Membrane tube formation from giant vesicles by dynamic association of motor proteins

Abstract

The tubular morphology of intracellular membranous compartments is actively maintained through interactions with motor proteins and the cytoskeleton. Moving along cytoskeletal elements, motor proteins exert forces on the membranes to which they are attached, resulting in the formation of membrane tubes and tubular networks. To study the formation of membrane tubes by motor proteins, we developed an in vitro assay consisting of purified kinesin proteins directly linked to the lipids of giant unilamellar vesicles. When the vesicles are brought into contact with a network of immobilized microtubules, membrane tubes and tubular networks are formed. Through systematic variation of the kinesin concentration and membrane composition we study the mechanism involved. We show that a threshold concentration of motor proteins is needed and that a low membrane tension facilitates tube formation. Forces involved in tube formation were measured directly with optical tweezers and are shown to depend only on the tension and bending rigidity of the membrane. The forces were found to be higher than can be generated by individual motor proteins, indicating that multiple motors were working together to pull tubes. We propose a simple mechanism by which individual motor proteins can dynamically associate into clusters that provide the force needed for the formation of tubes, explaining why, in contrast to earlier findings [Roux, A., Cappello, G., Cartaud, J., Prost, J., Goud, B. & Bassereau, P. (2002) Proc. Natl. Acad. Sci. USA 99, 5394–5399], motor proteins do not need to be physically linked to each other to be able to pull tubes.

Lipid bilayer membranes play an important role in the functional compartmentalization of the interior of the cell where membrane compartments of different shapes and sizes can be found. A prominent example is the endoplasmic reticulum, which is contiguous with the outer nuclear membrane and forms an elaborate network of interconnected tubes that extends throughout a large part of the cell (1). Membrane tubes have also been observed in connection with the Golgi apparatus (2), suggesting that the formation and maintenance of membrane tubes are important for intracellular trafficking as well. In vivo (3, 4) as well as in cell-free extracts (5–7) a close colocalization between the membrane tubes of the endoplasmic reticulum and the cytoskeleton is observed. The tubular membrane networks are dynamic in the sense that new tubes are continuously formed and existing ones disappear. The dynamic nature and the colocalization suggest that motor proteins in concert with the cytoskeleton play an important role in the formation and/or maintenance of the tubular membrane structures. This idea is supported by experiments in which the expression of the kinesin heavy chain was suppressed (8) or microtubules (MTs) were depolymerized (9), which showed the endoplasmic reticulum retracting toward the cell center while no tubes were newly formed. The hypothesis is that motor proteins exert forces on membranes while moving along the cytoskeleton and in this way shape the characteristic tubular membrane networks. However, the exact mechanism by which motor proteins are able to exert forces on the membrane and, consequently, how the cell may regulate this process is not understood. Note, also, that it has been shown that elaborate tubular membrane networks can be formed independent of cytoskeletal filaments (10) and that polymerization forces generated by the cytoskeleton itself can provide an alternative to motor proteins (4).

Thus far most studies on the formation of membrane networks were conducted either in vivo or in cytoplasmic cell extracts, making it difficult to determine which components are essential for the process. Recently, Roux et al. (11) reported the formation of membrane tubes from synthetic vesicles by purified motor proteins. In this work, clusters of motor proteins were formed by attaching kinesin motors to small beads, which were subsequently linked to the vesicles. It was concluded that multiple motors that are statically linked together are a prerequisite for tube formation and that attaching individual motor proteins to the lipids of the vesicle is not sufficient. We show here instead that an in vitro system, consisting of purified kinesin directly linked to synthetic lipid vesicles, is sufficient for the formation of membrane tubes and tubular networks when the vesicles are brought into contact with a network of stabilized MTs. To elucidate the mechanism involved we systematically varied different parameters and studied the resulting changes in the dynamics or the morphologies of the membrane structures that arose. We found that a critical concentration of motor proteins is needed for tube formation and that tubes form more easily when the membrane tension is low. In addition, we used optical tweezers to measure the forces involved in tube formation under different conditions directly, and we show that, as expected, these forces are determined by the bending rigidity and surface tension of the membrane. From our results we conclude that multiple motors have to cooperate in the process of tube formation, but that, in contrast to the findings by Roux et al. (11), they can do so without being physically linked to each other. We suggest a mechanism by which the membrane-bound motor proteins can spontaneously associate into stable clusters that exert enough force to form tubes.

Materials and Methods

All reagents were obtained from Sigma-Aldrich unless stated otherwise.

Giant Unilamellar Vesicles. 1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC) and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(cap biotinyl) (DOPE-Bio) were purchased from Avanti Polar Lipids. Seventy-five microliters of lipids in chloroform (2.78 mg/ml DOPC and 0.15 mg/ml DOPE-Bio) was spin-coated (at 2,000 rpm) onto each of two indium tin oxidecoated glass slides (2 × 33 cm²). After the slides were placed in vacuum for 1.5 h, a chamber (1 mm thick) was constructed from them and was filled with a solution of 200 mM sucrose. Giant unilamellar vesicles were formed by applying an AC voltage essentially as described (12). Cholesterol (40 mol%) was incorporated into the vesicle membrane for the proper functioning of streptolysin O (SLO) when appropriate (3.31 mg/ml DOPC, 0.23 mg/ml DOPE-Bio, and 1.14 mg/ml cholesterol). The presence of pores was verified by enclosing 2 μM sulforhodamine inside the vesicles. Shortly after the addition of SLO (13) this hydrophilic fluorescent dye was observed to diffuse out of the vesicles (data not shown). We used pipette tips with cut-off ends whenever handling giant unilamellar vesicles to reduce shear forces.

MTs and Motor Proteins. MTs were prepared from tubulin that was purified from pig brain by two cycles of cold and warm centrifugation followed by phosphocellulose chromatography (14). Tubulin (4 mg/ml) in MRB80 (80 mM K-Pipes/4 mM MgCl₂/1 mM EGTA, pH 6.8) with 1 mM GTP was incubated for 30 min at 35°C to polymerize. MTs were stabilized by mixing them 1:9 (vol/vol) with MRB80 containing 10 μM taxol. During the experiments, taxol was present in all buffers used when MTs were present. A truncated kinesin from Drosophila melanogaster, with a biotin and a triple hemagglutinin tag attached to it, was expressed in Escherichia coli and purified as described (15).

Sample Preparation. Coverslips were cleaned with 2 M NaOH in ethanol, rinsed with deionized H₂O, rinsed with ethanol, and dried at 100°C. Next, the coverslips were coated with poly-l-lysine by spin coating (4,000 rpm for 15 s) 200 μl of poly-l-lysine (2 μg/ml) in ethanol. A flow cell of a volume of 10 μl was constructed by drawing two parallel lines of vacuum grease (Hivac-G, Shin-Etsu, Tokyo) ≈5 mm apart on a microscope slide and by mounting the poly-l-lysine-coated coverslip on top.

MTs were introduced into the flow cell and incubated for 5 min to adhere. MTs that did not stick to the surface of the flow cell were removed by rinsing two times with MRB40 buffer (40 mM K-Pipes/4 mM MgCl₂/1 mM EGTA, pH 6.8) containing 10 μM taxol and 112 mM glucose to osmotically match this solution with the intravesicular buffer (3MO Microosmometer, Advanced Instruments, Needham Heights, MA) and α-casein (2.5 mg/ml) to minimize the interaction of binding the vesicles with the glass surfaces.

Vesicles were resuspended in MRB40 with 112 mM glucose and centrifuged at 7,000 rpm for 1 min to increase the concentration. Three microliters of this solution with giant vesicles was mixed with 1 μlof50 μg/ml streptavidin (Molecular Probes) and incubated for 3 min. Next, 1 μl of kinesin (concentration as required) was added and incubated for 5 min. The mixture was completed by adding 5 μl of MRB40 with 3 mM ATP/0.4 μM C₈-BODIPY 500/510-C₅/0.4 μM biotin/20 μM taxol/109 mM glucose and 8 mM DTT/0.4 mg/ml catalase/0.8 mg/ml glucose oxidase as an oxygen scavenger system. Finally, in some experiments SLO was added to a final concentration of 500 units/ml. This mixture was introduced into the flow cell. In some experiments fluorescent streptavidin (streptavidin–Alexa Fluor 488 conjugate, Molecular Probes) was used as a dye instead of BODIPY; this did not change the results.

Image Acquisition and Analysis. Observations were made on an inverted microscope (Leica Microsystems, Rijswijk, The Netherlands) by using epifluorescence and video-enhanced differential interference contrast microscopy. For the images in Fig. 1b a confocal microscope was used (Leica TCS NT-2). The total length of the tubes pulled from vesicles (Fig. 2) was measured as follows. A contiguous image of 300 × 500 μm² of the sample was made by acquiring a matrix (5 × 4) of fluorescent images (charge-coupled device camera, Kappa CF 8/4 DX, Kappa Optoelectronics, Gleichen, Germany) and stitching overlapping images together with imageassembler software (PanaVue, Quebec). By hand, lines were drawn along the lengths of all of the tubes in the field of view. After saving these lines as vector images, we analyzed the coordinates to find the total length of the tubes.

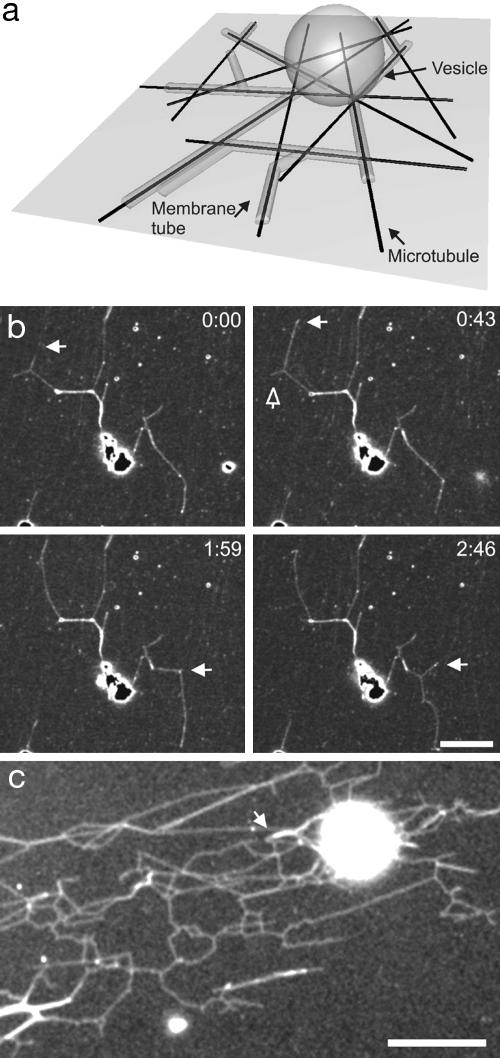
Fig. 1.

Overview of the experimental system. (a) Schematic representation of the assay (not to scale). Membrane tubes are formed from a vesicle that lies on top of a random network of MTs attached to the surface. (b) Time sequence of scanning confocal microscopy images of membrane tubes during the early stage of network formation (≈10 min after sample preparation). The network is dynamic: existing tubes disappear (open arrow) and new tubes appear and grow (white arrows), giving shape to three-way junctions. The fluorescence is due to fluorescently labeled streptavidin. Neither MTs nor motor proteins are visible. Time is given in minutes and seconds. (Bar, 5 μm.) (c) Fluorescence image of a large network of membrane tubes (with streptolysin). After 2 h, multiple three-way junctions can be observed and multiple membrane tubes are formed alongside each other, as can be seen from a stepwise increase in fluorescence (see arrow). Membranes are stained with BODIPY. (Bar, 10 μm.)

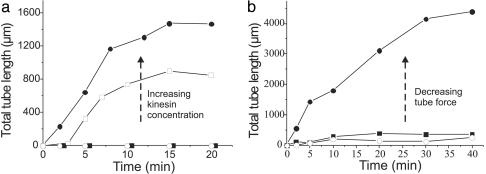
Fig. 2.

Evolution of tubular networks. (a) A typical example of the evolution of the total length of membrane tubes pulled from vesicles for different final concentrations of kinesin in the sample: 10 μg/ml (filled circles), 3 μg/ml (open squares), 1 μg/ml (open circles), and 0.1 μg/ml (filled squares). In each sample, ≈15 vesicles were present in the field of view. Time 0 corresponds to the end of sample preparation. No tubes are formed at the lower concentrations, whereas, for the higher concentrations, tubes start to form after sedimentation. (b) Typical example of the total tube length pulled from vesicles with the pore-forming drug SLO and cholesterol (filled circles), normal vesicles (filled squares), and vesicles with only cholesterol (open circles). In the presence of SLO the forces needed to pull tubes are much lower than for normal vesicles, whereas with only cholesterol present they are higher (see Fig. 3). The kinesin concentration is 2 μg/ml.

Optical Tweezers. The tweezers setup consists of an infrared trapping laser (1,064 nm, Nd:YVO₄, Spectra-Physics), which is focused into the sample by a ×100/1.3 numerical aperture oil immersion objective. A low-power red laser (633 nm, HeNe, 1125P, Uniphase, San Jose, CA) is superimposed on the IR beam and imaged onto a quadrant photodiode for stiffness calibration after passing through the trapped bead. The stiffness of the trap was determined by analysis of the power spectrum of the thermal fluctuations of the bead (16) and was controlled by attenuating the power of the laser beam that entered the microscope. Typically, the trap was operated with 0.01–0.40 pN/nm stiffness.

Force Measurements. In a solution containing biotin-labeled vesicles in MRB40 with 112 mM glucose, the position of a trapped streptavidin-coated polystyrene bead (SVP-20-5, Spherotech, Libertyville, IL) corresponding to a zero force was determined. Next, the bead was attached to a vesicle, which was stuck to the surface, either aspecifically or with another bead. After holding the vesicle against the bead for several seconds, a tube was formed by displacing the vesicle 10 μm at 0.1 or 1 μm/s with a Piezo stage (P-730.4C, Physik Instrumente, Karlsruhe, Germany) and holding it at this distance. The small deviation of the bead from the trap center was determined by cross-correlation analysis of the bead image (14). Together with the calibrated stiffness of the trap, this yielded the force on the bead.

Results

We developed a simplified in vitro system (Fig. 1a) in which kinesin motor proteins were linked directly to the lipids of giant vesicles. Within a few minutes after the kinesin-coated vesicles sedimented onto a network of randomly positioned, taxol-stabilized MTs, membrane tubes were observed to grow from the vesicles at velocities typical for the kinesin used (≈0.5 μm/s). Existing tubes were subsequently observed to branch and form three-way junctions (Fig. 1b). In addition, multiple tubes (up to three have been observed) would sometimes form on the same MT. This frequently resulted in an elaborate network of membrane tubes (Fig. 1c).

To elucidate the mechanism by which motor proteins are able to cooperate and exert the forces needed for tube formation, we varied the number of motors on the vesicle and the properties of the vesicle that determine the force needed to pull a tube. We quantified the extent of network formation by monitoring the total length of all of the tubes in a network under different conditions as a function of time (Fig. 2). The first parameter we varied was the density of motor proteins on the vesicle (Fig. 2a). Because a larger number of motor proteins should be able to exert a higher force, one may expect that more extensive networks will be formed at high motor densities. We found that more and longer tubes were formed for the higher concentrations, whereas below a certain threshold concentration no tubes were formed at all. In all cases, after some time the total tube length did not increase anymore and a plateau was reached (typically ≈20 min after start). In this plateau phase, the tubular network was still dynamic: existing tubes disappeared and new ones were formed. This indicates that the concentration of ATP was not limiting.

The second parameter we changed was the initial membrane tension. This parameter, together with the membrane-bending rigidity, determines the force needed to pull a tube from the vesicle (see below). In practice, our “normal” vesicles had a non-zero tension even before any tubes were formed. This tension corresponded to a small osmotic pressure difference between the inside and outside of the vesicles, even though our vesicles were created and used in isoosmotic buffers. The vesicles were impermeable to sucrose and glucose under normal circumstances and were thus unable to release this initial tension. The peptide SLO was used to form pores in the bilayer of the vesicle, making them permeable to solutes. The introduction of pores allowed the vesicles to adapt their fluctuating shape to the energetically most favorable one, thereby releasing the initial tension. In Fig. 2b the total tube length pulled from vesicles with SLO pores is plotted together with data for the total tube length pulled from control vesicles with no SLO. Many tubes were pulled from the vesicles with pores (filled circles), whereas many fewer tubes were formed from the normal vesicles (filled squares). Also, the formation of tubes continued for a longer time, and no clear plateau (as in Fig. 2a) was reached within the time of observation (40 min). It should be noted that, for SLO to be functional, 40 mol% cholesterol had to be added to the membrane. Cholesterol increases the bending rigidity of the membrane (see below), thereby influencing the tube formation force as well. In fact, when cholesterol was added without SLO (open circles) even fewer tubes were formed than for normal vesicles.

To verify the effect of the addition of SLO and cholesterol on the membrane tension and rigidity, the forces acting on short membrane tubes were evaluated directly by using optical tweezers (17). A streptavidin-coated bead was attached to a vesicle by using the optical tweezers, after which the vesicle and the bead were moved 10 μm apart and held at a fixed distance to allow the lipid bilayer to reach an equilibrium state. Typical measurements of tube formation forces for the different types of vesicles are presented in Fig. 3. The experiments showed that these forces are 18 ± 10 pN (n = 20 vesicles), 43 ± 18 pN (n = 11), and 0.73 ± 0.22 pN (n = 6) (average ± SD) for normal vesicles, vesicles with cholesterol, and vesicles with both cholesterol and SLO, respectively.

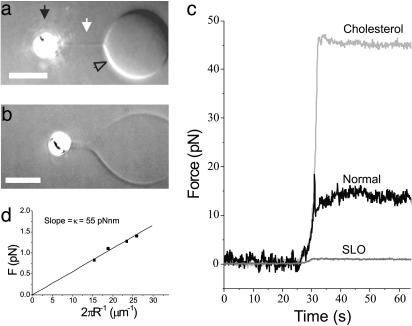
Fig. 3.

Force measurement of tube formation. (a) Video-enhanced differential interference contrast image of a normal vesicle (open arrow) from which a tube (white arrow) is pulled with a bead (black arrow) held in optical tweezers. The contrast has been enhanced to make the tube visible. (Bar, 5 μm.) (b) Tube formed from a vesicle with SLO and cholesterol. Note that the diameter of the tube is ≈800 nm. This is larger than the tube in a because of a lower membrane tension. (Bar, 5 μm.) (c) Examples of the tube formation forces for the different vesicles studied. After pulling a tube with the optical tweezers (around t = 30 s), the bead is held at a fixed position for several tens of seconds. The curves for the normal and SLO vesicles correspond to the images in a and b.(d) Tube force dependence on the radius for the SLO vesicle shown in b. Stepwise elongation of the tube results in an increased tension, which results in a smaller tube radius. The slope of the curve reveals the bending rigidity of the membrane.

The force, F, needed to support a static cylindrical membrane tube is expected to depend on the membrane tension, σ, and bending rigidity, κ, in the following way: 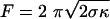(18-22). The radius of a membrane tube, R, is determined by these parameters according to 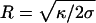, and hence F = 2πκ/R. The diameter of the tubes pulled from SLO vesicles was sufficiently large to be resolved by our microscope. Because we also know the force on the tube (Fig. 3c), the relationship F = 2πκ/R can be tested and used to estimate the bending rigidity for an SLO vesicle. When a tube was extended to 40 μm in 10-μm steps, an increasing force and a decreasing tube radius were found. The slope of these data, shown in Fig. 3d, yields a bending rigidity of 55 pNnm for the vesicle from Fig. 3b. Using this value and the measured force, we estimate the membrane tension for this SLO vesicle to be 1.6 × 10^–4 pN/nm (for a tube extension of 10 μm). The forces measured for the normal vesicles indicate that these vesicles have a much higher tension of on average 6.2 × 10^–2 pN/nm, where we have assumed a bending rigidity of 85 pNnm for a pure DOPC membrane (23). Bending rigidities are not available for DOPC vesicles containing cholesterol. However, when we assume a membrane tension equal to that of the normal vesicles, a bending rigidity of 376 pNnm can be inferred. This 4.4-fold increase corresponds well with literature data on the effect of adding cholesterol (24). The 55 pNnm found for vesicles containing both cholesterol and SLO indicates that, besides releasing the membrane tension, SLO also reduces the membrane rigidity.

In a separate attempt to vary the initial membrane tension, we varied the osmotic value of the extravesicular buffer by using different concentrations of glucose. Osmotic swelling and shrinking should result in different initial membrane tensions. Although we had some indication that a high osmolarity buffer facilitated tube and network formation (data not shown), these experiments and complementary force measurements showed too much spread to support strong conclusions. We believe that this variability was because of the practical problem of obtaining vesicles in their equilibrium state using the electroformation method. The tension in the vesicles is not always strictly related to the imposed area-to-volume ratio, as small uncontrollable amounts of area seem to be stored in “hidden reservoirs” of lipids (25).

Discussion

We developed a minimal system in which motor proteins moving along MTs can pull tubes from giant vesicles. We believe that multiple motor proteins are working together in the formation of membrane tubes for the following reasons. First, at low motor concentrations we do not observe any tube formation, even though the probability of having one kinesin pulling should still be significant. A rough estimate suggests that >10,000 motors per vesicle are still present at the lowest motor concentration used. Second, tubes are moving over much longer distances (sometimes >100 μm) than the known run length (≈1 μm) of one kinesin motor, especially when taking into account the decrease of a motor's processivity when a force is exerted on it (26–28). Finally, from the force measurements, it follows that the forces involved in tube formation from the normal vesicles are higher than the stall force of one kinesin protein (≈6 pN) (28–30). In addition, note that the tube formation forces we measured with the tweezers give a lower estimate of the forces involved in the formation of tubes by motors because the attachment of streptavidin (and kinesin) to the bilayer is likely to increase the bending rigidity of the membrane and therefore the tube formation force.

Because we conclude that multiple motor proteins must be working together, and because in our experiments the motor proteins are not physically linked to each other, we hypothesize in what follows on a mechanism through which individual motor proteins could dynamically form clusters that are able to exert enough force to form tubes. As shown schematically in Fig. 4a, we assume that motor proteins can participate in tube formation as soon as they are attached to a MT near the end of a membrane tube. The motors present at this location form a dynamic cluster, which constantly exchanges motors with the pool of motors attached to the vesicle. A stable cluster size can be formed only if at any time the number of motors leaving the cluster is balanced by the number of motors arriving in the cluster. If, in addition, the force per motor is lower than the stall force, a tube can be formed. Motor proteins can diffuse laterally on a vesicle because of the liquid nature of the bilayer. When a diffusing motor protein is in the proximity of a MT there will be a probability to attach, which will result in a certain number of motors that arrive in the cluster per second: the arrival rate. This arrival rate is expected to increase linearly with the concentration of motor proteins. Motor proteins that are attached to a MT will also have a probability to detach from the MT. This detachment probability becomes higher when a force is exerted on the motor protein (26–28). The total number of motor proteins that detach from the MT and leave the cluster per second defines the departure rate.

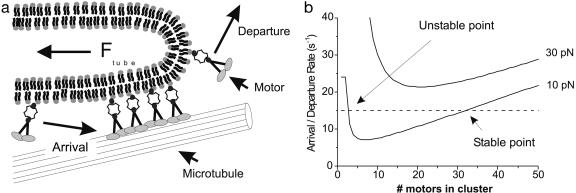
Fig. 4.

The mechanism of dynamic association. (a) Sketch of the mechanism of dynamic association of motor proteins. A cluster of motor proteins exerts a force on the tip of a tube. Each motor protein has a certain probability of detaching from the MT and leaving the cluster. This probability is force-dependent and will result in a certain departure rate. Motor proteins in the proximity of the MT will also have a probability of attaching and joining the cluster, characterized by an arrival rate. (b) Graph showing the feasibility of the formation of a stable clusters by dynamic association. The solid curves show the departure rate of motors from a cluster for two different forces (10 and 30 pN) as a function of the number of proteins present in the cluster (see text). The dashed line depicts a constant arrival rate. For the tube force of 10 pN, there is a stable point where a cluster can be formed. For high forces (e.g., a tube force of 30 pN), the departure rate is too high and no stable cluster can be formed.

Under what conditions a stable cluster of motor proteins at the leading end of a membrane tube can survive is shown in Fig. 4b, where the motor arrival and departure rates are plotted as a function of cluster size. We assume an exponential force dependence of the detachment probability for one motor: k_off = Ae^αFm, where F_m is the force per motor protein and the constants A = 0.38 s^–1 and α = 0.69 pN^–1 are obtained from a fit to results by Parmeggiani et al. (31). Note that the exact value of the constants is not critical for the mechanism. When N motors are present in the cluster this leads to the following expression for the departure rate: k_dep = NAe^αFtube/N, where we have assumed that the motors in the clusters share the load of the tube equally. In Fig. 4b we plot the departure rate for two different tube forces (10 and 30 pN). The shape of these curves can be understood in the following way: if a low number of motors is present in the cluster, the force per motor is high and the detachment probability as well as departure rate will be high. If the number of motors in the cluster is high, the force per motor will be low and the detachment probability per motor will become equal to the spontaneous detachment rate, A; however, because many motors are present in the cluster, even spontaneous detachment will result in a high departure rate. In contrast to the departure rate, the arrival rate will be independent of the size of the cluster and dependent only on the local motor concentration (in Fig. 4b an arbitrary value for the arrival rate was chosen). When the arrival and departure rates are equal, the cluster stays constant in size. For the tube force of 10 pN (in Fig. 4b), there are two points for which this is the case. One point (on the left) is unstable because small fluctuations in the number of motors in the cluster will enhance the difference between the arrival and departure rates. The other point represents a stable cluster. Here changes in the rates because of small fluctuations in the cluster size tend to drive the cluster back to the stable size. When the forces in the system become higher (e.g., 30 pN), the departure rate rises and no steady-state clusters can be formed anymore. This simple model does not take any geometrical constraints into account that may limit the number of motors in a cluster. A MT has multiple tracks along which motor proteins can move (13 filaments), but the number of filaments of a MT that are accessible to the motor proteins in our assay will presumably be six or seven because the MT is attached on one side to the coverslip. Along the MT, a high number of motor proteins could be present in rows. Because of the liquid nature of a lipid bilayer, only motors near the tip of a tube can exert force. However, it is not known how these motors will interact and how the force will be distributed over the different filaments and rows of motors.

Despite these simplifications, the proposed mechanism of dynamic association is in qualitative accordance with the observed dependence on the motor concentration and membrane composition (Fig. 2). When for a given membrane composition the motor concentration is too low, the arrival rate is too low for stable clusters to survive. When the concentration is increased, the arrival rate eventually passes a threshold value, after which stable clusters and membrane tubes can be formed (Fig. 2a). The composition of the membrane affects tube formation through the influence it has on the tube formation force. As shown in Fig. 3, the membrane tension and rigidity together determine the tube formation force. In the presence of SLO the initial membrane tension is very low, leading to an initial tube formation force that is ≈25-fold lower than for normal vesicles (Fig. 3c). Consequently, membrane tubes form much more easily in the presence than in the absence of SLO (Fig. 2b). When, in the absence of SLO, the bending rigidity is increased by the addition of cholesterol, the force instead goes up by, on average, a factor of 2.4, explaining why even fewer tubes are formed from these vesicles. The model also explains why network formation may stall. When more and longer tubes are being pulled from a vesicle, the membrane tension is expected to rise above the initial tension (Fig. 3d). For vesicles without SLO this is partly because of the fixed area-to-volume ratio of the vesicles (32). In addition, when increasing amounts of membrane material are withdrawn, the (visible and nonvisible) thermal undulations of the membrane are reduced, leading to an increase in membrane tension for vesicles with and without SLO (33–35). The rise in tension leads to a rise in force, which will increase the departure rate until the survival of a stable cluster that can support the tube is no longer possible. Collapse of a tube will release some of the tension, enabling the growth of a new tube. Thus, a dynamic steady state is reached. Because of the lack of volume constraints, the tension will rise less steeply in SLO vesicles, explaining the longer continuation of network growth.

The results presented here seem to be in contrast with the results of Roux et al. (11), who concluded that static linkers (beads) with multiple motors attached to them are a prerequisite for the formation of tubes. Although we agree that multiple motor proteins are needed for the formation of tubes (and these could in principle be statically bound clusters), we believe that in our assay these clusters arise from the dynamic association of motor proteins. If, as an artifact, kinesin aggregates were present in our sample, tubes should still occasionally be formed at very low kinesin concentrations. However, this was not observed. The absence of tubes after using individual motor proteins in the experiment of Roux et al. (11) may be because of a higher initial tension of their vesicles, opposing the formation of stable clusters. Their alternative way of introducing motors, by prebinding them to the MTs before the introduction of vesicles, may also have resulted in a lower motor concentration on the vesicles.

In living cells there are different mechanisms through which motor proteins may associate and join forces. Our experiments show the intrinsic ability of motor proteins to dynamically associate and form clusters without the requirement for cofactors. An alternative mechanism could be the binding of multiple motor proteins to membrane proteins that act as scaffolds to form static multimotor complexes (7, 11). The presence of rafts (36) could bias the mechanism of dynamic association. Certain kinesin motor proteins have been reported to directly bind to lipids, and subdomains of these lipids may function as a (dynamic) preclustering tool (37). Such rafts could thus combine properties of both clusters formed by dynamic association and static clusters. The magnitude of the forces that are needed to form and maintain membrane tubes should not depend on the exact mechanism by which motor proteins cluster, but only on the global bending rigidity and tension of the membrane. Regulation of the membrane tension, membrane composition, or the degree of expression of motor proteins may give the cell control of the ability to form tubes, and thus control of the structure of intracellular membranes.

In conclusion, we have shown that a minimal system consisting of MTs, kinesin, and giant vesicles is capable of forming an extensive network of membrane tubes that carries resemblance with intracellular membrane structures. Our results can be explained assuming a mechanism of dynamic association of individual motor proteins into clusters that are capable of generating sufficient forces. Our future in vitro experiments will be aimed at quantifying the forces in the network during evolution toward the final steady state. Our model would predict that inducing extra tension in the membrane when the network is fully developed (e.g., with a pipette) should cause a collapse of the network, because the motor clusters will no longer be stable. Similar experiments may also be performed in cytoplasmic cell extracts to test whether the same dynamic clustering of motor proteins is responsible for tube formation there as well.