Hydrogen bonding and spin density distribution in the Q_B semiquinone of bacterial reaction centers and comparison with the Q_A site

Abstract

In the photosynthetic reaction center from Rhodobacter sphaeroides, the primary (Q_A) and secondary (Q_B) electron acceptors are both ubiquinone-10, but with very different properties and functions. To investigate the protein environment that imparts these functional differences, we have applied X-band HYSCORE, a 2D pulsed EPR technique, to characterize the exchangeable protons around the semiquinone (SQ) in the Q_A and Q_B sites, using samples of ¹⁵N-labeled reaction centers, with the native high spin Fe²⁺ exchanged for diamagnetic Zn²⁺, prepared in ¹H₂O and ²H₂O solvent. The powder HYSCORE method is first validated against the orientation-selected Q-band ENDOR study of the Q_A SQ by Flores et al. (Biophys. J. 2007, 92, 671–682), with good agreement for two exchangeable protons with anisotropic hyperfine tensor components, T, both in the range 4.6–5.4 MHz. HYSCORE was then applied to the Q_B SQ where we found proton lines corresponding to T~5.2, 3.7 MHz and T~1.9 MHz. Density functional-based quantum mechanics/molecular mechanics (QM/MM) calculations, employing a model of the Q_B site, were used to assign the observed couplings to specific hydrogen bonding interactions with the Q_B SQ. These calculations allow us to assign the T=5.2 MHz proton to the His-L190 N_δH…O₄ (carbonyl) hydrogen bonding interaction. The T =3.7 MHz spectral feature most likely results from hydrogen bonding interactions of O1 (carbonyl) with both Gly-L225 peptide NH and Ser-L223 hydroxyl OH, which possess calculated couplings very close to this value. The smaller 1.9 MHz coupling is assigned to a weakly bound peptide NH proton of Ile-L224. The calculations performed with this structural model of the Q_B site show less asymmetric distribution of unpaired spin density over the SQ than seen for the Q_A site, consistent with available experimental data for ¹³C and ¹⁷O carbonyl hyperfine couplings. The implications of these interactions for Q_B function and comparisons with the Q_A site are discussed.

Introduction

The primary event in photosynthesis is light-driven charge separation, catalyzed by the reaction center (RC), a (bacterio)chlorophyll-containing protein complex. Light activation results in electron transfer from the primary donor, P, a dimer of (bacterio)chlorophyll, through a series of cofactors of low potential. On time scales longer than a nanosecond, the charge separation in RCs from purple bacteria resides on the primary donor and on the acceptor quinones. The primary quinone, Q_A, is tightly bound and functions as a one-electron redox species, whereas the secondary quinone, Q_B, is reversibly bound and can be doubly reduced via Q_A⁻, with the uptake of two protons (reviewed in^1–3). In spite of these marked functional differences, in Rba. sphaeroides the two quinones are chemically identical ubiquinone-10 molecules,^1–4 presenting an ideal opportunity to study the effect of protein structure on cofactor redox properties. The two neutral forms of Q_B – quinone and quinol – are rapidly exchangeable, but the semiquinone (SQ) intermediate, Q_B⁻, is tightly bound and stabilized, contributing to the redox properties of both reduction steps. It can be expected that hydrogen-bonding underlies this stability.

From the known structures of bacterial RCs, Q_A and Q_B are positioned symmetrically about an iron-histidine, Fe^II-(His)₄, complex and both quinones are bound by hydrogen bonds to the protein (Figure 1).^5,7,8 However, the plethora of X-ray structures now available does not provide unequivocal descriptions of the two quinone sites. The C₄ carbonyl of Q_A is hydrogen bonded to N_δ of His-M219 (an Fe-ligand), while the backbone NH of Ala-M260 is a H-bond donor to the C₁ carbonyl.⁷ On the other hand, the H-bond distances and the torsional angles of the two methoxy group substituents of the ubiquinone ring are quite variable in different structures (reviewed in³).

Figure 1.

Essential features of the Q_A and Q_B binding sites, showing putative hydrogen-bond donors to the quinone carbonyls. The structure is from 1dv3.pdb.⁸ The figure was prepared in VMD. ⁴²

For the Q_B site, crystal structures show even more diversity, including at least two different positions relative to the Fe^II-(His)₄ complex.^7–9 The functional position has been established to be the proximal location, essentially symmetrical to the position of Q_A. In the proximal position, Q_B is clearly hydrogen bonded through the C₄ carbonyl to N_δ of His-L190 (an Fe-ligand), but a second H-bond to the C₁ carbonyl is variously indicated from the backbone NH groups of Ile-L224 and/or Gly-L225 as potential donors (Figure 1).^7–9 The hydroxyl from Ser-L223 is also thought to form a hydrogen bond with either the quinone C₁ carbonyl - especially in the semiquinone state - or Asp-L213.^2,3,6,10 An additional H-bond from the peptide NH of Thr-L226 to one methoxy group was inferred from a recent structure.⁹ Thus, in addition to uncertainties in the geometry of the H-bonds to Q_B, even the number is uncertain.

Equivalent knowledge of the oxidized and reduced (SQ) states is necessary to understand the chemical reactivities and kinetic pathways of Q_A⁻ and Q_B⁻, but the H-bond environment around the semiquinone states is not indicated by the crystal structures. This, however, can be addressed through the application of pulsed EPR methods,^3,11 and the Q_A- and Q_B-sites have been amongst the most thoroughly explored by EPR techniques.^10–16 To observe the SQ signals directly by these techniques it is necessary to replace the native high spin Fe²⁺ with Zn²⁺, which does not perturb the function of the acceptor quinones.^11,12

Structural information about the SQs and their interactions with protein and solvent has mainly been obtained from proton ENDOR spectra in frozen solutions. Three classes of protons can contribute to the spectra: (i) non-exchangeable protons of substituents (isoprene chain, two methoxy groups, and a methyl group), (ii) exchangeable protons forming H-bonds to the quinone oxygens, and (iii) protons associated with the protein or solvent in the immediate vicinity. The major limitation of one-dimensional ENDOR spectroscopy, particularly for ubiquinones, is the large number of protons contributing to the spectra, with fully or partially overlapping frequencies¹¹, and the lack of an effective analysis of one-dimensional powder spectra in this situation. To address this, elaborate sample preparations have been required, involving combinations of fully protonated/deuterated protein with protonated/deuterated quinone. As a result, the hyperfine (and nuclear quadrupole) tensors in Rba. sphaeroides have been determined only for two protons (deuterons) H-bonded with the carbonyl oxygens of the Q_A SQ, using orientation-selected ¹H and ²H Q-band ENDOR.¹²

An alternative approach is the recently developed two-dimensional (2D) ESEEM spectroscopy, also called HYSCORE.^{17 1}H HYSCORE spectroscopy allows additional resolution by spreading out peaks that overlap in 1D spectra into 2D in the form of off-diagonal cross-peaks. This technique effectively resolves protons with substantially different anisotropic tensors, although complications remain for protons with close hyperfine couplings in X-band powder spectra.

We have previously used X-band HYSCORE to explore the structural neighborhood of the ubisemiquinones stabilized at the Q_i-site of the bc₁ complex of Rba. sphaeroides¹⁸ and the Q_H-site of the E. coli cytochrome bo₃ ubiquinol oxidase.¹⁹ These studies have shown that X-band ¹H HYSCORE spectra together with solvent deuterium exchange readily separate the cross-peaks of exchangeable hydrogen bonded protons from the lines of non-exchangeable protons, and allow quantitative analysis for determinations of the isotropic and anisotropic components of the hyperfine tensors. These parameters, especially when combined with couplings with nitrogen donors, can be used for the computational construction of structural models.²⁰

In this article we describe 1D and 2D ESEEM studies of the Q_A and Q_B SQs in reaction centers from Rba. sphaeroides. The work has three aims:

First, we demonstrate the resolution of powder ¹H HYSCORE spectra by analysing model spectral simulations for two protons hydrogen bonded to the Q_A SQ possessing anisotropic components of the hyperfine tensor that differ by only ~10%, using the Q-band ENDOR derived tensors¹². We then show the consistency between data for the Q_A SQ from orientation-selected Q-band ENDOR¹² and from powder X-band 2D ESEEM used in this work, despite partial overlap of individual cross-features from the two protons.

Second, we provide a quantitative characterization of the hyperfine tensors of exchangeable protons around the SQ in the Q_B site of the reaction center. The structural symmetry between the quinone sites allows the findings in the model Q_A SQ study to guide the analysis of the Q_B site, where a larger number of exchangeable protons contributes to the spectra.

Third, we utilize QM/MM calculations on a Q_B site model to assign the observed hyperfine tensors to specific hydrogen bond interactions in the Q_B site, and we compare this with the situation in the Q_A site. The QM/MM simulations also show a difference in the asymmetry of unpaired spin density distribution between the Q_A and Q_B sites, in agreement with available experimental data.

The hyperfine tensors for the exchangeable proton(s) provide a conclusive picture of the hydrogen bond network with the carbonyls of the SQ in the Q_B site. Previously, even the number of hydrogen bonds and the strength of coupling to the Q_B SQ were uncertain, which has frustrated the critical analysis of the spin density distribution and simulations exploiting different structural models.

Experimental Section

Sample preparations

In order to isolate SQ EPR signals, the native, high spin Fe²⁺ must be replaced by diamagnetic Zn²⁺. Procedures for biochemical metal exchange, along with the methods of bacterial cell growth and RC isolation, were as previously described.²¹ To eliminate cross suppression effects in the HYSCORE spectra and to facilitate resolution of the proton signals (see also Results), RCs were uniformly ¹⁵N labeled. ¹⁵N enrichment of RCs was accomplished during cell growth by using ¹⁵N-labeled ammonium sulfate (Cambridge Isotopes) in the growth medium. Prior to EPR sample generation, the detergent, LDAO, used in RC isolation, was exchanged for Triton X-100 by diluting approximately 100-fold and reconcentrating. Samples with Q_A⁻ were made by chemical reduction with 8 mM Na-dithionite. For samples with Q_B⁻ the RCs were combined with a 3-fold excess of both cytochrome c and ubiquinone-10. To trap the Q_B SQ, the sample was illuminated by a single laser flash at 532 nm and immediately frozen in liquid nitrogen. Routine optical assay of Fe/Zn-exchanged RC preparations showed a minimum of 80% reconstitution of Q_B activity. However, pulse EPR measurements showed no sign of Q_A SQ signals in Q_B SQ samples in either ¹H-HYSCORE (this work) or in ¹⁴N- or ¹⁵N-HYSCORE²¹, indicating that the functional reconstitution was complete, probably because of the much higher concentrations involved.

EPR and ESEEM experiments

The instrumentation for X-band and Q-band CW EPR measurements was as previously described.²¹ The instrumentation, pulse sequences and spectral processing for X-band 1D 4-pulse ESEEM (π/2-τ-π/2-t-π-t-π/2-echo) and 2D 4-pulse ESEEM (HYSCORE) (π/2-τ-π/2-t₁-π-t₂-π/2-echo) were also as described.^18,19,21 Spectral simulations were carried out using PC software developed by Dr. Alexei Tyryshkin (now at Princeton University).²¹

Computational Studies

Starting with the Rba. sphaeroides structure of Axelrod et al.⁸ (PDB file 1dv3), we created a model of the Q_B site. This model consisted of L subunit residues 177–242, and M subunit residues 218–220, 233–235 and 265–267 plus the non-heme Fe²⁺. Hydrogens were added and the native Fe²⁺ ion was replaced by Zn²⁺. The ubiquinone isoprene chain was reduced to CH₂CHCH₂. For the optimisation studies, two-layer ONIOM calculations ONIOM(B3LYP/6–31G(d):UFF) were performed. The QM layer contained the ubisemiquinone Q_B, His-L190, Gly-L225, Ile-L224, Ser-L223, Zn and its other ligands. The remaining atoms formed the MM layer. Linking between the QM and MM layers was achieved using hydrogen link atoms. Keeping all heavy atoms except the semiquinone fixed, we optimised the semiquinone geometry within the site. All hydrogen atom positions were optimised. Charges for the MM layer were generated using the qEq method and electrostatic embedding, i.e., ONIOM-EE was employed.²² This geometry was then used in a further single point ONIOM(B3LYP/EPR-II:UFF) calculation to obtain spin densities and hyperfine couplings. For the Zn atom the 6-31G(d) basis set was used. All calculations were performed using Gaussian 03 software.²³

Spectroscopic Background

Orientationally disordered ¹H HYSCORE spectra and their analysis

In this work, the proton environment of the SQs is best probed by the 2D ESEEM (HYSCORE) experiment.¹⁷ The essential advantage of the HYSCORE technique is the creation, in 2D spectra, of off-diagonal cross-peaks whose coordinates are nuclear frequencies from opposite electron spin manifolds. The cross-peaks significantly simplify the analysis of congested spectra by correlating the nuclear frequencies of individual nuclei. In addition, HYSCORE separates overlapping peaks along a second dimension and enhances the signal-to-noise ratio through a second Fourier transform. HYSCORE is also very valuable for the detection of extended, anisotropic, “ridge-like” features of low intensity, which are not seen in 1D ESEEM spectra. ^24–26

A nucleus with I = ½, such as ¹H, has two hyperfine nuclear frequencies, ν_α and ν_β, corresponding to two states m_s = ±1/2 of the electron spin system in the applied magnetic field. In HYSCORE, these may produce a pair of cross-features, (ν_α, ν_β) and (ν_β, ν_α).

The X-band (~9.7 GHz) EPR spectrum of a SQ is usually a single line with width ~0.8 mT.¹¹ This width is comparable with the excitation width of the microwave pulses, and the spectra obtained can be considered to be powder-type 1D or 2D ESEEM spectra because the resulting pattern contains contributions from all possible orientations of the SQ relative to the applied magnetic field. Orientationally disordered (i.e., powder) HYSCORE spectra of I = ½ nuclei reveal, in the form of cross-ridge projections, the interdependence of ν_α and ν_β belonging to the same orientations, and analysis of the ridges allows for direct, simultaneous determination of the nuclear isotropic and anisotropic components of the hyperfine tensor.²⁷

The contour lineshape of the cross-ridge in the powder 2D spectrum of a ¹H nucleus, for hyperfine interactions with the axially symmetric tensor (a−T, a−T, a+2T), is described²⁷ by Equation 1:

$${{\nu }_{\alpha }}^2=Q_{\alpha }{{\nu }_{\beta }}^2+G_{\alpha }$$ [1]

where $Q_{\alpha }=\frac{\text{T}+2a-4{\nu }_{\text{H}}}{\text{T}+2a+4{\nu }_{\text{H}}}$ and $G_{\alpha }=2{\nu }_{\text{H}}\left(\frac{4{\nu }_{\text{H}}^2-a^2+2{\text{T}}^2-a\text{T}}{\text{T}+2a+4{\nu }_{\text{H}}}\right)$ and ν_H is the ¹H Zeeman frequency. For each cross-feature, the frequency values along the ridge can be plotted as ν_α² versus ν_β², transforming the contour lineshape into a straight line segment whose slope and intercept are proportional to Q_α and G_α, respectively. These values can then be used to obtain two possible solutions of isotropic (a) and anisotropic (T) couplings with the same value of |2a+T| and interchanged A_⊥=|a-T| and A_||=|a+2T|.²⁷

Analysis of the HYSCORE spectra simulated using ENDOR data for the Q_A semiquinone

Orientation-selected Q-band ENDOR experiments with fully deuterated RC from Rba. sphaeroides in ¹H₂O buffer have provided the hyperfine tensors for two protons participating in H-bonds with O₁ and O₄ of the Q_A semiquinone.¹² The principal values of the anisotropic hyperfine tensors and isotropic couplings determined for these protons are summarized in Table 1. It is clear that the ENDOR data show one proton (H1) to possess a purely axial anisotropic tensor. For the second proton (H2), the rhombicity is only ≈4% and it, too, can be considered axial for spectral estimates. Table 2 shows the hyperfine tensors and nuclear frequencies for α and β manifolds assuming axial symmetry for both H1 and H2. These tensors support the previous assignment of the three couplings A₁=4.7 MHz, A₂=6.3 MHz, and A₃=9.0 MHz (±0.1 MHz) observed in powder ENDOR spectra, to two A_⊥ and one A_||.¹¹ The latter represents the overlap of two lines, with the predicted difference between A_|| for the two protons on the order of ~0.2 MHz (Table 2). Monitoring the time dependence of the ENDOR line intensities, following substitution of ¹H₂O by ²H₂O with fully protonated and fully deuterated RCs, confirmed that the three observed couplings belong to two protons. The ¹H/²H exchange times for the protons of the Q_A SQ were found to be τ₁~50 min and τ₂~1200 min in protonated RCs and τ₁~10 min and τ₂~90 min in fully deuterated RCs.¹³

Table 1.

ENDOR determined hyperfine tensors (MHz) for the hydrogen bonded protons H1 and H2 in the Q_A-site of the reaction center from Rba. sphaeroides R-26 (from refs.¹²,¹³)

Proton	H-bond	T33	T22	T11	a	Exchange rate
H1	O4-His (M219)	10.43	−5.23	−5.20	−1.28	slow
H2	O1–Ala (M260)	9.12	−4.75	−4.37	−0.17	fast

Table 2.

ENDOR derived hyperfine frequencies in the axial approximation (MHz) for protons H1 and H2^a (from ref.12)

Proton	H-bond	A⊥ =a-T	A||=a+2T	να||	νβ||	να⊥	νβ⊥
H1	O4-His (M219)	−6.50	9.15	19.29	10.15	11.47	17.97
H2	O1–Ala (M260)	−4.73	8.95	19.2	10.24	12.36	17.08

^ahyperfine frequencies were calculated for proton Zeeman frequency ν_H=14.73 MHz

On the other hand, for the Q_B SQ, couplings assigned to three exchangeable protons were detected by ENDOR, but their hyperfine tensors were not characterized.¹⁰

To illustrate the characteristics of powder ¹H HYSCORE and to identify the complications that arise when the spectra result from more than one nucleus (especially with similar hyperfine couplings) we use the ENDOR data for the Q_A SQ to generate simulated HYSCORE spectra for model analysis. Figure 2 shows, for two protons with principal values of the hyperfine tensors and corresponding nuclear frequencies provided in Tables 1 and 2, an idealized contour presentation of the powder HYSCORE spectra (A,C,E), and the corresponding calculated HYSCORE spectra, with time τ=136 ns between first and second microwave pulses (B,D,F). The idealized presentation just shows the location of full cross-ridges determined by the hyperfine parameters, as described by Eq. (1). The calculated spectra take into account suppression effects and show the distribution of intensity along the ridges, which depends on the selected time τ as determined by the intensity coefficient sin(πν_α τ)•sin(πν_β τ).^28,29 For each proton (H1, H2) there are two cross-ridges with permutated coordinates, (ν_α, ν_β) or (ν_β, ν_α), extending between (ν_α(β)||, ν_β(α)||) and (ν_α(β)⊥, ν _{β (α)⊥}). These are located symmetrically on both sides of the diagonal of the 2D spectrum and pass through the diagonal in the idealized presentation. The branches of the two ridges on the same side of the diagonal are located close to each other. In the calculated spectra, the cross-ridges are suppressed in the region of the diagonal. This effectively leads to the appearance of two isolated sub-ridges, 1_αβ and 1′_αβ, and 2_αβ and 2′_αβ, for H1 and H2, respectively. These sub-ridges can be correlated to each other using a linear regression approach based on Eq. (1) and illustrated below. Also shown is a superposition of the spectra from two protons in both presentations (Fig. 2E,F). The ν_α|| and ν_β|| frequencies are very close for both protons (Table 2). As a result, the upper parts of the ridges 1_αβ(βα) and 2_αβ(βα) are practically indistinguishable in the spectrum and are seen as one ridge (1+2)_αβ(βα). However, the presence of two protons can be recognized from the sub-ridges 1′_αβ(βα) and 2′_αβ(βα) located near the antidiagonal and corresponding to orientations approaching 90° between the magnetic field and the unique axis of the hyperfine tensor.

Figure 2.

The HYSCORE spectra for protons H1 and H2 identified by ENDOR. Left column (A,C,E): contour presentation of the full cross-peaks. Right column B,D,F: calculated HYSCORE spectra using Q-band ENDOR derived hyperfine tensors shown in Tables 1 and 2, and time between first and second microwave pulses τ=136 ns. ¹H Zeeman frequency is 14.73 MHz (see also text). The spectra qualitatively demonstrate the relative intensity of different ridges. The wider and more extended ridges possess greater intensity.

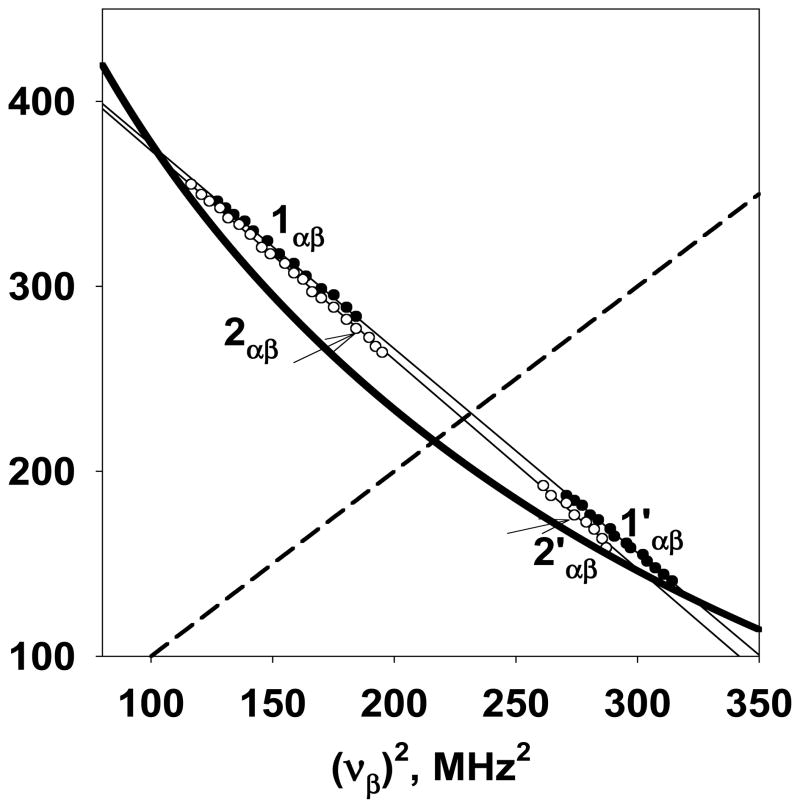
We illustrate the approach for determining the hyperfine tensor components by exploring the simulated HYSCORE spectra of Figure 2. The coordinates ν₁ and ν₂ of arbitrary points along cross-ridges were measured from the HYSCORE spectra calculated separately for H1 and H2 (Fig. 2B, D) and plotted as sets of values in ν_α² vs. ν_β². Figure 3 shows the plots where the larger frequency ν₁ of each point from sub-ridges 1_αβ and 2_αβ was arbitrarily selected as ν_α, and the smaller frequency ν₂ as ν_β. In contrast, for sub-ridges 1′_αβ and 2′_αβ, on the opposite side of the diagonal, the smaller coordinates should be assigned to ν_α and the larger ones to ν_β. This selection places the cross-ridges 1_αβ,2_αβ and 1′_αβ,2′_αβ on opposite sides of the graph relative to the dashed line corresponding to the diagonal in the spectra in Figure 2. In such a presentation, the points from 1_αβ and 1′_αβ fit the linear regression well, thus confirming that they are two parts of the same ridge from proton H1. The same is true for sub-ridges 2_αβ and 2′_αβ from proton H2. The slopes and intercepts for the linear regressions shown in Figure 3 are presented in Table 3, together with two possible sets of (a, T) satisfying Eq.(1) for protons H1 and H2, and A_⊥ and A_|| values. The curve |ν_α + ν_β| = 2ν_H (with ν_H =14.73 MHz, corresponding to the proton Zeeman frequency in a field of 346 mT) is also plotted in Figure 3 to explain the nature of the two solutions determined by Eq.(1). The points at which this curve crosses each extrapolated straight line correspond to the nuclear frequencies (ν_α||, ν_β||) or (ν_α⊥, ν_β⊥). There are two possible assignments of the parallel or perpendicular orientations for each point and, consequently, two sets of hyperfine tensors, one for each assignment. In this approach, the hyperfine couplings are identical to those determined from the slope and intercept. From the two solutions, one (marked by bold font in Table 3) gives a and T values close to the ENDOR derived values. In addition, Table S1 in Supporting Info shows that accurate estimates of the hyperfine tensors for H1 and H2 can be obtained from linear fitting of the 1′_αβ and 2′_αβ sub-ridges only. This is especially important when the extended sub-ridges 1_αβ and 2_αβ are not individually resolved.

Figure 3.

Plots of cross-peaks from the calculated HYSCORE spectra of Figure 2 in the ν_α² vs. ν_β² coordinate system (see text for detailed explanations). The straight lines show the linear fit of plotted data points. The thick curved line is defined by (ν_α+ν_β)=2ν_H with proton Zeeman frequency 14.73 MHz. The dashed line corresponds to the diagonal line in the spectra.

Table 3.

Parameters derived from contour lineshape analysis of the simulated HYSCORE spectrum in Figure 2

Proton	Qα	Gα, MHz2	(a,T)1, MHz	A⊥=a–T, MHz	A||=a+2T, MHz
H1 (ridges 1αβ,1′αβ)	−1.10 (0.002)	487.0 (0.5)	∓4.04, ±5.17 ∓1.13, ±5.17	∓9.2 ∓6.3	± 6.3 ±9.2
H2 (ridges 2αβ,2′αβ)	−1.13 (0.004)	486.4 (0.8)	∓4.13, ±4.65 ∓0.52, ±4.65	∓8.8 ∓5.2	± 5.2 ± 8.8

Results

Quantitative information about the proton environment around the SQ in the Q_A and Q_B sites of RC was obtained from 2D ESEEM (HYSCORE) experiments, because the simpler 1D approaches do not provide the necessary resolution of the multinuclear contributions from protons. In our studies of protons we used uniformly ¹⁵N labeled protein, because the ¹⁴N nuclei of atoms hydrogen bonded with carbonyl oxygens of the SQs produce deep ESEEM, especially for the Q_A SQ (Figure S1). ¹⁴N ESEEM completely suppressed the proton peaks in HYSCORE spectra of the Q_A SQ due to the cross-suppression effect.^30,31 The ¹⁵N nucleus, with spin I = ½ and no nuclear quadrupole moment, produces a modulation of the echo amplitude that is shallower than the ¹⁴N isotope. This allows the appearance of the proton peaks in HYSCORE spectra of the Q_A SQ. For the Q_B SQ in the RC sample with natural abundance ¹⁴N, the proton HYSCORE peaks are observed, but ¹⁵N labeling further improves the intensity and resolution of the proton spectra. The ¹⁴N and ¹⁵N X-band HYSCORE spectra of the Q_A and Q_B semiquinones are clearly different (see Figure S2, and ref.21) allowing one to draw convincing conclusions about the purity of the preparations containing Q_A or Q_B SQ.

Q_A semiquinone ¹H HYSCORE

The time, τ, which is kept constant in each individual experiment, influences the HYSCORE spectrum by modulating the intensity of cross-peaks. Therefore, measurements were performed at several values of τ to ensure that all cross-peaks were observed. Figure 4 shows the contour and 3D-like stacked presentations of the ¹H spectra recorded with τ=136 ns for the Q_A SQ prepared in ¹H₂O and ²H₂O buffer. To provide a better view of the different spectral features, in this figure (and others discussed below) only the half of the contour spectrum above the diagonal is shown. In addition, the sum of three spectra recorded with τ=136 ns, 200 ns and 400 ns in similar presentations is shown in Figure S3 to ensure adequate representation of all peaks. No new peaks appear in the sum spectrum although the relative intensities of the different peaks are changed. (Other views and presentations of the Q_A SQ spectra are provided in Supplemental Information, Figure S4.)

Figure 4.

Contour (A,B) and stacked (C,D) presentations of the experimental ¹H HYSCORE spectra of the Q_A SQ of Rba. sphaeroides reaction centers prepared in ¹H₂O and ²H₂O (magnetic field 345.9 mT (¹H₂O) and 346.0 mT (²H₂O), time between first and second pulses τ=136 ns, microwave frequency 9.702 GHz (¹H₂O) and 9.707 GHz (¹H₂O)). In the stacked presentation, in ¹H₂O, peak 3_A is hidden between ridges 1_A and 4_A.

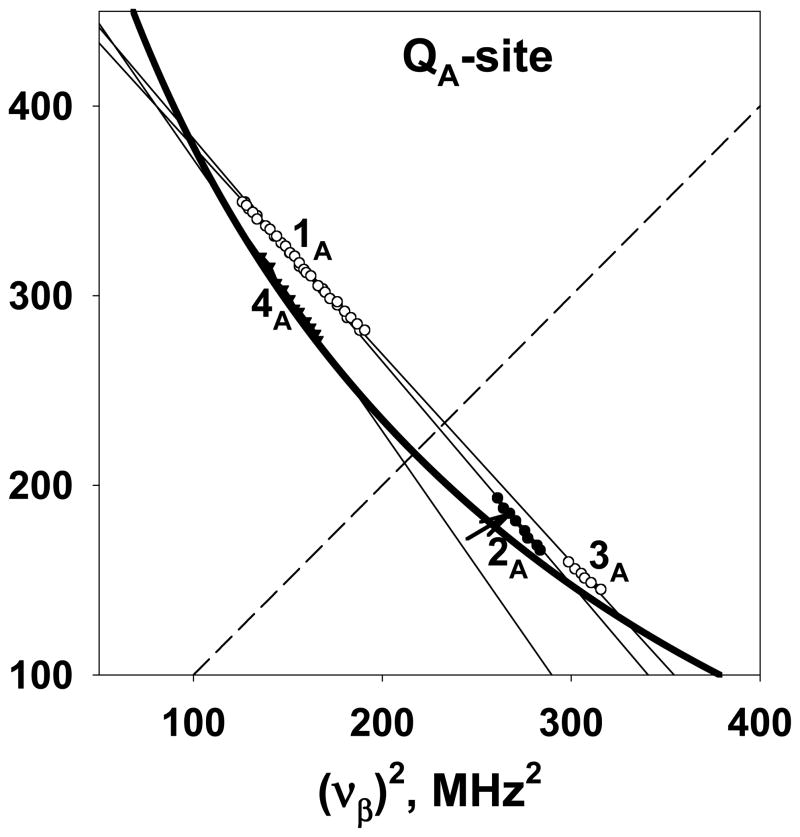
The spectrum in Figure 4 shows up to four pairs of resolved cross-ridges with different lengths and intensities located symmetrically relative to the diagonal. They are designated 1_A, 2_A, 3_A, and 4_A. The peaks or ridges of 1_A, 2_A, and 3_A deviate from the antidiagonal, indicating a significant anisotropic component (see full spectrum in Figure S3). In contrast, cross-peaks 4_A are approximately normal to the diagonal, suggesting smaller anisotropy.^24,25,,²⁷

The intensity of cross-ridges 1_A and 3_A (Figure 4) is substantially decreased in the HYSCORE spectra obtained under the same conditions but with the sample incubated in ²H₂O. The remaining ridge 1_A is also significantly narrower. Cross-peak 2_A (Figure 4) completely disappeared in this HYSCORE spectrum showing that it is produced by exchangeable proton(s). The same conclusion is probably applicable to cross-features 1_A and 3_A, taking into account the significantly different exchange rates for the two exchangeable protons H1 and H2 obtained in ENDOR experiments on the Q_A SQ. The remaining signals, therefore, could be assigned to the residue of slowly exchanging proton H1. The intensities of the diagonal peak and its shoulders spread along the antidiagonal (Figure 4C,D) are also partially suppressed in this spectrum, indicating contributions from weaker coupled exchangeable protons. Nevertheless, cross-peak 4_A and the diagonal peak, with its shoulders, still appear in all spectra, indicating contribution from protons of the SQ substituents and nonexchangeable protons of protein environment.

The HYSCORE spectra simulated using the ENDOR data (Figure 2) suggest that cross-ridge 1_A is the overlap of two cross-ridges, 1_αβ and 2_αβ, from protons H1 and H2, i.e., (1+2)_αβ. Then cross-peaks 2_A and 3_A correspond to cross-features 2′_βα and 1′_βα, respectively. These cross-features, defined by local maxima along the ridge, are plotted in ν² coordinates according to Eq. 1 (Figure 5). This presentation clearly shows that the points for 1_A and 3_A as well as 1_A and 2_A fall along two straight lines, indicating the presence of two protons contributing to these three cross-features. Permutation of the larger and smaller coordinates was performed for cross-peaks 2_A and 3_A, corresponding to the transformation of the sub-ridges 2′_βα and 1′_βα to 2′_αβ and 1′_αβ, for correlation with (1+2)_αβ (see Fig. 2F). The cross-features 4_A, produced by nonexchangeable protons, possess much smaller hyperfine anisotropy than protons responsible for cross-peaks 1_A-3_A and do not cross the diagonal. As a result only one cross-feature is used in the linear regression analysis of these points in Figure 5.

Figure 5.

Cross-peaks 1_A-4_A from ¹H HYSCORE spectrum in Figure 4 plotted in the ν_α² vs. ν_β² coordinate system (see text for detailed explanations). The straight lines show the linear fit of plotted data points. The thick curved line is defined by (ν_α+ν_β)=2ν_H with proton Zeeman frequency 14.73 MHz. The dashed line corresponds to the diagonal line in the spectra.

Quantitative analysis of the cross-peak contours provides two sets of a and T for exchangeable H1_A (ridges 1_A,3_A) and H2_A (ridges 1_A,2_A), and nonexchangeable H3_A (ridge 4_A) protons (see note to Table 4 regarding subscripts A). The full results of analysis are summarized in Table S2. The preferred set (Table 4) was selected on the basis of the ENDOR data, computational works and numerical simulations of HYSCORE spectra (see also Discussion). Particularly, the HYSCORE spectra simulated for H1_A and H2_A using the second solution, with large isotropic constants (Table S2), contain only sub-ridges similar to 1_αβ(βα) and 2_αβ(βα) in Figure 2 while sub-ridges 1′_αβ(βα) and 2′_αβ(βα) are absent, in contrast to the experimental spectra and the spectra simulated with the preferred parameter set.

Table 4.

Characteristics of hyperfine tensors of the protons H1_A-H3_A (MHz) derived from experimental HYSCORE spectra of the Q_A SQ.^a,^b

Proton(s)	a, T	A⊥=a–T	A||=a+2T
H1A (ridges 1A,3A)	−1.38±0.1, 5.41±0.17	−6.8	9.6
H2A (ridges 1A,2A)	−0.17±0.2, 5.07±0.35	−5.2	10
H3A (ridge 4A)	4.39±0.3, 1.71±0.5	2.7	7.8
H3A (ridge 4A)c	4.0±0.3, 1.6±0.5	2.4	7.2

^aThe subscript A indicates tensor assignments, and the corresponding protons, from experimental HYSCORE spectra of the Q_A semiquinone, in contrast to the ENDOR-derived tensors for H1 and H2 in Tables 1 and 2;

^berrors for a and T correspond to 95% prediction intervals for the linear regression results shown in Table S2;

^csample in ²H₂O.

Q_B semiquinone ¹H HYSCORE

Figure 6 shows contour (A) and stacked (C) presentations of the ¹H HYSCORE spectrum of the Q_B SQ prepared in ¹H₂O buffer, obtained as the sum of three spectra recorded with τ=136 ns, 200 ns and 400 ns. We use this presentation because not all cross-peaks possess observable intensity in the spectra at a single value of τ (see Figure S4 for comparison).

Figure 6.

Contour (A,B) and stacked (C,D) presentations of the experimental ¹H HYSCORE spectra of the Q_B SQ of Rba. sphaeroides reaction centers prepared in ¹H₂O and ²H₂O. Spectra were obtained as a sum of three individual spectra recorded with time between first and second pulses τ=136, 200, and 400 ns, (magnetic field 345.1 mT (¹H₂O) and 344.6 mT (²H₂O), microwave frequency 9.680 GHz (¹H₂O) and 9.666 GHz (²H₂O)).

Six pairs of cross-features 1_B-6_B can be identified in the spectrum. The cross-ridge 1_B shows similar length and deviation from the antidiagonal as cross-peak 1_A in the spectrum of the Q_A SQ although the width and intensity of the ridge are smaller than in the Q_A SQ spectrum. Using both contour and stacked spectra, careful examination of the line-shape for the cross-feature most closely approaching 1_B indicates that it is formed by the overlap of two ridges, marked 2_B and 3_B, from two different nuclei (this is also suggested by the 4-pulse ESEEM spectra discussed below). All three cross-features 1_B-3_B completely disappeared in the spectrum of the sample prepared in ²H₂O buffer, showing their relation to exchangeable protons. The spectrum of the Q_B SQ also shows two cross-peaks 4_B and 5_B, for which there are no counterparts in the spectrum of the Q_A SQ. These are also absent in the spectrum after ¹H/²H exchange. Only peak 6_B (similar to peak 4_A in the Q_A SQ spectrum) is still present in the spectrum after ¹H/²H exchange, together with the shoulders of the diagonal ¹H matrix line.

The ν_α² vs. ν_β² plot of the cross-features from the Q_B SQ ¹H HYSCORE spectrum (Figure 7) suggests that 1_B and 2_B, and 3_B and 4_B are the sub-ridges of cross-features belonging to two different protons. In terms of the designations used in Figure 2, 1_B and 2_B are similar to sub-ridges 1_αβ and 1′_βα from proton H1_B, and 3_B and 4_B are sub-ridges 2_αβ and 2′_βα from proton H2_B. The subscript B indicates assignments from experimental HYSCORE spectra of the Q_B semiquinone. In agreement with this suggestion 1_B and 2_B, and 3_B and 4_B (after permutation of the smaller and larger coordinates for 2_B and 4_B placing them to the opposite side of the spectrum relative to the diagonal), fall well along two straight lines and belong to two exchangeable protons H1_B and H2_B with T~5.2 and 3.7 MHz. There are no other cross-features in the spectrum that can be correlated with cross-peaks 5_B and 6_B. The characteristics of the slopes and intercepts for the linear regressions shown in Figure 5 are presented in Table S3, together with two possible sets of (a, T) that satisfy Eqn. (1). Table 5 shows the preferred sets of the hyperfine couplings.

Figure 7.

Cross-peaks 1_B-6_B from ¹H HYSCORE spectrum in Figure 6 plotted in the ν_α² vs. ν_β² coordinate system (see text for detailed explanations). The straight lines show the linear fit of plotted data points. The thick curved line is defined by (ν_α +ν_β)=2ν_H with proton Zeeman frequency 14.73 MHz. The dashed line corresponds to the diagonal line in the spectra.

Table 5.

Characteristics of hyperfine tensors of the protons H1_B-H4_B (MHz) derived from experimental HYSCORE spectra of the Q_B SQ.^a,^b

Proton	a, T	A⊥=a–T	A||=a+2T
H1B (ridges 1B,2B)	−0.83±0.08, 5.2±0.16	−6.0	9.6
H2B (ridges 3B,4B)	−0.88±0.14, 3.71±0.26	−4.6	6.5
H3B (ridges 5B)	1.09±0.35, 1.87±0.6	−0.8	4.9
H4B (ridges 6B)	4.27±0.25, 1.92±0.35	2.4	8.1
H4B (ridges 6B)c	4.8±0.12, 1.59±0.25	3.2	8.0

^aThe subscript B indicates assignments from experimental HYSCORE spectra of the QB semiquinone;

^berrors for a and T correspond to 95% prediction intervals for the linear regression results shown in Table S3;

^csample in ²H₂O.

Sum combination peaks in 1D 4-pulse ESEEM

Additional information about the exchangeable protons, supporting the HYSCORE data, was obtained from the 1D four-pulse ESEEM spectra (Figure 8). These spectra contain lines in the region of the double proton Zeeman frequency (2ν_H, at 29.4 MHz), which are sum-combination harmonics (ν_α+ν_β) of two basic frequencies ν_α and ν_β. These harmonics are not created in HYSCORE experiments. This approach is particularly useful for the resolution of protons with different anisotropic couplings.³²

Figure 8.

Stacked presentations of sets of four-pulse ESEEM spectra of the Q_A and Q_B SQs in Rba. sphaeroides reaction centers prepared in ¹H₂O and ²H₂O. The spectra show the modulus of the Fourier transform along the time (T) axis for different times between first and second pulses, τ. The initial time τ is 100 ns in the farthest trace, and was increased by 12 ns in successive traces. Microwave frequency and magnetic field were 9.711 GHz and 346.2 mT (Q_A in ¹H₂O), 9.705 GHz and 346.0 mT (Q_A in ²H₂O). 9.708 GHz and 346.1 mT (Q_B in ¹H₂O), and 9.664 GHz and 344.5 mT (Q_B in ²H₂O).

The four-pulse ESEEM spectrum of the Q_A SQ in ¹H₂O buffer contains two well resolved lines in the region of the proton 2ν_H, as shown in Figure 8. The most intense line appears exactly at the 2ν_H frequency and represents the contribution of weakly coupled protons from the protein environment with (ν_α+ν_β) ≅ 2ν_H. The spectrum also reveals a broad, asymmetrical peak of lower intensity shifted from 2ν_H to higher frequencies, with a shoulder on the high-frequency side. This peak does not possess a well-defined maximum and is consistent with two overlapping peaks with shifts of 0.8–1.1 MHz. This feature is greatly diminished in the spectrum of the sample prepared in ²H₂O, indicating that it contains a major contribution from exchangeable protons.

The four-pulse spectrum of the Q_B SQ shows a single, narrow peak shifted by ~0.9 MHz from 2ν_H. In addition, there is a distinct, shoulder-like feature located near the 2ν_H peak. The flat maximum indicates a shift of ~0.25–0.50 MHz. Both features disappear in ²H₂O.

The shifts observed in the four-pulse ESEEM are well described³² by Equation 2

$$\mathrm{\Delta }=9T^2/16{\nu }_{\text{H}}$$ [2]

which yields the anisotropic component T for the exchangeable protons producing shifted lines (Table 6). The T values determined from the shifts of the sum-combination lines are consistent with the values obtained from the HYSCORE analysis for Q_A and Q_B site semiquinones. Particularly, T ~4.6–5.4 MHz was found for the Q_A-site. In the Q_B SQ spectrum, the line with the larger shift corresponds to T ~5 MHz and relates to H1_B. The broad feature near the 2ν_H line corresponds to protons with T <3.7 MHz and can be accounted for by contributions of the exchangeable protons H2_B and H3_B, which possess significantly lower anisotropic hyperfine coupling than H1_B. This contrasts with the Q_A SQ where both detected exchangeable protons, H1_A and H2_A, exhibit similar hyperfine tensors.

Table 6.

Anisotropic hyperfine couplings for exchangeable protons in the Q_A- and Q_B-sites estimated from the shift of the sum combination harmonics

Site	Shift Δ, MHz	T, MHz
QA	0.8–1.1	4.6–5.4
QB	0.9–1.0 0.2–0.5	4.9–5.1 2.3–3.6

Discussion

Exchangeable protons

The principal values of the hyperfine tensors determined in our HYSCORE studies for the exchangeable protons around the Q_A SQ are fully consistent with previously published orientation-selected Q-band ENDOR data,¹² but were obtained with considerably greater ease of sample preparation, much shorter data acquisition time, and simpler analysis. We found the presence of two protons H1_A and H2_A, with similar anisotropic hyperfine couplings T~4.6–5.4 MHz, involved in the O₄–His (M219) and O₁–Ala (M260) hydrogen bonds.

Besides the cross-features assigned to these two protons, ¹H/²H exchange did not result in any other significant loss of spectral intensity in the Q_A SQ spectrum, e.g., in areas remote from the diagonal peak where distant nuclei mostly contribute. This is in agreement with the current vision of the Q_A site where only two hydrogen bonds, one to each carbonyl, are responsible for coupling the SQ to the protein.

The HYSCORE spectra of the Q_B SQ have resolved features assigned to exchangeable protons with distinct anisotropic couplings T~5.2 MHz and ~3.7 MHz. These values exceed the T~3 MHz observed for in-plane hydrogen bonded protons in alcoholic solutions.^33–35 Hydrogen bonding to the quinone carbonyl groups occurs via proton donation to one or both lone pairs on the sp²-hybridized carbonyl oxygen.³⁶ Besides these two protons discussed here for the Q_B SQ, we found a marked loss of spectral intensity after ¹H/²H exchange for a peak accompanying the antidiagonal, with a splitting of ~2.5 MHz (peak 5_B). This indicates the presence of an additional exchangeable proton with T~1.9 MHz estimated from contour lineshape analysis.

As expected from the simulated spectra, the powder X-band HYSCORE spectra did not resolve all the cross-ridges of the Q_A SQ protons, but the the linear analysis clearly identified them through the correlations between features (Figure 5). Similarly, the four-pulse ESEEM spectra did not fully separate all the shifted proton sum-combination peaks, due to line broadening, although our model simulations of the four-pulse spectra with ENDOR derived tensors did resolve peaks from two Q_A protons. One likely factor contributing to broadening of the lines and influencing the resolution is the “strain” of the hyperfine parameters, i.e., the static distribution of hyperfine parameters. Analysis of the lineshapes in the “single-crystal-like” Q-band ENDOR spectra from the protons of hydrogen bonds in the Q_A-site of RCs from Rba. sphaeroides¹² shows that the influence of this factor on the hyperfine coupling value would not exceed ±5%. For couplings of ~5 MHz, this could give broadening up to 0.5 MHz for basic frequencies and the spread in the position of line maximum for combination harmonics up to 0.3 MHz. In powder spectra such broadening does influence the resolution of the individual lines from protons H1_A and H2_A in the Q_A site.

Assignment of hyperfine couplings through QM/MM calculations

To help assign the observed hyperfine couplings to specific interactions within the Q_A and Q_B sites we have obtained calculated values using QM/MM density functional theory-based electronic structure calculations. The excellent ability of DFT-based calculations to accurately calculate hyperfine couplings for semiquinone free radicals has been demonstrated some time ago.³⁷ A recent report has shown how such calculations can be extended to model semiquinone protein binding sites using QM/MM calculations.²⁰ The carbonyl and hydrogen bonding distances calculated for SQ in the Q_A and Q_B sites are given in Table 7, while the calculated hyperfine couplings for the exchangeable protons are given in Table 8. For the Q_A site, T (T=T₃₃/2) values calculated for the His-M219 N_δ¹H (5.3 MHz) and Ala-M260 peptide N¹H (4.6 MHz) are in very good agreement with the respective T values of 5.2 MHz and 4.6 MHz from Q-band ENDOR,¹² and with our HYSCORE results, 5.4 and 5.1 MHz. We can therefore confidently assign the experimental T values to these proton interactions within the Q_A site. In addition the calculated ¹⁴N isotropic hyperfine couplings for the His-M219 N_δ (2.6 MHz) and the Ala-M260 peptide N (1.5 MHz) are in good agreement with the experimental values of 2.5 MHz and 1.9 MHz estimated from the ¹⁴N and ¹⁵N HYSCORE spectra of this work (Figure S2). A previous two- and three-pulse ESEEM study^14,15 reported hyperfine couplings of 1.8 and 1.1 MHz, which were not assigned to particular nitrogens due to uncertainty in the correlation of the single-quantum and double-quantum transitions from the same nitrogens in 1D ESEEM spectra.

Table 7.

SQ optimized carbonyl and hydrogen bonding distances in the Q_A and Q_B sites.^a,^b

Bond	QA site	QB site
C4-O4	1.29	1.28
C1-O1	1.27	1.28
O4 - HNδ His-M219/L190	1.62	1.58
O1 – HN Ala-M260/Gly-L225	1.84	2.00
O1 - HO Ser-L223		1.81
O1 - HN Ile-L224		2.30

^aQ_A data taken from ²⁰.

^bAll distances in ångstroms.

Table 8.

Calculated ¹H and ¹⁴N hyperfine couplings (MHz) for the Q_A and Q_B site hydrogen bonding interactions with SQ

QA sitea			QB site
Position	Anisotropic T33,T22,T11	Isotropic a	Position	Anisotropic T33,T22,T11	Isotropic a
1HN His-M219	10.4 −5.3 −5.0	0.6	1HN His-L190	10.2 −5.3 −4.9	−0.4
1HN Ala-M260	9.3 −4.7 −4.6	−1.8	1HN Gly-L225	6.6 −3.7 −2.9	−0.6
			1HN Ile-L224	3.9 −2.1 −1.8	−0.1
			1HO Ser-L223	7.6 −4.0 −3.7	−0.8
14Nδ His-M219	0.6 −0.3 −0.3	2.6	14Nδ His-L190	0.4 −0.2 −0.2	1.5
14NH Ala-M260	0.6 −0.3 −0.3	1.5	14NH Gly-L225	0.3 −0.2 −0.1	0.6
			14NH Ile-L224	0.2 −0.1 −0.1	0.1

^aQ_A data taken from ²⁰.

For the Q_B site, the largest ¹H tensor component in the calculations gives a value of 5.1 MHz for the coupling between the His-L190 N_δH group and the O₄ of the SQ (see Table 8). The experimentally observed T value of 5.2 MHz is therefore assigned to this interaction. Furthermore, the calculated ¹⁴N isotropic hyperfine coupling for the Q_B site N_δ His-L190 is 1.5 MHz, in agreement with the reported experimental value of 1.5 MHz.²¹ For the O₁ side in the Q_B site there are three ¹H hyperfine couplings calculated; two strong hydrogen bonding interactions, with the OH of Ser-L223 and the peptide NH of Gly-L225, and a weaker dipolar coupling with the peptide NH of Ile-L224. The calculated T value for the Ile-L224 peptide NH (1.9 MHz) is assigned to the same, experimentally observed T value of 1.9 MHz. The peptide NH of Gly-L225 is calculated to have a ¹⁴N isotropic value of 0.5 MHz whereas the corresponding value for Ile-L224 is 0.1 MHz. The experimentally observed ¹⁴N isotropic coupling of 0.5 MHz²¹ is therefore assigned to the NH Gly L-225 interaction. The much smaller value calculated for Ile-L224 would not be distinguishable from the matrix contributions on the diagonal.

The T values calculated for protons of Ser-L223 (3.8 MHz) and Gly-L225 (3.3 MHz) are both likely to contribute to the experimentally derived T=3.7 MHz value. The HYSCORE spectra calculated with the hyperfine coupling values for protons of Ser-L223, Gly-L225 and His-L190 from Table 8 showed that the cross-peaks from Ser-L223 and Gly-L225 protons are indistinguishable in the sum spectrum (Figure S7, A–F). The addition of the His-L190 proton gives the total spectrum, reproducing the shape of the overlapped cross-features (corresponding to the features assigned to 2_B and 3_B in the experimental spectra in Figures 6 and S5) and its location relative to the cross-ridge (equivalent to 1_B in Figure 6 and S5) from the His proton (Figure S7, G–L). Thus, these calculations qualitatively support the suggested contribution of the Ser-L223 and Gly-L225 protons to the feature with T=3.7 MHz in the experimental spectra. Further work using orientation-selected Q-band ENDOR or pulsed EPR at lower microwave frequencies is needed to confirm this result experimentally.

Nonexchangeable protons

The hyperfine couplings of nonexchangeable protons in the Q_A and Q_B semiquinones have been extensively studied by multifrequency (X-, Q-, and W-band) ENDOR in frozen solutions and X-band ENDOR in single-crystals.^11,38,39 These studies reported the couplings for the protons of a rotating methyl group (C₅′) and one proton from a methylene group of the isoprenoid chain of Q_A. All experiments with Q_A SQ have consistently shown that the maximum and minimum principal values of the hyperfine tensor are about 6.8 and 3.0 MHz for the methyl protons and 8.8 and 5.0 MHz for the methylene proton (Table S4). This suggests that the lines from methyl and methylene protons will partially overlap in powder X-band HYSCORE spectra.

ENDOR studies of the Q_B SQ have reported the coupling for methyl protons only, with larger isotropic coupling than for the Q_A SQ. Q- and W-band studies indicated maximum and minimum principal values of the hyperfine tensor of 7.8 and 3.9 MHz.^11,39

The HYSCORE spectra of the Q_A and Q_B semiquinones after deuterium exchange show only one pair of cross-peaks, i.e., 4_A and 6_B, respectively, along the antidiagonal and well-separated from the diagonal peak and remaining shoulders. Analysis of the contour line-shape of these peaks in the samples prepared in ¹H₂O and ²H₂O gives similar results for both SQs, and with only very minor contributions from exchangeable protons in this vicinity. The formal axial tensors are: (7.2, 2.4, 2.4) MHz with a=4.0 MHz and T=1.6 MHz for the Q_A SQ, and (8.0, 3.2, 3.2) MHz with a=4.8 MHz and T=1.6 MHz for the Q_B SQ. These values are in reasonable agreement with those derived from ENDOR, although the isotropic contributions are somewhat smaller and the anisotropic components larger (T~1.1–1.2 MHz for CH₃ and CH₂ protons). The HYSCORE analysis consequently yields a larger difference between the maximum and minimum principal values of the hyperfine tensors. The difference likely arises from the overlap of the methyl and methylene proton lines, which increases the apparent length of the HYSCORE cross-peak and leads to a larger anisotropic component in the formal analysis.

Proton resonances with smaller splittings have also been observed in ENDOR spectra, but have not been assigned. They should presumably belong to the second proton of the CH₂ group, other protons of the isoprenoid chain, the methoxy groups, and protons from the protein matrix. These protons contribute to the shoulders of the diagonal line in HYSCORE spectra.

From the QM/MM calculations (Table 9), the ¹H CH₃ values for Q_A are in good agreement with the experimentally determined values (see also²⁰). For Q_B the calculated isotropic hyperfine coupling is predicted to be larger than that found for Q_A in agreement with the experimental determinations. However, the Q_B value calculated is significantly higher than that observed experimentally, suggesting that the model in its current form overestimates the spin density at C₅ of the Q_B SQ. Since the ¹⁷O and ¹³C coupling values calculated for the carbonyls are in good agreement with experiment, the asymmetry along the C₁-C₄ quinone axis is well reproduced. However, asymmetry across the C₂-C₅ axis could be affected by the torsional angle of the C₂ methoxy group, which we have shown to be absolutely required for Q_B activity.^2,40 Proper understanding of the C₅ spin anomaly will require further knowledge of the unpaired spin density distribution over the ring carbons. This can be obtained from studies of ¹³C ring-labeled Q_A and Q_B SQs, and such experiments are under consideration.

Table 9.

Calculated ¹³C, ¹⁷O and ¹H hyperfine couplings (MHz) for the Q_A and Q_B semiquinones.^a,^b

QA sitea			QB site
Position	Anisotropic T33,T22,T11	Isotropic a	Position	Anisotropic T33,T22,T11	Isotropic a
13C1	20.1 −11.8 −8.3	−7.0	13C1	30.6 −16.6 −14.0	3.3
13C4	33.1 −17.6 −15.5	8.4	13C4	26.3 −14.4 −11.9	1.0
17O1	−78.8 39.7 39.1	−19.9	17O1	−66.9 −33.6 −33.3	−18.3
17O4	−54.0 27.3 26.7	−16.0	17O4	−62.6 −31.4 −31.2	−18.2
1H CH3(5′)	2.4 −1.6 −0.8	4.3	1H CH3(5′)	2.6 −1.7 −1.0	7.6

^aQ_A data taken from²⁰;

^bExperimentally determined hyperfine couplings from ¹¹:

¹³C couplings, A_obs=a+T₃₃, Q_A site: 22.7 MHz (C₁) and 35 MHz (C₄); Q_B site: 27.7 MHz (C₁) and 32.2 MHz (C₄).

¹⁷O couplings, A_obs=a+T₃₃, Q_A site: −94 MHz (O₁) and −75 MHz (O₄); Q_B site: −88 MHz (O₁) and −82 MHz (O₄).

Reported couplings for methyl group are summarized in Table S4.

Asymmetry in spin density distribution

Differences in the hydrogen bonding interactions with the quinone oxygens is expected to lead to asymmetry of the spin distribution in the radical anion. Comparison of the ¹H, ¹³C and ¹⁷O couplings for SQ in the Q_A and Q_B sites with those of ubiquinone-10 anion radicals in alcoholic solution led to the conclusion that the Q_A quinone binding site is more asymmetric than the Q_B site.¹¹ Based on the results and discussion above it can be inferred that the interactions with both SQs at the O₄ atom are similar, where a strong hydrogen bond is formed with the N_δ atom of a histidine residue. The O₁ interactions, however, are significantly different. For the Q_A site only one hydrogen bonding interaction is found with the peptide NH of Ala-M260, whereas in the Q_B site there are interactions with the peptide NH of Gly-L225 and the OH group of Ser-L223, and a weaker interaction with the peptide NH group of Ile-L224.

In the Q_A site, the stronger hydrogen bond to the O₄ oxygen gives rise to an asymmetric spin density distribution for the ubisemiquinone. For the Q_B site, the strong hydrogen bonding interaction to the O4 atom is balanced by the double hydrogen bond interaction at the O₁ atom in addition to a weaker interaction with the NH group of Ile-L224. This leads to a more symmetric spin density distribution for the Q_B SQ as previously indicated by the experimental ¹³C and ¹⁷O hyperfine couplings.¹¹

Table 9 gives the calculated isotropic and anisotropic ¹³C and ¹⁷O hyperfine couplings for the Q_A and Q_B SQs. Here the asymmetry difference between the two sites is clearly demonstrated by the large differences in the calculated values of the 1 and 4 positions for the Q_A SQ, whereas similar values are calculated for the Q_B SQ. The calculated total tensors show good agreement with the experimentally determined values of reference provided in the notes to Table 9.¹¹

The difference in methyl group hyperfine couplings is another indicator of the different spin density asymmetries exhibited by the Q_A and Q_B SQs. For Q_A, the stronger hydrogen bond at the O₁ atom leads to a low spin density at C₅ (see spin populations in Figure 9), which, in turn, leads to a lower hyperfine coupling for the methyl group protons. For the Q_B SQ, the more symmetric spin density distribution leads to a higher spin density value at C₅, which gives rise to a larger methyl group hyperfine coupling. This is similar to the situation in protic solvents where similar hydrogen bond strengths to each oxygen are expected.

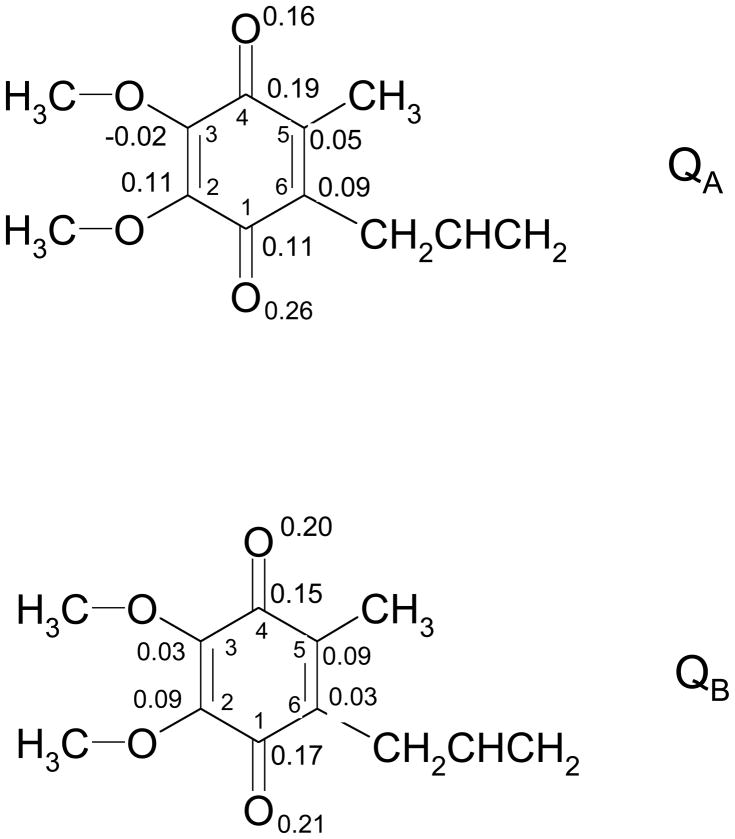
Figure 9.

Calculated Mulliken spin populations for the semiquinone in the Q_A and Q_B sites.

The difference in spin asymmetry for the Q_A and Q_B site semiquinones is well illustrated by the calculated Mulliken spin populations shown in Figure 9, where a much more symmetric spin population is shown for the Q_B SQ. This difference in spin density distribution for the two semiquinones may well contribute to their different functions in electron transfer. The asymmetry of the Q_A site in bacterial RCs polarizes the electron density of the Q_A SQ towards Q_B and it has been suggested that this might contribute to the electron transfer to Q_B.¹¹ However, in the similar, Type II reaction center of oxygenic photosystem II, the H-bond strengths that are presumed to underlie the spin density asymmetry have been reported to be opposite to that in bacterial RCs, i.e., the interaction with the peptide nitrogen was strongest.⁴¹ Thus, the directional component of the electron distribution in Q_A may not be a design requirement of functional Q_A to Q_B electron transfer. However, the asymmetry will likely affect the redox potential regardless of its particular polarity. For the Q_B site the more symmetric spin density resembles the in vitro SQ in protic solvents favoring double reduction and formation of the quinol form. The extra hydrogen bonding interactions found in the Q_B site will also increase the electron affinity of Q_B compared with Q_A, which should lead to a higher redox potential for Q_B, as observed experimentally.²

Conclusion

We have found that a principal difference between the SQ in the Q_A and Q_B sites of purple bacterial reaction centers is an increased number of hydrogen bond interactions at the O₁ atom for the Q_B SQ. This leads to a symmetric spin density distribution for the Q_B SQ and also an enhanced stabilization. The hydrogen bonding pattern in the binding site is able to control the reduction properties of the quinone. In other type II reaction centers, such as Photosystem II, the hydrogen bonding interactions with the Q_A semiquinone are also highly asymmetrical, suggesting that a similar control mechanism exists.⁴¹ The fine tuning of SQ properties through hydrogen bonding is likely to be a key mechanism for controlling quinone reduction in biological systems.