Molecular Simulations of Dodecyl-β-maltoside Micelles in Water: Influence of the Headgroup Conformation and Force field Parameters

Abstract

This paper deals with the development and validation of new potential parameter sets, based on the CHARMM36 and GLYCAM06 force fields, to simulate micelles of the two anomeric forms (α and β) of N-Dodecyl-ß-maltoside (C₁₂G₂), a surfactant widely used in the extraction and purification of membrane proteins. In this context, properties such as size, shape, internal structure and hydration of the C₁₂G₂ anomer micelles were thoroughly investigated by molecular dynamics simulations and the results compared with experiments. Additional simulations were also performed with the older CHARMM22 force field for carbohydrates (Kuttel, M. et al. J. Comp. Chem. 2002, 23, 1236-1243). We find that our CHARMM and GLYCAM parameter sets yields similar results in case of properties related to the micelle structure, but differ for other properties such as the headgroup conformation or the micelle hydration. In agreement with experiments, our results show that for all model potentials the β-C₁₂G₂ micelles have a more pronounced ellipsoidal shape than those containing α anomers. The computed radius of gyration is 20.2 Å and 25.4 Å for the α- and β-anomer micelles, respectively. Finally, we show that depending on the potential the water translational diffusion of the interfacial water is 7 - 11.5 times slower than that of bulk water due to the entrapment of the water in the micelle crevices. This retardation is independent of the headgroup in α- or β- anomers.

I. Introduction

Glycolipids (GLs) are glycosyl derivatives of lipids that belong to a large family of molecules known as glycoconjugates.¹ From a chemical point of view, GLs designate any molecule with surfactant properties containing a carbohydrate headgroup (with one or more monosaccharide unit) attached to a lipophilic tail. In particular, alkyl-glycosides are simple glycolipid molecules obtained, for instance, by condensation such as “Fischer glycosidation” of a sugar with a fatty alcohol.² Their tension-active properties depend on the length of the alkyl chain.^3,4 Because they are highly effective, ecologic and non toxic, this class of surfactants has a wide range of applications in food, cosmetic and pharmaceutical industries.^5-7 Similar to other surfactants, GLs can form different mesophases in water, such as micelles, lamellae, vesicles, etc; depending on experimental conditions (see for instance refs.3^,8-15).

During the last decades, alkyl-glucosides have also attracted a great deal of interest in the context of membrane protein extraction^16,17 given that they have a low critical micellar concentration (cmc) around 10 ^-3-10^-4 mol.1^-1 (see Table 2 of ref.7 for data and references), form large aggregates and keep the protein structure and its activity intact.^18,19 In particular, alkyl-glucosides have been successfully used for solubilization of large membrane protein complexes, such as rhodopsin²⁰, cytochrome c oxydase^21,22 and protein channel.^23,24

Among these detergents, N-Dodecyl-ß-maltoside (C₁₂G₂) (Figure 1) is one of the most used alkyl-glucosides in membrane protein extraction experiments.¹⁷ Two anomers, α- and β-, exist for C₁₂G₂ due to two possible connectivities of the dodecane chain (DOD) and of the anomeric carbon (C₁′) linking DOD to the maltose head. The β-isomer is in a linear conformation, whereas the α-isomer is in a right-angle bent formed between the maltose headgroup and the alkyl tail. The α-anomer is less soluble than the β^7,25 and is not commonly used in membrane protein studies, albeit with some notable exceptions. For instance, in the bacterial E.Coli Na⁺/H⁺ antiporter, it was reported recently ²⁴ that the α-C₁₂G₂ surfactant is needed to obtain a crystallized protein in its native state. To explain this feature, it is generally assumed that the orientation of the maltose head in the surfactant leads to differences in sterical constraints (i.e. due to different packing parameters) and, possibly, in hydration behaviors. SANS and SAXS scattering experiments have shown that the α-anomer of C₁₂G₂ forms small quasi-spherical micelle, while the β- conformation forms large oblate aggregates.^13,26

Figure 1.

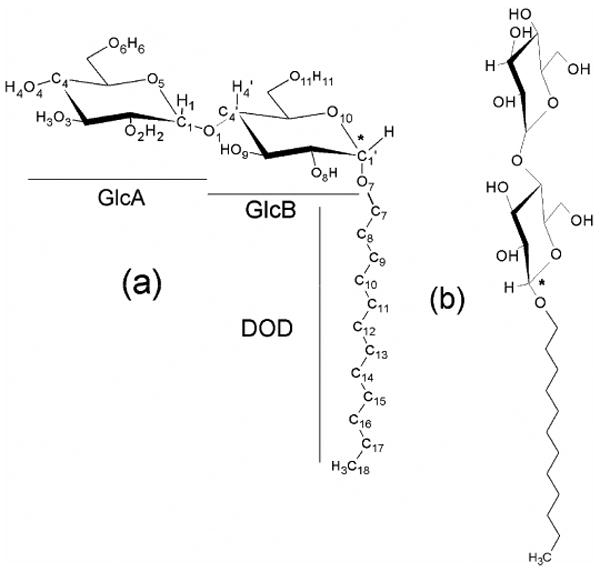
The α- (a) and β-anomers (b) of C₁₂G₂ surfactants with the atom numbering scheme used in the paper. The anomeric center C₁′ of the molecule is underlined with a star.

In the past few years, molecular dynamics simulations (MD) have been extensively used to study the structure and hydration of mono- and di-saccharides, in aqueous solutions (e.g., refs 27^{,28,29,30,31,32,33,34,35, 36,37,38,39,40}). MD with alkyl-glycosides (such as alkyl-β-O-glucoside (C₈Glc₁) or alkyl-β-O-galactoside (C₈Gal)) have been also performed in the past, involving bilayers,^{41, 42, 43} micelles ^{44,45, 46, 47} or interacting with a plant protein.⁴⁸ In the studies of Bogusz et al. ⁴⁴ and Chong et al. ⁴⁷, the influence of the surfactant headgroup conformation on the micelle structure and hydration has been thoroughly examined. It was reported that despite the conformational changes in the headgroup, several properties remain nearly unchanged for the aggregates, in particular micelle shape, surfactant tail length and conformation. In contrast, other properties directly related to the interaction between the solvent and the headgroup (i.e. solvent accessible surface area, headgroup cluster structure, number of isolated water at the micelle surface) are significantly modified by the stereochemistry of the carbohydrate head.^44,47 It was also noted that the sugar counterpart is responsible for strong perturbations of the water structure at the micelle surface and it affects the formation of a large hydrogen bond (HB) network at the micelle surface between water and the headgroups, and within the headgroups themselves (inter- and intra- HBs, respectively).^41,47,49 This HB network may also explain the good thermal stability of the surfactants⁴⁹ and cryoprotective effects.^36,50

Despite their crucial role in membrane protein extractions, C₁₂G₂ micelles have been rarely studied by computational methods, and to our knowledge, only a single MD study has been performed on these systems in the past.⁵¹ That investigation was mainly focused on the hydration properties of the micelles and used a thermodynamical approach to examine the micellisation behavior of surfactants with different chemical nature, and was compared with experiments. To simplify the calculations, the simulations were carried out starting from a spherical aggregate of 45 β-C₁₂G₂. This aggregation number is far from that of 130, commonly accepted in the literature.^13,14,26 Moreover, the authors used the OPLS-AA force field not fully optimized for glycolipid molecules.⁵² In absence of optimized parameters for the two C₁₂G₂ anomers for the widely used CHARMM and GLYCAM06 force fields, we have developed two sets of parameters compatible with these force fields for condensed-phase MD simulation studies. We expect that these new parameters will allow us to examine the influence of the headgroup stereochemistry in C₁₂G₂ micelle structures under experimental conditions. Our endeavour included the calculations of new RESP atomic charges for the current GLYCAM06 potential and an optimization of the dihedral angles for the acetal linkage between the maltose headgroup and the alkyl chain for both the α- and β-anomers compatible with the CHARMM36 force field (see next sections). These new CHARMM and GLYCAM parameters (named GLYCAM06 and CHARMM-Opt, respectively) have been tested and validated by performing different MD simulations of two realistic models of C₁₂G₂ micelles in explicit water. To compare our results with previous MD studies of glycolipid micelles,^44-46 we have also performed two simulations with the old CHARMM22 parameters taken from Kuttel et al.⁵³ and Reiling et al.⁵⁴, named throughout the paper with the acronym CHARMM-K.

This paper is organized as follows: in the next sections, we describe the procedures followed to derive RESP atomic charges as well as the optimization of the dihedral angles for the acetal linkage for the α-and β-anomers for the GLYCAM and CHARMM force fields. This is followed by sections covering MD simulations, the results, as well as the interpretations of these results.

II. Methods

1. RESP charge derivation for the α- and β-anomers of C₁₂G₂ for GLYCAM

RESP charge derivation for C₁₂G₂ GL for the GLYCAM force field was carried out using standard methods.^55-57 For this purpose, we have followed a similar approach than that described by Gouin et al.³⁹ Three molecules i.e. methyl α-D-glucopyranoside (AMG), methyl β-D-glucopyranoside (BMG) and 1-dodecanol (OH-DOD) were involved in charge derivation. For each glucose unit, two rotamers were selected for the ω (i.e. represented by the O₆C₆C₅C₄ and O₆C₆C₅O₅ rotational angles) in the gauche-gauche (gg, ω = -60°) and gauche-trans (gt, ω = +60°) conformations (see Figure S1 in the supplementary material) considering that they are the most populated in solution.⁵⁸ Optimized geometries presenting intramolecular HB were excluded from charge derivation to avoid over-polarization effect.⁵⁶ As a consequence, geometry optimization was carried out with dihedral angle constraints. The HO₄′O₄′C₄H′₄ dihedral angle of the glucosides AMG and BMG was constrained to 180°, whereas the HO₃-O₃-C₃-H₃ and HO₂-O₂-C₂-H₂ dihedrals of AMG and BMG were constrained to 180°, respectively. A single conformation for 1-dodecanol was considered in charge derivation, and the selected geometry was optimized in its extended conformation (i. e. “all trans dihedrals”). Indeed, it has been previously shown that the surfactant alkyl chain adopts mainly this conformation in the micelle core (see for instance refs.44^,59,60). Frequencies were calculated for all the molecules, and transition state structures were excluded from the charge derivation procedure. Geometry optimization, frequency calculation and molecular electrostatic potential (MEP) computation were carried out using the Gaussian03 quantum mechanics (QM) package in the gas phase,⁶¹ whereas charge fitting was performed using the RESP program.^55,56 The HF/6-31G** level of theory was used in the geometry optimization and frequency calculations⁶², while MEP computation was based on HF/6-31G* leading to implicit polarization required in condensed phase simulations when using the non-additive AMBER force field model.^55,56 The CHELPG algorithm was used to compute the grid of points involved in MEP computation.⁶³ The molecular orientation of each optimized geometries was controlled using the rigid-body reorientation algorithm implemented in the R.E.D. program.⁶³ Four molecular orientations for each optimized geometry of AMG and BMG (based on the glucose atom names C₁C₃C₅, C₅C₃C₁, C₂C₄O₅ and O₅C₄C₂, see Figure S1) and for the alkyl chain (based on the 1-dodecanol atom names C₁C₂C₃,C₃C₂C₁, C₁C₃C₅ and C₅C₃C₁, see Figure S1) were generated before MEP computation, and involved in the charge fitting procedure to yield reproducible atomic charges. Charge fitting was performed using a single RESP stage with a hyperbolic constraint value of 0.01. Intra-molecular charge constraints between the methyl and the C4 hydroxyl groups of AMG and BMG and inter-molecular charge constraints between the methyl group of each methyl glucoside and the hydroxyl group of OH-DOD (Figure S1) were set to a value of zero during charge fitting allowing the definition of the molecular fragments and force field libraries required to build C₁₂G₂ GL. Each hydrogen atom bound to a sp3 carbon was also constrained to a target value of zero during charge fitting to ensure a compatibility with the GLYCAM force field.⁶⁴ The charge derivation procedure was automatically carried out using version IV of the R.E.D program.⁶³ RESP charges for the α– and β–anomers of C₁₂G₂ are reported in the supplementary information, and are freely available from R.E.DD.B. server (http://q4md-forcefieldtools.org/REDDB/)⁶⁵ with the accession code “F-72”.

2. Optimization of the dihedral angle potentials for the acetal linkage in α- and β- C₁₂G₂ for CHARMM

Ethoxy tetrahydropyran (Et-THP) was used as a model compound to parameterize the acetal linkage in C₁₂G₂ GL. α- and β- substituted anomers were involved in the study (Figure S2). Tetrahydropyran (THP) parameters were those previously developed in the context of hexopyranoses.⁶⁶ The bond, angle, dihedral, Lennard-Jones, and partial charge parameters involving the acetal group were transferred by analogy to methoxy-THP (Met-THP) parameters developed previously⁶⁷ and existing linear ether parameters (Listing S1).⁶⁸ The optimization of these transferred parameters was undertaken as follows. QM MP2/cc-pVTZ//MP2/6-31G* Φ/Ψ scans for both α- and β-anomers were performed (Φ = O_R-C₁-O_E-C₆, Ψ = C₁-O_E-C₆-C₇) at 15 degree increments, thus giving rise to 576 conformations as target data. Figure S3 shows that the transferred parameters serve as a good initial guess as they reproduce the QM energy surface satisfactorily. The dihedral parameters involving the exocyclic heavy atoms were directly fit using the MCSA automated dihedral fitting procedure ⁶⁹ to the QM Φ/Ψ data, resulting in a marked improvement in the root mean square error (RMSE) from 2.01 (1.23) to 0.81 (0.83) kcal/mol for both α- and β- anomer. Figure S3 shows that the fit parameters reproduce well the QM Φ/Ψ potential energy surface for both anomers. Additionally, Figure S4 shows that the fit parameters reproduce the 1-D QM energy as a function of Ψ (Φ is kept constant at +/- 60 for α and β-anomer) much better than the transferred ones. Unconstrained MP2/6-31G* optimization of the molecules revealed the QM global minima for the α- anomer at values of (61.5°, 175.1°) and for the β-anomer at values of (-63.2°, -172°). These QM minima are correctly reproduced by our optimized dihedral parameters as seen in Table S2. We also notice that they also reproduce well the energy difference between the two anomers global minima, ΔE_α−β (ΔE_α-β= -1.52 kcal/mol for QM and ΔE_α−β= -1.85kcal/molforMM).

The transferred partial charge on the ether oxygen atom (O_E) was validated by performing water pair interaction energy calculation as performed in previous studies.⁶⁶ This consists of optimizing the solute/water interaction distance at the HF/6-31G* level theory, with constraints on all other degrees of freedom. Table S3 shows that our parameters reproduce well the scaled QM interaction energies and adjusted distances,⁶⁶ thus validating the transfer of charges. These new sets of parameters are provided in the supplementary information in the CHARMM readable format (Listing S1).

3. Simulation Methods

To be consistent with the force fields developed in this study, we used an “all-atom” approach to model all micellar systems. RESP charges derived in the section II. 1 were involved in GLYCAM-based MD simulations with the bonded and non-bonded parameters taken from the GLYCAM06 force field version f.⁶⁴ The 1-4 van der Waals and electrostatic scaling factors were set to 1.0, in agreement with the developer recommendations.⁶⁴ In the case of the CHARMM-K simulations, we used two sets of parameters to model the sugar headgroup and the exocyclic atom connecting the maltose head and the alkyl chain. For the maltose head we used the parameters of Kuttel et al.⁵³ (a revision of the CHARMM22 force field for sugars of Ha et al.)⁷⁰ and for the acetal atom those of Reiling et al.⁵⁴, which is assigned to an ether oxygen atom type with a partial charge of -0.30 e. These two sets of parameters were previously employed by Bogusz et al.^44,45 and Konidala et al. ⁴⁶ in MD simulations of C₈G₁ micelle in water. For the CHARMM-Opt simulations, we used the new set of parameters for hexopyranose⁶⁶ with optimized parameters for the Φ_H/Ψ_H glycosidic dihedral angles which significantly improves the CHARMM force field for simulations of polysaccharides.⁶⁷ For the connection between the maltose head and the alkyl chain, we adopted the optimized parameter set for ethers by Lee et al.⁷¹ combined with the optimized torsion parameters developed for Et-THP described in the previous section II.2. For all MDs performed with the CHARMM force fields, the alkyl chain of the surfactant was modeled with parameters developed by Klauda et al. for alkanes.⁷² This contrasts with previous investigations^44,45 and the work of Konidala et al.⁴⁶ where for alkyl chain the parameters⁷³ were used. Finally, the TIP3P water model⁷³ was adopted to model the solvent for all the simulations.

4. Construction of the Micelles and Simulation Techniques

In this paper, we made the choice of using two preassembled micelles with 75 and 132 monomers of α- and β-C₁₂G₂ respectively. For the three different force fields studied in this work, the same approach was used to construct the six micelles and an identical protocol was applied in MD simulations. The aggregation numbers (N_det) was obtained by Dupuy et al.¹³ by fitting the scattering curves from SAXS and SANS experiments at a temperature of 297 K and a concentration range between 20 and 100 mM for monodispersed micelles. We should emphasize that the N_det values may depend on the experimental methods and on the concentration. For example, the N_det value for the β-C₁₂G₂ micelle used here is higher than the value of 98 found by Rosevear et al.⁷⁴ using gel filtration method, the value of 82 to 120 obtained by SAXS measurements²⁶ at 310 K, and the value of 111 ± 10 derived by Time Resolved Fluorescence Quenching (TRFQ) spectroscopy.⁷⁵ On the other hand, our N_det is well within the findings of others experiments, e.g. N_det = 125 ± 10 was reported using others TRFQ results at 4.89 - 19.6 mM, at 289 K - 333 K,¹⁴ whereas N_det = 135-145 was found by Lipfert et al.⁷⁶ by SAXS at 298 K. In case of α-C₁₂G₂ micelle, only one aggregation number has been reported in the literature, N_det= 75.¹³

The starting configurations of the two aggregates were constructed using the Packmol program.⁷⁷ This program created an initial starting point for MD by packing in the sphere N_det C₁₂G₂ molecules in their extended conformation, with the first carbon atom (C₇) of the alkyl chain, near the headgroup at ∼17 Å from the center of the micelle. This is larger than the total length (∼14.0 Å) of the DOD chain in an extended conformation obtained with the DS Visualizer v2.0 (Accelrys Inc., San Diego) modeling program. In this way, the number of ‘steric clashes’ for the terminal ethyl groups of the C₁₂G₂ alkyl chain is reduced. To remove other inter- and intra-molecular overlaps, additional stages of conjugate gradient minimization followed by MD equilibration in vacuum with a small time step were carried out. Following this step, the headgroups were randomized by running MD simulation of the aggregates at 450 K for 300 ps, with the surfactant tail kept fixed to their minimized conformation. From this point on, in all cases the systems were solvated by adding TIP3P water at standard density in a truncated octahedron cell, corresponding to a simple cubic primitive cell unit with parameters a=b=c and α=β=γ=109.472°. Given the two different N_det used in our study, we chose a=85 Å and a=95 Å for the simulations of the α- and β- anomers, respectively. These box sizes were chosen to ensure that all the molecular systems were within the experimental L₁ phase (i.e. < 45% in weight concentration),⁷⁵ and that there was a sufficient distance (∼15 Å) between the micelle surface and the edge of the box to minimize interactions with periodic images.⁷⁸ As shown in Table 1, where we provide the composition of the two simulated systems, the simulated concentrations of the detergent are near 0.3 M and 0.40 M for the α- and β-C₁₂G₂ anomers, respectively. This is higher than the surfactant concentration used in the experimental study of Dupuy et al. ¹³ (0.02 - 0.04 mol·L^-1) and higher than the critical micelle concentration (cmc) for the α- and for β-C₁₂G₂ (∼1.5.10^-4 mol.L^-1 and ∼2.0.10^-4 mol.L^-1, respectively) ^13,75 at temperature 298 K. Indeed, simulations near the cmc would require about 2000 times more water in the simulation system leading to a dramatic increase of the calculation time. Furthermore, in order to equilibrate the solvent molecules, the systems were run for 300 ps at 450 K, with the ensemble of the micelles atoms fixed to their initial positions. Then, the constrained micelle atoms were released and the system slowly heated from 0 K to 297 K in 300 ps as described in ref.79 Finally, the resulting conformations were simulated in the NPT ensemble (T = 297 K and P = 0.1 MPa) for 14 ns after discarding the initial 300 ps. MD snapshots were saved every 240 fs for subsequent analysis.

Table 1. Simulations parameters for the micelle simulations.

N_C12G2, N_H2O, and N_atm are the numbers of N-dodecyl-ß-D-maltopyranoside monomers (C₁₂G₂), water and atoms composing the simulated systems. m_C12G2/m_Tot is the weight concentration (in %) of C₁₂G₂ in each system. t_sim is the simulation time (the 300 ps equilibration period was excluded from the analysis).

System	α-C12G2	β-C12G2
NC12G2	75	132
NH2O	13771	18389
Natm	47388	65859
mC12G2/mTot	13.4	16.9
T (K)	297	297
tsim (ns)	14.0	14.0
ρ (g/cm3)	1.02 ± 0.01	1.03 ± 0.01

5. Molecular Dynamics

For all the simulations and analysis performed in this study, a serial and parallel versions of the ORAC code were used.⁸⁰ To simulate in the NPT ensemble, ORAC uses a method based on the extended system approach by adding extra (virtual) coordinates and momenta in the system to control the temperature and the pressure.^81-85 To integrate the equation of motion, a five time step r-RESPA integration scheme with a Liouvillean separation in three non-bonded shells, was used.⁸⁶ The procedure combines a Smooth Particle Mesh Ewald (SPME) to handle electrostatic interactions,⁸⁷ and the method of constraints to keep the covalent bonds involving hydrogen's at their equilibrium length.⁸⁸ The SPME parameters were chosen to maintain a relative error of less than 0.1 % on the electrostatic interactions for all the micelles. For this purpose, a convergence parameter α = 0.43 Å^-1, a fifth-order B-spline and a 96 grid point in each cartesian direction to take care of the SPME charge interpolation for each simulated system was used.

III. Results

First, we consider the general structure of the α- and β-C₁₂G₂ aggregates at different simulation times: t_sim≈ 0 fs, t_sim= 7.0 ns and t_sim=14.0 ns of the production period. Figure 2 (a-f) provides three snapshots for each type of C₁₂G₂ micelles taken from the CHARMM-Opt simulations; these results are representative of the other simulations described in this paper. Visual inspection of the figures shows that at the beginning of the run, the micelles have rougher surfaces with some glycolipid protrusions (see Figures 2(a) and 2(d)). Thus, the micelles present large solvent-exposed surfaces where the alkyl chains of the surfactant are exposed to the solvent (see below). However, after typically 2-3 ns of production, Figs. 2(b-c) and 2(d-e), the surfactants arrange themselves to form compact aggregates where a major part of the alkyl tails are buried and the surface is covered with the glycolipid headgroups. These pictures also show that the α- and β-C₁₂G₂ micelles are not perfectly spherical and that β-C₁₂G₂ micelle is more ellipsoidal than α-one (see below). This finding has been observed in the various MD simulations performed in this study, regardless of the force field. Finally, in contrast with previous simulations ^46,47 of octyl-β-glucoside micelles, the integrity of the micelles studied with the GLYCAM and CHARMM force fields is maintained all along our simulation time window (14 ns), and no surfactant molecules escaped from the micelle. This is consistent with previous experimental results obtained for alkyl-maltoside micelles where it was found that monomer exchange between micelle and the solvent is in the order of 0.1 to 1.2 μs.⁸⁹

Figure 2.

Representative MD Snapshots of the α- (a-c) and β-anomers (d-f) of C₁₂G₂ micelles simulated with the CHARMM-Opt force field at t≈240 fs (a, d), t≈7.0 ns (b, e) and (c, f) and t ≈14 ns of the production period. Oxygen and hydrogen are in red, and white colors. Carbons in GlcA, GlcB and in the alkyl chain are blue, cyan and gray respectively. Water molecules are removed for visual clarity. Figures were produced with the PyMOL program.¹²²

A. Size of the micelles

To examine the stability and to measure the dimensions of the micelle in the six runs, we have computed their instantaneous radii of gyration, R_g, over the course of the simulations (Fig. 3) using the following expression:

Figure 3.

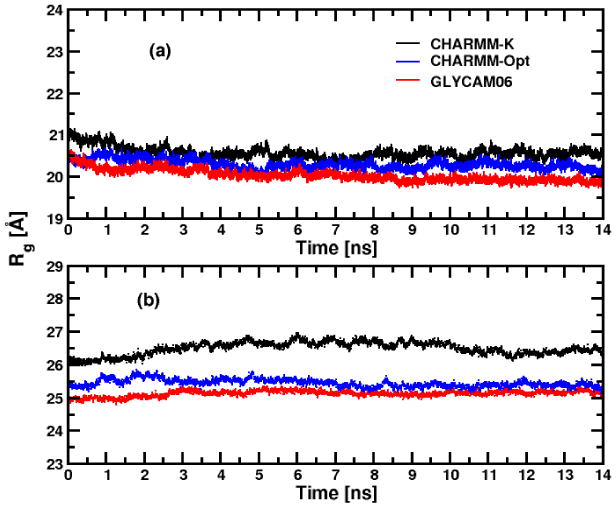
Time evolution of the radius of gyration, R_g, for α- (a) and β-anomers (b) of C₁₂G₂ micelles.

$${\text{R}}_{\text{g}}^2=\sum _{\text{i}}{\text{m}}_{\text{i}}{({\text{r}}_{\text{i}}-{\text{r}}_{\text{cm}})}^2/\sum _{\text{i}}{\text{m}}_{\text{i}}$$ (1)

Where m_i is the mass of the atom i of the micelle at the distance r_i from the center of mass r_cm. For all the micelles studied here, the R_g values are stable after typically ∼3 ns of production. As indicated previously, during the beginning of the productive run (i.e. between ∼ 0 and 3 ns time period), local arrangements and compaction of the surfactants on the micelle surfaces are observed. This feature was also observed in previous glycolipid micelle simulations.⁴⁷

The instantaneous R_g values for the α-C₁₂G₂ micelle in the three runs stabilizes after ∼ 3 ns around ∼20 -21 Å until the end of the trajectory. The average R_g values, 〈R_g〉, of the α-C₁₂G₂ micelles, computed from the last 11 ns of CHARMM-K, CHARMM-Opt and GLYCAM06 runs (20.5 ± 0.1 Å, 20.2 + 0.1 Å and R_g= 20.0 ± 0.1 Å, respectively) are close to the R_g experimental value (18.6 ± 0.6 Ź³ calculated from the semi-axis lengths of the micelle a_M, b_M and c_M and the expression ${\text{R}}_{\text{g}}^2=({\text{a}}_{\text{M}}^2+{\text{b}}_{\text{M}}^2+{\text{c}}_{\text{M}}^2)/5$ for an ellipsoid with an uniform density.⁷⁹ In the case of the β-C₁₂G₂ micelles, R_g reached stable values after ∼2.5–3 ns depending the force field used. In contrast to the α-C₁₂G₂ simulations, the three force fields lead to significant differences (up to 1.0 Å) for the instantaneous and averaged R_g, especially for the two CHARMM force fields versions. For β-C₁₂G₂, the 〈R_g〉 's are equal to 26.4 ± 0.1 Å, 25.4 ± 0.1 Å and 25.1 ± 0.1 Å, for the aggregates simulated with the CHARMM-K, CHARMM-Opt and GLYCAM06, respectively. The 〈R_g〉's obtained with the CHARMM-Opt and GLYCAM06 parameters are closer to the experimental value of 23.3 ± 0.6 Å.¹³

B. Shape of the Micelles

The micelle shape can be characterized by computing the instantaneous ellipsoidal axis ratio between the micelle major (a_M) and minor (c_M) semi-axis lengths, or a_M/c_M, obtained from the inertia tensors (see ref.79 for details). As shown in Figure 4, the six micelles present a stable ellipsoidal shape (i.e. a_M/c_M > 1.0) after typically ∼4.0 ns. For the α-C₁₂G₂ micelles, their shapes do not depend significantly on the force field. This contrasts with the behaviors of the β-C₁₂G₂ micelles where the ratio a_M/c_M shows a much larger fluctuations. To be consistent with the calculation of the R_g, the initial 3 ns of each trajectory were discarded in the calculation of a_M/c_M. The average values of the ratio, 〈a_M/c_M〉, are reported in the 7^th column of Table 2 for the different micelles studied. In our calculation, both α- and β-C₁₂G₂ are ellipsoidal, but α-C₁₂G₂ is the closest to the shape of a sphere. In the case of β-C₁₂G₂ aggregates, the instantaneous a_M/c_M values stabilize around ∼1.40 at the end of the simulations independently of the considered force field and the 〈a_M/c_M〉 values are close for the three micelles: 1.38 ± 0.03, 1.43 ± 0.01 and 1.38 ± 0.04 for CHARMM-K, CHARMM-Opt and GLYCAM06, respectively. In contrast, β-C₁₂G₂ micelles have a pronounced oblate shape (a_M>b_M≈c_M), which agrees well with the experimental observations.^13,26,75

Figure 4.

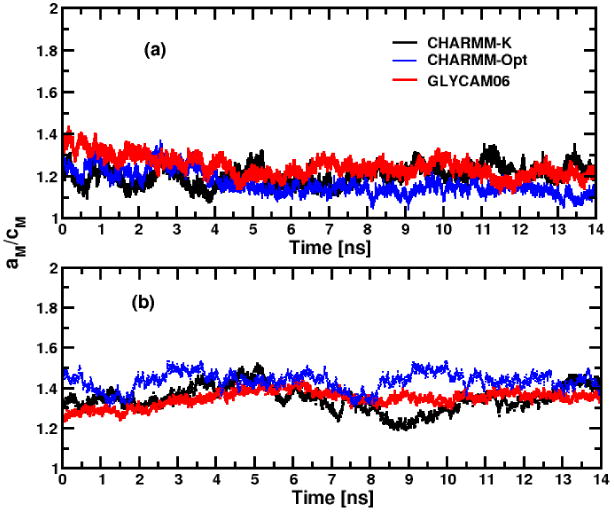
Time evolution of the major and minor semi-axis of inertia ratio for α- (a) and β-anomers (b) of C₁₂G₂ micelles.

Table 2. Average dimensions and shapes of the six micelles.

〈…〉 stands for the ensemble average. Values with M and HC subscripts were computed by including all the micelle atoms and those of the hydrophobic core, respectively. The radii of gyration and the semi-axis lengths were computed using the inertia tensor (e.g. see ref.79) and the main text for details. 〈l_pl〉 is the average polar layer thickness of the micelle in Å. The statistical errors (maximum errors) are always lower than 0.1 Å, 0.8 Å and 0.3 Å for the R_g, semi-axis lengths and polar layer thickness, respectively.

Force field	Micelle	〈Rg〉	〈aM〉	〈bM〉	〈cM〉	〈aM/cM〉	〈aHC〉	〈bHC〉	〈cHC〉	〈lpl〉
CHARMM-K	α-C12G2	20.5	28.4	25.6	23.8	1.20	22.1	19.1	16.5	6.7
	β-C12G2	26.4	38.8	34.7	28.1	1.38	33.1	27.3	20.0	7.2
CHARMM-Opt	α-C12G2	20.2	27.8	26.1	24.3	1.14	21.5	19.1	16.7	7.0
	β-C12G2	25.4	38.1	33.0	26.5	1.43	30.6	24.8	19.3	7.7
GLYCAM06	α-C12G2	20.0	28.4	25.5	23.1	1.23	22.3	18.6	16.5	6.5
	β-C12G2	25.2	37.2	32.0	30.1	1.38	30.1	24.4	19.2	7.2

However, we can underline that the 〈a_M/c_M〉 values for the β-C₁₂G₂ micelles remain, depending the force field between lower than the estimated experimental values (i.e. a_M/c_M =1.70 from Dupuy et al.).¹³ The instantaneous length values of the semi-axis of each micelle hydrophobic core (i.e. a_HC, b_HC and c_HC) have been also computed by including only the contributions from the surfactant hydrophobic chain in the calculations of the inertia tensors. The average values of the three semi-axes, (〈a_HC〉,〈b_HC〉 and 〈c_HC〉), are reported in the 8^th, 9^th and 10^th columns of Table 2. We find that the average major and minor semi-axis lengths 〈a_HC〉 and 〈c_HC〉 are in relative agreement with experimental values for α-C₁₂G₂ and β-C₁₂G₂ (i.e. 〈a_HC〉 =〈c_HC〉 = 18.6 Å ± 1.0 Å) and 〈a_HC〉 = 28.2 ± 1.0 Å and 〈c_HC〈 = 14.1 ± 1.0 Å, respectively).¹³ The average thickness of the polar outer layer, or 〈1_pl〉, computed by subtracting the semi-axis length of the hydrophobic core from those of the whole micelle (〈a_M〉,〈b_M〉 and 〈c_M〉), does not change significantly with the force field and is 6.7 ± 0.3 Å for the α-anomer of the C₁₂G₂ and increase up to 7.3 ± 0.4 Å for the β-anomer. Due to the partial folding of the maltose head, these values are 39.1 % and 33.4 % smaller than the calculated length of the maltose in its extended configuration (∼11.0 Å). The larger 〈1_pl〉 value for β-C₁₂G₂ is consistent with the fact that the β- anomer is linear and extends in the solvent, whereas α- is more folded, hence constrained on the micelle surface. In all cases, the 〈1_pl〉 values are within 1 Å of the experimental values estimated from SAXS and SANS experiments, i.e. 5.4 ± 0.1 Å and 6.2 ± 0.1 Å for α-C₁₂G₂ and β-C₁₂G₂, respectively.^13,76

C. Density profiles of the Micelles

To compare the spatial extent of the most relevant atomic group components of the micelles, we have computed their average radial mass density profiles ρ(r) as a function of the distance, r, of the group from center of mass (COM) of the micelle.⁷⁹ We discuss here the ρ(r) values obtained for the entire micelle (Micelle), the maltose headgroup (Maltose), the dodecane tail (DOD), the two maltose glucose rings (GlcA and GlcB), and the hydration water (H₂O). As previously discussed,⁷⁹ the non-spherical nature of the micelles will affect ρ(r) value to a certain extent, causing the broadening of these functions. ρ(r) values, averaged over the last 11 ns of each trajectory, are shown in Figure 5(a-b). The hydrophobic core ρ(r) profiles extend from 0 to ∼19.0 Å from the micelle COM, and present similar shapes regardless of the force field. For the hydrophilic maltose head, the ρ(r)'s present a strong peak with density maxima at 21.0 ± 0.5 Å and 25.0 ± 0.5 Å for the α- and β-C₁₂G₂ micelles, respectively. These values are close to those obtained previously for 〈R_g〉. We notice that the position of the main peaks for the GlcA and GlcB density profiles depend more strongly on the force field than that of the other groups studied here. Considering all the results, GlcA ρ(r)'s extend from 15.0 Å to 25.0 Å and from 18.0 Å to 28.0 Å for α- and β-C₁₂G₂ micelles, respectively. Larger values, of 1 to 2 Å, are found for all GlcB ρ(r) values. The water density profile in Fig. 5 shows that water molecules deeply penetrate into the micelle headgroup and solvates the maltose heads to a different degree with a preference for the outermost glucose ring (GlcA). We can also emphasize that water shares significant contact with the micelle hydrophobic core as seen by the intercepts of the water and DOD ρ(r) curves. Finally, the water ρ(r) curves reach their bulk density value (∼1.0 g/cm³) near the edge of the box at 35 Å (α-C₁₂G₂) and 38 Å (β-C₁₂G₂) from the micelle COM.

Figure 5.

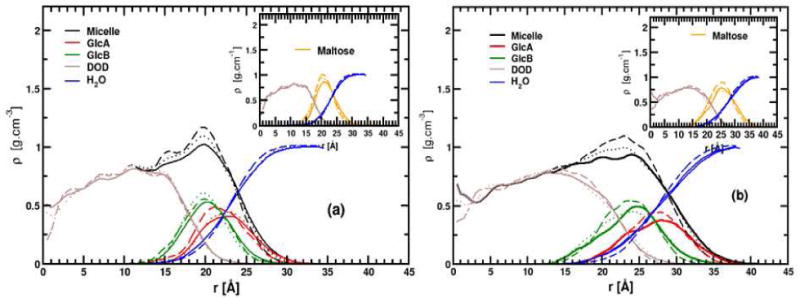
Average radial density profiles with respect to the center of mass (r = 0 Å) for simulations performed with CHARMM-K (continuous line), CHARMM-Opt (dotted lines) and GLYCAM06 force fields (dashed line) for micelles α- (a) and β-anomers (b) of C₁₂G₂ micelles. In the inset, the radial profiles for the micelle hydrophobic core (maroon), the maltose headgroup (orange) and water (blue) are plotted. A 0.5 Å bin width was used for both figures.

D. Hydration of the headgroup

As discussed in the previous section, radial mass density profiles show significant interaction between water and the C₁₂G₂ surfactant headgroups. To gain insights on this aspect, we provide in the Table 3 some surface area (SA) properties of the micelles computed from the last 11 ns of the simulations. We first compare the instantaneous value of the SA per surfactant headgroup (SA_HG^C12G2) with the results of Dupuy et al.¹³ obtained from SAXS and SANS experiments assuming that the α- and β-micelles are spherical. As described by these authors SA_HC^C12G2, the surface of the hydrophobic core of a sphere of radius R̄^HC was calculated. The average ellipsoid semi-axis of the micelle hydrophobic core 〈a_HC〉, 〈b_HC〉 and 〈c_HC〉 were used to calculate R̄^HCwith the expression: R̄^HC =(〈a_HC〉〈b_HC〉〈c_HC〉)^1/3. The average values of SA_HG^C12G2 ( $\langle {\text{SA}}_{\text{HG}}^{\text{C12G2}}\rangle$ are reported in the third column of the Table 3. We found that the $\langle {\text{SA}}_{\text{HG}}^{\text{C12G2}}\rangle$ values are in the range of 60.3 to 61.1 Ų and 55.5 to 65.1 Ų for the C₁₂G₂ α- and β-anomers, respectively. Values obtained with CHARMM-Opt and GLYCAM06 agree well with the experimental values (58 Ų and 52 Ų for the C₁₂G₂ α- and β-anomers, respectively), whereas the CHARMM-K results are further away.

Table 3. Surface properties of the micelles.

〈…〉 stands for the ensemble average. SA_HG^C12G2 (in Ų) are the average surface area per headgroup computed using the micelle oil core radius. SA_v^C12G2 and SA_e^C12G2 are the average micelle surfaces computed with the Voronoi polyhedron, ⁹⁰ assuming an ellipsoid-like geometry for the micelle. 〈f_tail〉 is the average surface fraction shared between the water and the C₁₂G₂ alkyl chain. The statistical errors (maximum errors) are always lower than 3.0 % and 0.2 % for the surfaces and 〈f_tail〉 values.

Force field	Micelle	$\langle {\text{SA}}_{\text{HG}}^{\text{C}12\text{G}2}\rangle$	$\langle {\text{SA}}_{\text{V}}^{\text{C}12\text{G}2}\rangle$	$\langle {\text{SA}}_{\text{e}}^{\text{C}12\text{G}2}\rangle$	〈ftail〉
CHARMM-K	α-C12G2	61.1	19425.0	9244.5	11.0
	β-C12G2	65.1	33237.6	16581.5	10.0
CHARMM-Opt	α-C12G2	60.4	17625.0	9013.2	10.9
	β-C12G2	56.8	29422.8	15894.6	9.3
GLYCAM06	α-C12G2	60.3	15675.0	9146.6	9.8
	β-C12G2	55.5	25726.8	15666.0	9.3

In the 4^th and 5^th columns of the Table 3 are reported the average surface areas (SA) for the whole micelles $\langle {\text{SA}}_{\text{V}}^{\text{C12G2}}\rangle$ and $\langle {\text{SA}}_{\text{e}}^{\text{C12G2}}\rangle$, respectively. The SA_v^C12G2 values were obtained from the Voronoi construction⁹⁰ by adding up the surface area of each Voronoi polyhedron shared between all surfactant atoms and water.⁹¹ Instead, $\langle {\text{SA}}_{\text{e}}^{\text{C12G2}}\rangle$ was the ellipsoidal surface of the micelle obtained from the average semi-axis lengths (〈a_M〉,〈b_M〉 and〈c_M〉) computed in section II.B. Comparison of the two values confirms that the micelle interfaces are corrugated (as also shown in Figure 1). Indeed, the surface rugosity factors f_s = SA_v^C12G2/SA_e^C12G2 was calculated between 1.7 and 2.1 and between 1.64 and 2.0 for the α- and β-anomers, respectively.

In the 6^th column of Table 3, we also provide the average C₁₂G₂ surface alkyl chain ratio of the micelles, 〈f_tail〉 in contact with the solvent. The 〈f_tail〉 values were calculated with the SA_v^C12G2 and the surface area of the alkyl chain atoms, SA_v^C12. 〈f_tail〉 values for all the micelles decrease by ∼1.0 % when the surfactant head changes from the α- to the β-anomer and are calculated between 9.8 and 11.1 % and between 9.3 and 10 % for the α- and β-anomers, respectively. The lower 〈f_tail〉 values of GLYCAM06 indicate that for those micelles the surfactant alkyl chains of the micelle are more protected from the solvent than those obtained in the simulations with the CHARMM force fields. In comparison, the 〈f_tail〉 values reported in this work are lower than those found by Stephenson et al.⁵¹ for a micelle with 45 β-C₁₂G₂ (∼17.0 %), and also lower than for micelles with 27 octyl-β-galactose⁴⁷ (∼30%) and 92 octyl-β-glucose monomers (20%).⁴⁶ The latter is probably due to the smaller size of the headgroup in those micelles, which shields less the micelle hydrophobic core from water.

The average number of water molecules, 〈n _w〉, in the first solvation shell of each surfactant, or hydration number, were also computed during the last 11 ns of each run. They are presented in Table 4. For each configuration, the hydration water molecules were selected using a simple cutoff radius criterion, as described in ref.92. Briefly, a water molecule is considered near the micelle surface if its distance with any of the detergent atoms is less than R_cut =f(R_w + R_C12G2), where R_w and R_C12G2 are the force field van der Waals radii of the water and of the C₁₂G₂ atoms, respectively, f is a parameter set arbitrarily to 1.1 in our calculations.⁹² Five hydration numbers were calculated here: for the whole C₁₂G₂ molecule $(\langle {\text{n}}_{\text{w}}^{\text{C12G2}}\rangle )$, for the headgroup $(\langle {\text{n}}_{\text{w}}^{\text{G2}}\rangle )$, for the GlcA $(\langle {\text{n}}_{\text{w}}^{\text{GlcA}}\rangle )$ and GlcB $(\langle {\text{n}}_{\text{w}}^{\text{GlcB}}\rangle )$ units and for the alkyl chain $(\langle {\text{n}}_{\text{w}}^{\text{C12}}\rangle )$. For all 〈n_w〉 's, higher values are found for the simulations obtained with CHARMM-K, whereas the〈n_w〉's of CHARMM-Opt and GLYCAM06 simulations are close to one another. The $\langle {\text{n}}_{\text{w}}^{\text{G2}}\rangle$ value for CHARMM-Opt and GLYCAM06 are computed around 8.2 - 7.2, respectively, and compare well with the estimation of $\langle {\text{n}}_{\text{w}}^{\text{C12G2}}\rangle$ obtained from SANS, SAXS (8.0)¹³ or TRFQ experiments for β-C₁₂G₂ micelle (7.9).⁷⁵ The bent conformation of the α-C₁₂G₂ slightly increases the headgroup hydration by 0.4 - 0.6 waters for the micelles simulated with the CHARMM-Opt and GLYCAM06 parameters, whereas for CHARMM-K the $\langle {\text{n}}_{\text{w}}^{\text{G2}}\rangle$ decreases by 0.3 units. For maltose molecules in water, hydration numbers between 5.7 and 22.6 are estimated by experimental studies, whereas values within 6.5 - 14.5 are obtained from computer simulations (see Table 3 of ref.33 and references therein). The validity of these results depends on the experimental techniques or the force field considered. Comparison of the hydration of the glucose rings GlcA and GlcB show that the number of water molecule around GlcB, connected to the alkyl chain, is, on average, ∼2.6 units lower than for GlcA. This is independent of the force field employed and the conformation of the headgroup. Finally, the low values for $\langle {\text{n}}_{\text{w}}^{\text{C12}}\rangle$ (< 1.0 water) confirm that the micelle hydrophobic core have only sporadic contacts with the solvent consistently with the 〈f_tail〉 value calculated in this work.

Table 4. Hydration numbers.

〈…〉 stands for the ensemble average. $\langle {\text{n}}_{\text{w}}^{\text{G}2}\rangle$, $\langle {\text{n}}_{\text{w}}^{\text{GlcA}}\rangle$, $\langle {\text{n}}_{\text{w}}^{\text{GlcB}}\rangle$, $\langle {\text{n}}_{\text{w}}^{\text{C}12}\rangle$ and $\langle {\text{n}}_{\text{w}}^{\text{C}12\text{G}2}\rangle$ give the average number of water molecule at 4.0 Å of the maltose head, the outermost and innermost glucose rings and the alkyl chain, respectively. The statistical errors (maximum errors) are always lower than 0.1 %.

Force field	CHARMM-K		CHARMM-Opt		GLYCAM06
System	α-C12G2	β-C12G2	α-C12G2	β-C12G2	α-C12G2	β-C12G2
$\langle {\text{n}}_{\text{w}}^{\text{G}2}\rangle$	8.3	8.6	8.2	7.6	7.6	7.2
$\langle {\text{n}}_{\text{w}}^{\text{GlcA}}\rangle$	5.2	5.6	5.2	5.1	4.7	4.9
$\langle {\text{n}}_{\text{w}}^{\text{GlcB}}\rangle$	3.1	3.0	3.0	2.5	2.9	2.3
$\langle {\text{n}}_{\text{w}}^{\text{C}12}\rangle$	0.8	0.8	0.8	0.7	0.6	0.6
$\langle {\text{n}}_{\text{w}}^{\text{C}12\text{G}2}\rangle$	9.1	9.4	9.0	8.3	8.2	7.8

To further examine the headgroup hydration, in Table 5 we provide the average number of nearest water for each maltose-oxygen, or 〈n_Ox−Ow〉, obtained from the computed radial pair density functions (RDF) of the maltose-oxygen (O_1-10) and water-oxygen (O_w) atoms. To obtain 〈n_Ox−Ow〉 the RDF functions were integrated until the first minimum at r ≈ 3.5 Å after the first peak. The 〈n_Ox−Ow〉 results indicate that water molecules solvate primarily the hydroxyl oxygen atoms (O₁, O₂, O₃, O₄,O₆, O₈, O₉ and O₁₁) of the maltose headgroup. This is consistent with previous simulation studies performed on other glycolipid micelles.^44,46,47 The number of water molecules in the first shell of these atoms are found between 1.9 and 3.7 as a function of the oxygen localization on the headgroup. These values vary little with the force field employed and the surfactant conformation. In general, the higher 〈n_Ox−Ow〉 values are obtained for the oxygen atoms O₃ (2.9 - 3.4) and for O₆ (3.2 - 2.4), the most the atoms are exposed to the solvent in GlcA. As an example, the hydroxyl oxygen O₁₁ in GlcB has about one water molecule in its first shell that the equivalent atom O₆ in GlcA. The hydration of the ring oxygen atoms O₅ and O₁₀ of GlcA and GlcB does not change much (∼0.3 water) when the surfactant conformation changes from the α- to β-anomer. Finally, for the oxygen atoms involved in the glycosidic bond (O₁) and the link between the headgroup and alkyl chain (O₇), present low〈n_Ox−Ow〉 values (< 0.8 and < 0.5) indicating that these oxygens are shielded from the solvent. This result is also consistent with another study, ⁴⁶ where a 〈n_Ox−Ow〉 value close to 0.2 – 0.3 for O₇ was observed.

Table 5. Nearest neighbors for the micelle oxygens.

The micelle oxygen atoms are labeled as it followed: O₁ and O₇ are the acetalic oxygens, O₅ and O₁₀ are the maltose ring oxygens and all the remaining are hydroxyl oxygens (see Figure 1). Also, Δ_β-α is the difference in the average number of nearest neighbors between the β- and α-anomers. The values have been obtained by integrating the O_x-O_w pair correlation functions g(r) up to the first minimum at around r≈3.5 Å. Total GlcA and Total GlcB give the average nearest neighbors for the outermost and innermost glucose unit of the molecule, respectively.

Force field	CHARMM-K			CHARMM-Opt			GLYCAM06
〈nOx−Ow〉	α-C12G2	β-C12G2	Δα→β	α-C12G2	β-C12G2	Δα→β	α-C12G2	β-C12G2	Δα→β
O1-Ow	0.7	0.8	0.1	0.5	0.5	0.0	0.5	0.4	-0.1
O2-Ow	2.3	2.7	0.4	2.5	2.3	-0.2	2.1	2.6	0.5
O3-Ow	3.6	3.7	0.1	2.9	3.2	0.3	3.0	3.4	0.4
O4-Ow	2.0	2.6	0.6	2.3	2.6	0.3	1.9	2.4	0.5
O5-Ow	1.1	1.3	0.2	1.3	1.0	-0.3	1.3	1.0	-0.3
O6-Ow	3.1	2.5	-0.6	2.6	2.3	-0.3	3.2	2.4	-0.8
Total GlcA	12.8	13.6	0.8	12.1	11.9	-0.2	12.0	12.2	+0.2
O7-Ow	0.2	0.5	0.3	0.3	0.3	0.0	0.2	0.4	0.2
O8-Ow	2.4	1.9	-0.5	1.9	1.6	-0.3	1.7	1.5	-0.2
O9-Ow	2.4	2.0	-0.4	2.2	1.8	-0.4	2.2	1.6	-0.6
O10-Ow	0.8	0.9	0.1	0.7	0.6	-0.1	0.6	0.8	0.2
O11-Ow	2.0	1.7	-0.3	1.7	1.6	-0.1	1.8	1.3	-0.5
Total GlcB	7.8	7.0	-0.8	6.8	5.9	-0.9	6.5	5.6	-0.9

Considering the strong interaction between the C₁₂G₂ headgroup atoms and water, it is clear that the headgroup oxygen atoms will form an extended network of hydrogen bonds with water molecules and with donor groups of the detergent themselves.⁹³ The average number of HB between water molecules and the maltose headgroup (WHB) and within the surfactant headgroups (HHB), were computed for the last 11 ns of the simulations, using the following geometrical criterion: a HB was considered if the oxygen-oxygen distance equals or is smaller than 3.5 Å and the angle O-H…O was between 120 and 180°.⁹⁴ These values are reported in Tables S4, S5 and S6 of the supplementary information. We observed that each α-C₁₂G₂ molecule presents 0.5 - 1.0 more WHB than the β-anomer. These values vary only slightly with the force fields, CHARMM-K having the largest number of HB in α-C₁₂G₂ followed by CHARMM-Opt and GLYCAM06. This result is in agreement with small variations of hydration water in the first shell of the C₁₂G₂ headgroup and the decrease of 〈n_Ox−Ow〉 reported in the previous paragraph. We found that each C₁₂G₂ headgroup makes, on average, ∼1.5 times more in the establishment of HB as an acceptor (∼7.0) than as a donor (∼5). This is consistent with previous computer simulations studies of C₈G₁ and C₈Gal in water.⁴⁷ As also expected the total number of WHB obtained in this work is lower than the total WHB found for maltose in TIP3P water where the number of WHB (∼15.9 and 22.4).^27,32 Further analysis of the individual HB donors and acceptors shows that the O₃ and O₆ (GlcA) and O₈ and O₉ (GlcB) hydroxyl oxygens make about one additional HB with water than the other oxygens. For these same oxygens, the number of WHB decreases by ∼0.2 when the headgroup changes from the α- to the β-anomer. Finally, due to the strong entanglement of the maltose head at the micelle surface and to the low hydration of some of the hydroxyl oxygen atoms, it is expected that a large network of inter- and intra- headgroup donor/acceptor HB (INHB and INTHB, respectively) will be favored. Several inter-headgroup HB have been computed (among these previously examined by Chong et al.⁴⁷) and are reported in the 5^th to 9^th columns in Tables S4, S5 and S6 in the supplementary information. The number of INHB is found to be much lower than the number of solvent-headgroup HB. On average, there are ∼0.10 and ∼0.25 HB per lipid for structures obtained from the CHARMM and GLYCAM force field simulations, respectively. The number of INHB is greater in β-C₁₂G₂ micelles and is due to the O₆-H…O₄, O₈-H…O₁₀ and O₈-H…O₉ HB. Furthermore, three other INTHB were previously observed (O₆H₆…O₅ and O₁₁H₁₁…O₁₀ in the first and second glucose rings and O₂H₂…O₉ between GlcA and GlcB).^27,28,94 These HB are correlated with the rotational freedom of the ω torsion angles and the α(l→4) glycosidic linkage flexibility. Our calculations indicate that these HB types exist during all of the simulations. In particular, O₂H₂…O₉ is present during approximately 70 - 80 % of the simulation times, whereas the two others INTHB only ∼30 - 40 % of the time.

E. Conformation of the Surfactant

To examine in more detail the hydration differences of the micelles, we have studied the surfactant conformation by computing the main peak of the average end-to-end distance probability distributions P(r). Specifically, we have computed the d_C12 and d_G2 by collecting from the trajectories the distances between the atoms C₇ and C₁₉ of the alkyl chain and between the O₄ and O₁₂ of the maltose head, respectively. Since the d_C12 and d_G2 end-to-end distances are strongly related to the conformations of the alkyl tail and headgroup of the surfactant, respectively, we have examined the conformation of several characteristics torsion angles of the tail (such as all the CCCC dihedral angles, the first C₇C₈C₉C₁₀, and last C₁₅C₁₆C₁₇C₁₈ dihedrals)⁴⁴, the torsion angles involved in the connection of the alkyl chain and the maltose head (i.e. O₇C₇C₈C₉ ⁴⁴, O₁₀C₁O₇C₇^27,95, C′₁O₇C₇C₈^28,96) and ω1 and ω2 angles (i.e. O₆C₆C₅O₅⁹⁵ and O₁₁C₆C₅O₁₀⁶⁴) by computing the corresponding normalized dihedral angle distribution P(ϕ). These functions were computed and averaged over the last 11 ns of each run. The relative gauche^+- (p_g^+-) and trans (p_t) populations were also extracted and are presented in Table 6. P(r) functions for the two CHARMM simulations (not shown here) display similar shapes with a strong peak at d_C12 ≈12.3 Å for all the micelles regardless of the surfactant headgroup anomer. This is ∼10.9 % smaller than the value (∼14.0 Å) calculated for an extended dodecane chain with the modeling program Discovery Studio Visualizer. In contrast to the CHARMM results, the alkyl tail P(r) functions for the two micelles simulated with GLYCAM06 parameters present two peaks at d_C12 ≈ Å and d_C12 ≈ 13.8 Å (figures not shown) indicating a coexistence of two populations for the alkyl chain length. In the literature, a smaller value for d_C12 is strongly related to the partial folding of the hydrophobic chain in the micelle core and existence of “gauche defaults”.^97,98 In this context, we found that the CCCC dihedral angles of the alkyl chain are mostly in their trans state with relative populations p_t close to 72.0 % and 84.6 % for the CHARMM and GLYCAM06 force fields, respectively. These results are consistent with previous simulations of micelles containing surfactant with a dodecane chain (see for instance refs 99^{, 100, 59}). As for the CHARMM simulations, the peaks in P(r) peaks do not change much (< 1 %) when going from an axial (α-) to an equatorial (β-) conformation of the surfactant headgroup (see Table 6). Further investigation shows that the outermost and innermost CCCC dihedral angles (i.e. C₇C₈C₉C₁₀ and C₁₅C₁₆C₁₇C₁₈) have a larger gauche^+- population, p_g+-≈ 27 %, than the others dihedrals in the alkyl chain, p_g+-≈15 %. Similar results were found in previous MD simulations of octyl-β-glucoside micelles⁴⁴, where the lower steric conflicts found at the extremities of the alkyl chains decrease the gauche conformation of the chain. Finally, we find only small differences, less than 12 % in p_t, in the CCCC angles between the CHARMM and GLYCAM06 simulations. Similar behaviors were obtained in simulations of LDAO micelles simulated with the CHARMM27 and AMBER94 force fields, p_t ≈ 71.0 % and p_t≈ 82.8 %, respectively.¹⁰¹

Table 6. Trans and Gauche populations.

Dihedral angles between -180° and -120°, between -120° and +120° and between +120° and +180° are defined as gauche⁺ (p_g⁺), trans (p_t) and gauche^- (p_g^-), respectively. The exponents a, b and c are for ^agauche^+-, ^bgauche⁺ and ^cgauche^-, respectively. The statistical errors (maximum errors) are always lower than 0.3 %. See the main text for details.

Force field	CHARMM-K		CHARMM-Opt		GLYCAM06
Micelle	α-C12G2	β-C12G2	α-C12G2	β-C12G2	α-C12G2	β-C12G2
CCCC	71.8, 28.2a	72.0, 28.0a	71.4, 28.6a	72.1, 27.9a	84.6, 15.4a	84.7, 15.3a
C7C8C9C10	67.4, 32.6a	70.9, 28.1a	66.7, 33.3a	67.7, 32.3a	82.0, 18.0a	80.0, 20.0a
C15C16C17C18	73.3, 26.7a	75.4, 24.6a	70.8, 29.2a	68.5, 31.5a	81.0, 19.0a	82.8, 17.2a
O7C7C8C9	80.5, 20.5a	80.6, 20.4a	54.4, 46.6a	53.3, 47.7a	61.8, 38.2a)	63.0, 37.0a
O10C′1O7C7	2.3, 97.7b	0.1, 99.9c	0.5, 99.5b	4.9, 95.1c	2.4, 97.6b	6.7, 93.3c
C′1O7C7C8	90.1, 8.9a	89.1, 10.9a	71.7, 28.3a	76.4, 23.6a	81.7, 18.3a	78.1, 11.9a
O6C6C5O5 (ω1)	59.0b, 43.7c	59.3 b, 39.4c	60.9b 35.0c	51.6b, 39.3c	51.7b, 44.7c	50.9b, 44.5c
O11C6C5O10 (ω2)	24.5c, 75.3c	37.0 b, 54.4c	36.7b, 60.0c	29.9b, 26.7c	30.9b, 65.9c	37.1b, 53.9c

In our simulations, the O₇C₇C₈C₉ dihedral angle remain in a trans state, in agreement with previous simulations of octyl-β-glucoside micelles.⁴⁴ Nevertheless, we found that CHARMM-Opt has a p_g+- 25 % smaller than that of CHARMM-K, closer to GLYCAM06 and in agreement with QM/MM calculations carried for the α- and β-anomers of maltose.⁶⁷ For the O₁₀C₁′O₇C₇ (Φ) dihedral angle we observed that for all the simulations, this angle is in gauche⁺ (> ∼ 90 %) for the α- and β-anomers. Also, our results show that for all the micelles the Ψ dihedral angle, C₁′O₇C₇C₈, is always found in a trans state. Compared to CHARMM-K, in CHARMM-Opt the p_t of this angle decreases by ∼13 units to 18 % depending on the anomer, and is closer to the values obtained for the GLYCAM force field.

In the last two rows of Table 6, we have listed for all the simulations, the average relative population of the two ω dihedral angle in the reducing (GlcA) (ω₁ = O₆C₆C₅O₅) and non-reducing (GlcB) (ω₂ = O₁₁C₆′C₅′O₁₀) glucose units of the maltose head. In glucopyranose, due to rotational freedom of the ω dihedral angle, three stable conformers exist, defined by the position of the OH oxygen relative to oxygen ring atoms (here, O₅ and O₁₀), termed gauche-gauche (gg), gauche-trans (gt), and trans-gauche (tg) which correspond to ω= -60°, -60° and 180°.^{102, 103,104} Computational results on maltose have shown that ω has a strong preference for gauche values.^58,105 This is due to steric repulsions between the hydroxyl groups in position 4 and 6, described as the “gauche effect”.¹⁰⁶

In contrast to maltose in vacuum, where the ω angle adopts preferentially a gt conformation, for maltose in solution, MD simulations performed in condensed phase^28,37 and experimental studies¹⁰⁷ have shown that the gg conformation is favored, Our results for CHARMM-K and CHARMM-Opt show a different behavior for ω, for which the conformation gt is favored with respect to gg (gt/gg ≈60:40). For GlcB, we find that these angles are mainly in its gg conformation except for the β- anomer where ω₂ highly similar gg and gt populations. These results, can be explained by the incomplete hydration of the maltose headgroup in the detergent and the existence of inter maltose HB.

Turning our attention to the maltose head linkage conformation, the P(r) functions (not shown here) present peaks at d_G2 ≈ 8.8 Å (α-anomer) and d_G2≈ 9.8 Å (β-anomer). These values change slightly (0.2 Å) with the potential employed and are smaller than the length for a maltose molecule in an elongated conformation (10.3 Å, with Φ_H = Ψ_H = 0.0°). On Figure 6, we have plotted the distribution maps of the P(Φ_H,Ψ_H) glycosidic dihedral angles pair in population percentage for all simulations. We find that, except for the α-C₁₂G₂ micelle simulated with the new CHARMM potential, all of the P(Φ_H,Ψ_H) present a compact elliptic shape with a maximum point near (-40°, -25°) ± 10°. In the former system, instead, two areas are sampled, around (-25°; -20°) and (-65°; -50°), for 70 % and 30 % of the total simulation time, respectively. It is difficult to validate these results, as no experimental data exist in the literature for P(Φ_H,Ψ_H) of C₁₂G₂ micelles and these results differ for a maltose molecule in water where experimental (such as NMR^{32,38,108,109} or optical rotation ¹¹⁰) and theoretical studies (such as QM^38,111,112 and MD ^{28,32,37,69,113}) predicted two peaks for P(Φ_H,Ψ_H) around (-50°; -30°) ± 20° and (-40°; -30°) ± 20°.

Figure 6.

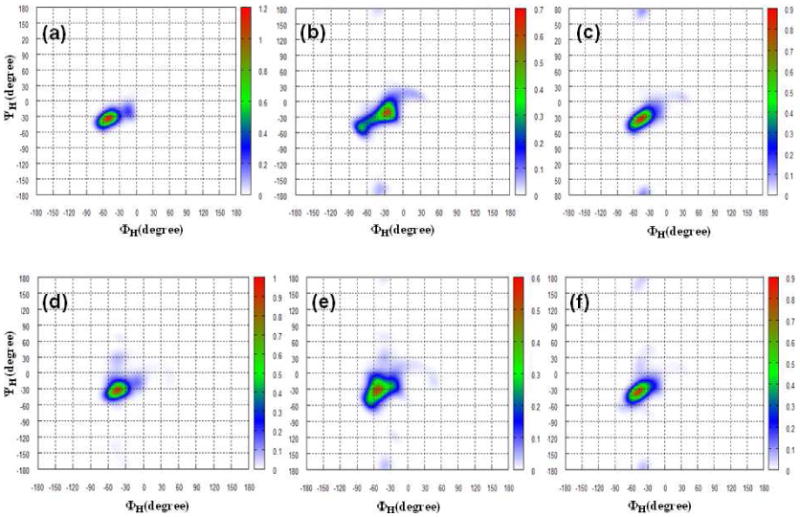
Distribution map of the Φ_H/Ψ_H glycosidic dihedral angles pairs in population percentage for α- (a) and β-anomers (b) of C₁₂G₂ micelles for the CHARMM-K ((a) and (d)), CHARMM-Opt ((b) and (e)) and GLYCAM06 ((c) and (f)) force fields, respectively. The grid interval is 5.0° and contour lines are spaced every 0.2 %.

F. Water Dynamics at the Micelle Surface

To examine the dynamic behavior of water molecules around the micelles, we have computed the mean square displacement (MSD) of the translational diffusion 〈|r(t) − r(0)|²〉 for water molecules at the micelle surface. Water molecules included in this calculation were at a distance of less than 4.0 Å from any detergent molecule at a given time of the trajectory (details about the calculation are available in ref.47). For the different micelles studied in this work, the MSD functions are shown in Figure 6 and the translational diffusion parameters are reported in Table 7. MSD functions are compared with the results obtained from a NPT simulation (T = 297 K and P = 0.1 MPa) for 1000 TIP3 water molecules simulated in a cubic box for 1 ns. As shown previously for water molecules near protein surfaces ^114,115, direct micelles^116,117 or reverse micelles^79,118 the water MSD presents a sub-diffusive regime and can be fitted with a power law (i.e. 〈|r(t) − r(0)|²〉 ∝ t^θ) rather than a linear dependence in time as observed in bulk water. This behavior is assumed to be the consequence of the geometric/energetic disorder found at the micelle and protein surfaces.¹¹⁴ For all micelles, the fit to a power law leads to similar values for θ, around 0.34 and 0.40. These values are comparable to the θ values found previously by one of us (MM) for water around the C₁₂E₆ micelle surface (0.3 and 0.4 at T = 283 K and 318 K, respectively).¹¹⁷ In this micellar system, it has been shown that the water interact with the long hydrophilic ethylene oxide (EO)₆ chain through a large hydrogen bonds network.¹¹⁹ For a subdiffusive regime, it is useful to define a rough estimate of the water residence time, τ_w, as the time needed by a water molecule to cover a distance of 9 Ų, i.e. corresponding to a path spanning a water molecular diameter.¹²⁰ The ratio, between τ_w and the residence time of the bulk water values (τ_w^b = 2.7 ps) are reported in the 4^th and 5^th rows in Table 7. We find that the τ_w values change significantly with the force field employed, but not with the surfactant headgroup conformation. τ_w values are calculated for all the simulations between 18.9 and 30.5 ps. In the GLYCAM06 simulations, water dynamic retardation, or τ_w^b/τ_w, are ∼ 11.3 for the α- and 11.7 for the β-anomers. The differences obtained for water diffusion is probably the results of the headgroup conformation variations and the number of trapped water at the micelle interface for the six micelles.

Table 7. Translational diffusion of the hydration waters.

θ is the dispersion regime parameter obtained by fitting the 〈|r(t) − r(0)|²〉 function to t^θ. τ_w is the water residence time, defined as the time (in ps) for a water to cover a distance equal to its own diameter (i.e. 3 Å) and τ_w/τ_w^b is the retardation or the ratio between the water residence time in the micelle and the bulk.

Force field	CHARMM-K		CHARMM-Opt		GLYCAM06
System	α-C12G2	β-C12G2	α-C12G2	β-C12G2	α-C12G2	β-C12G2
θ	0.39	0.40	0.34	0.36	0.38	0.35
τw (ps)	18.9	18.3	24.8	24.8	27.2	30.5
τw/τwb	6.7	6.5	8.5	8.5	11.7	11.3

To the best of knowledge, no experimental data on water dynamics are available for C₁₂G₂ micelles. Notwithstanding, Chong et al.⁴⁷ have computed the residence time of water near each headgroup oxygen atoms for micelles of octyl-glucose (C₈G₁) and galactose (C₈Gal). The authors found that τ_w maximum values are between 41.0 - 164.0 ps (C₈G₁) and 28.4 ps - 88.0 ps (C₈Gal) depending the localization of the hydroxyl group in the headgroup and the cutoff employed. The largest τ_w values are found for water molecules trapped within the crevices and clefts at the micelle surface. Finally, the τ_w values obtained here largely exceed the average residence time found by MD for water in the first shell of maltose (∼11.6 ps) in water ³¹ or in QENS experiments at 320 K (∼3.4 ps).¹²¹

IV. Conclusion

In this paper, we have presented the development of two new potential models, based on the CHARMM36 and GLYCAM06 force fields, to be used in the molecular modeling of the α- and β-anomers of C₁₂G₂ GL. These surfactants are widely employed to extract and solubilize membrane proteins. To validate these potentials, we have investigated the structure of significant C₁₂G₂ micelles by MD simulations. In particular, we have studied the structural properties of the micelles with the two anomeric forms, and described the dynamical properties of water molecules at the micelle/water interface. The results obtained for the new potentials were also compared with those obtained with older parameters developed for carbohydrate for CHARMM22.

We found that the three force fields studied here lead to different results particularly for the properties related to the headgroup conformation and micelle hydration. In particular, our calculations show that the α- and β-C₁₂G₂ micelles have a 〈R_g〉 close to 20.2 Å and 25.4 Å, respectively. The computed 〈R_g〉's agree reasonably well with SAXS and SANS experiments¹³ when the micelles are simulated with the new parameters developed for CHARMM36 CHARMM and GLYCAM06.

Concerning the global shape of the micelles, we observed no significant differences between the three force fields and the different micelles studied. The α-C₁₂G₂ micelles have an average major-to minor semi-axis ratio 〈a_M/c_M〉 close to 1.20 whereas the β-C₁₂G₂ micelle has a more pronounced oblate shape with 〈a_M/c_M〉 values around 1.38 - 1.43, in qualitative agreement with published experimental observations.^13,26,75 The computed radial density profiles indicate that water penetrates deeply at the micelle headgroup and hydrates preferentially the outermost glucose ring (GlcA). Due to the difference in the surfactant headgroup conformations, we also observed slight differences in the headgroup hydration. Consistently with previous simulations carried out with others glycolipid systems,^44,46,47 we found that the micelle/water interfaces are highly corrugated with a rugosity factor values around 1.6 - 2.0. The average solvent surface area for the α- and β-C₁₂G₂ anomers simulated with CHARMM-Opt and GLYCAM06 are found to be around 60.6 Ų and 55.5 Ų per molecule, respectively, which is close to experimental values.¹³

Concerning micelle hydration, we found that the alkyl chains of C₁₂G₂ are in all the cases sturdily protected from the solvent, as less than ∼10% of the water penetrate the micelle core. Due to the strong entanglement of the maltose head at the micelle surface, within each micelle we observed a large hydrogen bond network consisting in a complex combination of inter- and intra-HB between adjacent headgroups. HB between water and headgroups do not depend on the headgroup conformation, as we found a highly similar patterns for headgroup/water HB's for both α- and β-anomers (with only on average ~0.6 units of difference).

Finally, investigations of the dynamic behavior of the hydrating water for all the micelles show that the water translational diffusion is strongly retarded with respect to the bulk by a factor of 7.0 to 11.7, depending on the potential. Interestingly, the headgroup conformation does not affect the water diffusion for the three force fields examined here. In particular, water diffusion results near the micelle interface are similar for CHARMM-Opt and GLYCAM06 (∼ 8.5 and ∼ 11.7 smaller than for the bulk, respectively) and are ∼1.5 time larger than the diffusion values obtained in CHARMM-K based simulations

In conclusion, the molecular modeling and simulation results reported in this paper are a first and necessary step to improve our atomic level knowledge of the C₁₂G₂ micelles. In addition, because our potential parameters are consistent with two major protein force fields (CHARMM and AMBER) they offer a solid starting point for further studies on the interaction and aggregation of membrane proteins with C₁₂G₂ detergents.

Figure 7.

Interfacial water mean square displacement (MSD) as function of time for α- (continuous line) and β-anomers (dotted line). The black dashed line gives the distance for computing the residence time τ_w (see the main text).