Determination of the Optimal First-Order Gradient Moment for Flow-Sensitive Dephasing Magnetization-Prepared 3D Non-Contrast MR Angiography

Abstract

Flow-sensitive dephasing (FSD) magnetization preparation has been developed for black-blood vessel wall MRI and non-contrast MR angiography (MRA). The first-order gradient moment, m₁, is a measure of the flow-sensitization imparted by an FSD preparative module. Determination of the optimal m₁ for each individual is highly desirable for FSD-prepared MRA. This work developed a 2D m₁-scouting method that evaluates a range of m₁ values for their effectiveness in blood signal suppression in a single scan. The feasibility of employing the 2D method to predict blood signal suppression in 3D FSD-prepared imaging was validated on a flow phantom and the popliteal arteries of 5 healthy volunteers. Excellent correlation of the blood signal measurements between the 2D scouting and 3D FSD imaging was obtained. Therefore, the optimal m₁ determined from the 2D m₁-scouting scan may be directly translated to 3D FSD-prepared imaging. In vivo studies of additional 10 healthy volunteers and 2 patients have demonstrated the proposed method can help significantly improve the signal performance of FSD MRA, indicating its potential to enhance diagnostic confidence. Further systematic studies in patients are warranted to evaluate its clinical value.

INTRODUCTION

Flow-sensitive dephasing (FSD) magnetization preparation based on a driven equilibrium Fourier transform sequence was initially designed for imparting diffusion sensitization (1,2). It was later employed to suppress intravascular signal in perfusion MR imaging (3), vessel wall imaging (4-6), and cardiac imaging (7). More recently, an FSD-prepared balanced steady-state free precession (bSSFP) technique was developed for three-dimensional (3D) non-contrast (NC) MR angiography (MRA) of peripheral arteries that also relies on the FSD’s black-blood effect (8,9). The underlying mechanism of this effect is intravoxel phase dispersion of moving spins with different flow velocities along the FSD’s sensitizing direction (10).

Flow sensitization imparted by the FSD preparation is essential for the NC MRA technique, and its strength can be measured by the first-order gradient moment denoted as m₁ (6,8). As indicated in our previous studies (8), an unnecessarily large m₁ value may entail signal contamination from venous blood and, potentially, other static background tissues due to the associated diffusion effect, whereas incomplete delineation of arterial segments may result from an inadequate m₁ value. Consequently, a suboptimal m₁ tends to cause poor image quality, overestimation of stenosis, or false diagnosis in FSD MRA.

The optimal m₁, however, is subject and artery specific since dephasing of flowing spins is not only dependent on the m₁ of the FSD preparation but also on the local flow velocity profile (8,10). To obtain a satisfied MR angiogram, repeating FSD MRA with different m₁ values is time-consuming and impractical owing to 3D acquistions. An empirical m₁ value derived from a pilot study can be advantageous but might not work reliably for some clinical cases with complicated flow patterns. Therefore, an m₁ individually-tailoring procedure would be highly desirable.

The goal of this work was to develop a two-dimensional (2D) m₁-scouting method that can rapidly assess a range of m₁ values at their effectiveness in blood signal suppression and thus facilitate determination of an optimal m₁ value for FSD-prepared 3D NC MRA. Our focus was first on validating a theoretical basis, namely the predictive relationship between 2D m₁-scouting and 3D FSD MRA scans with respect to individual m₁’s blood signal-suppressing performance. The utility of the proposed method for improving imaging quality of FSD MRA was then demonstrated through signal comparison with the studies that simply used an empirical m₁ value.

THEORY

An FSD preparative module for blood signal suppression consists of a spatially nonselective RF pulse series (90°_x-180°_y-90°_−x), symmetric magnetic field gradients (referred to as FSD gradients hereafter) applied around the 180°_y RF pulse in the readout, phase encoding, and/or slice-select directions, respectively, and spoiler gradients applied right after the 90°_−x RF pulse (Fig. 1). A phase shift ϕ is introduced to moving spins by applied FSD gradients. For a single isochromat of spins with a velocity of $v\left(\overrightarrow{r}\right)$, ϕ can be expressed as

$$\varphi =\gamma \cdot v\left(\overrightarrow{r}\right)\cdot \int G\left(t\right)\cdot t\cdot dt=\gamma \cdot v\left(\overrightarrow{r}\right)\cdot m_{1q}$$ [1]

where γ is the gyromagnetic ratio and m₁ is the first-order gradient moment of the FSD preparation along the direction of $v\left(\overrightarrow{r}\right)$ (10). Signal attenuation due to flow is induced via intravoxel phase dispersion that, according to Eq. [1], is dependent on flowing spins’ velocity profile and m₁. As a result, FSD-induced flow signal suppression is voxel size-dependent: a voxel with a larger size in the flow cross-sectional dimension contains greater velocity variation and therefore higher-degree intravoxel phase dispersion. This has previously been demonstrated in the work by Nguyen et al. (7).

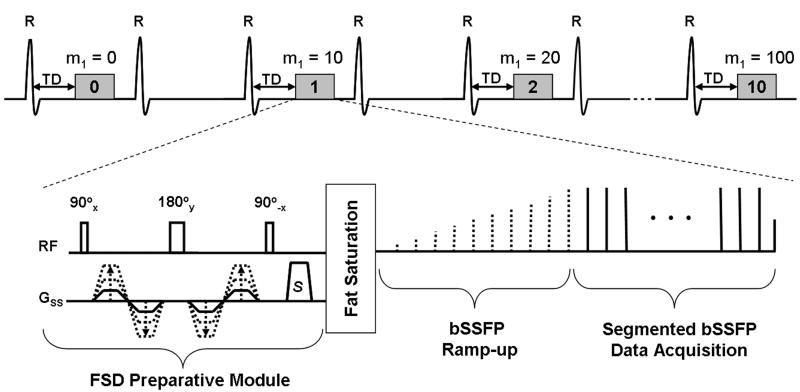
Figure 1.

Schematic diagram of the m₁-scouting sequence. FSD-prepared, ECG-triggered, segmented bSSFP acquisition is conducted every second (or third) heartbeat to continuously collect 11 measurements during a single scan. The FSD preparative module with FSD gradients applied in the slice-select direction only is used to impart flow-sensitization as measured by first-order gradient moment, m₁.The first measurement uses m₁ = 0 mT·ms²/m to provide reference signal intensity from the targeted blood vessel lumen, while the subsequent ones use incremental m₁ values, e.g. 10, 20, 30, …, 100 mT·ms²/m. A spectrally-selective fat saturation precedes the bSSFP ramp-up preparation and data acquisition to suppress the signal from perivascular fat. TD: trigger delay. S: spoiler gradient.

Hence, the voxel-size effect merits an attention when attempting to develop a method to predict flow signal-suppressing performance of individual m₁ values in 3D FSD imaging. For FSD-prepared 3D NC MRA, we hypothesized that the 3D imaging sequence can be switched to a 2D acquisition mode to rapidly scout a range of m₁ values, which are applied along the principal direction of blood flow, and predict their effectiveness in eliminating blood signal during 3D FSD MRA imaging. This requires (a) the 2D imaging plane to be perpendicular to the targeted vessel, (b) FSD gradients to be applied in the slice-select direction, and (c) in-plane spatial resolution to be identical to that of 3D imaging at the corresponding dimensions. In principle, a voxel in 2D imaging, although larger in size due to its thicker slice, has the same intravoxel phase dispersion as in 3D imaging, assuming the velocity variation in the slice-select direction (vessel long-axis) in a voxel is negligible and the intravoxel phase dispersion is independent of the slice thickness. Thus, the blood-suppressing performance of each m₁ value exhibited in 2D scouting imaging could be translated to 3D FSD MRA imaging.

MATERIALS AND METHODS

Pulse Sequence for m₁-Scouting

A pulse sequence for m₁-scouting, as shown in Figure 1, was implemented based on the sequence used in previous FSD-prepared 3D NC MRA studies (8). Specifically, an electrocardiography (ECG)-triggered, FSD-prepared segmented bSSFP acquisition was performed in a 2D transverse mode to continuously collect 11 measurements during a single scan. The first measurement used m₁ = 0 mT·ms²/m to provide reference signal intensity (SI) from a target flow, while the subsequent ones used incremental m₁ values, for example, starting with 10 mT·ms²/m in steps of 10 mT·ms²/m. FSD gradients were applied in the slice-select direction only, namely the principal direction of flow. Segmented acquisition was performed every second or third (if the R-R interval is short, e.g. 600-900 ms) heartbeat in an attempt to eliminate the potential interference of blood-suppressing performance from two successive m₁’s. By inspecting all acquired 2D images for intra-luminal flow SI, an optimal m₁ could be determined. Here, all relevant parameters, such as starting m₁ value (denoted as m_1,start) and step size (denoted as m_1,step) was allowed to specify through the sequence user-interface.

Flow Phantom Experiment

The flow phantom experiment was performed on a 1.5T MR system (MAGNETOM Espree; Siemens AG, Erlangen, Germany) using a 6-channel body matrix coil and spine coil. Gadolinium-doped water (0.25mM, T₁ = 670 ms) was pumped through a cylindrical silicone tube (internal diameter = 4.8 mm). A long segment of the tube (6 m) was used to ensure that velocity profiles were fully developed before entering the field of view (FOV) (11). A straight segment of the tube was placed in a tap-water bath and imaged, with its long-axis parallel to the bore of the magnet (B₀).

Various flow rates (15, 20, 30, 40, 50, 60 cm/s) were tested. For each flow rate, a 2D m₁-scouting scan was first performed and 11 transverse images at the middle of the target segment were acquired. Imaging parameters are provided in Table 1. The parameters m_1,start/m_1,step for all flow rates were empirically chosen as follows: 100/20 and 200/10 mT·ms²/m (flow rate 15 cm/s), 60/10 mT·ms²/m (flow rate 20 cm/s), 40/10 mT·ms²/m (flow rate 30 cm/s), 10/10 mT·ms²/m (flow rates 40, 50, and 60 cm/s).

Table 1.

Imaging parameters used in validation studies (flow phantom and healthy volunteer Group I) on a 1.5T Siemens Espree system and non-contrast FSD MRA studies on a 1.5T Siemens Avanto system (healthy volunteer Group II and patient).

	Flow phantom		Volunteer study (Group I)		FSD MRA (Group II and Patient)
	2D scouting	3D FSD	2D scouting	3D FSD	2D scouting	3D FSD
Orientation	Transverse	Coronal	Transverse	Sagittal	Transverse	Coronal
TE/TR (ms)	1.6/3.8	1.9/4.2	1.6/3.8	1.7/3.9	1.6/3.3	2.0/4.0
FOV (mm2)	186×300	225×225	180×360	169×210	150×300	310×316
Matrix size	198×320	240×240	192×384	180×224	160×320	330×336
Slice thickness (mm)	5.0	0.94	5.0	0.94	5.0	0.94
# of Segment per shot	37	56	54	51	46	60
# of shot per partition (slice)	3	3	2	2	2	3
Parallel factor (GRAPPA)	2	2	2	2	2	2
Flip angle (degree)	90	90	90	90	90	81
BW (Hz/pixel)	710	720	685	698	919	930
# of slice	1	22	1	48-56	1	64
Phase over- sampling (%)	0	30	0	0	0	0
Partition over- sampling (%)	0	6.7	0	25-28.6	0	12.5

To validate whether the m₁-scouting method can predict individual m₁’s blood signal-suppressing performance in FSD-prepared 3D imaging, six m₁ values (including m₁ = 0 mT·ms²/m) that appeared to provide distinct luminal SI on m₁-scouting images were respectively used in a segmented FSD-prepared 3D bSSFP coronal scan. FSD gradients were applied in the readout direction that was parallel to the long-axis of the target tube. Imaging parameters are given in Table 1. In both 2D and 3D scans, a simulated ECG signal was used for acquisition triggering, with an R-R interval of 1000 ms and a trigger delay of 200 ms.

Human Subject Experiment

Approved by our Institutional Review Board, 15 healthy volunteers and 2 patients (one diagnosed and the other suspected with peripheral arterial disease, PAD) were recruited with their written informed consent. The in vivo study consisted of the following two tasks, and accordingly the healthy subjects were divided into 2 groups.

a) To validate the predictive relationship between 2D m₁-scouting and FSD-prepared 3D black-blood imaging

On a 1.5T MR system (MAGNETOM Espree; Siemens AG, Erlangen, Germany) equipped with a 6-channel body matrix coil and spine coil, the left and right popliteal artery from each of five healthy subjects (Group I: 3 males, 19-46 years old) were imaged separately. Following a vessel localizer using multi-slice 2D time-of-flight, 2D m₁-scouting imaging was performed and 11 oblique transverse images were acquired using m₁ = 0, 5, 10, …, 50 mT·ms²/m, respectively. FSD-prepared 3D bSSFP oblique sagittal imaging was then performed with seven m₁ values (m₁ = 0, 5, 10, 15, 20, 25, 30 mT·ms²/m) imparted in the readout direction that was aligned with the target vessel. Imaging parameters for both 2D and 3D scans are given in Table 1. Both scans used the same ECG trigger delay time (i.e. peak systolic flow) as determined using a 2D gradient-echo phase contrast scan (velocity encoding = 90 cm/s) (8).

b) To systematically demonstrate the utility of the scouting method for improving imaging quality of 3D FSD MRA

Ten remaining healthy subjects (Group II: 7 males, 21-47 years old) and two patients (female, 89 years old; male, 53 years old) underwent NC MRA examinations using the FSD-prepared 3D bSSFP technique (8). Bilateral knees and calves, including the popliteal arteries, anterior and posterior tibial arteries, tibioperoneal trunk, and peroneal arteries, were covered with an oblique coronal acquisition orientation. Data were collected on a 1.5T MR system (MAGNETOM Avanto; Siemens AG, Erlangen, Germany) equipped with a 16-element peripheral matrix coil and spine coil.

An FSD MRA scan, referred to as Empirical Scan, was first performed using an m₁ of 35 mT·ms²/m, an empirical m₁ value according to literature (8). The m₁-scouting procedure was subsequently conducted at the level of mid tibial arteries (right below the center of the FOV used in MRA imaging), using the parameters m_1,start/m_1,step of 5/5 mT·ms²/m in healthy subjects, but 15/10 mT·ms²/m in patients to impart a larger scouting range for potentially slower flow. An optimal m₁ value was identified for the right and left leg, respectively, if arterial blood signal had been maximally suppressed with blood signal of neighboring veins barely attenuated. The application program “mean curve” available on the system console was used for the purpose. Compromise could be necessary when three or two arterial lumens had different optimal m₁ values. For each leg, a second FSD MRA scan, referred to as Optimized Scan, was performed using the selected optimal m₁ value only when it is different than the empirical value. Systolic and diastolic trigger delay times used in both m₁-scouting and 3D FSD MRA was determined using the aforementioned approach. Relevant imaging parameters are shown in Table 1.

Additionally, FSD MRA using a set of five m₁ values (including the optimal value) that have been scouted was obtained in two of the ten healthy subjects for demonstration purposes. The patient further underwent contrast-enhanced (CE) MRA using our institution’s routine protocol as described in previous work (8).

Image Processing and Data Analysis

All 2D and 3D image sets were processed and analyzed on a workstation (Leonardo; Siemens AG, Erlangen, Germany).

In the flow phantom and Group I volunteer studies, luminal SI was measured on images acquired in both 2D and 3D imaging. A region-of-interest (ROI) manually drawn in the tube or vessel lumen was used on 2D images, whereas three ROIs spreading over the tube or vessel lumen were used for 3D images to measure the mean SI. Pearson correlation analysis in SPSS (version 16.0, Chicago, IL) was used to determine the degree of correlation in SI’s between 2D m₁-scouting and FSD-prepared 3D bSSFP imaging. Statistical significance was set at p < 0.05.

In FSD MRA studies involving volunteers (Group II) and two patients, subtraction maximum intensity projection (MIP) was created from each 3D subtraction MRA image set. Arterial blood signal-to-noise ratio (SNR), artery-tissue contrast-to-noise ratio (CNR), and artery-vein CNR were evaluated on a per-leg basis in all 3D subtraction MRA image sets from the Empirical Scan and, if applicable, the Optimized Scan. Arterial blood signal (S_A) was measured from 5 ROI’s manually drawn within the lumen of five in-plane arterial segments, including the popliteal artery, the anterior and posterier tibial artery, tibioperoneal trunk, and peroneal artery, and then averaged. Venous blood signal (S_V) was derived in the same way from neighboring deep veins except that ROI’s were first prescribed on dark-artery image sets (before magnitude subtraction), where the veins were clearly depicted, and then propagated to subtraction image sets. Background tissue signal (S_B) was measured at the muscle area adjacent to the tibioperoneal trunk with a manually-drawn ROI no smaller than 2000 mm². At this similar level, image noise (σ_N) was estimated as the standard deviation of air signal between legs using a ROI no smaller than 1000 mm². Arterial blood SNR was then computed as SNR_A = S_A/σ_N. CNR between arterial blood and tissue was computed as CNR_A-B = (S_A – S_B)/σ_N. CNR between arterial blood and venous blood was computed as CNR_A-V = (S_A – S_V)/σ_N. To account for the spatial heterogeneity of noise in images reconstructed with parallel imaging (12), all corresponding ROI’s were matched in size and location when data from both the Empirical Scan and Optimized Scan were analyzed on a subject. Because these two scans have similar coil position, imaging volume, and reconstruction method, a relative comparison of SNR or CNR is possible (13). Hence, the above SNR and CNR measurements are referred to as relative SNR (rSNR) and relative CNR (rCNR), respectively. All rSNR’s and rCNR’s from Empirical Scans were time adjusted using the following equation in order to take the time efficiency into account when comparing to the measurements from Optimized Scans that essentially required extra time for m₁-scouting.

$$\mathit{rS}\left(C\right){\mathit{NR}}_{\text{Adjusted}}=\mathit{rS}\left(C\right)\mathit{NR}\times \sqrt{\frac{{\mathit{TA}}_{3D\mathit{MRA}}+{\mathit{TA}}_{2D\text{Scouting}}}{{\mathit{TA}}_{3D\mathit{MRA}}}}$$ [2]

where TA_{3D MRA} and TA_{2D Scouting} denote the acquisition time required for 3D FSD MRA and 2D m₁-scouting, respectively. The time-adjusted rSNR’s and rCNR’s from Empirical Scans were respectively compared with the corresponding measurements from Optimized Scans using a two-tailed paired Student’s t-test in SPSS (version 16.0, Chicago, IL). All subjects were included in t-tests; for the subjects whose optimal m₁ value equaled empirical value, the measurements from Empirical Scans were approximated as the values that would be obtained from Optimized Scans. Statistical significance was set at p < 0.05.

RESULTS

Flow Phantom Experiment

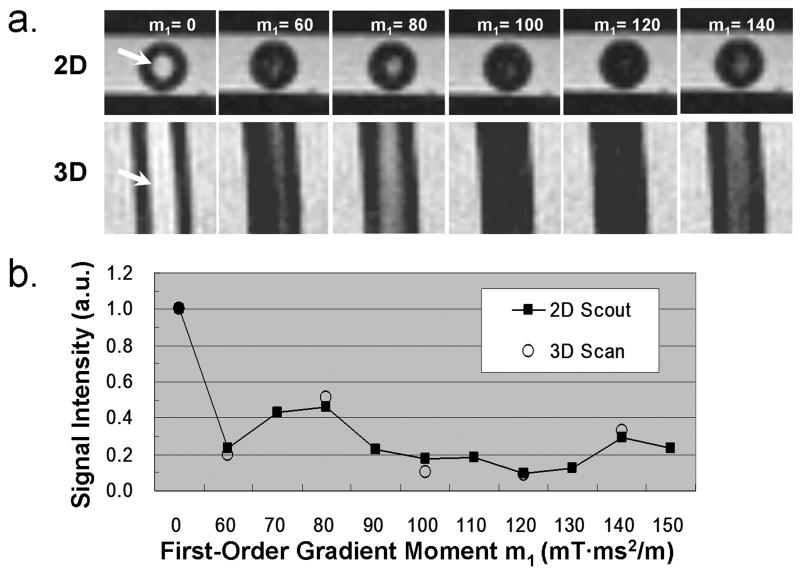
The luminal SI from 2D m₁-scouting images varied with the m₁ value (Fig. 2). The empirically chosen scouting m₁-range (defined by parameter m_1,start and m_1,step ) appeared to provide at least one measurement with the luminal SI reduced by 70-90%. Note that two m₁-scouting scans were necessary to derive the optimal m₁ at the flow rate of 15 cm/s; the first scan (rough tune) provided a large m₁-range, whereas the second one (fine tune) used a narrower range to derive an optimal m₁. The luminal SI from the 2D m₁-scouting and FSD-prepared bSSFP images were significantly correlated at all flow rates, with Pearson correlation coefficient = 0.99±0.01, p < 0.005 for all 6 cases. Figure 2 shows example images and flow SI-m₁ curves obtained from the case with flow rate = 20 cm/s.

Figure 2.

Example flow phantom experiment: flow velocity = 20 cm/s. a. 2D m₁-scouting transverse images and corresponding 3D reformatted coronal images using various m₁ values (in the units of mT·ms²/m) show similar flow (arrows: tube lumen) signal level; b, Good correlation of the flow signal intensity (SI) measurements (normalized by the reference flow SI) between the 2D and 3D scans. a.u.: arbitrary unit.

Human Subject Experiment

As with the flow phantom experiment, the luminal SI from 2D m₁-scouting images also varied with the m₁ value and the empirically chosen m₁-scouting range provided at least one measurement with the luminal SI reduced by 70-90%. Significantly high luminal SI correlation was obtained in all 10 popliteal arteries between the 2D and 3D image sets. Pearson correlation coefficient was 0.96±0.02, with p < 0.005 for all 10 cases. Typical images and corresponding flow SI-m₁ curves from a volunteer (male, 23 years old) are shown in Figure 3.

Figure 3.

Example human subject experiment: the popliteal artery at the left thigh. a. 2D m₁-scouting transverse images and corresponding 3D reformatted coronal images using various m₁ values (in the units of mT·ms²/m) show similar arterial blood (arrows) signal level; b, Good correlation of the arterial blood signal intensity (SI) measurements (normalized by the reference arterial blood SI) between the 2D and 3D scans. a.u.:arbitrary unit.

Data analyses for the 3D FSD MRA study are summarized in Table 2. Among all 12 subjects (including 2 patients), 4 subjects showed different optimal m₁ values at the right and left legs. Eighteen out of 24 legs (75%) were judged to have an optimal m₁ value different than 35 mT·ms²/m. With this optimization procedure, the measured rSNR_A, rCNR_A-B, and rCNR_A-V on resultant MRA’s were dramatically increased by 16.6%, 17.5%, and 19.0%, respectively. With time adjustment, such improvements were still significant (8.1%, 8.9%, and 10.2%, respectively) as indicated by the calculated p-values (0.044, 0.033, and 0.016, respectively) according to t-test analyses.

Table 2.

Comparison of signal measurements on 10 healthy volunteers and 2 patients who underwent FSD MRA using an empirical m₁ value and an m₁-scouting derived optimal m₁ value (highlighted in bold if different than 35 mT^.ms²/m).

Subject (Leg)	Optimal m1 (mT.ms2/m)	Scan Time of m1-scouting (s)	rSNRA		rCNRA-B		rCNRA-V
			Empirical: Adjusted (Unadjusted)	Optimized	Empirical: Adjusted (Unadjusted)	Optimized	Empirical: Adjusted (Unadjusted)	Optimized
V1 (R)	30	44	51.2 (48.1)	53.4	50.4 (47.3)	52.6	50.5 (47.4)	52.5
V1 (L)	30		45.3 (42.5)	49.4	44.2 (41.5)	48.3	43.5 (40.8)	47.8
V2 (R)	25	48	44.8 (42.2)	50.2	44.5 (41.9)	50.0	42.0 (39.5)	49.0
V2 (L)	25		45.4 (42.7)	47.1	44.5 (41.9)	46.7	42.2 (39.7)	46.0
V3 (R)	30	58	42.2 (39.5)	42.0	40.5 (37.9)	40.8	39.1 (36.6)	41.1
V3 (L)	30		32.6 (30.5)	35.5	30.8 (28.8)	34.2	30.0 (28.1)	34.6
V4 (R)	30	70	56.8 (52.1)	75.4	55.4 (50.8)	74.7	55.0 (50.5)	73.7
V4 (L)	30		54.3 (49.8)	77.1	53.1 (48.7)	76.2	52.1 (47.8)	75.0
V5 (R)	30	48	36.2 (33.9)	46.6	35.0 (32.8)	45.8	34.2 (32.1)	45.5
V5 (L)	30		33.9 (31.8)	43.0	32.4 (30.4)	42.0	31.2 (29.3)	41.5
V6 (R)	15	54	43.4 (39.5)	42.7	41.3 (37.6)	42.3	41.0 (37.3)	42.3
V6 (L)	20		34.7 (31.6)	36.1	32.7 (29.8)	34.6	31.2 (28.4)	33.0
V7 (R)	35	58	49.4 (45.3)	45.3	48.6 (44.6)	44.6	45.5 (41.7)	41.7
V7 (L)	30		49.4 (45.3)	40.3	48.5 (44.5)	38.8	47.0 (43.1)	38.1
V8 (R)	25	59	34.5 (31.5)	46.2	32.9 (30.0)	45.1	33.3 (30.4)	43.7
V8 (L)	35		31.8 (29.0)	29.0	30.1 (27.5)	27.5	29.8 (27.2)	27.2
V9 (R)	35	36	46.9 (44.2)	44.2	42.7 (40.2)	40.2	40.8 (38.5)	38.5
V9 (L)	35		46.5 (43.8)	43.8	42.0 (39.6)	39.6	39.8 (37.5)	37.5
V10 (R)	35	44	42.5 (40.0)	40.0	42.0 (39.6)	39.6	41.8 (39.4)	39.4
V10 (L)	35		44.5 (41.9)	41.9	44.1 (41.5)	41.5	42.9 (40.4)	40.4
P1 (R)	45	61	33.7 (30.7)	31.4	31.5 (28.7)	29.8	29.2 (26.6)	28.8
P1 (L)	55		27.3 (24.8)	26.0	25.4 (23.1)	24.8	23.2 (21.1)	24.0
P2 (R)	45	55	28.5 (25.9)	41.9	27.8 (25.3)	40.0	27.2 (24.7)	39.9
P2 (L)	45		24.9 (22.6)	33.0	24.2 (22.0)	30.7	23.8 (21.6)	30.1
Mean±Standard Deviation		52.9±9.3	40.9±8.8	44.2±11.9	39.4±8.8	42.9±12.2	38.2±8.8	42.1±12.1
Student t-test p-value			0.044		0.033		0.016

Note: Right (R) and left (L) legs are analyzed separately. V1-V10: 10 healthy volunteers. P1-P2: 2 patients. rSNR_A: relative arterial signal-to-noise ratio. rCNR_A-B: relative artery-tissue contrast-to-noise ratio. rCNR_A-V: relative artery-vein contrast-to-noise ratio.

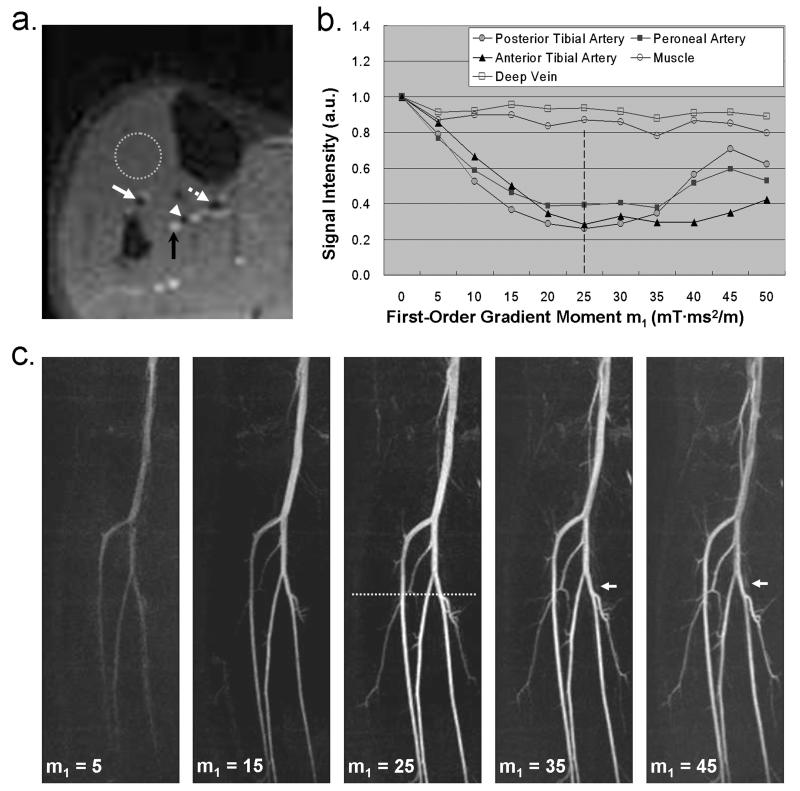
Figure 4 shows a set of MRA MIP’s from a healthy volunteer (male, 22 years old) who was imaged using m₁ = 5, 15, 25, 35, and 45 mT·ms²/m, respectively. In this case 25 mT·ms²/m was an optimal m₁ value providing a sharpest depiction of arterial segments without signal contamination from venous blood and background tissues. In contrast, MRA’s obtained with other m₁ values, including the empirical m₁ value, were degraded by inadequate or unsmooth signal enhancement of the arteries. Venous signal overlay became noticeable when using m₁ of 35 and 45 mT·ms²/m (arrows in Fig. 4c). This is expected to be more problematic when a large m₁ value is applied. Note that the image quality of all angiograms is well indicated by the SI-m₁ curves as derived from m₁-scouting imaging (Fig. 4a and b).

Figure 4.

An FSD MRA study on a healthy volunteer (male, 22 years old). From the m₁-scouting images (a), the signal intensity (SI) from three arteries (white arrows and arrow head), deep vein (black arrow), and muscle (dotted circle) is measured to provide SI-m₁ curves (b). The curves show that m₁ = 25 mT·ms²/m can suppress the arterial blood SI by up to 75%, with little sacrifice of SI from the vein and muscle. MRA (c) using this value is deemed optimal because of sharpest depiction of arterial segments without signal contamination from venous blood and background tissues. All other MRA images using m₁ = 5, 15, 35, and 45 mT·ms²/m are degraded by inadequate or unsmooth signal enhancement of the arteries. Venous signal overlay is also observed when using a higher m₁ value, i.e. 35 and 45 mT·ms²/m (arrows in c). Note: the values shown in (b) are the measured SI normalized by the reference SI; a.u.: arbitrary unit; the dotted line shown in (c) indicates the location of the 2D scouting plane; all images are displayed with the same window level.

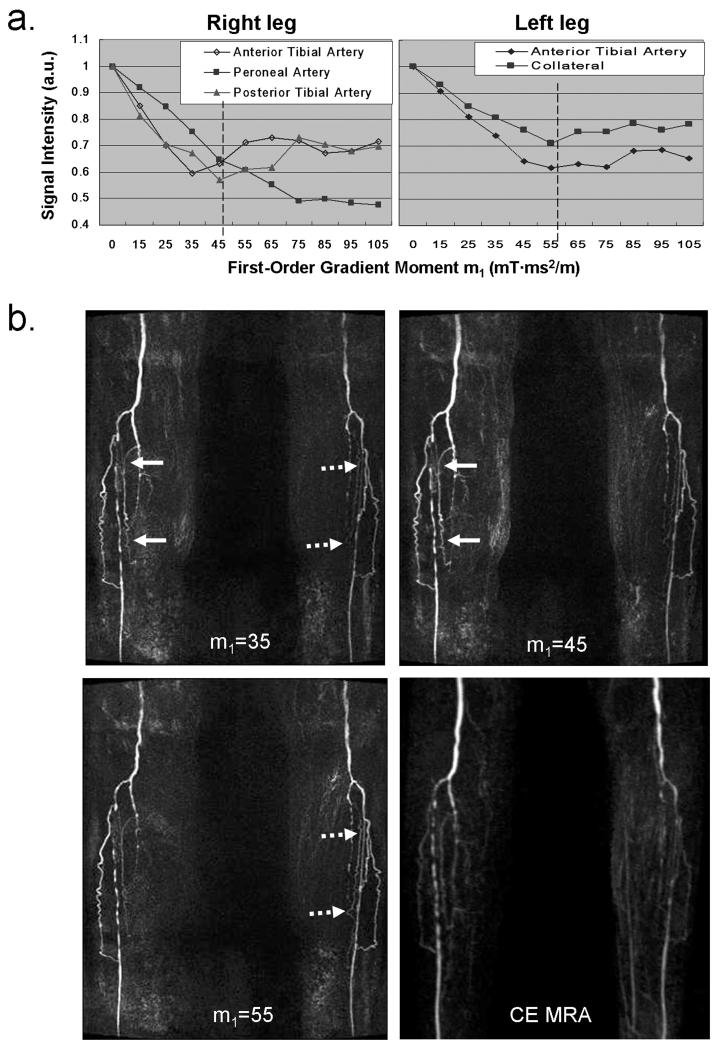
Figure 5 shows MRA MIP’s from the patient with known PAD. The right and left leg had different optimal m₁ values, namely 45 and 55 mT·ms²/m, respectively (dashed lines in Fig. 5a). Note that, on the right leg, the value of 45 mT·ms²/m is determined as a compromise since the major three arterial segments showed discordant flow SI-m₁ curve patterns (Fig. 5a). By using those optimal values the arteries exhibited higher signal on the corresponding legs compared to the case using empirical value, and in particular small collateral vessels were better depicted (Fig. 5b). In addition, there was excellent correlation in depiction of occlusion and stenoses between FSD MRA and CE MRA.

Figure 5.

MRA study on a patient (female, 89 years old) with known peripheral arterial disease. The m₁-scouting procedure (a) reveals that the patient has different optimal m₁ (marked by dashed line) on the right and left legs, namely 45 and 55 mT·ms²/m. Arterial segments exhibit higher signal on the corresponding legs when using these values, as compared to the case using the empirical value of 35 mT·ms²/m (Arrows). In particular, small collateral vessels are better depicted with the optimization procedure. Furthermore, there is excellent correlation in depiction of occlusion and stenoses between optimized FSD MRA and CE MRA. The blurring on CE MRA is likely due to non-isotropic, low spatial resolution. All NC MRA images are displayed with the same window level.

DISCUSSION

While CE MRA is currently a routine method for the evaluation of PAD, there is re-growing interest in NC MRA, given the frequency of renal functional impairment and risk of nephrogenic systemic fibrosis in this patient group (14,15). ECG-triggered FSD-prepared 3D bSSFP was recently proposed as a NC alternative for peripheral MRA. Proof-of-principle of this technique has been demonstrated in distal low extremities (8) and hands (9). The present work was aimed to continue to improve its performance by paying particular attention to signal suppression of blood flow by the FSD preparation.

The first-order gradient moment, m₁, is a determining factor for the effectiveness of blood signal suppression in FSD-prepared imaging (6,8,10). An empirical m₁ value was usually used in previous studies (5,16). In this work, the proposed method evaluates a range of m₁ values at their effectiveness in blood signal suppression in a quick scouting scan for each subject and specific vessel. One can choose an optimal m₁ value based on the SI from target vessels and apply it along the principal flow direction in 3D FSD MRA imaging, thus helping improve image quality.

The high signal correlation obtained from flow phantom and human subject experiments has verified that the proposed 2D method can be used to predict the performance of various m₁ values in flow signal suppression for 3D FSD-prepared imaging. This indicates that the optimal m₁ determined in 2D scouting imaging may be directly translated to 3D FSD MRA. This method seems similar to the approach previously used in fresh blood imaging (FBI) (17). Specifically, FBI employes a 2D projection scouting scan (30-40 mm thick), with the vessel of interest in plane, to scout and identify the appropriate strength of flow-spoiling gradients. Since through-plane spatial resolution (3-5 mm) in the 3D FBI scan is comparable to the vessel diameter, all blood spins over the entire lumen cross-section contribute to intravoxel dephasing in 3D imaging, which also occurs in the 2D scouting scan. Therefore, the intravoxel phase dispersion and thus blood signal suppression is approximately equivalent in both scans. However, this approach may not be applicable to 3D high-spatial-resolution (e.g. sub-millimeter) imaging in which case the 2D scouting imaging plane contains a larger velocity variation than 3D imaging. Instead, the 2D m₁-scouting method we proposed here combines several requirements as mentioned in THEORY section to ensure equivalent blood signal suppression in both 2D and 3D scans. It is noteworthy that this 2D m₁-scouting approach can also be applied in a coronal acquisition mode as long as its voxel dimensions can be matched in all three directions to 3D FSD MRA, thus providing an optimization for longer target vessels.

The blood flow SI-m₁ curve derived from the m₁-scouting scan clearly exhibits a sinc-function-like pattern (Fig. 2 and 3), which concurs with the underlying mechanism behind FSD-based flow signal suppression as mentioned in literature (10). Therefore, there could be several m₁ values showing sufficient signal suppression of arterial blood. In this case, one may also need to examine the signal change in accompanying veins and, possibly, other tissues and make a trade-off.

In this work, an optimal m₁ value different than 35 mT·ms²/m was identified in over half of the volunteer legs as well as in patients’. With the optimized flow sensitization, significant increases in arterial blood SNR, artery-vein CNR, and artery-tissue CNR were obtained, suggesting the necessity of the procedure. Due to the limited number of patient, we were not able to systematically investigate the favorable effect of the proposed method on disease evaluation. Nevertheless, the boosted SNR and CNR on resultant MRA would help enhance diagnostic confidence. We also anticipate that an optimal m₁ would minimize the likelihood that an arterial stenosis or occlusion is overestimated.

The proposed m₁-scouting approach can be flexibly adapted to various vascular anatomy by adjusting the relavant parameters m_1,start and m_1,step. In distal lower extremity imaging here, we have chosen m_1,start and m_1,step based on our previous experience. However, for other vascular territories, this approach would obviously require a pilot study to determine a proper scouting range. As indicated by the flow phantom study at 15cm/s, a slow flow scenario may require a large m_1,start and/or m_1,step and more than one scouting scans to derive an acceptable m₁. On the other hand, the approach could potentially be used in conjunction with other pulse sequqnces, such as turbo spin-echo and spoiled gradient echo, for FSD-based vessel imaging. In this particular application, an optimal m₁ value could be identified that results in sufficient signal suppression in target vessels while minimizing the signal loss in vessel wall, which is beneficial for characterizing plaques.

The proposed method has certain limitations. Firstly, it scouts m₁ values and identifies an optimal m₁ for a selected vessel or vessel segment only. Other vessels or vessel segments with a markedly different flow velocity or vessel caliber may have a different optimal m₁ value, which necessitates another scouting scan. We would suggest that the scouting plane be placed at the vessel segment which is expected to have the lowest flow velocity in the region of interest, and the optimal m₁ determined would likely be able to suppress blood signal throughout the region. The trade-off could be certain venous contamination at some locations. Secondly, in patients with severe arterial occlusive disease, blood flow in the normal segment and at the stenosis will be different. The fast or turbulent flow near stenoses is expected to result in better blood signal suppression than in normal segments, owing to a larger intravoxel velocity variation. However, the utility of the 2D method could be compromised by the stagnant flow distal to stenoses. In the patient case presented in this work, such a defect has not been noticed. Lastly, the method requires that flow be principally orthogonal to the 2D imaging plane, which may not be feasible for tortuous vessels.

In conclusion, a 2D imaging technique was developed to rapidly assess a range of first-order gradient moment values at their effectiveness in blood signal suppression. It was validated that individual m₁’s blood signal-suppressing performance is highly correlated between 2D m₁-scouting imaging and FSD-prepared 3D imaging such that the optimal m₁ determined by the 2D method may be directly translated to FSD-prepared 3D NC MRA. Preliminary results have demonstrated its potential to improve signal performance of FSD MRA. Further systematic studies in patients are warranted to evaluate its clinical value.