Abstract
Isotopic effects associated with molecular absorption are discussed with reference to natural phenomena including early solar system processes, Titan and terrestrial atmospheric chemistry, and Martian atmospheric evolution. Quantification of the physicochemical aspects of the excitation and dissociation processes may lead to enhanced understanding of these environments. Here we examine a physical basis for an additional isotope effect during photolysis of molecular nitrogen due to the coupling of valence and Rydberg excited states. The origin of this isotope effect is shown to be the coupling of diabatic electronic states of different bonding nature that occurs after the excitation of these states. This coupling is characteristic of energy regimes where two or more excited states are nearly crossing or osculating. A signature of the resultant isotope effect is a window of rapid variation in the otherwise smooth distribution of oscillator strengths vs. frequency. The reference for the discussion is the numerical solution of the time dependent Schrödinger equation for both the electronic and nuclear modes with the light field included as part of the Hamiltonian. Pumping is to all extreme UV dipole-allowed, valence and Rydberg, excited states of N2. The computed absorption spectra are convoluted with the solar spectrum to demonstrate the importance of including this isotope effect in planetary, interstellar molecular cloud, and nebular photochemical models. It is suggested that accidental resonance with strong discrete lines in the solar spectrum such as the CIII line at 97.703 nm can also have a marked effect.
Keywords: photodissociation, isotopic fractionation, UV photodissociation
Photochemical processes are particularly pervasive in nature. Measurements of isotopic compositions provide insights into a range of such processes, both terrestrial and extraterrestrial. To adequately interpret such measurements, characterization of relevant isotopically selective physicochemical processes associated with gas phase processes is desirable. In this paper we quantify an isotopic selectivity due to electronic reorganization following ligfht absorption. The results are compared to the solar spectrum for applications in nature.
There are a number of photodissociation processes that have been suggested where a more basic understanding of isotope effects could aid in the development of models. A striking example of observed, but presently not fully understood oxygen isotopic distribution occurs in the high temperature calcium aluminum rich inclusions of the Allende meteorite (1) and most oxygen bearing meteorites (see, for example, review in ref. 2). Although originally thought to be nucleosynthetic in origin based upon laboratory experiments, it was later suggested that the observed isotopic composition might arise from photochemical self-shielding (3–6). It has also been proposed that given the special properties of oxygen, symmetry related properties might produce the same fraction in the actual mineral formation process (7–11). A photochemical self-shielding mechanism has recently been tested utilizing short UV wavelength synchrotron light to dissociate CO after passage through a column of CO in a spectral region where self shielding is predicted (12), which has lead to discourse on the role of photochemistry in the early solar system (13–16).
The determination of isotopic selectivity during photoabsorption is important, for example, in the interpretation of the Martian atmospheric isotopic composition. The Viking Lander mission (17, 18) measured the Martian atmosphere composition, revealing a very high 15N isotopic enrichment (1.6 times terrestrial) that was suggested as deriving from dissociative recombination and photolysis of N2 and preferential gravitational escape of the lighter isotope, 14N (17,19–26). Recent work describing the nitrogen isotopic composition of the atmosphere of Titan has also been modeled to interpret its anomalous molecular nitrogen isotopic composition, which is a factor of two higher than the associated HCN (27). These careful calculations incorporated isotopic photoabsorption and photodissociation cross-sections for molecular nitrogen as well as consideration of coupling between Rydberg and valence states.
Meteoritic nitrogen observations have revealed extraordinarily high bulk heavy nitrogen isotopic enrichments (28, 29). High enrichments are also observed in spatially restricted hot spots within meteoritic material (30). The source of the enrichment remains unidentified and it is possible that a large nitrogen isotopic fractionation associated with photoabsorption of UV could be a relevant process in the early solar system or in circumstellar clouds. Identification and characterization of the process would better define the conditions associated with early nebular photochemistry.
In this paper we explore the possibility that N2 UV excitation may produce nitrogen isotope effects of potential applicability in nature. For this purpose we implemented a numerically accurate solution of the electronic and nuclear quantum dynamics of the far UV excited N2 molecule. We solve the time dependent Schrödinger equation so that we can follow in time the evolution of the populated excited electronic states during and after the pulse. We explicitly allow the atoms to move because it is the mass-dependent energies and couplings that are at the origin of the isotope effect.
The single UV photon excitation in N2 accesses the region of the lowest lying allowed transitions from the ground state (31, 32). In this energy region, optically accessible states are both valence and Rydberg excited states that qualitatively differ in the nature of the bonding in the molecule. This difference will be cardinal to what follows. The valence states are the gateway to dissociation via the repulsive triplet states (33–38) that cannot be optically directly accessed from the ground state. Essentially the same comments apply to the UV excited states of the isoelectronic molecule CO. Ref. 39 provides a recent example. In this paper we perform calculations for the N2 molecules because of the availability of the relevant potential energy curves at sufficient levels of precision. Relevant data for the isotopically substituted states is given in Table S1. The physical implications are applicable to CO given that the two diatoms are isoelectronic.
The lowest UV accessible excited states of the N2 molecule are in the 100,000–125,000 cm-1 frequency region (roughly 12.5–15 eV) (33, 37, 40–43). The excited states are of either Σ or Π symmetry and all are bound states. For each symmetry there are two Rydberg types and one valence-excited state that may be accessed optically directly from the ground state. The Rydberg states have a force constant and equilibrium distance that are comparable to those of the ground state of N2. The lower lying vibrational states within each Rydberg electronic state are thus in the frequency range of relatively intense transitions, the so-called Franck–Condon region (see figure 7 in ref. 44). The valence-excited states are more weakly bound so that the potential curves are shallower and have a larger equilibrium distance. Thus it is the higher vibrational states of the valence-excited electronic states that are in the Franck–Condon region (Fig. 1).
Fig. 1.
Potential energy curves and vibrational levels of the dipole-allowed excited Rydberg and valence diabatic states of N2. (Left) States of Σ symmetry. (Right) The Π symmetry. The energy scale, au, is relative to the ground vibrational state of the ground electronic state. The b and b′, red online, are the valence states of the two symmetries. Other potentials, black and blue online, are the two Rydberg states of each symmetry. The potential curves are adapted from ref. 42. Both panels contain an insert that is a blowup of the energy scale. The b(v) is the vibrational state v etc. The insert on the right shows that the isotope shift brings the b(5) level of 14N15N essentially into exact resonance with the c(0) level meaning that the best resonance is for the isotopically mixed molecule. Similarly, the insert on the left, for the b′(18) level and the e′(0) state. Note that the Σ states shown in the insert are at a higher energy compared to the Π states.
For diatomic molecules such as N2 and CO, potential energy curves of excited states of the same symmetry cannot cross (except for an unforeseen accident). The noncrossing property is valid when we determine the electronic states by clamping the nuclei and optimizing the motion of the electrons. This generates the adiabatic electronic or Born–Oppenheimer states. These states avoid one another and their potential energy curves do not cross. The adiabatic states are accessed in ordinary spectroscopy and specifically in solar/stellar UV irradiation. The designations “Rydberg” and “valence-excited” are labels of particular electronic configurations. The bonding patterns in such states are not optimized by the use of a variational principle, which means that whereas these states have a clear bonding character they are not really stationary because they do not fully diagonalize the electronic Hamiltonian. There is a residual interaction that is effective only in the region about the crossing (45). States of definite bonding character are here referred to as diabatic states. The weak nature of the coupling of the diabatic states and its localized effect is established by observing localized irregularities of level positions in the rovibrational spectrum (46) and in the nonmonotonic variations in the predissociation lifetimes for the rotational levels. The adiabatic and diabatic points of view are complementary to one another.
In this paper we quantify the origin of the isotope effect in photoexcitation using both a diabatic and the corresponding adiabatic approach. The advantages of invoking both points of view where diabatic potential energy curves cross is well-recognized (45). The diabatic potential energy curves are smoothly varying and the vibrational spectrum for such potentials is regular and systematic. These regular vibrational levels are shifted in a systematic manner due to isotopic substitution. The “Rydberg” and “valence” diabatic states have a rather different force constant. The spacing of states in their respective vibrational ladders therefore are quite different and alteration of the mass of the atoms alters the vibrational spacings. For different isotopomers, states that belong to different ladders permeate into or out of a resonance as a function of their energies. A resonance is expected to be highly advantageous for transitions between two diabatic states. As will be seen, our computations very much exemplify this point of view. The major shortcoming of the diabatic states is that they do not diagonalize the electronic Hamiltonian and such states are not stationary. The intrastate coupling continues after optical excitation is terminated.
The vibrational adiabatic states are obtained by diagonalizing the electronic Hamiltonian. When two diabatic states are in near resonance, the adiabatic states will be a mix of different electronic diabatic states. The different electronically excited diabatic states differ in bonding character and therefore have different transition strengths from the ground state. In the region of crossing of diabatic states the transition strengths vary irregularly as the frequency of excitation varies because successive adiabatic states contain variable amounts of different diabatic states. The alternation of strongly and weakly absorbing states is characteristic of energy regimes where the interacting states are nearly isoenergetic (SI Appendix). Such characteristic “windows” have been clearly observed in both the experimental and computed spectrum of N2, (see, for example, figure 9 of ref. 42) near the frequencies of 105,500, 111,000, or 116,000 cm-1 (See Fig. 2 and the window in Fig. 3). It is in this region of rapid alternation of oscillator strengths that we expect a noticeable isotope effect as a consequence of the extent of mixing of diabatic states. Therefore the transition strengths to the mixed adiabatic state are highly dependent upon the energy mismatching of the ladders of diabatic states.
Fig. 2.
Bar spectrum for neighboring energy regions that do not (top row of each symmetry), or do show a strong isotope-dependent mixing of diabatic states. (Top) The Π states. (Bottom) The Σ states. Each symmetry contains two nearby energy ranges. The light intensity is the same in all twelve panels. On the leftmost panel of each row is the absorption by the 14N14N isotopomer and serves as the reference. The two panels toward the right of each row are the absorption of the mixed, 14N15N isomer and the heavy 15N15N. These panels show the absorption relative to that of 14N14N. Therefore the scale of the ordinate on the right is the fractional isotope effect in absorption. For two of the Σ states the isotope effect is so large that it is written on top, as a fraction. To prevent a possible misunderstanding 91.2 is an isotope effect of 91,200 parts per thousand. The variation in the bar height = transition probability are due to the mixing of the diabatic states. The extent of mixing is spelled out within the bar for the more probable diabatic states. For states of very low intensity (e.g., at energy 114,851 cm-1) only the composition is shown. Computations at a field strength of 0.006 au resulting in a 0.5% depletion of the ground electronic state.
Fig. 3.
The role of the structured solar spectrum. Shown is the absorption spectrum of two isotopomers and the solar spectrum (50), golden line, in two frequency ranges. The spectrum is shown as the normalized oscillator strength. (Left) A low energy range where only low vibrational Π states of b symmetry can absorb. (Right) In the energy range of valence and low vibrational Rydberg state mixing corresponding to the region near the insert in Fig. 1, Right. The solar spectrum is in golden line, the  in blue whereas the
in blue whereas the  is in green. The spectrum of the isotopically mixed molecule is not shown for clarity. Its peaks are nestled in between the two. Energy scale in wave numbers from the ground state, with 100,000 cm-1 subtracted. On the two edges of the energy range shown are states that are of almost pure b character. These states have an order of magnitude larger transition strength from the ground state. Also see SI Appendix for a discussion of bright and dark states. All solar lines in the energy range are shown and are identified in the notation of ref. 50. For frequencies above about 109,000 cm-1 the solar spectrum is significantly denser. See SI Appendix for details of the computations. It is interesting to comment on the near resonance with the low vibrational states of the b valence-excited state as shown in the Left panel. These low lying states have been identified (33–38) as strongly predissociating due to spin orbit coupling to the bound triplet C state. This state is in turn coupled to the repulsive triplet C′ state.
is in green. The spectrum of the isotopically mixed molecule is not shown for clarity. Its peaks are nestled in between the two. Energy scale in wave numbers from the ground state, with 100,000 cm-1 subtracted. On the two edges of the energy range shown are states that are of almost pure b character. These states have an order of magnitude larger transition strength from the ground state. Also see SI Appendix for a discussion of bright and dark states. All solar lines in the energy range are shown and are identified in the notation of ref. 50. For frequencies above about 109,000 cm-1 the solar spectrum is significantly denser. See SI Appendix for details of the computations. It is interesting to comment on the near resonance with the low vibrational states of the b valence-excited state as shown in the Left panel. These low lying states have been identified (33–38) as strongly predissociating due to spin orbit coupling to the bound triplet C state. This state is in turn coupled to the repulsive triplet C′ state.
In an adiabatic approach it is the strength of optical coupling to the absorbing states that is the origin of a possible isotope effect. In the diabatic point of view we look at the energy gaps between the states for an explanation. (See also discussion in SI Appendix.) In neither scheme do we have a simple, “two-state” picture as there are always three or more diabatic states coupled to one another. Because both symmetries can be optically accessed from the ground state, the experimental spectrum is even more entangled than the theoretical one, where each symmetry can be separately studied. These considerations apply mutatis mutandis for CO.
The electronic coupling of the diabatic states is expected to slowly vary as a function of interatomic distance and has been accurately computed for N2 (42). At a given internuclear distance R, the effective coupling χ between the diabatic states α and β is determined by the electronic term Hαβ(R) where H is the electronic Hamiltonian. However, the magnitude of χ is scaled by the energy gap between the two potential energy curves of the two coupled diabatic states, χαβ(R) = Hαβ(R)/(Eα(R) - Eβ(R)) (45, 47). The energies of the diabatic electronic states are shown in Fig. 1 for both the Π and Σ states of N2.
The coupling χ can vary most dramatically with internuclear distance R because of how the energy gap (Eα(R) - Eβ(R)) varies. (In SI Appendix, we show a plot (Fig. S1) of the effective coupling, χ between the b′ and e′ diabatic electronic states). The isotope effect occurs around R values where the effective coupling is large. In the exact numerical computation we include all diabatic electronic-vibrational states in the Franck–Condon window of the ground state; 45 times 2 Π Rydberg states, 25 for the b valence state that is shallow and 45 times 3 Σ states. (See figure 7 in ref. 44 for a useful view of the entire manifold of vibrational states). The Hamiltonian matrix for the system is block diagonal as shown in Eq. S1, with one block for each diabatic state. Different blocks, each of them diagonal, constitute the vibrational spectrum of the diabatic states. Off-diagonal elements are allowed only between different blocks and these represent the coupling of vibrational states that belong to different diabatic states.
Here, we are specifically concerned with the role of mass in governing vibrational motion. The origin of the variations between different isotopomers is primarily due to the anharmonicity of the harmonic ladders of vibrational states for each diabatic electronic state. Anharmonicity requires vibrational spacings in a given ladder to decrease as the vibrational quantum number increases as observed in Fig. 1. The physics of the diabatic states means that ladders of vibrational states that belong to different diabatic states have different harmonic frequencies. Consequently, two vibrational states in different electronic ladders that are roughly close can be quite close or somewhat different in energy. The range of the possible variations is from near the vibrational frequency, which is high for N2, to almost zero. The isotope effect arises because the energies of vibrational states vary with isotopic substitution that alter the reduced mass by about 7%.
Fig. 1 is an example of the diabatic potential energy curves, [adapted from Spelsberg and Meyer (42)], one panel for each symmetry type, where the inserts expand the scale to show the isotopic variation in the positions of nearly isoenergetic vibrational states.
The numerical computation that demonstrates the isotope effect solves the time dependent Schrödinger equation for both the electronic and the nuclear motion. A pulsed UV light is included exactly as part of the Hamiltonian, (Eq. S2), and not as a perturbation. We mimic the pressure broadening of spectral lines in an atmosphere by using a short pulse. Such a pulse is broad in energy because of the time-energy uncertainty relation. During and following the pulse the nitrogen nuclei start to move because they abruptly encounter a potential not that of the ground state of the molecule.
Fig. 2 shows the isotope effect from the point of view of the adiabatic states. For each symmetry we show two panels, one with and one without a noticeable isotope effect due to state mixing. The height of each bar is the optical transition probability into that state using a laser pulse that is common to both panels of the same symmetry. There is no isotope effect when the diabatic vibrational states are not effectively coupled to states of a different diabatic ladder. When they are energetically near there is effective coupling as each adiabatic state is a mix of three or more diabatic states and the extent of mixing is highly isotope dependent. The degree of mixing influences both the probability to optically access the state and the lifetime for predissociation.
For the detection and interpretation of isotopic compositions associated with specific processes, the distribution patterns are conventionally expressed as ratios. For nitrogen, the distribution is expressed as the 15N14N/14N14N isotope ratio (mass 29/28). In the present computations, to conveniently express the isotope effect associated with coupling of the light pulse to the various states, we normalize to the case of light absorption for the isotopomer N14N14. The ratio of the absorption in the isotopomers to no isotope effect expresses the isotope effect associated with the primary absorption of light. The predissociation lifetimes are comparatively short compared to the lifetime for spontaneous emission and/or collisional deactivation. Consequently, most excited molecules will dissociate (48, 49) and the population is a reasonable approximation of the eventual isotope effect in dissociation.
The role of the discrete structure of the solar spectrum is illustrated in Fig. 3. The Left panel shows an energy regime where only the ground and very low excited vibrational states of Π symmetry can be accessed. These are valence-excited states of b type and they are effectively fully unperturbed by the higher lying Rydberg states. The isotope shift of the spectral lines is then entirely due to the familiar mass shift of harmonic oscillator like vibrational energies. Also shown in Fig. 3 is the solar spectrum, adapted from ref. 50. It is seen that the strong CIII solar line at 97.703 nm dominates the absorption of solar light in this region of frequency. The other frequency region shown in Fig. 3 is at a just somewhat higher energy near the extensive valence and Rydberg state mixing shown in Fig. 1, Right. In the higher energy regime there is a significant isotope effect due to state mixing. In summary of Fig. 3, the two panels illustrate the two isotope effects that we discuss. In the Left panel is the conventional effect of a mass shift of a vibrational frequency. In the Right panel is the region of strong state coupling. An accidental resonance with a solar line can make the shift quite important. In the Right panel, we show the isotope effect due to state mixing. Here too, the effect will be most pronounced for a structured light source.
The significant consequence of Figs. 2 and 3 is that the isotope effect in excitation, on a state by state basis, is very much a function of the energy, unambiguously demonstrating that such effects must be considered in photochemical models. There are relatively broad regions where there is no effect or only a weak effect, as shown in the topmost row for each symmetry type in Fig. 2. This correlates with little mixing of diabatic states. However, intermingled there are energy ranges where the isotope effect is large. There are very localized energies where the effect is exceptionally large that occurs whenever states of different bonding character are strongly mixed (21, 23). With the lifetime of the predissociation being relatively short these populated states will lead to a 15N enriched or depleted atomic nitrogen product of large order of magnitude. We expect that similar consideration will apply to other molecules and in particular to the isoelectronic molecule CO (51). Having said this we also draw attention to the role of the position of the strong solar lines as shown in Fig. 3. This means that every molecule must be examined as a case by itself.
The nature of the isotopic effect uncovered by the computations is important for models of atmospheric evolution, particularly Mars. Present models that account for the 15N/14N enrichment of 1.6 do not as yet incorporate the selective isotopic effect associated with the UV excitation discussed in the present paper (17, 21, 22, 24, 25). Nitrogen atoms produced by dissociative recombination of  and electrons result in production energetic atomic nitrogen atoms that possess energies exceeding the escape energy of about 1.72 eV, producing preferential escape for the lighter 14N and concomitant 15N enrichment in the residual atmospheric nitrogen. In this mechanism, assuming an initial terrestrial nitrogen isotopic composition, the atmosphere of Mars evolves over time with accrual of the heavy nitrogen isotope in the atmosphere. Recently it has been shown that molecular nitrogen photodissociation is the dominant mechanism for production of the nitrogen atoms that escape from the Martian thermosphere (25). In the energy range of the present calculations, photochemically produced atomic nitrogen is a significant source in the 250 km range during low solar activity and 300 km during high activity. In these models, it is assumed there is no isotope effect in the actual photolysis. As Fig. 2 displays, for a particular portion of the band spectrum, irradiation with light of a narrow spectral distribution the selective isotope effect may be quite large. Our computations show that across the entire nitrogen energy range, with a white light source, there is no significant net isotope effect. However, in the spectral region in the present consideration (12.5–15 eV), the solar spectrum is quite complex and consequently the convolution of the actual solar luminosity with the isotopic population as a consequence of the actual photoabsorption is quite significant. When the solar spectrum is included the effect could be substantial. Fig. 4 is an illustration of the computed effect for an atmosphere of pure N2 with additional graphical details provided in Fig. S2. Fig. 4 shows the rate of absorption, J, of the three different N2 isotopomers as a function of the pathlength l, logarithmic scale, of the solar light in N2 gas of density c. J is computed using Eq. S6. At low l hardly any light is absorbed. There is then a clear isotope effect due primarily to the accidental resonance with the strong solar line at 97.703 nm as shown in Fig. 3, Left. Fig. S2 provides a check of this statement: We, by hand, shift the solar line by roughly 120 cm-1 so that it overlaps better a different isotopomer. Whichever isotopomer best overlaps the solar line is the one that absorbs more. We emphasize that the entire solar spectrum is used in the computation but that at very low shielding the strong solar line that is nearly resonant dominates. As the pathlength l increases more light is absorbed and the extent of light absorbed diminishes exponentially. It is possible to plot the ratio of the light absorbed by different isotopes, say J(1415)/J(1414). If we do so, the ratio does not vary monotonically with l even though J itself does decrease monotonically, as seen in the graph and as can be shown analytically. A ratio of two exponentially small quantities is susceptible to amplification of the numerical error. We prefer, at the present level of accuracy of our quantum chemical computations of oscillator strengths, to show J itself and not the ratio.
and electrons result in production energetic atomic nitrogen atoms that possess energies exceeding the escape energy of about 1.72 eV, producing preferential escape for the lighter 14N and concomitant 15N enrichment in the residual atmospheric nitrogen. In this mechanism, assuming an initial terrestrial nitrogen isotopic composition, the atmosphere of Mars evolves over time with accrual of the heavy nitrogen isotope in the atmosphere. Recently it has been shown that molecular nitrogen photodissociation is the dominant mechanism for production of the nitrogen atoms that escape from the Martian thermosphere (25). In the energy range of the present calculations, photochemically produced atomic nitrogen is a significant source in the 250 km range during low solar activity and 300 km during high activity. In these models, it is assumed there is no isotope effect in the actual photolysis. As Fig. 2 displays, for a particular portion of the band spectrum, irradiation with light of a narrow spectral distribution the selective isotope effect may be quite large. Our computations show that across the entire nitrogen energy range, with a white light source, there is no significant net isotope effect. However, in the spectral region in the present consideration (12.5–15 eV), the solar spectrum is quite complex and consequently the convolution of the actual solar luminosity with the isotopic population as a consequence of the actual photoabsorption is quite significant. When the solar spectrum is included the effect could be substantial. Fig. 4 is an illustration of the computed effect for an atmosphere of pure N2 with additional graphical details provided in Fig. S2. Fig. 4 shows the rate of absorption, J, of the three different N2 isotopomers as a function of the pathlength l, logarithmic scale, of the solar light in N2 gas of density c. J is computed using Eq. S6. At low l hardly any light is absorbed. There is then a clear isotope effect due primarily to the accidental resonance with the strong solar line at 97.703 nm as shown in Fig. 3, Left. Fig. S2 provides a check of this statement: We, by hand, shift the solar line by roughly 120 cm-1 so that it overlaps better a different isotopomer. Whichever isotopomer best overlaps the solar line is the one that absorbs more. We emphasize that the entire solar spectrum is used in the computation but that at very low shielding the strong solar line that is nearly resonant dominates. As the pathlength l increases more light is absorbed and the extent of light absorbed diminishes exponentially. It is possible to plot the ratio of the light absorbed by different isotopes, say J(1415)/J(1414). If we do so, the ratio does not vary monotonically with l even though J itself does decrease monotonically, as seen in the graph and as can be shown analytically. A ratio of two exponentially small quantities is susceptible to amplification of the numerical error. We prefer, at the present level of accuracy of our quantum chemical computations of oscillator strengths, to show J itself and not the ratio.
Fig. 4.
The absorption of solar light, J, at different altitudes in a column of N2 at the concentration c that is the same as is observed in Titan (52). Computed using Eq. S6. We fit the data of the concentration, units of kg·m-3, vs. altitude to log(c) = -(h/150 + 2) where h is the altitude in km. The pathlength l in km is taken as l = 1500 km - h. At very low shielding there is a definite isotope effect due the absorption of the strong solar line at 97.703 nm; see also Fig. 3, Left, and the validation computations in Fig. S2. As more light gets absorbed, the isotope effect due to absorption of other solar lines that access mixed states, see Fig. 3, Right, becomes more important. See Fig. S2 for a similar plot for a gas at a constant density. Fig S2 also shows the effect of modest shift in the location of the solar line.
There will be spectral regions, typically windows of low absorption, where the three isotopomers, 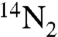 ,
,  and 14N15N, will not absorb to the same extent. Such a window is shown in Fig. 3, Right. It is evident that around 104,600 cm-1 the heavy isotopomer absorbs more than twice as much as the lightest one, however the sun delivers no light in that energy range. In the frequency range about 106,000 cm-1 the heavy isotope absorbs only about half as much as the lighter one. Here again there is almost no solar irradiance. For a very broad light excitation source the alternating preferences will tend to average out. However for a narrower light source the effect may be dramatic. The net isotope effect in the excitation depends not only on the molecule but also on the spectrum of the light. At higher frequencies, such as those displayed in Fig. 2, the reported solar spectrum is much less structured possibly due to lower spectral resolution. When a broad frequency spectrum light is applied the isotope effect will be averaged over many states and consequently decreases. For a narrower frequency spectrum of photoexcitation Fig. 2 shows that there can be a large isotope effect. The consequence of the calculations is that for any model of the isotopic evolution of the Martian atmosphere, the isotopic effect of the actual photoabsorption process must be accounted for as a highly resolved function of energy given the large effects associated with the photoabsorptive selectivity.
and 14N15N, will not absorb to the same extent. Such a window is shown in Fig. 3, Right. It is evident that around 104,600 cm-1 the heavy isotopomer absorbs more than twice as much as the lightest one, however the sun delivers no light in that energy range. In the frequency range about 106,000 cm-1 the heavy isotope absorbs only about half as much as the lighter one. Here again there is almost no solar irradiance. For a very broad light excitation source the alternating preferences will tend to average out. However for a narrower light source the effect may be dramatic. The net isotope effect in the excitation depends not only on the molecule but also on the spectrum of the light. At higher frequencies, such as those displayed in Fig. 2, the reported solar spectrum is much less structured possibly due to lower spectral resolution. When a broad frequency spectrum light is applied the isotope effect will be averaged over many states and consequently decreases. For a narrower frequency spectrum of photoexcitation Fig. 2 shows that there can be a large isotope effect. The consequence of the calculations is that for any model of the isotopic evolution of the Martian atmosphere, the isotopic effect of the actual photoabsorption process must be accounted for as a highly resolved function of energy given the large effects associated with the photoabsorptive selectivity.
There is another consequence implied by our computations. In an atmospheric column of pure N2, during light penetration of the column the light will necessarily be structured in that the highly absorbing states will have absorbed and the corresponding frequencies missing. The states that are highly absorbing are typically almost pure b or b′ states that do not exhibit a strong isotope effect in their absorption. Deeper down into the atmospheric column the light will be absorbed preferentially by the more weakly absorbing mixed states (Fig. 2), states that exhibit an additional isotope effect. The isotope effect can therefore strongly vary with altitude being stronger at low altitude where most of the light has been absorbed. This effect may perhaps be seen in figure. 2 of ref. 27. As emphasized in connection with Fig. 4, because at low altitudes the residual light intensity is exponentially small it requires considerable numerical accuracy for the effect to be seen in a computational modeling.
In summary, the calculations reported in this paper demonstrate that in the photoexcitation of N2, coupling of electronic states induces significant variations in the oscillator strength of individual isotopically substituted molecules. As a consequence, in a given energy regime there are large isotope effects, exceeding 91,000 per mil for a light source in the spectral range of Fig 2, Bottom Right. For structured light sources, specifically solar or stellar irradiation, such effects may be larger and consequently, models of the evolving Martian atmosphere should take this effect into account.
Supplementary Material
Acknowledgments.
We thank G.J. Wasserburg, R.N. Zare, J. Troe, T.J. Martinez, and Y. Yung for their comments on the manuscript. M.H.T. acknowledges numerous helpful discussions with S. Chakraborty, G. Dominguez, R. Shaheen, and Antra Priyadarshi. The work of B.H.M., F.R. and R.D.L. is supported by the James Franck Program for Laser–Matter Interaction. The work of R.D.L. and F.R. and the computational facilities for this project is also supported by the European Community Future Emerging Technology project Molecular Logic Circuits MOLOC (Nano-Informatino and Communication Technology). Support for M.H.T. was provided by the National Aeronautics and Space Administration Origins of Solar Systems and Cosmochemistry programs.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1102767108/-/DCSupplemental.
References
- 1.Clayton RN, Grossman L, Mayeda TK. Component of primitive nuclear composition in carbonaceous meteorites. Science. 1973;182:485–488. doi: 10.1126/science.182.4111.485. [DOI] [PubMed] [Google Scholar]
- 2.Thiemens MH. History and applications of mass-independent isotope effects. Annu Rev Earth Pl Sc. 2006;34:217–262. [Google Scholar]
- 3.Thiemens MH, Heidenreich JE. The mass-independent fractionation of oxygen—a novel isotope effect and its possible cosmochemical implications. Science. 1983;219:1073–1075. doi: 10.1126/science.219.4588.1073. [DOI] [PubMed] [Google Scholar]
- 4.Thiemens MH. Meteoritics—new isotopic evidence of early solar-system processes. Nature. 1983;306:18–19. [Google Scholar]
- 5.Clayton RN. Solar system—self-shielding in the solar nebula. Nature. 2002;415:860–861. [Google Scholar]
- 6.Lyons JR, Young ED. CO self-shielding as the origin of oxygen isotope anomalies in the early solar nebula. Nature. 2005;435:317–320. doi: 10.1038/nature03557. [DOI] [PubMed] [Google Scholar]
- 7.Marcus RA. Mass-independent isotope effect in the earliest processed solids in the solar system: A possible chemical mechanism. J Chem Phys. 2004;121:8201–8211. doi: 10.1063/1.1803507. [DOI] [PubMed] [Google Scholar]
- 8.Thiemens MH. Mass-independent isotope effects and their use in understanding natural processes. Isr J Chem. 2002;42:43–54. [Google Scholar]
- 9.Thiemens MH. Atmosphere science—mass-independent isotope effects in planetary atmospheres and the early solar system. Science. 1999;283:341–345. doi: 10.1126/science.283.5400.341. [DOI] [PubMed] [Google Scholar]
- 10.Thiemens MH. Mass-independent isotopic fractionations and their applications. ACS Sym Ser. 1992;502:138–154. [Google Scholar]
- 11.Heidenreich JE, Thiemens MH. A non-mass-dependent oxygen isotope effect in the production of ozone from molecular-oxygen—the role of molecular symmetry in isotope chemistry. J Chem Phys. 1986;84:2129–2136. [Google Scholar]
- 12.Chakraborty S, Ahmed M, Jackson TL, Thiemens MH. Response to comments on “Experimental test of self-shielding in vacuum ultraviolet photodissociation of CO”. Science. 2009;324:1516. doi: 10.1126/science.1159178. [DOI] [PubMed] [Google Scholar]
- 13.Lyons JR, Lewis RS, Clayton RN. Comment on “Experimental test of self-shielding in vacuum ultraviolet photodissociation of CO”. Science. 2009;324:1516. doi: 10.1126/science.1167717. [DOI] [PubMed] [Google Scholar]
- 14.Yin QZ, Shi XY, Chang C, Ng CY. Comment on “Experimental test of self-shielding in vacuum ultraviolet photodissociation of CO”. Science. 2009;324:1516. doi: 10.1126/science.1170488. [DOI] [PubMed] [Google Scholar]
- 15.Federman SR, Young ED. Comment on “Experimental test of self-shielding in vacuum ultraviolet photodissociation of CO”. Science. 2009;324:1516. doi: 10.1126/science.1169923. [DOI] [PubMed] [Google Scholar]
- 16.Chakraborty S, Ahmed M, Jackson TL, Thiemens MH. Experimental test of self-shielding in vacuum ultraviolet photodissociation of CO. Science. 2008;321:1328–1331. doi: 10.1126/science.1159178. [DOI] [PubMed] [Google Scholar]
- 17.McElroy MB. Mars—evolving atmosphere. Science. 1972;175:443–445. doi: 10.1126/science.175.4020.443. [DOI] [PubMed] [Google Scholar]
- 18.Nier AO, McElroy MB. Composition and structure of Mars upper atmosphere—results from neutral mass spectrometers on Vikings 1 and 2. EOS T Am Geophys Un. 1977;58:827–827. [Google Scholar]
- 19.Owen T. Mars. Tucson: University of Arizona Press; 1992. p. 1485. [Google Scholar]
- 20.Owen T, Mahaffy PR, Niemann HB, Atreya S, Wong M. Protosolar nitrogen. Astrophys J. 2001;553:L77–L79. [Google Scholar]
- 21.Fox JL, Hac A. The N-15/N-14 isotope fractionation in dissociative recombination of N-2(+) J Geophys Res-Planet. 1997;102:9191–9204. [Google Scholar]
- 22.Brinkman RT. Mars—has nitrogen escaped. Science. 1971;174:944–945. doi: 10.1126/science.174.4012.944. [DOI] [PubMed] [Google Scholar]
- 23.Fox JL, Dalgarno A. Production of nitrogen-atoms on Mars and their escape. Planet Space Sci. 1980;28:41–46. [Google Scholar]
- 24.Bakalian F, Hartle RE. Monte Carlo computations of the escape of atomic nitrogen from Mars. Icarus. 2006;183:55–68. [Google Scholar]
- 25.Bakalian F. Production of hot nitrogen atoms in the martian thermosphere. Icarus. 2006;183:69–78. [Google Scholar]
- 26.Liu X, et al. Experimental and coupled-channels investigation of the radiative properties of the N(2)c(4)′(1)Σ(+)(u)-X-1 Σ(+)(g) band system. J Geophys Res-Space. 2008;113:A02304. [Google Scholar]
- 27.Liang MC, Heays AN, Lewis BR, Gibson ST, Yung YL. Source of nitrogen isotope anomaly in HCN in the atmosphere of Titan. Astrophys J. 2007;664:L115–L118. [Google Scholar]
- 28.Ivanova MA, et al. The Isheyevo meteorite: Mineralogy, petrology, bulk chemistry, oxygen, nitrogen, carbon isotopic compositions, and Ar-40-Ar-39 ages. Meteorit Planet Sci. 2008;43:915–940. [Google Scholar]
- 29.Prombo CA, Clayton RN. A striking nitrogen isotope anomaly in the Bencubbin and Weatherford meteorites. Science. 1985;230:935–937. doi: 10.1126/science.230.4728.935. [DOI] [PubMed] [Google Scholar]
- 30.Briani G, et al. Pristine extraterrestrial material with unprecedented nitrogen isotopic variation. Proc Natl Acad Sci USA. 2009;106:10522–10527. doi: 10.1073/pnas.0901546106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ermler WC, Clark JP, Mulliken RS. Ab initio calculations of potential-energy curves and transition moments of 1-Epsilon+/G-State and 1-Epsilon+/U-State of N-2. J Chem Phys. 1987;86:370–375. [Google Scholar]
- 32.Ermler WC, McLean AD, Mulliken RS. Ab initio study of valence state potential-energy curves of N2. J Phys Chem. 1982;86:1305–1314. [Google Scholar]
-
33.Stark G, et al. Oscillator strengths and line widths of dipole-allowed transitions in
 between 89.7 and 93.5 nm. J Chem Phys. 2008;128:114302–114310. doi: 10.1063/1.2834933. [DOI] [PubMed] [Google Scholar]
between 89.7 and 93.5 nm. J Chem Phys. 2008;128:114302–114310. doi: 10.1063/1.2834933. [DOI] [PubMed] [Google Scholar] -
34.Haverd VE, Lewis BR, Gibson ST, Stark G. Rotational effects in the band oscillator strengths and predissociation linewidths for the lowest
 —X1
—X1  transitions of N2. J Chem Phys. 2005;123:214304. doi: 10.1063/1.2134704. [DOI] [PubMed] [Google Scholar]
transitions of N2. J Chem Phys. 2005;123:214304. doi: 10.1063/1.2134704. [DOI] [PubMed] [Google Scholar] -
35.Lewis BR, et al. Lifetime and predissociation yield of

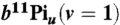 revisited: Effects of rotation. J Chem Phys. 2005;123:236101. doi: 10.1063/1.2137722. [DOI] [PubMed] [Google Scholar]
revisited: Effects of rotation. J Chem Phys. 2005;123:236101. doi: 10.1063/1.2137722. [DOI] [PubMed] [Google Scholar] - 36.Lewis BR, et al. Structure and predissociation of the 3p sigma D-u(3)Σ(+)(u) Rydberg state of N-2: First extreme-ultraviolet and new near-infrared observations, with coupled-channels analysis. J Chem Phys. 2008;129:204304. doi: 10.1063/1.3023034. [DOI] [PubMed] [Google Scholar]
- 37.Wu CYR, et al. Fluorescence excitation spectra of the b(1)Pi(u), b′(1)Σ(+)(u), c(n)(1)Pi(u), and c(n)′(1)Σ(+)(u) states of N-2 in the 80–100 nm region. J Chem Phys. 2007;127:084314. doi: 10.1063/1.2768923. [DOI] [PubMed] [Google Scholar]
- 38.Ubachs W, Velchev I, Lange Ad. Predissociation in b(1)Pi(u),v (v = 1, 4, 5, 6) levels of N-2. J Chem Phys. 2000;112:5711–5716. [Google Scholar]
-
39.Vazquez GJ, Amero JM, Liebermann HP, Lefebvre-Brion H. Potential energy curves for the
 and 1,3Π states of CO. J Phys Chem A. 2009;113:13395–13401. doi: 10.1021/jp902730d. [DOI] [PubMed] [Google Scholar]
and 1,3Π states of CO. J Phys Chem A. 2009;113:13395–13401. doi: 10.1021/jp902730d. [DOI] [PubMed] [Google Scholar] -
40.Sprengers JP, Ubachs W, Baldwin KGH, Lewis BR, Tchang-Brillet WUL. Extreme ultraviolet laser excitation of isotopic molecular nitrogen: The dipole-allowed spectrum of
 and 14N 15N. J Chem Phys. 2003;119:3160–3173. [Google Scholar]
and 14N 15N. J Chem Phys. 2003;119:3160–3173. [Google Scholar] -
41.Stahel D, Leoni M, Dressler K. Nonadiabatic representations of the
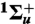 and
and  states of the N2 molecule. J Chem Phys. 1983;79:2541–2558. [Google Scholar]
states of the N2 molecule. J Chem Phys. 1983;79:2541–2558. [Google Scholar] - 42.Spelsberg D, Meyer W. Dipole-allowed excited states of N2: Potential energy curves, vibrational analysis, and absorption intensities. J Chem Phys. 2001;115:6438–6449. [Google Scholar]
-
43.Stark G, Huber KP, Yoshino K, Smith PL, Ito K. Oscillator strength and linewidth measurements of dipole-allowed transitions in
 between 93.5 and 99.5 nm. J Chem Phys. 2005;123:214303–214311. doi: 10.1063/1.2134703. [DOI] [PubMed] [Google Scholar]
between 93.5 and 99.5 nm. J Chem Phys. 2005;123:214303–214311. doi: 10.1063/1.2134703. [DOI] [PubMed] [Google Scholar] - 44.Ajello JM, James GK, Franklin BO, Shemansky DE. Medium-resolution studies of extreme ultraviolet emission from N-2 by electron-impact—vibrational perturbations and cross-sections of the C’4 1-Sigma-U+- and B’1-Sigma-U+- State. Phys Rev A. 1989;40:3524–3556. doi: 10.1103/physreva.40.3524. [DOI] [PubMed] [Google Scholar]
- 45.Levine RD. Molecular Reaction Dynamics. Cambridge, UK: Cambridge University Press; 2005. [Google Scholar]
- 46.Geiger J, Schroder B. Intensity perturbations due to configuration interaction observed in the electron energy-loss spectrum of N2. J Chem Phys. 1969;50:7–11. [Google Scholar]
- 47.Faist MB, Levine RD. Collisional ionization and elastic-scattering in alkali-halogen atom collisions. J Chem Phys. 1976;64:2953–2970. [Google Scholar]
- 48.Sprengers JP, et al. Pump-probe lifetime measurements on singlet ungerade states in molecular nitrogen. Chem Phys Lett. 2004;389:348–351. [Google Scholar]
- 49.Walter CW, Cosby PC, Helm H. Predissociation quantum yields of singlet nitrogen. Phys Rev A. 1994;50:2930–2936. doi: 10.1103/physreva.50.2930. [DOI] [PubMed] [Google Scholar]
- 50.Curdt W, et al. The SUMER spectral atlas of solar-disk features. Astron Astrophys. 2001;375:591–613. [Google Scholar]
- 51.Lefebvre-Brion H, Lewis BR. Comparison between predissociation mechanisms in two isoelectronic molecules: CO and N2. Mol Phys. 2007;105:1625–1630. [Google Scholar]
- 52.Fulchignoni M, et al. In situ measurements of the physical characteristics of Titan’s environment. Nature. 2005;438:785–791. doi: 10.1038/nature04314. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.






