Inherent randomness of cell division patterns

In 1665, Robert Hooke described the arrangement of plant cells to be “much like a Honey-comb, but [that] the pores of it were not regular; yet it was not unlike a Honey-comb in these particulars” (1). Since then, the semiregular patterns of cell arrangements have been extensively studied due to their fundamental role in plant morphogenesis and their visual beauty. Cell division is a key factor determining cellular patterns, which raises the question of what mechanisms control when and how a cell divides. Rules that aim at predicting the position of the division plane, given the shape or growth directions of the cell, have been proposed since the 19th century (2, 3). More recently, the quest for such rules has been aided by computational models that facilitate the comparison of different rules (4). However, all these rules and models have failed to reproduce patterns that match the observations exactly. One possible interpretation of this discrepancy may be that some essential ingredient of the deterministic patterning mechanism is yet to be discovered. In an elegant PNAS paper, Besson and Dumais (5) propose a fundamentally different perspective, according to which the discrepancies between the models and real patterns are due to the inherent randomness of the patterning process. This randomness also explains the variability of patterns produced in similar conditions. Seeking an exact prediction of a cell division pattern is thus as futile as attempting to predict the exact sequence of numbers produced by repetitively throwing a die. Only the statistical characteristics of these processes, as opposed to individual outcomes, can be meaningfully anticipated.

Besson and Dumais (5) focus on the Errera rule, which postulates that a cell divides along the surface of the least area that halves the cell's volume (2–6). Previous studies have shown that in the absence of other cues, such as the preestablished polarity of a tissue, the Errera rule describes well the general visual appearance and statistical properties of the cell division patterns observed in experiments (4). However, departures from this rule are also commonly observed. To explain these departures, Besson and Dumais modified the Errera rule by proposing that a new wall need not have a globally minimal area, but may also be inserted in positions that correspond to local minima. Given this set of alternatives, a specific wall position is selected at random, with probabilities depending on the differences in the areas of candidate walls. The probability that a wall will be selected as predicted by the Errera rule is thus high in cells in which the difference between the area of the globally minimal wall and the other candidate walls is large. This probability is decreased in cells that have several candidate walls with an area close to the global minimum (Fig. 1).

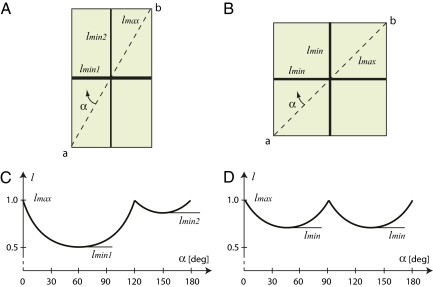
Fig. 1.

Principle of the stochastic extension of the Errera rule. Schematic cells (A and B) and the size l of a hypothetical division plane rotating with respect to the original orientation ab by angle α (C and D). In the elongated cell (A), the global minimum l_min1 is much smaller than the local minimum l_min2. In this case, the division plane will likely correspond to the global minimum l_min1, as predicted by the Errera rule. In the square cell (B), both minima l_min are equal, and either orientation can be chosen with the same probability.

To quantify the selection process, Besson and Dumais (5) consider a stochastic biomechanical model of cytoskeleton strands that link the cytoplasm surrounding the nucleus with the cortical cytoplasm and anticipate the position of the division plane. As first observed by Lloyd (3), these strands behave like stretched springs that minimize their energy by forming the shortest path possible. This minimization takes place in the presence of random fluctuations that dynamically reconfigure and reallocate the strands to different walls while preserving their combined length. The formation of shorter strands is thus favored, but the formation of longer strands is not precluded. This process is analogous to distributing particles subject to both gravity and random motion in a landscape with hollows of different depth. Most particles will be concentrated in the deepest hollows, but some may appear in shallower hollows as well.

Within a cell, the distribution of strands is calculated by maximizing the entropy of the system. Calculations show that the number of strands between the nucleus and a particular wall decreases exponentially with the length of the strands. By associating this number with the probability of forming a specific division plane, Besson and Dumais (5) conclude that this probability also decreases exponentially with the size of the plane. The rate of decrease was determined experimentally by fitting the exponential formula to data obtained for a green alga, a fern, and two flowering plants. The formula captures well the distribution of the division planes in these diverse, taxonomically distant organisms.

The idea that departures from the Errera rule represent stochastic fluctuations that can be elegantly quantified by maximizing entropy is beautiful in its simplicity. It addresses the long-standing problem of characterizing the patterns of cell divisions by reducing a biological process to statistical mechanics. The results of Besson and Dumais (5) have important methodological implications, as they suggest that finding a deterministic rule that predicts the patterns of cell divisions exactly is fundamentally impossible. These findings are also relevant to computational plant models, in which tissues with dividing cells provide a basis for models of higher-level processes, such as phyllotaxis (7) or the formation of leaf venation patterns (8).

The innovative perspective afforded by the work of Besson and Dumais (5) gives rise to numerous research questions, one of which concerns extensions to asymmetric divisions, such as those preceding the formation of stomata. Could such divisions be characterized as maximization of entropy in situations where the nucleus is moved from the centroid of the cell? Another problem is the nature of the constant that characterizes the decrease in the probability of division plane selection accompanying the increase in its area. Could this constant be derived from the fundamental biomechanical properties of the macromolecules forming the cytoskeleton? Finally, the notion of entropy has interwoven meanings in statistical mechanics and information theory. Could the process of division plane selection, which is presented by Besson and Dumais (5) in the language of statistical mechanics, be alternatively described as a decision-making process where the information discerning the options is more or less significant? It is exciting to see that studies of cell patterns, initiated by 17th-century microscopic observations and augmented with 19th-century geometric rules, continue to inspire modern research, bridging traditional and current biology.