Symmetry considerations and development of pinwheels in visual maps

Abstract

Neurons in the visual cortex respond best to rod-like stimuli of given orientation. While the preferred orientation varies continuously across most of the cortex, there are prominent pinwheel centers around which all orientations are present. Oriented segments abound in natural images and tend to be collinear; neurons are also more likely to be connected if their preferred orientations are aligned to their topographic separation. These are indications of a reduced symmetry requiring joint rotations of both orientation preference and the underlying topography. We verify that this requirement extends to cortical maps of monkey and cat by direct statistical analysis. Furthermore, analytical arguments and numerical studies indicate that pinwheels are generically stable in evolving field models that couple orientation and topography.

The preferential response of cells in the primary visual cortex to lines of a particular orientation has been known for >40 years (1) yet remains a subject of intense experimental study and modeling. Early models were simple structural arrangements of local isoorientation columns into regular arrays (2–4). Intricate maps of global patterns of orientation preference over the cortex, obtained by optical imaging (5, 6), revealed more complex arrangements. Thus, later models focused on the development of orientation preference (OP) in networks of neurons whose connectivity is modified in response to stimuli (7–9). Obtaining large-scale patterns of OP with many pinwheels is computationally costly with the later models (10); drastically simplified models generate large static maps essentially from bandpass-filtered white noise (11–13).

Analytical understanding of the development of visual maps and its connections to other problems in pattern formation is best obtained in terms of evolving fields. In this framework, OP is modeled by a director field, 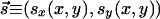, indicating the preferred orientation at location 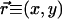on the cortex. The field 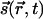then evolves in time according to some development rule that depends on its configurations at earlier times (14, 15). Wolf and Geisel (WG) (16) have shown that a large number of such evolutions can be summarized through a dynamical equation, 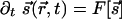. [WG combine the two components into a single complex field, z = (s_x + is_y)².] Common elements in models of evolving fields are: (i) Starting from an initial condition with little OP, there is rapid onset of selectivity governed by 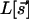, the linear part of the functional 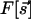. The characteristic length scale observed in cortical maps is implemented by a linear operator that causes maximal growth of features of wavelength Λ, i.e., acting as a band-pass filter, in the parlance of circuits. It is possible to follow the linear development analytically: WG (16) show that the density of pinwheels [zeros of the field 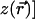] has to be larger than π/Λ² in this regime. (ii) Because the linear evolution leads to unbounded growth of OP, nonlinearities are essential for a proper saturation of the field. Although analytical studies of nonlinear development are difficult, numerical simulations indicate that the OP patterns continue to change (albeit more slowly) even after their magnitudes have saturated. More importantly, the pinwheels typically annihilate in pairs, giving way to a rainbow pattern of wavelength Λ. To maintain pinwheels, development has to be stopped, or extrinsic elements such as inhomogeneities that trap the pinwheels have to be introduced. Constant stirring by sufficiently strong external noise can also lead to dynamic creation and annihilation of pinwheels, but our focus is on evolving fields where the only randomness is in the choice of initial conditions. Because the neural processes that lead to OP are still not fully understood, the stability of pinwheels has not been a topic of much study among neuroscientists. Nevertheless, the search for intrinsically stable pinwheel patterns has motivated some recent studies (17, 18). We propose here an alternative explanation, demonstrating that evolving field models with proper rotational symmetry generically lead to patterns with stable pinwheels.

Symmetry considerations are paramount in problems of pattern formation. Because all directions are more or less equally present in cortical maps, practically all models of OP [certainly those summarized in WG (16)] assume that different orientations are equivalent. In fact (as we also found in our analysis of monkey map), not all orientations are equally represented. This type of anisotropy indicates the absence of any form of rotation symmetry and should not be confused with the distinction between full and joint rotation symmetries, which is the subject of this article. The former is compatible with rainbow patterns and does not appear to play a role in the stability of pinwheels. We verified this explicitly by numerical simulations in models with a preference for the horizontal direction (also available as supporting information, which is published on the PNAS web site). 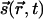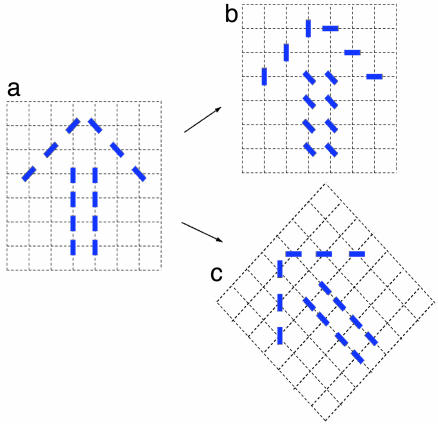The full rotational symmetry is implemented by requiring the evolution of to be unchanged if all angles are rotated together. This rotation is independent of the topographic space 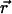, which is also assumed to be isotropic (no preferred directions). Two versions of rotation are illustrated in Fig. 1. Fig. 1b displays a collection of oriented lines that are rotated independently of the background grid from Fig. 1a. We propose that the appropriate symmetry for OP maps is simultaneous rotations of the orientations and the underlying space, as illustrated in Fig. 1c.

Fig. 1.

(a) The image of an arrow formed by oriented solid lines on a topographic grid of dotted lines. (b) Each solid line is rotated counterclockwise by 45° independent of the grid. The thus rotated image bears little resemblance to the original. (c) There is simultaneous rotation of the grid and the solid lines as the whole image is rotated.

The observational evidence for the reduced symmetry is reviewed in Observational Evidence of Reduced Symmetry in Cortical Maps. As suggested by Fig. 1, the absence of full rotation symmetry in natural images is expected and in fact demonstrated in ref. 19. There is also evidence that neural connectivities are preferentially linked along the axis of OP (20). We present a statistical analysis of OP maps from monkey and cat, which also supports the lack of full rotation symmetry. Consequences of reduced symmetry in evolving field models are discussed in Modeling Joint Rotation Symmetry. A linear analysis indicates that the reduced symmetry introduces an additional time scale into the problem and an interval in which the pinwheel density can actually increase by pair creations. Vectorial versions of center-surround interactions are then used in numerical simulations of models with joint rotation symmetry. The simulations result in patterns with intrinsically stable pinwheels and histograms of OP similar to those obtained from cat and monkey maps.

Observational Evidence of Reduced Symmetry in Cortical Maps

Casual consideration of scenes strongly suggests that the persistence of edges of stationary objects (as in Fig. 1) or of tracks of moving ones leads to oriented segments that cannot be rotated independent of their background. This expectation has been confirmed and quantified by statistical tests in ref. 19, where an orientation was assigned to each pixel of images from the natural world. The primary query of ref. 19 was the range and directionality of correlations in orientation. Sigman et al. observed that correlations depend on the relative angles in the topographic space, in a manner consistent with a collection of circles.

Because the task of the visual system is to extract information from observed images, it is likely that the neural connections that carry out the associated computations are influenced by symmetries and anisotropies of the natural scenes. Contemplation of the Hebbian rule (21), “neurons that fire together wire together,” suggests that there should be more connections between neurons whose shared OP is collinear to their topographic separation. Indeed, biocytin injections that map the horizontal connections of neurons have been combined with optical imaging of the primary visual cortex of the tree shrew (20). Connections from an injection site are anisotropic, preferentially extended along the axis of OP at the site. Although less pronounced, similar anisotropies are also observed in maps from monkey (22) and cat. Such connectivities are incompatible with rotations of OP independent of the underlying topography. A map with all OPs rotated by a fixed angle would require a different set of horizontal connections.

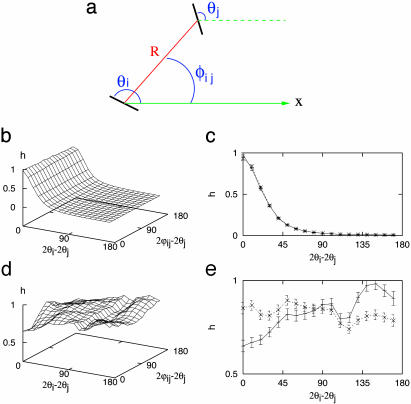
To test the hypothesis that cortical maps of OP also reflect the reduced rotation symmetry, we undertook statistical tests of a map of monkey (in the form of 360 × 480 pixels; provided by K. Obermeyer, Technical University of Berlin, Berlin). At each point i of the map, there is an orientation angle θ_i, measured relative to an arbitrary axis; and two points i and j, separated by a distance R form an angle φ_ij with the same axis, as indicated in Fig. 2a. Binning into intervals of 10°, we make joint histograms of the form 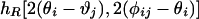. (The factor of two is introduced because the orientation is defined from 0 to π.) The second argument measures the angle relative to the line-joining points i and j. If the orientations are independent of topography, the histograms should be independent of their second argument. This is not the case for the monkey histograms shown on the left column in Fig. 2; the right column of Fig. 2 shows cross sections at 2(φ_ij - θ_j) = 0° and 90°, which display maximal contrast for parallel orientations. The larger probability for 2(φ_ij - θ_j) = 90° does not violate expectations based on collinear orientations, because we do not know the actual topographic axis in our monkey map. The choice of an arbitrary axis does not modify θ_i - θ_j but shifts the histograms along 2(φ_ij - θ_j). The advantage of our method is the ability to detect lack of full rotation symmetry in the absence of knowledge of topographic axis, but the lack of this information prevents making a connection to correlations in visual inputs.

Fig. 2.

Histograms of OP from a cortical map of monkey. (a) The relative orientation between two pixels i and j at a distance R is one argument of the histogram; the second is the OP of one point measured relative to the line joining the two pixels (at angle φ_ij). Full histograms are shown on the left, whereas the right is for 2(φ_ij - θ_j) = 0° (solid line) or 90° (dotted line) (b and c) Short separations of 5–10 pixel spacings with no dependence on the relative angle. By contrast, there is a small but clear indication of a coupling to the underlying topography in d and e, which are taken at distances of 70–75 pixels, comparable to the separations of pinwheels. Such dependence indicates the lack of full rotation symmetry in the map.

Fig. 2 b and c are at separations R, which are a fraction of the typical distance between pinwheels and show no indication of any dependence on topography. By contrast, Fig. 2 d and e correspond to values of R comparable to pinwheel separations. There is now a small but distinct dependence on the orientation of the line between two points, indicating that the OPs do not follow a distribution with full rotational symmetry. Similar results were obtained for maps from cat (204 × 372 pixels; provided by M. Sur and J. Schummers, Massachusetts Institute of Technology, Cambridge) and are available as supporting information. In both cases, the dependence on the second argument is small (at most ≃20%), and some assessment of its statistical significance is needed. Because we had access to only one map in each case, we made an indirect estimate of statistical error by constructing an artificial ensemble of 2,000 histograms though random samplings of 2.9% of total pixels in the monkey map. (As described in the supporting information, we tested this sampling procedure on maps generated by numerical simulations.) From the thus-included error bars in Fig. 2e, we conclude that the differences fall outside statistical errors.

Modeling Joint Rotation Symmetry

We believe that the restriction to joint rotation symmetry is an essential aspect of the OP maps and should be incorporated into models and analytical studies. In computational models with neural networks (10), this reduction in symmetry is naturally achieved through the choice of a proper training set of images. How should this be implemented in analytical models of evolving fields? If the inputs to locations (such as i and j in Fig. 2) are predominantly parallel, a Hebbian interaction between them would evolve to minimize θ_i - θ_j. If the OP at i is indicated by a vector 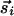, this interaction can be written as 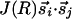. Such an interaction, however, makes no reference to the relative orientation 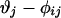and thus cannot represent a response to a preponderance of inputs that are collinear with the topographic (unit) vector r̂_ij. 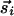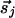To account for the latter, we could have distinct interactions between components of and that are parallel or perpendicular to r̂_ij; the difference between them can be represented by a new interaction of the form 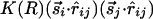. 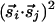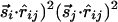[More precisely, we should use interactions of the form and that are invariant under 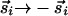, because both vectors indicate the same orientation. Such modifications unduly complicate the presentation and analysis without changing the essence of our results.] With this distinction, when 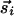and 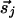are parallel (perpendicular) to r̂_ij, the strength of interaction is J(R) + K(R)(J(R)).

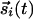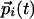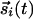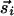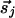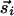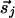As a specific model, let us assume a set of , stimulated by inputs , and interactions between them that reflect the average activity of over previous times. The joint activity of and contributions can be decomposed into two components, and , that are parallel to r̂_ij or perpendicular to it. Both cases contribute to the isotropic interaction 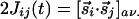, whereas the component parallel to r̂_ij gives rise to the interaction 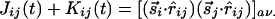. In the initial stages, the couplings are small, and 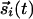merely follow the inputs 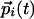. The couplings then evolve to reflect the statistics of inputs: A tendency for the 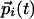and 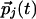to be parallel leads to a positive J_ij, whereas if and only if these inputs also tend to be collinear, a finite K_ij is generated. 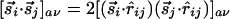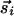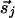Note that if K_ij = 0, we have due to equal contribution from and that are parallel to r̂_ij, and perpendicular to r̂_ij. As the dynamics proceeds further, the increased couplings could well freeze 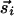to a particular pattern. The interactions then follow suit and become correlated to the frozen orientations. Such a scenario could well account for the correlations between OP and connectivity observed in the tree shrew (20). Other procedures for obtaining synaptic couplings from input activities (23–25), once generalized to orientations with proper correlations, lead to similar results. However, our intention is not to promote a particular scenario but to emphasize that any interactions not specifically ruled out by symmetry will generically be present. In the following, we shall explore some consequences of joint rotation symmetry on the evolution of the patterns.

Linear Analysis. To underscore the difference between the two forms of rotation symmetry, let us consider the regime of linear evolution, which is analytically tractable. Due to translation symmetry, the problem is simplified in terms of the Fourier modes 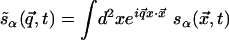, where α = 1, 2 (or x, y) labels the two components of the vector s̃. After Fourier transforming the interactions J(R) and K(R) introduced above, the linear evolution equation takes the form

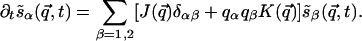[1]

Due to the assumed isotropy, the functions J and K depend only on the magnitude of the vector 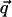. For example, they can be band-pass filters peaked at q̄ = 2π/Λ to reproduce the power spectrum of cortical maps. In the case of full rotation symmetry, invariance of the equations under independent rotations of 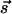and 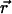requires K(q) = 0. However, if 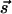and 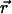can only be rotated together, a finite K(q) is possible and should be generically present. (One way to see this is that 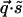is invariant under joint rotations but not separate rotations of 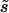and .)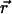

A finite K(q) mixes the evolution of the two components s̃₁ and s̃₂. This mixing can be removed by decomposing the field s̃ into longitudinal and transverse components. For a given 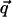, the longitudinal component is parallel to 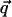, and the transverse component is perpendicular to it. Under the action of the linear operator in Eq. 1, the two components grow as e^{[J(q)+q2K(q)]t} and e^J(q)t. If K(q) = 0 (full rotation symmetry), the two modes grow at the same rate, over a time scale τ₁(q) ∼ 1/J(q). Even a small K(q) breaks this degeneracy, introducing a second time scale τ₂(q) ∼ 1/[q²K(q)], over which the effects of anisotropy become apparent.

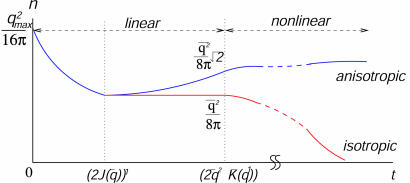
Note that when the two modes grow at the same rate [K(q) = 0], an equal superposition to these modes is compatible with a rainbow pattern that does not contain any nodes. (Of course, the rainbow is one of many possible patterns.) However, K(q) is generically nonzero for a joint rotation symmetry, and one of the two modes eventually dominates the other. The dominance of transverse or longitudinal components increases the density of zeros and is incompatible with rainbow patterns. We repeated the analysis of WG (16) for the density of pinwheels in the linear regime, in the presence of a small K(q). The calculation is cumbersome and relegated to the supporting information, but the final result for the evolution of pinwheel density is depicted in Fig. 3. The initial random pattern has a high density that rapidly decreases in a time of order τ₁ ∼ J(q̄)^-1 to the limiting value of π/Λ² predicted by WG. This is the case for both isotropic [K(q) = 0] and anisotropic [K(q) ≠ 0] cases. However, pinwheel density then goes up by a factor of 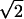for the anisotropic case on a time scale of τ₂ ∼ [q̄² K(q̄)]^-1, whereas it remains as π/Λ² for the isotropic case. As explained in the supporting information, the factor of 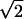is the outcome of an approximate evaluation of density, which is analytically tractable. We also performed simulations that confirmed an increase in density by a small factor of ≈1.12. Although the increase in density is small, it nonetheless implies (pair) creation of pinwheels in the anisotropic case, a phenomenon that is absent in the isotropic models. Note that the ultimate density ratio between isotropic and anisotropic cases is a universal number, independent of the degree of anisotropy. The strength of K(q) dictates only the time scale over which the density increases and not its ultimate value.

Fig. 3.

Schematic depiction of the evolution of the density of zeros for isotropic (red line) and anisotropic (blue line) interactions. Anisotropy results in an increase of the density of pinwheels in the latter stages of linear regime. The nonlinear extrapolation is based on simulation results.

Simulations. Although the above arguments from the linear regime strongly suggest that joint rotational symmetry promotes pinwheel stability, verification of this hypothesis comes from simulations of the nonlinear evolution. For the latter, 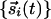was placed on a lattice of points of locations 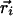and evolved in time according to

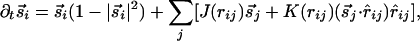[2]

where 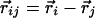has magnitude r_ij along the unit vector r̂_ij. The nonlinearity appearing in the first term on the right-hand side stabilizes the magnitude of 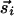to unity. The linear evolution is governed by a vectorial center-surround filter, composed of two parts: (i) A standard center-surround filter with positive couplings J_s in a circle of size R/2 ∼ Λ and negative values J_l in an annulus from R/2 to R. (ii) Additional couplings in the annular region that explicitly depend on orientations relative to the lines joining lattice points and invariant only under joint rotations. We use positive long-range couplings K to mimic the preferential horizontal connectivity of cooriented coaxially aligned receptive fields, as reported in ref. 20. [Similar kinds of anisotropic interactions were also used in a model for dynamics of neural activity in the visual cortex (26). The anisotropic coupling by lateral neural connectivities was also obtained and associated with pinwheel structure in ref. 24.]

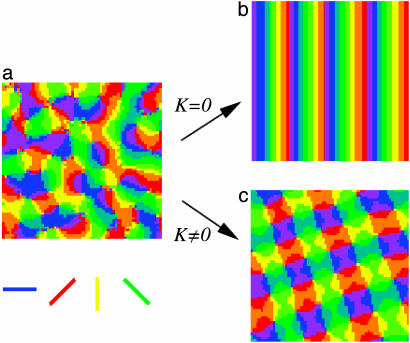
Simulations are started on an L × L lattice with initial values of 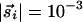, equally distributed over all angles, with J_s = 0.01, J_l = -0.0039, and R = 10. As shown in Fig. 4a, undifferentiated initial conditions quickly develop into a pattern with pinwheels reminiscent of actual maps. Further evolution depends on the symmetry of development rules. Full rotation symmetry with K = 0, and the action of ii above turned off, leads to a rainbow state with no pinwheels at long times, as in Fig. 4b. However, reduction of this symmetry by adding interactions in ii with K = 0.0039 above eventually results in a square lattice of pinwheels, as in Fig. 4c. Naturally, we do not imply that pinwheels in cortical maps form a square lattice (various inhomogeneities could easily trap these vortices in a distorted arrangement), but that they are intrinsically stable under such development rules. The precise choice of long-range couplings is not important in this regard, and we observed pinwheel patterns with other types of anisotropic coupling (some are also available in the supporting information).

Fig. 4.

(a) The development of a random initial condition by typical center-surround (bandpass) filter leads to a collection of pinwheels. The filter used in b has full rotation symmetry [K(r) = 0 in Eq. 2]. In this case, the pinwheels annihilate in pairs, giving way to a rainbow pattern at long times. (c) By contrast, a model with joint rotation symmetry evolves to a stable pattern of pinwheels. This figure was generated by the vectorial center–surround filter in Eq. 2, with a nonzero K(r).

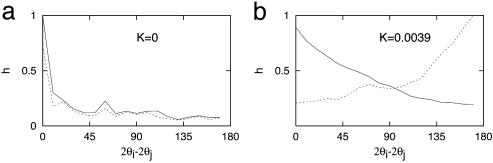
Not surprisingly, the anisotropic couplings lead to correlations between OP and the topographic angles. We repeated the histogram analysis of actual maps with those generated by numerical simulations, and some results are plotted in Fig. 5. There is no dependence on topography for K = 0, as depicted in Fig. 5a, which shows two relative angle histograms for 2(φ_ij - θ_j) = 0° and 2(φ_ij - θ_j) = 90°. For K ≠ 0, there are positive correlations in relative angles for 2(φ_ij - θ_j) = 0° and negative correlations for 2(φ_ij - θ_j) = 90° (Fig. 5b). The topographic dependence is robust and does not significantly depend on the strength of the anisotropic coupling.

Fig. 5.

Histograms of relative angles for 2(φ_ij - θ_j) = 0° (solid line) and 2(φ_ij - θ_j) = 90° (dotted line) with isotropic (K = 0) (a) and anisotropic (K = 0.0039) (b) interactions.

Conclusion

Collinearity is a prominent characteristic of line segments in natural images. It is reasonable to expect that cortical maps of OP reflect a corresponding tendency. A basic consequence of the tendency of line segments to be collinear is the absence of a full rotation symmetry, independent of the underlying topography. We demonstrate the lack of full symmetry by analyzing histograms of monkey and cat maps. We then explore consequences of reduced symmetry on the behavior of evolving fields of OP. In the linear regime, we find that the interactions allowed generate a time scale over which the pinwheel density can actually increase. Numerical simulations confirm that this tendency persists in the nonlinear regime, resulting in patterns with stable pinwheels.

Although the stability problem of pinwheels in OP maps is not widely appreciated, it has been the motivation for two other recent studies. In ref. 17, a different coupling between neurons is used based on a wiring length minimization principle, whereas in ref. 18 higher-order nonlinearities are used in place of the stabilizing 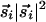term in Eq. 2. Although these models lead to stable patterns of pinwheels, they cannot account for the anisotropic features of actual OP maps, because both have full rotation symmetry. A potential relation between the symmetries and correlations of line segments in natural images and the statistics of OP maps (including stability and arrangement of pinwheels) may provide further clues to how visual information is processed by the brain.