Single-molecule resolution of interfacial fibrinogen behavior: Effects of oligomer populations and surface chemistry

Abstract

Using single-molecule total internal reflection fluorescence microscopy, the dynamic behavior of fibrinogen was observed at the interface between aqueous solution and various solid surfaces. Multiple populations of objects were observed, as characterized by surface residence times, interfacial diffusion, and fluorescence intensity. On all surfaces, populations exhibited direct links between surface residence time, rate of diffusion and fluorescence intensity. In particular longer-lived populations diffused more slowly and exhibited greater fluorescence intensity, leading to the conclusion that the objects represented fibrinogen monomers and discrete oligomer populations (dimers, trimers, etc.), and that these oligomer populations play an important role in the protein-surface interaction because of their long surface residence times. Two or three diffusive modes were observed for most populations, indicating that protein aggregates have multiple mechanisms for interaction with solid substrates. In addition, the fastest diffusive mode is believed to represent a hopping mode that often precedes desorption events. Surprisingly, a monolayer of PEG(5000) increased surface residence time and slowed diffusion of fibrinogen relative to bare fused silica or hydrophobically-modified fused silica, suggesting that the mechanism of PEG resistance to protein adhesion is more sophisticated than the simple repulsion of individual proteins.

Introduction

Biomaterials used for in vivo applications are often chemically inert with respect to specific interactions with cells and proteins. Nonspecific protein adsorption at the solid-liquid interface is problematic, however, as proteins may functionalize the inert biomaterial surface to support more pathological processes such as inflammation and thrombosis. In particular, fibrinogen adsorption is of primary concern due to its abundance in plasma. Fibrinogen is a 340 kDa glycoprotein that consists of two identical subunits that each contain three unique chains (α,β,γ).^{1, 2} Two sequences on the γ chain (γ_190–202 and γ_377–395) are recognized synergistically by the phagocyte integrin, Mac-1, and can lead to inflammatory and wound-healing responses.^{3, 4} These sequences were found to be inaccessible to Mac-1 in native fibrinogen but are presented upon fibrinogen denaturation or polymerization to fibrin.^{3, 5} Additionally, the platelet integrin, GPIIa-IIIb, binds to both an RGD (arg-gly-asp) sequence on the a-chain and a 12 amino acid sequence on the C-terminus of the γ chain.^{2, 6, 7} Aggregation of activated platelets at the biomaterial surface can lead to thrombosis due to increased thrombin production and conversion of solution phase fibrinogen to fibrin.⁸

Due to its importance for the biocompatibility of surfaces in contact with blood, fibrinogen adsorption at solid-liquid interfaces has been extensively studied.^9–15 A qualitative picture has emerged suggesting that some protein molecules in an adsorbed fibrinogen monolayer exhibit reversible binding at the interface while others remain adsorbed for longer than experimentally accessible timescales. Early studies explained this observation by assuming a single adsorbing fibrinogen species that either desorbs or converts to an irreversibly bound state through unfolding or other relaxation processes.^{10, 11, 14} Subsequent work allowed for a single adsorbing species to assume a distribution of protein “footprints” on the surface that correlated with the reversibility of binding.¹⁵ From this later work, it was concluded that the fraction of reversibly-bound proteins increased with protein flux as increased flux decreased the available area for any one protein to spread and relax on the surface.

Surface chemistry has also been shown to affect the behavior of adsorbed fibrinogen. In the work of Hu, Eaton, and Tang, polyethylene terepthalate, polyvinyl chloride and low-density polyethylene were effective at exposing Mac-1 binding sequences while fibrinogen on polyether urethane or polydimethyl siloxane was substantially less immunoreactive.³ In the work of Wertz and Santore, surface chemistry was found to affect the relaxation rates and maximum observable footprint of fibrinogen.¹⁵ Fibrinogen relaxation on hydrophobic surfaces was attributed to slow unfolding events while proteins on hydrophilic surfaces increased their binding strength via reorientations on timescales shorter than those for unfolding.

While protein denaturation and spreading on a surface seems to be an important factor in determining the irreversibility and pathology of adsorbed fibrinogen, the role of heterogeneity in the adsorbing population has received less attention. Light scattering data has shown that monomeric bovine fibrinogen cannot be the only species in solution as the average weight of soluble species is twice that of the monomer.¹⁶ Here and throughout this work, the term monomer refers to the entire 340 kDa protein, rather than one of its two identical subunits mentioned in the introductory paragraph. Although there is disagreement on the exact fractions of monomers and aggregates, size exclusion chromatography data has also shown the presence of soluble aggregates in bovine fibrinogen solutions.¹⁷ This work will test the idea that soluble protein aggregates, small oligomers in particular, with more ways to interact favorably with a surface, have longer residence times than monomers and predispose its constituent proteins to spread and become irreversibly bound.

Experimental studies of the role of aggregation in fibrinogen monolayer formation are possibly absent from the literature because it is difficult to determine the properties of an adsorbing or desorbing species using the ensemble-averaged techniques that have been employed previously (i.e. studying net adsorption or desorption). In the present work, total internal reflectance microscopy (TIRFM) is used at very low surface coverage to track individual species as they adsorb to, diffuse along, and desorb from the solid-liquid interface. This allows a direct measurement of a protein object’s surface residence time, independent of transport phenomena in solution. When combined with analysis of that object’s diffusive behavior and fluorescence intensity, an accurate and direct assessment of protein-surface interactions for oligomeric proteins is possible. This detailed picture of the initial stages of fibrinogen monolayer formation demonstrates that heterogeneity in the adsorbing fibrinogen population leads to diversity in protein-surface interactions.

The role of surface chemistry in this process is also studied due to its importance for biomaterial design. Model hydrophilic and hydrophobic surfaces will be compared along with a protein-resistant polyethylene glycol (PEG) layer due to the ubiquity of PEG in drug-delivery and biomaterial applications.^18–20 It is generally accepted that a densely grafted PEG layer inhibits recognition of PEGylated surfaces by proteins and cells although this inhibition is often incomplete.^21–23 Commonly cited mechanisms for this protein resistance are that stable water layers near the PEG surface or that the steric barrier presented by the flexible polymer chain makes protein adsorption thermodynamically unfavorable.^{24, 25} This work will further explore the PEG-fibrinogen interaction as it pertains to initially adsorbing proteins.

Experimental

Fibrinogen solution

Human fibrinogen, labeled with AlexaFluor® 488 was purchased from Molecular Probes, Inc. The manufacturer-specified degree of labeling was approximately 15 dye molecules per fibrinogen. Phosphate buffered saline (PBS) was purchased from Invitrogen (calcium and magnesium free). Fibrinogen solutions were prepared at concentrations in the range 0.5 × 10⁻¹³ to 0.5 × 10⁻¹² M in order to achieve low surface densities for single-molecule experiments.

Surface preparation

Fused silica (FS) wafers were washed with cationic detergent (Micro 90, International Product Corp.) and thoroughly rinsed with water purified to 18 MΩ cm⁻¹. Wafers were then immersed in warm piranha solution for 1 hour followed by UV-ozone treatment for 1 hour. Following this treatment, FS wafers were either used without further treatment or were coated with monolayers of trimethyl silane (TMS) or methoxy-terminated PEG(5000) silane. To form TMS monolayers, wafers were exposed to hexamethyldisilazine (Sigma) vapors for 18 hours at room temperature. PEG(5000) silane monolayers were formed via a 2 hour solution deposition in which PEG(5000) triethoxysilane (Nanocs) was dissolved in toluene at a concentration of 0.1 mg / mL.

Surface characterization

Contact angle measurements

Static contact angles of functionalized surfaces were measured with a custom-built contact angle goniometer. A 1 μL drop of deionized water was deposited on the surface and at least six drops on three independent samples were averaged for reported values here. Almost complete wetting was observed on bare fused silica to the point that contact angles could not be measured. The static contact angle of the TMS substrate was 94 ± 4°. This value is consistent with a hydrophobic surface and with previous characterization of TMS coated surfaces but smaller than the ~110° contact angle, typical of highly ordered, long chain self-assembled monolayers.^{26, 27} The static contact angle of the PEG(5000) monolayer was found to be 35 ± 1°.^{28, 29} This value is in good agreement with contact angles of methoxy-terminated PEG (MW = 460–590) monolayers (36 ± 1°) and methoxy-terminated PEG(5000) monolayers (33 ± 3°).³⁰

Ellipsometry for PEG monolayers

A single wavelength (632.8 nm), variable angle, null ellipsometer (Multiskop, Optrel, Sinzing, Germany) was used to measure surface density of PEG chains in air. For ellipsometry experiments, PEG(5000) surfaces were prepared on silicon wafers (2” intrinsic, Wafer Reclaim Services, San Jose, CA) as previously described for fused silica substrates. A three layer planar model of the solid surface, considering air and its refractive index, n = 1.003, PEG (n = 1.45), the native silicon dioxide (n = 1.457), and silicon (n = 3.881), was used to simultaneously fit the amplitude ratios, tan Ψ, and phase shifts, Δ, measured at angles between 45° and 70°.³¹ The thickness of the native oxide layer was measured by ellipsometry prior to PEG(5000) functionalization. This technique gave a PEG(5000) layer thickness of 2.4 ± 0.3 nm. At a density of 1 g/cm³, this leads to a grafting density of 0.28 ± 0.04 chains/nm², or 31 ± 4 monomer units/nm². This monomer density is believed to confer protein resistance in human blood serum.³² Higher monomer densities, resulting in an extended brush in which the methoxy terminus of the PEG chain is forced to the PEG-water interface, have been shown to support protein adsorption.²²

Image acquisition

TIRFM measurements were performed using a custom-built prism-based illumination system, flow cell, Nikon TE-2000 microscope with 60x objective and 488 nm Ar ion laser that have been described previously.³³ The flow cell was maintained at 37 ± 0.1 °C and flow was stopped after introduction of the fibrinogen solution. The intensity of the laser illumination was high enough to resolve individual objects in sequential images with a 2 second acquisition time, but low enough to permit continuous observation of objects for several minutes without photobleaching.

The evanescent wave created by total internal reflection has a penetration depth of less than 100 nm and consequently only objects near the surface are excited. While any object within this penetration depth may be excited and fluoresce, those that are not adsorbed to the surface are typically not observed. This is because diffusion coefficients in solution are 2–3 orders of magnitude higher than even the fastest surface diffusion coefficients observed in these experiments and the residence time of any one molecule in the capture region of a single imaging pixel is negligible unless it is adsorbed to the surface. Consequently, objects in solution contribute to higher background levels but are not identified as objects themselves.

Diffraction-limited objects were identified in each frame via convolution with a disk matrix and thresholding.³⁴ Object positions were calculated as the centroid of intensity. Object tracking was accomplished by identifying the closest objects in sequential frames while requiring the distance between closest objects to be less than 3 pixels (810 nm). Surface residence times were calculated as the number of frames on which the object was identified, multiplied by the exposure time of each frame. The error in this measurement was assumed to be the exposure time divided by √2 due to the fact that an object is not necessarily present for the entire first and last frames in which it is observed. Objects that were not observed to both adsorb and desorb were ignored due to the uncertainty in assigning their residence time. The intensity of an object in each frame was determined by integration of all pixels assigned to that object by the disk convolution and thresholding algorithm and local background subtraction was also performed.

Data analysis

Residence times

The surface residence time of a given fibrinogen population is assumed to follow first-order desorption kinetics and consequently the integrated or cumulative residence time distribution can be described as the sum of all such populations

$$p(t)=\sum _{i=1}{f}_i{e}^{-t/{\tau }_i},$$ (1)

where p(t) is the probability that a given object will have a residence time greater than or equal to time t. Each population is denoted with the subscript, i, and τ_i is the inverse of the first-order desorption rate constant for that population (i.e. that population’s mean surface residence time). The relative fraction of all analyzed objects represented by population i is f_i. In this work, cumulative distributions are preferable to raw desorption probability distributions because experimental data can be displayed and modeled without artifacts from binning into discrete residence time groups (for residence time data) or squared-displacement groups (for diffusion data).

The experimental residence time distribution was constructed by first accounting for the finite length of a movie whereby the adsorption and desorption of an object has a lower a priori probability of being observed for longer residence times because there are fewer opportunities to observe both events in a finite window. The number of objects observed to have a given residence time (n_t) was multiplied by a correction factor, c(t), given by

$$c(t)={\left[H(T-t)\left(1-\frac{t}{T}\right)\right]}^{-1}$$

where T is the length of the movie and H is the Heavyside step function. After correcting for finite movie length, the cumulative residence time distribution was therefore given by

$$p(t)=\sum _{t^{\prime }>t}{n}_{t^{\prime }}c(t^{\prime })/\sum _{t^{\prime }}{n}_{t^{\prime }}c(t^{\prime }).$$

Counting the number of objects with a given residence time (n_t) is assumed to follow Poisson statistics and the error shown for each data point in the cumulative distribution represents 68% confidence intervals for a Poisson distribution with a mean of ${\displaystyle \sum _{t^{\prime }>t}}{n}_{t^{\prime }}$ scaled using the appropriate correction factor. Cumulative residence time distributions from multiple movies were averaged with a relative weight of the number of objects observed in that movie.

Diffusion

By default, one expects interfacial diffusion to follow two-dimensional Gaussian random-walk statistics where the probability of finding an object at a distance, r, away from its initial position after a time interval of Δt is given by

$$p(r,\mathrm{\Delta }t)={(2D\mathrm{\Delta }t)}^{-1}{re}^{-\frac{r^2}{4D\mathrm{\Delta }t}}$$

where D is the diffusion coefficient. Often it is more convenient to view this probability distribution in its integrated form (the so-called cumulative squared-displacement distribution),

$$C(R^2,\mathrm{\Delta }t)=e^{-\frac{R^2}{4D\mathrm{\Delta }t}},$$

which represents the probability that an object will diffuse a distance ≥ R in a time interval Δt.

If a diffusing object is capable of multiple modes of diffusion each characterized by a diffusion coefficient, D_j, its cumulative squared-displacement distribution is simply the sum of the cumulative distributions for each mode weighted by the fraction of observed steps, x_j, corresponding to that mode

$$C(R^2,\mathrm{\Delta }t)=\sum _j{x}_j{e}^{-\frac{R^2}{4D_j\mathrm{\Delta }t}}$$ (2)

and the average diffusion coefficient is taken to be the fraction-weighted average of each mode,

$$\overline{D}=\sum _j{x}_j{D}_j.$$

The experimental cumulative squared-displacement distribution is calculated as described previously³³ by sorting the squared displacement data in ascending order and ranking each data point. Thus, C(R_k², Δt) is given by

$$C\left(R_k^2,\mathrm{\Delta }t\right)=1-k/N$$

where k is the rank in the sorted order and N is the total number of sorted data points. The error shown for each data point in the cumulative distribution represents 68% confidence intervals for a Poisson distribution with a mean of N+1-k.

Data fitting

The experimental cumulative distribution of either residence time data or squared-displacement data was fit to equation (1) or (2) by minimizing the variance weighted by the squared error for each data point. For a given dataset, the number of populations used for the fit was increased until populations were found with either characteristic residence time constants or diffusion coefficients that were not statistically different from each other as determined by a t-test to 90% confidence. This modest confidence value was generally found to exclude models with characteristic residence time constants or diffusion coefficients that had the same first significant digit.

Results and Discussion

Heterogeneity in adsorbing fibrinogen

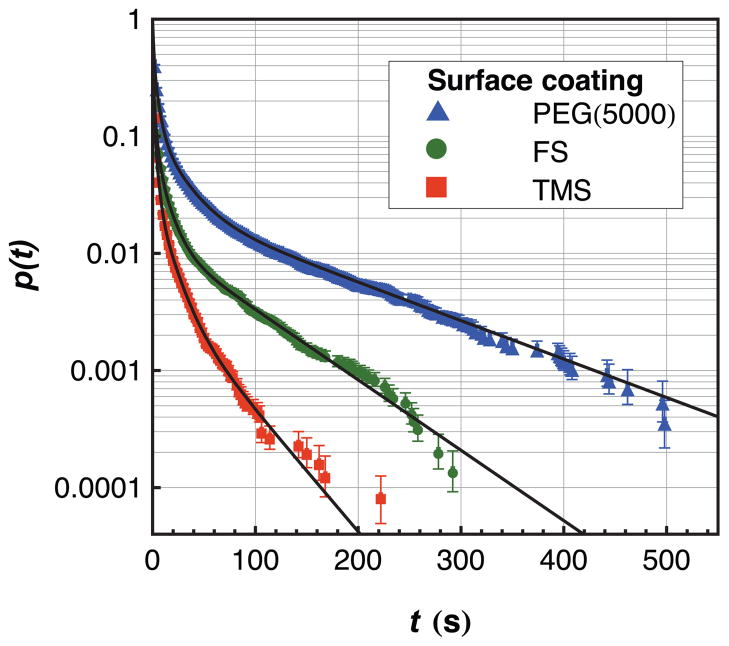
Each object observed in these experiments was characterized by its residence time, median intensity, and surface trajectory. Of these, residence time distributions were examined first in order to identify unique populations of adsorbed fibrinogen. The experimental cumulative residence time distributions on FS, TMS, and PEG(5000) surfaces are shown in Figure 1 along with experimental fits using equation 2 and parameters given in Table 1. These data represent observations of more than 35,000 fibrinogen objects on each type of surface chemistry. Numbers given in parentheses following each value represent uncertainty in the last significant figure given.

Figure 1.

A semi-log plot of the cumulative residence time distribution of fibrinogen on fused silica that has been functionalized with PEG(5000), TMS, or left unfunctionalized after acid treatment. Quadruple-exponential fits to the data (parameters given in Table 1) are shown using solid lines.

Table 1.

Parameters used to fit equation 1 to the cumulative residence time distribution accounting for four sub-populations

Population	Fused Silica		TMS		PEG(5000)
	fi	τi (s)	fi	τi (s)	fi	τi (s)
A	0.73(3)	0.59(5)	0.81(2)	0.65(3)	0.54(2)	1.18(4)
B	0.19(3)	2.6(3)	0.16(2)	2.9(2)	0.31(1)	5.0(3)
C	0.069(7)	10.6(6)	0.028(3)	13(2)	0.104(6)	20.4(9)
D	0.0135(5)	69(2)	0.004(2)	45(8)	0.0437(8)	109(1)

Data from a homogeneous fibrinogen population with a single characteristic residence time would appear as a straight line on the log-linear scale used for Figure 1. This is clearly not the case for any surface chemistry, and this effect is quantified using the parameters in Table 1 where four populations were identified with distinct characteristic residence times. Although population A typically has a characteristic residence time that is shorter than 1 frame (2 seconds), the assignment of this parameter comes from the tail of the distribution that extends to longer residence times. On all surfaces, there is an inverse relationship between characteristic residence time and the relative fraction of that population suggesting that proteins with more favorable surface interactions are increasingly rare compared to those with weaker surface affinity. An obvious explanation for this phenomenon is that larger fibrinogen aggregates have greater surface affinity and are also increasingly rare in solution due to their larger aggregation numbers. Alternatively, one could argue that aggregation is unimportant in the determination of residence time and this phenomenon is caused by preferential adsorption to anomalous “defect” sites. This latter hypothesis is ruled out, however, by the direct correlation between intensity and residence time that is presented in Figure 2 and discussed in the following section. That is, objects with longer residence times appear brighter and the intensity of populations A–D increases in roughly integer multiples moving from A to D.

Figure 2.

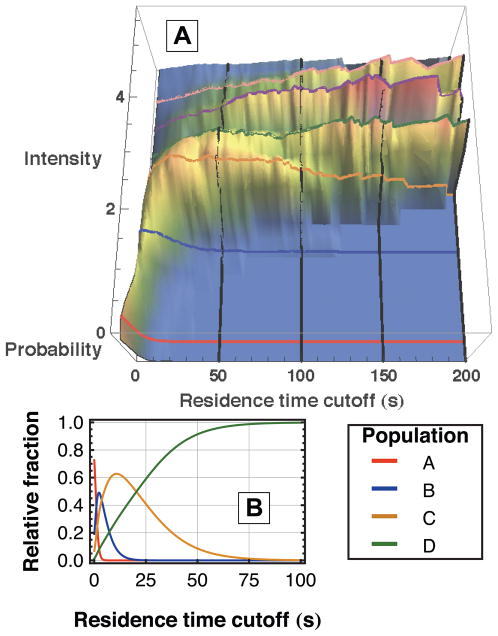
Characteristic intensities exist for fibrinogen populations indicating different aggregation states. (A) The probability distribution of intensities on fused silica is shown as a function of the lowest residence time included in the distribution. Distinct ridges appear in the direction of increasing residence time cutoff that correspond to the values given in Table 2. (B) From the fit parameters to residence time data given in Table 1, the relative fractions of populations A–D are shown as a function of residence time cutoff. This helps to explain the growth and disappearance of the first 4 ridges in (A).

With regards to the population fractions, f_i, in Table 1, little significance should be placed in the comparison of values between different surfaces. Because fibrinogen aggregation in solution may be a kinetic phenomenon, with the protein aggregating over time, details of solution preparation can affect the solution fractions of each aggregate. This means that slight variations in solution preparation could lead to different oligomer fractions that impinge on the surface. Alternatively, one might imagine that surface chemistry somehow affects the observed relative fractions of oligomeric species. This latter hypothesis is ruled out by the observation that experiments done on the same type of surface but on different days frequently had different relative fractions of populations A–D but gave the same characteristic residence times, relative intensity values, and diffusion coefficients.

Fibrinogen aggregates are responsible for heterogeneous behavior

The intensity data for each object provides direct evidence that aggregation is responsible for the heterogeneous behavior observed in the residence time data. In particular, objects with longer surface residence times were observed to have systematically greater fluorescence intensities. In the subsequent analysis, objects were collected that had a residence time greater than a given cutoff value. The probability distribution of fluorescence intensity for these objects was then calculated and normalized. Figure 2A shows these intensity distributions as a function of residence time cutoff for the fused silica surface. It is clear that the distributions associated with longer residence time cutoffs are dominated by objects with greater fluorescence intensity. Notably, ridges of approximately constant intensity are visible, suggesting the presence of discrete populations with unique characteristic intensities. Of course, larger fluorescence intensities are likely to be associated with aggregates containing a greater number of protein molecules, and therefore more fluorescent labels. At the relatively low level of fluorophore loading used in these experiments, intra-protein fluorophore quenching is expected to be negligible and inter-protein quenching in oligomeric species is expected to be a minor effect. These assumptions predict a linear relationship between intensity and aggregate size to a first approximation.

A direct connection can be made between the populations identified via surface residence time (shown in Table 1) and the populations associated with specific fluorescence intensities. Figure 2B shows the fractional contribution of each population to the total object distribution as a function of residence time cutoff, calculated from the residence time parameters in Table 1. The result is the appearance and disappearance of populations as a function of the residence time cutoff axis and allows identification of characteristic intensities for these populations (as the intensity coordinate of each ridge backbone) by direct comparison with the visible ridges in Figure 2A. Variation in the number of fluorophores per protein in addition to uncertainty in the intensity measurement results in broadening of each ridge but does not shift the intensity value of the ridgeline.

Prominent intensity ridges were observed at approximate positions of 2, 3, 4 and 5 intensity units where 1 unit is believed to represent the intensity of a monomer. Units were arbitrarily chosen so the ridge with the smallest width in the residence time direction and lowest intensity was assigned a value of 2 units. When the residence time cutoff was 2 seconds (i.e. all objects were included), an additional peak existed in the probability distribution at approximately 0.5 intensity units which is believed to represent the intensity of the large number of objects with a residence time less than the frame acquisition time that consequently appear to be less intense. although 4 populations were identified in analysis of residence time data, a 5^th, and occasionally a 6^th, ridge was also observed in the intensity analysis. They have been identified in Figure 2A but not considered in other analyses (e.g. residence time, diffusion) because there were typically not enough of these objects for sufficient statistical significance. The exact values for intensity determinations are given in Table 2. It should be noted that the characteristic intensity values of species C, D, and E are all slightly less than the assumed aggregation numbers for these species. This is likely due to a combination of the following effects: self-quenching between nearby fluorophores on different proteins (as was previously discussed), increased bleaching in objects with longer residence times, and saturation of the CCD camera (primarily with population E). The fact that the intensity ratios are in good agreement with the integer series 2:3:4:5 in many experiments on three different surfaces strongly suggests that the heterogeneity in the residence time data is due to the presence of discrete fibrinogen oligomers, specifically dimers, trimers, and tetramers.

Table 2.

Relative fluorescence intensity values for populations with the intensity of population B defined as 2. Population E was not seen in residence time data and is ignored in analysis of diffusive motion

Population	Fused Silica	TMS	PEG(5000)
A	0.4(1)	0.4(1)	0.6(1)
B	2	2	2
C	2.9(2)	2.8(2)	2.9(2)
D	3.8(2)	3.7(2)	3.9(2)
E	4.7(2)	4.5(3)	5.0(4)

To confirm that protein aggregates are present in bulk solution, both analytical centrifugation and size exclusion chromatography were performed on the labeled human fibrinogen solutions used in this work (see Supporting Information, Figures S1 and S2). Consistent with results from the present residence time analysis and previous experiments on bovine fibrinogen,^{16, 17} these results showed a large monomer fraction coexisting with a smaller fraction of larger aggregates of dimer size or greater. That oligomers were observed in both labeled fibrinogen studied here and unlabeled fibrinogen studied previously demonstrates that labeling is not the cause of the observed aggregation and that preexisting aggregates in solution are likely in physiological environments.

The idea that fibrinogen oligomers in solution result in interfacial objects with different characteristic residence times sheds new light on the discussion of fibrinogen-surface interactions. In particular, Wertz and Santore found that relaxation to an irreversibly bound state was slow, on the order of 10³ seconds for hydrophilic and hydrophobic surfaces.¹⁵ This work provides strong evidence that the vast majority of fibrinogen aggregates with aggregation numbers less than four do not remain on the surface long enough to relax. As larger aggregates may have exponentially increasing characteristic residence times, these may be the proteins that are more likely to relax to irreversibly bound states. Furthermore, oligomers observed in these experiments must pre-exist in solution as it is nearly impossible for two proteins to aggregate on the surface given the extremely low surface coverage used in these experiments and the relatively slow observed diffusion coefficients.

While the work of Wertz and Santore used higher solution concentrations and surface densities than in this work, AFM experiments have also observed slow fibrinogen relaxation of individual proteins.³⁵ Given the results in this work, it seems likely that monomeric fibrinogen observed by AFM over hour-long timescales represents a vanishingly small fraction of the total number of monomers that interact with the surface. These monomers may have long residence times because they adsorbed to anomalous defect sites, because there is something inherently different about these monomers (e.g. partial denaturation), or because they merely represent the extreme tail end of the monomer population A that is described in this work. It is worth further study to identify which of these explanations is most likely, and the subsequent implications for the interpretation of previous studies on fibrinogen-surface interactions.

In the above-mentioned AFM study and in several others, there is seemingly evidence of a small fraction of fibrinogen aggregates.^35–37 Potential aggregates may appear as individual proteins that are extremely close to each other or as groups where individual proteins cannot be distinguished. Given the results in this work, it may be worthwhile for future AFM studies to compare the properties of these aggregates to those of the monomers. Finally, the work of Siegsmund and colleagues considers the importance of cluster formation due to surface diffusion in the growth of a fibrinogen protein layer.³⁸ Although their modeling technique considers fibrinogen at higher solution concentrations and surface densities than in this work, it may be important, in light of the present results, to include the possibility that small clusters may also originate in solution.

The present work has demonstrated the presence of fibrinogen aggregates at low concentrations and the previous work discussed above suggests that these species are also present at higher concentrations. It therefore seems appropriate to consider the possible effects of fibrinogen aggregates in the interpretation of in vitro adsorption experiments despite the fact that quantitative modeling is obscured by uncertainty in f_i. It is also interesting to consider the possibility that fibrinogen aggregates might exist in blood as well. In particular, a small fraction of oligomers would be virtually unseen by aggregate-detecting techniques like scattering, centrifugation, or chromatography in such a heterogeneous environment. In light of the present demonstration of the importance of fibrinogen aggregates, this work hopes to motivate further exploration of these aggregates in blood.

Influence of surface functionalization

Surface functionalization also influences the behavior of fibrinogen at the interface. Table 1 shows that the characteristic residence times are comparable for fibrinogen on fused silica and TMS but that the residence times of fibrinogen on PEG(5000) were longer for each population by about a factor of two. This result is surprising because it is generally believed that PEGylated surfaces resist the adsorption of individual protein molecules as discussed in the introduction. One possible theory for this observation is that partial insertion of fibrinogen into the PEG layer may increase van der Waals attractions and possibly even permit entanglements between PEG and protein, overwhelming the repulsive forces of steric repulsion and water layer formation. However, this work presents no direct mechanistic evidence for the attraction between PEG and fibrinogen and further study is necessary on this front. Although the mechanism remains unknown, it is important to note that this observation is believed to be the first of its kind because the single molecule techniques employed here directly assess protein-surface interactions, independently of protein-protein interactions, through residence time measurements at extremely low surface coverage.

The broad conclusion that should be drawn from the observation of increased residence times on PEG is that PEG does not appear to decrease protein adsorption at the level of direct protein-surface repulsion or attraction. This is not to cast doubt on the well-established fact that PEG is protein-resistant but rather to suggest that protein-protein interactions may be important in determining ultimate surface coverage and that surface chemistry may indirectly affect these interactions. Surface chemistry may play an indirect but nevertheless important role at this level by influencing the orientation of proteins relative to the surface as well as their secondary, tertiary, or quaternary structures and their subsequent propensity to form a stable protein layer. However, this is not the same as saying that PEG decreases the residence time of individual proteins, a statement that the current work does not support. This is an important distinction because while PEG’s protein resistance in physiological environments is well documented, it is also known that some protein still does adsorb to most PEG-coated surfaces.²³ A more sophisticated understanding of the ability of PEG to permit protein adsorption but prevent protein layer formation may lead to surface coatings with improved biocompatibility.

Diffusion provides an independent assessment of protein-surface interactions

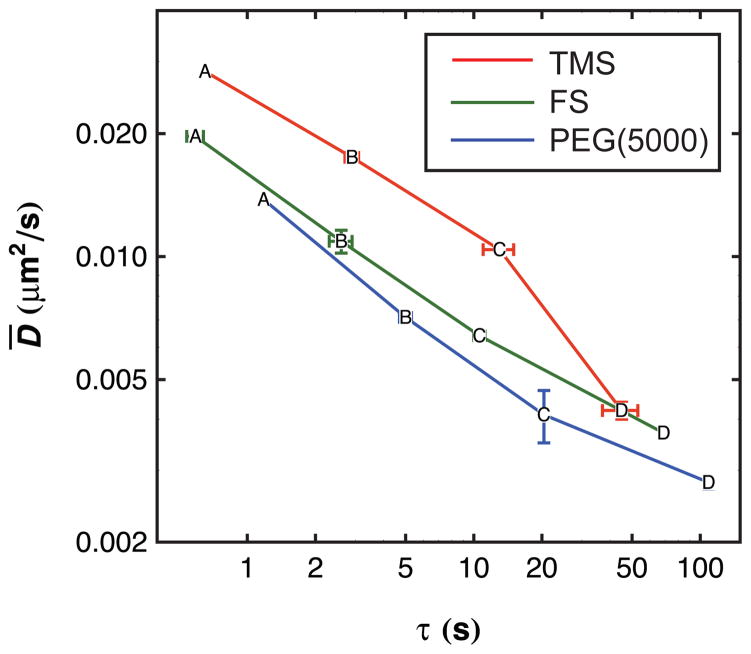
Like residence time analysis, diffusive behavior provides another way to assess fibrinogen-surface interactions. This stems from the fact that an object must detach partially or completely from a solid surface in order to change its lateral position at the interface, as was suggested in previous work on surfactant molecules by Honciuc and Schwartz.²⁶ Therefore, one might expect some correlation between trends in desorption kinetics and interfacial diffusion coefficients. In order to make a direct comparison, the diffusive behavior of each population A–D was determined. Given the characteristic intensities and residence times of each population determined previously, trajectories were grouped using both properties to assess which population they belong to. Although, in principle, populations can be identified solely by intensity, in practice the intensity distribution is broad due to heterogeneity in labeling and photophysical effects like blinking and intra-protein self-quenching. As a result, binning by residence time and intensity helps to increase the accuracy of population identification (the details of the intensity and residence time ranges used to define populations are given in the Supporting Information, Tables S1 to S3). Figure 3 shows a direct comparison of mean surface residence time and mean interfacial diffusion coefficient for the four populations on the three types of surfaces studied in this work. There is a dramatic similarity in the trends of these two dynamic properties with population. Notably, on all three surfaces, the mean surface residence time increases by a factor of 4.6 ± 0.9 and the mean diffusion coefficient decreases by a factor of 1.8 ± 0.3 as the aggregation state increases by one protein monomer (i.e. from population A to B to C to D). The fact that these quantities scale so similarly suggests a deep mechanistic connection associated with the energy barriers for full and partial detachment. Future temperature-dependent studies will directly probe these energy barriers.

Figure 3.

The average diffusion coefficient is plotted on a log-log scale as a function of characteristic residence time for each population (labeled as “A” through “D”) on each surface. Error bars represent uncertainty in each coordinate where this value is larger than the data marker. Lines are drawn as a visual guide.

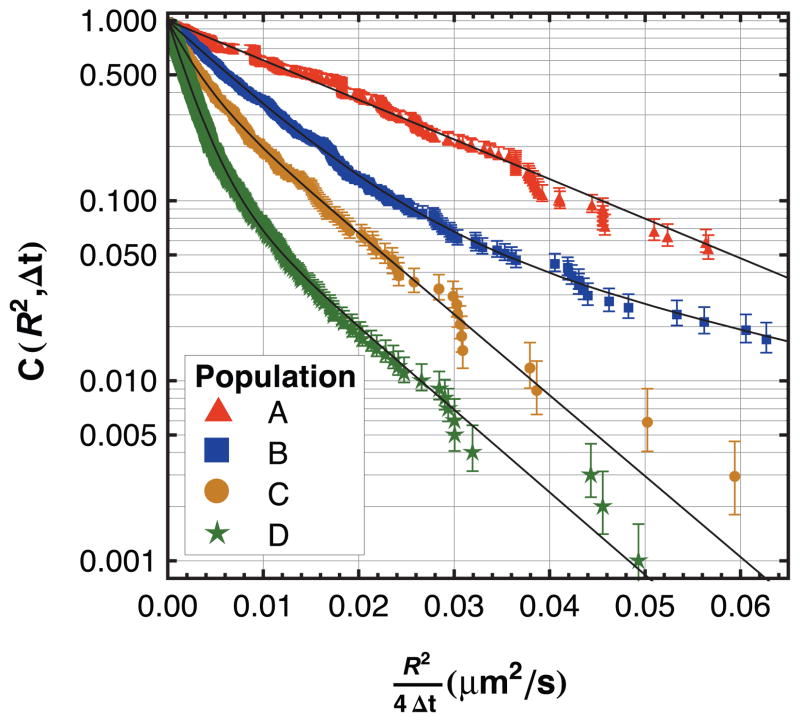
Interestingly, the diffusion of an individual population was not typically described by simple two-dimensional Brownian motion. For example, Figure 4 shows the cumulative squared-displacement distribution for each population on a fused silica surface. Parameter values used in fitting the data with equation (2) are shown in Figure 5A. This analysis was repeated for the TMS and PEG(5000) surfaces and these parameters are shown in Figures 5B and 5C, respectively. The tabulated values of these parameters are given in the Supporting Information, Tables S1 to S3.

Figure 4.

The cumulative squared-displacement distribution on fused silica is shown for trajectories that have been binned by intensity and residence time. From top to bottom (moving from A to D), brighter objects with longer residence times diffuse more slowly.

Figure 5.

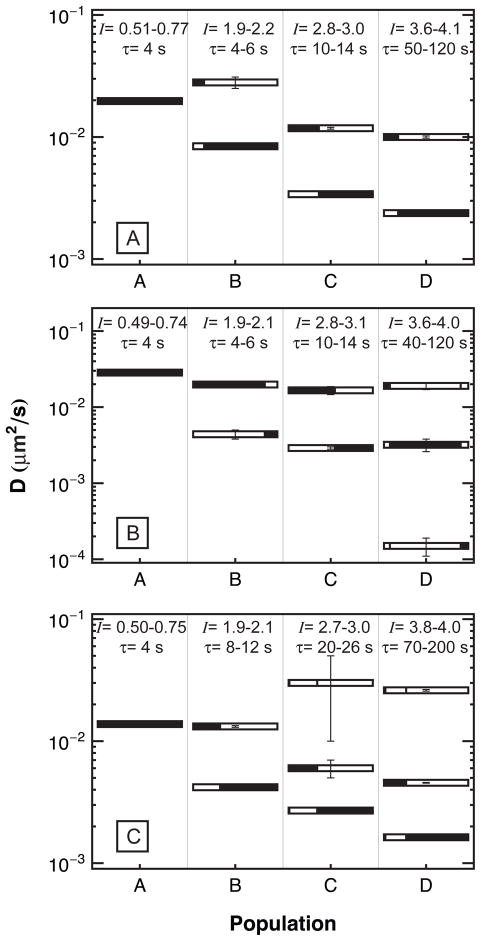
The diffusion coefficients for the multiple diffusive modes of populations A through D are shown on different surfaces: (A) FS, (B) TMS, (C) PEG(5000). The black area of each bar represents the fraction of steps observed with the diffusion coefficient given by the bar’s position on the vertical axis. The intensity and residence time binning criteria used to define each population are shown along the top of each figure.

Multiple diffusive modes are necessary to explain the diffusive behavior of all populations except A. This means that the correlation time for diffusive motion must be at least as long as the frame acquisition time. If diffusive motion were uncorrelated on this time scale, all steps from each diffusive mode would be averaged in a single frame, leading to a single apparent diffusion coefficient. The presence of multiple diffusive modes has previously been linked to different types of association between adsorbate molecule and the surface. For example, a pancake-shaped molecule might associate with the surface in an edge-on or a face-on geometry and might switch between the two on a characteristic time scale.³⁹ During periods of edge-on association, the barrier to partial detachment would be relatively small, and so the molecule would diffuse more rapidly than during periods of face-on association. Given this picture, multiple diffusive modes are expected for increasingly large aggregates, as there are more ways for a larger protein to interact favorably with a surface than a smaller one.

Although the diffusive behavior as shown in Figure 5 is complicated, one can make some generalizations. For example, in all cases there appears to be a “fast” mode with a diffusion coefficient in the range 0.01–0.03 μm²/s. Oligomers of all sizes exhibit this mode to some extent, and the diffusion coefficient associated with this mode changes only modestly with aggregation number on a given surface. However, while monomers exhibit this fast mode exclusively, the fast mode represents a systematically smaller fraction of trajectories for progressively larger aggregates. This suggests that while oligomers may occasionally visit configurations where they are weakly bound (and therefore diffuse rapidly), these configurations are increasingly rare for larger aggregates.

Figure 5 also exhibits a second cluster of “slow” diffusive modes in the range 0.002–0.006 μm²/s, and sometimes a third set of even slower modes for the larger aggregates. Again, the diffusion coefficients within a given set decrease modestly with aggregate size, but there is a clear trend suggesting that the trajectories of larger aggregates systematically exhibit a greater fraction of steps associated with the slower modes. Roughly speaking, it is possible to say that while monomers and oligomers of all sizes exhibit both fast and slow diffusive modes, the dominant mechanism for the slower interfacial diffusion of larger aggregates is associated with the fact that their trajectories are increasingly dominated by the slower modes. It is also worth mentioning that aggregates were found on TMS surfaces that exhibited diffusive behavior that was anomalous for their aggregation number. While this observation is not important for the discussion at hand, further discussion on these populations is provided in the supporting information.

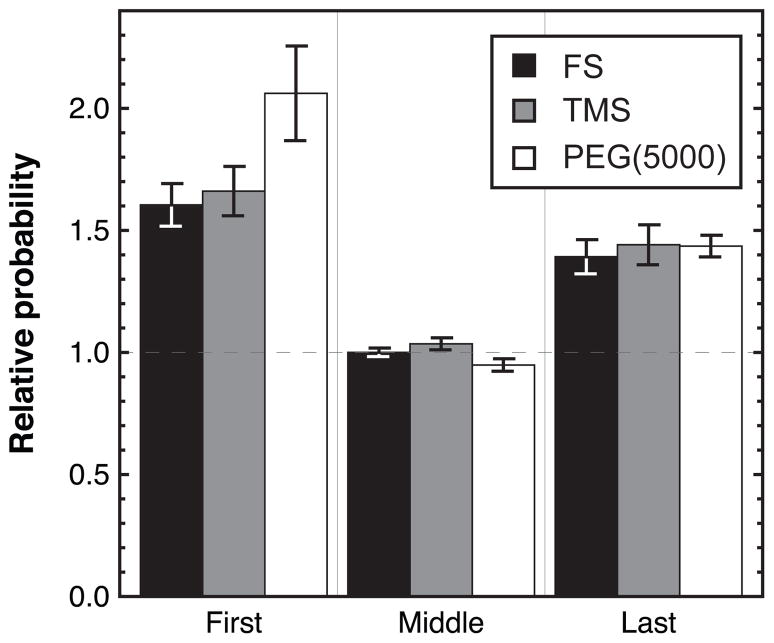
If the various diffusive modes truly correspond to different types of molecule-surface associations, one might expect to see a direct correlation between the diffusive mode and the processes of adsorption and desorption. For example, if faster diffusion corresponds to a weaker binding mode, molecules should be more likely to desorb while executing fast diffusion than slow diffusion. Since the correlation time for diffusive motion is at least as long as the frame acquisition time, it is possible to directly probe this question by looking at the characteristic diffusive behavior immediately prior to desorption. Specifically, objects with a residence time of at least 10 seconds were collected. Their diffusion steps were divided into four groups: 1) the first step after adsorption, 2) the middle step of the trajectory (as a control), 3) the last step prior to desorption and 4) a weighted average of all steps. Trajectories for group 4 were weighted so that each trajectory contributed an equal number of statistical steps to the observed diffusive behavior, regardless of the actual length of the trajectory. This was done to mimic the statistical bias induced by taking one step from each trajectory in groups 1–3 but to take advantage of the greater statistics provided by including all observed steps in a trajectory. Diffusive steps for these groups were analyzed by arbitrarily choosing a cutoff value for R² to denote a “large” step. The probability of observing this value of R² or greater was determined for groups 1–3 and normalized by that of group 4 to get the relative probability of a large step. The results of this analysis are shown in Figure 6 where the error bars represent the standard deviation in the calculated relative probability when the large step cutoff value is varied over a reasonable range. Here, a reasonable range was determined by identifying the values of R² that gave a probability of a large step in group 4 between 0.01–0.05. The cumulative squared-displacement distributions for groups 1–4 are shown in the Supporting Information, Figure S3. The analogous graph to Figure 6, giving the relative probabilities of “small” steps, is not shown, as all probabilities are within statistical error of unity.

Figure 6.

The relative probabilities of a “large” step are shown for the first, middle and last steps in a trajectory on FS, TMS and PEG(5000). Probabilities are relative to the distribution of all observed steps and error bars represent the error introduced by choosing an arbitrary cutoff for a “large” step.

From Figure 6, it is evident that the first and last steps in a trajectory are more likely to be “large” than all other steps in the trajectory. This is true for all surfaces studied. The fact that the diffusion immediately prior to desorption is fast suggests that desorption is more likely to occur during periods of fast diffusion, and is consistent with the notion that fast diffusion corresponds to relatively weak surface association. The fact that diffusion immediately following adsorption is also fast suggests that an adsorbing molecule does not immediately adopt a favorable orientation on the surface. It may be that favorable surface orientations are easier to come by in larger aggregates and consequently larger aggregates that interact with the surface are more likely to stick before they diffuse back into solution. These observations also provide an explanation for the data in Figure 5, which show that the trajectories of monomers (population A) are dominated by the fast diffusive mode; since the surface residence time of these molecules is small, their diffusion does not have time to become uncorrelated from the fast diffusion that follows adsorption and precedes desorption. In contrast, population D typically has time to settle on the surface and explore slower modes of diffusion.

As discussed above, a comparison of the average diffusion coefficient for each population shows a consistent trend whereby diffusion on TMS is faster than on FS which is faster than on PEG(5000). It is expected that diffusion on the PEG(5000) surface would be slowest from both the residence time data and the earlier discussion on the similarity between the fast diffusion mode and desorption, and this is observed in the data. Residence time data also leads to the expectation that fibrinogen should diffuse similarly on TMS and FS but this prediction is not supported by the data. This discrepancy suggests that protein-surface interactions on TMS and FS surfaces are fundamentally different types of interaction and that it is mere coincidence that their residence times are similar. It is possible that the sum of interactions between fused silica and fibrinogen (such as hydrogen bonding) equals the sum of a different type of interactions between TMS and the protein (such as hydrophobic effects), leading to comparable probabilities for desorption. However, these two fundamentally different types of interactions may allow fibrinogen to diffuse more quickly on TMS than on FS because of the length scales involved in each type of interaction. More specifically, if hydrophobic patches on fibrinogen can feel an attractive force towards a hydrophobic TMS surface from a distance of several water molecules (e.g. via water depletion effects), it will diffuse quickly through the near-surface liquid (i.e. parallel to the surface) but long-range attractions will keep it from leaving the near-surface region completely. In contrast, on a hydrogen-bonding surface like fused silica, once fibrinogen is no longer close enough to hydrogen bond to the surface, it is free to desorb. It should be noted that this is only one possible explanation for the observed results and further work is necessary to clarify the mechanism of fibrinogen diffusion on each surface. However, this type of analysis illustrates the power of comparing residence time data with diffusion data. While a simplistic view of protein-surface interactions predicts an inverse relationship between residence time and diffusion coefficient, instances where this does not hold true is evidence of more sophisticated interactions that would merit further study through the use of temperature variation to determine activation barriers for diffusion and desorption.

Conclusions

Single-molecule resolution of fibrinogen-surface interactions illustrates the ability of this technique to unravel complex behavior involving multiple populations with a variety of surface residence times and diffusive modes. In particular, fibrinogen behavior is much more complicated than the conventional picture of a single protein molecule adsorbing to the surface, exhibiting a simple Brownian random walk at the interface, and either desorbing (with a single characteristic residence time) or relaxing to an irreversibly bound state. The single-molecule approach permits strong connections between observable behavior and the physical significance attributed to these observations are provided by the correlation between different types of information.

Analysis of protein residence times, fluorescence intensities, and diffusive motion has identified soluble fibrinogen aggregates/oligomers with the propensity for varied behavior at the interface. Oligomers with increasing aggregation number were found to have longer surface residence times and to diffuse more slowly. Multiple modes of diffusion were observed for many of the aggregated populations, indicating that a large protein oligomer has multiple ways to interact with a solid surface. The inclusion of fibrinogen aggregates into the analysis of other types of experiments and models of fibrinogen-surface interactions may help to clarify mechanisms of protein layer formation on biomaterial surfaces.

This work studied proteins that had surface residence times typically less than 600 seconds and therefore cannot provide direct information on long-lived species that may also be important for protein-layer formation. However, these experiments were able to directly assess protein-surface interactions through residence time and diffusion data. The results showed that a monolayer of PEG5000 actually extended the surface residence time and slowed diffusion of fibrinogen relative to a bare fused-silica surface (or to a hydrophobically-modified surface). This contrast with conventional wisdom regarding the protein resistance of PEG monolayers suggests that PEG’s biocompatibility is not primarily a product of its ability to decrease the mean residence time of isolated fibrinogen molecules. We speculate that an important factor in the protein resistance of PEG layers may involve their ability to mediate post-adsorption protein behavior, perhaps by influencing fibrinogen orientation and its propensity to form a stable layer with other proteins via protein-protein interactions in the near-surface environment.

A comparison of fused silica and TMS surfaces indicated that the two chemistries lead to similar surface residence times. However, diffusive data indicated that this was merely a coincidence because fibrinogen exhibited significantly faster diffusion on TMS monolayers than on fused silica, indicating fundamentally different types of interactions on each. Further studies will seek to elucidate the mechanisms of interaction with each type of surface chemistry.