Propensity Score-Based Nonparametric Test Revealing Genetic Variants Underlying Bipolar Disorder

Abstract

Association analysis has led to identification of many genetic variants for complex diseases. While assessing the association between genes and a disease, other factors can play an important role. The consequence of not considering covariates (such as population stratification and environmental factors) is well-documented in genetic studies. We introduce a nonparametric test of association that adjusts for covariate effects. Specifically, the adjustment is realized through weights that are constructed from genomic propensity scores that summarize the contribution of all covariates. The benefit of our test is demonstrated through an important dataset on bipolar disorder (BD) collected by the Wellcome Trust Case Control Consortium (WTCCC). When compared to other tests, our test identified an un-reported region with three single nucleotide polymorphisms (SNPs) on chromosome 16 that show strong evidence of association (p-value < 5×10⁻⁷). This region is near the RPGRIP1L gene known to be associated with bipolar disorder. A haplotype block including these three SNPs was further discovered to be strongly associated with bipolar disorder. It is also interesting to note that our nonparametric test did not reveal strong signals at two SNPs that were detected by a covariate-adjusted parametric test. This suggests that different methods of covariate adjustment can complement each other. Thus, we recommend using both parametric and nonparametric testing. Additionally, we performed simulation studies to compare our proposed test with the unadjusted test and an adjusted parametric test. Our finding underscores the importance of accommodating and controlling for covariate effects in discovering genetic variants associated with complex disorders.

INTRODUCTION

Over the past several years, genome-wide association studies (GWAS) have been successful in localizing and identifying important genes that contribute to common human diseases [Klein et al., 2005; Arking et al., 2006; Duerr et al., 2006; Chen et al., 2007]. To test the association between a genetic variant and a disease, it has become increasingly clear that environmental factors may have important confounding effects [Amos et al., 1996; Lu and Cantor, 2007; Vansteelandt et al., 2009]. For example, population stratification is a special case of confounding caused by ethnicity or ancestry differences that a failure to account for this stratification can lead to a spurious association. There are many methods specifically designed to address population stratification such as genomic control, structured association, and the principal component method [Devlin and Roeder, 1999; Pritchard and Rosenberg, 1999; Price et al., 2006]. It remains important, however, to develop a general method to assess association in the presence of covariates.

A common method of accounting for covariates is to regress phenotypic values against the covariates, and then to perform an association analysis using the residuals against the genotypes [Wang et al., 2006; Lu and Cantor, 2007]. While this two-step approach is convenient, the theoretical properties of this approach are difficult to study due to the lack of an integrated model. Additionally, this framework may not be suitable when the covariates themselves are correlated with the genes. Another useful approach is to fit a parametric model of the relationship between phenotype and all risk factors. Here, the risk factors include both genotypes and covariates. For example, logistic regressions are typically used to test genetic contribution while adjusting for the covariates in a case-control study. The underlying assumptions of parametric models however, can be difficult to verify, especially so for discrete outcomes that usually involve the choice of link function. The shortcomings of these parametric methodologies motivate our nonparametric approach that tests the association between the phenotype and a genetic variant, while adjusting for the covariates.

Score tests are particularly useful in genetic studies and many of them are unified under the U-statistics [Laird et al., 2000; Zhang et al., 2010]. Most of these statistics evaluate the direct association between the phenotype and a genetic variant without adjusting for the covariates. Meanwhile, the concept of propensity score has been proven useful to remove the bias of the treatment effect caused by confounding variables, enabling causal inference [Rosenbaum and Rubin, 1983; Zhao et al., 2009]. Recall that the balance property of propensity scores [Rosenbaum and Rubin, 1983, Theorems 1–2] indicates that if a subclass of units is homogeneous in propensity score, then the treated and control units in that subclass will have the same distribution of covariates.

Thus, we propose a weighted nonparametric statistic of association by using propensity scores. Instead of exactly matching the samples using propensity scores, we choose to weigh each sample pair in the U-statistic in Zhang et al. (2010) according to their propensity scores. In this way, we are aiming to achieve the balance property without losing power of the test. In particular, we use propensity scores to summarize the contribution of all covariates, and then derive the weights from these scores. From the viewpoint of U-statistic, the weights increase the contribution of each sample pair if they share similar propensity scores, and they reduce that contribution otherwise. Taking into account the covariates, we use this weighted statistic to test the null hypothesis that there is no association between the phenotype and a genetic variant conditional on the covariates.

MATERIALS AND METHODS

Bipolar Disorder Dataset and Quality Control

We were given permission to use the bipolar disorder data set collected by WTCCC to demonstrate the utility of our test. The data contain 1998 cases and 3004 controls. The control samples came from two sources: half from the 1958 Birth Cohort (58C) and the remainder from a new UK Blood Service (UKBS) sample. The genotyping was performed using GeneChip 500K arrays at the Affymetrix Services Lab (California). After proper quality control/quality assurance (QC/QA), WTCCC (2007) identified a strong signal (p-value < 5×10⁻⁷) for bipolar disorder at SNP rs420259 on chromosome 16p12, and 13 other SNPs with moderate association (p-value between 10⁻⁵ and 5×10⁻⁷) genome-widely.

Following the same QC/QA procedure as in WTCCC (2007), we used a quality score threshold for inclusion of SNPs at 0.9, treating the genotype as missing when the most probable call fell below this threshold. Furthermore, we removed 130 samples from the BD cohort, 24 samples from the 58C cohort, and 42 samples from the UKBS cohort, due to low call rates, overall heterozygosity, and evidence of non-European ancestry. Additionally, SNPs were excluded from our analysis according to the exclusion list provided by WTCCC, including missing data rates and departures from Hardy-Weinberg equilibrium. We performed further quality controls based on minor allele frequency (MAF > 5%) and Hardy-Weinberg equilibrium in both cases and controls (p-value > 0.0001). As the WTCCC investigators, we set 5×10⁻⁷ as the genome-wide significance threshold for strong association, and p-values between 10⁻⁵ and 5×10⁻⁷ as moderate association.

Unadjusted Association Test

First, the SNP association is evaluated using the unadjusted association test in Zhang et al. (2010). To introduce the notation, suppose that we have data from n subjects, and for subject i, let Y_i denote the trait and G_i a genotypic score. Here, Y can be the case/control status or a quantitative trait, and G can be the number of mutant alleles. The association test is based on the U-statistic generalized from Kendall’s tau to measure the association between Y and G, namely, $U={\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}{\displaystyle \sum _{i<j}(G_i-G_j)(Y_i-Y_j)}$. In the absence of covariates, the test statistic U follows an asymptotically normal distribution under the null hypothesis conditioning on all phenotypes [Rabinowitz and Laird, 2000]. Once the asymptotic mean and variance of U are evaluated, it can be used to test the null hypothesis H₀ that there is no association between Y and G.

Covariate-Adjusted Nonparametric Association Test

Before we propose the covariate-adjusted nonparametric test of association, we provide a brief review of genomic propensity scores [Zhao et al., 2009]. For a SNP marker with two alleles A and a, the genomic propensity score is the probability of an individual having a particular test-locus genotype (AA, Aa, or aa) based on each specific individual’s covariates Z, p_g(z) = P(G = g | Z = z), where g and z are observed values of G and Z. Specifically, for a dominant or a recessive model with g = 0 or 1, the propensity score becomes p(z) = p₁(z) = P (G = 1|Z = z), where p₀(z) = 1 − p₁(z). For an additive model with g = 0, 1, or 2, the propensity score p(z) is a vector p(z) = (p₁(z),p₂(z)) = (P(G = 1|Z = z),P(G = 2|Z = z)), where p₀(z) = 1 − p₁(z) − p₂(z).

As in matching subjects according to their propensity scores [Rosenbaum and Rubin, 1984], we propose a weighted U-statistic by imposing weights to each observation pair (i, j). In particular, the propensity scores are used to summarize the contribution of all covariates; weights are then derived from these scores. Sample pairs that share similar propensity scores are more heavily weighed than sample pairs that do not share similar propensity scores. That is, for the sample pair (i, j), we first evaluate p(z_i) and p(z_j), then a weight function is derived using a positive weight function, W : w(p(z_i),p(z_j)) = W(p(z_i) − p(z_j)). Thus, the proposed weighted test statistic is: $U_w={\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}{\displaystyle \sum _{i<j}(G_i-G_j)(Y_i-Y_j)}w(p(z_i),p(z_j)).$.

To account for covariates, this weighted test statistic is used to test the null hypothesis, H₀′, that there is no association between the phenotype and the genetic marker conditional on the covariates, that is, Y and G are independent conditional on the covariates, Z. The mean and variance of the weighted test statistic under this null hypothesis can be calculated conditioning on all phenotypes and covariates. Then the calculations become similar to those in Zhang et al. (2010) except that we need to evaluate P(G_i = g|Z_i = z_i) for each subject i, which are exactly the genomic propensity scores p_g(z_i). After calculating the mean and variance, a χ² test statistic can be obtained from U_w for testing purpose.

When analyzing the bipolar disorder data set, the propensity scores were estimated from the data using proportional odds logistic model as log it(P(G_i ≤ g | Z_i = z_i)) = λ_g + β'z_i, i = 1,…,n, using covariates gender and age at recruitment, with g = 0,1. The weight function was chosen as $W(u_1,u_2)=\text{exp}(-u_1^2/2-u_2^2/2)$ after standardizing the corresponding propensity scores such that they have a unit sample standard deviation.

RESULTS

Genome-wide Association Results

Our analyses confirmed previous results by WTCCC (2007) and further revealed other regions associated with bipolar disorder. Using the non-weighted test statistic U under the null hypothesis H₀, Table 1 suggests that three SNPs show strong evidence of association. One of these three SNPs is rs420259 on chromosome 16 which was detected by WTCCC (2007); the other two SNPs are rs9378249 on chromosome 6 and rs12938916 on chromosome 17, which to the best of our knowledge, have not been reported previously using the same data.

Table 1.

SNPs Showing Strong Evidence of Association (P < 5×10⁻⁷)

Chr	SNP	Position	P1a (addd)	P1 (dome)	P1 (recf)	P2b (add)	P2(dom)	P2 (rec)	P3c (add)	P3 (dom)	P3 (rec)
6	rs9378249	31435680	1.21E-08	5.11E-08	5.06E-03	1.39E-08	3.41E-08	7.55E-03	1.71E-09	7.70E-09	8.87E-04
16	rs4202591	23541527	2.19E-04	9.66E-02	8.51E-09	6.47E-04	1.20E-01	6.59E-08	4.26E-04	1.51E-01	3.33E-09
16	rs2387823	51445620	2.90E-06	4.63E-05	3.98E-04	1.30E-07	5.32E-05	2.98E-04	1.77E-06	3.11E-05	3.11E-04
16	rs1344485	51469833	1.78E-06	3.09E-05	3.77E-04	1.79E-07	1.34E-05	6.29E-04	1.41E-06	1.80E-05	5.12E-04
16	rs11647459	51473252	2.93E-06	3.64E-05	6.33E-04	2.76E-07	4.16E-06	8.39E-04	1.89E-06	1.83E-05	7.59E-04
17	rs12938916	53221286	8.15E-07	4.80E-07	2.81E-01	2.05E-06	1.11E-06	3.75E-01	1.47E-06	8.89E-07	1.82E-01
20	rs48156032	3720527	7.51E-05	3.00E-06	2.05E-01	9.33E-04	1.42E-05	6.39E-02	1.82E-05	4.80E-07	1.69E-01
20	rs37612181	3724175	4.44E-05	1.13E-06	2.14E-01	5.30E-04	3.27E-06	7.13E-02	1.16E-05	2.16E-07	1.73E-01

^aP-value from non-weighted test under H₀.

^bP-value from weighted test under H₀′.

^cP-value from a logistic regression model.

^dAdditive genotype coding.

^eDominant genotype coding.

^fRecessive genotype coding.

¹The SNPs identified by WTCCC with strong or moderate association.

²The SNPs identified by WTCCC with p-value between 10⁻⁴ and 10⁻⁵.

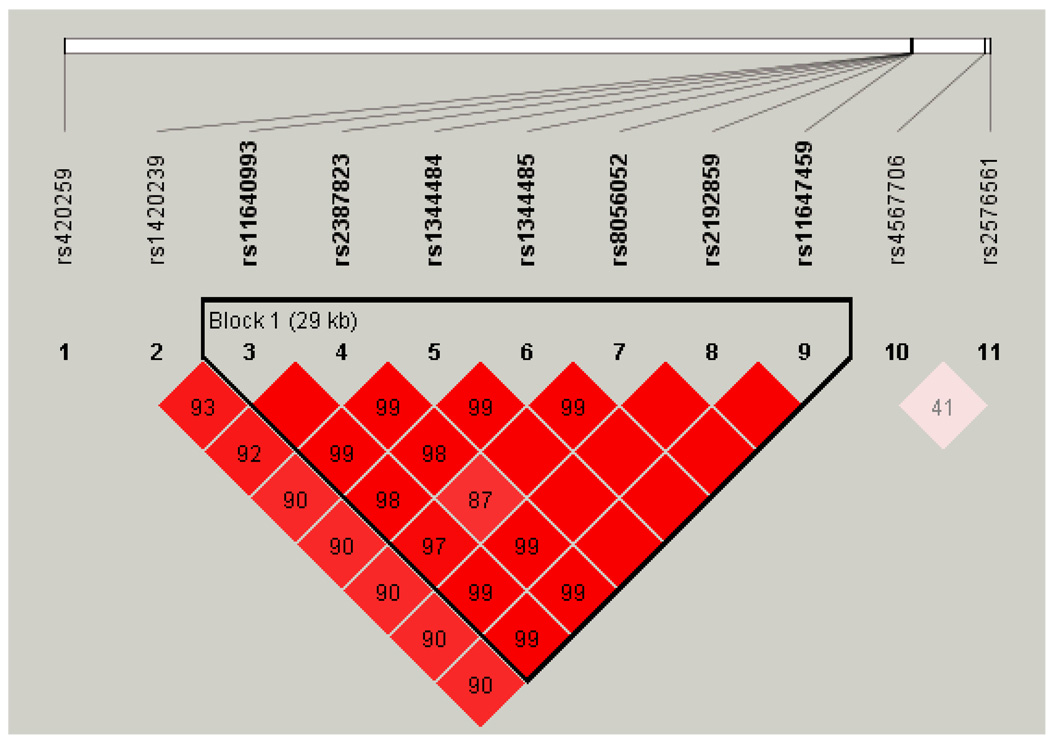
Next, we considered gender and age at recruitment as covariates. Compared with the previous test, the adjusted nonparametric test confirmed rs9378249 and rs420259 as signals with strong association, but did not pick up rs12938916. Moreover, the adjusted nonparametric test identified three additional SNPs (rs2387823, rs1344485, and rs11647459, all on chromosome 16) with strong evidence of association. These three SNPs were neither detected by the unadjusted test nor reported by WTCCC (2007). It is noteworthy that the three additional SNPs are in strong linkage disequilibrium, but not with the reported rs420259 (Figure 1).

Figure 1.

Linkage disequilibrium heat map for the identified SNPs on chromosome 16

To make our comparisons more comprehensive, we further analyzed the bipolar disorder data set using a logistic regression model, adjusting for gender and age at recruitment. The results corroborated the results of the nonparametric method. The results of the logistic regression confirmed the genome-wide significance of exactly the same two SNPs and excluded the other SNP identified by the unadjusted test (see Table 1).

Two additional strong signal SNPs were detected using the logistic regression as opposed to the nonparametric adjusted test: rs4815603 and rs3761218, both on chromosome 20. Note that WTCCC (2007) identified rs3761218 as showing moderate evidence of association and rs4815603 had a p-value between 10⁻⁴ and 10⁻⁵. Additionally, both SNPs showed only moderate associations using unadjusted and nonparametric adjusted tests. Nonetheless, the logistic regression model missed the three SNPs (rs2387823, rs1344485, rs11647459) on chromosome 16 that were identified by our nonparametric approach as discussed above. These findings show that different methods of adjusting for covariates can lead to different insights. Although parametric adjustment is commonly used in the literature, nonparametric adjustment can be more robust to the model specification. Thus, these two approaches serve as complements to each other in the identification of important SNPs.

We further examined the three new SNPs rs2387823, rs1344485, and rs11647459 (all on chromosome 16) that were identified by the covariate-adjusted nonparametric test, and also the two new SNPs rs4815603 and rs3761218 (both on chromosome 20) that were identified by the parametric test. Recall that we fitted the proportional odds logistic model to estimate the genomic propensity scores. Thus we can evaluate the correlations between the genotype and the covariates through this model. On one hand, the three SNPs on chromosome 16 did not appear to be associated with the covariates, implying that almost no confounding effect exists. The adjustment was mainly for the effects of covariates on trait, producing a more significant p-values than the unadjusted test (this phenomenon is supported by the simulations reported here). One the other hand, the two SNPs on chromosome were associated with the covariates, resulting confounding effects and increasing the p-values of the weighted test (see Table 1). However the logistic regression achieved the genome-wide significance, possibly because of the efficiency of the parametric method when the underlying model assumption is valid (see more discussions for the simulation results).

In addition to Table 1, Table 2 lists all SNPs showing moderate evidence of association identified by any of the above three methods (with p-values between 10⁻⁵ and 5×10⁻⁷). Although there exist some non-overlapping results, most findings are consistent among these three methods.

Table 2.

SNPs Showing Moderate Evidence of Association (5×10⁻⁷ < P < 10⁻⁵)

Chr	SNP	Position	P1 (add)	P1 (dom)	P1 (rec)	P2 (add)	P2 (dom)	P2 (rec)	P3 (add)	P3 (dom)	P3 (rec)
1	rs1461356	60749036	2.76E-05	4.63E-06	3.91E-02	3.05E-05	4.85E-06	6.37E-02	3.92E-05	6.74E-06	4.20E-02
1	rs29894761	60771280	2.27E-05	2.20E-06	4.61E-02	2.66E-05	2.25E-06	7.27E-02	4.03E-05	3.23E-06	6.06E-02
1	rs107792792	213314367	3.99E-05	6.08E-05	7.89E-02	8.93E-06	2.29E-05	9.67E-02	2.65E-05	3.62E-05	9.11E-02
2	rs40271321	11988090	1.31E-05	9.20E-03	3.09E-06	1.74E-05	7.03E-03	1.42E-05	1.35E-05	6.56E-03	5.61E-06
2	rs75706821	104441785	3.12E-06	3.37E-05	9.06E-04	8.75E-06	1.60E-04	1.95E-04	8.01E-06	1.44E-04	4.14E-04
2	rs11123306	115948011	2.79E-06	7.60E-05	2.24E-04	3.76E-05	9.80E-05	8.86E-04	2.45E-06	5.67E-05	2.75E-04
2	rs13751441	115957416	2.44E-06	5.83E-05	2.68E-04	4.71E-05	2.63E-04	1.10E-03	2.02E-06	4.24E-05	3.11E-04
2	rs2421104	115958495	9.55E-06	3.32E-04	1.72E-04	4.76E-05	1.03E-03	1.57E-04	5.37E-06	2.04E-04	1.27E-04
2	rs6741692	116020161	4.65E-06	4.01E-05	1.36E-03	7.48E-05	1.39E-04	4.56E-03	5.85E-06	5.00E-05	1.47E-03
2	rs2953146	241235242	6.73E-06	4.42E-04	1.21E-05	3.42E-05	1.01E-03	4.73E-05	1.57E-05	8.64E-04	1.17E-05
2	rs2953174	241242257	6.43E-06	1.34E-04	1.15E-04	5.30E-06	1.27E-04	1.40E-04	7.82E-06	1.26E-04	1.75E-04
3	rs42762271	32305690	4.59E-06	2.64E-05	2.04E-03	1.12E-05	3.41E-05	5.62E-03	5.15E-06	4.65E-05	1.24E-03
3	rs4627791	32322828	2.38E-06	7.73E-06	3.50E-03	6.34E-06	1.59E-05	1.91E-03	4.60E-06	2.18E-05	2.84E-03
3	rs130745752	61558323	3.49E-05	1.16E-05	7.90E-01	8.74E-05	2.00E-05	9.58E-01	3.17E-05	8.77E-06	9.50E-01
3	rs589445	184351697	4.45E-06	8.34E-07	8.27E-01	5.56E-05	5.14E-06	8.17E-01	4.99E-06	1.22E-06	6.75E-01
3	rs6833951	184352520	2.30E-06	8.57E-07	5.44E-01	2.29E-05	3.88E-06	4.72E-01	2.74E-06	1.21E-06	4.56E-01
3	rs514636	184353138	2.50E-06	7.45E-07	7.22E-01	2.64E-05	4.70E-06	9.49E-01	4.45E-06	1.31E-06	6.74E-01
3	rs6414498	184353916	4.73E-06	8.95E-07	8.76E-01	5.36E-05	4.85E-06	7.25E-01	5.38E-06	1.17E-06	7.94E-01
3	rs6414500	184354001	5.14E-06	8.10E-07	9.75E-01	6.59E-05	4.22E-06	9.00E-01	5.86E-06	1.06E-06	9.46E-01
4	rs6844851	181063149	3.76E-05	9.41E-07	2.71E-01	1.98E-03	6.25E-05	2.96E-01	4.15E-05	1.24E-06	2.67E-01
5	---	169013376	1.42E-04	1.79E-04	2.44E-01	8.11E-06	2.22E-05	9.97E-02	1.89E-04	2.36E-04	2.56E-01
6	rs64583071	42839093	3.43E-01	2.11E-01	2.82E-05	1.67E-01	2.60E-01	7.87E-06	2.84E-01	2.44E-01	1.90E-05
7	rs22864922	22758250	5.06E-01	6.98E-01	8.40E-06	3.56E-01	8.80E-01	8.58E-06	4.73E-01	7.36E-01	9.35E-06
8	rs26096531	34356534	6.87E-06	2.10E-05	1.41E-02	3.48E-05	4.11E-05	3.83E-02	1.57E-05	4.62E-05	1.54E-02
8	rs4739466	37060700	1.99E-01	6.56E-01	3.60E-06	6.17E-01	9.15E-01	1.76E-05	2.00E-01	6.19E-01	1.14E-05
9	rs914715	79540452	2.28E-06	1.26E-06	9.56E-01	1.71E-06	2.14E-06	7.66E-01	1.02E-06	7.05E-07	7.29E-01
9	rs109822561	114340388	8.82E-06	5.85E-04	1.21E-04	5.29E-06	3.51E-04	2.01E-04	1.05E-05	4.11E-04	2.39E-04
10	rs17600642	72133000	5.19E-06	8.07E-06	3.34E-02	2.38E-05	3.78E-05	5.38E-02	5.01E-05	7.44E-05	5.43E-02
10	rs78961312	94539655	1.56E-04	1.35E-05	8.25E-01	2.65E-04	2.40E-05	7.17E-01	1.14E-04	9.12E-06	8.29E-01
11	rs1568889	27966039	1.45E-03	1.01E-01	2.32E-06	2.94E-03	1.52E-01	2.77E-05	3.05E-03	1.57E-01	2.28E-06
12	rs7136898	23945839	1.32E-05	1.30E-05	8.33E-03	2.24E-05	7.44E-05	2.19E-02	6.84E-06	1.11E-05	4.34E-03
12	rs11168839	47743902	2.38E-04	2.63E-05	1.80E-01	8.72E-05	8.75E-06	1.24E-01	7.06E-05	1.10E-05	9.48E-02
12	rs7296288	47766235	4.92E-04	2.76E-05	1.72E-01	2.05E-04	9.60E-06	8.15E-02	1.91E-04	1.49E-05	9.92E-02
13	rs28069222	45416060	7.90E-03	3.42E-01	1.82E-05	3.42E-02	4.00E-01	2.40E-05	5.54E-03	3.63E-01	4.61E-06
13	rs9530460	75157071	1.86E-03	4.12E-01	1.40E-05	4.58E-04	2.87E-01	2.16E-06	7.88E-04	2.94E-01	7.02E-06
14	rs101349441	57188949	3.22E-06	1.15E-06	4.79E-01	3.96E-06	7.45E-07	6.78E-01	2.46E-06	7.93E-07	5.07E-01
14	rs12890287	57191398	2.06E-05	1.10E-05	3.85E-01	7.09E-06	2.63E-06	4.63E-01	1.52E-05	6.13E-06	4.91E-01
14	rs11622600	57194142	1.70E-05	1.02E-05	3.66E-01	5.31E-06	2.06E-06	3.93E-01	1.18E-05	5.51E-06	4.61E-01
14	rs6574988	87629745	5.66E-06	4.22E-06	3.70E-01	3.11E-05	1.57E-05	5.10E-01	1.59E-05	1.05E-05	4.77E-01
14	rs8021692	103498329	2.98E-06	3.62E-06	1.67E-02	1.60E-05	1.97E-05	9.39E-03	3.64E-06	9.48E-06	7.58E-03
14	rs116224751	103578829	2.10E-06	2.20E-06	1.95E-02	7.78E-06	9.07E-06	1.42E-02	2.41E-06	5.26E-06	9.26E-03
15	rs8031347	31377909	7.82E-05	7.69E-05	6.46E-02	7.99E-06	1.93E-05	3.09E-02	2.53E-05	3.16E-05	3.66E-02
16	rs14202392	51434112	4.48E-05	1.14E-04	1.38E-02	7.56E-06	5.12E-05	6.03E-03	5.49E-05	1.44E-04	1.43E-02
16	rs11640993	51444106	3.42E-06	4.77E-05	5.57E-04	1.35E-06	1.25E-05	1.70E-04	2.05E-06	2.79E-05	5.01E-04
16	rs13444841	51469800	1.65E-06	2.62E-05	3.97E-04	9.60E-07	7.49E-06	6.74E-04	1.07E-06	1.28E-05	4.98E-04
16	rs8056052	51470239	4.23E-06	9.10E-05	3.57E-04	2.73E-06	1.10E-04	4.39E-04	4.47E-06	8.47E-05	4.27E-04
16	rs2192859	51472250	1.88E-06	2.82E-05	4.41E-04	2.44E-06	3.51E-06	9.14E-04	1.26E-06	1.45E-05	5.46E-04
16	rs45677062	53859772	1.55E-05	7.46E-05	4.88E-03	4.01E-06	2.63E-05	4.89E-03	6.22E-06	3.73E-05	2.46E-03
16	rs2576561	54028475	2.99E-05	2.91E-05	1.26E-01	1.22E-05	4.50E-06	2.51E-01	7.81E-05	6.31E-05	1.90E-01
17	rs203097	47368276	2.01E-03	7.33E-02	4.50E-05	3.72E-04	2.48E-02	9.59E-06	1.55E-03	6.64E-02	2.23E-05
18	rs18931462	8977427	8.15E-05	1.71E-04	4.50E-02	5.83E-06	1.58E-05	7.92E-03	5.05E-05	1.00E-04	4.79E-02
19	rs7247513	12552185	2.07E-06	8.94E-05	1.08E-04	5.54E-06	2.02E-04	1.10E-04	3.96E-06	1.90E-04	9.19E-05
19	rs74081692	48485993	6.10E-05	2.07E-04	7.96E-03	4.32E-05	1.87E-04	3.31E-03	9.84E-06	3.66E-05	4.08E-03
19	rs72484932	63402920	3.08E-05	4.30E-05	4.24E-02	1.40E-05	2.46E-05	1.08E-02	6.04E-06	2.31E-05	6.78E-03

¹The SNPs identified by WTCCC (2007) with strong or moderate association.

²The SNPs identified by WTCCC (2007) with p-value between 10⁻⁴ and 10⁻⁵.

Haplotype Analysis Results

Among all SNPs showing strong or moderate evidence of association, we found that some SNPs are in close proximity within a chromosome. This motivates a haplotype analysis for these SNPs. We focus on the SNPs on chromosome 16 that are tabulated in Tables 1 and 2. The linkage disequilibrium (LD) heat map in Figure 1 displays that seven out of the eleven SNPs were in a 29kb region. They were identified as a haplotype block [Barrett et al., 2005]. Using the seven SNPs within the block, the haplotype frequency was estimated [Zhao, 2004]. The top haplotypes are “GGTTCGG”, “ACCCGAA”, “GCTTCGG”, and “GGTTGGG”, with probabilities 0.535, 0.381, 0.049, and 0.027, respectively. Next, a pair of haplotypes was estimated for each subject using EM algorithm, and the haplotype association analysis was performed. We chose to dichotomize haplotype H as 1 or 0 according to whether it is equal to “ACCCGAA”. Then, the previous association tests can be applied simply by replacing genotype G with haplotype H. Using the non-weighted test under H₀, the p-value was 3.45×10⁻⁶. The weighted test determined the p-value at 2.64×10⁻⁷ as a genome-wide strong association between this block and bipolar disorder, highlighting the power of the weighted test and further confirming the importance of this region. Moreover, using the logistic regression model adjusting for the covariates determined the p-value of this block at 2.16×10⁻⁶, which did not achieve the genome-wide significance. We note that this region is close to the RPGRIP1L gene, which encodes the protein that localize to the basal body-centrosome complex or to primary cilia and centrosomes in ciliated cells. The RPGRIP1L gene was previously identified to be associated with schizophrenia as well as bipolar disorder [O’Donovan et al., 2008; Riley et al., 2009].

SIMULATIONS

Simulation Settings

To further evaluate our method, we performed a proof-of-principle simulation study to assess the influences of the weighted test to the confounding effects. First, a continuous covariate Z^co was simulated from N(0,1) distribution, and a categorical covariate Z^ca was simulated as P(Z^ca = 1) = 1 − P(Z^ca = 0) = 0.7. To then introduce the correlation between the covariates and the test-locus genotype G, we generated G according to Binomial distribution Binomial(2, p) with probability p satisfying it(p) = μ +ν_co Z^co + ν_caZ^ca where ν_co and ν_ca control the correlation between the genotype and the covariates, and u ~ N(0,1) is random noise. Lastly, conditional on the genotype G and the covariates Z^co and Z^ca, a binary trait Y was generated according to a logistic model including genetic effect, environmental effects, and gene-environment interactions, logit(P(Y = 1)) = α + β_gg + β_coz^co + β_caz^ca + β_g,cogz^co + β_g,cagz^ca + ε, where ε ~ N(0,1). The interaction terms were added purposely to evaluate the robustness of different testing methods.

In the simulation, we set μ = α = −0.5. The choices of the coefficients (ν_co,ν_ca) and (β_g,β_co,β_ca,β_g,co,β_g,ca) were provided as in Table 3 as different settings and models. The weight function was chosen as $W(u_1,u_2)=\text{exp}(-u_1^2/2-u_2^2/2)$ after standardizing the corresponding propensity scores such that they have a unit sample standard deviation. We compared our weighted test to the non-weighted test to assess the influence of adjustment for covariates. In addition, as in the analysis of bipolar disorder data, we provided results from logistic regression model including marginal effects from both gene and covariates.

Table 3.

Simulation Settings and Models

	Coefficients
Setting S1	νco = νca = 0
Setting S2	νco = νca = 0.5
Setting S3	νco = νca = −0.5
Model N1	βg = βco = βca = βg,co = βg,ca = 0
Model N2	βg = 0, βco = βca = 1, βg,co = βg,ca = 0
Model A1	βg = 0.5, βco = βca = 1, βg,co = βg,ca = 0
Model A2	βg = 0.5, βco = βca = 2, βg,co = βg,ca = 0
Model A3	βg = 0, βco = βca = 0, βg,co = βg,ca = 1
Model A4	βg = 0, βco = βca = 1, βg,co = βg,ca = 1
Model A5	βg = 0.5, βco = βca = 0, βg,co = βg,ca = 1
Model A6	βg = 0.5, βco = βca = 1, βg,co = βg,ca = 1

Simulation Results

Tables 4, 5 and 6 report the empirical type I error and power of the three tests: the non-weighted test using H₀, the weighted test using H₀′, and the test from the logistic regression. Tables 4, 5 and 6 correspond to Settings S1, S2 and S3 (see Table 3), respectively.

Table 4.

Type I Error and Power (Setting S1)

	α	n	T a	$T_w^{\text{'}}$ b	Tlc	T	$T_w^{\text{'}}$	Tl
Type I Error			Model N1			Model N2
	0.05	200	0.075	0.070	0.074	0.055	0.042	0.047
		400	0.052	0.049	0.055	0.046	0.037	0.053
	0.01	200	0.016	0.019	0.018	0.013	0.004	0.009
		400	0.006	0.010	0.007	0.002	0.007	0.010
Power			Model A1			Model A2
	0.05	200	0.422	0.420	0.512	0.255	0.268	0.395
		400	0.748	0.743	0.796	0.485	0.540	0.680
	0.01	200	0.212	0.196	0.254	0.103	0.104	0.175
		400	0.501	0.494	0.589	0.254	0.269	0.420
Power			Model A3			Model A4
	0.05	200	0.701	0.769	0.746	0.294	0.398	0.397
		400	0.939	0.969	0.955	0.516	0.684	0.673
	0.01	200	0.448	0.555	0.493	0.116	0.149	0.180
		400	0.822	0.878	0.853	0.296	0.433	0.428
Power			Model A5			Model A6
	0.05	200	0.980	0.988	0.988	0.725	0.826	0.847
		400	1.000	1.000	1.000	0.951	0.986	0.992
	0.01	200	0.899	0.936	0.928	0.456	0.591	0.650
		400	0.999	0.999	1.000	0.832	0.931	0.951

^aNon-weighted test under H₀.

^bWeighted test under H₀′.

^cLogistic regression.

Table 5.

Type I Error and Power (Setting S2)

	α	n	T a	$T_w^{\text{'}}$ b	Tlc	T	$T_w^{\text{'}}$	Tl
Type I Error			Model N1			Model N2
	0.05	200	0.058	0.058	0.061	0.348	0.054	0.053
		400	0.044	0.049	0.052	0.585	0.047	0.053
	0.01	200	0.012	0.013	0.008	0.150	0.008	0.008
		400	0.010	0.005	0.005	0.332	0.014	0.014
Power			Model A1			Model A2
	0.05	200	0.926	0.459	0.507	0.957	0.319	0.363
		400	0.998	0.762	0.794	0.998	0.609	0.675
	0.01	200	0.798	0.227	0.261	0.854	0.133	0.173
		400	0.988	0.527	0.583	0.993	0.366	0.418
Power			Model A3			Model A4
	0.05	200	0.973	0.754	0.732	0.944	0.441	0.387
		400	1.000	0.967	0.948	0.998	0.743	0.669
	0.01	200	0.882	0.545	0.497	0.824	0.220	0.193
		400	0.995	0.866	0.826	0.993	0.518	0.426
Power			Model A5			Model A6
	0.05	200	1.000	0.980	0.976	0.995	0.854	0.833
		400	1.000	1.000	1.000	1.000	0.994	0.983
	0.01	200	0.993	0.927	0.919	0.975	0.660	0.637
		400	1.000	0.998	0.998	1.000	0.963	0.938

^aNon-weighted test under H₀.

^bWeighted test under H₀′.

^cLogistic regression.

Table 6.

Type I Error and Power (Setting S3)

	α	n	T a	$T_w^{\text{'}}$ b	Tlc	T	$T_w^{\text{'}}$	Tl
Type I Error			Model N1			Model N2
	0.05	200	0.059	0.053	0.058	0.326	0.052	0.050
		400	0.049	0.045	0.046	0.544	0.054	0.045
	0.01	200	0.012	0.014	0.015	0.138	0.005	0.006
		400	0.006	0.009	0.007	0.328	0.010	0.007
Power			Model A1			Model A2
	0.05	200	0.066	0.437	0.490	0.158	0.320	0.384
		400	0.072	0.720	0.773	0.230	0.614	0.674
	0.01	200	0.013	0.205	0.261	0.044	0.136	0.167
		400	0.010	0.470	0.542	0.084	0.330	0.416
Power			Model A3			Model A4
	0.05	200	0.225	0.603	0.557	0.111	0.328	0.289
		400	0.403	0.865	0.830	0.153	0.622	0.535
	0.01	200	0.081	0.367	0.323	0.024	0.134	0.112
		400	0.186	0.705	0.646	0.049	0.343	0.284
Power			Model A5			Model A6
	0.05	200	0.759	0.967	0.944	0.072	0.796	0.778
		400	0.974	1.000	1.000	0.103	0.987	0.979
	0.01	200	0.547	0.868	0.840	0.023	0.598	0.549
		400	0.898	0.998	0.996	0.026	0.943	0.909

^aNon-weighted test under H₀.

^bWeighted test under H₀′.

^cLogistic regression.

From the perspective of type I error, for model N1, since β_g = β_co = β_ca = β_g,co = β_g,ca = 0, there was neither genetic effect nor covariate effect. We found that all three tests behaved fairly well in terms of the accuracy for type I errors as noted in all three settings (Tables 4, 5 and 6). For model N2, since β_g = 0, β_co = β_ca = 1, β_g,co = β_g,ca = 0, there was no genetic effect but there were covariate effects. If there are correlations between the genotype and covariates, we expect that the non-weighted test using H₀ cannot control the type I error at the significance level because of the confounding effects caused by the covariates. In Table 4, since there were no correlations between the genotype and the covariates, all three tests performed reasonably well. However, in Tables 5 and 6, the type I errors of the non-weighted test were always much higher than the significance level. By contrast, the weighted test using H₀′ and the logistic regression performed well in controlling the type I errors.

From the perspective of power, we considered a collection of models representing different situations. Models A1 and A2 only have marginal effects from both genotype and covariates, while Models A3–A6 all include gene-environment interactions. Since the non-weighted test using H₀ cannot control the type I error in Tables 5 and 6, the power is not truly comparable. Nonetheless, we tabulated the power results for all three tests. The non-weighted test using H₀ sometimes had a higher power (as seen in Table 5), and sometimes had a lower power (as seen in Tables 4 and 6). In Setting 2, due to the confounding effects enhancing the overall genetic effects, a false positive occurred. We have the opposite situation in Setting 3 as the false negative occurred. This suggests that to adjust for confounders, the null hypothesis must be conditional, as is H₀′. It is noteworthy that, even if there were no confounders as in Setting 1, we still observe the advantage of adjusting for covariates when there exist environmental effects to the trait.

The comparison between the weighted test using H₀′ and the logistic regression falls into the classic framework of comparing nonparametric and parametric tests. In Models A1 and A2, due to the correctness of underlying model assumptions, the logistic regression performed slightly better than the weighted test. By contrast, when the underlying model assumptions were violated as in Models A3–A6, the nonparametric test performed better than the parametric test due to its robustness to model specifications. In summary, the weighted test is robust to the model assumptions compared with the logistic regression, and it performed consistently well in our simulation studies.

DISCUSSION

In conclusion, we applied a propensity score-based nonparametric test to analyze an important data set on bipolar disorder made available to us by the WTCCC. By analyzing the bipolar disorder data, we not only confirmed the results reported by the WTCCC (2007), but also identified other regions at the genome-wide significance level, including the haplotype block identified on chromosome 16. It is important to note that the identified haplotype block is near the RPGRIP1L gene that was reported to be associated with bipolar disorder. Simulation studies provide further supporting evidence for the weighted test. Compared with the non-weighted test, the weighted test can not only correctly control the type I error at the significance level to avoid false positives, but also increase the power when false negatives occur. Compared with other parametric test such as logistic regression, the weighted test has the merit of robustness to model specifications. Our approach provides a promising way of adjusting for general covariates in genome-wide association studies, and has demonstrated its usefulness in an existing GWAS data set. In this analysis, we examined age and gender as two potentially important covariates. There are likely other covariates that are worthy consider investigation.