A Spring-loaded Release Mechanism Regulates Domain Movement and Catalysis in Phosphoglycerate Kinase

Abstract

Phosphoglycerate kinase (PGK) is the enzyme responsible for the first ATP-generating step of glycolysis and has been implicated extensively in oncogenesis and its development. Solution small angle x-ray scattering (SAXS) data, in combination with crystal structures of the enzyme in complex with substrate and product analogues, reveal a new conformation for the resting state of the enzyme and demonstrate the role of substrate binding in the preparation of the enzyme for domain closure. Comparison of the x-ray scattering curves of the enzyme in different states with crystal structures has allowed the complete reaction cycle to be resolved both structurally and temporally. The enzyme appears to spend most of its time in a fully open conformation with short periods of closure and catalysis, thereby allowing the rapid diffusion of substrates and products in and out of the binding sites. Analysis of the open apoenzyme structure, defined through deformable elastic network refinement against the SAXS data, suggests that interactions in a mostly buried hydrophobic region may favor the open conformation. This patch is exposed on domain closure, making the open conformation more thermodynamically stable. Ionic interactions act to maintain the closed conformation to allow catalysis. The short time PGK spends in the closed conformation and its strong tendency to rest in an open conformation imply a spring-loaded release mechanism to regulate domain movement, catalysis, and efficient product release.

Introduction

Phosphoglycerate kinase (PGK)² catalyzes the transfer of phosphate from 1,3-bisphosphoglycerate (1,3BPG) to ADP in the first ATP-generating step of the glycolytic pathway. As a major controller of flux through the pathway, PGK is a viable target for drugs against anaerobic pathogens, such as Trypanosoma and Plasmodium species, which depend solely on glycolysis for energy metabolism (1). In addition to its metabolic role, the phosphoryl transfer activity of PGK is important in the processing of antiretroviral prodrugs that take the form of l-nucleoside analogues (2). The rate-limiting step in the in vivo activation of such compounds has been demonstrated to be the addition of a third phosphate by PGK (3). A third activity of PGK is as a signaling molecule in chordates. It is integral in the response to hypoxia, when it is secreted from the cell and inhibits angiogenesis through a disulfide reductase activity that activates plasminogen autoproteolytic activity, producing angiostatin (4). This activity apparently uses the same mechanism as the normal metabolic reaction and can be inhibited competitively by 3-phosphoglycerate (3PG) or ADP (5). Consequently, PGK has a crucial role in oncogenesis and its development.

PGK is composed of two similarly sized domains, both with Rossmann fold topology, termed the N-terminal domain, which binds the phosphoglycerate species 3PG and 1,3BPG, and the C-terminal domain, which binds the nucleotides ADP and ATP. In early crystal structures of PGK (6–9), it was apparent that this state of the enzyme was incapable of catalysis. The relative orientation of the two domains meant that the two substrates would be too distant from each other to allow phosphoryl transfer. Therefore, significant “hinge bending” was suggested to be required for catalysis to occur (6). A major step forward in the understanding of catalysis by PGK was the determination of partially (10, 11) and fully closed (12) crystal structures of the enzyme. The latter, in complex with transition state analogues (TSAs), defined for the first time the state of PGK responsible for its catalytic activity, in particular demonstrating that a catalytic triad of positively charged residues surrounds the transferring phosphoryl group. On adopting a fully closed conformation, the separation of donor and acceptor atoms is between 3.9–4.3 Å, as predicted to be required for catalysis (13, 14). In the closed conformation of PGK, the two domains reorient by 33°, compared with the open form, about central hinge regions to bring the substrates together. Much effort has been put into elucidating the mechanism of this hinge bending and the role that substrate binding plays in inducing the conformational changes needed for catalysis to occur (15–19).

Here, we present small angle x-ray scattering (SAXS) data on complexes of human PGK (HsPGK) in solution. In combination with deformable elastic network (DEN) refinement (20, 21) a new “fully open” conformation of the apoenzyme is defined, and details are revealed of the relative time spent by the enzyme in the open and closed conformations during catalytic turnover. Together with the crystal structures of the binary (3PG) and ternary (3PG-ADP and 3PG-AMP-PCP) complexes in a half-open conformation, it is demonstrated that, in addition to the role of substrate binding in domain closure, the enzyme strongly favors the open conformation. The exposure of a hydrophobic patch may be important in promoting domain opening. A complete reaction pathway for the enzyme can thus be presented.

EXPERIMENTAL PROCEDURES

SAXS Experiments

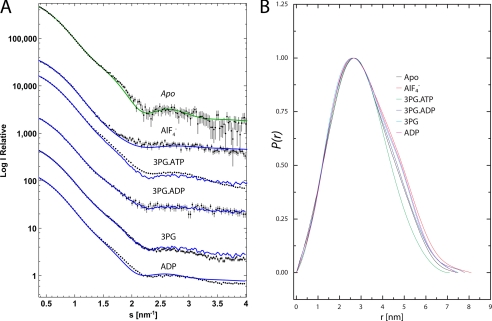
Expression, purification, and activity measurements of recombinant wild type HsPGK were performed as described previously (18, 22). Small angle x-ray scattering data were collected at the bioSAXS beamline ID14-3 (23) at the European Synchrotron Radiation Facility (Grenoble, France) with a Pilatus 1M detector (Dectris Ltd., Baden, Switzerland) at a wavelength of 0.931 Å and a camera length of 2.42 m. Scattering curves were measured from solutions of HsPGK without substrates; the binary complexes with either 50 mm 3PG or 10 mm ADP; a quaternary complex inhibited with the TSA 3PG-AlF₄⁻-ADP (50 mm 3PG, 10 mm ADP, 25 mm MgCl₂,10 mm NH₄F, and 2 mm AlCl₃ added 3 h before measurements); the 3PG-ADP ternary complex (50 mm 3PG, 10 mm ADP, and 25 mm MgCl₂) and the 3PG-ATP ternary complex (50 mm 3PG, 10 mm ATP, and 25 mm MgCl₂, nucleotide added just before measurements) in SAXS buffer (50 mm Tris, pH 7.5, and 20 mm DTT). Measurements were performed at protein concentrations between 5 and 15 mg/ml to verify whether any interparticle effects that may have been present could be accounted for and rule out their influence on the analysis. To exclude the possibility of radiation damage, 10 frames, each of a 10-s duration, were collected while continuously exposing fresh sample to the beam, the resulting frames were then compared with ensure no differences in the SAXS profiles were induced by exposure to x-rays. All data were processed using the ATSAS program package (24). Radii of gyration (R_g) were evaluated from Guinier plots using PRIMUS and pair distance distribution functions, P(r), were computed with GNOM (see Fig. 1 and supplemental Fig. S1) (25). The solution shapes of HsPGK were reconstructed from the experimental data (GNOM functions) using the ab initio method. For each sample, 12 independent DAMMIN reconstructions were aligned, averaged, and filtered using the program package DAMAVER. A homology model of the apo form of HsPGK was created from the mouse crystal structure (Protein Data Bank code 2P9Q (26)). The N- and C-terminal domains were then treated as rigid bodies, and their positions were refined against the scattering curve using SASREF (24). The model produced was then used to calculate an electron density map to 8 Å resolution as an alternative representation of the scattering data. The apo homology model was then fitted to this density map using the real space refinement program DireX (21), which uses DEN restraints (20) to balance the model deformations and the fit to the density. The fitted model was then energy minimized with CNS. The DireX refinement removed numerous atom clashes and improved local geometry in the rigid body fitted model with almost no change to the chi-square value of the fit to the scattering curve (0.97–1.08). As the structure was refined against the 8 Å density map (i.e. indirectly against the scattering curve) the limited amount of data did not allow for a cross-validation procedure, therefore no “free chi-square” value could be computed. The final structure had 90% of backbone torsion angles in the allowed region (and 2% outliers) of the Ramachandran plot. The relative contributions of models to scattering curves was assessed with OLIGOMER (27) (Table 1 and supplemental Fig. S2).

FIGURE 1.

Scattering curves and pair distance distribution functions. A, comparison of SAXS curves and the two component fits from OLIGOMER. The experimental curves for the samples are shown with the two component fits from OLIGOMER (blue lines). For the apo data, the fit of the DEN refined structure as calculated using CRYSOL is also shown (green line). The curves are displaced for visualization and therefore log (I) values are relevant for the apo sample only. B, pair distance distribution function, P(r), plots calculated by an indirect Fourier transformation of the SAXS data using GNOM.

TABLE 1.

SAXS experimental data, oligomer fits, and comparison with crystal structures

Protein complex	Rg	% Open	% Closed	Chi-square of fit
	nm
Apo	2.42	N.D	N.D	1.08 (DEN model)
3PG-AlF4−-ADP	2.24	39.3	60.6	1.36
3PG-ATP	2.34	92.5	7.5	7.55
3PG-ADP	2.37	96.5	3.5	0.9
3PG	2.40	96.6	3.4	2.75
ADP	2.42	96.7	3.3	5.15
3PG-AlF4−-ADP crystal structure	2.17
Binary complex crystal structure	2.33

Crystallization

Lyophilized HsPGK was resuspended in 50 mm Tris, pH 7.0, 20 mm DTT, 20 mm MgCl₂, and 20 mm 3PG, and the protein concentration was adjusted to 20 mg/ml. Crystals with approximate dimensions 0.9 × 0.3 × 0.1 mm³ were obtained by vapor diffusion in 4 μl hanging drops consisting of a 50:50 mix of protein and precipitant (26–31% PEG 4000 and 0.1 m Tris, pH 7) solutions. Crystals of this complex diffracted poorly after cryoprotection (d_min = 3.0 Å) and were therefore conditioned by controlled dehydration using a HC1b dehydration device mounted on beamline ID14-2 at the European Synchrotron Radiation Facility (28). Crystals were harvested on micromeshes at a relative humidity of 98.5% (the equilibrium relative humidity with the mother liquor), and excess mother liquor was removed. A reduction in the relative humidity to 97.5% resulted in an increase in the diffraction limit of crystals and a small reduction in the a axis of the unit cell by ∼3 Å. After conditioning, crystals were cryo-cooled by plunging directly into liquid nitrogen, without the use of a cryo-protectant, and stored at 100 K. To obtain the ADP and AMP-PCP open ternary complexes, crystals were transferred to a buffer containing 50 mm Tris, pH 7.0, 20 mm DTT, 20 mm MgCl₂, and 20 mm 3PG, 31% PEG 4000, and 10 mm ADP or AMP-PCP for 10 min prior to conditioning with the HC1b device as described above.

Data Collection and Structure Solution

Diffraction data were collected from cryo-cooled crystals to resolutions of between d_min = 2.2 and 1.74 Å on an ADSC Q210 CCD detector at beamline ID14-2 (λ = 0.933 Å) at the European Synchrotron Radiation Facility (Grenoble, France) (Table 2). The half-open conformation crystallized in the orthorhombic space group P2₁2₁2 with unit cell dimensions of a = 61.6 Å, b = 73.0 Å, and c = 93.6 Å with one molecule in the asymmetric unit (Table 2). Data were processed with MOSFLM (29) and programs from the Collaborative Computational Project Number 4 (CCP4) suite (30). The structures were solved by molecular replacement with MolRep (31) using the HsPGK structure (Protein Data Bank code 2ZGV (32)), stripped of ligands and water molecules, as a search model. In all subsequent refinement steps, 5% of the data, chosen at random, were excluded for calculating the free R-factor. Refinement was carried out alternately with REFMAC5 (31) and by manual rebuilding with the program COOT (33). Some solvent molecules were included using the ARP/water function of ARP/wARP (34). The models contain residues 4–416 for the HsPGK-3PG-open structure and 5–416 for the HsPGK-3PG-ADP-open and HsPGK-3PG-AMP-PCP-open structures. The final electron density maps for all the structures were of good quality, omit maps for all ligands are shown in supplemental Figs. S3–S5. Stereochemistry was assessed with COOT (33) with all residues in preferred or allowed regions. Figs. 2–4 and S2–S5 were produced with PyMOL (35). Hinge bending analysis and interpolation of structures for movies were performed using the MORPH server (36).

TABLE 2.

Data processing and refinement statistics

Structure	3PG	3PG-ADP	3PG-AMP-PNP
Space group	P21212	P21212	P21212
Wavelength	0.933 Å	0.933 Å	0.933 Å
Unit cell dimensions (Å) a, b, c	61.6, 73.0, 93.6	58.6, 73.4, 93.4	59.3, 71.2, 91.5
Resolution range (Å)	20–1.74	20–2.2	20–1.79
No. of unique reflections	43561	20841	36815
Multiplicitya	4.1 (3.7)	3.9 (4.0)	2.9 (2.7)
Completenessa (%)	98.9 (100.0)	99.1 (99.8)	98.6 (97.1)
Rmergea,b	0.10 (0.29)	0.06 (0.29)	0.07 (0.29)
〈I/σ(I)〉a	8.1 (3.2)	12.8 (4.0)	10.1 (3.6)
Wilson B factor	22.6 Å2	32.8 Å2	19.4 Å2
Water molecules	363	65	140
R-factorc (%)	20.6	22.4	19.8
Free R-factord (%)	25.3	28.8	24.3
Bonds (Å)e	0.023	0.017	0.023
Anglese	1.85°	1.61°	1.96°

^a Statistics for the highest resolution bin (3PG, 1.83–1.74; 3PG-ADP, 2.32–2.20; 3PG-AMP-PNP, 1.88–1.79) are shown in parentheses.

^b R_merge = Σ_hΣ_i|I_h − I_(h)i|/Σ_hΣ_iI_(h)i, where I_(h) is the mean weighted intensity after rejection of outliers.

^c R = Σ_hkl‖F_obs| − k|F_calc‖/Σ_hkl|F_obs|, where F_obs and F_calc are the observed and calculated structure factor amplitudes.

^d R_free = Σ_hkl⊂T‖F_obs| − k|F_calc‖/Σ_hkl⊂T|F_obs|, where F_obs and F_calc are the observed and calculated structure factor amplitudes, and T is the test set of data omitted from refinement (5% in this case).

^e Root mean square deviation.

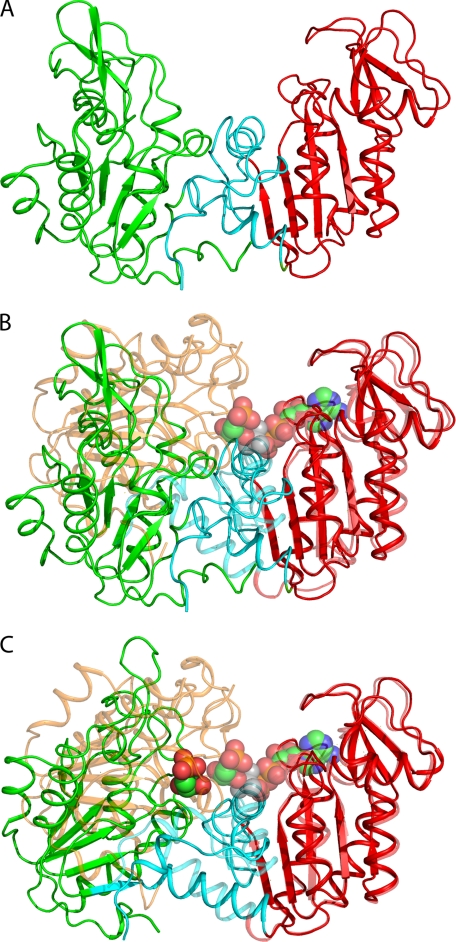
FIGURE 2.

A, the structure of the fully open apo-HsPGK (ribbon; green, N-terminal domain; red, C-terminal domain; cyan, interdomain region) determined by rigid body and DEN refinement against SAXS data. B, the structure of the SAXS-observed fully open apo-HsPGK aligned with the structure of the fully closed HsPGK-3PG-MgF₃⁻-ADP complex (Protein Data Bank code 2WZB). The N-terminal domain of the closed conformation is colored orange for clarity. Structures were aligned on residues 200–400 of the C-terminal domain and are related by a 56° rotation of the N-terminal domain. The substrates 3PG, MgF₃⁻, and ADP are shown as spheres (green carbon atoms). C, the crystal structure of the half-open conformation of the HsPGK-3PG binary complex (ribbon; colored as above) aligned as before with that of the fully closed HsPGK-MgF₃⁻-ADP complex. The half-open and fully closed structures are related by a 28° rotation of the N-terminal domain. Substrates are shown as spheres (green carbon atoms).

FIGURE 3.

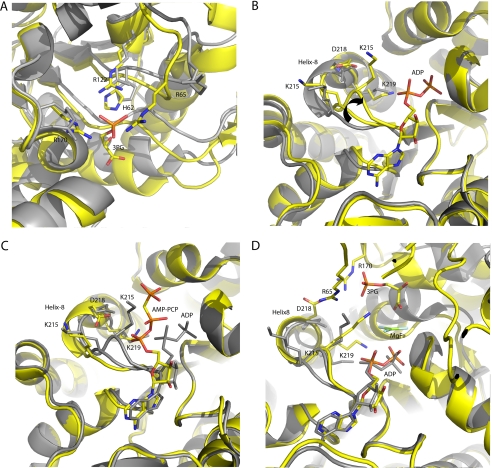
Conformational changes induced by substrate binding in PGK. A, the binding of 3PG. An alignment of residues 10–150 of the half-open conformation binary complex (yellow) and the mouse apoprotein. 3PG is bound by three arginines and a histidine. Residues Arg⁶⁵ and Arg¹⁷⁰ are crucial in stabilizing the closed conformation and are only positioned correctly on ligand binding. B, the binding of ADP to the binary complex. An alignment of residues 200–400 of the half-open conformation binary (gray) and 3PG ADP ternary (yellow) complexes. On binding of ADP the catalytic loop (residues 214–219) adopts two conformations, the end of helix-8 moves 2 Å toward the nucleotide leading to the preparation of Lys²¹⁵ for catalysis (arrow). The closed conformation is also prepared for by the positioning of Asp²¹⁸ to form an essential salt bridge with Arg⁶⁵ from the N-terminal domain. C, an alignment of residues 200–400 of the ADP (gray) and AMP-PCP (yellow) half-open conformation ternary complexes. The catalytic loop resumes the conformation observed in the binary complex and the ATP analogue is ready for release. D, comparison of the half-open 3PG ADP ternary complex (gray) and the fully closed 3PG-MgF₃⁻-ADP TSA complex (yellow). On domain closure, a salt bridge is formed between Asp²¹⁸ and Arg⁶⁵, Lys²¹⁵ is positioned for catalysis, and helix-8 is extended. The alternative position of Lys²¹⁵ is very similar to that observed in the closed conformation and prepares the enzyme to form an interaction with the 3-phosphate of 3PG to stabilize the closed conformation. In the half-open conformation, the catalytically essential residue Lys²¹⁹ remains coordinated to the α-phosphate of ADP as there is no γ-phosphate or 3-phosphate present and is not involved in stabilizing the closed conformation.

FIGURE 4.

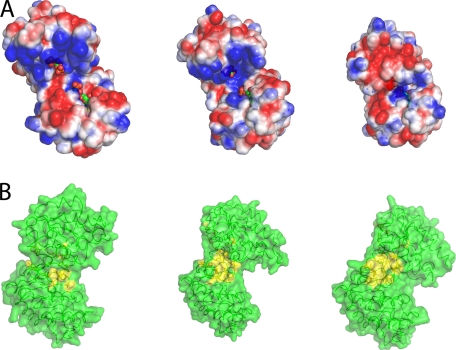
Changes in the solvent exposed surface upon domain closure. A, electrostatic potential representation (blue, positive; red, negative; white, neutral; values from +2 kcal/mol to −2 kcal/mol) of the solvent accessible surface (probe radius, 1.4 Å) of the fully open apoenzyme conformation, the half-open binary complex, and the fully closed conformation. In the fully open conformation, the binding sites for ligands are well separated and exposed to the bulk solvent. The complementary charged areas that stabilize the closed conformation can be seen easily. Ligands are shown as spheres (green carbon atoms). B, surface representation of the transition from fully open to fully closed state. Residues involved in hydrophobic interactions are colored yellow. As the enzyme moves to the fully closed state, a hydrophobic patch is exposed.

RESULTS

Solution Structure of Apo-PGK and Domain Movements in Solution

The x-ray crystal structures of PGK available define snapshots in the catalytic cycle but lose detail on the extent and timing of the domain movements that occur in solution. To determine the events during the reaction cycle in solution, SAXS was employed to determine the conformations of the protein at different stages of the reaction cycle. Scattering curves of the apoenzyme, the 3PG and ADP binary complexes, the ATP-3PG ternary complex (equivalent to the enzyme in catalytic turnover), the ADP-3PG ternary complex (a dead-end complex), and the 3PG-AlF₄⁻-ADP complex (the fully closed conformation) were measured (Fig. 1). Although similar experiments have been performed previously (18, 19), the experiments described here benefit from the ability to trap the fully closed conformation in solution by inhibition with aluminum fluoride (the ADP-AlF₄⁻-3PG complex) and compare the curves to the crystal structure of this complex and to the various open forms from the same species. In this respect, the study provides a full explanation of domain movement during catalysis. The radius of gyration (R_g) of the apoprotein was found to be larger than that calculated from crystal structures of the open conformation (Table 1). Ab initio modeling for the apoenzyme produced a molecular envelope close to that obtained from crystal structures of the open conformation but with a greater angle between the two domains (supplemental Fig. S1). To define the domain orientation in this new conformation, a homology model of the HsPGK apoenzyme was constructed from the crystal structure of the mouse apoenzyme (26), and the N- and C-terminal domains refined as rigid bodies against the scattering curves to define their relative orientation in solution. DEN refinement (20, 21) was then used to further characterize the resting state of the enzyme (Fig. 2). The model obtained gives an excellent fit to the data (Table 1, coordinates available in supplemental material) and shows a conformation considerably more open than observed in crystal structures, with a 56° rotation required to form the catalytically active conformation (as opposed to a maximum of 33° from the most open crystal structure (Fig. 2B) (37). The validity of the model produced is supported molecular dynamics studies (16) that detected a further opening of PGK, when compared with “open” crystal structures. The domains also exhibit a 5° twist such that amino acids in the two domains that interact in the closed conformation are “misaligned” relative to each other. Without the constraints of a crystal lattice, the protein thus adopts its fully open resting state. Scattering curves of the binary complexes, with either 3PG or ADP alone, show an R_g close to that of the apoprotein implying a requirement for both substrates to bind before domain closure, in agreement with previous suggestions (11, 19). Scattering curves obtained from the AlF₄⁻-TSA complex have a similar R_g to the crystal structure of the same complex, and ab initio modeling confirms a more closed conformation of this complex (supplemental Fig. S2). SAXS data therefore define both the fully open and fully closed states of PGK in solution. The curves obtained from of the ATP-3PG ternary complex do not match any of the crystal structures, even though the R_g is similar to the half-open crystal structure (Table 1). The ab initio model calculated from these data presents a shape reminiscent of both open and closed conformations (supplemental Fig. S2C) as SAXS scattering curves originate from an average of all the particles in solution, and the enzyme was in full catalytic turnover throughout the measurements. It is possible, however, to calculate the contribution of conformational states from each stage of the catalytic cycle to the overall scattering curves observed. In this manner, the relative time that the enzyme spends in each conformation during catalysis can be determined. The program OLIGOMER was used to determine the relative contributions of conformational states to the scattering curves of the protein. The degree of inhibition in the TSA complex was also determined (Table 1) by calculating the percentage of particles inhibited in the closed conformation. Both two-component (fully open and fully closed) and three-component (including the half-open crystal structure) models were applied to the data to see whether there was significant time spent in the half-open state. The results of the fit suggest that when the enzyme is in full catalytic turnover it spends 92% of its time in the fully open conformation and only 8% of the time in the catalytically competent fully closed conformation. This figure is even lower for the binary and ADP-3PG dead end complexes with 97% of time spent in the open conformation, presumably because these complexes cannot form all of the interactions needed to stabilize the closed conformation. The TSA complex was found to be only 60% closed. This would account for the larger R_g compared with the crystal structure of the same complex and is probably due to incomplete inhibition by aluminum fluoride.

These results imply that although the enzyme moves between the open and closed state, it has an energetic preference for the open conformation. A model of cycling and catalysis may be proposed where unliganded PGK remains open (ready to bind substrates or release products) most of the time. This assertion is supported by isothermal calorimetric titration experiments, where a very small energy difference could be calculated between the open and the closed conformations of the enzyme (38). The binding of substrates induces structural changes that allow the stabilization of the closed state for sufficient time to enable catalysis.

Preparation of Closed Conformation by Binding of Ligands

If PGK has a preference for an open conformation, and only the binding of both substrates affects this conformation, what is the role of substrate binding in the formation of the closed conformation? Previous studies have pointed to an induction of hinge bending upon ligand binding (17–19); however, this model does not adequately describe how products are subsequently released. To investigate the effects of ligand binding on the open conformation, crystals of the 3PG-HsPGK binary complex in an open conformation (HsPGK-3PG-open) were grown, and ADP and the nonhydrolyzable ATP analogue, AMP-PCP, were introduced, by soaking, to investigate the effect of their binding on the open conformation. The diffraction properties of the crystals were significantly improved by controlled dehydration using the HC1b dehydration device (28). Crystal structures were then solved of the 3PG binary complex and of the 3PG-ADP and 3PG-AMP-PCP ternary complexes. The complexes obtained are in a half-open conformation with an opening angle between the two domains of 28° relative to the closed conformation observed in the crystal structure of the MgF₃⁻-TSA complex (Fig. 2C). This conformation is very similar to previously observed crystal structures of open forms of PGK from various species (8, 9, 39). Comparison of the structures of these half-open binary complexes with the open structure of apo-PGK shows how binding of 3PG prepares the enzyme for catalysis. The conclusions drawn are entirely consistent with previous findings derived from the crystal structure of the 3PG binary complex of pig muscle PGK (9). Upon binding of 3PG, residues Arg⁶⁵ and Arg¹⁷⁰ (located in the N-terminal domain) are aligned to be able to form essential salt bridges (present only in the closed conformation) with a reoriented Asp²¹⁸ (located in the C-terminal domain, see below). These salt bridges stabilize the catalytically active closed conformation (Fig. 3, A and B). In the half-open ternary complex with 3PG and ADP (HsPGK-3PG-ADP-open) binding of the nucleotide effects changes that provide information on the catalytic cycle. On binding ADP, the loop region at the N terminus of helix-8 (C-terminal domain) composed of residues 214–219 adopts two conformations, one moving ∼2 Å toward the nucleotide. This motion may assist in domain movement and leads to the positioning of the catalytic residue Lys²¹⁵ to interact with the 3-phosphate of 3PG (or both the 1- and 3-phosphate groups of 1,3BPG), bound in the N-terminal domain, upon closure and stabilize this conformation (an arrangement not observed previously in other open conformation structures). A reorientation of Asp²¹⁸ to a position ready to form a salt bridge with Arg⁶⁵, another interaction important in stabilizing the closed conformation, also occurs (Fig. 3, B and C). This movement leads to an extension of helix-8. Therefore, the binding of ADP moves essential catalytic residues on a “catalytic loop” into position by extending helix-8 and prepares the C-terminal domain for stabilizing the closed conformation.

In contrast, in the half-open ternary complex of PGK with AMP-PCP and 3PG (HsPGK-3PG-AMP-PCP-open), the 214–219 loop adopts the same conformation seen in the binary complex (Fig. 3C). The adenosine moiety is bound in a similar manner to the ADP ternary complex, but the β- and γ-phosphate groups protrude into the solvent and are poorly ordered: A conformation that is similar to the same complex of pig muscle PGK (40). As the γ-phosphate has been shown to possess a high extent of mobility, it could temporarily interact with Lys²¹⁵, even in the open conformation (22). Thus, ATP may be able to stabilize the conformation seen in the HsPGK-3PG-ADP-open structure, which is similar to that observed in the closed conformation (3PG-MgF₃⁻-ADP TSA complex) with Lys²¹⁵ interacting with the phosphate groups of 3PG and the transition state analogue (Fig. 3D). Before the enzyme closes, binding of ADP has positioned this residue to form the interactions needed to stabilize the closed conformation, in its absence, Lys²¹⁵ is not positioned correctly, and the closed conformation cannot be stabilized. Therefore, both 3PG and the nucleotide, bound in the open conformation, act to prepare the interactions that will exist only in the catalytically competent closed form.

DISCUSSION

A Hydrophobic Spring May Favor Open Conformation

The data presented here point to a new model of catalysis in PGK. SAXS data demonstrate that the protein remains mostly in an open conformation, with (even in the apo form) short bursts of closure, whereas the x-ray structures reveal that ligand binding prepares the interactions needed to stabilize the closed conformation for the 8% of time spent on catalysis, rather than actually inducing closure. The need for both ligands to be bound in order for the closed conformation to be stabilized and for catalysis to occur also is shown. Analysis of the solvent accessible area and electrostatic potential of the different conformations (Fig. 4A) shows that the fully open SAXS-observed conformation is needed for efficient substrate exchange. Only in this conformation are the substrate binding sites fully accessible to solvent with large positive and negative patches available for binding. The transition to the crystallographically observed half-open conformation occludes the binding sites implying that this conformation would not be able to efficiently exchange ligands. No significant time is spent in this conformation in solution, and it is therefore part of the transition between open and closed and not functionally significant itself. Movement to the catalytically active conformation completely excludes the ligands from the solvent. The fully open conformation is clearly optimal for ligand exchange, but how is this conformation maintained/readopted in the presence of the strong electrostatic interactions present when ligands are bound? A detailed comparison of the fully open and fully closed structures points to a possible “spring” that drives the preference for the open conformation. The N- and C-terminal domains are linked by a single helix (helix-7, residues 187–198) that is highly conserved across all kingdoms of life. Many of these residues are hydrophobic. Analysis of the fully open conformation shows extensive interaction between these residues and other conserved hydrophobic residues in the core of the protein (for a full list of residues, see supplemental Table S1). When the enzyme moves to the half-open and fully closed conformations, some of these interactions are disrupted, and many residues form a solvent-exposed hydrophobic patch (see supplemental Movie 1 and Fig. 4B). This hydrophobic patch has a solvent exposed area of 502 Ų in the fully closed conformation, which reduces to 150 Ų in the half-open conformation and has a minimum of 92 Ų in the open state (masking 82% of the area from solvent, supplemental Table S1). These residues only become buried when the opening angle between the domains is >50°. This masking of the hydrophobic region from solvent could account for the preference of PGK to adopt an open conformation, as this will be thermodynamically more stable.

An analysis of seven amino acid sequences of PGKs show that the hydrophobic nature of almost all of the residues in this region is conserved across all kingdoms, implying an essential role (Fig. 5). The exposure to solvent of this hydrophobic patch in the catalytically competent closed conformation, stabilized when both substrates are bound, suggests that this conformation will exist only long enough for catalysis to occur and that the overall thermodynamic preference for the open conformation will eventually destabilize the closed conformation, causing it to spring open, leading to the release of products and rebinding of substrates. The hydrophobic patch could act as a spring by constantly applying pressure to the closed conformation, leading to the release of products after catalysis.

FIGURE 5.

Multiple sequence alignment of PGK from all kingdoms of life. Residues colored yellow are the same as those shown in Fig. 4B. Residues that form the hydrophobic patch are almost completely conserved from archaea to human. Residues involved in catalysis are shown in red. Species are as follows: Sus, Sus scrofa; Homo, Homo sapiens; Saccharomy, Saccharomyces cerevisiae; Arabidopsi, Arabidopsis thaliana; Trypanosom, Trypanosoma brucei; Escherichi, Escherichia coli; Pyrococcus, Pyrococcus furiosus. The trypanosome-specific insertion (residues 69–84) was removed for clarity.

The “spring-loaded” release mechanism suggested here has parallels with ATP synthase. In this enzyme, a domain movement of 19° is effected mechanically, using the energy of an electrochemical gradient to produce the catalytically competent conformation (41). The majority of the energy used is in the subsequent mechanical transformations to the open conformation that are required to release the newly synthesized ATP molecule. In PGK, the production of ATP is a less efficient process as the transformation between conformations is not controlled mechanically. Instead, a balance between thermodynamically stable states could be used to ensure that a tightly bound state is opened in order to release ATP and 3PG and allow binding of 1,3BPG and ADP for the next cycle. However, if the enzyme has a stable state that is noncatalytic and spends most of its time in this state, how can it act as an efficient catalyst? As the actual phosphoryl transfer reaction occurs extremely fast (13, 14), the closed state does not need to be stabilized for too long. Therefore, for catalysis to be efficient, the open conformation needs to be dominant. The destabilizing effect of the hydrophobic patch on the closed conformation may act like a powerful spring, allowing the protein to efficiently bind and, importantly, release substrates and products. As the catalytic trap will only be primed when all ligands are bound, this prevents any time lost in futile stabilization of the closed conformation.

Reaction Pathway

Using the experimental evidence presented here, a complete reaction cycle for PGK can be proposed. From the SAXS data, it can be seen that the protein has a “normal state” with a large angle between the domains that maintains the substrates at a distance of 16 Å (nucleophile to phosphate atom) and that even during full catalytic turnover, this conformation is preferred by the enzyme. Brownian motion will, presumably, provide energy to cycle the two domains between the open and closed conformations, but in the absence of substrates, the interactions required to maintain the closed conformation away from the low energy open conformation are not present. However, upon substrate binding, the charged residues that form the important salt bridges, which stabilize the closed conformation, are all positioned correctly. Therefore, the closed conformation is “primed” on substrate binding. Substrate binding may also assist in the interdomain communication and domain closure by the aid of well described interaction networks (17–19) and acts in concert with the internal dynamics of the protein. Therefore, as soon as the domains come together, the salt bridges are formed, and the closed conformation will be stabilized sufficiently for catalysis to occur. The tendency for the protein to return to the open conformation will avert any energy minima preventing substrate release or rehydrolysis of the product. With all catalytic residues coordinating the transferring phosphate, the catalytic loop becomes an extension of helix-8 completing the continuing stabilization of this region by the subsequent binding of substrates and its interaction with the N-terminal domain. The substrates are now aligned for catalysis, and three positively charged residues (Arg³⁸, Lys²¹⁵, and Lys²¹⁹) are positioned trigonally around the transferring phosphate, perfectly balancing the charge of the transition state. After phosphoryl transfer has occurred pressure to return to the open conformation from the exposed hydrophobic patch could destabilize them. As the domains begin the next cycle of opening, ATP bound to the C-terminal domain and 3PG bound to the N-terminal domain are exposed to the bulk solvent. The removal of the interaction with Arg³⁸ and a destabilization of helix-8, removing the interaction with Lys²¹⁹, coupled with the lower affinity fully open conformation, leads to the release of ATP (movies defining all steps in the reaction cycle are available in the supplemental material). Competition between the higher affinities for ADP over ATP and 1,3BPG over 3PG may also play a part in the release of products (18).

The fast spring-loaded release mechanism with the majority of time spent in an open conformation would ensure the efficient binding and release of substrates and products with short periods ensuring catalysis. Thus, the temperature-driven internal motion of protein structure seems to be essential for functioning of PGK, as also suggested for more complex allosteric proteins (42, 43). Although it has been assumed that the open, or unliganded, conformations of proteins that act through domain movements will be favored (44), a mechanism for this equilibrium has not been proposed. Here, we show that the equilibrium between open and closed is greatly biased toward the open conformation of PGK, and a hydrophobic spring may be responsible. This mechanism may prove general for some of the large number of enzymes that act by domain movements.