Abstract
A model is proposed to describe the polarization dependence of second harmonic generation (SHG) from type I collagen fibrils. The model is based on sum-frequency vibrational spectrum experiments that attribute the molecular origins of collagen second-order susceptibility to the peptide groups in the backbone of the collagen α-helix and the methylene groups in the pyrrolidine rings. Applying our model to a polarization SHG (P-SHG) experiment leads to a predicted collagen I peptide pitch-angle of 45.82° ± 0.46° and methylene pitch-angle of 94.80° ± 0.97°. Compared to a previous model that accounts for only the peptide contribution, our results are more consistent with the x-ray diffraction determination of collagen-like peptide. Application of our model to type II collagen from rat trachea cartilage leads to similar results. The peptide pitch-angle of 45.72° ± 1.17° is similar to that of type I collagen, but a different methylene pitch-angle of 97.87° ± 1.79° was found. Our work demonstrates that far-field P-SHG measurements can be used to extract molecular structural information of collagen fibers.
Introduction
Collagen molecules are the most common protein found in the body. Among the 28 known types of collagen, type I is the most common. Type I collagen is a major constituent of bone, tendon, skin dermis, cornea, and artery walls and plays a central role in maintaining tissue homeostasis (1). Structurally, a single type I collagen molecule is composed of three α-helix intertwined in forming a coil which is 1.5 nm in diameter and 290 nm in length. In tissue, the collagen molecules self-assemble in a staggered fashion into microfibrils which further aggregate in forming fibrils. Variations in the collagen supramolecular assemblies directly affect their properties in different tissues ranging from the high tensile strength of the tendon and elasticity of skin, to the transparency of the cornea. Due to its molecular and supramolecular structure, fibrillar collagen such as type I and II collagen produces a strong second harmonic generation (SHG) signal that has led to effective nonlinear imaging of many tissues including skin, bone, tendon, cartilage, and cornea (2–5). In addition to providing morphological contrast for SHG microscopy, the coherent nature of second harmonic generation is sensitive to the molecular and macromolecular structures, experimentally detectable in the SHG emission directionality and polarization dependence (6–10). The strength of the SHG and its polarization dependence is characterized by the bulk susceptibility tensor χ(2) which in turn depends on the molecular hyperpolarizability β. In cases of small molecules, the hyperpolarizability can be associated with a single molecule. For macromolecules such as collagen, there can be several moieties within the molecule, each making a contribution to the hyperpolarizability of a single collagen molecule.
Quantitative SHG measurements of polypeptide α-helix at air/water interface and hyper-Rayleigh scattering experiment have attributed the physical origin of SHG to the amide groups in the polypeptide bonds (11–13). Based on this, Plotnikov et al. (14), Tiaho et al. (15), Odin et al. (16), and Psilodimitrakopoulos et al. (17) have constructed a single axis model for the susceptibility tensor of α-helix that associates the polarization dependence of SHG with the pitch-angle of the α-helix. Applications of this model have led to pitch-angle predictions that are consistent with x-ray diffraction results for muscle myosin, but less accurate for collagen. Furthermore, a recent sum-frequency study by Rocha-Mendoza et al. (18) have found that in addition to the amide group in the peptide bonds, the methylene groups in the pyrrolidine groups of proline and hydroxyproline amino acids also make major contributions to the second-order susceptibility tensor.
Based on experimental results of collagen sum-frequency measurements, we construct what we believe to be a new model for the collagen second-order susceptibility tensor that accounts for the contribution from both the peptide and the methylene groups. We show that application of our model leads to prediction of collagen peptide and methylene pitch-angle that are in better agreement with x-ray diffraction data in comparison with a previous model. Furthermore, the model improves the ability to separate type I and type II collagen in pixel-resolved P-SHG imaging (19,20).
Theoretical Background
Cylindrical symmetry of collagen molecules
In general, the second-order nonlinear polarization Pi induced by an incident electric field E for the bulk second-order susceptibility χijk is Pi = χijk EjEk. For macromolecules such as collagen, the contribution for the bulk second-order susceptibility χijk comes from the chemical bonds of the smaller molecular groups such as C=O and N-H groups in the peptide bonds. We can write χijk in terms of a sum of molecular hyperpolarizabilities as
| (1) |
where N is the number density of the collagen molecule, is the hyperpolarizability for the molecular group s, in the molecular group's (primed) coordinate system, and Rijk i′ j′ k′ (ϕ,θ,ψ) is a sixth-rank tensor that transforms the hyperpolarizability from the molecular group's coordinate to the laboratory coordinates. Fig. 1 A is a drawing of the cross-section view of collagen molecule showing the position of the peptide bonds and the location of the methylene group within the collagen molecule. We chose a coordinate system where the z axis (pointing out of page) is along the α-helix. The angles (ϕ,θ,ψ) corresponds to the x-convention Euler angles (21) (Fig. 1 B), and the angular averaging denoted by 〈〉 accounts for the angular distribution of molecular group s. For collagen molecules that are well aligned within the point-spread function of a focused laser light source, we can make the cylindrical symmetry assumption (invariance under ϕ-rotation) for the bulk second-order susceptibility. If z axis is the axis of symmetry, we are left with only four independent χ-tensor elements (14)
and
Figure 1.
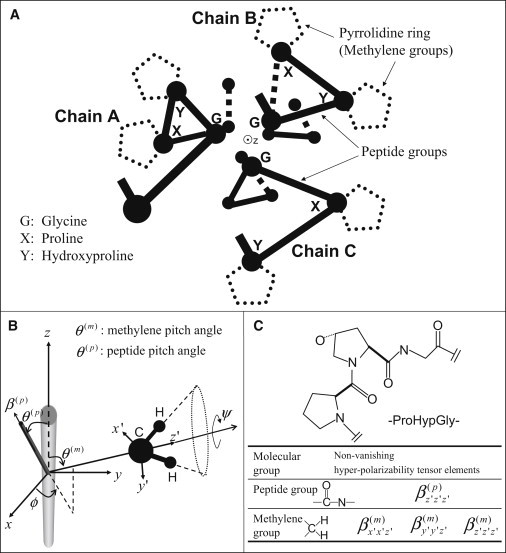
Molecular structure of collagen. (A) Schematic drawing for a cross-section of a collagen molecule showing two segments of the G-X-Y sequence for each α-helix. G, X, and Y correspond to glycine, proline, and hydroxyproline, respectively. (Sticks) Peptide groups. (Balls) The α-carbon. (Dotted-line pentagons) Pyrrolidine rings where the methylene groups are located, at the side chains of X and Y and pointing outward and away from the axis of the helix. The z axis points out of the page along the α-helix. (B) θ(p) and θ(m), respectively, denote the orientations of peptide and methylene groups relative to the symmetry z axis. The other two Euler angles ϕ and ψ are drawn for the methylene group. (C) A segment of single-strand collagen peptide, -proline-hydroxyproline-glycine-, is shown. The nonvanishing hyperpolarizability tensor elements are listed for the associated peptide and methylene groups.
Molecular origins of second-order susceptibility: peptide groups
Early SHG polarization and recent hyper-Rayleigh scattering experiments have suggested that the molecular origins of second-order susceptibility come mainly from peptide groups in the backbone (12,14,22,23). Following Plotnikov et al. (14), we can model the hyperpolarizability contribution from the peptide group by assuming β(p) to have only one nonvanishing hyperpolarizability tensor element, β(p) = βz′z′z′ distributed evenly around the collagens axis of symmetry at a constant pitch-angle θ(p), corresponding to the steepness of the rise for a single α-helix inside the collagen molecule. The superscript p denotes peptide. This assumption further reduces the nonvanishing independent χ-tensor elements from four to two (14):
| (2) |
| (3) |
As discussed by Plotnikov et al. (14), although Kleinman symmetry has not been explicitly assumed in this model, the resulting χ-tensor elements satisfy the Kleinman condition. By experimentally determining the χ-tensor ratio χzzz/χzxx = 2cot2 θ(p), the pitch-angle of the α-helix can be obtained. SHG polarization measurements for myosin molecule have led to results consistent with the model, and have led to pitch-angle predictions in good agreements with x-ray diffraction studies. However, SHG polarization measurements for collagen from rat tail tendons show that the χ-tensor elements χzxx and χxxz are not equal and lead to a pitch-angle of 5–7°-greater than the known pitch-angle of 45.3° (10,14,24,25).
Molecular origins of second-order susceptibility: methylene groups
A recent sum-frequency study showed that in additional to the peptide groups, the symmetric stretch of the methylene groups in the side chain of the collagen molecule also contributes significantly to the bulk susceptibility (18). The hyperpolarizabilities for the methylene group can be described by three nonvanishing tensor elements,
where m denotes methylene and the z′ axis is along the methylene group's symmetry axis (Fig. 1 B) (26). The hyperpolarizability elements are related by (26,27)
Using a custom MATLAB (The MathWorks, Natick, MA) program to perform the angular transformation in Eq. 1, we obtain the contribution of the methylene group (denoted by the subscript m) to the bulk second-order susceptibility,
| (4) |
where we have let , and integrated over 2π around the molecular axis of symmetry, z′. Assuming that the methylene groups are distributed uniformly around the collagen fibril z axis at a pitch-angle θ(m) from the z axis, we integrate ϕ from 0 to 2π. The resulting nonvanishing susceptibility elements contributed by the methylene groups are
| (5) |
Molecular origins of second-order susceptibility: peptide and methylene groups combined
Finally, combining the nonvanishing susceptibility contributions from the peptide (Eqs. 2 and 3) and the methylene groups (Eq. 5), we obtain three independent elements for the bulk second-order susceptibility of collagen:
| (6) |
| (7) |
| (8) |
and are the number density of the peptide and methylene groups, respectively. Equations 7 and 8 show that as a result of adding the methylene contribution, χzxx and χxxz are no longer equal, as is the case of the single-axis model proposed by Plotnikov et al. (14), or by making the Kleinman symmetry assumption. Using Eqs. 6–8, the pitch-angle for the peptide groups, θ(p), can be determined from the ratios of the bulk susceptibility tensor elements a ≡ χzzz/χzxx and b ≡ χxxz/χzxx as
| (9) |
If the methylene contribution to the susceptibility tensor were zero, then b = 1, and Eq. 9 reduces to the result of the single-axis model or the result under the Kleinman symmetry assumption. To determine the pitch-angle for the methylene groups (θ(m)) using Eqs. 6–8, the ratio t = N(m)β(m)/N(p)β(p) is also needed:
| (10) |
Because the second-order polarization of collagen fiber can be expressed as
| (11) |
the dependence of the SHG intensity, ISHG ∼ Pz2 + Px2, on the excitation polarization angle θe is then represented as
| (12) |
with c as the proportional constant and the θo as the fiber orientation angle. Schematic illustrating the orientation of excitation polarization and the fibril are shown at Fig. 2 A.
Figure 2.
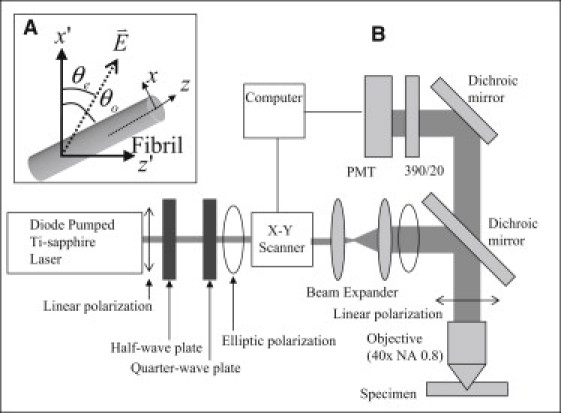
(A) Schematic illustration of excitation polarization angle and the orientation of the fibril. (B) Experimental setup of excitation polarization-resolved second harmonic generation (SHG) microscopy.
Materials and Methods
Excitation polarization-resolved SHG microscope
Fig. 2 B shows the imaging setup of our custom-built epi-illuminated P-SHG microscope that has been described in detail elsewhere (20,24,28). In short, a pulsed, femtosecond, titanium-sapphire laser (Tsunami; Spectral Physics, Mountain View, CA) tuned to 780 nm was used as the excitation source. A set of half-wave plate and quarter-wave plate was used to compensate the depolarization of the main dichroic mirror and to control the directions of the linear polarization incident on the specimen (24). Next, the laser source was guided by the pair of galvanometer scanning mirrors (Model 6220; Cambridge Technology, MA), and reflected by a main dichroic mirror (700DCSPXRUV-3P; Chroma Technology, Rockingham, VT) onto the back aperture of the objective (Fluor, 40×/NA 0.8; Nikon, Tokyo, Japan). The relatively small numerical aperture (NA) of 0.8 avoids a depolarization effect by the objective (29). The backward SHG signal was collected by the same focusing objective and selected by a secondary dichroic mirror (435DCXR; Chroma Technology) and a narrow band-pass filter (HQ390/20; Chroma Technology), before detection by single-photon-counting photomultiplier tubes (R7400P; Hamamatsu, Hamamatsu City, Japan).
Sample preparation: pure type I and II collagens in tissues and mixed tissue culture
The type I and type II collagen used in the study were from rat tail tendon and rat trachea cartilage, respectively. Fascicle of rat tail tendon and C-shaped cartilage (Fig. 3, A and B) rat trachea were removed with tweezers and surgical knife, and immersed into phosphate-buffered saline solution. C-shaped cartilage was cut from trachea and imaged at the position indicated by the asterisk in Fig. 3 B. For imaging, the wet tendon and cartilage were placed on a glass slide, and sealed with a cover glass. Fig. 3 C is the imaging of C-shaped trachea cartilage by SHG. To demonstrate our approach in distinguishing between collagen I and II fibers in the same tissue, polarization SHG data from an engineered cartilage tissue specimen that was synthesized and used in a previous study was further analyzed using the model described in this work (20).
Figure 3.
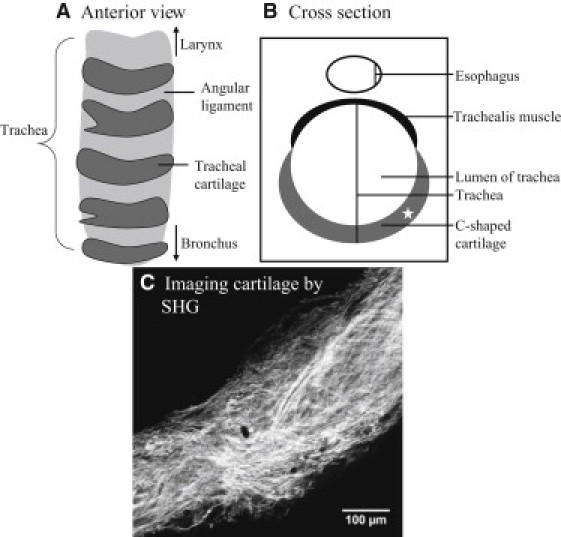
(A and B) Schematic illustration of trachea cartilage structure. (C) SHG image for the C-shaped cartilage acquired at location close to the asterisk in the cross-section (B).
In our study, the SHG images were acquired at the surface for tendon and at the depth 15μm below the surface for trachea cartilage. Because the scattering coefficients of cartilage can be neglected within a depth of 20 μm (30), we do not expect that the excitation polarization is drastically affected at these depths. Furthermore, we verified the polarization of the excitation source before entering our 40× and NA 0.8 objective. As has been described, the depolarization effect by can be neglected for objectives of numerical aperture below 0.85 (29).
Data analysis
SHG images of the samples at 12 different excitation polarizations were obtained by rotating the half-wave plate and the quarter-wave plate. To improve the signal/background ratio, we scanned each of the 12 angles three times. The data were processed with a custom IDL (Research Systems, Boulder, CO) program to determine the susceptibility tensor element ratios and the fiber orientation angle at each pixel. Because we used the single-photon-counting approach to analyze the SHG signal, a threshold was used to reduce the effect of background noise. For the pixel residence time used, the noise level is estimated to <1 count per pixel. Because the SHG signal depends on the excitation polarization, the SHG photon counts varied over the 12 excitation polarizations.
To properly fit the variation with our model (Eq. 12), those pixels with the lowest photon count below the chosen threshold level were not used in the second-order susceptibility analysis. Using Eq. 12, we analyzed the SHG data for tendon and cartilage with different threshold levels of one, two, and six photon counts per pixel and found no significant differences on the results of the second-order susceptibility components. Specifically, the different thresholds lead to the same second-order susceptibility ratios and pitch-angles in both rat tail tendon and rat trachea cartilage. Therefore, the results presented in this work correspond to the threshold level of two photo counts per pixel. We also presented the susceptibility tensor elements ratios as images to visualize the spatial distribution of the model parameters of χzzz/χzxx, χxxz/χzxx, peptide pitch-angle θ(p), and methylene pitch-angle θ(m).
Results and Discussion
To compare the predictions of our model to the properties of collagen, we used rat tail tendon as the source of type I collagen known to be uniform in direction and size (31). The dependence of SHG intensity from collagen at different excitation orientation was determined for 12 angles. Shown in Fig. 4, A–C, are the SHG images of the rat tail tendon and those in Fig. 4, D–F, are for rat trachea cartilage at three different polarization rotations of the incident laser light. The double-headed arrows in the images indicate the directions of the excitation polarization. As Fig. 5 shows, fitting the excitation polarization dependence of the SHG intensity variation through the use of Eq. 12 allows us to determine the χ-tensor element ratios χzzz/χzxx and χxxz/χzxx for each pixel in the image (19).
Figure 4.

SHG images for rat tail tendon (A–C) and rat trachea cartilage (D–F) at different angles of polarization of excitation. (White-headed arrow) Direction of excitation polarization.
Figure 5.
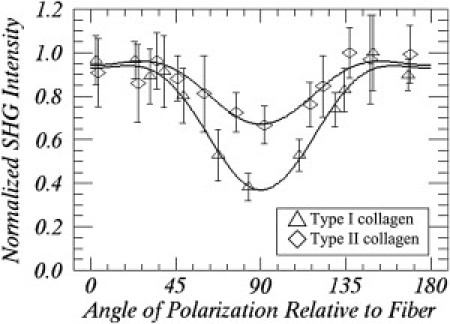
Variation of SHG intensities with the angles of polarization relative to fiber at the selected points indicated by the squares in Fig. 4, A and D. Chi-squares for the curve fit of type I and II collagen data are 1.00 and 1.12, respectively (8° of freedom).
For rat tail tendon, we determined the average value of the SHG image and obtained χzzz/χzxx = 1.59 ± 0.12, χxxz/χzxx = 0.76 ± 0.19, and fiber orientation angle θo = 133.67° ± 0.35° in the selected square point of Fig. 4 A. The obtained fiber orientation angle is also well consistent with SHG intensity image. Substituting the values of χzzz/χzxx and χxxz/χzxx into Eq. 9 leads to a pitch-angle for the collagen α-helix of θ(p) = 46.27° ± 0.55°. To determine the pitch-angle for the methylene groups (θ(m)) through the use of Eq. 10, we substitute t = N(m)β(m)/N(p)β(p) ≈ 0.8 as estimated by the sum-frequency vibration spectra of collagen I (18). Together with our values for the χ-tensor ratios, we obtained θ(m) = 93.10° ± 3.90°. In Fig. 6, A–D, results of χzzz/χzxx, χxxz/χzxx, peptide pitch-angle θ(p), and methylene pitch-angle θ(m) analysis are expressed as images to allow visualization of their spatial distribution. The corresponding histograms for each of those images are plotted in Fig. 7. The values of model parameters are χxxz/χzxx = 0.62 ± 0.08, χzzz/χzxx = 1.51 ± 0.04, θ(p) = 45.82° ± 0.46°, and θ(m) = 94.80° ± 0.97° for type I collagen (Fig. 7).
Figure 6.
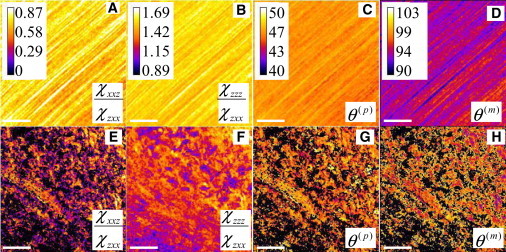
Respective images ofχxxz/χzxx, χzzz/χzxx, peptide pitch-angle θ(p), and methylene pitch-angle θ(m) for type I collagen (A–D) and type II collagen (E–H). Scale bar is 20 μm.
Figure 7.
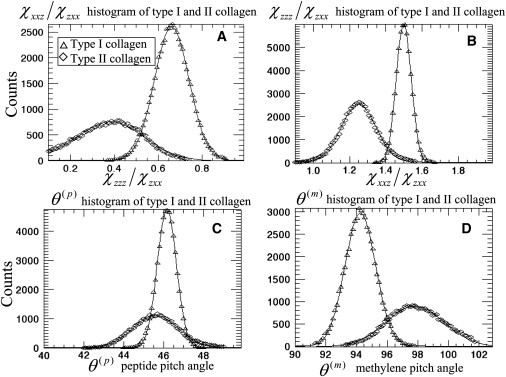
Histograms of (A) χxxz/χzxx, (B) χzzz/χzxx, (C) peptide pitch-angle θ(p), and (D) methylene pitch-angle θ(m) of type I collagen and type II collagen shown in Fig. 6.
For type II collagen from rat trachea cartilage, the images of χxxz/χzxx, χzzz/χzxx, peptide pitch-angle θ(p), and methylene pitch-angle θ(m) are shown in Fig. 6, E–H, with the corresponding histograms shown in Fig. 7. From the histograms, we determined the peptide and methylene groups pitch-angles for type II collagen to be χzzz/χzxx = 1.26 ± 0.11, χxxz/χzxx = 0.39 ± 0.15, θ(p) = 45.72° ± 1.17°, and θ(m) = 97.87° ± 1.79°, respectively.
Because the tendon collagen is known to be well aligned, therefore, SHG imaging of such a well-organized structure would ensure that the tendon collagen is aligned in the focal plane. However, such organization appears missing in trachea collagen. Therefore, to validate our results, the trachea cartilage image chosen for analysis was selected from a three-dimensional image stack (Fig. 8, A and B), 95 × 95 × 30 μm3 in size). The chosen plane (Fig. 8 C), at 15-μm depth below the tissue surface, contained fibers that were well aligned and lie within the image plane (indicated by arrows in Fig. 8, A–C). The fibers within the boxed region (Fig. 8 C) were analyzed and compared with the results obtained from the entire image. Specifically, we found that within the boxed region, the average angle of fibril orientation is 39.26° ± 6.24°, χxxz/χzxx = 0.38 ± 0.14, χzzz/χzxx = 1.23 ± 0.05, θ(p) = 45.99° ± 0.96°, and θ(m) = 97.94° ± 1.64°. The results of the boxed region are similar to the results of the entire image (Table 1). Therefore, we arrive at two conclusions: first, the type II collagen fibers from trachea that we analyzed lie mostly in a plane; and second, the fiber orientation is uniform within the point-spread function.
Figure 8.
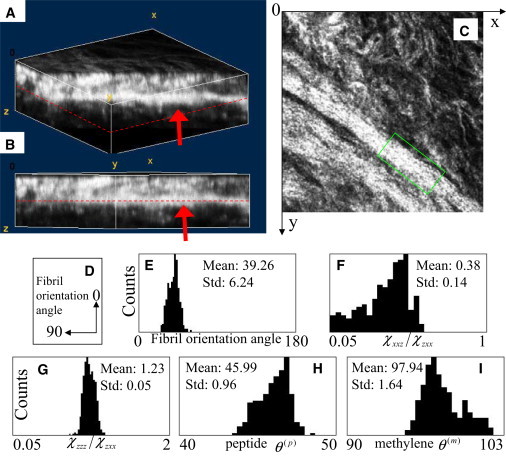
Three-dimensional SHG imaging and second-order susceptibility analysis of trachea cartilage. (A and B) Three-dimensional SHG image stack (95 × 95 × 30 μm3) of trachea cartilage. (C) SHG image of a section at 15 μm below the surface (indicated by dashed lines in A and B). Boxed region indicates region of well-aligned fiber used for localized second-order susceptibility analysis. (D) The definition of fibril orientation. (E–I) Histograms of fibril orientation angle, χxxz/χzxx, χzzz/χzxx, peptide pitch-angle θ(p), and methylene pitch-angle θ(m), respectively. Mean and standard deviations are summarized at Table 1 .
Table 1.
Summary of second-order susceptibility ratios and the determined pitch-angles for the peptide and methylene group in native type I and II collagens
| Collagen types | χzzz/χzxx | χxxz/χzxx | Peptide pitch-angle θ(p) | Methylene pitch-angle θ(m) |
|---|---|---|---|---|
| Type I collagen (entire area) | 1.51 ± 0.04 | 0.62 ± 0.08 | 45.82° ± 0.46° | 94.80° ± 0.97° |
| Type II collagen (entire area) | 1.26 ± 0.11 | 0.39 ± 0.15 | 45.72° ± 1.17° | 97.87° ± 1.79° |
| Type II collagen (region of well-aligned fibril; Fig. 8, green box) | 1.23 ± 0.05 | 0.38 ± 0.14 | 45.99° ± 0.96° | 97.94° ± 1.64° |
| Engineered type I collagen | 1.54 ± 0.20 | 0.64 ± 0.19 | 45.05° ± 1.24° | 94.47° ± 2.23° |
| Engineered type II collagen | 1.23 ± 0.05 | 0.38 ± 0.14 | 46.04° ± 1.52° | 98.10° ± 1.79° |
Our experimental result of χxxz/χzxx ≠ 1 suggests that methylene contributes significantly to the second-order susceptibility of collagen. In an attempt to compare our results with x-ray structure, we found that detailed structures at atomic resolution of collagen in native tissues are not currently available. While x-ray scattering have been applied to tissues, atomic-level resolution could not be obtained. This is most likely due to the fact that perfectly periodic structure is absent in native tissue. Instead, what we found is that various groups used collagen-like model peptides in an effort to study this class of important protein molecules. The first atomic resolution structure of such a molecule (proline-hydroxyproline-glycine)n was obtained by Bella et al. in 1994 (32). Therefore, the best effort in comparing our SHG results of collagen-containing tissues to high-resolution structures was made by investigating the structures of two collagen-like molecules to model collagen I and II.
Because collagen I is a heterotrimer composed of two α1(I) α-helices and one α2(I) α-helix, we selected a heterotrimer rich in proline (Protein DataBank (PDB) No. 1ITT, GPPGPPG) where G and P, respectively, denote glycine and proline (33). However, because collagen II is a homotrimer composed of three α1(II) α-helices which are deficient in proline, we chose a homotrimer model composed of hydroxyprolines (PDB No. 1WZB, HHGHHGHHGH) in which H denotes the hydroxyproline to model collagen II (34). The peptide and methylene pitch-angles from our SHG results of the native collagen I and II fibers can be compared to those of the respective collagen-like polypeptides. We found that both two types of collagen-like molecules were seven amino acids per two helix turns and had similar peptide pitch-angles (Table 2) and these results were close to our measurements of native tissues (Table 1).
Table 2.
Helix parameters and pitch-angles of peptide and methylene groups determined from x-ray diffraction data (Protein DataBank (PDB)) of collagen-like model peptides
| Collagen-like model peptide | Residues per helix turn | Rise per residue (Å) | Helix radius (Å) | Peptide pitch-angle θ(p) | Methylene pitch-angle θ(m) |
|---|---|---|---|---|---|
| Heterotrimer(collagen I-like) | 3.5 | 2.57 | 1.5 | 46.34° | 97.46° ± 43.87° |
| Homotrimer(collagen II-like) | 3.5 | 2.71 | 1.5 | 44.82° | 108.98° ± 57.83° |
The heterotrimer corresponds to PDB No. 1ITT (GPPGPPG) while the homotrimer is PDB No. 1WZB (HHGHHGHHGH).
Specifically, we found that the methylene pitch-angles for collagen I and II from were, respectively, 94.80° ± 0.97° and 97.87° ± 1.79° where the results of the heterotrimer and homotrimer models are 97.46° ± 43.87°and 108.98° ± 57.83° (Tables 1 and 2). The histograms of methylene orientations of the model peptides are shown in Fig. 9. Therefore, although our results do not match perfectly with that of the model peptides, the trend that the methylene pitch-angle for the homotrimer is higher than that of the heterotrimer is consistent with our collagen I, II results. Until the exact high-resolution structures are available for native collagen I and II molecules, exact comparison with the SHG results cannot be made.
Figure 9.
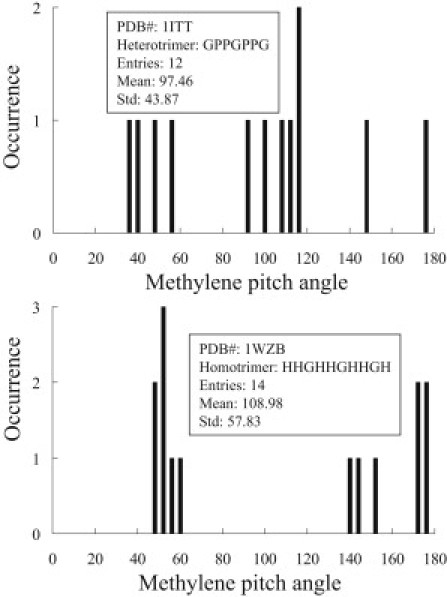
Histograms of methylene pitch-angles for collagen-like heterotrimer and homotrimer as determined from x-ray diffraction data. G denotes glycine, P is proline, and H is hydroxyproline.
To demonstrate the validity of our approach in distinguishing the two fiber types, the mixed type I and II collagen in engineered cartilage tissue are performed. Such a system is important in chondrogenesis where both collagens I and II are produced although native cartilage is primarily composed of type II collagen (20). Therefore, the ability to distinguish both fiber types noninvasively will lead to a better understanding of the fibrogenesis process and may contribute to the production of improved tissue engineering products. Fig. 10 A shows the multiphoton image of the engineered tissue which we have previous synthesized (20) where the red color represents the SHG from collagen and green color is autofluorescence from chitosan scaffold. The two collagen types cannot be discriminated from SHG intensity imaging.
Figure 10.
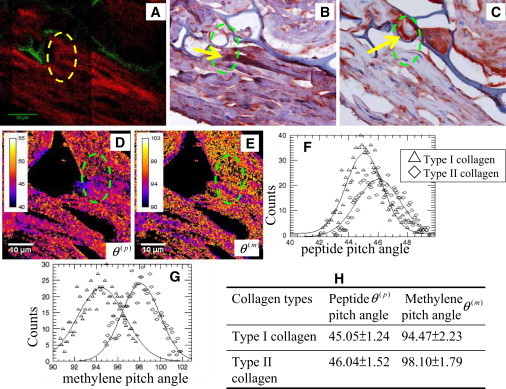
Localizations of type I and II collagens in engineered cartilage tissues through immunohistochemical staining, peptide, and methylene pitch-angle imaging. (A, Red) SHG from collagen and (A, green) autofluorescence from chitosan scaffold. (B and C) Immunohistochemical images for type I and II collagen, respectively. (Yellow arrows) Type I collagen (B) and type II collagen (C). (D and E) Peptide and methylene pitch-angle imaging. (F and G, histograms) Peptide and methylene pitch-angles in the dashed-circled region, respectively. (H) Summary of the peptide and methylene pitch-angles for type I and II collagen in engineered cartilage tissue.
In an effort to apply our model, we have reanalyzed the experimental results with the model presented in this work along with immunohistochemical images of adjacent tissue sections. Fig. 10, B and C, shows the immunohistochemical images of type I and II collagen, respectively. Red represents the positive stain for collagen and purple is the chitosan scaffold and the chondrocyte-like cell. Yellow arrows indicate the type I collagen in Fig. 10 B and type II collagen in Fig. 10 C. Spatial distributions of type I and II collagen can be observed by immunohistochemical staining. Peptide and methylene pitch-angle-resolved images of the same location in adjacent tissue sections are shown in Fig. 10, D and E. Second-order susceptibility analysis of selected regions (green dashed regions in Fig. 10, D and E) are shown in Table 1. We found that the peptide pitch-angles (Fig. 10 F) are close to the results of the native type I and II collagen (Table 1). Moreover, the histograms of methylene pitch-angles (Fig. 10 G) show the presence of two peaks (Fig. 10 E). One is 94.47° ± 2.23° and the other is 98.10° ± 1.79°. These results are similar to the values measured from the native type I and II collagens (Table 1).
Although we obtained different values of χ-tensor ratios for the two collagen types, their peptide pitch-angles calculated from Eq. 9 are similar. The similarity in the peptide pitch-angle is expected as the positioning of glycine at every third amino acid of the amino-acid sequence of fibrillar collagen dictates similar α-helical structure (35). The difference in the amino-acid sequence of the two types of collagen, however, can lead to differences in the side chains that are likely responsible for the 3.07° difference between the methylene pitch-angles of type I and type II collagens (Fig. 7 D). The ability of the methylene tilt angle to separate distinctly the two types of collagen can lead to better contrast in second-order susceptibility tensor (19,20) imaging of type I and type II mix samples.
Conclusions
In this work, we propose what we believe to be a new model to resolve the collagen nanostructure through far-field P-SHG measurement. The model accounts for the second-order susceptibility contributions from both the peptide groups in the α-helix and methylene groups in the side chains. The predicted pitch-angles of the peptide group and the methylene groups from P-SHG measurement are in good agreement with x-ray results of model peptides. Application of this model to type I and II collagen leads to similar pitch-angle for the peptide group, and a different pitch-angle for the methylene group. The ability of this method to probe nanostructure changes in wet collagen samples using far-field measurements makes it a valuable tool for in vitro and dynamical studies of collagen biophysics.
Acknowledgments
We acknowledge the financial support of the National Science Council (grant Nos. NSC-99-2221-E-002-096-MY3 and NSC-98-2112-M-002-008-MY3), the Center for Quantum Science and Engineering (grant No. CQSE-99R80870), National Taiwan University (grant No. NTU-99R70409), and the National Health Research Institute (grant No. NHRI-EX100-10041EI) in Taiwan. In addition, we acknowledge Professor Yi-You Huang and Professor Hsuan-Shu Lee for providing the engineered cartilage tissue from Institute of Biomedical Engineering and Internal Medicine, National Taiwan University.
Contributor Information
Yang-Fang Chen, Email: yfchen@phys.ntu.edu.tw.
Chen-Yuan Dong, Email: cydong@phys.ntu.edu.tw.
References
- 1.Shoulders M.D., Raines R.T. Collagen structure and stability. Annu. Rev. Biochem. 2009;78:929–958. doi: 10.1146/annurev.biochem.77.032207.120833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cox G., Kable E., Gorrell M.D. Three-dimensional imaging of collagen using second harmonic generation. J. Struct. Biol. 2003;141:53–62. doi: 10.1016/s1047-8477(02)00576-2. [DOI] [PubMed] [Google Scholar]
- 3.Yeh A.T., Nassif N., Tromberg B.J. Selective corneal imaging using combined second-harmonic generation and two-photon excited fluorescence. Opt. Lett. 2002;27:2082–2084. doi: 10.1364/ol.27.002082. [DOI] [PubMed] [Google Scholar]
- 4.Lin S.J., Jee S.H., Dong C.Y. Discrimination of basal cell carcinoma from normal dermal stroma by quantitative multiphoton imaging. Opt. Lett. 2006;31:2756–2758. doi: 10.1364/ol.31.002756. [DOI] [PubMed] [Google Scholar]
- 5.Lee H.S., Teng S.W., Dong C.Y. Imaging human bone marrow stem cell morphogenesis in polyglycolic acid scaffold by multiphoton microscopy. Tissue Eng. 2006;12:2835–2841. doi: 10.1089/ten.2006.12.2835. [DOI] [PubMed] [Google Scholar]
- 6.Roth S., Freund I. 2nd harmonic-generation in collagen. J. Chem. Phys. 1979;70:1637–1643. [Google Scholar]
- 7.Mertz J., Moreaux L. Second-harmonic generation by focused excitation of inhomogeneously distributed scatterers. Opt. Commun. 2001;196:325–330. [Google Scholar]
- 8.Williams R.M., Zipfel W.R., Webb W.W. Interpreting second-harmonic generation images of collagen I fibrils. Biophys. J. 2005;88:1377–1386. doi: 10.1529/biophysj.104.047308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brasselet S., Le Floch V., Ibanez A. In situ diagnostics of the crystalline nature of single organic nanocrystals by nonlinear microscopy. Phys. Rev. Lett. 2004;92:207401. doi: 10.1103/PhysRevLett.92.207401. [DOI] [PubMed] [Google Scholar]
- 10.Stoller P., Kim B.M., Da Silva L.B. Polarization-dependent optical second-harmonic imaging of a rat-tail tendon. J. Biomed. Opt. 2002;7:205–214. doi: 10.1117/1.1431967. [DOI] [PubMed] [Google Scholar]
- 11.Mitchell S.A., McAloney R.A., Zgierski M.Z. Second-harmonic generation optical activity of a polypeptide α-helix at the air/water interface. J. Chem. Phys. 2005;122:114707. doi: 10.1063/1.1862613. [DOI] [PubMed] [Google Scholar]
- 12.Deniset-Besseau A., Duboisset J., Schanne-Klein M.C. Measurement of the second-order hyperpolarizability of the collagen triple helix and determination of its physical origin. J. Phys. Chem. B. 2009;113:13437–13445. doi: 10.1021/jp9046837. [DOI] [PubMed] [Google Scholar]
- 13.Pena A.M., Boulesteix T., Schanne-Klein M.C. Chiroptical effects in the second harmonic signal of collagens I and IV. J. Am. Chem. Soc. 2005;127:10314–10322. doi: 10.1021/ja0520969. [DOI] [PubMed] [Google Scholar]
- 14.Plotnikov S.V., Millard A.C., Mohler W.A. Characterization of the myosin-based source for second-harmonic generation from muscle sarcomeres. Biophys. J. 2006;90:693–703. doi: 10.1529/biophysj.105.071555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tiaho F., Recher G., Rouède D. Estimation of helical angles of myosin and collagen by second harmonic generation imaging microscopy. Opt. Express. 2007;15:12286–12295. doi: 10.1364/oe.15.012286. [DOI] [PubMed] [Google Scholar]
- 16.Odin C., Le Grand Y., Baffet G. Orientation fields of nonlinear biological fibrils by second harmonic generation microscopy. J. Microsc. 2008;229:32–38. doi: 10.1111/j.1365-2818.2007.01868.x. [DOI] [PubMed] [Google Scholar]
- 17.Psilodimitrakopoulos S., Santos S.I., Loza-Alvarez P. In vivo, pixel-resolution mapping of thick filaments' orientation in nonfibrillar muscle using polarization-sensitive second harmonic generation microscopy. J. Biomed. Opt. 2009;14:014001. doi: 10.1117/1.3059627. [DOI] [PubMed] [Google Scholar]
- 18.Rocha-Mendoza I., Yankelevich D.R., Knoesen A. Sum frequency vibrational spectroscopy: the molecular origins of the optical second-order nonlinearity of collagen. Biophys. J. 2007;93:4433–4444. doi: 10.1529/biophysj.107.111047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen W.L., Li T.H., Dong C.Y. Second harmonic generation χ-tensor microscopy for tissue imaging. Appl. Phys. Lett. 2009;94:183902. [Google Scholar]
- 20.Su P.J., Chen W.L., Dong C.Y. The discrimination of type I and type II collagen and the label-free imaging of engineered cartilage tissue. Biomaterials. 2010;31:9415–9421. doi: 10.1016/j.biomaterials.2010.08.055. [DOI] [PubMed] [Google Scholar]
- 21.Goldstein H. Addison-Wesley; Reading, MA: 1980. Classical Mechanics. [Google Scholar]
- 22.Kriech M.A., Conboy J.C. Label-free chiral detection of melittin binding to a membrane. J. Am. Chem. Soc. 2003;125:1148–1149. doi: 10.1021/ja028577z. [DOI] [PubMed] [Google Scholar]
- 23.Freund I., Deutsch M., Sprecher A. Connective tissue polarity. Optical second-harmonic microscopy, crossed-beam summation, and small-angle scattering in rat-tail tendon. Biophys. J. 1986;50:693–712. doi: 10.1016/S0006-3495(86)83510-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chou C.K., Chen W.L., Dong C.Y. Polarization ellipticity compensation in polarization second-harmonic generation microscopy without specimen rotation. J. Biomed. Opt. 2008;13:014005. doi: 10.1117/1.2824379. [DOI] [PubMed] [Google Scholar]
- 25.Beck K., Brodsky B. Supercoiled protein motifs: the collagen triple-helix and the α-helical coiled coil. J. Struct. Biol. 1998;122:17–29. doi: 10.1006/jsbi.1998.3965. [DOI] [PubMed] [Google Scholar]
- 26.Hirose C., Akamatsu N., Domen K. Formulas for the analysis of surface sum-frequency generation spectrum by CH stretching modes of methyl and methylene groups. J. Chem. Phys. 1992;96:997–1004. [Google Scholar]
- 27.Hirose C., Yamamoto H., Domen K. Orientation analysis by simulation of vibrational sum-frequency generation spectrum—CH stretching bands of the methyl-group. J. Phys. Chem. 1993;97:10064–10069. [Google Scholar]
- 28.Su P.J., Chen W.L., Dong C.Y. Discrimination of collagen in normal and pathological skin dermis through second-order susceptibility microscopy. Opt. Express. 2009;17:11161–11171. doi: 10.1364/oe.17.011161. [DOI] [PubMed] [Google Scholar]
- 29.Richards B., Wolf E. Electromagnetic diffraction in optical systems. 2. Structure of the image field in an aplanatic system. Proc. Royal Soc. London A Math. Phys. Sci. 1959;253:358–379. [Google Scholar]
- 30.Mansfield J.C., Winlove C.P., Matcher S.J. Collagen fiber arrangement in normal and diseased cartilage studied by polarization sensitive nonlinear microscopy. J. Biomed. Opt. 2008;13:044020. doi: 10.1117/1.2950318. [DOI] [PubMed] [Google Scholar]
- 31.Parry D.A.D., Barnes G.R.G., Craig A.S. A comparison of the size distribution of collagen fibrils in connective tissues as a function of age and a possible relation between fibril size distribution and mechanical properties. Proc. R. Soc. Lond. B Biol. Sci. 1978;203:305–321. doi: 10.1098/rspb.1978.0107. [DOI] [PubMed] [Google Scholar]
- 32.Bella J., Eaton M., Berman H.M. Crystal and molecular structure of a collagen-like peptide at 1.9 Å resolution. Science. 1994;266:75–81. doi: 10.1126/science.7695699. [DOI] [PubMed] [Google Scholar]
- 33.Hongo C., Nagarajan V., Nishino N. Average crystal structure of (Pro-Pro-Gly)(9) at 1.0 Ångstrom resolution. Polym. J. 2001;33:812–818. [Google Scholar]
- 34.Kawahara K., Nishi Y., Kobayashi Y. Effect of hydration on the stability of the collagen-like triple-helical structure of [4(R)-hydroxyprolyl-4(R)-hydroxyprolylglycine]10. Biochemistry. 2005;44:15812–15822. doi: 10.1021/bi051619m. [DOI] [PubMed] [Google Scholar]
- 35.van der Rest M., Garrone R. Collagen family of proteins. FASEB J. 1991;5:2814–2823. [PubMed] [Google Scholar]


