An efficient EM-ICP algorithm for symmetric consistent non-linear registration of point sets

Abstract

In this paper, we present a new algorithm for non-linear registration of point sets. We estimate both forward and backward deformations fields best superposing the two point sets of interest and we make sure that they are consistent with each other by designing a symmetric cost function where they are coupled. Regularisation terms are included in this cost function to enforce deformation smoothness. Then we present a two-step iterative algorithm to optimise this cost function, where the two fields and the fuzzy matches between the two sets are estimated in turn. Building regularisers using the RKHS theory allows to obtain fast and efficient closed-form solutions for the optimal fields. The resulting algorithm is efficient and can deal with large point sets.

1. Introduction

The most popular methods in the literature for the non-rigid registration of two point sets are probably those extending the original ICP algorithm of Besl & McKay [1], such as the EM-ICP of Granger & Pennec [2] or the TPS-RPM of Chui & Rangarajan [3]. The common viewpoint of these methods is to consider the points of the first set as the means of a Gaussian Mixture Model (GMM) and the points of the other set as samples of this GMM. The unknown non-rigid transformation best superposing the two point sets can then be estimated according to the maximum likelihood principle and using (typically) the EM algorithm. This optimisation then boils down to a simple iterative estimation of fuzzy point-to-point correspondences (encoded in what is often termed the match matrix) and of the non-rigid transformation in turn. This simple two-step (point matching and transformation estimation) algorithm is very attractive, but inherently asymmetric, which makes it difficult to obtain inverse consistent registration (i.e. the registration of one set to the other provides the inverse transformation of that obtained when switching the two sets) in this EM-ICP framework. Such a property is very desirable, especially when building an atlas from a set of anatomical structures. First trials towards a symmetric point matching include the work by Rangarajan et al. who used the Sinkhorn theorem to enforce the match matrix to be doubly stochastic [3]. Most other works focused on the estimation of the transformation: Joshi & Miller [4] showed how to build a diffeomorphism between two sets of matched points, but without guaranteeing inverse consistency. In parallel, Johnson & Christensen proposed a method towards this goal, but using thin-plate splines where invertibility is not ensured [5]. These solutions are theoretically attractive but computationally redhibitory in case of large point sets, which limits their use to simple anatomical structures.

In this paper, we propose a symmetric formulation of the registration problem in an EM-ICP framework, that allows to jointly compute the forward and the backward deformation fields linking the two point sets (Section 2). Our cost function is composed of two data attachment terms, two consistency terms (to enforce both transformations to be compatible with each other) and two regularisation terms over both fields. We provide an iterative two-step algorithm to minimise this new criterion, in which the first step is quite similar to that of the original EM-ICP algorithm and the second step consists of two interleaved approximation problems. Using the Reproducing Kernel Hilbert Space (RKHS) theory and the Fourier analysis, we devise efficient regularisers leading to closed-form solutions based on sparse linear algebra for these two problems (Section 3). This results in an efficient algorithm allowing non-linear registration on large 3D point sets (Section 4). Finally, we give some perspectives (Section 5).

2. A framework for a consistent & symmetric EM-ICP

2.1. Cost function

Let X = {x₁, …, x_N} and Y = {y₁, …, y_M} be two point sets representing two anatomical structures to be registered. Let T^X and T^Y be respectively the backward and forward unknown transformations superposing X and Y. Let A^X (resp. A^Y) be the match matrix describing the correspondences between T^X(X) and Y (resp. T^Y (Y) and X). Let α and β be real positive values weighing the influence of the different terms. Following the EM-ICP framework in its energetic formulation [3], we consider the matrices A^X and A^Y as hidden variables of the problem and we design our cost function as :

$$\mathcal{E}(T^X,T^Y,A^X,A^Y)=[{\mathcal{E}}_d(Y,T^X(X),A^X)+{\mathcal{E}}_d(X,T^Y(Y),A^Y)+\alpha {\mathcal{E}}_c(T^X\circ T^Y,I)+\alpha {\mathcal{E}}_c(T^Y\circ T^X,I)+\beta {\mathcal{E}}_r(T^X)+\beta {\mathcal{E}}_r(T^Y)],$$ (1)

where:

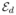• (Y, T^X(X), A^X) is a data attachment term defined as:

  $${\mathcal{E}}_d(Y,T^X(X),A^X)=1/N[\sum _{i,j}{A}_{i,j}^X{\left|\right|y_i-T^X(x_j)\left|\right|}^2+{\sigma }^2\sum _{i,j}{A}_{i,j}^{X}log(A_{i,j}^X)],$$ (2)

  where Σ_i,j is the sum over the points y_i ∈ Y and x_j ∈ X, and ${\sum }_i{A}_{i,j}^X=1\forall j$. The parameter σ can be seen as the Gaussian noise variance on X and Y. In practice σ controls the fuzziness of A.

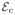• (T^Y ◦ T^X, I) is a consistency term that measures the discrepancy between transformations T^X and T^Y. Without this term, estimations of T^X and T^Y would be completely independent. This new term couples them and forces them to be compatible with each other. We design it as: 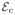(T^Y ◦ T^X, I) = 1/N Σ_xj∈X ||T^Y ◦ T^X(x_j) − x_j||².

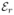• (T^X) = R(T^X) is a regularisation term penalising discontinuities of T^X.

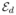• (X, T^Y (Y), A^Y), 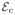(T^X ◦ T^Y, I) and 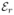(T^Y) are built the same way.

2.2. Minimisation

The cost function (1) can be optimised by an iterative two-step algorithm that consists in minimisation over A^X;A^Y and T^X; T^Y in turn:

• initT̃^X and T̃^Y as the identity function
• i)Ã^X; Ã^Y = arg min_A^X,A^Y 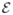(T̃^X, T̃^Y,A^X,A^Y)
• ii)T̃^X; T̃^Y = arg min_T^X,T^Y 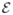(T^X, T^Y,Ã^X,Ã^Y)

  Step i) has a closed-form solution. To achieve robustness, we replace the square cost function in 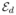by a truncated quadratic cost function. Then Step i) can be efficiently solved using a kd-tree [2]. For Step ii), we optimise iteratively the criterion with respect to each one of the two unknowns T^X and T^Y :

• ii.a)T^X = T̃^X and T^Y = T̃^Y
• ii.b)T̃^X = arg min_T^X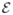(T^X, T^Y,Ã^X,Ã^Y)
• ii.c)T̃^Y = arg min_T^Y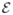(T^X, T^Y,Ã^X,Ã^Y)

Intuitively, this algorithm consists in alternatively estimating T^X as a compromise between data attachment (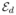(Y, T^X(X),A^X)), regularisation (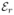(T^X)) and consistency with T^Y (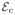(T^Y ◦T^X, I)) and T^Y as a compromise between the three other symmetric terms. Implementing this last scheme requires further specification of T and R. We define the transformation T^X as the initial position plus a displacement field: T^X(x_j) = x_j +t^X(x_j) and R is a regulariser on t^X (similarly for T^Y and t^Y). Then Step ii.b) can be written as:

• ii.b) ${\stackrel{\sim }{t}}^X=arg{min}_{t^X}1/N{\sum }_{i,j}{A}_{i,j}^X{\left|\right|y_i-x_j-t^X(x_j)\left|\right|}^2+\beta R(t^X)+\alpha /N{\sum }_j{\left|\right|{\stackrel{\sim }{t}}^Y(x_j+t^X(x_j))+t^X(x_j)\left|\right|}^2+\alpha /M{\sum }_i{\left|\right|t^X(y_i+{\stackrel{\sim }{t}}^Y(y_i))+{\stackrel{\sim }{t}}^Y(y_i)\left|\right|}^2$

  Step ii.c) has a similar expression.

Due to the terms Σ_j ||t̃^Y (x_j+t^X(x_j))+t^X(x_j)||² in step ii.a) and Σ_i ||t̃^X(y_i+ t^Y (y_i)) + t^Y (y_i)||² in Step ii.b), which are somewhat redundant with their symmetric counterparts, the two problems are very intricate. Thus, similarly to what is done by Chui et al. [7] in a related context, we drop them, which allows to reformulate Steps ii.a) and ii.b) as two independent approximation problems:

• ii.b) ${\stackrel{\sim }{t}}^X=arg{min}_{t^X}1/N{\sum }_{i,j}{A}_{i,j}^X{\left|\right|y_i-x_j-t^X(x_j)\left|\right|}^2+\beta R(t^X)+\alpha /M{\sum }_i{\left|\right|t^X(y_i+{\stackrel{\sim }{t}}^Y(y_i))+{\stackrel{\sim }{t}}^Y(y_i)\left|\right|}^2$
• ii.c) ${\stackrel{\sim }{t}}^Y=arg{min}_{t^Y}1/M{\sum }_{i,j}{A}_{i,j}^Y{\left|\right|x_i-y_j-t^Y(y_j)\left|\right|}^2+\beta R(t^Y)+\alpha /N{\sum }_j{\left|\right|t^Y(x_j+{\stackrel{\sim }{t}}^X(x_j))+{\stackrel{\sim }{t}}^X(x_j)\left|\right|}^2$

In practice, only a few iterations are necessary to decrease importantly the criterion. Then, R could be chosen as a TPS regulariser and then the two approximations problems would consist in solving linear systems of size proportional to N × M, which would be impracticable in terms of time and memory complexity for large point sets. Below, we propose an alternative efficient strategy.

3. Efficient solutions for the approximation problems

3.1. Formalism

One can show that the two above mentioned problems can be restated as:

$$\stackrel{\sim }{f}=\underset{f}{argmin}\sum _{i,j}{p}_j{A}_{i,j}{\left|\right|u_i-(v_j+f(v_j))\left|\right|}^2+\beta R(f).$$ (3)

where U = {u₁, …, u_N}, V = {v₁, …, v_M} and Σ_i A_i,j = 1 ∀ j. The positive values (p_j) are introduced for the sake of generality and allow to consider some points of V as outliers by simply fixing p_k = 0 when v_k is an outlier.

First, one can show that this problem is equivalent to (considering that the derivatives vanish at the optimum and noting that Σ_i A_i,j = 1, ∀j):

$$\stackrel{\sim }{f}=\underset{f}{argmin}\sum _{j=1}{p}_j{\left|\right|c_j-(v_j+f(v_j))\left|\right|}^2+\beta R(f),\text{with}{c}_j=\sum _i{A}_{i,j}{u}_i.$$ (4)

This reduces the size of the problem from card(U) × card(V) to card(V).

Now, we focus on building a tractable (in terms of minimisation) and powerful (in terms of reliability of the model) regulariser R. For that, we consider our problem in a space of admissible solutions 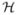that we span using a positive definite kernel (pdk) k¹: $\mathcal{H}={\{f\mid f(·)={\sum }_{i=0}^{\infty }k(q_i,·)w_i,w_i\in {IR}^3,,q_i\in \mathrm{\Omega };{\left|\right|f\left|\right|}_{\mathcal{H}}<\infty \}}^C$ where S^C denotes the completion of the set S and where Omega; ⊂ IR³. This space is endowed with the inner product: $<f,h{>}_{\mathcal{H}}={\sum }_{i,j=0}^{\infty }{w}_i^{T}k(q_i,q_j)w_j$. The space 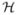is a Hilbert space with reproducing kernel k (or more compactly a RKHS) [8].

Then we assume that f ∈ 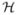and define our regulariser R(f) as || f ||:

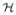$$\stackrel{\sim }{f}=\underset{f\in \mathcal{H}}{argmin}\sum _{j=1}{p}_j{\left|\right|c_j-(v_j+f(v_j))\left|\right|}^2+\beta {\left|\right|f\left|\right|}_{\mathcal{H}}.$$ (5)

One of the key advantage of RKHS is that one can show [9] that the values taken by the solution f̃ at the points v₁, …, v_j,…, v_M can be expressed as $\stackrel{\sim }{f}(v_j)={\sum }_{i=1}^{M}k(v_i,v_j)w_i$ and then formulate the last minimisation problem as:

$$(\stackrel{\sim }{w})=\underset{(w)}{argmin}\sum _{j=\mathrm{1..}M}{p}_j{\left|\right|c_j-(v_j+\sum _{i=\mathrm{1..}M}k(v_j,v_i)w_i)\left|\right|}^2+\beta \sum _{i,j=\mathrm{1..}M}{w}_i^{T}k(v_j,v_i)w_j$$

Vanishing the derivatives gives a linear system whose solution can be expressed in a closed-form as: W = (d(P)K +βI)⁻¹ d(P)[C −V ], where V = [v₁, …, v_M]^T, C = [c₁, …, c_M]^T, W = [w₁, …,w_M]^T, K = (k(v_i, v_j)_i,j) is the M by M matrix associated to kernel k and d(P) is the diagonal matrix formed by the p_j values. The challenge is now to choose a kernel corresponding to a relevant regulariser.

3.2. Choosing a kernel

In order to design a suitable k, one can use an interesting relationship with Fourier-based stabilisers. Let ∀f = (f₁, f₂, f₃) integrable, R(f) = R(f₁)+R(f₂)+ R(f₃), with $R(f_i)=\frac{1}{{(2\pi )}^3}{\int }_{-\infty }^{\infty }\frac{{\mid f_i^{\ast }(\omega )\mid }^2}{{\phi }^{\ast }(\mid \omega \mid /b)}d\omega$, where ^* is the Fourier transform operator, φ: IR → IR is an integrable function and b is a real positive rescaling factor. Let 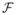= {f: IR³ → IR³|R(f) < ∞}. Interestingly, one can state that if φ^* is symmetric, positive and if φ ∈ 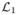thus 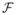is a RKHS whose reproducing kernel is given by k(q_i,.) = b × φ(b × (q_i − .)) and such that ∀ f ∈ 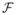, 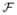= R(f) [8, 10]. This dual view is convenient as it allows to design a wide variety of efficient regularisers directly into the Fourier domain.

In order to design an efficient regulariser, we have to choose $\frac{1}{{\phi }^{\ast }}$ as a high-pass filter. This way, high frequencies of the deformation will be drastically penalised whereas low frequencies will only be penalised a little. Generally, ${\phi }_{[0,\infty ]}^{\ast }$ is a monotonically decreasing function and the most important element that characterises its influence on the regularisation is the way it decreases that indicates the amount of penalisation with respect to frequencies. Particularly, the frequencies for which φ*(||ω||/b) is null are forbidden. The two parameters β and b allow to handle the regularisation properties: β is a quantitative parameter (it indicates the amount of smoothness) whereas b is more qualitative (in a way, it defines what the term “smoothness” means). Finally, note that an undesirable effect of this approach is to penalise the null frequency i.e. the average of the field (as 1/φ*(0) is not null). One removes this penalisation by simply ensuring that the deformation field has the same norm before and after regularisation. Figure 1 shows the influence of b and β when approximating a noisy field when choosing φ as the Wu kernel [8].

Fig. 1.

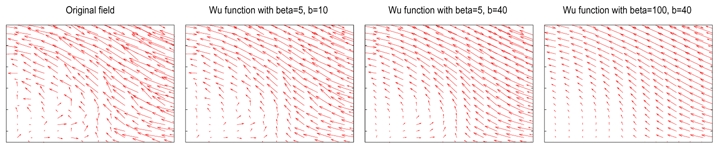
Effect of parameters β and b on the approximation of a noisy field.

3.3. Efficient choices

Although we propose a closed-form solution for the approximation problem, it consists in solving a M×M system. This is can be problematic when M increases (in term of memory usage and of computational time). Suppose that we choose a compactly supported pdk (i.e. for ∀x, ∀y such that ||y|| > r; k(x, y) = 0), then i) d(P)K + βI is a sparse matrix that can be computed using a kd-tree and ii) computing W consists in solving a sparse system. Some interesting compactly supported pdk corresponding to low-pass filters have been proposed in the literature (such as Wendland, Wu or Buhmann functions). Moreover, techniques to generate a wide variety of them have been proposed [8]. Alternatively one can use a highly decreasing function and approximate it by zeroying all its values over a given threshold. We experimentally find the compact support kernel of Wu (φ_2,3) as the one providing the best results and we will use it in the following.

4. Evaluation & Application

We use three databases of 20 surfaces each, composed of pairs of lateral ventricles of control subjects (15,000 points, segmented from T1-weighted MRI using itksnap.org), caudate nuclei of patients with dysphasia (2,000 points, segmented from T1-weighted MRI with an in-house software) and osseous labyrinths of modern H. sapiens (30,000 points, segmented from CT images with amira.com). We perform the following validation experiments.

Experiment 1

We choose one surface in each dataset and deform these 3 surfaces 100 times using randomly generated non-linear transformations (using TPS). Then we register the original and deformed surfaces and compute the overall residual distance between the known corresponding points and the Hausdorff distance between the surfaces. These two error measures are then averaged over the 100 simulations for each of the three surfaces.

Experiment 2

We manually select 6 landmarks on each of the 40 pairs of ventricles and labyrinths (the 20 nuclei are not used in this experiment). Then we choose one of the surfaces in each of the two datasets to be the template, and register all the 19 other surfaces to this template. We evaluate the mean residual errors on the landmarks, the Hausdorff distance between the surfaces, and we average these errors over the 19 subjects for each of the two datasets.

For both sets of experiments, we evaluate 3 strategies: asymmetric EM-ICP formulation using an order-one Tikhonov regularisation [6] (Method 1), asymmetric formulation using RKHS-based regularisation (Method 2) and symmetric-consistent formulation using RKHS (Method 3). The results are displayed on Tab. 1. Fig. 2 and Fig. 3 illustrate the added value of the symmetric consistent RKHS formulation compared to the asymmetric one on ventricles and nuclei.

Table 1. Average registration errors for the 3 tested methods and the two experiments on the 3 datasets.

The first error is the mean point-to-point (for Exp. 1) or landmark-to-landmark (Exp. 2) error, and the second error is the Hausdorff distance. Both errors are averaged over the 100 (Exp. 1) or 19 (Exp. 2) registrations. Method 3 (symmetric-consistent EM-ICP with RKHS regularisation) gives the lowest error for each experiment and dataset.

	Experiment 1			Experiment 2
	Method 1	Method 2	Method 3	Method 1	Method 2	Method 3
nuclei	2.26/1.87	0.73/1.76	0.64/1.37	-	-	-
ventricles	2.15/7.80	1.55/5.15	1.53/1.48	2.21/3.41	1.84/2.23	1.67/1.01
labyrinths	0.29/0.85	0.23/0.75	0.21/0.23	0.32/0.65	0.28/0.62	0.24/0.19

Fig. 2. Registration of lateral ventricles.

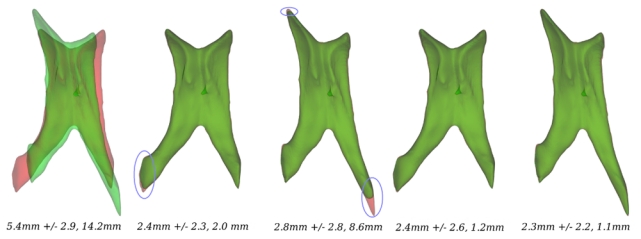
From left to right: (i) two misaligned pairs of lateral ventricles A and B (from Exp. 1); (ii) A to B and (iii) B to A with the asymmetric EM-ICP with RKHS; (iv) A to B and (v) B to A with the symmetric-consistent EM-ICP with RKHS. Point-to-point and Hausdorff registration errors are given below each figure. The asymmetric formulation leads to registration errors close to the horns. The location of these errors depends on what surface is used as the template. With the symmetric consistent formulation, no order-dependent registration error is visible, and the overall registration quality is visually and quantitatively improved.

Fig. 3. Registration of caudate nuclei.

Same display as in Fig. 2, but with caudate nuclei and a color mapping of the point-to-point errors. We draw the same conclusions as in Fig. 2.

The parameters for Method 3 are initialised as: α= 8, β = 400, σ² = 20×S, b = 250 × S where S is the size (in metre) of the object; β, σ², b are then decreased throughout the algorithm until they reach the respective values of 20, 5×S and 150×S. The same is done for Method 1 for β and σ² and for Method 2 for β, σ² and b. The run time to register point sets of 5,000 points is 2 min for Method 1, 5 min for Method 2 and 12 min for Method 3 on a standard PC.

Application to statistical shape modeling

Two major tracks have been followed in the literature to extend the EM-ICP formalism to build statistical shape models [7, 12]. By using our contributions, these methods can be made symmetric and consistent (allowing to reduce the bias during the computation of the mean shape) and one can drastically increase the size of the input data. Fig. 4 shows the mean shape and the first mode of variation for 20 caudate nuclei by adapting the method of Hufnagel et al. [12].

Fig. 4. Mean shape and first mode of variation ( $\pm \mathbf{2}\sqrt{{\lambda }_1}$) on 20 caudate nuclei.

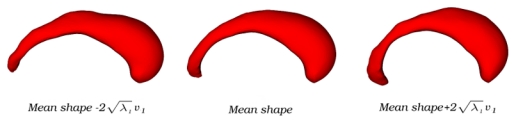
The first mode can be interpreted as a bending.

5. Conclusion

Our contributions are twofold. First, we proposed a symmetric and consistent EM-ICP framework where we enforce coherency between backward and forward deformations. Note that none of these transformations is guaranteed to be invertible, though. Second, we designed new efficient regularisers for EM-ICP based registration. These new regularisers are expressed within the RKHS formalism which leads to computationally attractive solutions (especially when using kernels with compact support). A particular class of kernels provides regularisers with a simple interpretation in the frequency domain. Overall, our algorithm allows to perform registration on large data sets. Future works will include i) comparing our regulariser with others such as Coherent Point Drift [11] or TPS; ii) comparing our statistical shape modelling with other techniques [7, 12].