Abstract
Most of the existing intelligibility measures do not account for the distortions present in processed speech, such as those introduced by speech-enhancement algorithms. In the present study, we propose three new objective measures that can be used for prediction of intelligibility of processed (e.g., via an enhancement algorithm) speech in noisy conditions. All three measures use a critical-band spectral representation of the clean and noise-suppressed signals and are based on the measurement of the SNR loss incurred in each critical band after the corrupted signal goes through a speech enhancement algorithm. The proposed measures are flexible in that they can provide different weights to the two types of spectral distortions introduced by enhancement algorithms, namely spectral attenuation and spectral amplification distortions. The proposed measures were evaluated with intelligibility scores obtained by normal-hearing listeners in 72 noisy conditions involving noise-suppressed speech (consonants and sentences) corrupted by four different maskers (car, babble, train and street interferences). Highest correlation (r=−0.85) with sentence recognition scores was obtained using a variant of the SNR loss measure that only included vowel/consonant transitions and weak consonant information. High correlation was maintained for all noise types, with a maximum correlation (r=−0.88) achieved in street noise conditions.
I. INTRODUCTION
A number of measures have been proposed to predict speech intelligibility in the presence of background noise. Among these measures, the articulation index (AI) [1–4] and speech-transmission index (STI) [5,6] are by far the most commonly used today for predicting speech intelligibility in noisy conditions. The AI measure was further refined to produce the speech intelligibility index (SII) [4]. The SII measure is based on the idea that the intelligibility of speech depends on the proportion of spectral information that is audible to the listener and is computed by dividing the spectrum into 20 bands (contributing equally to intelligibility) and estimating the weighted (geometric) average of the signal-to-noise ratios (SNRs) in each band [3,4,7–9]. The SNRs in each band are weighted by band-importance functions which differ across speech materials [4]. The SII measure has been shown to predict successfully the effects of linear filtering and additive noise on speech intelligibility. It has, however, a number of limitations. For one, the computation of the SII measure requires as input the levels of speech and masker signals at the eardrum of the listeners, something that might not be available in situations wherein we only have access to recorded (digitized) processed signals. Second, the AI measure has been validated for the most part only for steady (stationary) masking noise since it is based on the long-term average spectra (computed over 125-msec intervals) of the speech and masker signals. As such, it cannot be applied to situations in which speech is embedded in fluctuating maskers (e.g., competing talkers). Several attempts have been made to extend the SII measure to assess speech intelligibility in fluctuating maskers [10–13]. Rhebergen et al. [11], for instance, have proposed to divide the speech and masker signals into short frames (9–20 ms), evaluate the instantaneous AI value in each frame, and average the computed AI values across all frames to produce a single AI metric. Other extensions to the SII index were proposed in [14,15] for predicting the intelligibility of peak-clipping and center-clipping distortions in the speech signal, such as those found in hearing aids. Modifications to the AI and speech-based STI indices to account for fluctuating masker environments (e.g., train noise) were also proposed in [13] based on the use of signal- and segment-dependent band-importance functions.
With the exception of the coherence-based index [15] that assessed non-linear distortions, most of the existing intelligibility measures do not account for the distortions present in processed speech, such as those introduced by speech-enhancement algorithms. The majority of speech-enhancement algorithms operate in the frequency domain and are based on multiplication of the noisy speech magnitude spectrum by a suppression function, which is designed/optimized based on certain error criteria (e.g., mean squared error). The multiplication of the suppression function with the noisy magnitude spectra introduces two types of distortions, spectral attenuation (i.e., enhanced spectral components are smaller in magnitude than corresponding clean spectral components) and/or spectral amplification (i.e., enhanced spectral components are larger in magnitude than corresponding clean spectral component). These two types of distortions coexist within and across consecutive time frames, leading in some cases to the well known distortion of “musical noise” [16,17]. The perceptual implications and impact on speech intelligibility of these distortions are not clear, and most objective measures (e.g., Itakura-Saito measure, Quackenbush et al., 1988) lump these two types of distortions into one, as they are primarily based on the squared error criterion. The only notable measure that provides different weights to these two distortions is the PESQ measure (ITU-T, 2000). Other objective measures that attempted to balance the tradeoff between the two distortions were proposed in [18,19], but did not yield high correlation with subjective speech quality [18] (these measures were not evaluated with speech intelligibility scores). These measures were computed in the time-domain and not in the frequency (critical-band) domain, as done with the proposed measures.
In the present paper, we propose a new measure which treats the two types of spectral distortion differently, thus providing us with the possibility of assessing the individual contribution of the two distortions on speech intelligibility. It uses a critical-band spectral representation of the clean and noise-suppressed signals and is based on the measurement of the SNR loss incurred in each critical band after the corrupted signal goes through a speech enhancement algorithm. The proposed measure is flexible in that it can provide different weights to the two types of spectral distortions introduced by enhancement algorithms, and can also limit the amount of distortion that should be accounted for in its calculation. A second measure is also investigated based on the normalized correlation between the clean and enhanced critical-band spectra. This measure was chosen as it can detect inconsistencies in the two types of distortions introduced in the spectrum. It is based on the hypothesis is that if the enhanced spectra are uniformly attenuated or amplified across all bands, then intelligibility should not suffer as the overall spectral envelope is preserved. Consequently, the correlation coefficient will be high since the clean and enhanced spectra will be linearly related. On the other hand, when both spectral attenuation and amplification distortions are present (as is often the case), the impact on intelligibility ought to be higher and subsequently the correlation coefficient will be lower. A measure that combines the attractive features of the SNR loss and normalized correlation measures is also proposed.
The proposed measures are evaluated using a total of 72 noisy conditions. The 72 conditions included distortions introduced by 8 different noise-suppression algorithms and noise-corrupted (i.e., unprocessed) conditions operating at two SNR levels (0 and 5 dB) in four types of real-world environments (babble, car, street and train). The intelligibility scores obtained by human listeners in the 72 conditions [20] were used in the present study to evaluate the predictive power of the newly proposed objective measures.
II. PROPOSED OBJECTIVE MEASURES FOR PREDICTING SPEECH INTELLIGIBILITY
Let y(n) = x(n) + d(n) denote the noisy signal, with x(n) indicating the clean signal and d(n) indicating the masker (noise) signal. After windowing the observed signal with a function h(n), (i.e., Hamming window) we compute the short-time Fourier transform of y(n) as follows:
| (1) |
where ωk = 2πk/N (k=0,1,..,N−1) is the frequency bin index, m is the time frame index, N is the frame size in samples, and R is the update rate in samples. The excitation (or critical-band) spectrum of y(n) is computed by multiplying the FFT magnitude spectra, |Y(ωk, m)|, by 25 overlapping Gaussian-shaped windows [17, Ch. 11] spaced in proportion to the ear’s critical bands and summing up the power within each band. This results in the following critical-band spectra representation of the signals:
| (2) |
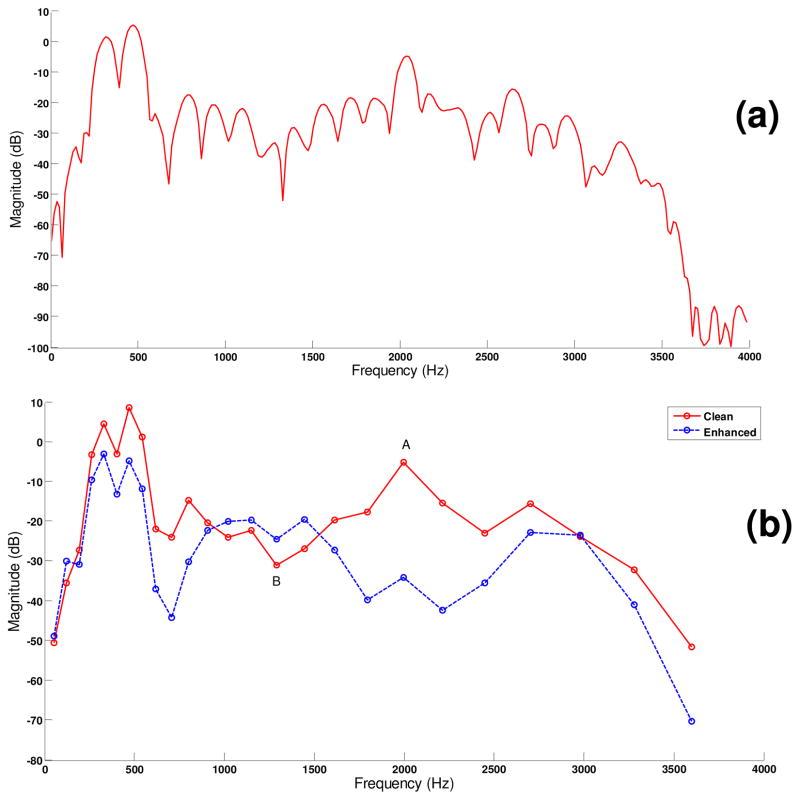
where K is the number of bands, X (j, m) is the excitation spectrum of the clean signal in band j at frame m, and D(j, m) is the excitation spectrum of the masker (noise). Figures 1(a) and 1(b) show respectively example FFT magnitude spectra and associated excitation spectra for a vowel segment excised from the word “kick”. The proposed objective measures are based on the above derived excitation spectra.
Figure 1.
Top panel (a) shows the FFT magnitude spectrum of a vowel segment excised from the word “trick” in quiet. Bottom panel (b) shows the excitation spectra of the clean signal and enhanced signal obtained using the RDC spectral-subtractive algorithm [22]. The band labeled A in panel (b) shows an example of spectral attenuation distortion, while the band labeled B shows an example of spectral amplification distortion.
A. SNR Loss
The SNR loss in band j and frame m is defined as follows:
| (3) |
where SNRX (j, m) is the input SNR in band j, SNRX̂ (j, m) is the effective SNR of the enhanced signal in the j th frequency band, and X̂(j, m) is the excitation spectrum of the processed (enhanced) signal in the j th frequency band at the mth frame. The first SNR term in Eq. (3) provides the original SNR in frequency band j before processing the input signal x(n), while the second SNR term provides the SNR of the processed (enhanced) signal. The term L(j, m) in Eq. (3) thus defines the loss in SNR1, termed SNRLOSS, incurred when the corrupted signal goes through a noise-suppression system. Clearly, when X̂ (j,m) = X(j,m), the SNRLOSS is zero. It is reasonable to expect with most noise-suppression algorithms that as the SNR level increases, i.e., SNR → ∞, the estimated spectrum X̂(j,m) approaches the clean spectrum X(j,m), i.e., X̂(j,m) → X̂(j,m) (see proof in Chen, et al., 2008) for the Wiener filter enhancement algorithm), and consequently the SNRLOSS is zero. On this regard, the value of the above SNRLOSS measure depends on the input SNR value. This is tested in the present study by assessing the correlation of the SNRLOSS measure with speech intelligibility scores obtained in different SNR level conditions.
Figure 1 shows an example excitation spectrum of a signal that has been processed via a spectral subtraction algorithm [22]. As can be seen from this example, the SNR loss can be positive in some bands (see label A in panel b) suggesting the presence of spectral attenuation distortion or could be negative in others (see label B in panel b) suggesting spectral amplification distortion.
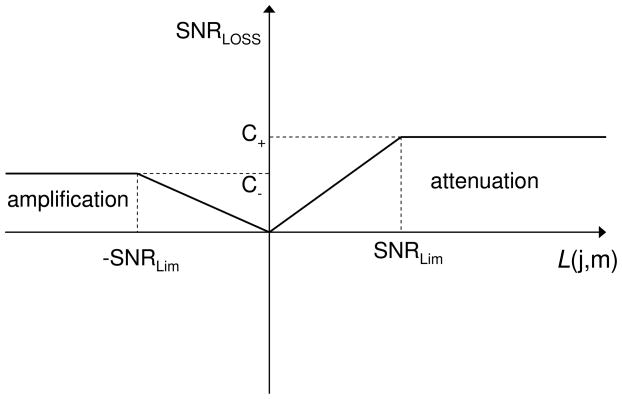
Following the computation of the SNR loss in Eq. (3), the L(j, m) term is limited to a range of SNR levels. In the SII index [4], for instance, the SNR calculation is limited to the range of [−15, 15] dB, prior to the mapping of the computed SNR to the range of [0,1]. Assuming in general the restricted SNR range of [−SNRLim, SNRLim] dB, the L(j, m) term is limited as follows:
| (4) |
and subsequently mapped to the range of [0, 1] using the following equation:
| (5) |
where C+ and C− are parameters (defined in the range of [0, 1]) controlling the slopes of the mapping function (see Figure 2). Note that the SNRLim values in the above equation do not denote the assumed speech dynamic range but rather the limits imposed to the computed SNR values. The above equation normalizes the frame SNRLOSS to the range of 0 ≤ SNRLOSS(j, m) ≤ 1 since 0 ≤ C+, C− ≤ 1. The average SNRLOSS is finally computed by averaging SNRLOSS(j,m) over all frames in the signal as follows:
| (6) |
where M is the total number of data segments in the signal and fSNRLOSS(m) is the average (across bands) SNR loss computed as follows:
| (7) |
where W(j) is the weight (i.e., band importance function [4]) placed on the j th frequency band. The weighting function W(j) can be signal dependent [13], but in our case we set it equal to band-importance functions similar to those given in [4]. The band-importance functions were taken from Table B.1 in the ANSI standard [4]. For the consonant materials, we used the nonsense syllable functions and for the sentence materials we used the short-passage functions given in Table B.1 in [4]. The functions were linearly interpolated to reflect the range of band center-frequencies adopted in the present study (the values for the 50 and 120 Hz bands were extrapolated). It should be noted that due to the smaller bandwidth and the use of interpolated values, the sum of the articulation index weights given in Table B.1 does not add up to 1. Despite that, due to the normalization term used in the denominator of Eq. 7, the fSNRLOSS(m) measure is always smaller than 1.
Figure 2.
Mapping of the difference L(j,m) (in dB) between the clean and enhanced signals to SNRLOSS. The parameters C+ and C−, and the SNR range ([−SNRLIM, SNRLIM] dB) control the slope of the mapping function.
Based on Eq. (5), it is easy to show that Eq. 7 can be decomposed into two terms as follows (assuming for convenience that W(j) = 1 for all j):
| (8) |
where the terms SNR− and SNR+ are used to indicate the isolated SNR loss due to amplification and attenuation distortions respectively. As it will be shown later (see Sec. VI), the SNR+ and SNR− measures can be used as a diagnostic tool when analyzing the performance of speech enhancement algorithms.
From Equations (4) and (5), it is clear that the SNRLOSS measure depends on the SNRLim and the parameters C+ and C−, both of which control the slope of the mapping function (see Figure 2). The parameters C+ and C− are quite important, as they can tell us about the individual contribution of the spectral attenuation (occurring when X (j, m) > X̂ (j, m)) and spectral amplification (occurring when X(j,m) < X̂ (j,m)) distortions introduced by noise-suppression algorithms to speech intelligibility (see example in Figure 1). By setting C+=1 and C− =0, for instance, we can assess whether we can better predict speech intelligibility when accounting only for spectral attenuation distortions while ignoring spectral amplification distortions. Similarly, by setting C+=1 and C−=1, we can assess whether both distortions (spectral amplification and attenuation) should be weighted equally. In brief, the parameters C+ and C− can help us assess the perceptual impact of the spectral distortions introduced by noise-suppression algorithms. Given the importance of the parameters C+ and C−, we varied independently their values from 0 to 1 (in steps of 0.2) and examined the resulting SNRLOSS correlation with speech intelligibility.
While the parameters C+ and C− in Eq. (5) can be used to control the importance of the type of spectral distortion (spectral amplification and/or attenuation) introduced by noise-suppression algorithms, the SNRLim parameter can be used to assess the amount of spectral distortion that should be included in the SNRLOSS calculation. In the computation of the SII measure, for instance, the SNRLim parameter is set to 15 dB, suggesting that band SNRs larger than 15 dB do not contribute further to intelligibility and should not be included in the calculation of the SII index. Hence, by varying the SNRLim parameter in the present study we can examine the lower/upper limits of spectral distortions that should be included in the calculation of the SNRLOSS measure. In the example shown in Figure 1, for instance, band A (see panel b) was attenuated by nearly 30 dB. Had this band been attenuated by say 5 dB, would it make the processed speech stimulus more intelligible or does there exist a critical “saturation” point beyond which the distortions do not contribute further to intelligibility loss? To answer these questions, we will vary the SNRLim parameter (and associated SNR dynamic range) in the present study from a low of 2 dB to a high of 50 dB, and examine the resulting correlations with speech intelligibility scores.
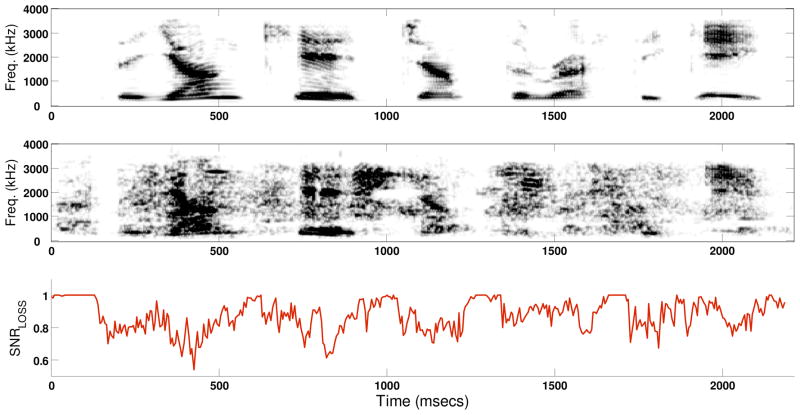
Figure 3 shows an example frame SNRLOSS values for a sentence (in 0 dB SNR babble) processed via the RDC spectral-subtractive algorithm [22]. The spectrograms of the clean and enhanced signals are also shown for comparison. The average SNRLOSS value for this example was 0.87. For this example, the SNRLOSS value was high during the unvoiced segments and was relatively low during voiced segments. This is consistent with the fact that most speech-enhancement algorithms do not perform well during unvoiced segments, as those low-SNR segments are heavily masked by noise.
Figure 3.
Top two panels show spectrograms of a sentence in quiet and corrupt sentence processed by the RDC spectral-subtractive algorithm [22] respectively. The input sentence was corrupted by babble at 0 dB SNR. Bottom panel shows the frame SNRLOSS values. The average SNRLOSS was 0.86 (SNRLIM was set to 5 dB).
The SNRLOSS measure bears some resemblance to the intelligibility-weighted gain in SNR [23] which is computed as follows:
| (9) |
where Wk denote the weights (i.e., band-importance functions) applied to band k, SNROUT is the output SNR (expressed in dB) in band k computed using the processed clean and noise signals, and SNRIN is the input SNR computed using the input (clean) signal. Note that unlike the enhanced signal’s SNR used in Eq. (3), the SNROUT term is computed using the processed (by the algorithm’s suppression function) clean and noise signals, and is not based on the enhanced output signal (e.g., [24]). Furthermore, the SNR calculations in Eq. (9) are not restricted to a finite range (e.g., 30 dB). In contrast, the band SNRs used in the SNRLOSS measure are restricted to a small range (see Eq. (4) and Figure 2) and are mapped nonlinearly to the range of [0,1] after the subtraction operation. The above measure was originally intended to characterize an effective signal-to-noise ratio in speech transmission systems, and not to predict speech intelligibility [23].
The SNRLOSS measure given in Eq. (3) also bears some resemblance to the spectral distortion (SD) measure often used in speech coding particularly in the design of vector quantizers [25,26]:
| (10) |
where PX (f) and PX̂ (f) denote the power spectra of the clean and coded (processed) spectra respectively, and Fs denotes the sampling frequency. There is one fundamental difference between the definition of SD and Eq. (3). The spectral log difference in Eq. (10) is squared, while the log difference in Eq. (3) is not. As mentioned earlier, when the difference is squared, no distinction is made between the amplification and attenuation distortions as they are both lumped into one. The SD measure is also used sometimes for evaluating noise-suppressed speech [27]. For comparative purposes, we will also evaluate in the present study a critical-band based version of Eq. (10), denoted as SDCB, and implemented as follows:
| (11) |
where L(j,m) is given by Eq. (3). Aside from the spectral distortion given in Eq. (10), a number of other spectral distortion measures were proposed in [28,29]. These measures were computed for the most part in the context of Wiener filtering, and more generally, in the context of linear estimators of speech including those applied in the KLT domain. Some measures were also proposed for non-linear estimators of the speech spectrum (Benesty, 2009). The proposed SNRLOSS measure can be used for speech processed by either linear or non-linear estimators. Furthermore, the spectral distortion measures proposed in [28,29] were not validated with human intelligibility tests, hence it remains uncertain as to how reliably can these measures predict speech distortion or speech intelligibility.
B. Excitation Spectra Correlation (ESC)
The excitation spectral correlation (ESC) measure at frame m is computed as follows:
| (12) |
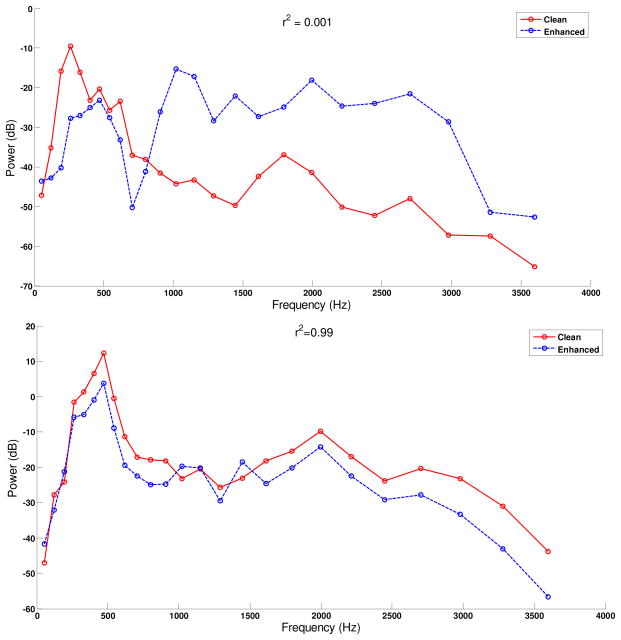
where K is the number of bands (K=25 in our study). Note that the above equation gives the squared Pearson’s correlation between the clean and enhanced excitation spectra (assuming that these spectra have a zero mean). As such, the r2(m) values are limited to 0 ≤ r2(m) ≤ 1. A value of r2(m) close to 1 would suggest that the input and processed signals are linearly related, while a value of r2(m) close to 0 would indicate that the input and processed signals are uncorrelated. At the extreme case wherein X̂ (j,m) = α · X(j,m) for all bands, then it is easy to show from Eq. (12) that r2(m) =1. Hence, if α > 1 that would suggest that X̂ (j,m) is uniformly amplified across all bands, and similarly if α < 1 that would suggest that X̂ (j, m) is uniformly attenuated across all bands. Uniform spectral distortion, across all bands, would indicate that the shape of the spectral envelope (which includes the formant peaks, F1 and F2, in voiced segments, e.g., vowels) is grossly preserved, and consequently intelligibility should not be degraded. On the other hand, if the spectral distortions vary across bands (as is often the case) in that speech is attenuated in some bands and amplified in others, then intelligibility would likely suffer and the resulting correlation will be low or lie somewhere between 0 and 1. Figure 4 shows two example spectra in which the correlations are high and low, demonstrating the above concept and motivation for the use of the ESC measure.
Figure 4.
Example excitation spectra of the clean and enhanced signals in two different scenarios. Top panel shows an example in which the spectral amplification and attenuation distortions are non-uniformly distributed across the spectrum. Bottom panel shows an example in which the enhanced spectrum is for the most part uniformly (across nearly all bands) attenuated. The resulting excitation spectrum correlation (ESC) is indicated in the top of each figure.
The average ESC is computed by averaging r2(m) over all frames in the signal as follows:
| (13) |
Based on the assumption that the excitation spectra have zero mean, it is easy to show that r2(m) (Eq. (12)) is related to the signal-to-residual noise ratio (SNRES) as follows (see Appendix A):
| (14) |
Note that the denominator provides the power of the residual spectrum, which is not necessarily the same as the masker spectrum. For that reason, we refer to the above term as SNRES rather than as SNR. The time-domain counterpart of SNRES is the segmental SNR (SNRseg), often used in the evaluation of speech enhancement and speech coding algorithms [30].
The excitation spectra, X(k, m) and X̂ (k, m), are positive quantities and have a non-zero (and time-varying) mean. Consequently, we also considered the following covariance measure which accounts for the means of the excitation spectra:
| (15) |
where μX(m) and μX̂(m) denote the means of X(k,m) and X̂ (k,m) respectively (e.g., ). The average covariance (across the whole utterance) of the excitation spectra is computed as in Eq. (13) and is denoted as ESCμ.
The average ESC measure (Eq. (13)) was computed by averaging r2(m) over all frames in the signal, putting equal emphasis on low-energy (e.g., fricatives) and high-energy (e.g., vowels) phonetic segments. Higher correlations were obtained in [14], when dividing the M speech segments into three level regions, and computing separately the measure for each region. The high-level region consisted of segments at or above the overall RMS level of the whole utterance. The mid-level region consisted of segments ranging from the overall RMS level to 10 dB below the overall RMS level, and the low-level region consisted of segments ranging below RMS-10 dB. The three-level ESC measures obtained for the low-, mid- and high-level segments were denoted as ESCLow, ESCMid and ESCHigh respectively. A linear combination of the three ESC values (based on linear regression analysis) can subsequently be used to model the intelligibility scores. Hence, in addition to the average ESC measure which puts equal emphasis to all phonetic segments, we will also investigate the performance of the three-level ESC measures.
III. COMBINING THE SNRLOSS AND ESC MEASURES
The ESC measure has an attractive feature that is absent from the SNRLOSS measure. As illustrated in Figure 4, when the enhanced output signal is uniformly (across all bands) attenuated/amplified, the resulting correlation is near one. In contrast, the SNRLOSS measure reaches its maximum value (since it is limited by SNRLim), and consequently yields a high SNR loss value (near one), which is inappropriate for uniform distortions and likely inconsistent with intelligibility scores. For that reason, we propose to combine the two measures as follows:
| (16) |
where SNRLESC(m) is the new measure at frame m, and fSNRLOSS(m) is the average frame SNRLOSS given by Eq. (7). The SNRLESC measure is bounded within the range of 0 to 1, and assumes a high value (i.e., near one) when both the terms (1 − r2(m)) and SNRLOSS assume a high value, and assumes a small value when either of the two measures takes on a small value (i.e., near zero). The average, across the whole utterance, SNRLESC measure is computed as in Eq. (13). Depending on the implementation of r2 (m), two different measures are produced, denoted as SNRLESC (based on Eq. (12)) and SNRLESCμ (based on Eq. (15)). Figure 5 shows as an example, the frame SNRLESC values superimposed to the frame SNRLOSS values for an utterance processed by the spectral-subtractive algorithm in [22]. As can be seen, the SNRLESC curve follows for the most part the SNRLOSS curve with the exception when (1 − r2(m)) is close to zero.
Figure 5.
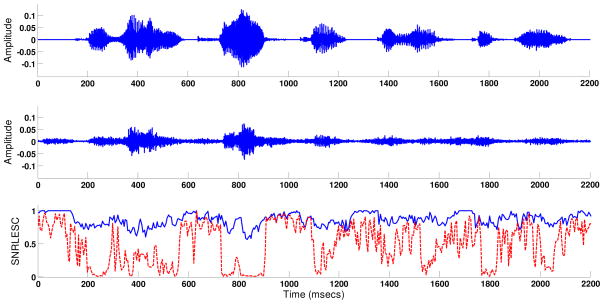
The top two panels show time-domain waveforms of a sentence in quiet and processed by the RDC spectral-subtractive algorithm respectively. The input sentence was corrupted by babble at 0 dB SNR (same as in Figure 3). Bottom panel shows the frame SNRLESC values (dashed lines) superimposed to the frame SNRLOSS values (solid lines). The average SNRLOSS was 0.86 and the average SNRLESC value was 0.48 (SNRLIM was set to 5 dB).
As will be shown later, the SNRLOSS measure performs quite well despite the above limitation in dealing with uniform distortions. This is perhaps because uniform distortions occur significantly less often in noise-suppressed speech than non-uniform distortions. The proposed SNRLESC measure is meant to enhance the prediction power of the SNRLOSS measure.
V. INTELLIGIBILITY LISTENING TESTS
In order to properly evaluate the predictive power of the proposed objective measures, we need intelligibility scores obtained from human listeners. For that, we will be using the intelligibility evaluation study of noise-corrupted speech processed through eight different noise-suppression algorithms as reported in Hu and Loizou [20]. This study is summarized briefly below.
IEEE sentences [31] and consonants in /a C a/ format were used as test material. The consonant test included 16 consonants recorded in /a C a/ context, where C = /p, t, k, b, d, g, m, n, dh, l, f, v, s, z, sh, dj/. These recordings were originally sampled at 25 kHz, but were downsampled to 8 kHz and are available in [17]. The masker signals were taken from the AURORA database [32] and included the following real-world recordings from different places: babble, car, street, and train. The maskers were added to the speech signals at SNRs of 0 and 5 dB. A total of 40 native speakers of American English were recruited for the sentence intelligibility tests, and 10 additional listeners were recruited for the consonant tests. A total of 40 native speakers of American English were recruited for the sentence intelligibility tests. The 40 listeners were divided into four panels (one per type of noise), with each panel consisting of 10 listeners. The processed speech files (sentences/consonants), along with the clean and noisy speech files, were presented monaurally to the listeners in a double-walled sound-proof booth (Acoustic Systems, Inc) via Sennheiser’s (HD 250 Linear II) circumaural headphones at a comfortable level. The intelligibility study by Hu and Loizou [20] produced a total of 72 noisy conditions including the noise-corrupted (unprocessed) conditions. The intelligibility scores obtained in the 72 conditions were used in the present study to evaluate the predictive power of the newly proposed objective measures.
VI. RESULTS
Two figures of merit were used to assess the performance of the above objective measures in terms of predicting speech intelligibility in noise. The first figure of merit was the Pearson’s correlation coefficient, r, and the second figure of merit was an estimate of the standard deviation of the error computed as , where σd is the standard deviation of the speech recognition scores in a given condition, and σe is the computed standard deviation of the error. A smaller value of σe indicates that the objective measure is better at predicting speech intelligibility.
The average intelligibility scores obtained by normal-hearing listeners in the 72 different noisy conditions (see Section III), were subjected to correlation analysis with the corresponding mean values obtained with the objective measures. A total of 1440 processed speech samples were included in the correlations encompassing two SNR levels (0 and 5 dB), four different types of background noise and speech/noise distortions introduced by 8 different speech enhancement algorithms (1152 processed speech samples were used for consonants). The intelligibility scores for each speech sample were averaged across all listeners involved in that test. Similarly, the values from the objective measures were averaged across the speech material (20 sentences or 16 consonants) used in each condition. A logistic function was used to map the values obtained by the objective measures to speech intelligibility scores.
As mentioned earlier, these conditions involved noise-suppressed speech (consonants and sentences) originally corrupted by four different maskers (car, babble, train and street interferences) at two different SNR levels. The computed correlation coefficients (and prediction error) are tabulated separately for the consonants and sentence materials and are given in Table 2. For the computation of the SNRLOSS measure, we initially set SNRLim = 15 dB (as used in [4]) and C+ = C− = 1. Further experiments were carried out using different values of SNRLim and C+, C− (see later sections). All measures were computed by segmenting the sentences using 20-msec duration Hamming windows with 75% overlap between adjacent frames.
Table 2.
Correlations between the proposed measures and consonants/sentence recognition scores. The SNR range used in the computation of the SNRLOSS and SNRLESC measures was fixed at [−15, 15] dB.
| Speech Material | Objective measure | r | σe |
|---|---|---|---|
| Consonants | SNRLOSS | −0.67 | 0.09 |
| ESC | 0.70 | 0.09 | |
| ESCHigh | 0.61 | 0.10 | |
| ESCMid | 0.73 | 0.08 | |
| ESCLow | 0.29 | 0.12 | |
| ESCμ | 0.68 | 0.09 | |
| ESCμ-High | 0.60 | 0.10 | |
| ESCμ–Mid | 0.71 | 0.09 | |
| ESCμ–Low | 0.56 | 0.10 | |
| SNRLESC | −0.71 | 0.09 | |
| SNRLESCμ | −0.66 | 0.09 | |
| SDCB | −0.33 | 0.12 | |
| Sentences | SNRLOSS | −0.61 | 0.14 |
| ESC | 0.82 | 0.10 | |
| ESCHigh | 0.83 | 0.10 | |
| ESCMid | 0.84 | 0.09 | |
| ESCLow | 0.46 | 0.15 | |
| ESCμ | 0.83 | 0.10 | |
| ESCμ-High | 0.83 | 0.10 | |
| ESCμ–Mid | 0.83 | 0.10 | |
| ESCμ–Low | 0.57 | 0.14 | |
| SNRLESC | −0.72 | 0.12 | |
| SNRLESCμ | −0.72 | 0.12 | |
| SDCB | −0.26 | 0.17 |
As shown in Table 2, of the three measures proposed, the SNRLESC measure performed the best (r=−0.71) in predicting consonant recognition scores, while the ESCμ measure performed the best (r=0.83) in predicting sentence recognition scores. The SNRLOSS measure performed modestly well, at least for the SNRLim range tested (SNRLim = 15 dB). Significant improvements in correlation were noted, however, when the SNRLim range was reduced (see Table 3 and later experiments). The spectral log difference measure (SDCB in Eq. (11)), which is often used to assess speech distortion introduced by speech enhancement algorithms [27] or vector quantizers [25] yielded the lowest correlation (|r| = 0.26–0.33) for both consonant and sentence recognition. This outcome highlights the negative implications of lumping the amplification and attenuation distortions into one, as done when the log difference between the clean and processed spectra is squared.
Table 3.
Correlations between the SNRLOSS measure and consonants/sentence recognition scores as a function of the SNR dynamic range.
| Speech material | SNR Range (dB) | r | σe |
|---|---|---|---|
| Consonants | [−1,1] | −0.73 | 0.08 |
| [−3,3] | −0.77 | 0.08 | |
| [−5,5] | −0.76 | 0.08 | |
| [−10,5] | −0.75 | 0.08 | |
| [−10,10] | −0.72 | 0.09 | |
| [−10,35] | −0.33 | 0.12 | |
| [−15,5] | −0.72 | 0.09 | |
| [−15,10] | −0.71 | 0.09 | |
| [−15,15] | −0.67 | 0.09 | |
| [−15,35] | −0.39 | 0.11 | |
| [−20,5] | −0.68 | 0.09 | |
| [−20,10] | −0.69 | 0.09 | |
| [−20,20] | −0.62 | 0.10 | |
| [−25,10] | −0.66 | 0.09 | |
| [−30,10] | −0.63 | 0.10 | |
| Sentences | [−1,1] | −0.77 | 0.11 |
| [−3,3] | −0.82 | 0.10 | |
| [−5,5] | −0.80 | 0.10 | |
| [−10,5] | −0.76 | 0.11 | |
| [−10,10] | −0.71 | 0.12 | |
| [−10,35] | −0.31 | 0.17 | |
| [−15,5] | −0.69 | 0.139 | |
| fl−15,10] | −0.67 | 0.13 | |
| [−15,15] | −0.61 | 0.14 | |
| [−15,35] | −0.36 | 0.16 | |
| [−20,5] | −0.62 | 0.14 | |
| [−20,10] | −0.62 | 0.14 | |
| [−20,20] | −0.53 | 0.15 | |
| [−25,10] | −0.57 | 0.14 | |
| [−30,10] | −0.52 | 0.15 |
Among the three-level ESC measures, the mid-level ESC (ESCMid) measure yielded the highest correlation for both consonant (r=0.73) and sentence materials (r=0.84), consistent with the outcome reported in [14]. The ESCMid measure captures information about envelope transients and spectral transitions, critical for the transmission of information regarding place of articulation. Subsequent logistic transformations of the ESC3 measure did not improve the correlations.
Further experiments were conducted to assess the influence of the SNR range (SNRLim) and the parameters C+ and C− involved in the computation of the SNRLOSS and SNRLESC measures. These experiments are discussed next.
A. Influence of mapped SNR range
To assess the influence of the mapped SNR range on the performance of the SNRLOSS measure, we varied the SNR range from a low of 2 dB to a high of 50 dB. The parameters C+ and C− were both set to one. The resulting correlation coefficients are given in Table 3. As can be seen, the highest correlations were obtained when the SNR range was limited to [−3, 3] dB. Significant improvement was noted on the prediction of sentence recognition scores; the correlation coefficient improved from r=−0.61, based on the SNR range of [−15, 15] dB (adopted in the SII index computation), to r=−0.81 based on the SNR range of [−3, 3] dB. This outcome suggests that, unlike the SII index [4], the spectral distortions introduced by noise-suppression algorithms do not contribute proportionally, within a 30 dB dynamic range, to speech intelligibility loss. The contribution of SNR loss to speech intelligibility seems to reach a saturation point at the [−3, 3] dB limits. Put differently, processed speech with a measured SNR loss of say 10 dB is not less intelligible than processed speech with an SNR loss of 5 dB. Based on Table 3, we can thus conclude that only spectral distortions falling within a 6 dB range (i.e., within [−3, 3] dB) should be included in the computation of the SNRLOSS measure.
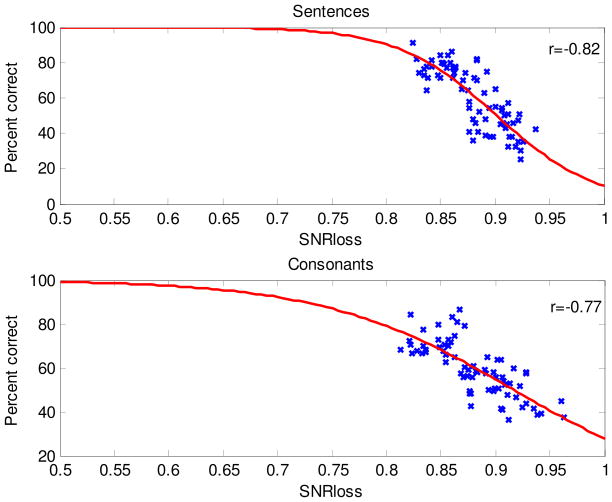
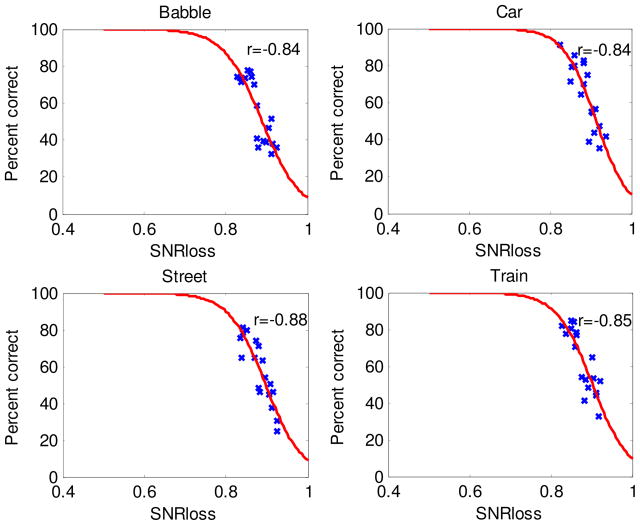
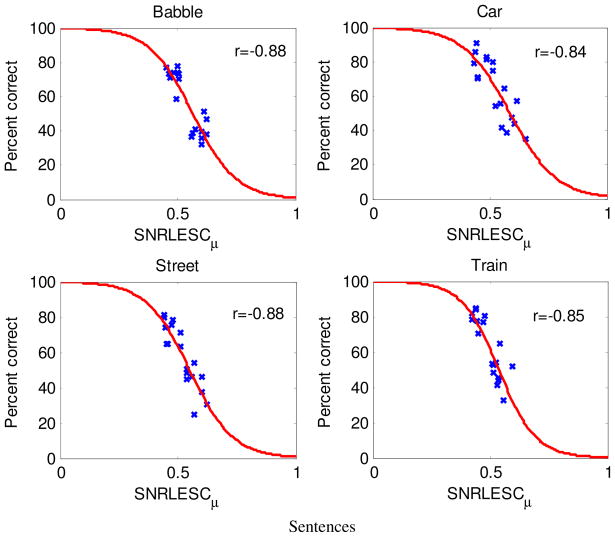
Figure 6 shows the scatter plot of the predicted SNRLOSS scores (obtained using the [−3, 3] dB range) against the listeners’ recognition scores for consonants and sentences. Figures 7 and 8 show the individual scatter plots broken down by noise type for sentence and consonant recognition respectively. A logistic function was used to map the objective scores to intelligibility scores. As can be seen, a high correlation was maintained for all noise types, including modulated (e.g., train) and non-modulated (e.g., car) maskers. The correlations with consonant recognition scores ranged from r=−0.81 with babble to r=−0.87 with street noise. The correlations with sentence recognition scores ranged from r=−0.84 with car noise to r=−0.88 with street noise. The correlations were obtained with logistic-type fitting functions. Only two SNR levels (0 and 5 dB) were examined in this study, neither of which yielded saturation or flooring effects.
Figure 6.
Scatter plots of the intelligibility scores obtained by human listeners and predicted SNRLOSS values for the sentence and consonants materials.
Figure 7.
Individual scatter plots of the sentence intelligibility scores and predicted SNRLOSS values for the four maskers tested.
Figure 8.
Individual scatter plots of the consonant intelligibility scores and predicted SNRLOSS values for the four maskers tested.
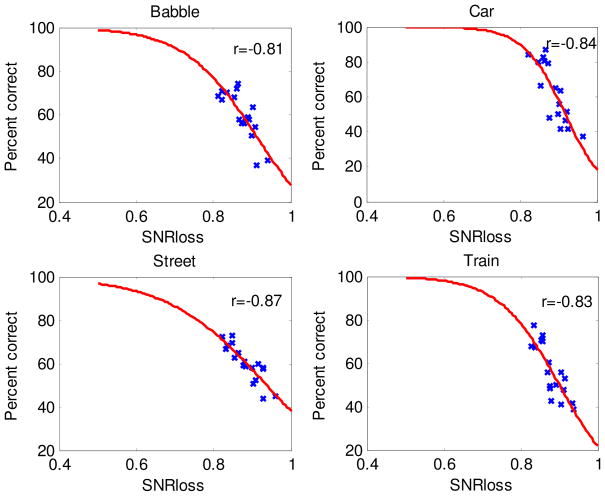
Having determined the optimum SNR range to use in the computation of the SNRLOSS measure, we re-examined the correlations of the SNRLESC measure based on the [−3, 3] dB range. The resulting correlation coefficients are shown in Table 4. Consistent improvements in the correlation coefficient were noted for both consonants and sentence materials. The correlation coefficient obtained using the SNRLESC measure was higher than obtained with either the ESC or SNRLOSS measures alone. The highest correlation (r=−0.84) with sentence materials was obtained with the SNRLESCμ measure. Figure 9 shows the individual scatter plots of the predicted SNRLESCμ values broken down by noise type for sentence recognition. Further improvements were obtained with the three-level SNRLESCμ and SNRLESC measures. Similar to the approach taken for the ESC measures, a multiple-regression analysis was run on the three SNRLESC measures, yielding the following predictive models for consonant and sentence intelligibility.
Table 4.
Correlations between the SNRLESC measure and consonants/sentence recognition scores. The SNR range was set to [−3, 3] dB.
| Speech Material | Objective measure | r | σe |
|---|---|---|---|
| Consonants | SNRLESC | −0.73 | 0.08 |
| SNRLESCHigh | −0.64 | 0.09 | |
| SNRLESCMid | −0.74 | 0.08 | |
| SNRLESCLow | −0.39 | 0.11 | |
| SNRLESCμ | −0.70 | 0.09 | |
| SNRLESCμ–High | −0.63 | 0.10 | |
| SNRLESCμ–Mid | −0.73 | 0.08 | |
| SNRLESCμ–Low | −0.59 | 0.10 | |
| Sentences | SNRLESC | −0.82 | 0.10 |
| SNRLESCHigh | −0.84 | 0.09 | |
| SNRLESCMid | −0.85 | 0.09 | |
| SNRLESCLow | −0.51 | 0.15 | |
| SNRLESCμ | −0.84 | 0.09 | |
| SNRLESCμ–High | −0.84 | 0.09 | |
| SNRLESCμ–Mid | −0.85 | 0.09 | |
| SNRLESCμ–Low | −0.58 | 0.14 |
Figure 9.
Individual scatter plots of the sentence intelligibility scores and predicted SNRLESCμ values for the four maskers tested.
B. Influence of parameter values C+ and C−
In the previous experiments, the parameters C+ and C− were fixed to one. To assess the influence of the parameters C+ and C− on predicting speech intelligibility, we varied independently the values of the parameters from 0 to 1, in steps of 0.2. The resulting correlation coefficients are shown in Table 5. As can be seen from Table 5, the optimum values for the parameters C+ and C− are 1 and 1 respectively. This suggests that both spectral attenuation and amplification distortions need to be included in the SNRLOSS calculation and that these distortions contribute equally to loss in intelligibility. It is interesting to note however that the correlation coefficient dropped significantly (near zero) when C+ was set to a small value, and the C− value was fixed at 1. The resulting correlation (r=−0.03) obtained, for instance, with C+=0.4 and C−=1, did not differ significantly from zero (p=0.829). A relatively smaller decrease in correlation coefficient was obtained when C− was set to a small value, and the C+ value was fixed at 1 (resulting correlations were significant, p<0.05). This indicates that, when limited to the [−3, 3] dB range, the spectral attenuation distortions carry a larger perceptual weight compared to the spectral amplification distortions. Nevertheless, both distortions need to be included in the computation of the SNRLOSS measure for maximum correlation.
Table 5.
Correlations between the SNRLOSS measure and consonants/sentence recognition scores for various values of the parameters C+ and C−.
| Material | C− | C+ | r | σe |
|---|---|---|---|---|
| Consonants | 1 | 0 | 0.11 | 0.12 |
| 1 | 0.2 | 0.08 | 0.12 | |
| 1 | 0.4 | 0.02 | 0.12 | |
| 1 | 0.6 | −0.10 | 0.12 | |
| 1 | 0.8 | −0.42 | 0.11 | |
| 1 | 1 | −0.77 | 0.08 | |
| 0 | 1 | −0.24 | 0.12 | |
| 0.2 | 1 | −0.27 | 0.12 | |
| 0.4 | 1 | −0.31 | 0.12 | |
| 0.6 | 1 | −0.39 | 0.11 | |
| 0.8 | 1 | −0.55 | 0.10 | |
| Sentences | 1 | 0 | 0.06 | 0.17 |
| 1 | 0.2 | 0.03 | 0.17 | |
| 1 | 0.4 | −0.03 | 0.17 | |
| 1 | 0.6 | −0.13 | 0.17 | |
| 1 | 0.8 | −0.41 | 0.16 | |
| 1 | 1 | −0.82 | 0.10 | |
| 0 | 1 | −0.18 | 0.17 | |
| 0.2 | 1 | −0.21 | 0.17 | |
| 0.4 | 1 | −0.25 | 0.17 | |
| 0.6 | 1 | −0.33 | 0.16 | |
| 0.8 | 1 | −0.51 | 0.15 |
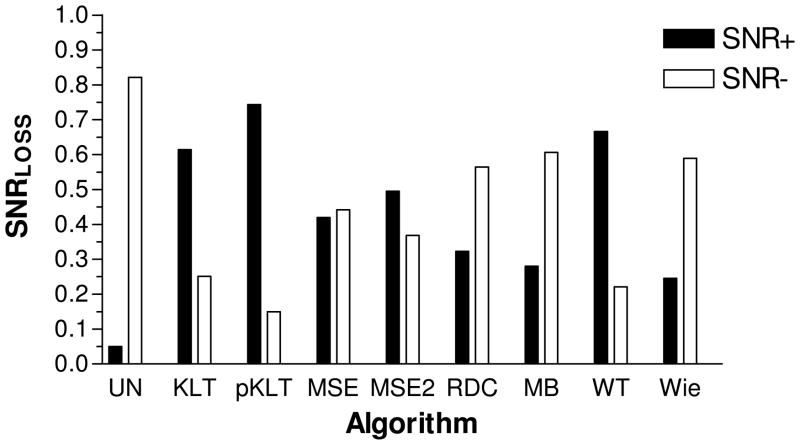
The overall SNR loss introduced by speech enhancement algorithms can be written, based on Eq. (5), as the sum of the loss due to spectral amplification distortion and the loss due to the spectral attenuation distortion (see Eq. (8)). As shown in Eq. (8), the overall SNR loss can be decomposed as: SNRLOSS =SNR+ + SNR− where SNR+ indicates the loss in intelligibility due to spectral attenuation distortions alone, and SNR− indicates the loss in intelligibility due to spectral amplification distortions alone. This decomposition of the SNR loss values can provide valuable information when analyzing the performance of individual algorithms as it can be used to create an intelligibility-loss profile for the algorithm tested. To illustrate this, we computed the SNR+ and SNR− values for the 8 enhancement algorithms used in the 5-dB SNR car noise condition in [20]. The results are shown in Figure 10. The (unprocessed) corrupted files (indicated as UN in Figure 10) had the highest spectral amplification distortion and the lowest attenuation. This is to be expected given that no suppression function was applied to the corrupted signals. The amplification distortions present in the corrupted signals reflect the masking of the signal by the noise. In contrast, the pKLT algorithm [33] yielded the highest spectral-attenuation distortion loss. Incidentally, the pKLT algorithm also yielded the lowest intelligibility score (69% correct with pKLT vs. 81% correct with unprocessed and corrupted sentences) for this condition [20]. Relative to the corrupted signals, the Wiener filtering algorithm [34] reduced the spectral attenuation distortion and introduced only modest spectral amplification. The Wiener filtering algorithm yielded the lowest spectral attenuation distortion among all algorithms tested, while maintaining modest amplification loss. Largest improvements in intelligibility were obtained with the Wiener algorithm compared to all other algorithms. In fact, performance with the Wiener algorithm was higher (by 10% points) than performance obtained with the corrupted (unprocessed) signals. The statistical model-based algorithms (e.g., [35]) maintained a good balance between the two distortions. From the SNRLOSS profile depicted in Figure 10 and the associated intelligibility scores, we can conclude that the loss due to spectral amplification is not as detrimental to speech intelligibility as is the loss due to spectral attenuation distortions, at least when the distortions are limited within the [−3, 3] dB range. This is consistent with the data in Table 5 assessing the influence of the parameters C+ and C−. As illustrated in Table 5, the correlation coefficient dropped significantly (near zero) when the parameter C+, which controls the weight placed on spectral attenuation distortion, was set to a small value. In brief, the SNR+ and SNR− measurements of the two distortions can serve as a valuable tool when analyzing individual algorithms in terms of identifying potential loss in intelligibility caused by spectral distortions.
Figure 10.
Plot of the SNR+ and SNR− values for the 8 enhancement algorithms used in the 5-dB SNR car noise condition [20]. SNR+ indicates the predicted loss in intelligibility due to spectral attenuation distortions, and SNR− indicates the predicted loss in intelligibility due to spectral amplification distortions. The unprocessed (corrupted) sentences are indicated as UN, and the enhancement algorithms include the KLT [40], pKLT [33], MSE [41], MSE2 [41], RDC [22], MB [42], WT [43] and Wie [34] algorithms.
C. Effect of window duration
Unlike the SII standard [4] which uses a 125-ms integration window, a 20-ms integration window was used in our present study for the implementation of the SNRLOSS measure. The study in [13] noted a positive influence of window duration on the performance of AI-based objective measures, in that a longer window produced higher correlation with intelligibility scores. The study in [36] revealed that an analysis window duration of 15–35 ms seems to be the optimum choice, in terms of intelligibility, when speech is reconstructed from its short-time magnitude spectrum. To examine the influence of window duration on the performance of the SNRLOSS measure, we varied the window duration from 4 ms to 125 ms. Results showed that the window duration did not seem to influence greatly the resulting correlation coefficients for either consonants or sentences.
D. Comparison with other objective measures
Table 6 compares the correlation obtained with the SNRLOSS, ESC and SNRLESC measures against the correlations obtained with other conventional objective measures including the PESQ measure [37]. The comparison additionally includes an AI-based measure (indicated as AI-ST) and an STI-based measure (indicated as NCM). These measures have been evaluated with the same data used in the present study and were previously reported in [13]. As can be seen, the proposed SNRLOSS measure performed better than the PESQ and AI-based measures on predicting sentence recognition, but did not perform as well as the STI-based measure (NCM). The PESQ measure was reported in [38] to produce higher correlations (r>0.9) than those shown in Table 6, however, it was only evaluated with binaurally-processed speech, and the evaluation did not include the many different variations of distortions that can be introduced by noise-suppression algorithms. Computationally, the proposed SNRLOSS measure offers the advantage that it can be computed on a frame-by-frame basis, whereas the PESQ and STI-based measures require first access to the whole signal prior to computing the measure.
Table 6.
Comparison of correlations with the proposed SNRLOSS, SNRLESC and ESC measures, against other conventional objective measures reported in Ma et al., 2009.
| Speech Material | Objective measure | r | σe |
|---|---|---|---|
| Consonants | SNRLOSS | −0.77 | 0.08 |
| SNRLESC | −0.73 | 0.08 | |
| SNRLESCμ–Mid | −0.73 | 0.08 | |
| ESC | 0.70 | 0.09 | |
| PESQ | 0.77 | 0.08 | |
| AI-ST(Ma et al., 2009) | 0.68 | 0.10 | |
| NCM (Ma et al., 2009) | 0.77 | 0.08 | |
| Sentences | SNRLOSS | −0.82 | 0.10 |
| SNRLESC | −0.82 | 0.10 | |
| SNRLESCMid | −0.85 | 0.09 | |
| ESC | 0.82 | 0.10 | |
| PESQ | 0.79 | 0.11 | |
| AI-ST(Ma et al., 2009) | 0.80 | 0.11 | |
| NCM (Ma et al., 2009) | 0.89 | 0.07 |
VII. SUMMARY AND CONCLUSIONS
The present study evaluated the performance of three new objective measures (SNRLOSS, ESC and SNRLESC) for predicting speech intelligibility in noisy conditions. The objective measures were tested in a total of 72 noisy conditions which included processed sentences and nonsense syllables corrupted by four real-world types of noise (car, babble, train, and street). The distinct contributions and conclusions of the present work include the following:
Unlike traditional intelligibility indices (e.g., SII and STI) the proposed objective measures operate on short-time intervals (20 ms) and can predict well the intelligibility of speech processed in fluctuating maskers (e.g., train, street noise) by noise-suppression algorithms. Consistently high correlations (|r|=0.84–0.88) scores were found across the four maskers tested (see Figures 7–9).
Of the three measures proposed, the SNRLESC measure yielded the highest overall correlation (r=−0.84) for predicting sentence recognition in noisy conditions. High correlation was maintained for all four maskers tested, and ranged from r=−0.84 obtained in car-noise conditions to r=−0.88 in street noise conditions. Further improvement in correlation was attained when including only mid-level energy frames (i.e., frames with RMS energy in the range of 0 to −10 dB relative to the overall RMS level) in the calculation of the SNRLESC measure. The resulting correlation improved to r=−0.85 (see Table 4).
Experiments with the SNRLOSS measure indicated that the spectral distortions introduced by noise-suppression algorithms do not contribute proportionally, within a 30 dB dynamic range, to the loss in speech intelligibility. Only spectral distortions falling within a 6 dB range (i.e., within [−3, 3] dB) were found to contribute the most to intelligibility loss, at least for the two input SNR levels (0 and 5 dB) tested in this study.
When limited within the [−3, 3] dB range, the spectral attenuation distortions were found to carry a larger perceptual weight compared to the spectral amplification distortions (see Table 5 and Figure 10). Equal weight, however, needs to be applied to the two spectral distortions (amplification and attenuation) for maximum correlation with the SNRLOSS measure (see Table 5).
Comparison of the correlations obtained with the proposed SNRLOSS measure against other conventional measures, revealed that the SNRLOSS measure yielded a higher correlation than the PESQ and AI-based measures with sentence recognition scores, but did not perform as well as the STI-based measure (NCM).
The squared spectral log difference measure (Eq. (10)), which is often used to assess speech distortion introduced by speech enhancement algorithms [27] or vector quantizers [25], yielded the lowest correlation (|r|=0.26–0.33) for both consonant and sentence recognition tasks. This result demonstrates the negative implications of lumping the amplification and attenuation distortions into one, as done when the difference between the clean and processed magnitude-spectra is squared. This outcome thus highlights the importance of isolating the two types of distortions introduced by enhancement algorithms, as done in the implementation of the SNRLOSS measure.
The decomposition of the SNR loss measure into the intelligibility loss introduced by spectral attenuation and spectral amplification distortions can serve as a valuable tool for analyzing the performance (in terms of intelligibility loss) of enhancement algorithms.
Table 1.
Band-importance functions [4] used in the implementation of the SNRLOSS and SNRLESC measures for consonants and sentence materials.
| Band | Center frequencies (Hz) | Consonants | Sentences |
|---|---|---|---|
| 1 | 50.0000 | 0.0000 | 0.0064 |
| 2 | 120.000 | 0.0000 | 0.0154 |
| 3 | 190.000 | 0.0092 | 0.0240 |
| 4 | 260.000 | 0.0245 | 0.0373 |
| 5 | 330.000 | 0.0354 | 0.0803 |
| 6 | 400.000 | 0.0398 | 0.0978 |
| 7 | 470.000 | 0.0414 | 0.0982 |
| 8 | 540.000 | 0.0427 | 0.0809 |
| 9 | 617.372 | 0.0447 | 0.0690 |
| 10 | 703.378 | 0.0472 | 0.0608 |
| 11 | 798.717 | 0.0473 | 0.0529 |
| 12 | 904.128 | 0.0472 | 0.0473 |
| 13 | 1020.38 | 0.0476 | 0.0440 |
| 14 | 1148.30 | 0.0511 | 0.0440 |
| 15 | 1288.72 | 0.0529 | 0.0470 |
| 16 | 1442.54 | 0.0551 | 0.0489 |
| 17 | 1610.70 | 0.0586 | 0.0486 |
| 18 | 1794.16 | 0.0657 | 0.0491 |
| 19 | 1993.93 | 0.0711 | 0.0492 |
| 20 | 2211.08 | 0.0746 | 0.0500 |
| 21 | 2446.71 | 0.0749 | 0.0538 |
| 22 | 2701.97 | 0.0717 | 0.0551 |
| 23 | 2978.04 | 0.0681 | 0.0545 |
| 24 | 3276.17 | 0.0668 | 0.0508 |
| 25 | 3597.63 | 0.0653 | 0.0449 |
APPENDIX A
In this Appendix we prove the relationship given in Eq. (14) between the signal-to-residual noise ratio (SNRES) and the excitation spectral correlation, r2(m).
First, we assume that the excitation spectra have zero mean, and that
| (17) |
where X̂(j,m) is the enhanced spectrum and R(j,m) denotes the residual excitation spectrum in the jth band. We further assume that X(j,m) and R(j,m) are uncorrelated, i.e., that E[X(j,m) · R(j,m)] = 0. After dropping the band and frame indices (j, m) for convenience, we compute the normalized correlation between X and X̂ as follows:
| (18) |
where denotes the variance of X and denotes the variance of X̂. Substituting Eq. (17) into the above equation, we get:
| (19) |
where is the signal-to-residual noise ratio. Solving for SNRES in the above equation, yields Eq. (14). Note that a similar equation was derived in [39], but based on the normalized correlation between the clean and noisy signals, rather than the clean and enhanced signals.
In practice, the excitation spectra X and X̂ have non-zero means, which we denote by μX and μX̂ respectively. Consequently, we have:
| (20) |
and the non normalized covariance between X and X̂ becomes:
| (21) |
After some algebraic manipulation and utilizing the following new definition of SNRES which accounts for the non-zero means:
| (22) |
we get:
| (23) |
where the terms C and D are given by:
| (24) |
| (25) |
It is clear from Eq. (24) and (25), that if μX = μX̂ = 0, then Eq. (23) reduces to Eq. (19). Solving for SNRE in Eq. (23), we get:
| (26) |
Footnotes
The term “SNR loss” also refers to the increased signal-to-noise ratio required by hearing-impaired listeners to understand speech in noise relative to that required by normal-hearing listeners [21]. In the present study, we use this term to indicate the SNR loss introduced by noise suppression algorithms rather than acoustic noise alone.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Jianfen Ma, Taiyuan University of Technology, Shanxi, 030024, China, and Department of Electrical Engineering, University of Texas at Dallas, Richardson, TX 75083.
Philipos C. Loizou, Department of Electrical Engineering, University of Texas at Dallas, Richardson, TX 75083-0688.
References
- 1.French NR, Steinberg JC. Factors governing the intelligibility of speech sounds. J Acoust Soc Am. 1947;19:90–119. [Google Scholar]
- 2.Fletcher H, Galt RH. the perception of speech and its relation to telephony. J Acoust Soc Am. 1950;22:89–151. [Google Scholar]
- 3.Kryter K. Methods for calculation and use of the articulation index. J Acoust Soc Am. 1962;34(11):1689–1697. [Google Scholar]
- 4.ANSI. Technical Report S3.5-1997. American National Standards Institute; 1997. Methods for calculation of the speech intelligibility index. [Google Scholar]
- 5.Steeneken H, Houtgast T. A physical method for measuring speech transmission quality. J Acoust Soc Am. 1980;67:318–326. doi: 10.1121/1.384464. [DOI] [PubMed] [Google Scholar]
- 6.Houtgast T, Steeneken H. A review of the MTF concept in room acoustics and its use for estimating speech intelligibility in auditoria. J Acoust Soc Am. 1985;77:1069–1077. [Google Scholar]
- 7.Kryter K. Validation of the articulation index. J Acoust Soc Am. 1962;34:1698–1706. [Google Scholar]
- 8.Pavlovic CV. Derivation of primary parameters and procedures for use in speech intelligibility predictions. J Acoust Soc Am. 1987;82:413–422. doi: 10.1121/1.395442. [DOI] [PubMed] [Google Scholar]
- 9.Allen JB. How do humans process and recognize speech. IEEE Trans Speech Audio Process. 1994;2:567–577. [Google Scholar]
- 10.Rhebergen K, Versfeld N. A speech intelligibility index based approach to predict the speech reception threshold for sentences in fluctuating noise for normal-hearing listeners. J Acoust Soc Am. 2005;117:2181–2192. doi: 10.1121/1.1861713. [DOI] [PubMed] [Google Scholar]
- 11.Rhebergen K, Versfeld N, Dreschler W. Extended speech intelligibility index for the prediction of the speech reception threshold in fluctuating noise. J Acoust Soc Am. 2006;120:3988–3997. doi: 10.1121/1.2358008. [DOI] [PubMed] [Google Scholar]
- 12.Kates J. The short-time articulation index. J Rehabil Res Dev. 1987;24:271–276. [PubMed] [Google Scholar]
- 13.Ma J, Hu Y, Loizou P. Objective measures for predicting speech intelligibility in noisy conditions based on new band-importance functions. J Acoust Soc Am. 2009;125(5):3387–3405. doi: 10.1121/1.3097493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kates J, Arehart K. Coherence and the speech intelligibility index. J Acoust Soc Am. 2005;117:2224–2237. doi: 10.1121/1.1862575. [DOI] [PubMed] [Google Scholar]
- 15.Kates J. On using coherence to measure distortion in hearing aids. J Acoust Soc Am. 1992;91:2236–2244. doi: 10.1121/1.403657. [DOI] [PubMed] [Google Scholar]
- 16.Berouti M, Schwartz M, Makhoul J. Enhancement of speech corrupted by acoustic noise. Proc. IEEE Int. Conf. Acoust., Speech, Signal Processing,; 1979. pp. 208–211. [Google Scholar]
- 17.Loizou P. Speech Enhancement: Theory and Practice. Boca Raton: Florida: CRC Press LLC; 2007. [Google Scholar]
- 18.Paajanen E, Ayad B, Mattila V. New objective measures for characterization of noise suppression algorithms. IEEE Speech Coding Workshop. 2000:23–25. [Google Scholar]
- 19.Mattila V. Objective measures for the characterization of the basic functioning of noise suppression algorithms. Proc. of online workshop on Measurement Speech and Audio Quality in Networks; 2003. [Google Scholar]
- 20.Hu Y, Loizou P. A comparative intelligibility study of single-microphone noise reduction algorithms. J Acoust Soc Am. 2007;22(3):1777–786. doi: 10.1121/1.2766778. [DOI] [PubMed] [Google Scholar]
- 21.Yoon Y-S, Allen J. SNR-loss with hearing impaired ears. Abstracts of Assoc Research Otolaryng. 2006 [Google Scholar]
- 22.Gustafsson H, Nordholm S, Claesson I. Spectral subtraction using reduced delay convolution and adaptive averaging. IEEE Trans on Speech and Audio Processing. 2001;9(8):799–807. [Google Scholar]
- 23.Greenberg J, Peterson P, Zurek P. Intelligibility-weighted measures of speech-to-interference ratio and speech system performance. J Acoust Soc Am. 1993;94(5):3009–3010. doi: 10.1121/1.407334. [DOI] [PubMed] [Google Scholar]
- 24.Spriet A, Moonen M, Wouters J. Robustness analysis of multichannel Wiener filtering and generalized sidelobe cancellation for multimicrophone noise reduction in hearing aid applications. IEEE Trans Speech Audio Process. 2005;13(4):487–503. [Google Scholar]
- 25.Paliwal K, Atal B. Efficient Vector Quantization of LPC Parameters at 24 Bits/Frame. IEEE Trans Speech Audio Proces. 1993;1(1):3–14. [Google Scholar]
- 26.Nein H, Lin C-T. Incorporating Error Shaping Technique into LSF Vector Quantization. IEEE Trans Speech Audio Proces. 2001;9(2):73–86. [Google Scholar]
- 27.Cohen I, Gannot S. Spectral enhancement methods. In: Benesty J, Sondhi M, Huang Y, editors. Handbook of Speech Processing. Berlin: Springer Verlag; 2008. pp. 873–901. [Google Scholar]
- 28.Chen J, Benesty J, Huang Y, Doclo S. New insights into the noise reduction Wiener filter. IEEE Trans on Speech and Audio Processing. 2006;14(4):1218–1234. [Google Scholar]
- 29.Benesty J, Chen J, Huang Y, Cohen I. Noise reduction in speech processing. Berlin Heidelberg: Springer Verlag; 2009. [Google Scholar]
- 30.Quackenbush S, Barnwell T, Clements M. Objective measures of speech quality. Englewood Cliffs, NJ: Prentice Hall; 1988. [Google Scholar]
- 31.IEEE Subcommittee. IEEE Recommended Practice for Speech Quality Measurements. IEEE Trans Audio and Electroacoustics. 1969;AU-17(3):225–246. [Google Scholar]
- 32.Hirsch H, Pearce D. The AURORA experimental framework for the performance evaluation of speech recognition systems under noisy conditions. Proc ISCA ITRW ASR200. 2000 [Google Scholar]
- 33.Jabloun F, Champagne B. Incorporating the human hearing properties in the signal subspace approach for speech enhancement. IEEE Trans Speech Audio Process. 2003;11:700–708. [Google Scholar]
- 34.Scalart P, Filho J. Speech enhancement based on a priori signal to noise estimation. Proc IEEE Int Conf Acoust, Speech, Signal Processing. 1996:629–632. [Google Scholar]
- 35.Ephraim Y, Malah D. Speech enhancement using a minimum mean-square error log-spectral amplitude estimator. IEEE Trans Acoust, Speech, Signal Process. 1985;ASSP-33(2):443–445. [Google Scholar]
- 36.Paliwal K, Wojcicki K. Effect of analysis window duration on speech intelligibility. IEEE Signal Proces Letters. 2008;15:785–789. [Google Scholar]
- 37.ITU. . Perceptual evaluation of speech quality (PESQ), and objective method for end-to-end speech quality assessment of narrowband telephone networks and speech codecs. ITU-T Recommendation P 862. 2000 [Google Scholar]
- 38.Beerends J, Larsen E, Lyer N, Van Vugt J. Measurement of speech intelligibility based on the PESQ approach. Proc of Workshop on Measurement of Speech and Audio Quality in Networks (MESAQIN) 2004 [Google Scholar]
- 39.Benesty J, Chen J, Huang Y. On the importance of the Pearson correlation coefficient in noise reduction. IEEE Trans Audio, Speech, Lang Process. 2008;16(4):757–765. [Google Scholar]
- 40.Hu Y, Loizou P. A generalized subspace approach for enhancing speech corrupted by colored noise. IEEE Trans on Speech and Audio Processing. 2003;11:334–341. [Google Scholar]
- 41.Ephraim Y, Malah D. Speech enhancement using a minimum mean-square error short-time spectral amplitude estimator. IEEE Trans Acoust, Speech, Signal Process. 1984 Dec;ASSP-32(6):1109–1121. [Google Scholar]
- 42.Kamath S, Loizou P. A multi-band spectral subtraction method for enhancing speech corrupted by colored noise. IEEE International Conference on Acoustics, Speech, and Signal Processing; Orlando, FL. 2002. [Google Scholar]
- 43.Hu Y, Loizou P. Speech enhancement based on wavelet thresholding the multitaper spectrum. IEEE Trans on Speech and Audio Processing. 2004;12(1):59–67. [Google Scholar]