An improved coarse-grained model of solvation and the hydrophobic effect

Abstract

We present a coarse-grained lattice model of solvation thermodynamics and the hydrophobic effect that implements the ideas of Lum–Chandler–Weeks theory [J. Phys. Chem. B 134, 4570 (1999)] and improves upon previous lattice models based on it. Through comparison with molecular simulation, we show that our model captures the length-scale and curvature dependence of solvation free energies with near-quantitative accuracy and 2–3 orders of magnitude less computational effort, and further, correctly describes the large but rare solvent fluctuations that are involved in dewetting, vapor tube formation, and hydrophobic assembly. Our model is intermediate in detail and complexity between implicit-solvent models and explicit-water simulations.

INTRODUCTION

This is a technical paper that addresses how the hydrophobic effect may be understood quantitatively. Despite its technical nature, the physical ideas and final model we formulate should be accessible and potentially interesting to a wide audience of researchers who are confronted with the many manifestations of the hydrophobic effect, and are in need of an effective quantitative tool for treating them.

The hydrophobic effect is presumed to be an important driving force in biology and nanoscale self-assembly.^{1, 2, 3} Because of its collective nature and its length-scale dependence,⁴ and because of its nonlocal dependence on solute surface moeities,^{5, 6, 7} modeling the hydrophobic effect remains a challenge. To treat it theoretically, one could track the explicit position of possibly tens of thousands of water molecules around solutes of interest,^{8, 9} but the computational cost of this approach limits its applications. Alternatively, at significantly reduced cost, one could replace explicit waters by an implicit solvent model, as is done in the generalized Born and surface area (GBSA) approach.^{10, 11} In this paper, building on previous efforts,^{12, 13, 14} we propose a coarse-grained model intermediate in detail between these two extremes, one that retains most of the computational advantage of implicit solvent models and overcomes two of their significant conceptual flaws: their incorrect scaling behavior and their neglect of rare but large solvent density fluctuations that play pivotal roles in the dynamics of assembly.

Solvation free energies^{15, 16} of solutes with sub-nanometer features, exactly the size prevalent in biological regimes, do not in general^{17, 18} scale as surface area.^{12, 19, 20, 21} By construction, models that assume such scaling significantly underestimate the driving force for hydrophobic assembly.^{4, 22} Our model, on the other hand, captures the correct scaling behavior with solute size for generic solute geometries.

Since hydrophobicity is a solvent property as much as it is a solute property, it is important to consider the solvent on length-scales dictated by the solute(s). Numerous studies of hydrophobicity^{4, 14, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33} have shown that rare solvent motions and dewetting transitions in confining environments play a critical role in solute assembly and function. Our model adequately captures these rare and important fluctuations. To demonstrate this, we consider the water number distribution P_V(N) in a probe volume V. Hummer et al. introduced the idea of characterizing this distribution in the context of solvation theory,³⁴ and the utility of this function has been demonstrated subsequently.^{33, 35, 36, 37}

The GBSA model,^{10, 11} widely used in biological settings, captures the effect of electrostatics with reasonable accuracy, but its treatment of the hydrophobic effect is less adequate,^{20, 38, 39, 40} for the reasons discussed above. Interesting examples of solutes for which hydrophobicity is essential, and for which GBSA is unsuitable, include large classes of proteins, such as those involved in transmembrane protein recognition and insertion,⁴¹ and versatile chaperones.⁴² It is these kinds of solutes for which our approach may eventually prove most useful.

The ideas behind our model are those of Lum-Chandler-Weeks (LCW) theory.¹² Ten Wolde et al.^{13, 14} generalized this theory by casting it in terms of a Hamiltonian for a lattice field theory. The motivation for that development was to facilitate treatments of large length-scale dynamics. The motivation of the current work is similar, though in this paper we confine our attention to time-independent properties. The main contribution of this paper is to improve upon these previous attempts, and to introduce concrete implementations of the underlying theory that illustrate the improvements, which are significant.

The paper is organized as follows. In Sec. 2, we sketch the physical ideas behind our model and present their implementation in a tractable format. The derivation and approximations made therein are left to the Appendix. In Sec. 3, we consider the accuracy of our model by computing the solvation free energies of solutes and P_V(N) distributions for various geometries, with and without adhesive solute-solvent interactions. Finally, in Sec. 4 we conclude with a discussion of the merits and limitations of the present implementation of the model.

MODEL

Density fields and Hamiltonian

In this section we first consider general features of a liquid solvent, specializing to water only later. We focus on the solvent density, ρ(r). For water in particular, ρ(r) refers to the instantaneous positions of water oxygen atoms. Effects of other variables such as molecular orientations appear implicitly in terms of parameters. We decompose density into large and small length-scale contributions ρ_ℓn(r) and δρ(r), respectively,

$$\rho \left(\mathbf{r}\right)={\rho }_{\ell }n\left(\mathbf{r}\right)+\delta \rho \left(\mathbf{r}\right).$$ (1)

Here, ρ_ℓ is the bulk liquid density, and n(r) is an Ising-like field that is 1 in regions that are locally liquidlike and 0 in regions that are locally vaporlike. The field takes on intermediate values only around interfacial regions. This large length-scale field describes extended liquid-vapor interfaces, while the small length-scale field describes more rapidly varying density fluctuations. This separation implies some form of space-time coarse-graining to define n(r), a coarse-graining which is most reasonable for dense fluids far from their critical points. The key development of LCW was to describe how to (a) perform this decomposition, and (b) couple the two separate fields.

Building on the work of ten Wolde et al.,¹³ we construct a Hamiltonian for the solvent density that captures the dominant physics. We have

$$\begin{array}{ccc}\hfill H\left[n\right(\mathbf{r}),\delta \rho (\mathbf{r}\left)\right]& =& H_{\mathrm{large}}\left[n\left(\mathbf{r}\right)\right]+H_{\mathrm{small}}[\delta \rho \left(\mathbf{r}\right);n\left(\mathbf{r}\right)]\hfill \\ \hfill & & +H_{\mathrm{int}}[n\left(\mathbf{r}\right),\delta \rho \left(\mathbf{r}\right)],\hfill \end{array}$$ (2)

where H_large[n(r)] captures the physics of interface formation in n(r). We estimate this contribution using a Landau–Ginzburg Hamiltonian

$$H_{\mathrm{large}}\left[n\left(\mathbf{r}\right)\right]={\int }_{\mathbf{r}}\left[w(n\left(\mathbf{r}\right),\mu )+\frac{m}{2}{\left|\nabla n\left(\mathbf{r}\right)\right|}^2\right],$$ (3)

where w(ρ∕ρ_ℓ, μ) is the grand free energy density for the liquid solvent at a given density, ρ, and chemical potential, μ, relative to that of the gas. The parameter m reflects surface tension and intrinsic interfacial width. For conciseness, we use an abbreviated integration notation, where the integration variable is denoted with a subscript to the integral sign, and the integration domain is all of space unless otherwise stated.

For the term H_small[δρ(r); n(r)], we exploit the observation that small length-scale density fluctuations in homogeneous liquids obey Gaussian statistics.^{34, 43, 44} Thus, for a given configuration of n(r), we assume that δρ(r) has Gaussian statistics with variance

$$\chi [\mathbf{r},{\mathbf{r}}^{\prime };n\left(\mathbf{r}\right)]={⟨\delta \rho \left(\mathbf{r}\right)\delta \rho \left({\mathbf{r}}^{\prime }\right)⟩}_{n\left(\mathbf{r}\right)}.$$

Here, the right-hand side denotes the thermal average of δρ(r)δρ(r′) under the constraint of fixed field n(r). The term H_small[δρ(r); n(r)] is then a Gaussian with this variance, namely,

$$\begin{array}{c}\hfill H_{\mathrm{small}}[\delta \rho \left(\mathbf{r}\right);n\left(\mathbf{r}\right)]=\frac{k_{\mathrm{B}}T}{2}{\int }_{\mathbf{r}}{\int }_{{\mathbf{r}}^{\prime }}\delta \rho \left(\mathbf{r}\right){\chi }^{-1}[\mathbf{r},{\mathbf{r}}^{\prime };n\left(\mathbf{r}\right)]\delta \rho \left({\mathbf{r}}^{\prime }\right),\end{array}$$ (4)

where k_BT is temperature, T, times Boltzmann’s constant. We approximate the variance with

$$\chi [\mathbf{r},{\mathbf{r}}^{\prime };n\left(\mathbf{r}\right)]\approx \left\{\begin{array}{cc}\hfill {\chi }_0(\mathbf{r}-{\mathbf{r}}^{\prime }),& \hfill n\left(\mathbf{r}\right)=n\left({\mathbf{r}}^{\prime }\right)=1,\\ \hfill 0,& \hfill \mathrm{otherwise},\end{array}\right.$$ (5)

where χ₀(r) can be written in terms of the radial distribution function g(r) as

$${\chi }_0\left(\mathbf{r}\right)={\rho }_{\ell }\delta \left(\mathbf{r}\right)+{\rho }_{\ell }^2\left[g\right(\left|\mathbf{r}\right|)-1].$$ (6)

For the uses we make of the approximation in Eq. 5, corrections have quantitative but not qualitative effects, as discussed in the Appendix and also Ref. 45.

In the absence of large solutes, fluctuations in n(r) are unlikely. The only fluctuations of significance in that case are those described by δρ(r). In the presence of large solutes, however, n(r) will often differ significantly from its bulk mean value. In that case the statistics of δρ(r) is modified and the coupling H_int[n(r), δρ(r)] between n(r) and δρ(r) becomes significant. As argued by Weeks and coworkers,^{12, 13, 46, 47, 48, 49, 50} this coupling arises from unbalanced attractive forces wherever n(r) is nonuniform, which results in solvent molecules experiencing an effective attraction toward denser regions, or equivalently, an effective repulsion from less dense regions. The repulsion is well-modeled by an effective interaction of the field δρ(r) with an external unbalancing potential, ϕ(r), given by

$$H_{\mathrm{int}}[n\left(\mathbf{r}\right),\delta \rho \left(\mathbf{r}\right)]={\int }_{\mathbf{r}}\phi \left(\mathbf{r}\right)\delta \rho \left(\mathbf{r}\right)+H_{\mathrm{norm}}\left[n\left(\mathbf{r}\right)\right],$$ (7)

where

$$\phi \left(\mathbf{r}\right)=-2a{\rho }_{\ell }[\overline{n\left(\mathbf{r}\right)}-1].$$ (8)

Here, a determines the strength of the potential, and the overbar operator smears n(r) over the effective range of solvent-solvent attractive interactions, as described in more detail in the Appendix. The potential is shifted so that it is zero for the uniform liquid. When δρ(r) is integrated out, a renormalized Hamiltonian for n(r) results. The term H_norm[n(r)] is chosen so that, in the absence of a solute, this renormalized Hamiltonian is identical to H_large[n(r)].

LCW theory¹² is a mean-field theory for the average large length-scale field, 〈n(r)〉, so it ignores the effects of large-scale fluctuations in n(r). Subsequent lattice implementations of LCW theory^{13, 14, 51} have incorporated fluctuations in the simplest possible manner. The present model refines these previous attempts to achieve near-quantitative accuracy for solvation free energies and correct behavior of fluctuations in n(r). Most importantly, we improve the calculation of the interfacial energies due to n(r).

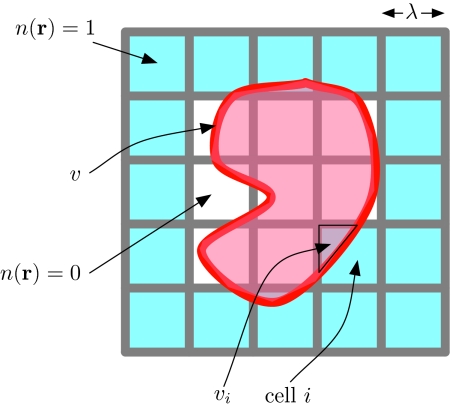
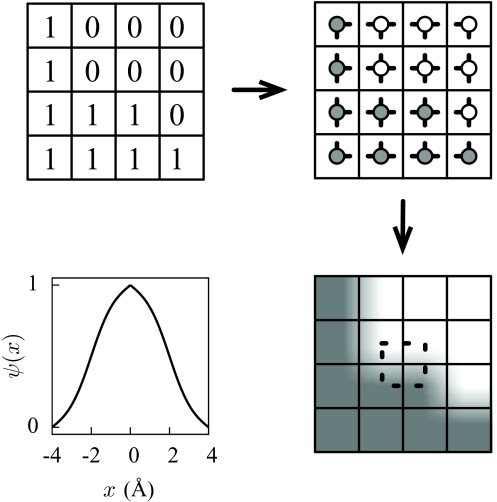
To write down the renormalized Hamiltonian that results from integrating out the field δρ(r), we begin by describing n(r) with reference to a cubic grid of spacing λ, depicted in Fig. 1, and we denote its value at the center of cell i by n_i. Then, n(r) is given by

$$n\left(\mathbf{r}\right)=\sum _i{n}_i\Psi (\mathbf{r}-{\mathbf{r}}_i),$$ (9)

where r_i is the center of cell i and n_i is 1 or 0, and the sum is over all cells i. The function Ψ(r) is maximal with value 1 at r = 0; it is cubic symmetric about the origin; and it is zero when the magnitude of any of the Cartesian components of r is greater than λ. The value of λ, about which we will say more later, should be roughly the size of the bulk correlation length of the liquid solvent. The typical size of interfacial energies between cells on this grid is γλ², where γ is the liquid-vapor surface tension of the solvent.

Figure 1.

Schematic showing the solute and the large length-scale density field on a grid.

With this particular representation for n(r), we proceed to evaluate the integral in H_large[n(r)]. At liquid-gas phase coexistence, μ = 0, the value of the integral is conveniently expressed as the sum γλ²∑_ih_i with the local integrals

$$\begin{array}{ccc}\hfill h_i& =& \frac{1}{\gamma {\lambda }^2}{\int }_{x_i}^{x_i+\lambda }\mathrm{d}x{\int }_{y_i}^{y_i+\lambda }\mathrm{d}y{\int }_{z_i}^{z_i+\lambda }\mathrm{d}z\hfill \\ & & \times \left[w(n(x,y,z),0)+\frac{m}{2}{\left|\nabla n(x,y,z)\right|}^2\right].\hfill \end{array}$$ (10)

The quantity h_i depends only on the values of n_j for cells j that share one of the corners of cell i. There are only 14 distinct possible values of h_i, which can be precalculated numerically for a given free energy density w(n, 0) and cell size λ, as detailed in the Appendix. In previous modeling, the simpler Ising model estimate γλ²∑_〈ij〉(n_i − n_j)² has been used, where the sum is over nearest-neighbor pairs of cells. For reasons discussed in the Appendix, this simpler estimate proves less accurate than the one used here.

The dissolved solute excludes solvent density from a volume v, and we define $\overline{v}$ to be its complement, so that the total volume of the system is the union of v and $\overline{v}$. The excluded volume can be of any shape, and it can be composed of disconnected parts. In Ref. 43, regions within v are called “in,” and regions within $\overline{v}$ are called “out.” For any volume V, we have the projector b_V(r),

$$b_V\left(\mathbf{r}\right)=\left\{\begin{array}{cc}\hfill 1,& \hfill \mathbf{r}\in V,\\ \hfill 0,& \hfill \text{otherwise},\end{array}\right.$$ (11)

so that $b_V\left(\mathbf{r}\right)+b_{\overline{V}}\left(\mathbf{r}\right)=1$. We denote the overlap of v or $\overline{v}$ with cell i by v_i or ${\overline{v}}_i$, respectively.

In the absence of a solute, the Gaussian nature of δρ(r) results in solvent number fluctuation correlations. The correlations between the portions of cells i and j that overlap with two volumes V and V′, respectively, form the elements of a matrix

$${\chi }_{ij}(V,V^{\prime })={\int }_{\mathbf{r}\in i}{\int }_{{\mathbf{r}}^{\prime }\in j}{b}_V\left(\mathbf{r}\right){\chi }_0(\mathbf{r},{\mathbf{r}}^{\prime })b_{V^{\prime }}\left({\mathbf{r}}^{\prime }\right).$$ (12)

Here, the domains of the r and r′ integrals are restricted to the volume of cells i and j, as indicated. A way to estimate these elements is outlined in the Appendix. The resulting matrix is used to calculate entropic effects due to solvent exclusion and the linear response of solvent density to external fields.

With the above notation, we now write the Hamiltonian for our model, which constitutes the main result of the paper,

$$\begin{array}{ccc}\hfill H_{\mathrm{eff}}\left[\left\{n_i\right\}\right]& =& \gamma {\lambda }^2\sum _i{h}_i-\mu {\rho }_{\ell }{\lambda }^3\sum _i{n}_i-K\sum _i{\phi }_i{\rho }_{\ell }{n}_i{v}_i\hfill \\ \hfill & & +k_{\mathrm{B}}T[{⟨N⟩}_v^2∕2{\sigma }_v+C∕2],\hfill \end{array}$$ (13a)

where

$$\begin{array}{c}\hfill {\phi }_i=2a{\rho }_{\ell }\left[1-\frac{1}{2}{n}_i-\frac{1}{12}{\sum _{j\left(\mathrm{nn}\mathit{i}\right)}}^{\prime }{n}_j\right],\end{array}$$ (13b)

$$\begin{array}{c}\hfill {⟨N⟩}_v={\rho }_{\ell }\sum _i{n}_i{v}_i,\end{array}$$ (13c)

$$\begin{array}{c}\hfill {\sigma }_v=\sum _{i,j}{n}_i{\chi }_{ij}(v,v)n_j,\end{array}$$ (13d)

$$\begin{array}{c}\hfill C=\left\{\begin{array}{cc}\hfill \ln \left(2\pi {\sigma }_v\right),& \hfill {⟨N⟩}_v>1,\\ \hfill \max [\ln \left(2\pi {\sigma }_v\right),{⟨N⟩}_v],& \hfill \mathrm{otherwise}.\end{array}\right.\end{array}$$ (13e)

The primed sum over j(nni) is a sum over the six cells j that are nearest neighbors to cell i. The final expression for ϕ_i shown above, with renormalization constant K, is the result of an accurate and computationally convenient approximation to the coupling arising from H_int[n(r), δρ(r)], which is described in detail in the Appendix.

The terms on the right-hand side of Eq. 13a, respectively, approximate: the free-energy cost of establishing interfaces in n(r), the pressure-induced bias toward the liquid phase, the effective coupling between n(r) and δρ(r) induced by the presence of a solute, and the entropic cost of setting ρ_ℓn(r) + δρ(r) to zero whenever r is in v and n(r) is 1. As the total number of waters to be excluded, 〈N〉_v, approaches zero, the statistics of solvent number fluctuations in v changes from Gaussian to Poisson, so that its variance, σ_v, also approaches zero. Equation 13e captures this change continuously and prevents H_eff[{n_i}] from becoming infinitely negative in this limit.

Incorporating solute-solvent attractions

The above Hamiltonian pertains to the simplest case, where the solute interacts with the solvent only by hard-core repulsion. Realistic solutes additionally have attractive interactions with the solvent that can be modeled as an external potential u(r) that couples to ρ(r). Such a potential induces an additional term in our Hamiltonian, which we denote by H_u[{n_i}]. To describe this term, we define a discretized analogue u_i of u(r),

$$u_i=\frac{1}{{\overline{v}}_i}{\int }_{\mathbf{r}\in i}{b}_{\overline{v}}\left(\mathbf{r}\right)u\left(\mathbf{r}\right).$$ (14)

Notice that u_i is independent of u(r) for values of r in v_i. The apparent divergence, where v completely overlaps cell i, has no effect in the final expression. In particular,

$$\begin{array}{ccc}\hfill H_u\left[\left\{n_i\right\}\right]& =& \sum _i{u}_i{n}_i[{\rho }_{\ell }{\overline{v}}_i-\sum _j{\chi }_{ij}(\overline{v},v)n_j{⟨N⟩}_v∕{\sigma }_v\hfill \\ & & -\sum _j{\chi }_{ij}(\overline{v},\overline{v})n_j\beta (u_j+{\phi }_j)]\hfill \\ & & +\frac{k_{\mathrm{B}}T}{2}\sum _{i,j}\beta u_i{n}_i{\chi }_{ij}(\overline{v},\overline{v})n_j\beta u_j,\hfill \end{array}$$ (15)

where β is the reciprocal of k_BT. The first part is the mean-field contribution ∫_ru(r)〈ρ(r)〉, while the last term is the entropic cost of the external potential modifying the average solvent density in the vicinity of the solute.

Parameters of the Hamiltonian

We now specialize our model to water at ambient conditions, T = 298 K and 1 atm pressure, p. Further, we comment upon what changes are required for applications at different states of water.

The cell size length λ should be no smaller than the intrinsic width of the liquid-vapor interface. Based upon the interfacial profile of the SPC∕E model,^{19, 52} we therefore pick λ = 4 Å. This is the minimal scale over which the time-averaged solvent density can transition from liquidlike to vaporlike values. Following Ref. 53, we use the free-energy density

$$w(n,\mu )=\frac{2m}{d^2}{(n-1)}^2{n}^2-\mu {\rho }_{\ell }n,$$ (16)

with d = 1.27 Å because this choice reproduces the sigmoidal density profile of water-vapor interfaces at coexistence. The resulting values of h_i are tabulated in the Appendix. The bulk liquid density ρ_ℓ is the experimental value,⁵⁴ whereby a liquid cell contains ρ_ℓλ³ ≈ 2.13 waters on average. The value of m is chosen such that the interfacial energy of vapor spheres of radius R tends to 4πγR² for large R. At ambient conditions, the experimental value for the surface tension⁵⁴ yields γλ² ≈ 2.80 k_BT. Finally, the relative chemical potential is given by μ ≈ (p − p_vap)∕ρ_ℓ, where p_vap is the vapor pressure at 298 K. This relationship gives μ ≈ 7.16 × 10⁻⁴ k_BT, which is quite small, reflecting that water at ambient conditions is nearly at coexistence with its vapor.

The matrix elements χ_ij(V, V′) are computed from the radial distribution function, g(r), and we derive this function from Narten and Levy’s tabulated data.⁵⁵ It is a convenient data set because it covers a broad range of temperatures for the liquid at and near p = 1 atm. At one temperature, 25°C, we have checked that a different estimate of the radial distribution function, that of the SPC∕E model, yields similar matrix elements, and the resulting solvation properties are essentially identical to those obtained when the χ_ij(V, V′)’s are computed from the Narten–Levy data at the same temperature.

The only parameters that we estimate through fitting are the strength a of the unbalancing potential and the renormalization constant K. In the absence of solute-solvent attractions, only the product of a and K is relevant. Values of a and K with Kaρ_ℓ = 2.1 k_BT allow us to match the solvation free energies of hard spheres in SPC∕E water (see below). By comparing the average value of the computationally convenient approximate expression involving ϕ_i in Eq. 13a with that of its complete and unrenormalized counterpart, as is done in the Appendix, we find that K is about 1∕2, so that aρ_ℓ ≈ 4.2 k_BT. This value for a is close to the original LCW estimate,¹² arrived at from a different criterion.

These values are applicable at ambient conditions. As temperature and pressure vary, only γ, μ, and g(r) vary appreciably, while K varies slightly. In particular, surface tension decreases roughly linearly with temperature⁵⁴ (with dγ∕dT ≈ −0.15 mJ∕m² K, or alternately, βλ²dγ∕dT is −5.8 × 10⁻³∕K at T = 298 K). As noted above, μ increases roughly linearly with pressure. The pair correlation function g(r) loses some structure for temperatures above 50°C. The terms that are modeled by the renormalization constant K reflect the degree to which solvent density layers next to a solute. Since this layering reflects the structure of g(r), we expect K to be slightly state-dependent, with its value increasing with temperature.

Conversely, liquid water has a nearly constant density and bulk correlation length at the temperatures and pressures where our model would be useful, so ρ_ℓ and λ can be taken as constant as well. Theoretical estimates for a in simple liquids [Eq. (4) in Ref. 46] are state-independent, so we expect that in water, a will be nearly state-independent as well.⁵⁶

APPLICATIONS AND RESULTS

Solvation free energies

To test our model’s ability to capture the length-scale dependence of solvation, and to parameterize the strength of the unbalancing potential, we have calculated the solvation free energy of hard spheres of different radii. Whether within our model or using explicit water simulations, we calculate the solvation free energy of a solute following the guidelines of Ref. 57. Briefly, we first define a series of M + 1 solutes S₀ through S_M that slowly interpolate from an empty system (S₀) to the final solute of interest (S_M). We then sequentially calculate the free energy difference between solute m and solute m + 1 using the Bennett acceptance ratio estimator⁵⁸ (BAR), and, where necessary, the linear interpolation stratification procedure of Ref. 57. Error estimates are calculated using BAR, and are generally smaller than 0.5%.

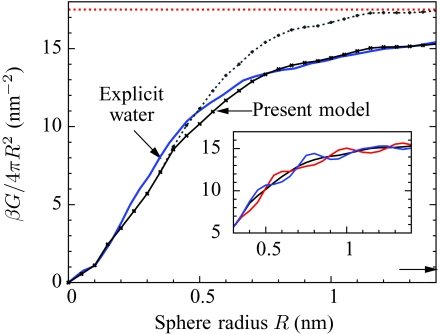
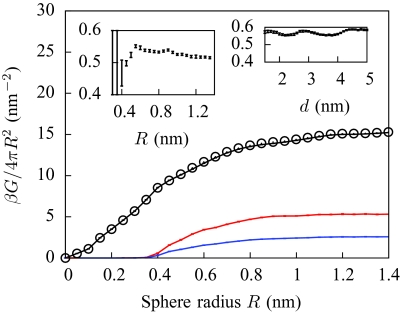
Our model (Eq. 13a) involves only simple arithmetic, so free energies can be calculated with little computational effort. For example, calculating the solvation free energy of hard spheres of up to 14 Å in radius in increments of 0.5 Å (Fig. 2) takes about 1 hour on a single 2 GHz machine with a code that has not been fully optimized, whereas a similar calculation in explicit SPC∕E waters with GROMACS (Ref. ⁵⁹) would take around 600 hours on the same machine to obtain a similar statistical accuracy.

Figure 2.

Solvation free energies G of hard spheres of increasing radii, as calculated from explicit SPC∕E water simulations (Ref. ¹⁹) (solid blue), from the coarse-grained model (solid black), and from one of the most common variants of GBSA (Ref. ⁶¹) (arrow at bottom right). Different parameterizations of GBSA yield nonpolar solvation energies that may differ by as much as a factor of ten, reflecting the crudeness of the SA portion of the model (Ref. ⁶¹). When the coarse-grained model has no unbalancing potential (a = 0, dashed gray), the intermediate-size regime is only qualitatively reproduced. For large spheres, the ratio of G to surface area tends to the liquid-vapor surface tension γ (horizontal red dots). Inset: illustration of lattice artifacts. The spheres are centered at different offsets from the lattice: a generic position (0.98, 0.79, 1.89 Å) that breaks all rotational and mirror symmetries (black), a lattice cell corner (blue), and a lattice cell center (red). All three curves are identical for R ⩽ 0.35 nm.

Hard-sphere solvation free energies scale as solute volume for small spheres, and as surface area for large spheres, with a smooth crossover at intermediate sizes.⁴ Figure 2 illustrates this behavior and compares the results of our model to previous simulation results using SPC∕E water.¹⁹ As the model manifestly reproduces the small and large length-scale limits, the most significant feature illustrated in Fig. 2 is the gradual crossover from volume to surface area scaling. Ignoring the unbalancing potential leads to a qualitatively correct scaling behavior. However, adjustment of the single parameter a, which determines the strength of the unbalancing potential, yields a near-exact agreement between our model and the SPC∕E results for all sphere sizes. In all subsequent results, the parameter a is fixed at this value.

The model results have small lattice artifacts—results that depend upon the position of the solute relative to that of the coarse-grained lattice—as shown in the inset of Fig. 2. When studying stationary solutes, lattice artifacts may be mitigated by performing multiple calculations, differing only by small displacements of the solutes, and then averaging the results. When studying dynamical phenomena, lattice artifacts tend to pin solutes into alignment with the coarse-grained lattice. For arbitrary molecular solutes, we expect that pinning forces acting on one portion of the molecule will generically oppose pinning forces on other parts of the molecule, so that the total pinning forces will largely cancel out. However, when treating many identical molecules, lattice artifacts can add constructively, and additional steps are needed to mitigate them.⁶⁰

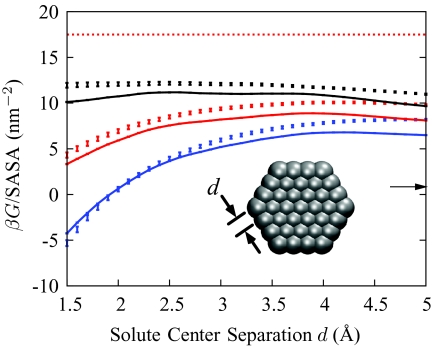
Since the unbalancing potential is explicitly parameterized with the solvation free energy of hard spheres, it is useful to evaluate the accuracy of the results in other geometries. To this effect we computed the solvation free energies of a family of hexagonal plates, consisting of 37 methanelike oily sites arranged into three concentric rings. We control the size of these plates, depicted in Fig. 3, by varying the distance d between neighboring oily sites. For our calculations with explicit SPC∕E water, the sites are uncharged and interact with the solvent molecules via a standard^{63, 64} water-CH₂ Lennard-Jones potential. To study the role of attractive interactions, we split this Lennard-Jones potential using the Weeks–Chandler–Andersen (WCA) prescription⁶⁵ into a repulsive part u₀(r) and an attractive part Δu(r). The magnitude of the attractive tail can be varied systematically with a scaling parameter η, such that

$$u_{\eta }\left(r\right)=u_0\left(r\right)+\eta \Delta u\left(r\right).$$ (17)

For the ideal hydrophobic plate, we set η to zero.

Figure 3.

Solvation free energies G of hexagonal plates, as a function of plate size, as calculated by the coarse-grained model (solid lines), by explicit SPC∕E water simulations (points), and by the same GBSA variant as in Fig. 2 (arrow on right). Three values of the attractive interaction strength η are shown: 0.0 (black), 0.5 (red), and 1.0 (blue). Solvent-accessible surface areas (SASAs) were calculated using VMD (Ref. ⁶²) with a particle radius of 1.97 Å, a solvent radius of 1.4 Å, and 1 000 000 samples per atom. The bulk liquid-vapor surface tension of water (horizontal red dots) is shown. Inset: detail of the hexagonal plate. The solvent-excluded volume of each oily site is a sphere of radius R₀ = 3.37 Å.

In the coarse-grained model, the repulsive core of the solute is represented as an excluded volume. To construct it, we replace each solute particle by a thermally equivalent hard sphere, whose radius R₀ is estimated according to

$$R_0={\int }_0^{\infty }\mathrm{d}r[1-\exp (-\beta u_0\left(r\right))],$$

which is a first approximation to the WCA value of this radius,^{66, 67} and is essentially the radius at which u₀(r) is k_BT. The excluded volume is then the union of the hard-sphere volumes of each solute site.

Figure 3 compares the solvation free energies for this family of solute plates computed from our atomistic simulations with those computed from the coarse-grained model with the unbalancing parameter a determined above for solvated hard spheres. Now, with this different geometry, the coarse-grained model continues to perform well. The discrepancies are primarily due to the small underestimation, shown in Fig. 2, of the solvation free energy of small spheres. Figure 3 also compares the solvation free energies of plates with increasing attractions to the corresponding results from explicit-water simulations.

Fluctuations

A more detailed probe of solvent behavior than solvation free energies is the probability P_V(N) of finding N waters in a given volume V. The solvation free energy G of an ideal, volume-excluding hydrophobe is simply³⁴ βG = −ln P_V(0), and we can glean information about hydrophobicity and dewetting from the behavior at nonzero N.

In the present model, we estimate P_V(N) by a two-step procedure. For any given solvent configuration {n_i}, the small length-scale fluctuations of δρ(r) give rise to a Gaussian distribution in the number of waters, so that

$$P_V\left(N\right|\left\{n_i\right\})\propto \exp \left[-{(N-{⟨N⟩}_V)}^2∕2{\sigma }_V\right],$$ (18)

where

$${\sigma }_V=\sum _{ij}{n}_i{\chi }_{ij}(V,V)n_j,$$ (19)

and the mean number of solvent particles in the volume V, 〈N〉_V, is computed from Gaussian statistics subject to the constraint that no solvent exists in the excluded volume v. That computation⁴³ gives

$$\begin{array}{ccc}\hfill {⟨N⟩}_V& =& \sum _i{n}_i[{\rho }_{\ell }{V}_i-\sum _j{\chi }_{ij}(V,v)n_j{⟨N⟩}_v∕{\sigma }_v\hfill \\ & & -\sum _j{\chi }_{ij}(V,\overline{v})n_j\beta (u_j+{\phi }_j)].\hfill \end{array}$$ (20)

Here, V_i is the overlap of the probe volume with cell i. Notice the use of the probe volume V in the χ_ij matrices. Formally, we then thermally average the above result over all possible solvent configurations to obtain

$$P_V\left(N\right)\propto \sum _{\left\{n_i\right\}}{P}_V\left(N\right|\left\{n_i\right\})\exp (-\beta H_{\mathrm{eff}}\left[\left\{n_i\right\}\right]).$$

In practice, we estimate this sum by sampling a lattice variable n that closely correlates with N, given by

$$n=\sum _{i\in V}{n}_i.$$

We divide the range of possible values of n into small overlapping windows, and sample relevant configurations at every value of n using Wang–Landau sampling⁶⁸ along n, together with replica exchange,⁶⁹ to obtain good sampling and avoid kinetic traps. We then used the multistate Bennet acceptance ratio estimator⁷⁰ (MBAR) to reconstruct from these runs the probability distribution P(n). During the umbrella sampling runs, lattice configurations with equal n are observed in proportion to their Boltzmann weight. Using the notation {n_i} ∈ n to denote all observed lattice gas configurations with a particular value of n, we finally obtain

$$P_V\left(N\right)=\sum _{n}P\left(n\right)\sum _{\left\{n_i\right\}\in n}{P}_V\left(N\right|\left\{n_i\right\}).$$

To estimate the statistical errors in our procedure, we calculate P_V(N) in five independent Monte Carlo runs, and estimate the standard error in the mean of ln P_V(N).

For comparison, we also calculate these distributions in SPC∕E water using LAMMPS (Ref. ⁷¹) as described previously,³³ paying careful attention to good sampling around free energy barriers. Errors were estimated with MBAR.

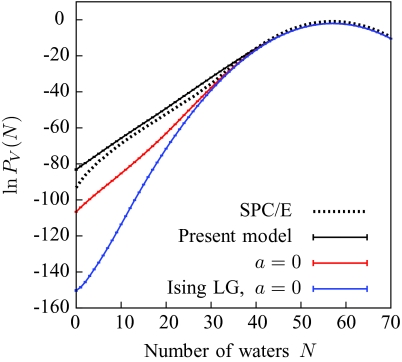
In the absence of a solute, P_V(N) is sensitive only to the interfacial energetics of the lattice gas. Figure 4 compares the P_V(N) curve obtained using the present model for a 12 × 12 × 12 ų volume with results that we have previously obtained from simulation of SPC∕E water,³³ and with (a) a version of the coarse-grained model that lacks an unbalancing potential (a is set to zero), and (b) a version that additionally uses the naive Ising lattice gas for estimating interfacial energetics in n(r). Our present model captures the observed deviations from Gaussian behavior better than these simpler models, which reflects its higher accuracy in estimating interfacial energetics and microscopic curvature effects.

Figure 4.

Water number distribution in a 12 × 12 × 12 ų cube, as obtained using explicit SPC∕E water simulations (Ref. ³³), the present model, the present model without the unbalancing potential (a = 0), and a model with an Ising lattice gas and no unbalancing potential.

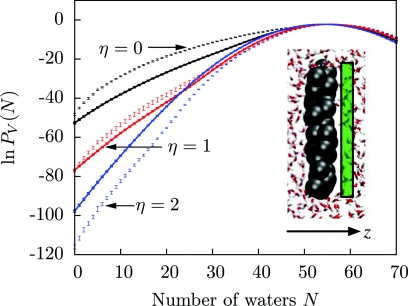
We have also previously examined how hydrophobic solutes affect water number fluctuations in nearby probe volumes.³³ To evaluate the performance of our model in that scenario, we use the model hydrophobic plate solute described in Ref. 33. The plate is made up of oily particles with the same number density as water, whose centers lie inside a 24 × 24 × 3 ų volume.⁷² Taking into account the van der Waals radii of the oily particles, the plate has approximate dimensions 28 × 28 × 7 ų. We model this solute in the same way as the hexagonal plates described above. As before, we explore the role of attractive interactions by varying the attraction strength parameter η.

Figure 5 shows the water number distribution in a 24 × 24 × 3 ų probe volume adjacent to the plate. With no solute-solvent attractive interactions, the probability computed from the lattice model has a clear fat tail toward lower numbers of waters in the probe volume. This fat tail is the hallmark of a soft vapor-liquid interface, in this case a soft interface next to the hydrophobic solute.^{73, 74, 75, 76} At higher attractive interactions, this fat tail is correspondingly depressed, but not entirely suppressed. Accordingly, in Ref. 33, the fat tail is only fully suppressed when η exceeds 3.0.

Figure 5.

Water number distributions in a probe volume of size 24 × 24 × 3 Å³ immediately adjacent to a model plate solute (inset) of varying attractive strength η, in the coarse-grained model (solid lines) and in explicit SPC∕E water (points). Defining z = 0 to be the plane passing through the plate center, points in the probe volume (green) satisfy 5 Å < z < 8 Å, so that a water molecule touching the plate is located at the edge of the probe volume (Ref. ³³).

Figure 5 also evidences some of the limitations of the present model. The probe volume being less than one lattice cell thick, large lattice artifacts are inevitable. Moreover, since P_V(N) distributions are much more detailed probes of solvent structure than solvation free energies, we expect more room for disagreement with simulation. Nevertheless, we emphasize that, by construction, no implicit solvation models can capture the above effects on solvent structure, which underlie the pathways of hydrophobic assembly. Other coarse-grained solvation models (for example, see Ref. 77), on the other hand, can probe rare solvent fluctuations, and it would be useful to evaluate their accuracy in this respect as compared to explicit-water models and the present lattice model.

Confinement

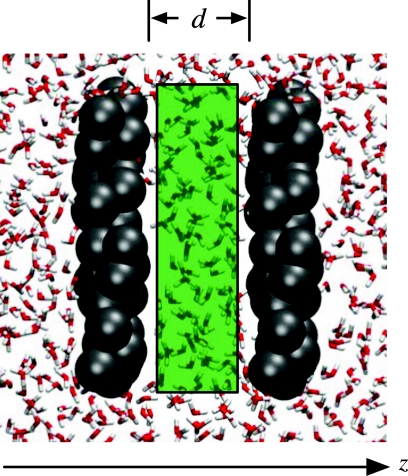
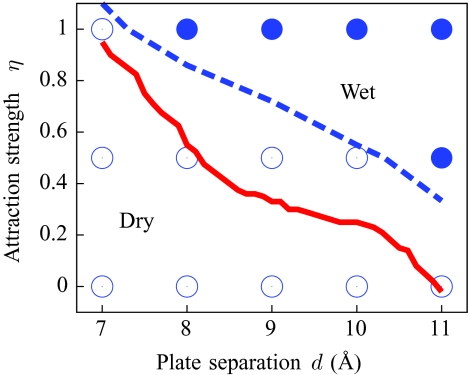
To examine confinement in detail, we place two of the model hydrophobic plates at a distance d from each other, as shown in Fig. 6, and calculate the water number distribution in a 24 × 24 × (d − 3) ų probe volume between them as a function of interplate separation d and attraction strength η. Figure 7 summarizes the results in the form of a phase diagram. At small separations and low attractive strengths, the dry state (low N) is most stable, whereas high attractive strengths and large separations stabilize the wet state (high N). Generically, the hydrophobic association of two such plates proceeds through a dewetting transition in the interplate volume.^{23, 24, 25, 27}

Figure 6.

Setup for examining water fluctuations under confinement (here, d = 8 Å). The model hydrophobic plates (Ref. ³³) (gray particles) are placed d Å apart: taking into account the van der Waals radii of about 2 Å of the plates’ oily particles and the 3 Å thickness of each plate, the center of the first plate is placed at z = 0, the center of the second plate is placed at z = d + 7 Å. The van der Waals radius of water (red and white sticks) being about 1.5 Å, the 24 × 24 × (d − 3) ų probe volume (green) extends from z = 5 Å to z = d + 2 Å. The plates are not perfectly flat, so some waters fit between the plates and the probe volume.

Figure 7.

Phase diagram for the interplate region of the system depicted in Fig. 6. For the explicit SPC∕E water simulations (blue), each symbol corresponds to an individual P_V(N) distribution that we have calculated (filled: wet state stable; open: dry state stable). The phase boundary (blue dashes) is estimated from a linear interpolation of the relative stability of the wet and dry states. The relative stability is determined from the relative depths of the basins in −ln P_V(N). The phase boundary for the present model (red solid line) was estimated from a dense sampling of P_V(N) distributions, and is accurate to ±0.1 Å in d and ±0.1 in η.

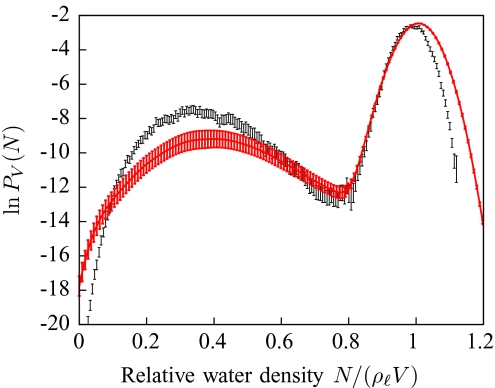
The general, though not quantitative, agreement between the coarse-grained model and the SPC∕E data is very encouraging: bistability is observed in the P_V(N) distributions in both cases, with the barriers at the nearly equal values of N, and with barrier heights that track the SPC∕E barrier heights. The phase boundary in Fig. 7 closely tracks the phase boundary observed in explicit water, with a shift of less than 2 Å for all η. Moreover, as shown in Fig. 8, once the general shift in the phase boundaries is accounted for, the P_V(N) distributions for systems near that boundary obtained by the coarse-grained model and the SPC∕E simulations agree reasonably well. Hence, the present model is better suited than implicit solvation models for studies of nanoscale self-assembly or protein–protein interactions driven by the hydrophobic effect. A recently developed coarse-grained model of water (mW water) has been used to extensively probe these rare fluctuations, and their predictions also display the characteristic bistability of dewetting transitions that we observe.^{37, 78}

Figure 8.

Water density distribution of confined water 1 Å from coexistence. These distributions are for the system depicted in Fig. 6 when η = 0.5. Coexistence lines are shown in Fig. 7. The explicit water simulation data (black) correspond to d = 11 Å, while the coarse-grained model (red) results correspond to d = 9 Å. The remaining P_V(N) distributions are included in the Supplementary Data (Ref. ⁷²).

DISCUSSION

We have presented a coarse-grained model of solvation thermodynamics that correctly reproduces the length-scale dependence of solvation free energies, and, moreover, correctly captures the behavior of the slow and rare solvent fluctuations that are pivotal in pathways to hydrophobic assembly. Our model is applicable to generic solute shapes, and addresses the effects of solute-solvent attractive interactions.

While our model successfully describes various aspects of the hydrophobic effect, some technical challenges remain to be addressed before it can be applied in biological settings. Most notably, electrostatic forces are missing from our model. Dzubiella et al.⁷⁹ have highlighted the importance of coupling hydrophobic solvation and electrostatics. They have proposed a way of modeling this coupling in mean field. Marchi and coworkers⁸⁰ have proposed, based upon the bilinear Marcus–Felderhof free energy functional,^{81, 82} an alternate method for including polarization fluctuations, an approach closely related to the Gaussian field model of Song et al.^{83, 84} Any one of these approaches, or even the simpler GB method, would suitably augment our model of hydrophobic interactions. Electrostatics would be coupled to hydrophobic solvation by defining the low-permittivity cavity to include both the solute’s excluded volume and the regions where n(r) is zero.

A second notable technical hurdle is to find efficient algorithms for calculating the gradient of H_eff[{n_i}] with respect to the position of the solute’s atomic centers, necessary for implementing realistic solute dynamics, such as Brownian dynamics. In the context of solvent lattice models, the problem is tractable for spherical solutes with limited overlap,^{14, 51} but the implementation of a solution for generic solutes is more challenging.

Finally, as with implicit solvation models, our own model does not attempt to capture solvent dynamics. For thermodynamically driven processes, almost any reasonable dynamics may suffice when estimating the kinetic prefactor of rate constants of interest. Indeed, in a previous lattice model,¹⁴ the solvent’s dynamics is approximated by Glauber dynamics, the solute’s by Langevin dynamics, and the relative rates at which the two dynamics are advanced are calibrated through physical arguments. However, it is known, as evidenced in the form of the Oseen tensor, that hydrodynamic interactions can be long-ranged⁸⁵ and can influence timescales of molecular processes by an order of magnitude or more.⁸⁶ This observation may prove important in nanoscale assembly processes that are kinetically driven, rather than thermodynamically driven.⁸⁷ Approaches to implementing coarse-grained dynamics in a lattice setting include multiparticle collision dynamics,⁸⁸ fluctuating hydrodynamics,⁸⁹ and lattice Boltzmann methods,⁹⁰ among others. We leave all dynamical considerations to future work.

APPENDIX A: DERIVATION OF THE MODEL

Continuum formulation

In this appendix, we derive Eq. 13 starting from the microscopic ideas of LCW theory embodied in Eq. 2. Here, we integrate out the field δρ(r) to obtain the effective Hamiltonian H_eff[n(r)]. In Appendix A2, we discretize the result.

For notational simplicity, we suppress the dependence of χ(r, r′) on n(r) manifest in Eq. 5. The total density ρ_ℓn(r) + δρ(r) is constrained to be zero for all points r in v, so the effective Hamiltonian is given by

$$\begin{array}{ccc}\hfill \exp \{-\beta H_{\mathrm{eff}}\left[n\left(\mathbf{r}\right)\right]\}& =& \int \mathcal{D}\delta \rho \left(\mathbf{r}\right)\exp \{-\beta H[n\left(\mathbf{r}\right),\delta \rho \left(\mathbf{r}\right)\left]\right\}\hfill \\ & & \times \prod _{\mathbf{r}\in v}\delta ({\rho }_{\ell }n\left(\mathbf{r}\right)+\delta \rho \left(\mathbf{r}\right)).\hfill \end{array}$$ (A1)

A long but straightforward calculation⁴³ yields

$$\begin{array}{ccc}\hfill H_{\mathrm{eff}}\left[n\left(\mathbf{r}\right)\right]& =& H_{\mathrm{large}}\left[n\left(\mathbf{r}\right)\right]+k_{\mathrm{B}}T\ln \sqrt{\det 2\pi {\chi }_v}\hfill \\ \hfill & & -{\int }_{\mathbf{r}\in v}\phi \left(\mathbf{r}\right){\rho }_{\ell }n\left(\mathbf{r}\right)+\frac{k_{\mathrm{B}}T}{2}{\int }_{\mathbf{r}\in v}{\int }_{{\mathbf{r}}^{\prime }\in v}\hfill \\ \hfill & & \times \left[{\rho }_{\ell }n\left(\mathbf{r}\right)-{\int }_{{\mathbf{r}}^{\prime \prime }\in \overline{v}}\chi (\mathbf{r},{\mathbf{r}}^{\prime \prime })\beta \phi \left({\mathbf{r}}^{\prime \prime }\right)\right]{\chi }_v^{-1}(\mathbf{r},{\mathbf{r}}^{\prime })\hfill \\ \hfill & & \times \left[{\rho }_{\ell }n\left({\mathbf{r}}^{\prime }\right)-{\int }_{{\mathbf{r}}^{\prime \prime \prime }\in \overline{v}}\chi ({\mathbf{r}}^{\prime },{\mathbf{r}}^{\prime \prime \prime })\beta \phi \left({\mathbf{r}}^{\prime \prime \prime }\right)\right]\hfill \\ \hfill & & -\frac{k_{\mathrm{B}}T}{2}{\int }_{\mathbf{r}\in \overline{v}}{\int }_{{\mathbf{r}}^{\prime }\in \overline{v}}\beta \phi \left(\mathbf{r}\right)\chi (\mathbf{r},{\mathbf{r}}^{\prime })\beta \phi \left({\mathbf{r}}^{\prime }\right)\hfill \\ \hfill & & +H_{\mathrm{norm}}\left[n\left(\mathbf{r}\right)\right].\hfill \end{array}$$ (A2)

Here, χ_v(r, r′) is the restriction of χ(r, r′) to the volume v. As such, ${\chi }_v^{-1}(\mathbf{r},{\mathbf{r}}^{\prime })$ satisfies

$${\int }_{{\mathbf{r}}^{\prime }\in v}{\chi }_v^{-1}(\mathbf{r},{\mathbf{r}}^{\prime })\chi ({\mathbf{r}}^{\prime },{\mathbf{r}}^{\prime \prime })=\delta (\mathbf{r}-{\mathbf{r}}^{\prime \prime }),\mathbf{r},{\mathbf{r}}^{\prime \prime }\in v.$$ (A3)

To make H_eff[n(r)] equal to H_large[n(r)] in the absence of a solute,

$$H_{\mathrm{norm}}\left[n\left(\mathbf{r}\right)\right]=\frac{k_{\mathrm{B}}T}{2}{\int }_{\mathbf{r}}{\int }_{{\mathbf{r}}^{\prime }}\beta \phi \left(\mathbf{r}\right)\chi (\mathbf{r},{\mathbf{r}}^{\prime })\beta \phi \left({\mathbf{r}}^{\prime }\right).$$ (A4)

It is useful to recast Eq. A2 into a form where the physical significance of each term is manifest. To do so, we first note how the constraint of zero solvent density inside v modifies the solvent density and its fluctuation spectrum outside of v. As described in Ref. 43, the average of δρ(r)δρ(r′) in the presence of the constraint, denoted by χ^(m)(r, r′), is given by

$$\begin{array}{ccc}\hfill {\chi }^{\left(\mathrm{m}\right)}(\mathbf{r},{\mathbf{r}}^{\prime })& =& \chi (\mathbf{r},{\mathbf{r}}^{\prime })-{\int }_{{\mathbf{r}}^{\prime \prime }\in v}{\int }_{{\mathbf{r}}^{\prime \prime \prime }\in v}\chi (\mathbf{r},{\mathbf{r}}^{\prime \prime })\hfill \\ & & \times {\chi }_v^{-1}({\mathbf{r}}^{\prime \prime },{\mathbf{r}}^{\prime \prime \prime })\chi ({\mathbf{r}}^{\prime \prime \prime },{\mathbf{r}}^{\prime }).\hfill \end{array}$$ (A5)

From Eq. A3, it follows that χ^(m)(r, r′) is zero whenever r or r′ is in v, as required by the solvent exclusion constraint. To describe the constraint’s effect on the average density, we introduce an auxiliary field c(r) that satisfies

$$\begin{array}{cc}\hfill {\int }_{{\mathbf{r}}^{\prime }\in v}\chi (\mathbf{r},{\mathbf{r}}^{\prime })c\left({\mathbf{r}}^{\prime }\right)={\rho }_{\ell }n\left(\mathbf{r}\right),& \mathbf{r}\in v,\end{array}$$ (A6a)

$$\begin{array}{cc}\hfill c\left(\mathbf{r}\right)=0,& \mathbf{r}\in \overline{v}.\end{array}$$ (A6b)

In terms of c(r) and χ^(m)(r, r′), the average density in the presence of the solute is given by

$$\begin{array}{ccc}\hfill ⟨\rho \left(\mathbf{r}\right)⟩& =& {\rho }_{\ell }n\left(\mathbf{r}\right)\hfill \\ \hfill & & -{\int }_{{\mathbf{r}}^{\prime }\in v}\chi (\mathbf{r},{\mathbf{r}}^{\prime })c\left({\mathbf{r}}^{\prime }\right)-{\int }_{{\mathbf{r}}^{\prime }\in \overline{v}}{\chi }^{\left(\mathrm{m}\right)}(\mathbf{r},{\mathbf{r}}^{\prime })\beta \phi \left({\mathbf{r}}^{\prime }\right).\hfill \end{array}$$ (A7)

Equation A2 can now be written much more simply as follows:

$$\begin{array}{ccc}\hfill H_{\mathrm{eff}}\left[n\left(\mathbf{r}\right)\right]& =& H_{\mathrm{large}}\left[n\left(\mathbf{r}\right)\right]-{\int }_{\mathbf{r}\in v}\phi \left(\mathbf{r}\right){\rho }_{\ell }n\left(\mathbf{r}\right)\hfill \\ \hfill & & +k_{\mathrm{B}}T\ln \sqrt{\det 2\pi {\chi }_v}+\frac{k_{\mathrm{B}}T}{2}{\int }_{\mathbf{r}\in v}{\rho }_{\ell }n\left(\mathbf{r}\right)c\left(\mathbf{r}\right)\hfill \\ \hfill & & -{\int }_{\mathbf{r}\in \overline{v}}{\int }_{{\mathbf{r}}^{\prime }\in v}\phi \left(\mathbf{r}\right)\chi (\mathbf{r},{\mathbf{r}}^{\prime })c\left({\mathbf{r}}^{\prime }\right)\hfill \\ \hfill & & +\frac{k_{\mathrm{B}}T}{2}{\int }_{\mathbf{r}}{\int }_{{\mathbf{r}}^{\prime }}\beta \phi \left(\mathbf{r}\right)(\chi -{\chi }^{\left(\mathrm{m}\right)})(\mathbf{r},{\mathbf{r}}^{\prime })\beta \phi \left({\mathbf{r}}^{\prime }\right).\hfill \end{array}$$ (A8)

For the geometries we considered, the sum of the last two terms of this equation is, on average, opposite in sign but nearly proportional to the much simpler remaining term involving ϕ(r) (see Appendix D). Physically, these three terms capture the energetic bonus of driving δρ(r) to 0 inside v where ϕ is positive, the energetic cost of the consequent density enhancement just outside of v, and the small difference between (a) the entropic cost associated with ϕ modifying the solvent density in the presence of a solute and (b) that same cost in the absence of a solute. In typical configurations, the three terms are roughly proportional to the subvolume of v where n(r) = 1, and capture how solvation free energies are modified by the microscopic curvature of v. We have found it accurate to model the effect of these three terms using only the second term of Eq. A8, whose strength is then renormalized by a factor K. The resulting approximation for H_int[n(r)] is

$$H_{\mathrm{int}}\left[n\left(\mathbf{r}\right)\right]\approx -K{\int }_{r\in v}\phi \left(\mathbf{r}\right){\rho }_{\ell }n\left(\mathbf{r}\right).$$ (A9)

Finally, we introduce an important simplification in H_small[n(r)]. Instead of solving Eq. A6a to obtain the value of the field c(r) in v, we replace c(r) there by its average value, c₁, and obtain the much simpler relation

$$c_1={⟨N⟩}_v∕{\sigma }_v,$$ (A10)

where

$$\begin{array}{c}\hfill {⟨N⟩}_v={\int }_{\mathbf{r}\in v}{\rho }_{\ell }n\left(\mathbf{r}\right),\end{array}$$ (A11)

$$\begin{array}{c}\hfill {\sigma }_v={\int }_{\mathbf{r}\in v}{\int }_{{\mathbf{r}}^{\prime }\in v}\chi (\mathbf{r},{\mathbf{r}}^{\prime }).\end{array}$$ (A12)

Equivalently, in Eq. A1 we enforce the single constraint that ∫_{r ∈ v}ρ_ℓn(r) + δρ(r) be zero, instead of enforcing the multitude of constraints that ρ_ℓn(r) + δρ(r) be zero at every point r in v. We have verified that this approximation, dubbed the “one-basis set approximation” in previous works,¹³, ⁵³ does not appreciably change the solvation free energies and P_V(N) distributions that we have obtained. Crucially, this approximation replaces the large (though sparse) linear system of Eq. A6a with the trivial relation of Eq. A10, and is therefore very advantageous computationally. With it, the term H_small[n(r)] is given by

$$H_{\mathrm{small}}\left[n\left(\mathbf{r}\right)\right]=k_{\mathrm{B}}T[{⟨N⟩}_v^2∕2{\sigma }_v+C∕2].$$ (A13)

The normalization constant C is defined by Eq. 13e. When the value of 〈N〉_v becomes small, the integral defining σ_v is dominated by the δ-function in Eq. 6 and takes the value σ_v ≈ 〈N〉_v. The value ln (2πσ_v) of C that is applicable for larger 〈N〉_v thus tends unphysically to negative infinity as 〈N〉_v tends to zero. This deficiency arises from a breakdown of Gaussian statistics for solvent number fluctuations in sub-Angstrom volumes. Since solvent molecules are discrete entities, these statistics are instead Poissonian. A small cavity v can contain either one solvent molecule, with probability 〈N〉_v, or no solvent molecules, with probability 1 − 〈N〉_v. The free-energy cost of evacuating that cavity is thus −k_BTln (1 − 〈N〉_v) ≈ 〈N〉_vk_BT. The definition of C given in Eq. 13e is a simple, continuous way of capturing this difference in fluctuation statistics at tiny length-scales. The crossover occurs at 〈N〉_v ≈ (2π − 2)⁻¹ ≈ 0.23.

Lattice formulation

Using Eq. 9, we express H_eff[n(r)] and its components in terms of the lattice variables n_i, so that

$$H_{\mathrm{eff}}\left[\left\{n_i\right\}\right]=H_{\mathrm{large}}\left[\left\{n_i\right\}\right]+H_{\mathrm{int}}\left[\left\{n_i\right\}\right]+H_{\mathrm{small}}\left[\left\{n_i\right\}\right].$$ (A14)

The integrals that define each term are then approximated through lattice sums, with continuous fields replaced by either their average values or their integrals over each cell.

Equation A13 for H_small[δρ(r); n(r)] is the easiest to tackle. We begin by discretizing Eq. 5, which defines χ(r, r′), when the domains of integration for r and r′ are V and V′, respectively. In terms of the matrix χ_ij(V, V′) defined by Eq. 12, our prescription yields

$$\chi (\mathbf{r},{\mathbf{r}}^{\prime })\to n_i{\chi }_{ij}(V,V^{\prime })n_j,\mathbf{r}\in V,{\mathbf{r}}^{\prime }\in V^{\prime }.$$

Equation 13d for σ_v then follows immediately from Eq. A12. Equation 13c for 〈N〉_v reasonably approximates the integral in Eq. A11.

To discretize Eq. A9 for H_int[n(r)], we need to choose a concrete implementation of the overbar operation that is used to define ϕ(r). Following Ref. 13, we approximate it as a weighted average involving the cell and its nearest neighbors,⁹¹ given by

$$\overline{n\left(\mathbf{r}\right)}\to \left[\frac{1}{2}{n}_i+\frac{1}{12}{\sum _{j\left(\mathrm{nn}\mathit{i}\right)}}^{\prime }{n}_j\right],$$

where the notation for the sum is as in Eq. 13.

The average, ϕ_i, of ϕ(r) over cell i follows immediately from Eq. 8, and is given by Eq. 13b. Following our prescription, Eq. A9 is then reasonably discretized as the lattice sum

$$H_{\mathrm{int}}\left[\left\{n_i\right\}\right]\approx -K\sum _i{\phi }_i{\rho }_{\ell }{n}_i{v}_i.$$

Discretizing H_large[n(r)] correctly is a surprisingly subtle challenge. Previously,¹³, ¹⁴, ⁵¹ it has been approximated by an Ising Hamiltonian with nearest-neighbor coupling

$$H_{\mathrm{large}}\left[\left\{n_i\right\}\right]\stackrel{?}{\to }\gamma {\lambda }^2\sum _{⟨ij⟩}{(n_i-n_j)}^2-\mu {\rho }_{\ell }{\lambda }^3\sum _i{n}_i.$$

Unfortunately, the use of this Hamiltonian results in serious artifacts. Consider, for instance, the energetics of a convex vapor bubble embedded in the liquid, as represented by the field {n_i}. Many configurations of the field that are physically distinct have nonetheless equal projections onto the xy, yz, and xz-planes, so they will be given equal statistical weight by the Hamiltonian. Hence, the use of this Hamiltonian results in an unphysical excess of entropy, as shown in detail in Appendix E. Moreover, the energetic cost of common configurations of the field {n_i} is substantially overestimated. The Ising Hamiltonian assigns a large vapor bubble of radius R an interfacial energy of about 6πγR², not 4πγR². Whereas using a renormalized γ can alleviate this latter problem,²⁸ the problem of excess entropy is more fundamental.

Motivated by the above deficiencies of the Ising Hamiltonian, we have instead chosen to evaluate the Landau–Ginzburg integral in Eq. 3 numerically. To proceed, we need to construct the basis function Ψ(r) used in Eq. 9. Our choice, depicted in Fig. 9 for water, approximates the usual van der Waals construction⁹² at a local level. We first construct a 1D basis function ψ(x) satisfying

$$w^{\prime }(\psi \left(x\right),0)-m{\psi }^{\prime \prime }\left(x\right)=0,$$ (A15)

with boundary conditions ψ(0) = 1 and ψ(λ) = 0. We then extend the range of ψ(x) and symmetrize it so that

$$\psi (x>\lambda )=0$$ (A16)

and

$$\psi (x<0)=\psi (-x).$$ (A17)

Finally, the three-dimensional basis function Ψ(r) is constructed from the one-dimensional profiles ψ(x) to give

$$\Psi (x,y,z)=\psi \left(x\right)\psi \left(y\right)\psi \left(z\right).$$

The field n(r) constructed from Eq. 9 using this basis function has many useful properties: the value of n(r) at the center of each cell i corresponds to the state encoded in n_i; the density interpolates smoothly between adjacent cells; and the density profile of a configuration representing an axis-aligned wall, where all n_i’s are 1 on one side of a plane and 0 on the other, nearly reproduces the interface profile given by the van der Waals construction.

Figure 9.

Constructing n(r) from {n_i}. The binary field specifies whether the density at the center of each lattice cell should be that of the liquid or that of the vapor. Between cell centers, the density is interpolated using the basis function ψ(x) (whose form for water is shown in the lower left panel). The dashed lines delineate the domain of integration of the local free energy h_i given by Eq. 10.

For water, we use the function w(n, μ) given in Eq. 16. This choice results in both sides of Eq. A15 being proportional to m, so the function ψ(x) is independent of m. In the free van der Waals theory, where the boundary conditions on Eq. A15 are ψ( − ∞) = 1 and ψ( + ∞) = 0, the density profile ψ₀(z) that results is

$${\psi }_0\left(z\right)=[1+\tanh (z∕d)]∕2,$$

which accurately describes the average density profile of an SPC/E water slab at ambient conditions. The thickness parameter d can thus be determined from simulation. A complication due to capillary waves is that d grows logarithmically with simulation box size,⁷³, ⁹³ so different authors quote different values of d: 1.27 Å for a 19 × 19 Ų interface in Ref. 53 and 1.54 Å for a 30 × 30 Ų interface in Ref. 94. We choose the smaller value because the instantaneous configuration of n(r) should be blurred only by small-scale fluctuations, not by large-scale capillary waves, which correspond instead to different conformations of n(r). The profile shown in Fig. 9 corresponds to the solution of Eq. A15 when the more restrictive boundary conditions described above are imposed, with λ = 4 Å and d = 1.27 Å.

With concrete choices of Ψ(r), w(n, 0), m and λ, the integrals h_i defined by Eq. 10 can be evaluated. We discuss the choice of m below. As outlined in the main text, the value of h_i depends only on the values of n_j for the 8 cells j that share one of the corners of cell i. Out of the 256 possible configurations of {n_j}, only 14 are unique when one accounts for reflection, rotation and inversion symmetry. Thus, only 14 distinct integrals need to be evaluated numerically. This decomposition bears a strong resemblance to the marching cubes algorithm⁹⁵ that reconstructs interfaces in volumetric data, and is widely used in computerized tomography.

In principle, the value of m is related to the surface tension by the relation⁹²

$$\gamma ={\int }_0^{\lambda }\left[w(\psi \left(x\right),0)+m{\psi }^{\prime }{\left(x\right)}^2∕2\right]\mathrm{d}x.$$ (A18)

On a lattice, as exemplified above by the Ising Hamiltonian, this choice results in perfect interfacial energies for flat axis-aligned interfaces at the expense of more common curved interfaces. Thus, we instead choose m self-consistenly such that ψ(x) satisfies Eq. A15 and the calculated interfacial energy of some reference geometry of surface area A is γA. Eq. A18 corresponds to a cubic reference geometry. Since curved surfaces are far more common than flat ones in realistic solutes, we instead use large spheres as our reference geometry.

For the specific form of w(n) that we use for water, h_i is proportional to m and ψ(x) is itself independent of m. The above self-consistent procedure can hence be implemented quite simply. We first calculate the h_i quantities up to a factor of m, and then pick m to obtain the correct interfacial energies. The resulting values of h_i are given in Table 1.

Table 1.

Relative interfacial free energy h_i for each distinct neighboring cell configuration (diagrams after Ref. 95). Highlighted corners denote cells j with n_j = 1, whereas the others refer to cells with n_j = 0; cell i is the lower-left corner in the back. To aid the eye, a schematic of the implied liquid-vapor interface of each configuration is shown in orange. The values of h_i are inversion-symmetric: interchanging highlighted and unhighlighted corners yields the same interface and interfacial energy. Also shown are the values of h_i that would reproduce the energetics of the standard Ising lattice gas, namely γλ²∑_〈ij〉(n_i − n_j)².

Local {nj} configuration
hi (Present model)	0.000	0.387	0.676	0.725	0.754	0.851	0.965
hi (Ising model)	0.000	0.750	1.000	1.500	1.500	1.250	1.750
Local {nj} configuration
hi (Present model)	0.983	0.857	0.910	1.104	0.965	1.040	1.134
hi (Ising model)	2.250	1.000	1.500	2.000	1.500	2.000	3.000

Incorporating solute-solvent interactions

A generic solute interacts with a solvent molecule through a potential u(r). This interaction is reflected in the microscopic Hamiltonian of Eq. 13b as an additional term H_u[n(r), δρ(r)] given by

$$H_u[n\left(\mathbf{r}\right),\delta \rho \left(\mathbf{r}\right)]={\int }_{\mathbf{r}}u\left(\mathbf{r}\right)[{\rho }_{\ell }n\left(\mathbf{r}\right)+\delta \rho \left(\mathbf{r}\right)].$$

Upon integrating out the density fluctuations, an additional term H_u[n(r)] appears in H_eff[n(r)]. Physically, the total solvent density responds linearly to the external field u(r) according to the density fluctuation spectrum given by χ^(m)(r, r′), so that

$$\begin{array}{ccc}\hfill ⟨\rho \left(\mathbf{r}\right)⟩& =& {\rho }_{\ell }n\left(\mathbf{r}\right)-{\int }_{{\mathbf{r}}^{\prime }}\chi (\mathbf{r},{\mathbf{r}}^{\prime })c\left({\mathbf{r}}^{\prime }\right)\hfill \\ & & -{\int }_{{\mathbf{r}}^{\prime }}{\chi }^{\left(\mathrm{m}\right)}(\mathbf{r},{\mathbf{r}}^{\prime })\beta [\phi \left({\mathbf{r}}^{\prime }\right)+u\left({\mathbf{r}}^{\prime }\right)].\hfill \end{array}$$ (A19)

The resulting free energy change H_u[n(r)] arises from the direct interaction of the solute and the solvent, and from the entropic cost of modifying the mean solvent density around the solute. It is given by

$$\begin{array}{ccc}\hfill H_u\left[n\left(\mathbf{r}\right)\right]& =& {\int }_{\mathbf{r}}u\left(\mathbf{r}\right)⟨\rho \left(\mathbf{r}\right)⟩\hfill \\ & & +\frac{k_{\mathrm{B}}T}{2}{\int }_{\mathbf{r}}{\int }_{{\mathbf{r}}^{\prime }}\beta u\left(\mathbf{r}\right){\chi }^{\left(\mathrm{m}\right)}(\mathbf{r},{\mathbf{r}}^{\prime })\beta u\left({\mathbf{r}}^{\prime }\right).\hfill \end{array}$$ (A20)

Note that the integrands is zero whenever r or r′ is inside the solute.

To implement the previous equation on a lattice, we have found it useful to approximate χ^(m)(r, r′) by

$$\begin{array}{c}\hfill {\chi }^{\left(\mathrm{m}\right)}(\mathbf{r},{\mathbf{r}}^{\prime })\approx \left\{\begin{array}{cc}\hfill {\chi }_0(\mathbf{r}-{\mathbf{r}}^{\prime }),& \hfill \mathbf{r},{\mathbf{r}}^{\prime }\in \overline{v},n\left(\mathbf{r}\right)=n\left({\mathbf{r}}^{\prime }\right)=1,\\ \hfill 0,& \hfill \mathrm{otherwise}.\end{array}\right.\end{array}$$ (A21)

We also use the one-basis set approximation, c(r) ≈ c₁, given in Eq. A10. Discretizing Eq. 20 as in Appendix A2 then immediately yields Eq. 15.

APPENDIX B: ESTIMATING χ_ij(V, V′)

An essential ingredient of the model we present is the matrix χ_ij(V, V′), given by the integral in Eq. 12. The terms involving the delta-functions of Eq. 5 are trivial. Owing to the rapid oscillations in g(r) − 1, the remaining integrals are harder to estimate. We employ a two-step procedure to estimate these integrals efficiently. We begin by subdiving the λ = 4 Å-resolution grid of cells into a much finer grid of resolution λ_f = 1 Å. For clarity, below we explicitly distinguish between cells in the coarse grid, indexed by the letters i and j, and cells in the fine grid, indexed by the letters a and b. We evaluate the integrals of the non-delta-function portion of χ₀ on the fine grid without otherwise restricting the arguments to particular volumes V and V′, and denote the result by χ_ab. Each fine cell is so small that the effect of a restriction on the integration domain can be estimated accurately with a simple interpolation formula. We then use these interpolated values in the fine grid to build up the elements of χ_ij(V, V′) over the coarse grid.

To evaluate χ_ab, we use the Narten–Levy data for the structure factor S(k) of water.⁵⁵ Since the S(k) is unavailable for wave-numbers k higher than 16 Å⁻¹, we blur the domains of integration over a range of about 2π∕16 Å, which makes the values of the integrals practically insensitive to this missing data. Concretely, we introduce a basis function Φ, given by

$$\Phi (x,y,z)=\varphi \left(x\right)\varphi \left(y\right)\varphi \left(z\right),$$

with

$$\varphi \left(x\right)=\frac{1}{2}\left[\tanh \frac{x-{\lambda }_f∕2}{\Delta }-\tanh \frac{x+{\lambda }_f∕2}{\Delta }\right].$$

The function φ is unity around x = 0, and goes rapidly to zero as |x| ≳ λ_f∕2, with Δ controlling the range of x over which this transition occurs. We have found that a value of 0.1 Å for Δ is adequate. Using the notation r_a to denote the center of fine cell a, the value of χ_ab is given by

$${\chi }_{ab}={\rho }_{\ell }^2{\int }_{\mathbf{r}}{\int }_{{\mathbf{r}}^{\prime }}\Phi (\mathbf{r}-{\mathbf{r}}_a)\left[g\right(|\mathbf{r}-{\mathbf{r}}^{\prime }\left|\right)-1]\Phi ({\mathbf{r}}^{\prime }-{\mathbf{r}}_b).$$ (B1)

The integral is best evaluated in Fourier space, where the term in square brackets appears as the experimental S(k) profile. We overcome the convergence problems of a rapidly oscillating integrand by using the Haselgrove–Conroy integration algorithm.⁹⁶, ⁹⁷ To properly account for g(r) being exactly zero for r ≲ 2.35 Å, we further set χ_ab to exactly $-{\rho }_{\ell }^2$ if all points in a are within r_c = 2.35 Å from all points in b. To limit the range of χ_ab, we also set it to zero if all points in a are more than 10 Å from all points in b. The values of χ_ab need only be calculated once at each state point of water, and we have spent considerable effort in compiling them at ambient conditions. Our results are included in the Supplementary Data.⁷²

For specific volumes V and V′, we estimate the value of χ_ij(V, V′) as a weighted average of the pertinent values of χ_ab,

$$\begin{array}{c}\hfill {\chi }_{ij}(V,V^{\prime })\approx {\rho }_{\ell }(V\cap V^{\prime })+\sum _{a\in i}\sum _{b\in j}(V_a∕{\lambda }_f^3){\chi }_{ab}(V_b^{\prime }∕{\lambda }_f^3),\end{array}$$ (B2)

where (V∩V′) is the volume of the overlap between V and V′. This interpolation formula for χ_ij is manifestly linear in its arguments, so that

$${\chi }_{ij}(V,V^{\prime })+{\chi }_{ij}(V,V^{\prime \prime })={\chi }_{ij}(V,V^{\prime }\cup V^{\prime \prime }),$$

whenever V′ and V″ do not overlap. Most importantly, the interpolation procedure is simple, convenient, and correct for the limiting cases of where all the values of V_a are either 0 or ${\lambda }_f^3$.

For comparison, we have also calculated values of χ_ab from an explicit SPC/E water simulation in GROMACS at temperature T = 298 K and pressure p = 1 atm. The values are also included in the Supplementary Data.⁷² For the quantities we have studied in the main text, using these values for χ_ab instead of those derived from the Narten–Levy data yields nearly identical results.

APPENDIX C: FLUCTUATION VARIANCE

The variance of the field δρ(r) given in Eq. 5 is a simplification of the LCW interpolation formula,

$${\chi }_{\mathrm{LCW}}(\mathbf{r},{\mathbf{r}}^{\prime })={\rho }_{\ell }n\left(\mathbf{r}\right)\delta (\mathbf{r}-{\mathbf{r}}^{\prime })+{\rho }_{\ell }^{2}n\left(\mathbf{r}\right)\left[g\right(|\mathbf{r}-{\mathbf{r}}^{\prime }\left|\right)-1]n\left({\mathbf{r}}^{\prime }\right),$$

to the case where n(r) only takes the values 0 or 1. The discrepancies arising from using Eq. 5 and more precise expressions for the variance are mostly quantitative and limited to the vicinity of liquid-vapor interfaces.⁴⁵

One possible improvement to Eq. 5 is given in Ref. 43:

$$\begin{array}{ccc}\hfill \chi (\mathbf{r},{\mathbf{r}}^{\prime })& =& {\chi }_0(\mathbf{r},{\mathbf{r}}^{\prime })\hfill \\ & & -{\int }_{{\mathbf{r}}^{\prime \prime }\in E}{\int }_{{\mathbf{r}}^{\prime \prime \prime }\in E}{\chi }_0(\mathbf{r},{\mathbf{r}}^{\prime \prime }){\chi }_E^{-1}({\mathbf{r}}^{\prime \prime },{\mathbf{r}}^{\prime \prime \prime }){\chi }_0({\mathbf{r}}^{\prime \prime \prime },{\mathbf{r}}^{\prime }),\hfill \end{array}$$ (C1)

where E is the empty (i.e., gaseous) region of space where n(r) is 0, and ${\chi }_E^{-1}(\mathbf{r},{\mathbf{r}}^{\prime })$ satisfies

$${\int }_{{\mathbf{r}}^{\prime \prime }\in E}{\chi }_E^{-1}(\mathbf{r},{\mathbf{r}}^{\prime \prime }){\chi }_0({\mathbf{r}}^{\prime \prime },{\mathbf{r}}^{\prime })=\delta (\mathbf{r}-{\mathbf{r}}^{\prime }),\mathbf{r},{\mathbf{r}}^{\prime }\in E.$$

Equations C1, 5 are in qualitative agreement: both are zero when r or r′ is in the gaseous region, and both reduce to χ₀(r, r′) well into the liquid phase. The differences are, as expected, concentrated near the boundaries of E. In this refined expression, the integrand oscillates significantly within a lattice cell, so a lattice approximation to Eq. C1 proves unreliable. Because using Eq. 5 gives accurate results for all quantities we have examined, we regard the approximate Eq. 5 to be acceptable, and we have not pursued algorithms by which Eq. C1 can be accurately evaluated.

APPENDIX D: HOW WELL IS THE EFFECT OF UNBALANCED FORCES CAPTURED BY EQ. A9?

Above, we replaced the three terms involving ϕ_i in Eq. 8 by the simpler expression given in A9. We now justify this replacement.

Denote by H₊[n(r)] the terms dropped from Eq. 8. They are

$$\begin{array}{ccc}\hfill H_{+}\left[n\left(\mathbf{r}\right)\right]& =& -{\int }_{\mathbf{r}\in \overline{v}}{\int }_{{\mathbf{r}}^{\prime }\in v}\phi \left(\mathbf{r}\right)\chi (\mathbf{r},{\mathbf{r}}^{\prime })c\left({\mathbf{r}}^{\prime }\right)\hfill \\ \hfill & & +\frac{k_{\mathrm{B}}T}{2}{\int }_{\mathbf{r}}{\int }_{{\mathbf{r}}^{\prime }}\beta \phi \left(\mathbf{r}\right)(\chi -{\chi }^{\left(\mathrm{m}\right)})(\mathbf{r},{\mathbf{r}}^{\prime })\beta \phi \left({\mathbf{r}}^{\prime }\right).\hfill \end{array}$$ (D1)

Using the approximation for χ^(m)(r, r′) given in Eq. A21 and the one-basis set approximation of Eq. A10, we discretize these terms to obtain a lattice version of H₊[n(r)],

$$\begin{array}{ccc}\hfill H_{+}\left[\left\{n_i\right\}\right]& =& -\sum _{i,j}{\phi }_i{n}_i{\chi }_{ij}(\overline{v},v)n_j{⟨N⟩}_v∕{\sigma }_v\hfill \\ \hfill & & +k_{\mathrm{B}}T\sum _{i,j}\beta {\phi }_i{n}_i[{\chi }_{ij}(v,v)∕2+{\chi }_{ij}(\overline{v},v)]n_j\beta {\phi }_j.\hfill \end{array}$$

Because of the double sums in the formula, calculating H₊[{n_i}] is by far the most computationally demanding part of calculating H_eff[{n_i}]. Since a single cell flip changes the value of ϕ_i in up to 7 cells, calculating incremental changes to H₊[{n_i}] is also much more expensive than calculating incremental changes to H_u[{n_i}] (Eq. 15), which has a similar structure.

Figure 10 presents the solvation free energies of hard spheres calculated when the H₊[{n_i}] term is included and the renormalization constant K is set to 1. As can be seen, the term corresponding to H_int[{n_i}] has a much larger absolute value, and in the region where their values are not negligible, the average values of H_int[{n_i}] and H₊[{n_i}] are, as claimed, essentially proportional. The renormalization procedure we implement thus seems justified, a conclusion borne out by the results in the text. For completeness, we have verified that the solvation free energies of the hexagonal plate solute (Fig. 3) calculated when H₊[{n_i}] is included and K is 1 are essentially identical to the ones calculated using Eq. 13.

Figure 10.

Solvation free energies G of hard spheres as a function of sphere radius, where the term H₊[{n_i}] (Eq. D1) has been included and the renormalization constant K has been set to 1 (solid black), compared to the simpler model in Eq. 13 (circles). The averages of −〈H_int[{n_i}]〉 (red) and 〈H₊[{n_i}]〉 (blue) are nearly proportional to each other. Left inset: implied renormalization constant K, equal to 〈H_int[{n_i}] + H₊[{n_i}]〉∕〈H_int[{n_i}]〉. Note that both the numerator and denominator take on essentially zero value for R ≲ 0.4 nm. Right inset: implied value of K for hexagonal plate solute (Fig. 3) with η = 1.0. The implied value of K is similar for different η.

APPENDIX E: COMPARISON TO THE MODEL OF TEN WOLDE AND CHANDLER

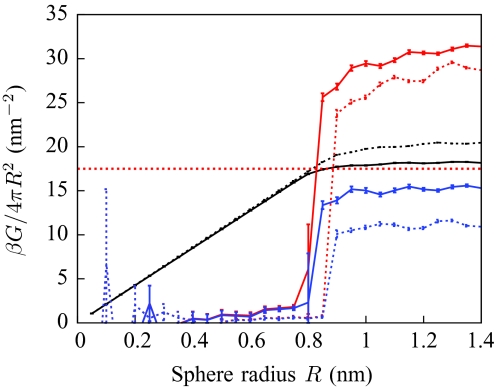
Above, we argued that the Ising Hamiltonian estimate for H_large[n(r)] overestimates the interfacial energy of a sphere of radius R by a factor of 3∕2. However, the lattice version of LCW theory presented by ten Wolde and Chandler¹⁴ uses precisely this Hamiltonian, yet the solvation free energy of spheres seems to tend to the correct value as R grows. Here we explain this apparent paradox.

Figure 11 shows the solvation free energies of spheres in the model of Ref. 14, and shows how they differ when the lattice cell size of λ = 2.1 Å is changed to λ = 2.3 Å. As claimed, 〈H_large[{n_i}]〉 is much larger than it should be, but for λ = 2.1 Å, the excess entropy resulting from the unphysical degeneracies of the Ising Hamiltonian exactly cancels this excess energy. This fortuitous cancellation does not occur for different cell sizes, and will not, in general, hold for solutes of different geometries.

Figure 11.

Solvation free energies G of spheres in the model of Ref. 14 (black), for cell sizes λ = 2.1 Å (solid) and λ = 2.3 Å (dashes). The use of the Ising Hamiltonian causes the average value of H_large[{n_i}] (red) to significantly exceed the solvation free energy, but also leads to large excess entropies (blue, TS = 〈H〉 − G). At λ = 2.1 Å, but not at λ = 2.3 Å, a fortuitous cancellation leads to correct solvation free energies.