Validation of a Non-Invasive Technique to Precisely Measure In Vivo Three-Dimensional Cervical Spine Movement

Abstract

Study Design

In vivo validation during functional loading.

Objective

To determine the accuracy and repeatability of a model-based tracking technique that combines subject-specific CT models and high-speed biplane X-ray images to measure three-dimensional (3D) in vivo cervical spine motion.

Summary of Background Data

Accurate 3D spine motion is difficult to obtain in vivo during physiological loading due to the inability to directly attach measurement equipment to individual vertebrae. Previous measurement systems were limited by two-dimensional (2D) results and/or their need for manual identification of anatomical landmarks, precipitating unreliable and inaccurate results. All previous techniques lack the ability to capture true 3D motion during dynamic functional loading.

Methods

Three subjects had 1.0 mm diameter tantalum beads implanted into their fused and adjacent vertebrae during ACDF surgery. High resolution CT scans were obtained following surgery and used to create subject-specific 3D models of each cervical vertebra. Biplane X-rays were collected at 30 frames per second while the subjects performed flexion/extension and axial rotation movements six months after surgery. Individual bone motion, intervertebral kinematics, and arthrokinematics derived from dynamic RSA served as a gold standard to evaluate the accuracy of the model-based tracking technique.

Results

Individual bones were tracked with an average precision of 0.19 mm and 0.33 mm in non-fused and fused bones, respectively. Precision in measuring 3D joint kinematics in fused and adjacent segments averaged 0.4 mm for translations and 1.1° for rotations, while anterior and posterior disc height above and below the fusion were measured with a precision ranging between 0.2 mm and 0.4 mm. The variability in 3D joint kinematics associated with tracking the same trial repeatedly was 0.02 mm in translation and 0.06° in rotation.

Conclusions

3D cervical spine motion can be precisely measured in vivo with sub-millimeter accuracy during functional loading without the need for bead implantation. Fusion instrumentation did not diminish the accuracy of kinematic and arthrokinematic results. The semi-automated model-based tracking technique has excellent repeatability.

Introduction

It is difficult to accurately determine three-dimensional (3D) spine motion in vivo during physiological loading due to the inability to directly attach measurement equipment to individual vertebrae. Previously, cervical spine motion has been measured in vivo under static conditions using MRI,¹ CT,² single plane X-ray,^3,4 and biplane X-ray.⁵ Two-dimensional (2D) fluoroscopic video has also been used to quantify dynamic sagittal plane motion.⁶ These techniques have significant limitations. First, methods that rely on single plane X-ray images can only measure 2D vertebral motion. Second, methods that require manual identification of anatomical landmarks can be unreliable and inaccurate. Third, these previous approaches all lack the ability to capture true three-dimensional (3D) motion during dynamic functional loading. Furthermore, these techniques have not been rigorously validated using in vivo data and an appropriate, highly accurate “ground truth” reference for comparison. Numerous authors have noted the necessity for three-dimensional,^1,5,7–10 in vivo^5,9,11,12 measurements of the cervical spine under dynamic load.^6,7,12,13 Currently there is a complete absence of data regarding in vivo, 3D movement of cervical vertebrae during functional loading. The present study presents a technique that can be applied to address this shortcoming.

This study compares a previously validated bead-based method of tracking bone motion in vivo¹⁴ (dynamic radiostereophotogrammetric analysis (D-RSA)¹⁵) to a new model-based method. The model-based method relies on a computer algorithm to maximize the correlation between biplane radiographic images and digitally reconstructed radiographs (DRRs). The DRRs are created by placing a volumetric model of the bone, obtained from CT, in a virtual biplane X-ray system proportionally identical to the laboratory system.

Validation of this system has been previously published for the study of gleno-humeral motion,¹⁶ patella-femoral motion,¹⁷ and femo-acetabular motion¹⁸ in cadaver specimens, and for the study of tibio-femoral motion in vivo during running.¹⁹ In spite of these previous validations, it was not clear how the model-based technique would perform when tracking vertebrae, nor was it clear how the method would perform when instrumentation was present in the spine. Several unique factors, including the morphologic complexity of the bones and the overlapping of vertebrae in radiographs, regardless of viewing angle, make spine tracking using a model-based approach a unique challenge.

The objective of the present study was to determine the accuracy of a non-invasive model-based tracking technique that combines subject-specific CT models and high-speed biplane X-ray images to measure three-dimensional in vivo cervical spine motion during functional loading. The ability of the model-based tracking system to measure 1) individual bone motion, 2) intervertebral six degree of freedom kinematics, and 3) intervertebral arthrokinematics (in this case, anterior and posterior disc height during movement) was evaluated. Additionally, repeatability of the semi-automated tracking process was measured by tracking the movement of one spinal motion segment three times to assess variability associated with the tracking process.

Materials and Methods

Following Institutional Review Board (IRB) approval, three subjects had 1.0 mm diameter tantalum beads implanted into their fused and adjacent cervical vertebrae during single-level anterior cervical discectomy and fusion (ACDF) surgery (3–5 beads per vertebral body). Biplane X-rays were collected six months after surgery within a system comprised of cardiac-cine angiography generators (EMD Technologies, CPX-3100CV), two 0.3/0.6 mm focal spot X-ray tubes, two 16-inch Thalus image intensifiers, and two high-speed digital cameras (4 megapixel Phantom v10, Vision Research) (Figure 1). The high-speed cameras collected data only from the central 12-inches of the image intensifers and mapped this data to images of dimensions 1800 x 1824 pixels, resulting in images with pixel size of approximately 0.17 mm. Biplane X-ray images were downsampled to 1024 x 1024 pixel resolution, producing images with pixel size of approximately 0.30 x 0.30 mm.

Figure 1.

Biplane radiography system configuration for a) the flexion/extension trials, and b) the axial rotation trials. For flexion/extension trials, imaging systems were aligned horizontally and the angle between X-ray tube/image intensifier pairs was approximately 55°. For the axial rotation trials, the angle between imaging systems was 90° and the system imaging from anterior to posterior was tilted up 15°.

Dynamic flexion/extension images were collected from two oblique views (Figure 1a) while axial rotation images were collected from one lateral and one anterior/posterior view (Figure 1b). The anterior/posterior view was directed upward 15° to improve visualization of vertebral bodies, as is done in conventional clinical cervical spine X-rays. Biplane X-rays were collected for two seconds at 30 frames per second for 3–4 trials each of continuous flexion/extension and axial rotation movement. All movements were performed to the beat of a metronome set at 40 beats/minute. Subjects were instructed to time their movement so they achieved full flexion (or rotation to the right) on one beat followed by full extension (or rotation to the left) on the next beat, maintaining smooth, continuous motion throughout. The high-powered cardiac-cine angiography generators (70 kV, 160 mA) produced X-ray pulses 2.5 ms in duration each frame, synchronized with the high-speed cameras, resulting in high-contrast, blur-free images.

Implanted beads were tracked in the biplane X-ray images using dynamic radiostereophotogrammetric analysis (D-RSA), as described previously,^14,16,19 to provide a “ground truth” for vertebral movement each trial. A best-fit algorithm was implemented to define bone motion when more than three beads were implanted in any single vertebra. For each bone of every subject, the inter-bead distances were determined every frame of data. The average inter-bead distance for each pair of markers within each bone over all movement tests was then determined. Frames in which an inter-bead distance deviated outside the 95% confidence interval for that bead pair were eliminated from further analysis, as the bead tracking was no longer a reliable “gold standard” for that frame.

Accuracy of tracking the implanted beads was determined by calculating the bias and precision in inter-bead distances within each bone over the entire dynamic trial, using procedures identical to those already published.¹⁴ Bias was defined as the average difference in inter-bead spacing determined using either CT slices or radiographs for each frame of an entire trial. Precision was defined as the standard deviation of these differences over the entire trial. Bead-based tracking was then used as the “gold standard” to calculate the accuracy of the model-based tracking. Kinematic and arthrokinematic validations of the model-based technique were not performed on bones in which the beads were inserted in a nearly straight line.

Subject-specific bone models were generated from CT images using a combination of manual and automated segmentation (Mimics Inc., Ann Arbor, MI). The original axial scans (0.29 x 0.29 x 1.25 mm) were interpolated to 0.29 x 0.29 x 0.29 mm to create 3D bone models with voxel dimensions close to the biplane radiograph resolution. Tantalum bead locations were identified in the CT scans and bead signatures were manually removed from the CT slices by replacing pixels containing bead signal with pixels containing surrounding bone tissue so they would not influence model-based tracking results. Bone models were placed within a proportionally identical virtual data collection system (Figure 2) and a computerized matching process reproduced bone location and orientation in 3D space each X-ray frame (Figure 3). Extensive details on the bead-based and model-based tracking process, including hardware and software specifications, calibration and distortion correction procedures, and computational algorithms have been described previously.^16,19,18 To briefly summarize the model-based tracking algorithm, the laboratory-based 3D location and orientation of the high-speed cameras and x-ray sources were recreated within the computer to generate a virtual test configuration identical to the actual biplane radiographic imaging system. Given the x-ray source and camera locations, a digitally reconstructed radiograph (DRR) was created by placing the subject-specific CT bone volume in the virtual testing configuration. As the CT volume was translated and rotated within the virtual testing configuration, the DRRs changed accordingly. The DRRs overlaid the distortion corrected biplane radiographic data and provided visual feedback to the operator regarding the similarity between the DRRs and radiographic images (Figure 2). Initially, the operator interactively positioned the CT volume reconstruction in two consecutive frames. Custom computer code used these initial estimates to begin a search to optimize the correlation between the DRRs and radiographic images. Once the optimum correlation was calculated, the computer program performed the same optimization procedure for successive frames, using a linear extrapolation of previously solved frames as the initial guess for each unsolved frame. The product of the correlation coefficients of the two DRRs with their respective radiographs was the objective function. The correlation was calculated only in the actual footprint of the DRR. A cluster of 24 computers using parallel processing performed these calculations.

Figure 2.

Virtual X-ray system for model-based tracking. A 3D CT reconstruction of the bone was placed in a computer-generated reproduction of the X-ray system. Simulated X-rays were then passed through the 3D CT reconstruction to generate digitally reconstructed radiographs (DRRs). Bone position and orientation was determined by optimizing the correlation between the DRRs (green in image) and the edge-enhanced radiographs (red in figure).

Figure 3.

Magnified view of distortion-corrected X-rays with overlaid DRR in red. Note the “interior” anatomical features (e.g. lateral mass edge, pedicles) that can assist the model-based matching algorithm to properly position the bone. These interior features would not exist in a silhouette bone model.

Model-based tracking accuracy was expressed in terms of bias and precision²⁰, where bias was the average difference between bead-based and model-based motion, and precision was the standard deviation of these differences. Three distinct comparisons were made between bead-based and model-based tracking results in order to evaluate the model-based tracking technique. First, the accuracy in tracking individual bones was determined by calculating the centroid of the tantalum beads within each bone for every frame of each trial using each tracking technique. Second, for each frame of every trial, relative translation and rotation between adjacent vertebrae was calculated (joint kinematics) using each tracking technique, with results expressed relative to anatomical coordinate systems created in each bone (Figure 4). Third, accuracy in measuring dynamic disc height was evaluated by comparing bead-based and model-based tracking results from flexion/extension trials. In addition to the assessments of accuracy described above, repeatability of the model-based tracking technique was evaluated by tracking C6 and C7 three times each for one flexion/extension trial. Repeatability was determined by calculating the within frame standard deviation for each of the six degrees of freedom (3 rotations, 3 translations) among the three sets of tracking results.

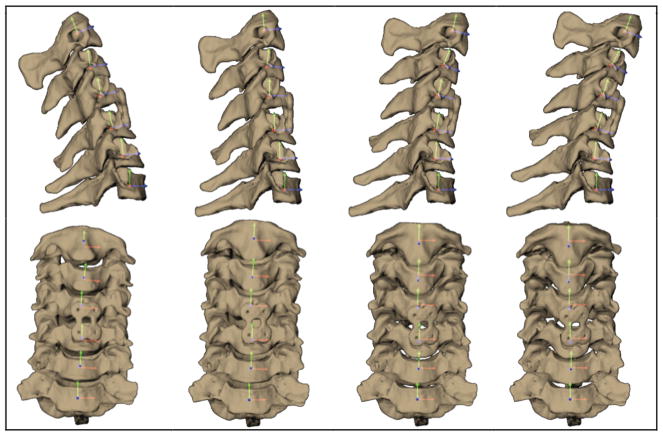
Figure 4.

Cervical vertebrae and fusion plate at four instants of flexion viewed from the sagittal (top) and anterior (bottom) directions. Rotation and translation of adjacent segments were determined with respect to anatomical coordinate systems imbedded within each vertebra

For all evaluations, accuracy results were grouped according to bone location (above the fusion, fused, or below the fusion) to investigate variability due to implanted fusion instrumentation. A total of seven flexion/extension trials and seven axial rotation trials were included as part of this validation. In all cases, raw data were filtered at 3 Hz using a fourth-order, low-pass Butterworth filter. One-sample, two-tailed t-tests with alpha set at 0.05 were used to test for statistically significant bias in all cases.

Results

The average inter-bead distance for all bones of all subjects was 7.2 ± 2.8 mm. Averaging over all bones, no bias in inter-bead distance measures was observed when comparing bead locations identified in CT slices to bead locations identified in biplane radiographs. However, a statistically significant bias of −0.12 mm was observed in inter-bead distance within the superior fused bone.

Implanted beads were tracked in biplane radiographs with precision of 0.10 mm and 0.08 mm during flexion/extension and axial rotation, respectively, with no difference among fused and adjacent bones, providing a highly accurate “ground truth”. Two bones were not included in kinematic (3D translation and rotation) and arthrokinematic (dynamic disc height) accuracy analysis calculations due to the beads being placed in a nearly straight line.

Individual bones were tracked with an average precision of 0.19 mm in non-fused bones and a precision of 0.33 mm in fused bones (Table 1). Statistically significant bias (0.35 mm or less) was observed in the non-fused and the fused bones (Table 1).

Table 1.

Model-based tracking accuracy (bias and precision) when tracking individual bones during flexion/extension (7 trials) and axial rotation (7 trials). For each trial, the difference in bead centroid location between the bead-based method and the model-based method was calculated for each data frame. This time history of differences was used to calculate mean difference between methods (bias) and standard deviation of these differences (precision). Data from all trials from the same subject were averaged to obtain a single average for each subject. The averages of all subjects were then calculated and appear in this table.

Activity	Bias			Precision
	Above Fusion	Fused	Below Fusion	Above Fusion	Fused	Below Fusion
Flexion/extension	0.11 ± 0.12	0.35 ± 0.26*	0.15 ± 0.10*	0.19 ± 0.04	0.34 ± 0.14	0.17 ± 0.03
Axial rotation	0.27 ± 0.13*	0.19 ± 0.24	0.26 ± 0.09*	0.23 ± 0.06	0.32 ± 0.07	0.19 ± 0.06

^*indicates bias statistically different from zero. All units are in millimeters.

Precision in measuring 3D joint kinematics in fused and adjacent segments averaged 0.4 ± 0.1 mm for translations and 1.1 ± 0.1 degrees for rotations (Table 2, Table 3). Statistically significant bias was indicated in both translation (0.7 mm or better) and rotation (−3.0 degrees or better) for both flexion/extension (Table 2) and axial rotation (Table 3) movements.

Table 2.

3D joint kinematic measurement accuracy (bias and precision) during flexion/extension. Data is from 3 subjects performing 7 trials of flexion/extension. For each of the 3D joint kinematic variables, bias and precision were calculated as described in Table 1.

Measurement	Bias			Precision
	Above Fusion	Fused	Below Fusion	Above Fusion	Fused	Below Fusion
Medial-lateral translation (mm)	0.2 ± 0.6	1.0 ± 1.1	0.7 ± 0.5*	0.3 ± 0.1	0.3 ± 0.1	0.3 ± 0.2
Superior-inferior translation (mm)	0.4 ± 0.4	−0.2 ± 0.4	−0.7 ± 1.2	0.2 ± 0.1	0.2 ± 0.1	0.4 ± 0.3
Anterior-posterior translation (mm)	0.4 ± 0.7	−0.1 ± 0.6	0.7 ± 0.9	0.2 ± 0.2	0.3 ± 0.1	0.3 ± 0.3
Flexion-extension (deg)	2.1 ± 0.3*	0.3 ± 2.4	−2.5 ± 5.5	1.3 ± 0.2	1.1 ± 0.5	1.3 ± 0.6
Axial rotation (deg)	1.4 ± 1.2*	−3.0 ± 2.6*	−0.4 ± 2.0	0.6 ± 0.1	0.7 ± 0.4	0.8 ± 0.3
Lateral bend (deg)	1.5 ± 1.0*	−1.0 ± 2.8	−1.2 ± 2.9	1.0 ± 0.3	1.0 ± 0.1	1.2 ± 0.3

^*indicates bias statistically different from zero.

Table 3.

3D joint kinematic measurement accuracy (bias and precision) during axial rotation. Data is from 2 subjects performing 7 trials of axial rotation. For each of the 3D joint kinematic variables, bias and precision were calculated as described in Table 1.

Measurement	Bias			Precision
	Above Fusion	Fused	Below Fusion	Above Fusion	Fused	Below Fusion
Medial-lateral translation (mm)	0.1 ± 1.1	0.5 ± 0.8	0.6 ± 0.4*	0.2 ± 0.1	0.3 ± 0.1	0.2 ± 0.1
Superior-inferior translation (mm)	−0.2 ± 0.8	0.3 ± 0.2*	0.2 ± 0.3	0.6 ± 0.4	0.6 ± 0.6	0.5 ± 0.5
Anterior-posterior translation (mm)	0.5 ± 0.5	0.7 ± 0.1*	1.0 ± 1.8	0.6 ± 0.1	0.4 ± 0.1	0.4 ± 0.2
Flexion-extension (deg)	1.7 ± 1.1*	−0.8 ± 1.1	−1.1 ± 2.6	1.8 ± 0.1	1.7 ± 0.3	1.3 ± 0.8
Axial rotation (deg)	0.3 ± 0.5	0.7 ± 2.7	−0.1 ± 0.8	1.2 ± 0.3	1.2 ± 0.1	0.8 ± 0.2
Lateral bend (deg)	−0.6 ± 0.5*	0.6 ± 3.5	−0.1 ± 0.9	0.9 ± 0.1	1.1 ± 0.1	0.7 ± 0.3

^*indicates bias statistically different from zero.

Anterior disc height during in vivo motion was measured with a precision of 0.4 ± 0.2 mm and 0.3 ± 0.2 mm above and below the fused segment, respectively, while posterior disc height during in vivo motion was measured with a precision of 0.3 ± 0.2 mm and 0.2 ± 0.1 mm above and below the fused segment, respectively (Figure 5). Significant bias was not identified in any disc height measurements.

Figure 5.

Anterior and posterior disc height during the flexion/extension movement using bead-based (blue) and model-based (red) tracking results from a representative trial.

The variability associated with tracking the same trial repeatedly was 0.02 mm in translation (average variability in the medial/lateral, superior/inferior and anterior/posterior translation directions) and 0.06° in rotation (average variability about the flexion/extension, axial rotation and lateral bend axes).

Discussion

On average, no bias was observed when comparing inter-bead distances from the CT scans to those found in the bead-tracking results. Implanted bead tracking precision (0.09 mm) was excellent, and similar to previous reports using dynamic RSA (0.07 mm¹⁴, 0.12 mm¹⁹, 0.13 mm¹⁸). Therefore, the bead-based results provided a highly accurate “gold standard” reference for evaluation of the model-based tracking technique.

It is not surprising that accuracy results were slightly better when tracking individual bones without instrumentation than when tracking bones containing instrumentation (Table 1). Metal plates and screws have the potential to distort bone tissue on CT scans, resulting in less accurate bone models for the model-based tracking process. Second, due to the placement of bone graft during fusion surgery, it was not possible to conclusively differentiate the native bone from the bone graft, again leading to slightly less accurate bone models for the fused motion segment.

The objective of model-based tracking is to obtain accurate three-dimensional kinematic (i.e. 3D translation and rotation) and arthrokinematic (i.e. motions at the joint surface) measurements of the joint, not simply the three-dimensional location of an individual bone. The clinically relevant joint kinematic (Table 2, Table 3) and arthokinematic (Figure 5) results reveal the accuracy that can be expected following application of the model-based tracking. Precision values were excellent for translation (average 0.4 mm), rotation (average 1.1°), and disc height (average 0.3 mm) measurements.

The extremely high repeatability of the semi-automated model-based tracking technique (0.02 mm in translation and 0.06° in rotation) provides support for computerized, automated measurement techniques, rather than manual techniques, which have much worse repeatability due to human error.^3,21 Furthermore, the repeatability associated with the model-based tracking implemented in the present study is an order of magnitude better than a previous report using a two-dimensional automated matching technique for tracking cervical spine motion.⁶

Statistically significant bias measurements were likely attributable to misidentified bead signatures in the CT scan and in the radiographic images, and not associated with a systematic error in the model-based tracking technique. Bead signature centroids may have been slightly misidentified in the original CT scan slices due to the relatively large original scan spacing of 1.25 mm and due to scatter associated with each bead signature. Second, bead signature identification in the CT of the fused motion segment was further hampered due to scatter associated with instrumentation. Third, bead identification in the radiographic images was challenging due to occlusion produced by the fusion screws as the subjects moved. This is believed to be the dominant factor contributing to the statistically significant bias values observed in this study.

The overall precision value of 0.09 mm indicates the bead-based tracking results were sufficiently accurate to serve as a gold standard to evaluate the model-based technique. In fact, the magnitude of the precision values observed with model-based tracking is in a range very similar to that observed in the bead-based tracking. As such, any bias observed in the model-based tracking may in fact be due to inherent bias in the bead-based tracking data. Therefore, it is difficult to determine which technique is more accurate. At best, we can conclude that these techniques demonstrated similar precision.

The model-based tracking technique described here has accuracy similar to previously reported techniques for measuring cervical spine motion. Reitman et al. moved two frozen cervical spines (without soft tissue) through a planar motion path within their single-plane fluoroscopic system and reported accuracy of 0.5°in rotation and 0.3 mm in translation.⁶ Single-plane fluoroscopic systems allow for data collection during functional flexion-extension with the subject in the upright position. However, single-plane systems do not account for out of plane motion and cannot be applied to investigate any arthrokinematic measures that are not parallel to the imaging plane, such as foramen size. Additionally, movements that involve combined motions, such as axial rotation, cannot be investigating using single-plane systems. Ishii et al. placed ceramic balls on a subject’s diving mask to validate a MRI voxel-based registration technique and reported rotational errors between 0.24° and 0.43° and translational errors between 0.41 mm to 0.52 mm.²² While the MRI system avoids radiographic exposure to the subject and enables 3D data collection for combined motions, the data must be collected while the subject is motionless and supine. The current technique overcomes the limitations of these previous methods by enabling data collection during three-dimensional, dynamic functional motion.

When evaluating measurement system validation reports, it is crucial for the reader to keep in mind not only the reported accuracy of the system, but also the means employed to perform the validation. Validations performed using animal or cadaver specimens, using “simulated” test conditions, and using mechanical equipment to create movement may lead to impressive estimations of accuracy that cannot be obtained in vivo. Alternatively, validations performed under real-world testing conditions (i.e. in vivo, dynamic, 3D muscle-driven motion) using multiple subjects and test configurations provide a more reliable indication of system accuracy.

A limitation of this study is that the “gold standard” bead tracking precision was 0.09 mm. Ideally, the accuracy of the reference standard should be an order of magnitude better than the accuracy of the technique being evaluated. However, in this case, it was believed it was better to validate the model-based technique during dynamic, in vivo motion with a gold standard of “only” 0.09 mm rather than devise a test arrangement unlike the conditions that will be in place during the application of this technique. A second limitation is that the validation numbers presented in this study are representative of the model-based tracking accuracy only for camera configurations and movements closely resembling those tested. Further validation may be necessary when using alternative camera configurations or when the subject performs significantly different spine movements. Additionally, it should be noted that although soft tissue response to movement and loading can be inferred (such as disc height), soft tissue movement can not be directly measured by dynamic stereoradiography.

There are several unique characteristics of the biplane radiography system and the model-based tracking algorithm described above that make this technique particularly well suited to spine motion tracking. First, the short-duration, high power X-rays generated by the cardiaccine angiography generators result in high contrast, blur free images, using X-ray pulses 2.5 ms in duration. Typical fluoroscopy units produce 8 ms X-ray pulses, resulting in motion blur at even moderate movement speeds. An additional advantage of the short duration pulses is that patient exposure to radiation is significantly reduced. Using commercial software (PCXMC, STUK, Helskini, Finland), given the radiographic parameters listed above, the effective radiation dose from one three-second trial within our biplane X-ray system was calculated to be 0.19 mSv. For comparison, in the United States we receive about 3.0 mSv of exposure from natural background radiation every year²³, and the average effective dose associated with a cervical spine CT scan is 4.36 mSv²⁴. Therefore, 22 biplane radiography trials, each lasting three seconds, result in radiation exposure similar to one CT scan. Second, the ray-tracing process that simulates X-rays passing through the subject-specific volumetric bone models yields “interior” bone morphology information, as opposed to simple edge-based information (Figure 3). Due to the highly complex morphology of vertebrae, including structures of varying size and shape such as the vertebral body, pedicles, lateral masses, and spineous process, a DRR that includes “interior” bone morphology provides a large amount of information that the computer can use to match the DRRs to the biplane radiographs. Third, the flexibility of the biplane X-ray system described here is advantageous when attempting to obtain two unobstructed views of the cervical spine during motion. The ability to tilt the system up (Figure 1b) is particularly useful as it directs X-rays below the chin and yields images that clearly show the separation between vertebral bodies from the anterior aspect (due to the curvature of the spine). The resulting superior and inferior vertebral body bone edge information is helpful to the model-based tracking algorithm. Finally, in contrast to MRI, data can be collected during active functional motion with the patient in an upright position, thereby recording vertebral movement that occurs in the presence of muscular and inertial loads.

A multitude of spinal implants have been developed recently and are now available to the spine surgeon for treating various disorders of the spine. Although many theoretical reasons have been hypothesized for their use, there is very little in vivo data that measures and documents the effects of these spinal implants on the 3D kinematics of the spine, especially under physiologic loading conditions. Our described technique will now allow for precisely measuring the true in vivo 3D spine movement not only in patients that have undergone fusion surgery, but also those that have or will undergo “motion preservation” surgery. Such careful in vivo kinematic analysis will provide critical information on either refuting or confirming the theoretical biomechanical benefits of various surgical procedures. This will be particularly important in the emerging field of motion preservation spine surgery as it challenges the standards historically set in fusion surgery.

This study has shown 3D cervical spine motion can be precisely measured in vivo with sub-millimeter accuracy during functional loading without the need for bead implantation. Fusion instrumentation did not diminish the precision of motion segment kinematic and arthrokinematic results. The semi-automated model-based tracking technique is highly repeatable. In the future, this technique may be applied to assess in vivo vertebral motion in asymptomatic subjects to define “normal” intervertebral in vivo kinematics and arthrokinematics, to evaluate surgical subjects while they perform functional tasks, to assess the performance of instrumentation such as dynamic fusion plates and disc replacements, and to investigate the effects of different conservative treatment options on cervical spine motion.