A model for the prediction of breathiness in vowels

Abstract

The perception of breathiness in vowels is cued by multiple acoustic cues, including changes in aspiration noise (AH) and the open quotient (OQ) [Klatt and Klatt, J. Acoust. Soc. Am. 87(2), 820–857 (1990)]. A loudness model can be used to determine the extent to which AH masks the harmonic components in voice. The resulting “partial loudness” (PL) and loudness of AH [“noise loudness” (NL)] have been shown to be good predictors of perceived breathiness [Shrivastav and Sapienza, J. Acoust. Soc. Am. 114(1), 2217–2224 (2003)]. The levels of AH and OQ were systematically manipulated for ten synthetic vowels. Perceptual judgments of breathiness were obtained and regression functions to predict breathiness from the ratio of NL to PL (η) were derived. Results show that breathiness can be modeled as a power function of η. The power parameter of this function appears to be affected by the fundamental frequency of the vowel. A second experiment was conducted to determine if the resulting power function could estimate breathiness in a different set of voices. The breathiness of these stimuli, both natural and synthetic, was determined in a listening test. The model estimates of breathiness were highly correlated with perceptual data but the absolute predicted values showed some discrepancies.

INTRODUCTION

Voice quality plays an important role in speech and serves to cue several indexical properties such as age, emotions, speaker identity, etc. A change in voice quality can arise as a symptom of some diseases or laryngeal conditions and is often the focus of rehabilitative efforts. Therefore, quantification of voice quality has several important applications. These range from commercial applications such as the development and evaluation of speech compression∕coding techniques, speech synthesis, or speech understanding systems to clinical tools that serve as screening or diagnostic measures or as indices of treatment∕rehabilitative outcome. Although the measurement of voice quality has been the focus of many experiments over the last several decades, no standardized approach to quantify voice quality exists. The research described here attempts to understand how listeners perceive “breathy” voice quality. A computational model is used to quantify this particular dimension of voice quality and to serve as a guide to future investigations of voice quality perception.

Voice quality is a perceptual construct that results from specific acoustic cues in speech. These cues may be a product of the glottal source, the vocal tract filter, or a combination of the two. Modifications to the glottal source are believed to result in three major subtypes or dimensions of voice quality: “breathy,” “rough,” or “strain” (e.g., Takahashi and Koike, 1976; Hirano, 1981; ASHA, 2002). The present report attempts to understand the perception of breathy voice quality, which results from lax adduction of vocal folds and an incomplete glottal closure resulting in greater turbulence noise in the vowel acoustic signal (de Krom, 1995; Hammarberg et al., 1986; Klatt and Klatt, 1990).

Several different measures have been proposed to quantify the degree or magnitude of breathiness in a vowel. These include measures of short-term perturbation (e.g., Eskenazi et al., 1990; Prosek et al., 1987; Martin et al., 1995), relative noise level (de Krom, 1993; Hirano et al., 1988), relative amplitude of the first harmonic (de Krom, 1994; Hillenbrand et al., 1994), spectral slope (Hammarberg et al., 1980), glottal source characteristics (Childers and Lee, 1991; Klatt and Klatt, 1990), and the relative amplitude of the cepstral peak (Hillenbrand et al., 1994). However, none of these measures has shown a consistent and high correlation with perceptual judgments of breathy voice quality when tested across multiple experiments using different speakers and listeners (Kreiman and Gerratt, 2000). Few reports have attempted to develop a formal predictive or computational model for breathiness. Instead, most report only the correlation between perceptual judgments of breathiness and one or more acoustic measures derived from the speech signal. Such data, although necessary, are not sufficient to develop a formal tool for the quantification of breathiness that may be widely used for multiple applications.

More recently, an auditory-processing front-end has been used as a preprocessing step prior to computing acoustic correlates for breathiness (Shrivastav, 2003; Shrivastav and Sapienza, 2003). This intermediate step represents the non-linear transformation between the acoustic signal and perception following processing by the auditory system. These reports show that the use of a loudness model (described by Moore et al., 1997) as a signal processing front-end resulted in measures that were better correlated with perceptual judgments of breathiness than other metrics used for this purpose [such as the cepstral peak prominence, short-term perturbation, and harmonic-to-noise ratio (HNR)]. Briefly, the loudness model attempts to predict the loudness of a signal by simulating the processes involved in the transduction of an acoustic signal into its corresponding neural representation. The loudness model also has the advantage of separating the loudness due to a signal of interest, referred to as “partial loudness” (PL), from the loudness due to background activity not associated with the signal of interest, referred to as “noise loudness” (NL). There are four basic elements of the model. The outer and middle ears are represented by separate passive band-pass filter functions. The cochlear mechanics are represented by a non-linear filter bank, analogous to critical band filtering. Subsequent neural transduction is represented by a compressive non-linear transformation of the output of the cochlear filter bank. The loudness estimate from each filter bank is summed to obtain the total loudness of a signal and is proportional to the total neural activity in response to that input.

The vowel acoustic signal can be viewed as having a periodic (harmonic) and an aperiodic (noise) component. The total loudness of the vowel includes contributions of both the harmonic and the noise components. The PL of the harmonic energy reflects the loudness of the periodic component in vowels, when these are masked by the aperiodic components in the same voice. The NL reflects the loudness resulting from the aperiodic components present in that voice. These two measures computed from the output of this loudness model were observed to correlate with perceptual judgments of breathiness. Breathiness was observed to be inversely related to PL and related directly to NL (Shrivastav, 2003; Shrivastav and Sapienza, 2003). Shrivastav and Sapienza (2003) reported that for low to moderate perceptual judgments of breathiness, PL had the most predictive leverage, but NL better predicted breathiness for stimuli judged to have high levels of breathiness.

To better understand the perception of breathiness in vowels, Shrivastav and Camacho (2010) evaluated breathiness of synthetic vowels that varied in the level of aspiration noise (AH) using an unanchored direct magnitude estimation task. The magnitude of perceived breathiness was compared to the PL and NL for these stimuli. It was observed that perceptual judgments of breathiness for these stimuli were best predicted by a power function of the ratio of NL to PL.

The power of these functions varied with fundamental frequency but was always observed to be below 1.0, resulting in a compressive relationship between NL∕PL and breathiness. NL∕PL (henceforth referred to as η) proved to be a good predictor of breathiness in vowels and Shrivastav and Camacho (2010) suggested that a computational model to predict breathiness in vowels would take the following form:

$$b={(k\eta )}^p+b_{\text{TH}},$$ (1)

where b was the breathiness of a vowel, k was a constant, η was the ratio of NL to PL, p was a power, and b_TH was defined as a threshold breathiness below which changes in AH levels had no effect on perceived breathiness. Furthermore, two of the model parameters (p and b_TH) were observed to vary with the stimulus fundamental frequency.

While the initial evaluation of this model by Shrivastav and Camacho was promising, the full power of the model requires evaluation using a broader set of conditions. Specifically, while Shrivastav and Camacho evaluated synthetic vowel stimuli so they could precisely control specific stimulus parameters, a general model of breathiness must also predict the perception of naturally occurring voices. Furthermore, the synthesized vowels used by Shrivastav and Camacho (2010) manipulated breathiness by changing the level of AH alone. In contrast, natural voices along the continuum of breathiness often show multiple acoustic changes (e.g., Klatt and Klatt, 1990). In addition to changes in AH, acoustic changes associated with breathiness include an increase in the spectral slope and an increase in the amplitude of the first harmonic relative to the second harmonic (e.g., Hanson, 1997). Such acoustic changes often interact with each other to cue the perception of breathiness. For example, in unpublished pilot experiments, we observed that an increase in the amplitude of the first harmonic relative to that of the second harmonic (H1-H2) was effective in cuing changes in breathiness when the AH levels were low. However, at higher levels of AH, changes in H1-H2 did not affect the perceived breathiness in vowels.

Accounting for such complex acoustic-to-perceptual relationships may require development of models based on a more realistic simulation of breathy voice quality. Alternatively, one may attempt to study the perception of breathy voice quality using natural voices alone (such as using machine learning algorithms to determine the acoustic-to-perceptual relationship). The former allows a high degree of control over stimuli, allowing the experimenter to draw inferences that are more conclusive from their data. The later allows the use of more naturalistic stimuli, but the high variability across stimuli makes it difficult to draw firm conclusions about the resulting data. A third alternative, applied in the present study, is to develop a computational model based on synthesized voices and to evaluate it against natural voices.

Therefore, the goal of this study was to develop a model for the perception of breathiness in vowels using synthesized stimuli that showed co-variation of two different acoustic cues previously associated with changes in breathiness (Klatt and Klatt, 1990; Hillenbrand et al., 1994; Hanson, 1997). These included changes in AH level and changes in the H1-H2, simulated through the manipulation of the glottal source open quotient (OQ). A comparison of the resulting model with that proposed by Shrivastav and Camacho (2010) based on changes in AH alone would help to identify the contribution of changes in H1-H2 to the perception of breathiness. A second objective of this study was to evaluate the extent to which a model based on the analysis of synthesized voices would generalize to a novel set of stimuli consisting of both synthesized and natural voices.

EXPERIMENT 1: MODEL DEVELOPMENT

Methods

Stimuli

The stimuli consisted of ten synthetic vowel series (∕ɑ∕) generated using the Klatt synthesizer with the Liljencrants–Fant model (Fant et al., 1985) as the sound source. This allowed systematic manipulation of the amplitude of AH and the OQ, two parameters shown to be correlated with the perception of breathy voice quality. Note that changes in the OQ of the glottal source are related to changes in H1-H2 in the output spectrum (e.g., see Hanson, 1997). Thus, changes in the OQ parameter of the Klatt synthezier were incorporated to indirectly manipulate the H1-H2 for these stimuli.

The synthetic vowels simulated ten talkers selected from the Kay Elemetrics Disordered Voice Database (Kay Elemetrics, Lincoln Park, NJ). These vowels have been used in previous experiments on breathiness, and more details about their selection and synthesis have been provided in Shrivastav and Camacho (2010). Briefly, the ten vowel samples corresponded to five male and five female talkers who exhibited a wide range of breathiness, from normal to extremely dysphonic. These were selected through a pilot listening test where 4 listeners rated the breathiness of 50 voices that were randomly selected from the Kay Elemetrics database. The stimuli were rank ordered based upon the average ratings and then grouped into five bins varying in breathiness. Finally, two stimuli—one male and one female—were selected from each bin. Synthesized versions of these talkers were generated by recreating the fundamental frequency (f₀) and first three formant frequencies (F1, F2, F3) of the natural voices. Certain other source and filter parameters (AH, OQ, tilt, formant bandwidths) were adjusted subjectively to obtain approximately equal perceived breathiness. It is emphasized that the goal was not to produce an exact match between the natural and the synthesized voices but to obtain the same range of breathiness between the two groups of stimuli.

For the present experiment, the ten synthetic vowels were systematically manipulated to obtain ten sets of vowel continua. Each vowel continuum consisted of 11 samples co-varying in AH and OQ, thus resulting in a total of 110 synthetic stimuli (10 vowel continua × 11 stimuli∕continuum). The AH ranged from approximately 0 dB to 80 dB, whereas the OQ ranged from approximately 25% to 99% for most of the vowel continua. However, for two stimuli, the range of AH and OQ was restricted to a smaller range because pilot listening tests showed the resulting output to be judged as being highly unnatural. The exact range of AH and OQ for each vowel is shown in Table TABLE I.. These ranges of AH and OQ were used to generate 11 stimuli, for each vowel where each AH level was combined with the corresponding OQ. Thus, for example, the first stimulus in a particular vowel continuum had the lowest AH level combined with the lowest OQ permissible for that continuum. The second stimulus in that continuum had the next permissible values based on the step-size for AH and OQ for that series (where step-size = permissible range∕10). All other synthesis parameters were kept constant for all stimuli within each vowel continuum. The goal was to obtain a set of vowels that vary in breathiness, without any regard to linearity of the change in breathiness. For the purpose of this experiment, it was not critical to have stimuli that were equidistant in terms of perceived breathiness within or across various vowel continua.

Table 1.

The range and step-sizes used to generate the AH and OQ continua used in experiment 1.

	Stimuli	FEML5	FEML4	FEML3	FEML2	FEML1	MALE5	MALE4	MALE3	MALE2	MALE1
AH (dB)	Range	55–80	0–80	0–75	0–80	0–80	55–80	0–80	0–75	0–80	0–75
	Step-size	2.5	8	7.5	8	8	2.5	8	7.5	8	7.5
OQ (%)	Range	30–99	25–99	35–99	35–99	30–99	30–85	35–99	25–99	25–99	25–99
	Step-size	6.9	7.4	6.4	6.4	6.9	5.5	6.4	7.4	7.4	7.4

All vowel stimuli were generated at a sampling rate of 10 000 Hz and with 16-bit quantization. These were then up-sampled to 12 207 Hz to match the permissible sampling rate of the hardware used. Stimuli were 500 ms in duration and were adjusted in amplitude to have equal root-mean-square (rms) energy. This was done to ensure that the loudness of the stimuli was relatively similar and that large differences in loudness did not bias perceptual data. The stimuli were shaped with 20-ms cosine-squared onset and offset ramps to avoid audible transients.

Finally, the synthesizer was also used to generate two additional waveforms for each stimulus—one for the AH with no voicing and another for the harmonic signal with no AH. These waveforms were used in the development and evaluation of the predictive model described below. The noise waveform was generated by re-synthesizing the vowel with the amplitude of voicing (AV) set to zero and leaving all other parameters at the same value as the original stimulus. The harmonic signal was generated by setting the AH value to zero. Neither of these two signals was used in any listening test.

Listeners

Ten listeners, nine females and one male, were recruited to participate in this experiment. The mean age of the listeners was 21.3 yr and ranged from 20 to 26 yr. All listeners were native speakers of American English and had normal hearing (hearing thresholds below 20 dB hearing level (HL) at octave frequencies between 250 and 8000 Hz). Listeners were recruited from the undergraduate and graduate program in Communication Sciences and Disorders at the University of Florida. These listeners had completed a minimum of one course that discussed various voice disorders and were familiar with the concept of breathiness. However, they had limited prior experience in listening to breathy voice quality. They received a small monetary compensation for participating in the study.

Procedures

The listening test was completed in a single-walled sound attenuating chamber. Each stimulus was presented 5 times in random order for a total of 550 listening trials (10 vowel continua × 11 stimuli∕continuum × 5 presentations). The order of stimulus presentation was randomized across listeners. All stimuli were presented monaurally to the right ear at an intensity of 75 dB sound pressure level (SPL). Stimuli were presented through the TDT System III (Tucker-Davis Technologies, Inc., Alachua, FL), consisting of a high-fidelity DSP board (RP2), programmable attenuators (PA5), and a preamplifier (HB7). Stimuli were presented through ER2 ear inserts (Etymotic, Inc., Elk Grove Village, IL), which have a flat frequency response at the eardrum. The experiment was controlled by the software sykofizx (Tucker-Davis Technologies, Inc.), and the listeners responded by entering the desired rating using a computer keyboard.

Judgments of severity of dysphonic voice quality, including breathiness, form a prothetic continuum since these can be judged on a scale of low to high (e.g., Eadie and Doyle, 2002). For such continua, a magnitude estimation task provides better perceptual data than a standard rating scale task, which may result in ordinal data (Shrivastav et al., 2005). Therefore, listeners were asked to judge the magnitude of breathiness for each stimulus using a free direct magnitude estimation task. In this task, listeners were asked to assign a number between 1 and 1000 to the stimulus to indicate the magnitude of its breathiness. Listeners were free to choose any number but were required to use the numbers in such a way that these reflected the magnitude of change in breathiness across stimuli. Thus, for example, if a stimulus was perceived to have twice the breathiness as another, it should be assigned a number that is twice as large as that assigned to the first stimulus. The task was explained to the listeners, but no specific practice session was implemented. The listening test commenced after the listener confirmed clear comprehension of test instructions and was comfortable with the required task. The judgment data thus obtained were logarithmically scaled, and the preferred estimate of central tendency for such data is the geometric mean. Therefore, the geometric mean of all ratings from all listeners was computed and used for describing changes in breathiness within and across different vowel continua.

Signal processing

As described in the Introduction, two measures were computed for each stimulus: the PL of the harmonic energy and the loudness of the AH (NL). These measures were computed using the loudness model proposed by Moore et al. (1997) as described above. The PL of the signal and loudness of the noise (NL) were used as independent variables to generate a model of breathiness.

Note that both PL and NL require estimation of the AH in a vowel stimulus. As described previously, one way to obtain the noise is through the Klatt synthesizer (by selecting AV = 0). This provides the most accurate estimation of the AH, and measures computed through this approach are henceforth referred to as the “ideal” noise loudness (NL_ideal) and the “ideal” partial loudness of the harmonic energy (PL_ideal). In a previous experiment (Shrivastav and Camacho, 2010), the ratio of NL_ideal to PL_ideal was found to be successful in predicting changes in breathiness for vowels. This ratio is henceforth referred to as the loudness ratio (η). To indicate that η was computed using ideal estimates of AH, an appropriate subscript is used (η_ideal).

Finally, the fundamental frequency (f₀) of the vowel was included in the model. However, instead of expressing it in hertz, a quasi-logarithmic transformation of it produced by the equivalent rectangular bandwidth (ERB) scale was used corresponding to the same ERB scale used in the formulation of the filter-bank portion of the loudness model (Moore et al., 1997). This was computed using the following formula:

$$\phi =21.4{\text{log}}_{10}\left(1+\frac{f}{229}\right),$$ (2)

where ϕ is the frequency in ERB units and f is the frequency measured in kilohertz.

Analyses and results

Breathiness judgments

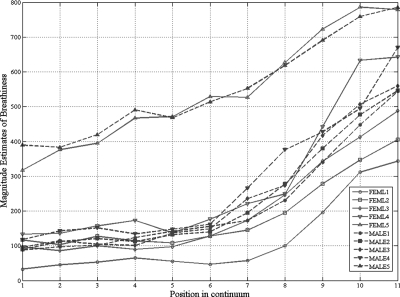
In general, breathiness was judged to increase with increasing OQ and AH along the 11-point continuum. However, the rate of change in breathiness varied across the ten vowel continua, with some continua showing minimal changes in breathiness for the initial few stimuli. The absolute values of the listener judgments ranged from 32 to 786. For ease of computation, these raw data were first converted to a log₁₀ scale, transforming majority of the nominal values (those ranging from 100 to 1000) to a range from 2 to 3. Then, the log-transformed data was rescaled by subtracting a constant value of 2, resulting in data ranging from 0 to 1 for majority of the stimuli. Such transformation of the data had no effect on its dispersion but made it considerably simpler to model using linear and non-linear equations. The log-transformed magnitude estimation data are shown in Fig. 1.

Figure 1.

(Color online) Magnitude estimate data for the ten synthetic voice continua.

Intra-listener reliability was estimated by obtaining the mean Pearson’s correlation between one set of ratings (one repetition of the stimuli) and the remaining four sets of ratings within a listener. Thus the mean was computed over ten correlations, since each stimulus was rated five times {for n = 5 sets of ratings, there are [n × (n − 1)]∕2 unique pairs}. The mean intra-listener reliability measure across ten listeners was 0.81 (standard deviation = 0.10; range = 0.67–0.96). Inter-listener reliability was estimated as the average Pearson’s correlation between the geometric mean ratings from one listener and the remaining nine listener (thus, the average was computed across nine correlations). This was found to average 0.72 (standard deviation = 0.07; range = 0.57–0.79).

Model development

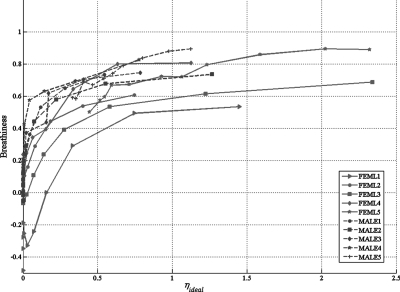
Figure 2 shows the change in breathiness as a function of changes in η_ideal for the ten vowel continua. For most continua, breathiness shows a monotonic but non-linear increase with an increase in η_ideal, except at the low end, where no clear pattern is noted. At the low end of the continuum, stimuli show little or no change in η_ideal despite reasonably large changes in AH and OQ, and random (at least, non-monotonic) variation in breathiness. This can be also be inferred from Fig. 1, which shows little change in breathiness for the first 3–6 positions in many vowel continua. This mismatch between the acoustic and perceptual data may be explained by the large difference limen observed for the perception of changes in AH, particularly at low AH levels (Kreiman and Gerratt, 2003; Shrivastav and Sapienza, 2006). However, the output of the loudness model is presumed to be sensitive to such perceptual limitations, thus accounting for some of these mismatches.

Figure 2.

(Color online) Change in breathiness as a function of η_ideal for the ten synthetic vowel continua.

Figure 2 also shows that the same η_ideal resulted in greater breathiness for the male vowel continua than for female continua, suggesting a possible inverse relationship with the pitch of the vowels. This possibility was further examined by using pitch as an independent variable for predicting breathiness. This is described in more detail below.

Finally, note that perceptual scores for one vowel continuum (FEML1) showed a large non-monotonic trend in perceptual data for the first few stimuli in the continuum despite minimal changes in η_ideal. Therefore, this stimulus continuum was excluded from the curve-fitting operations described below but was included for all subsequent evaluations. Two other continua that were excluded when constructing the model were FEML5 and MALE5. This is because these continua started at η_ideal values very far from zero,1 which made it impossible to determine a breathiness threshold b₀ for them (see curve-fitting process below).

The data in Fig. 1 were modeled using a set of curve-fitting operations. These procedures have been used previously to model vowel continua that vary only in AH (Shrivastav and Camacho, 2010). First, an equation was generated for each individual vowel continuum. A power relationship of the following form was observed to produce a good fit to the data for each continuum:

$$b=b_0+k{\left({\eta }_{\text{ideal}}\right)}^p,$$ (3)

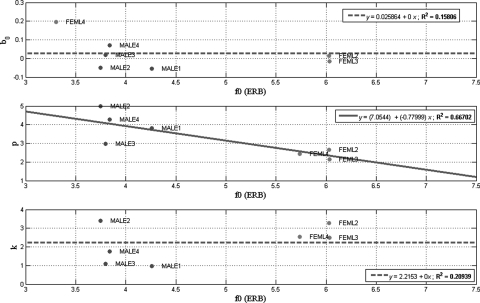
where b is the translated logarithm of breathiness magnitude, p is the power, and b₀ and k are constants. Next, to determine if any of the parameters in Eq. 3 varied systematically with fundamental frequency, linear regressions between the vowel f₀ (ϕ measured in ERB units) and the three equation parameters (p, k, and b₀) were computed. These regressions are displayed in Fig. 3 and show that only p was systematically related to ϕ (R² = 0.667). Therefore, Eq. 3 was modified to include the linear regression function relating p to ϕ. The parameters b₀ and k did not vary systematically with ϕ (R² values of 0.158 and 0.209, respectively) and their average values across the seven vowel continua were used. Figure 3 shows the regression for p and its R². The figure also shows the R² for k and b₀, but their respective linear equations (and lines) were replaced by their means (and horizontal lines) to give a better idea of the value used for these parameters. Finally, the breathiness (b) of a vowel with a known loudness ratio (η_ideal) and f₀ (ϕ expressed in ERB units) was described by the following formula:

$$b({\eta }_{\text{ideal}},\phi )=0.45{\eta }_{\text{ideal}}{}^{1∕(7.054-0.78\phi )}+\mathrm{0.026.}$$ (4)

Figure 3.

(Color online) Regression functions predicting model parameters (b₀, p, and k) from vowel fundamental frequency. Solid line shows the linear regression prediction. Dashed line shows the average value for the nine stimulus continua.

As in Eq. 3, Eq. 4 describes a power function between breathiness and η_ideal, but the power is now a linear function of f₀.

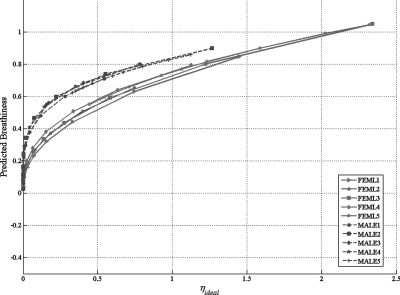
To evaluate the success of Eq. 4 in describing the perceptual data, this equation was used to estimate the breathiness of each stimulus on each of the ten vowel continua. The predicted breathiness values are shown in Fig. 4. The goodness of the fit was evaluated by computing the mean absolute error (MAE) and the amount of variance in perceptual data accounted for by the model (R²). A perfect fit would result in MAE = 0 and R² = 1. Higher values of MAE and lower values of R² indicate a poor fit between the predicted and perceptual data. These values were found to be 0.0625 and 0.9248, respectively, suggesting that Eq. 4 was generally able to model the perceptual data with high accuracy. However, the predicted data did not fit the continuum endpoints well. As noted previously, the perceptual data at the low end of the breathiness continuum showed high variability which was not accounted for by Eq. 4. Similarly, Eq. 4 failed to account for stimuli with very high levels of η_ideal (η_ideal > 1.2 for females and η_ideal > 0.8 for males) because stimuli with such high values of n were not utilized for generating the regressions functions of the model (MALE5 and FEML5 were excluded from the model development).

Figure 4.

(Color online) Change in breathiness as a function of η_ideal for ten synthetic vowel continua as predicted by Eq. 4.

Discussion

In experiment 1, listeners judged the breathiness of a set of synthetic vowel continua created by systematic co-variation of AH and OQ to simulate naturally occurring vowels that vary in breathiness. These judgments were used as the basis for a model of the relationship between perceived breathiness and the ratio of NL and PL (η_ideal). The resulting model was a power function relating η_ideal and breathiness. The power was observed to be inversely related to fundamental frequency (measured in ERB units), so that the same change in η_ideal led to greater changes in breathiness for the male speakers than for female speakers. It is also possible that changes in p resulted from factors other than the fundamental frequency (such as the formant ratios resulting from differences in vocal tract length). However, such interactions were not evaluated in the present experiment.

The general form of the equation, including the inverse relationship between the power and fundamental frequency, are consistent with the functions reported by Shrivastav and Camacho (2010) for vowels that vary in AH alone [see Eq. 1]. However, unlike Shrivastav and Camacho (2010), the model generated by simultaneous manipulation of AH and OQ did not require a stimulus-dependent breathiness-threshold point (b₀) and only one parameter (p) was observed to vary systematically with stimulus f₀. This is presumably because of an interaction between AH and H1-H2 (resulting from changes in OQ) in cuing breathiness. An interaction between OQ and AH levels in cuing breathiness has been documented by other experiments as well. For example, Kreiman and Gerratt (2005) found that listeners performing a method-of-adjustment task showed significantly greater variance in adjusting the noise-to-harmonic ratio (NSR) for stimuli with lower H1-H2 (which results from a smaller OQ), possibly suggesting a smaller difference limen for breathiness for stimuli with steeper spectral slopes. By accounting for such interactions amongst various acoustic cues, the breathiness model described here is likely to better capture variability in breathiness judgments for natural stimuli.

Although f₀-dependent, the exponential term was always less than 1.0, consistent with a compressive relationship between η_ideal and breathiness. Such a compressive relationship is typical for many psychophysical phenomena such as those obtained for loudness or brightness (e.g., Stevens, 1975, p. 15) and suggests that the perception of breathiness may follow the same general psychophysical rules that are observed for many other sensory stimuli. Certain other constants in the computational model were derived by averaging values from individual vowel continua. Despite this, the high R² and low MAE in predicted breathiness suggest that the model was a good representation of the relationship between breathiness and η_ideal.

Finally, note that the ten vowel continua used to generate this model provide limited variability in f₀. These stimuli essentially result in a bimodal distribution of f₀ corresponding to the male and female speakers. Thus, the linear regression function used to estimate the relationship between f₀ and p should only be considered preliminary. Further experimentation with stimuli that vary systematically in f₀ is necessary to confirm or modify this relationship.

EXPERIMENT 2: MODEL EVALUATION

The goal of this experiment was to evaluate the success of the model obtained in experiment 1 in predicting breathiness for novel stimuli. The computational model described in Eq. 4 was used to predict breathiness for a set of natural and synthetic stimuli, and the resulting estimates of breathiness were compared against perceptual data.

Methods

Stimuli

A total of 39 stimuli (29 natural and 10 synthetic vowels) were used in this experiment. The natural vowels were randomly selected from the Kay Elemetrics Disordered Voice database (Kay Elemetrics, Inc., Lincon Park, NJ). This database consists of approximately 700 disordered voices, recorded at a sampling rate of 50 000 Hz and with 16-bit quantization. For the purpose of this experiment, these were down-sampled to 24 414 Hz to match the permissible sample rate of the hardware. A 500-ms segment was extracted from each speaker. The stimuli were scaled to have equal rms and the onset and offset were shaped by 20-ms cosine-squared ramps.

Ten synthetic vowels were also tested in this experiment. These were included because synthetic stimuli, unlike natural samples, permit accurate estimation of AH. Testing the model with both natural and synthetic stimuli may help determine the extent to which inaccuracies in AH estimation in natural stimuli affect the model performance. Ten synthetic stimuli were modeled after ten natural voices selected using stratified sampling procedures from the set of 29 natural voices described above. A pilot listening test was completed to rank order the natural voices in order of magnitude of breathiness. The rank order was divided into five linearly spaced categories and two stimuli from each category were randomly selected. These stimuli were modeled with a Klatt synthesizer using the procedures described in experiment 1. Note that an exact match to the target voice was not essential for the purpose of this experiment. Rather, the synthetic stimuli were designed to have the same range of breathiness as observed in the natural voices. Also note, that unlike the natural voices, these stimuli were synthesized using a 10 kHz sampling rate and were therefore limited to a 5 kHz bandwidth.

Listeners

Eight listeners, all females, with a mean age of 21 yr (range = 18–28 yr) were tested in this experiment. None of these listeners participated in experiment 1. Listeners were recruited from the undergraduate and graduate program in Speech-Language Pathology or Linguistics at the University of Florida. All listeners were native speakers of American English and were screened for normal hearing. These listeners had little to no prior experience in making perceptual judgments of breathiness. Listeners received a small monetary compensation for participation in the study.

Procedures

A free direct magnitude estimation procedure, identical to the one used in experiment 1, was completed. Each of the 39 stimuli was presented 5 times resulting in a total of 195 presentations (39 stimuli × 5 repetitions). The order of presentation was randomized across listeners. Stimulus presentation and response collection was identical to experiment 1.

Prior to testing, a brief training session was completed to familiarize the listeners with the test procedures. In this training session, listeners were asked to complete a free direct magnitude estimation task for a set of 17 (14 natural and 3 synthetic) vowels randomly selected from the Kay Elemetrics Disordered Voice Database. The stimuli used for training did not include any items from the test set. The goal of this training was merely to familiarize the listeners with breathiness and the direct magnitude estimation procedure. No feedback was provided.

The geometric means of the magnitude estimates of breathiness obtained in the listening test were transformed to a logarithmic scale and translated to the range 0–1. This was essential because Eq. 4 derived during the development of the model was also generated on log-transformed and translated data.

Signal processing

The signal processing steps were generally identical to those described in experiment 1. The goal was to separate each vowel into its periodic and aperiodic components. These components were given as input to the loudness model to estimate the loudness of the noise (NL) and the PL of the harmonic energy. The fundamental frequency (ϕ) was measured in ERB units for all stimuli as described in experiment 1. Finally, ϕ and η (the ratio of NL to PL) were used as the predictors of breathiness using Eq. 4.

As described in experiment 1, the estimation of AH in synthetic voices was done through re-synthesis of the stimuli with AV set to zero. Since this approach was not feasible when using natural stimuli, the AH was estimated using an algorithm described by Milenkovic (1995, 1997) and implemented in the software CSPEECH (Milenkovic; University of Wisconsin—Madison, WI). This algorithm has been used in prior experiments on breathiness (e.g., Shrivastav and Sapienza, 2003). Briefly, this algorithm attempts to determine a perfectly periodic glottal source within a small temporal window and estimates the AH by subtracting the actual vowel waveform from the ideal waveform. For the natural stimuli used in this experiment, the AH was estimated using this algorithm and the measures computed from these estimates were referred to as the “estimated” partial loudness of the harmonic energy (PL_estimate) and the “estimated” noise loudness (NL_estimate). In order to predict breathiness for natural stimuli, the ratio of NL_estimate and PL_estimate (referred to as η_estimate) was substituted for η_ideal in Eq. 4.

Analyses and results

Breathiness judgments

The magnitude estimation scores ranged from 72 to 753 for natural stimuli and from 90 to 877 for synthetic stimuli. As in experiment 1, the raw scores were rescaled by first converting to a logarithmic scale (base 10) and then subtracting a constant value of 2 from each score. The synthetic and natural stimuli were observed to span approximately similar range of breathiness. A weak correlation between the fundamental frequency of the stimuli and perceptual judgments of breathiness were observed (Pearson’s correlation was −0.16 and +0.31 for natural and synthetic stimuli, respectively).

As in experiment 1, intra-listener reliability was estimated by obtaining the mean Pearson’s correlation between one set of ratings (one repetition of the stimuli) and the remaining four sets of ratings within a listener. Thus, the mean was computed over ten correlations, since each stimulus was rated five times [(5 × 4)∕2 = 10 unique pairs]. The intra-rater reliability was found to average 0.76 (standard deviation = 0.11) across the eight listeners and ranged from 0.63 to 0.87. Inter-listener reliability, estimated as the Pearson’s correlation between the average ratings from each listener was found to average 0.74 (standard deviation = 0.10) and ranged from 0.55 to 0.83. These values were very similar to those obtained in experiment 1 and showed moderately high inter- and intra-listener reliability.

Model evaluation

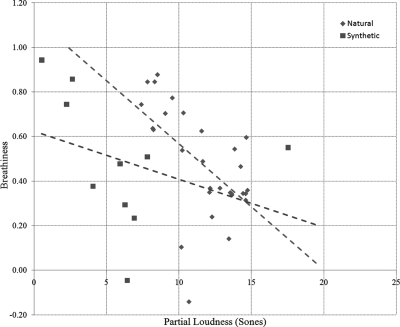
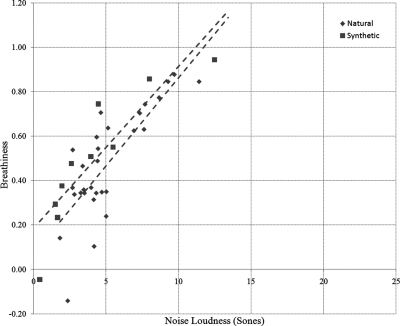
The relationships between perceived breathiness and each of PL and NL are shown in Figs. 56. Note that different methods were used to separate the periodic and noise components for the synthetic and natural stimuli. Therefore Figs. 56 show PL_estimate and NL_estimate for the natural stimuli, but PL_ideal and NL_ideal for the synthetic stimuli. For natural stimuli, both PL_estimate and NL_estimate show a moderate correlation (Pearson’s correlation of −0.57 and 0.77, respectively) with perceived breathiness. For synthetic stimuli, PL_ideal is moderately correlated with breathiness (Pearson’s r = −0.47), but NL_ideal shows a high correlation with breathiness (r = 0.95). Except for the synthetic stimulus that was judged to have the highest breathiness, NL_ideal spans the same range as the NL_estimate. However, PL_ideal obtained from synthetic vowels is generally lower than the PL_estimate estimated from natural vowels.

Figure 5.

(Color online) Perceived breathiness as a function of PL for the natural and synthetic stimuli tested in experiment 2.

Figure 6.

(Color online) Perceived breathiness as a function of NL for the natural and synthetic stimuli tested in experiment 2.

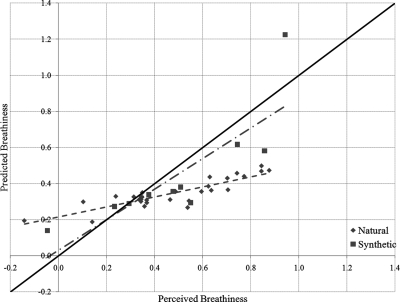
To evaluate the success of Eq. 4 in predicting breathiness for novel voices, it was used to predict the breathiness of all stimuli used in the present experiment. Figure 7 compares the breathiness estimated from Eq. 4 to the perceptual data obtained through the listening test. For all data, a correlation of 0.773 was obtained between the predicted and perceived breathiness scores. Thus, the model accounted for 59.8% of the variance in the perceptual data. Some differences were observed between the synthetic and natural stimuli. For synthetic stimuli, the model predictions were generally lower than perceived breathiness resulting in high absolute error (MAE = 0.31), but the predicted scores showed a high correlation with perceptual data (Pearson’s r = 0.828; R² = 0.686). The correlation between the model predictions and the perceptual judgments was adversely affected by one stimulus that was judged to have the highest breathiness. Exclusion of this stimulus increased the Pearson’s correlation to 0.922 and the corresponding R² to 0.851. For natural voices, the model overestimated the breathiness for some of the least breathy stimuli but underestimated perceptual data for voices with higher magnitude of breathiness. The MAE between breathiness predicted by Eq. 4 and perceptual data was 0.1765. The correlation between the predicted and perceived data was 0.873, accounting for 76.2% of the variance in perceptual data.

Figure 7.

(Color online) Perceptual judgments of breathiness vs breathiness predicted by the model for natural and synthetic stimuli tested in experiment 2. The solid line indicates model output if the predicted values were identical to perceptual data. The dashed and the dashed-dot lines show best fitting linear regression for the natural and synthetic stimuli, respectively.

Discussion

The goal of experiment 2 was to evaluate the success of the model described by Eq. 4 in predicting breathiness for novel stimuli. The breathiness values of the 39 vowels were computed using this model and were compared against perceptual judgments from a panel of listeners. Although the predicted values of breathiness show a high correlation with perceptual data, the absolute values obtained from the model differ from those obtained by averaging listener data. The high correlation between the perceptual data and the model predictions for novel test stimuli suggest that η is a good candidate for the development of a computational model for breathiness. Furthermore, the general form of the predictive equation is consistent with prior experiments on breathiness using synthesized vowels varying in AH levels alone (Shrivastav and Camacho, 2010) and show that breathiness is related to a power function of η. The power of this function appears to be f₀-dependent but was always less than 1.0, suggesting a compressive relationship between η and breathiness. This computational model successfully described breathiness for novel stimuli, with the exception of one synthetic vowel, which was perceived to have the greatest magnitude of breathiness. This discrepancy likely resulted because the development of the model [Eq. 4] excluded extremely high levels of breathiness (FEML5 and MALE5 in experiment 1). Thus, it is possible that further modifications to the model are necessary to extend its accuracy to stimuli with very high breathiness.

Computing breathiness using Eq. 4 requires accurate estimation of AH spectra. However, the algorithm used for this estimation may introduce some errors in model output. To approximate the magnitude of error resulting from inaccurate estimation of AH, the R² between predicted breathiness and perceptual scores were compared for synthetic and natural stimuli. The breathiness model accounted for 85% of the variance in perceptual data for synthetic stimuli when discarding one outlier (as described above). Therefore, inaccuracies in estimating AH spectra may have contributed a maximum of 9% error in model performance. However, note that differences in sampling rate between natural and synthetic voices complicate a direct comparison between the two sets of data. The natural voices tested in this experiment had a higher bandwidth than the synthetic stimuli. Few experiments have examined the contributions of high frequency components (over 5 kHz) to voice quality perception, and it is difficult to speculate how the differences in stimulus bandwidths might have affected model performance.

Despite the high R² between predicted breathiness and perceptual scores, the MAE was moderately high. This incongruence—good correlation but poor absolute judgment—is primarily a reflection of the experimental methods employed in this experiment. The mismatch between R² and MAE likely arise because perceptual data obtained using free magnitude estimation tasks does not result in consistent values when used across different stimulus sets (e.g., Guilford, 1954). This is because the absolute values are affected by a number of biases, such as the centering bias or range- and frequency-effects (Guilford, 1954; Parducci and Wedell, 1986) and are influenced by variables such as the number and type of stimuli used in an experiment. Since experiments 1 and 2 used different sets of stimuli, these biases likely contributed to an increase in the MAE between the predicted breathiness and perceptual scores. Note that Eq. 4 overestimated perceptual data at low levels of breathiness and underestimated it for stimuli judged to have high breathiness (Fig. 6), which may reflect a possible centering bias. The MAE may also be affected by differences in sampling rate between the natural and synthetic stimuli. However, as mentioned above, the exact nature of this discrepancy remains unknown because the contributions of high frequency components to voice quality perception have not been studied in much detail.

In summary, the breathiness predicted by Eq. 4 was highly correlated with perceptual data for novel stimuli, suggesting that η is a good candidate for predicting breathiness. Breathiness appears to be a power function of η. The model developed from stimuli co-varying in AH and OQ generalized well to both natural and synthetic test stimuli. Errors in estimating AH spectra may contribute up to 9% error in model performance. The model may need to be further modified to accommodate stimuli with the very high magnitude of breathiness.

SUMMARY AND FUTURE DIRECTIONS

A computational model to predict breathiness in vowels was developed based on perceptual data for a set of ten synthetic vowel continua that co-varied in the OQ of the glottal source and the level of the AH. Both of these changes have been observed to correlate with changes in breathiness in vowels and co-variation of these parameters was assumed to approximate naturally occurring vowels closely. Based on the findings of Shrivastav and Sapienza (2003), an auditory-processing front-end was used for preprocessing the vowel spectrum prior to the computation of predictor variables. Two measures computed from the auditory spectrum (PL and NL) and the vowel fundamental frequency (measured in ERB units) were used to predict breathiness. PL is an estimate of the loudness of the periodic components in the vowels when these are masked by the AH. Therefore, in a broad sense, PL is somewhat similar to the HNR computed from the vowel. However, unlike HNR, it accounts for the non-linear loudness growth and masking functions observed in the auditory system. The perceived magnitude of breathiness is inversely related to PL. The NL is an estimate of the loudness resulting from the AH alone; greater NL typically results in the perception of greater breathiness.

The computational model for predicting breathiness described here is similar to that proposed by Shrivastav and Camacho (2010) where breathiness was modeled as a power function of the loudness ratio (η). The power of this function appears to vary with the fundamental frequency of the vowel, such that vowels with lower fundamental frequency show a greater increase in breathiness for an equal change in η. However, unlike Shrivastav and Camacho (2010), the inclusion of stimuli co-varying in AH and OQ resulted in a monotonic increase in breathiness even at very low AH levels. It appears that changes in OQ (which lead to a change in the first harmonic amplitude in the vowel spectrum) is an effective cue for discriminating breathiness at low levels of AH.

The success of the model developed using synthetic stimuli was evaluated in a separate experiment using a novel set of stimuli. Results show a high correlation between perceived breathiness and model predictions, but the absolute predicted values did not match the perceptual data. These differences are partly related to the nature of the experimental task employed to obtain perceptual data. Additionally, some errors in model prediction likely arise from inaccuracies in decomposing natural voices into its periodic and aperiodic components as well as differences in the bandwidth of the natural and synthetic stimuli.

The findings of the experiments described here also help identify future directions for research. First, various biases inherent to the direct magnitude estimation task makes it inappropriate for research to model the perception of voice quality or to develop tools for voice quality measurement. This is because the measurements across multiple experiments cannot be directly compared to one another. Alternate approaches to evaluate the perception of voice quality, such as the matching tasks (Gerratt and Kreiman, 2001; Patel et al., 2010) need to be developed and standardized. Second, more accurate algorithms need to be developed to decompose voices into its periodic and aperiodic components. Goor et al. (2004) showed that the accuracy of various algorithms to estimate the noise level in stimuli varies with the level of AH in voices. Improving the accuracy of these algorithms can further improve the performance of models to describe voice quality perception. Finally, additional research needs to be done to evaluate the role of high frequency components on the perception of breathiness as well as other voice quality dimensions.

CONCLUSIONS

A model to predict breathiness in vowels is reported. In this model, breathiness is modeled as a power function of the ratio of NL to PL. The power of this function is linearly related to the vowel f₀. This model was tested with a set of novel voices and a high correlation was achieved between predicted breathiness and perceptual data. Sources of error in model predictions include the experimental tasks employed to generate perceptual data and the inaccuracies in decomposing voices into its periodic and aperiodic components.