Abstract
Background and Aims
Functional–structural modelling can be used to increase our understanding of how different aspects of plant structure and function interact, identify knowledge gaps and guide priorities for future experimentation. By integrating existing knowledge of the different aspects of the kiwifruit (Actinidia deliciosa) vine's architecture and physiology, our aim is to develop conceptual and mathematical hypotheses on several of the vine's features: (a) plasticity of the vine's architecture; (b) effects of organ position within the canopy on its size; (c) effects of environment and horticultural management on shoot growth, light distribution and organ size; and (d) role of carbon reserves in early shoot growth.
Methods
Using the L-system modelling platform, a functional–structural plant model of a kiwifruit vine was created that integrates architectural development, mechanistic modelling of carbon transport and allocation, and environmental and management effects on vine and fruit growth. The branching pattern was captured at the individual shoot level by modelling axillary shoot development using a discrete-time Markov chain. An existing carbon transport resistance model was extended to account for several source/sink components of individual plant elements. A quasi-Monte Carlo path-tracing algorithm was used to estimate the absorbed irradiance of each leaf.
Key Results
Several simulations were performed to illustrate the model's potential to reproduce the major features of the vine's behaviour. The model simulated vine growth responses that were qualitatively similar to those observed in experiments, including the plastic response of shoot growth to local carbon supply, the branching patterns of two Actinidia species, the effect of carbon limitation and topological distance on fruit size and the complex behaviour of sink competition for carbon.
Conclusions
The model is able to reproduce differences in vine and fruit growth arising from various experimental treatments. This implies it will be a valuable tool for refining our understanding of kiwifruit growth and for identifying strategies to improve production.
Keywords: Actinidia deliciosa, kiwifruit, L-systems, plant architecture, carbon allocation, functional–structural plant model
INTRODUCTION
Kiwifruit (Actinidia deliciosa) originated from China, but was first grown commercially in New Zealand and has become the country's most important export horticultural crop (Ferguson and Bollard, 1990). The kiwifruit vine is characterized by vigorous growth and intense competition for carbohydrates between vegetative and reproductive components. Controlling the vegetative growth of the canopy and channelling carbohydrates into fruit is a major challenge for kiwifruit growers (Miller et al., 2001; Thorp et al., 2003). Traditionally, developing new training and pruning strategies to control canopy vigour and maximize production of high-quality fruit involves multiple field trials, which are costly and time consuming. Our long-term goal is to use functional–structural plant modelling for improving management techniques by exploring the vine's behaviour under hypothetical management practices in different environmental conditions (e.g. temperature and light). The aim of the research reported in this paper was to develop a functional–structural kiwifruit vine model, incorporating existing knowledge on kiwifruit architecture and physiology, which can be used to guide future experimental work by increasing our understanding of how different aspects of the plant interact.
To this end, a model was developed that represents the following features of kiwifruit vine growth and function: (a) plasticity of kiwifruit architecture and, in particular, effects of genotype and temperature on shoot growth and shoot tip abortion (Foster et al., 2007); (b) effects of management practices on shoot growth, light distribution within the canopy and fruit dry weight; (c) the role of reserves in the vine carbon dynamics; and (d) effects of fruit position within the canopy on its dry weight.
In earlier work, Buwalda (1991) constructed a process-based compartment model of the kiwifruit vine that included maintenance respiration, growth of organs, and synthesis and hydrolysis of carbon reserves, along with canopy net photosynthesis. The model's main focus was on the carbon economy of the vine, including predicting the effects of plant–environment interactions; however, it had a number of simplifying assumptions: (a) a common pool of carbon; (b) no representation of 3-D structure and light distribution; and (c) the rate of photosynthesis was considered proportional to total leaf area. Although the model was able to reproduce several observed phenomena [such as resource-limited growth, depletion and regeneration of reserves, and root system turnover (Buwalda, 1991)], the common carbon pool model cannot adequately account for the architectural plasticity of the vine [as demonstrated for grapevine (Pallas et al., 2010)] and the variations in fruit size caused by differences in local carbon supply within the vine (Tombesi et al., 1993; Piller and Meekings, 1997). Thus, a process-based model is unable to reproduce fully the desired features of kiwifruit vine growth and development.
Greaves et al. (1999) investigated the importance of carbon reserve distribution in parent branches on axillary shoot growth. They modelled a single parent branch as a linked system of discrete elements, with each element comprised of a labile, reserve and structural pool. They considered carbon transport between the labile pools of connected elements, carbon synthesis and hydrolysis between reserve and labile pools, and the growth of shoots (not the parent branch itself) by movement of carbon from the labile pool into the structural pool. Output from their model showed general agreement with data from their own experiments on mature kiwifruit vines. Although this model is theoretically capable of meeting the features of the vine, it was designed for the sole purpose of investigating the effect of carbon reserves on early shoot growth (before the leaves become sources of carbon). Therefore, without substantial changes to the simple mechanism used to drive growth, it is unable to produce all the desired features of the vine's growth (Greaves et al., 1999).
Greer et al. (2004) modelled canopy leaf area development and daily amount of carbon acquisition of kiwifruit vines from a mathematical model of shoot leaf area expansion and photosynthesis of individual leaves. They extended the shoot leaf area expansion model of Seleznyova and Greer (2001) by including architectural components (e.g. shoot type, node number and probability of budbreak), and used a rectangular hyperbolic function to model daily photosynthesis for leaves. Measurements of canopy leaf area development and rates of photosynthesis from vines grown in an orchard were in close agreement with the output from their model, and the estimated total carbon acquisition over the growing season was close to the measured biomass of the vine over that season. They concluded that their physiological model is scalable to whole vines but requires further development for carbon partitioning between individual organs. In other words, their model does not take into account the structure of the vine.
In order to integrate structure with carbon dynamics, functional–structural plant models (FSPMs) can be used. FSPMs are computational models that explicitly account for the 3-D architecture of a plant as it is governed by physiological processes and the environment (Sievänen et al., 2000; Godin and Sinoquet, 2005; Vos et al., 2007, 2010). The L-system modelling approach (Lindenmayer, 1968) is widely used to implement FSPMs (Fourcaud et al., 2008; Vos et al., 2010), as it can represent development, growth and carbon allocation processes at the organ level, taking into account effects of organ position within the canopy (Prusinkiewicz et al., 1997). Also, an L-system model can be interfaced with external models to incorporate environmental effects (Měch and Prusinkiewicz, 1996), such as light distribution (Cieslak et al., 2008), and allows for interaction with the model as the simulation progresses: first, by user-driven modification of the numerical parameters in the model (Prusinkiewicz, 2004), and, secondly, by direct manipulation of the visual representation of the model on the computer screen (Prusinkiewicz et al., 2007b).
In this paper, a functional–structural kiwifruit vine model is presented that integrates architectural development with mechanistic modelling of carbon transport and allocation. The model was implemented using the L-system-based modelling platform, L-studio (Prusinkiewicz et al., 2000), in the L + C modelling language (Karwowski and Prusinkiewicz, 2003). The focus here is on the modelling concepts used to incorporate existing biological knowledge and hypotheses on kiwifruit architecture and physiology into the model. In order to demonstrate the model's capabilities and show its potential to reproduce the desired features of kiwifruit growth, the qualitative behaviour of the model is investigated through several simulations. The parameter values used in these simulations are either taken directly from existing experimental work or are fitted manually. Because of the complexity of the kiwifruit vine model, calibration and quantitative validation require the design of new experiments for parameter fitting, concentrating on just one particular aspect of the vine at a time [e.g. competition between reproductive and vegetative components (Minchin et al., 2010)], and is beyond the scope of this paper. Nevertheless, a comparison is made between model output and observed data.
METHODS: DESCRIPTION OF THE MODEL
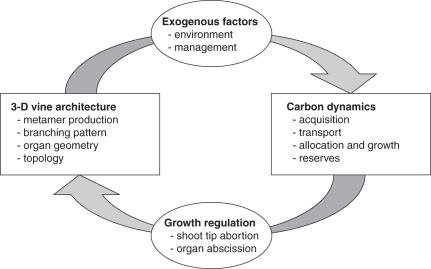
The kiwifruit vine model combines aspects of the vine's architecture, carbon dynamics and the interactions between them (Fig. 1). For the architectural component, it includes a representation of individual organs and their topological connections, with rules for production of metamers (Cieslak et al., 2007). For the carbon dynamics component, it includes carbon acquisition by leaves, transport throughout the plant, allocation and growth dependent on availability, and the role of carbon reserves (Cieslak et al., 2010). The model accounts for exogenous factors, such as light distribution, temperature and horticultural manipulation (pruning and training), and other endogenous factors, such as shoot tip abortion and organ abscission. All of these aspects are detailed in the remainder of this section, and Tables 1 and 2 summarize the various parameters and variables of the model, respectively.
Fig. 1.
Diagram of the kiwifruit vine model structure, showing the architectural and carbon dynamics aspects with the interactions between them.
Table 1.
The model parameters (by order of appearance in the text): symbols, definitions, units and values used in the simulations
| Symbol | Definition | Value and units | Reference |
|---|---|---|---|
| Shoot development | |||
| pbb(n, m) | Probability of budbreak by node on parent cane | Empirical function (dimensionless) | Seleznyova et al. (2002) |
| psd(n, m) | Probability of shoot development by node on parent cane | See eqn (1) (dimensionless) | |
| cmin | Carbon concentration threshold for shoot development | 0·01 g C m−3 | |
| P(T) | Phyllochron as function of temperature | Fig. 5 (days) | Morgan et al. (1985) |
| T | Temperature over time | Empirical function (°C) | Greer et al. (2004) |
| θ | Leaf phyllotaxis angle | 144 ° | Ferguson (1990) |
| ϕ | Leaf inclination angle | 33 ° | Morgan and McNaughton (1991) |
| cmin,flower | Carbon concentration threshold for flower abortion | 0·01 g C m−3 | |
| Photosynthesis | |||
| Pmax | Maximum photosynthetic rate | 15·2 µmol CO2 m−2 s−1 | Greer et al. (2004) |
| φapp | Apparent photon yield | 0·039 mol CO2 mol−1 | Greer et al. (2004) |
| D | Maximum potential photon flux density above the canopy | 1300 µmol PAR m−2 s−1 | Greer et al. (2004) |
| Leaf growth | |||
| qleaf | Sink priority for leaf growth | 0·01 g C m−3 | |
| τleaf(T) | Duration of rapid leaf growth | Fig. 5 (days) | Seleznyova and Halligan (2006) |
| B(n) | Leaf growth parameter | Fig. 7 (g C) | Seleznyova and Greer (unpubl. res.) |
| L | Specific leaf area | 3·69e-6 m2 g−1 C | Seleznyova and Greer (unpubl. res.) |
| Internode growth | |||
| ρ | Internode volumetric density | 1·89e-7 g C m−3 | Seleznyova and Greer (unpubl. res.) |
| qinde,pri | Sink priority for internode elongation | 0·01 g C m−3 | |
| qinde,sec | Sink priority for internode thickening | 0·05 g C m−3 | |
| τinde(T) | Duration of rapid internode growth | τleaf(T)/2 (days) | Seleznyova (unpubl. res.) |
| ksec | Long-term internode thickening rate | 0·003 (dimensionless) | |
| klogistic | Rapid initial internode thickening rate | 0·28 (dimensionless) | |
| Internode flow resistance | |||
| kΩ | Transport resistance coefficient | 0·025 s m−3 | |
| Fibrous root growth | |||
| qroot | Sink priority for fibrous root growth | 30 g C m−3 | |
| kprgr | Potential fibrous root growth rate | 0·003 g C g−1 C d−1 | Buwalda (1991) |
| Tprgr | Root growth temperature response coefficient | ln(2)/10 (dimensionless) | Buwalda (1991) |
| Fruit growth | |||
| qfruit | Sink priority for fruit growth | 30 g C m−3 | |
| Sfmax | Maximum potential final fruit size | 14·5 g C | |
| k1, k2, k3 | Fruit growth parameters | 0·02 d−1, 22·21 g−2 C, 0·64 g C | Gandar et al. (1996) |
| Maintenance respiration | |||
| qrsp,i | Sink priority for maintenance respiration of organ type i (leaf, internode, roots, fruit) | 1e-4 g C m−3 | |
| mleaf | Leaf maintenance respiration coefficient | 8·06e-3 g C g−1 C d−1 | Walton and Fowke (1995) |
| minde | Internode maintenance respiration coefficient | 5·27e-3 g C g−1 C d−1 | Walton and Fowke (1995) |
| mroot | Root maintenance respiration coefficient | 1·84e-3 g C g−1 C d−1 | Walton and Fowke (1995) |
| mfruit | Fruit maintenance respiration coefficient | 1·43 g C g−1 C d−1 | Walton and Fowke (1995) |
| Trsp,i | Respiration temperature response coefficient for organ type i | ln(2)/10 (dimensionless) | Buwalda (1991) |
| cmin,abs | Carbon concentration threshold for organ abscission due to insufficient supply for maintenance | 0·01 g C m−3 | |
| Leaf carbon supply | |||
| σ | Constant for converting units of Pgross to g C m−2 d−1 | 1·04 g C s μmol−1 CO2 d−1 | Calculated |
| qsrc | Leaf carbon supply rate | 1·0 g C m−3 | |
| Carbon reserves | |||
| smax,inde | Maximum starch content per unit of structural carbon in an internode | 0·06 g starch g−1 C | Smith et al. (1992) |
| smax,roots | Maximum starch content per unit of structural carbon in roots | 0·22 g starch g−1 C | Smith et al. (1992) |
| qsyn | Sink priority for starch synthesis | 0·1 g C m−3 | |
| qhyd | Reserve carbon supply rate | 1·0 g C m−3 | |
| ksto | Starch synthesis rate | 0·1 d−1 | |
| khyd | Starch hydrolysis rate | 1·0 d−1 | |
The symbol n represents the developmental step, which corresponds to the number of nodes on a shoot, and m represents node number on a parent cane. A reference is provided for some parameter values, while the remainder were set manually and must be calibrated.
Table 2.
The state variables used in the model, with symbols, definitions and units given in order of appearance in the text
| Symbol | Definition | Initial value with units |
|---|---|---|
| nP | Phyllochron index | 0 (dimensionless) |
| Pgross | Leaf photosynthetic rate | 0 µmol CO2 m−2 s−1 |
| I | Absorbed photosynthetic photon flux density per leaf | 0 µmol PAR m−2 s−1 |
| c | Carbon concentration in transport pathway for each sink/source | 0 g C m−3 |
| Leaf growth | ||
| sleaf | Leaf sink size (structural carbon) | 3·69e-4 g C |
| αleaf | Leaf developmental age | Fig. 7 (dimensionless) |
| Aleaf | Leaf area | (L·sleaf) m2 |
| Internode growth | ||
| V | Internode volume | (πr2l) m3 |
| l | Internode length | (empirical function) m |
| r | Internode radius | 1·5e-3 m |
| αinde | Internode developmental age | –6/τinde(T) (dimensionless) |
| sinde | Internode sink size (structural carbon) | (ρ·V) g C |
| Ω | Internode resistance along transport pathway | Eqn (14) s m−3 |
| Fibrous root growth | ||
| sroot | Fibrous root sink size (structural carbon) | 4779 g C |
| Fruit growth | ||
| sfruit | Fruit sink size (structural carbon) | 0·1 g C |
| Maintenance respiration | ||
| Mrsp | Amount of carbon required to meet maintenance respiration | Eqn (17) g C |
| Leaf carbon supply | ||
| ssrc | Acquired carbon in a leaf | 0 g C |
| Carbon reserves | ||
| sres,inde | Carbon reserves in an internode | (sinde·smax,inde) g C |
| sres,roots | Carbon reserves in roots | (sroot·smax,roots) g C |
Some initial values are given explicitly, and the remainder are set according to calculation.
Aspect integration using L-systems
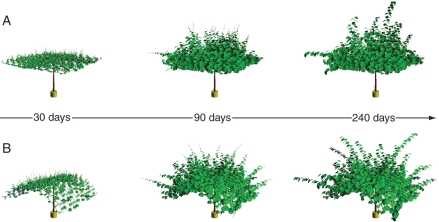
L-systems (Prusinkiewicz et al., 1997) are used to create a 3-D virtual plant representation (Room et al., 1996) of the annual growth cycle of a managed mature kiwifruit vine (Sale and Lyford, 1990) (Fig. 2), and to integrate the aspects of this model at different spatial and temporal scales. At the beginning of each cycle, the structure consists of the main trunk, two leaders and a specified number of canes trained on a support structure (Fig. 3). After budbreak and creation of the initial cluster of leaves, the appearance of new metamers on each shoot depends on environmental conditions and carbon availability. The simulation of shoot development and organ growth continues until the end of the annual growth cycle, when the fruit is ready for harvest. Since the simulation ends at this stage, the model does not currently take into account organ senescence, but nothing precludes including it if necessary.
Fig. 2.
A 3-D visualization of the kiwifruit vine (A. deliciosa) over one season's growth shown at the following times: 30, 90 and 240 d after budbreak. The vine was trained on a pergola support structure (A) and a T-bar support structure (B).
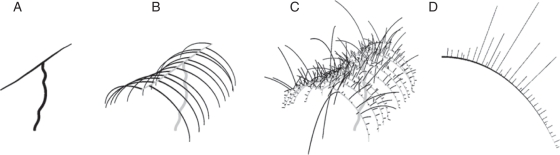
Fig. 3.
Schematic of a mature kiwifruit vine trained on a T-bar support structure. In a standard management scheme, a single trunk is maintained with two horizontally trained relay axes, called leaders, in opposite directions along a support structure (A). New relay axes from these leaders are left to bend under their own weight and eventually tied down to support structures, which are called replacement or parent canes (B). The axillary shoots that grow from these parent canes (C) will produce the fruit. Generally, the parent canes are replaced with one of the vigorous axillary shoots during winter pruning, bringing the vine back to a similar form at the beginning of each season (B). In this kiwifruit vine model, the permanent structure (B) is assumed to be present at the start of the simulation, but the branching pattern of the axillary shoots on a parent cane (D) is a result of the simulation.
The allocation of carbon to various sinks is computed with a time step of 0·1 d (selected as a compromise between the accuracy and speed of the computation), whereas the light distribution in the canopy is only calculated at daily time steps. In principle, the time steps could be the same for both of these aspects; however, calculating light distribution at the organ level is computationally intensive at the required precision, and the accuracy of the numerical method used to compute carbon allocation is limited by the size of the time step (a daily time step would lead to a large approximation error). To combine these aspects at different time scales, the average daily amount of carbon acquired by each leaf is calculated once per day, and then the amount is distributed to the leaves uniformly over the entire day (using a time step of 0·1 d).
Shoot development and vine architecture
Axillary shoots develop from mature first-order axillary buds on the cane. Their structure, as described by Walton et al. (1997), is as follows: nodes 1–4 have second-order axillary buds; nodes 5–12 have axillary meristems that differentiate into inflorescences and flowers; and nodes 13 onwards have axillary meristems that produce next season's axillary buds. The first four nodes are subtended by bud scales, while nodes from 5 up are subtended by leaf primordia. The transition from pre-formed to neoformed nodes usually occurs between node 15 and 25, with all kiwifruit buds resuming organogenesis during budbreak (Foster et al., 2007). Not all pre-formed organs expand during shoot development, as the shoot apex can abort at any stage. The likelihood of axillary meristem differentiation into flowers is dependent on many factors, such as node number along the shoot and application of chemical agents (Walton and Fowke, 1993). Second-order axillary buds only develop if the apical meristem of the first-order axillary bud is damaged (Walton, 1996).
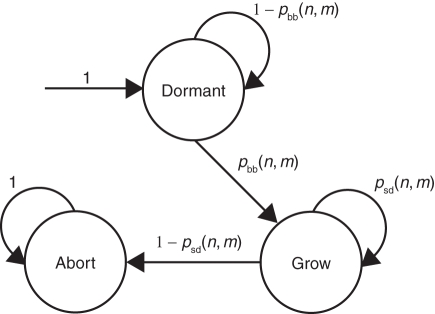
Each individual axillary bud and its potential shoot are modelled by a discrete-time Markov chain (Taylor and Karlin, 1998), with three states: dormant, growing and aborted (shown in Fig. 4). The time between state transitions in the Markov chain corresponds to the rate of metamer appearance on the axillary shoot and is determined by phyllochron, which is the time interval between the appearance of successive leaves. At the start of the season, each axillary bud is in a dormant state, with a transition probability for budbreak, pbb(n, m), defined as a function of the developmental step, n, nodal position on the parent cane, m, and of the bud's orientation on the cane [so only buds on the topside of the cane will produce a shoot (Snowball and Considine, 1986)]. Modelling the effect of bud position along the parent cane is based on a theoretical probability of latent bud obtained (in tabulated form) by fitting a hidden semi-Markov model (HSMC) to architectural data (Seleznyova et al., 2002: fig. 12A). It was assumed that all buds can break at n = 0, with probability pbb(0, m) set by a user-defined function and the bud's orientation on the cane (1 for buds on the topside and 0 for the underside). The buds that break will produce an axillary shoot, and any remaining buds will stay dormant, with pbb(n, m) = 0 when n > 0. An axillary shoot produced after budbreak will continue growing with a specified probability of shoot development [denoted by psd(n, m)], otherwise the shoot will abort growth.
Fig. 4.
The Markov chain representation of axillary shoot growth. The probability of budbreak is given by pbb(n, m). The probability of shoot development is given by psd(n, m) and is modulated by initial bud vigour, positional effects along the cane and resource availability. From Cieslak et al. (2010), © 2010 IEEE.
The non-stationary transition probability, psd(n, m), is modulated by several factors. First, there is an associated vigour (growth potential) with each shoot, e.g. a very vigorous kiwifruit shoot can have a final length of 4·54 m compared with a mean final shoot length ( ± s.e.) of 0·71 ± 0·06 m on the vine (Snowball, 1997). The kiwifruit vine conforms to Champagnat's architectural model (Hallé et al., 1978), so that vigorous shoots are most likely to develop in the central region of the parent cane (Seleznyova et al., 2002). This is captured in the model by a function, v(m), which modulates a shoot's vigour depending on its position along the parent cane, where 0 ≤ v(m) < 1. In the current paper, v(m) is defined in a graphical form using the function editor in L-studio (Prusinkiewicz, 2004) to be increasing from zero at the basal node to one at nodes 18–25, and then decreasing to zero at the apical node. Secondly, there is an intrinsic variation in the shoot vigour emerging during budbreak, as the variation in the number of neoformed metamers in a bud increases through successive stages of budbreak (Foster et al., 2007). This variation is captured in the model by randomizing the vigour using a normally distributed random variable, V, with mean 0·95 and s.d. 0·24, estimated according to data collected by Foster et al. (2007). The third factor modulating shoot development is that a shoot will abort growth with different probabilities during any of three developmental stages (Foster et al., 2007): opening of the initial cluster of leaves (p0), expansion of the pre-formed metamers (p1), and expansion of the neoformed metamers (p2). The values of these probabilities are dependent on the Actinidia species, and must be fitted from experimental data, as was done by Foster et al. (2007).
According to the three shoot development factors given above, the non-stationary transition probability, which changes with developmental step n (equivalent to the number of nodes in the developing shoot), is defined as
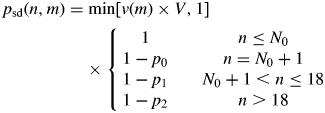 |
(1) |
where N0 is the number of nodes in the initial cluster, and it is assumed there are 18 pre-formed nodes in all buds. The value of N0 is generated per shoot from a binomial distribution with a mean of 5·7 and an s.d. of 2·1, which are taken directly from the architectural analysis by Seleznyova et al. (2002) of short axillary shoots that terminated after opening of the initial cluster. Finally, regardless of the value of psd(n, m), the shoot will abort when the carbon supply is low (Piller et al., 1998; Greaves et al., 1999), i.e. when the carbon concentration at the shoot tip falls below a certain threshold cmin.
In kiwifruit, phyllochron responds non-linearly to temperature (Morgan et al., 1985; Seleznyova and Halligan, 2006) (see Fig. 5). Therefore, the growing degree-days concept for modelling leaf appearance cannot be applied, as it can only be used in the case of a linear response. In our model, the rate of metamer appearance is governed by a phyllochron index defined as
| (2) |
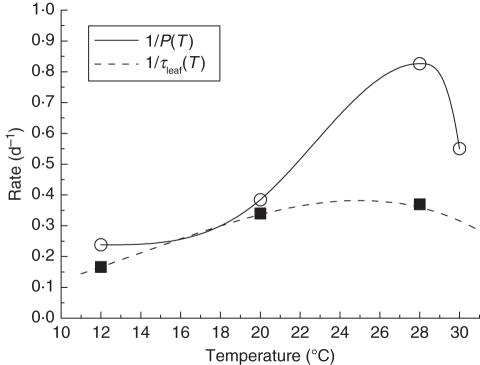
where P(T) is phyllochron as a function of average daily temperature, T, and the integer part of nP corresponds to the developmental step at time t, n = int(nP). The form of 1/P(T) is defined by the user; we used the empirical function given in Fig. 5. Eqn (2) is numerically integrated using the explicit Euler method (Press et al., 1992), with step size 0·1 and nP initially set to zero. Thus, a new leaf appears when nP increases by one, but this is subject to the probability of shoot development, psd(n, m), given above. As the leaves appear, they are arranged in a spiral phyllotaxis of 2/5 (Ferguson, 1990) (the angle between successive leaves is θ = 144°) and have an inclination angle of ϕ = 33° (Morgan and McNaughton, 1991).
Fig. 5.
The rate of kiwifruit leaf appearance (solid line) and specific leaf growth rate (dashed line) as a function of temperature. The functions are fitted to data (squares, circles), collected by Seleznyova and Halligan (2006) and Morgan et al. (1985). From Cieslak et al. (2010), © 2010 IEEE.
The production of flowers and ultimately fruit on the axillary shoot is dependent on node number (as given in the description of first-order axillary bud above), so there are potentially eight reproductive meristems in the axillary bud (Hopping, 1990). Not all of these meristems develop into flowers, and the details of the mechanisms that control flower bud abortion/evocation are not fully known (Hopping, 1990; Walton and Fowke, 1993; Snelgar et al., 2007). For this reason, flower production is modelled as a binomial process with the probability of an axillary bud switching physiologically from vegetative to reproductive dependent on node number. For nodes 5–12, this probability is set according to data collected by Walton and Fowke (1993), while for the remaining nodes it is set to zero. Every flower on the shoot is capable of setting and developing into a fruit (Hopping, 1990). The model takes into account the effect of local carbon supply, so a flower will abort if the carbon supply is too low, i.e. if the carbon concentration at the flower's point of attachment to the transport pathway is below a threshold, cmin,flower, it aborts. This captures the suggestion proposed by Walton and Fowke (1993) that increased supply of metabolites reduces flower abortion. Also, the model assumes successful pollination of all the flowers.
Canopy light distribution and photosynthesis
To study the effects of canopy structure on light distribution and to estimate carbon acquisition through photosynthesis, the kiwifruit vine model is interfaced with a light environment model using the open L-system formalism (Měch and Prusinkiewicz, 1996). The light environment model estimates the amount of absorbed irradiance for each leaf in the canopy using a quasi-Monte Carlo path-tracing algorithm (Cieslak et al., 2008). It approximates the incoming light from the sky based on the CIE standard clear sky or overcast sky models (CIE-110, 1994), parameterized by the day of year, time of day and geographical location.
Gross photosynthesis for each leaf is estimated using a light response curve. The following rectangular hyperbolic function is used (Greer et al., 2004)
| (3) |
where Pmax = 15·2 µmol CO2 m−2 s−1 is the maximum rate of photosynthesis, φapp = 0·039 mol CO2 mol−1 PAR is the apparent photon yield and I (μmol PAR m−2 s−1) is the photon flux density absorbed by the leaf (determined by the light environment model), with the potential maximum at the top of the canopy assumed to be D = 1300 µmol PAR m−2 s−1, approximated in midsummer (Greer et al., 2004). The effect of temperature on the light response curve is not currently included in the model, as Laing (1985) has noted minimal variation in photosynthetic rate for temperatures in the range 10–25 °C. Consequently, application of the current model is limited to this temperature range.
Carbon dynamics
Prusinkiewicz et al. (2007a) presented an algorithm for simulating the acquisition, transport and partitioning of carbon within a plant based on an analogy between pressure-driven flow and current flow in an electric circuit, originally developed in the functional–structural peach tree model, L-PEACH (Allen et al., 2005). The essence of this carbon transport resistance allocation model (herein referred to as C-TRAM) is to compute the concentration and flow of carbon throughout the plant based on the resistances between sink/source elements and within each element. Their compact L-system implementation shows the benefit of L-system-based models; as the structure develops, the system of equations (in this case, controlling the flow of carbon throughout the plant) is automatically expanded. The semi-implicit Euler method (Press et al., 1992) was used to solve the equations representing flow of carbon, which was essential to avoid the limitation of the explicit Euler method for solving stiff equations. As the system of equations may be non-linear, the Newton–Raphson method was used to find a solution iteratively through linearization (Press et al., 1992).
In C-TRAM, each metamer was modelled as a conduit element, representing an internode, with a single sink or source element attached at its distal end, representing a lateral organ such as a fruit or a leaf. We extended this approach, so that for each plant organ (e.g. internode, leaf, fruit and roots) several source/sink elements are defined to take into account growth, maintenance, reserve dynamics and, in the case of leaves, carbon acquisition. Specifically, the extension uses multiscale modelling to apply one set of L-system rules representing plant development at the organ scale and another set of rules representing carbon dynamics at the sink/source scale. The advantage of this multiscale approach is that the L-system rules implementing C-TRAM can be applied to all sinks/sources at one scale without modification of the original underlying method for solving the non-linear system of equations. Otherwise, only linear responses to carbon limitation can be considered, as in the latest version of L-PEACH (Lopez et al., 2008), or the Newton–Raphson method must be applied twice: first at the organ scale to determine carbon allocation to different sinks within each organ, and then at the whole-plant scale. All that remains now is to define the equations for influx of carbon into the different sink types and outflow of carbon from sources.
Influx into organ growth sinks
C-TRAM allows for the mechanistic modelling of effects of carbon limitation on organ growth via appropriate definition of the functional forms of growth rates for different sink types. The growth rate is determined by the influx of carbon into the sink, depending on its intrinsic potential growth rate and the carbon concentration outside the organ in the transport pathway. This growth rate is modulated by two functions, as given by the following equation
| (4) |
where si is the size (structural carbon) of the sink of type i, dsi/dt is the change in sink size, f(qi, c) is a non-linear resource-limiting function of carbon concentration, c, outside the sink in the transport pathway that depends on sink type, and Gmax(…) is a maximum potential growth rate that depends on environmental factors (e.g. temperature) and the organ's intrinsic properties. The form of the resource-limiting function f(qi, c) is the same for all sink types and is defined by
| (5) |
where qi can be interpreted as a sink priority parameter (given the same carbon concentration in the vicinity of the sink, a low value of qi indicates a higher carbon influx into the sink). This function captures the complex behaviours that are likely to occur for different sink types in a hierarchical arrangement (Wardlaw, 1990). If carbon concentration outside the sink is high, the carbon flux into the sink is at or near saturation, but, when the concentration is low, the carbon flux of individual sinks falls with different rates depending on the type. Although the form of this resource-limiting function is similar to the Michaelis–Menten equation derived for enzyme kinetics (Thornley and Johnson, 1990) and used to model sink unloading by Minchin et al. (1993), its application is different. In our model, eqn (5) is used in a more phenomenological sense to represent the aggregated sink responses, with the parameter qi controlling sink priority dependent on sink type.
The form of the function Gmax(…) depends on the sink type, and will be described next for vegetative and reproductive components of the vine.
Vegetative growth
Leaf and internode growth under carbon limitation is modelled using two state variables as proposed by Seleznyova (2008): sink size, si, and developmental age, αi, where i is the type (leaf or internode). The developmental age variable eliminates the need for specifying an organ's potential final size, so that organ size is only determined by its initial state at the time of appearance, si,0 and αi,0, and duration of rapid growth, τi, which is centred around the time of maximum growth t0 (i.e. it is the time period when most of the growth occurs) (Seleznyova and Greer, 2001). Developmental age extends the thermal time concept by accounting for the various effects of the environment on the duration of growth (not only temperature), and it can be applied when the response is non-linear (Seleznyova, 2008). In this model, the developmental age of a leaf or an internode is used to determine the organ's non-linear growth response to temperature, which is not possible using the thermal time (degree-days) concept (Seleznyova and Halligan, 2006).
Developmental age relates time to temperature via a direct relationship (as temperature increases/decreases internal ageing increases/decreases), and the change in developmental age of an organ over time is modulated by the organ's specific growth rate, which is inversely related to the duration of growth. More precisely, it is governed by the following equation (Seleznyova, 2008)
| (6) |
where τi(T) is now a function of temperature. Before describing the specific equations for modelling kiwifruit leaf and internode growth, let us consider how the developmental age variable can be used as input into a growth function.
Simple logistic-type growth can be modelled as a relative growth rate by
| (7) |
where s is the size of the organ, 1/τ is the specific growth rate, and Γ(α), the growth function, is defined as (Seleznyova, 2008)
| (8) |
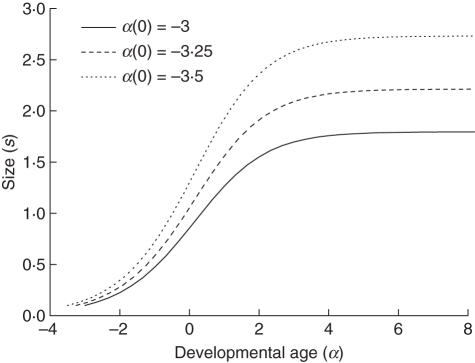
Note that these variables are used to explain the concept and are not part of the kiwifruit vine model. By numerically integrating eqn (7) using the explicit Euler method for different initial values of developmental age, we can examine the differences in resulting final sizes. Figure 6 shows the size of an organ with respect to its developmental age. The first solution is used as a control, with τ = 3, and initial values α(0) = –3 and s(0) = 0·1. The developmental age is fixed to zero (α = 0) at the time of maximum expansion t0, which is why it is initially negative (Seleznyova, 2008). In the remaining two solutions, only the initial value of developmental age was changed: α(0) = –3·25 and α(0) = –3·5, respectively. The final sizes were s(tF) = 1·8, s(tF) = 2·2 and s(tF) = 2·7, respectively, where tF is the final simulation time. Assuming the initial sizes are the same, decreasing the initial developmental age, α(0), causes an increase in final size, and increasing α(0) causes a decrease in final size, irrespective of the duration of rapid growth, τ. It is precisely this characteristic of the developmental age variable that allows organ growth to be modelled without specifying final size.
Fig. 6.
The change in size of an organ with respect to its developmental age for different initial values of developmental age: α(0) = –3, α(0) = –3·25 and α(0) = –3·5. Given the same initial size, s(0) = 0·1, the resulting final size of the organ is different irrespective of α, the duration of rapid growth. If the initial developmental age is decreased (given that the time of maximum growth is when α = 0), the final size increases.
As kiwifruit leaf growth rate is characterized by logistic-type growth (Seleznyova and Greer, 2001), the leaf sink size, sleaf, is modelled according to a maximum potential relative growth rate derived from data (Seleznyova, 2008). The following equation is used to capture the change in leaf size [with Gmax(…) given as the second term on the right-hand side of the equation],
| (9) |
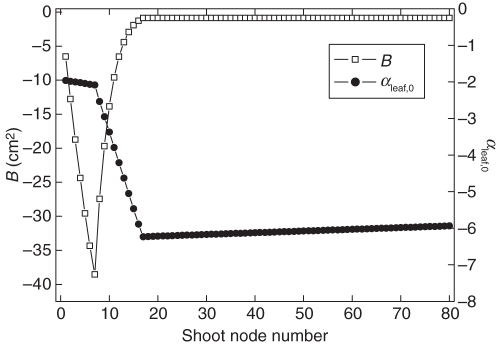
where B(n) is a coefficient that controls the initial growth rate of the leaf by node number n (see Fig. 7), and Γ(αleaf) is defined as before in eqn (8). The B(n) coefficient is necessary to include positional effects on leaf size, because a leaf's initial size at time of appearance, sleaf,0, is the same for all leaves. In addition, the specific growth rate, 1/τleaf(T) is included in this equation to set a leaf's maximum relative growth rate. Figure 5 shows the value of 1/τleaf(T), which is an empirical function defined by the user. The initial developmental age for an organ can be determined from data as described by Seleznyova (2008). Figure 7 shows this value, αleaf,0, for kiwifruit leaves by node number. Together with the τleaf parameter, the initial developmental age determines the duration of the exponential expansion phase of the leaf. Lastly, leaf area, Aleaf, is approximated from leaf sink size according to the equation Aleaf = Lsleaf, where L is the specific leaf area (m2 g−1 C) and is assumed to be constant.
Fig. 7.
The initial leaf developmental age, αleaf,0, and leaf growth parameter, B, by node number. The values are fitted from data collected by Seleznyova and Greer (Plant & Food Research, Palmerston North, New Zealand, unpubl. res.). From Cieslak et al. (2010), © 2010 IEEE.
Internode growth rate is characterized by its increasing volume due to expansion of cells and formation of new phloem and xylem (Pallardy, 2008). The internode sink size is proportional to internode volume, sinde = ρV, where ρ is volumetric density (assumed to be constant) and V is internode volume, and can be described by growth rates for radial and axial components separately. Thus, based on preliminary observations, internode elongation is described by a relative growth rate (as for a leaf, but with B = 0), and thickening is given in two parts: short-term logistic expansion for young internodes, and long-term radial expansion that is proportional to the internode's surface area. In practice, the length, l, and radius, r, are governed by the following two equations:
| (10) |
and
| (11) |
where qinde,pri and qinde,sec are parameters controlling sink priority of primary and secondary growth, respectively, and both ksec and klogistic are thickening growth rate parameters. The former regulates long-term radial growth and the latter regulates a rapid initial growth. The value of τinde(T) for internodes is half that of leaves (Seleznyova, Plant & Food Research, Palmerston North, New Zealand, unpubl. res.). The initial developmental age for internodes is αinde,0 = –3·64, initial length depends on node number and is defined in tabulated form based on shoot growth data analysis, and initial radius is set to 1·5e-3 m (Seleznyova and Greer, Plant & Food Research, Palmerston North, New Zealand, unpubl. data). Now, the two equations above can be combined to get the change in internode sink size, given by
| (12) |
This equation can be rewritten in terms of carbon units only, as the following
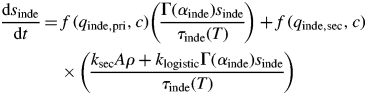 |
(13) |
where A = 2πrl is the internode's surface area.
Resistance along the transport pathway, Ω, is directly proportional to the length of the internode, and inversely proportional to its circumference, as the phloem is a layer near the surface of the internode. Assuming the thickness of the layer is constant and much smaller than the internode's radius, it is given by the following equation
| (14) |
where kΩ is a coefficient that includes the phloem's thickness, l is internode length and r is its radius.
Root growth is modelled according to the method proposed by Buwalda (1991), where only the growth of fibrous roots is considered, because, in a mature kiwifruit vine, growth of structural roots is negligible (Buwalda, 1993) and it is speculated that fibrous roots turn over within 1 year (Buwalda and Hutton, 1988). The relative elongation rate of fibrous roots in late summer, the peak period of growth (Buwalda and Hutton, 1988), is assumed to represent potential growth rate. Then, the change in root sink size is modelled as a relative growth rate that responds to changes in temperature, and is given by
| (15) |
where kprgr is a parameter representing the potential root growth rate for the peak period of growth in late summer, and Tprgr is a parameter controlling the response of root growth to temperature (Buwalda, 1991). A value of 0·003 g C g−1 C d−1 for kprgr at 20 °C was reported by Buwalda and Hutton (1988). The temperature response coefficient is assumed to double the growth rate for every 10 °C increase in temperature, as proposed by Buwalda (1991).
Fruit growth
Kiwifruit growth rate is characterized by a double-sigmoid curve, where the growth rate is more rapid in the first phase than in the second phase (Davison, 1990). In accordance with this characteristic, the change in fruit sink size is modelled as a relative growth rate by the following equation
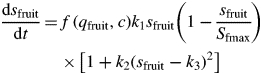 |
(16) |
where the form of the potential growth rate, identified as Gmax(…) in eqn (4), is the one proposed by Gandar et al. (1996) for change in fruit weight over time. The parameter Sfmax gives the maximum size of the fruit, and k1, k2, and k3 are parameters that are fitted to data (Gandar et al., 1996). These parameters are necessary to capture the bimodal relationship between growth rate and size in kiwifruit. The shape of the peaks (points of inflection on the growth rate) is determined by k1 and k2, and the trough in between them is determined by k3 (Gandar et al., 1996). Compared with the model for vegetative growth (described above), the fruit growth model is currently constrained by the specification of the maximum potential fruit size and by the exclusion of temperature effects. Addressing this limitation is challenging as it is difficult to show a consistent effect of temperature on kiwifruit growth in the field; nevertheless, progress is being made (Snelgar et al., 2005; Bebbington et al., 2009).
Maintenance respiration
The carbon demand required to meet maintenance respiration, Mrsp, of a specific organ is defined by the total biomass of that organ and the ambient temperature. It is modelled as the influx of carbon into a maintenance sink by the following equation (Buwalda, 1991)
| (17) |
where qrsp,i is the sink priority for organ type i, si is current sink size (corresponding to structural carbon), mi is a maintenance coefficient for organ type i, Trsp,i is a temperature response coefficient, and T is the temperature. Grossman and DeJong (1994) give values of mi for various plant organs in peach, which may also be used for kiwifruit (Walton and Fowke, 1995). The temperature-dependent parameter is set so that the respiration rate doubles for every 10 °C increase in temperature. Finally, insufficient supply of carbon for maintenance respiration results in organ abscission, when the carbon concentration at the organ's point of attachment to the transport pathway falls below the threshold cmin,abs. This value must be set through optimization.
Carbon acquisition
The carbon acquired through photosynthesis and stored in a leaf is modelled as a source of size ssrc. Carbon is loaded from the source into the transport pathway dependent on the carbon concentration outside the leaf, c, and is assumed to involve active transport (Cannell and Dewar, 1994). Therefore, the amount of carbon the leaf will acquire and store, and then supply into the transport pathway is modelled by
| (18) |
where the first term captures carbon acquisition through photosynthesis limited by overloading, with the constant σ = 1·04 used to convert Pgross from units of μmol CO2 m−2 s−1 to g C m−2 d−1, and g(qsrc, c) is a resource-limiting function, which is currently defined as
| (19) |
Parameter qsrc sets the carbon supply rate so that the leaf maintains a high carbon concentration outside itself in the transport pathway (Cannell and Dewar, 1994). There is a maximum amount of carbon a leaf can store based on its current size, i.e. if ssrc approaches a state of saturation (when sleaf = ssrc), carbon acquisition by the leaf is reduced because it is unable to store more carbon.
Reserve dynamics
Carbon reserves, in internodes and roots, are modelled as an active competing sink driving starch synthesis (Cannell and Dewar, 1994; Daudet et al., 2002). The rate of starch synthesis depends on organ size, but may be limited by overloading. Remobilization of stored carbon is proportional to the amount of starch in the organ. The change in size of the storage sink is given by the following equation
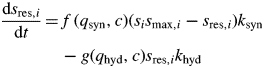 |
(20) |
where i is organ type (internode or roots). The first half of the equation limits carbon storage owing to starch overloading and the organ storage capacity, which is proportional to the current organ structural biomass, si, and maximum starch content per unit of structural carbon, smax,i, for organ i (internodes or roots). The other half governs carbon remobilization depending on the amount of stored carbon. The two parameters ksyn and khyd control the rate of starch synthesis and hydrolysis, respectively. Maximum starch content, smax,i, was calculated from the reported budbreak starch concentration of 0·06 g starch g−1 dry weight for internodes and 0·22 g starch g−1 dry weight for roots (Smith et al., 1992).
RESULTS: MODEL SIMULATIONS
In order to demonstrate the capability of the kiwifruit vine model to produce the vine's growth features and simulate experimental scenarios, several simulations were performed. The first simulation is of the branching patterns of A. deliciosa and A. chinensis observed by Snowball (1997) and Seleznyova et al. (2002), which highlights the performance of the architectural component of the model. The second simulation emphasizes the role of relative distances between sinks and sources based on the whole cane defoliation experiments of Tombesi et al. (1993). In the last two simulations, the effect of local carbon supply on early shoot growth is shown by manipulating carbon reserves for isolated shoots and for competing adjacent shoots on the basis of experiments performed by Piller et al. (1998) and Greaves et al. (1999), respectively. The parameters of the model are set manually according to experimental data or from observations (see Table 1).
Since the focus of these simulations is only on showing the capabilities of the model, the effect of temperature was excluded so that parameters dependent on temperature could be kept constant, with P = 2·9 d, τinde = 2·77 d, τleaf = 5·53 d, while the remaining parameters were set as given in Table 1. The initial values for state variables were set as given in Table 2. The light model was set to simulate the PAR domain for a clear sky averaged over the entire day, with the absorbance ratio of the leaves set to 78 % (Greer and Laing, 1992).
Simulation of the entire vine over one growing season (240 d) with 28 canes and 392 shoots (totalling 6370 metamers) took about 57 min on a notebook PC with a 1·73 GHz processor and 2 GB of memory. During this simulation, computation of the light distribution within the canopy took about 18 min using 262 144 light path samples. Also, the final number of sinks and sources was 71 500. As the L-system simulator, lpfg, automatically handles addition/removal of the model's components (organs and sinks/sources), there is no theoretical restriction on the maximum number; the only limit is set by the computer's capacity.
Branching pattern: distributions of shoot node number and axillary shoot types
An illustration of the model's architectural component, without the effects of resource limitation, is necessary to provide a basis for further simulation of the entire vine. The model calculates the final number of nodes for each axillary shoot and the probability distributions of axillary shoot types along the cane. This model output can be directly compared with biological data, which can be used to calibrate the architectural parameters of the model manually.
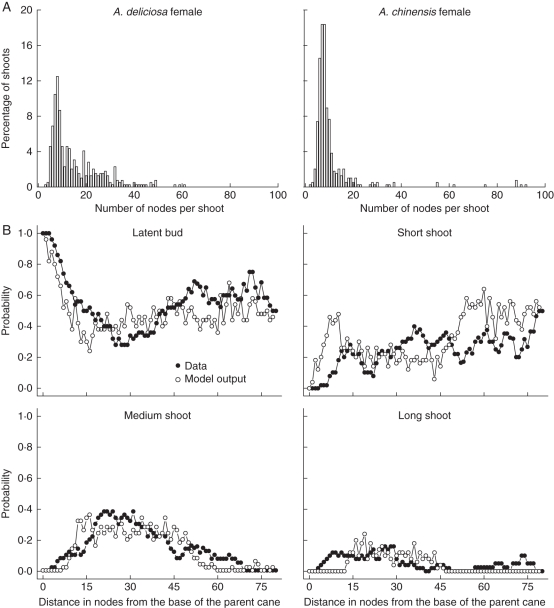
Snowball (1997) collected data for the seasonal cycle of shoot development for ten Actinidia species, which were pruned to standard commercial practice on a T-bar support structure. Among other things, she calculated the frequency distribution of shoot node number for A. deliciosa and A. chinensis vines. To calibrate the model parameters manually and compare the model output with these data, a simulation of axillary shoot growth from parent canes was performed for a female vine of both species. The architectural parameters were identical for each of these simulations, except for the probabilities of growth cessation, which differed between A. deliciosa and A. chinensis as follows: p0 for cessation after opening of the initial cluster (0·02 vs. 0·35), p1 for cessation after expansion of pre-formed metamers (0·005 vs. 0·1) and p2 for cessation after expansion of neoformed metamers (0·09 vs. 0·01), where values given in parentheses are for A. deliciosa and A. chinensis, respectively. All three parameters have been shown to be species dependent by Foster et al. (2007).
Figure 8A gives the frequency distribution of node numbers for a simulation of shoots growing on 28 canes each for the two female Actinidia vines. Table 3 gives the mean number of nodes ( ± s.e.) per shoot, the median number and the maximum number for both species, along with the values reported by Snowball (1997) for comparison. The similarity of the values suggests that the probabilities for growth cessation are reasonably set.
Fig. 8.
Model output for simulation of the kiwifruit branching pattern: (A) the final node number distribution of shoots growing from 28 canes (each) of two different species of Actinidia vines, and (B) the probability distributions of axillary shoot types for long parent shoots of A. chinensis. In the latter, the filled symbols are from data (Seleznyova et al., 2002) and open symbols are from model output.
Table 3.
Statistical properties of final shoot node number distributions for two Actinidia species: A. deliciosa and A. chinensis
| A. deliciosa | A. chinensis | |
|---|---|---|
| Data | ||
| Mean ± s.e. | 15 ± 0·6 | 11 ± 0·9 |
| Maximum | 56 | 97 |
| Median | 13 | 7 |
| Model | ||
| Mean ± s.e. | 15·19 ± 0·52 | 10·77 ± 0·58 |
| Maximum | 61 | 92 |
| Median | 11 | 8 |
The mean with s.e., maximum and median number of nodes as reported by Snowball (1997) are given, and can be compared with model output.
Seleznyova et al. (2002) collected architectural data on 2-year-old branches of an unpruned A. chinensis vine and calculated probability distributions of different shoot types along the parent cane. Kiwifruit axillary shoot types were classified as short, medium and long (based on architectural analysis). Short and medium shoots produce only pre-formed leaves and are called terminated shoots, while long shoots are non-terminating and have leaves arising from neoformed primordia.
To demonstrate the capability of the model to produce the branching pattern observed by Seleznyova et al. (2002) on 2-year-old branches of A. chinensis, a simulation of axillary shoot growth from an unpruned parent cane was performed. The difference from the previous simulation was that the number of nodes on the parent cane was much larger (80 nodes vs. 30 nodes for a pruned cane). This meant that, relative to the previous simulation, the vigour function, v(m), had to account for the extra nodes, but otherwise the parameters were kept the same. Figure 8B gives the model output and corresponding data (Seleznyova et al., 2002: fig. 12) for probability distributions of different axillary shoot types grown from long parent canes of the A. chinensis vine. As in the previous simulation, the model parameters were set manually and the probability of budbreak along the parent cane was empirically set using a tabulated output of an HSMC model fitted to architectural data (Seleznyova et al., 2002: fig. 12A).
Influence of distance between sink and source
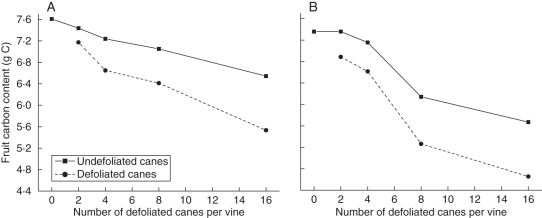
Tombesi et al. (1993) investigated the effects of different source–sink ratios on fruit growth and quality by defoliating A. deliciosa vines with varying intensity. Four treatments were applied: shoots on two, four, eight and 16 canes from 28–30 canes per vine were defoliated over the growing season, starting 48 d after budbreak. To show the effect that source proximity has on fruit, they recorded the average fruit weight on the defoliated and undefoliated canes. The results showed a statistically significant difference in fruit weight between treatments with ≥4 defoliated canes and the undefoliated canes.
This defoliation treatment was simulated using the kiwifruit model. The same parameters were used as in the simulation of axillary shoot growth of the A. deliciosa vine, but axillary shoots on selected canes were defoliated 48 d after budbreak. Tombesi et al. (1993) did not report which canes were defoliated in their experiments, so, for this simulation, canes were chosen for defoliation starting at the apical end of each leader, i.e. for the first treatment (two canes per vine), the most distal canes from the main trunk on each leader were selected for defoliation. For the second treatment (four canes per vine), the very next cane following the most distal one on each leader was also selected for defoliation. In subsequent treatments (eight and 16 canes per vine), pairs of canes on opposite sides of a leader were selected for defoliation, always ensuring that one pair of undefoliated canes existed between defoliated canes.
Figure 9 shows the predicted average fruit carbon content for undefoliated and defoliated canes for all four treatments and for a vine without any defoliation. It shows both the model output and the observed data, which were estimated from the average fruit fresh weight reported by Tombesi et al. (1993). These estimates where calculated using a 15 % dry matter content found by Tombesi et al. (1993) (there were no significant differences in percentage dry matter between treatments) and a conversion factor of 45 % g C g−1 dry weight. The model reproduces the considerable difference in fruit carbon content between the two types of canes, especially for high levels of defoliation.
Fig. 9.
(A) Model output for a simulation of defoliation treatments, showing the effect on fruit carbon content for defoliated and undefoliated canes, and (B) estimated average fruit carbon content for the experimental defoliation treatments by Tombesi et al. (1993), assuming 15 % dry matter and 45 % g C per g dry weight.
Competition for carbon reserves in shoot growth
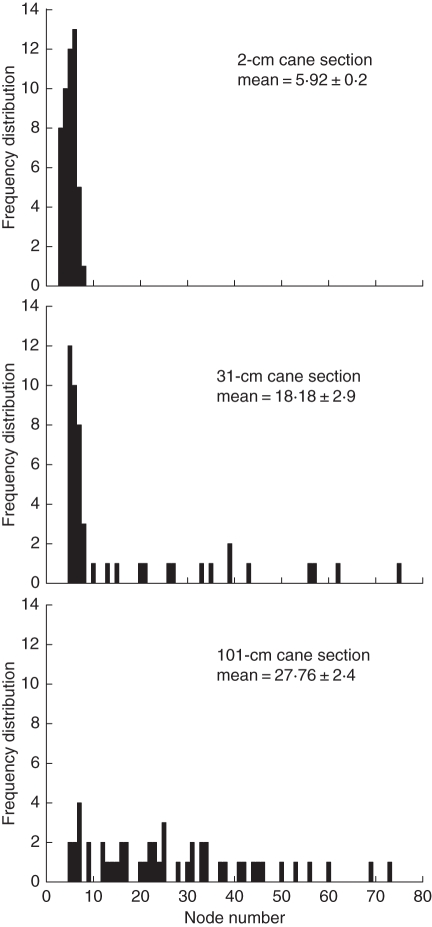
Early shoot growth in kiwifruit relies significantly on reserves, because carbon acquisition by leaves is insufficient at that stage (Greer et al., 2003). To test the sensitivity of shoot growth to reserves, Piller et al. (1998) performed girdling experiments on parent canes to manipulate the amount of resources available to the shoot. In one of the experiments, a single shoot was isolated within a girdled section of a parent cane 2 weeks after budbreak by removing all other shoots within the section. Three treatments were applied: a girdle 1, 30 or 100 cm away from the shoot towards the cane's base, with a 1 cm girdle beyond the shoot towards the cane's tip in each case, resulting in 2, 31 and 101 cm total lengths of the girdled section of cane attached to the shoot. These experiments can be replicated using the kiwifruit model on a computer by simulating shoot growth from a girdled cane.
For each girdling treatment, 50 simulations of shoot growth were performed (see Fig. 10). The only difference between the three sets of simulations was the length of the parent cane, i.e. the amount of carbon available to a growing shoot was manipulated by changing the parent cane's length. Each shoot was assigned the same vigour, so the probability of growth cessation was only modulated by resource availability.
Fig. 10.
The node number distribution for simulation of kiwifruit shoots grown under three cane-girdling treatments, with the mean number of nodes ± s.e. For each simulation, a single shoot was grown within a girdled section of cane of length 2, 31 or 101 cm. From Cieslak et al. (2010), © 2010 IEEE.
Figure 10 shows the distribution of node number per shoot generated from the simulations. For the 2 cm cane, the mean node number is 5·92 ± 0·2 s.e. For the 31 cm cane, the mean is 18·18 ± 2·9, and for the 101 cm cane the mean is 27·76 ± 2·4. Piller et al. (1998) reported that shoots with a 2 cm girdle section were significantly shorter than controls. The shoots in the 31 cm girdle section were not significantly different from controls, but the shoots in the 100 cm girdle section were longer and showed a significant increase in growth rates 8 weeks after budbreak. Although a direct comparison between shoot lengths from the data and node number distributions from the model is not feasible, qualitatively the model is able to simulate the effect of carbon reserves on shoot growth; growth is directly proportional to the amount of reserves available.
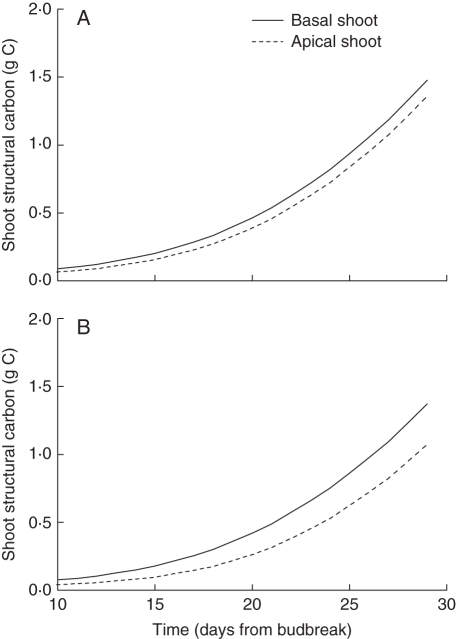
Greaves et al. (1999) investigated the effect of carbon reserve distribution in parent canes on axillary shoot growth. One of their experiments showed how growth of adjacent shoots is affected during the time of reserve dependence (when net photosynthesis is smaller than supply from reserves). In this experiment, pairs of shoots were isolated by applying two girdling treatments to parent canes 1 week after budbreak. The two treatments differed by the location of the shoots in the girdled section: (1) central location, the shoots were in the middle of the cane (30 cm of cane on either side of the shoots); and (2) apical location, the shoots were located towards the apical end of the cane (54 cm of cane before the basal shoot and 6 cm after the apical shoot). They found that for both treatments the shoot nearest the apical end of the cane had significantly less growth than the basal shoot, with no significant effect resulting from the location of the pair (i.e. central or apical) within the girdled section.
The functional–structural kiwifruit vine model presented here was used to simulate this experiment as well. All the parameters were kept the same as in the previous simulation of individual shoot growth from a girdled cane. For this simulation two identical shoots were placed 15 cm apart on a 60 cm section of cane. The vigour of each shoot was set to the same value so that the only difference between the shoots was the radius of the cane section it was growing from, i.e. the amount of locally available reserves. Canes were treated as a sequence of eight internodes with length set to 7·5 cm and radius set to 0·7 cm for the base internode, which reduced linearly to 0·05 cm for the last internode.
Figure 11 shows the amount of structural carbon in vegetative components of the two simulated shoots. On the centrally located shoot pair, growth of the apical shoot was slowed down by competition for reserves from the basal shoot. The simulation of an offset shoot pair showed a similar effect, but the difference was larger. Greaves et al. (1999) reported a significant difference in length of the shoot pair for both the centrally located and offset shoots, with the basal shoot being about 33 cm longer 20 d after girdling in both cases.
Fig. 11.
Model output of the amount of structural carbon in vegetative components of a pair of identical shoots growing from a 60 cm long section of a girdled cane in two locations: (A) in the centre of the cane, and (B) offset to the apical end. In both cases, the shoots were 15 cm apart.
DISCUSSION
A number of plant models are based on the ‘common pool theory’ (Buwalda, 1991; Letort et al., 2008), which does not account for topological distances between sinks and sources of carbon. While useful for some purposes, the application of this theory is not always possible, as some studies have shown that topological distances play an important role in carbon allocation (Lacointe, 2000). In kiwifruit, for example, Tombesi et al. (1993) have shown the importance of source–sink distance for fruit weight, budbreak and flower differentiation when carbon availability is reduced. Moreover, studies indicate that early kiwifruit shoot development (before anthesis) is particularly sensitive to local carbon supply (Piller and Meekings, 1997), and there is a highly plastic developmental response to trophic competition in fruiting shoots (Greer et al., 2003). Based on experimental data, Pallas et al. (2010) have shown the inadequacy of the common pool theory for modelling this type of plastic response in grapevine development, and suggested that a more suitable approach should include the topological distance between sources and sinks. Our model satisfies this requirement, and is suitable for modelling the types of responses seen in kiwifruit and grapevine.
Plasticity of kiwifruit architecture
A new aspect of the kiwifruit model is the inclusion of the plastic response of shoot growth cessation to local carbon supply. The model of shoot development was integrated with the carbon dynamics model to include effects of carbon availability on metamer production. This method is similar to the one used by Mathieu et al. (2008), except that, instead of a single variable (source–sink ratio) controlling production of all metamers on the plant, in the current model the fate of each apex is determined by carbon availability in its immediate vicinity. Owing to this method, simulations of shoots growing from three different levels of available reserves reproduced the expected response of shoots to local carbon supply. Thus, the model reproduces the effect of resource availability on shoot growth, and is capable of producing the observed patterns, such as those reported by Piller et al. (1998).
Another aspect of the model is the inclusion of the vine's architectural plasticity as determined by species. The branching pattern of the vine is an emergent property of the model, with the number of metamers on a shoot not pre-determined but resulting from the simulation. This is based on the assumption that branching pattern emerges from the overall vigour of the parent cane and the likelihood of shoot tip abortion during axillary bud outgrowth, which is species specific. Using this feature, the shoot growth of two female Actinidia vines was simulated by manually calibrating model parameters according to data collected by Snowball (1997: fig. 2) for the same species, resulting in a qualitatively similar final node number distribution. Simulated distributions of axillary shoot types along parent canes for A. chinensis were similar to those observed by Seleznyova et al. (2002). However, adjustment of the vigour function was required to improve representation of positional effects on branching. In the future, the architectural parameters could be modified to compare model output further with data for other Actinidia species (Snowball, 1997; Foster et al., 2007) or for effects of rootstocks on shoot growth (Clearwater et al., 2006).
In this kiwifruit vine model, the fate of an axillary shoot (whether it remains dormant, or develops into a short, medium or long shoot) is captured at the individual shoot level by modelling the physical state of the shoot apical meristem, so the distributions of different shoot types along the parent cane and node number distributions for axillary shoots are emergent properties of the model. The model differs from that of the peach tree model, L-PEACH (Lopez et al., 2008), and the apple tree model, MAppleT (Costes et al., 2008), where the branching patterns are modelled at a parent shoot level by specifying branching zones along the parent shoots based on experimental data, resulting in the fates of axillary shoots being largely pre-determined by the branching zones they belong to. This approach would be too restrictive for modelling shoot growth in kiwifruit, because axillary bud fate is highly plastic and depends on environmental conditions and horticultural manipulations (Clearwater et al., 2006; Foster et al., 2007).
Effects of horticultural manipulation
Orchard management practices for improving fruit size and quality may involve changing the leaf–fruit ratio on the vine by optimizing leaf distribution and fruit exposure (Tombesi et al., 1993). The effects of reduced carbon availability and topological distance, however, incur limits on these sink–source manipulations. The experimental result of Tombesi et al. (1993) showed the limitations of this management practice; when carbon availability in the vine is low, sinks, such as fruit, take advantage of proximity to sources. In the model presented here, this effect was taken into account through the use of a transport resistance model of carbon allocation (C-TRAM), and the model was able to reproduce the reduction in fruit size as observed by Tombesi et al. (1993: fig. 1) for whole cane defoliation treatments (Fig. 9). Even with the limited knowledge of the mechanisms underlying transport resistance in plants, our basic assumption that carbon flow through an internode is modulated by the length and surface area of this internode was enough to reproduce the effect of source proximity on fruit size. Being able to reproduce this kind of result demonstrates the model's capability to increase our understanding of transport resistance between sink and source, and to simulate some vine management practices.
Although only the effects of distance on major sinks, under reduced carbon availability, were considered in the present model, other sinks, such as buds during flower evocation, are also affected by distance to sources during competition for carbon (Tombesi et al., 1993). Including this effect in the model will be important for further study of management practices over multiple years, since it means a possible reduction in flowers for next season's growth.
Sink competition
The kiwifruit vine model uses a mechanistic approach to modelling sink competition and growth under resource limitation. It is general enough to take into account non-linear growth responses to temperature and carbon availability, and organ growth rates for vegetative components of the vine are specified without final sizes. Some models are based on the proportional allocation of resources to sinks independent of the level of availability (Buwalda, 1991; Letort et al., 2008); however, experimental data suggest this is not always the case, as there is a hierarchy of sinks based on competitive ability to attract limited resources (Wardlaw, 1990; Minchin et al., 1993). Our model is capable of capturing the complex behaviour of sink competition for carbon, because the fraction of carbon allocated to a sink depends on its type and the carbon concentration outside the sink at its point of attachment to the transport pathway.
Due to this approach, the simulation of competition for carbon reserves between adjacent shoots (Fig. 11) showed the capability of the model to produce the observed difference in the growth rate of the two shoots (Greaves et al., 1999: table 2), but, it predicted a larger difference in structural carbon for the shoot pair located towards the apical end of the cane. A simulation model that Greaves et al. (1999) created to investigate the importance of carbon reserve distribution in a single cane on axillary shoot growth similarly predicted a larger difference in the shoot pair located at the apical end of the cane. There was a suggestion from their data that a larger difference does occur, though a more thorough experiment would need to be done to confirm this (Greaves et al., 1999).
Internode secondary growth
An additional feature of the current model, which was not illustrated in this paper, is the mechanistic approach to modelling internode thickening. Secondary growth of internodes is often represented using the pipe model (Shinozaki et al., 1964) as a teleonomic approach (Thornley, 1999). In the alternative model used here, long-term secondary growth is based on an absolute growth rate proportional to internode surface area [similar to the model of Deleuze and Houllier (1997) and to the model of Thornley (1999)]. This is a mechanistic approach because only the local carbon supply and intrinsic properties of each internode define secondary growth.
Conclusions and future work
The functional–structural kiwifruit vine model described herein has been successful in integrating existing knowledge on the architecture and carbon dynamics of a managed and mature vine with effects of the environment. As illustrated by several simulations, it is able to simulate vine growth responses qualitatively similar to those observed in biological experiments, demonstrating its ability to mimic features of the vine's growth and function. Our approach was to formulate mechanistic hypotheses for modelling growth at an organ level that would lead to output consistent with biological data at the plant level. This resulted in a model that is primed for calibration and quantitative evaluation, meeting our objectives of developing a robust kiwifruit vine model that allows for in silico experiments testing our hypotheses of the behaviour of the real plant. In the long term, the model will help in finding and testing new horticultural management techniques, especially for new cultivars where the techniques have not yet been established and the genotype growth habit may be largely unknown.
At this stage the model parameters were set manually, but, in the future, the model needs to be calibrated with appropriate data and evaluated against existing experimental results. Such data will come from experiments similar to those performed by Minchin et al. (2010) on sink behaviour during limited carbon supply. Then, the model will be used for identifying knowledge gaps and designing experiments for obtaining the data essential for further model calibration and for performing a sensitivity analysis. Once the kiwifruit vine model is calibrated, it will be studied in a systematic manner by simulating the kiwifruit vine's development, and performing experiments that predict the behaviour of the system under the influence of various parameters.
ACKNOWLEDGMENTS
We thank Drs Alistair Hall and Hamish Brown and the anonymous referees for useful appraisal of the manuscript, and Drs Przemyslaw Prusinkiewicz and Theodore DeJong for the original implementation of C-TRAM and helpful discussions. We gratefully acknowledge the support of this research by the New Zealand Institute for Plant & Food Research Limited (M.C. and A.N.S.).
LITERATURE CITED
- Allen MT, Prusinkiewicz P, DeJong TM. Using L-systems for modeling source–sink interactions, architecture and physiology of growing trees: the L-PEACH model. New Phytologist. 2005;166:869–880. doi: 10.1111/j.1469-8137.2005.01348.x. [DOI] [PubMed] [Google Scholar]
- Bebbington M, Hall AJ, Lai CD, Zitikis R. Dynamics and phases of kiwifruit (Actinidia deliciosa) growth curves. New Zealand Journal of Crop and Horticultural Science. 2009;37:179–188. [Google Scholar]
- Buwalda J. A mathematical model of carbon acquistion and utilisation by kiwifruit vines. Ecological Modelling. 1991;57:43–64. [Google Scholar]
- Buwalda JG. The carbon costs of roots systems of perennial fruit crops. Environmental and Experimental Botany. 1993;33:131–140. [Google Scholar]
- Buwalda JG, Hutton RC. Seasonal changes in root growth of kiwifruit. Scientia Horticulturae. 1988;36:251–260. [Google Scholar]
- Cannell M, Dewar R. Carbon allocation in trees: a review of concepts for modelling. Advances in Ecological Research. 1994;25:59–101. [Google Scholar]
- CIE-110. Spatial distribution of daylight – luminance distributions of various reference skies. Vienna, Austria: Commission Internationale de l'Eclairage; 1994. [Google Scholar]
- Cieslak M, Seleznyova AN, Hanan J. Virtual kiwifruit: modelling annual growth cycle and light distribution. In: Prusinkiewicz P, Hanan J, Lane B, editors. Proceedings of the 5th International Workshop on Functional–Structural Plant Models. 46–1. Napier, New Zealand: Print Solutions Hawke's Bay Limited; 2007. 46–2. [Google Scholar]
- Cieslak M, Lemieux C, Hanan J, Prusinkiewicz P. Quasi-Monte Carlo simulation of the light environment of plants. Functional Plant Biology. 2008;35:837–849. doi: 10.1071/FP08082. [DOI] [PubMed] [Google Scholar]
- Cieslak M, Seleznyova AN, Hanan J. A functional–structural kiwifruit vine model. In: Li B, Jaeger M, Guo Y, editors. The Third International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications. Beijing, China: IEEE Computer Society; 2010. pp. 206–213. [Google Scholar]
- Clearwater M, Seleznyova AN, Thorp TG, Blattmann P, Barnett AM, Lowe R, Austin P. Vigor-controlling rootstocks affect early shoot growth and leaf area development of kiwifruit. Tree Physiology. 2006;26:505–515. doi: 10.1093/treephys/26.4.505. [DOI] [PubMed] [Google Scholar]
- Costes E, Smith C, Renton M, Guédon Y, Prusinkiewicz P, Godin C. MAppleT: simulation of apple tree development using mixed stochastic and biomechanical models. Functional Plant Biology. 2008;35:936–950. doi: 10.1071/FP08081. [DOI] [PubMed] [Google Scholar]
- Daudet F, Lacointe A, Gaudiller J, Cruiziat P. Generalized Munch coupling between sugar and water fluxes for modelling carbon allocation as affected by water status. Journal of Theoretical Biology. 2002;214:481–498. doi: 10.1006/jtbi.2001.2473. [DOI] [PubMed] [Google Scholar]
- Davison R. The physiology of the kiwifruit vine. In: Warrington IJ, Weston GC, editors. Kiwifruit: science and management. Auckland: Ray Richards Publisher and New Zealand Society for Horticultural Science; 1990. pp. 127–154. [Google Scholar]
- Deleuze C, Houllier F. A transport model for tree ring width. Silva Fennica. 1997;31:239–250. [Google Scholar]
- Ferguson AR. Stem, branches, leaves and roots of the kiwifruit vine. In: Warrington IJ, Weston GC, editors. Kiwifruit: science and management. Auckland: Ray Richards Publisher and New Zealand Society for Horticultural Science; 1990. pp. 58–70. [Google Scholar]
- Ferguson AR, Bollard EG. Domestication of the kiwifruit. In: Warrington IJ, Weston GC, editors. Kiwifruit: science and management. Auckland: Ray Richards Publisher and New Zealand Society for Horticultural Science; 1990. pp. 165–246. [Google Scholar]
- Foster TM, Seleznyova AN, Barnett AM. Independent control of organogenesis and shoot tip abortion are key factors to developmental plasticity in kiwifruit (Actinidia) Annals of Botany. 2007;100:471–481. doi: 10.1093/aob/mcm140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fourcaud T, Zhang X, Stokes A, Lambers H, Körner C. Plant growth modelling and applications: the increasing importance of plant architecture in growth models. Annals of Botany. 2008;101:1053–1063. doi: 10.1093/aob/mcn050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandar PW, Hall AJ, de Silva HN. Deterministic models for fruit growth. Acta Horticulturae. 1996;416:103–112. [Google Scholar]
- Godin C, Sinoquet H. Functional–structural plant modelling. New Phytologist. 2005;166:705–708. doi: 10.1111/j.1469-8137.2005.01445.x. [DOI] [PubMed] [Google Scholar]
- Greaves AJ, Henton SM, Piller GJ, Meekings JS, Walton EF. Carbon supply from starch reserves to spring growth: modellling spatial patterns in kiwifruit canes. Annals of Botany. 1999;83:431–439. [Google Scholar]
- Greer D, Laing W. Photoinhibition of photosynthesis in intact kiwifruit (Actinidia deliciosa) leaves: changes in susceptibility to photoinhibition and recovery during the growth season. Planta. 1992;186:418–425. doi: 10.1007/BF00195323. [DOI] [PubMed] [Google Scholar]
- Greer DH, Cirillo C, Norling CL. Temperature-dependence of carbon acquistion and demand in relation to shoot and fruit growth of fruiting kiwifruit (Actinida deliciosa) vines grown in controlled environments. Functional Plant Biology. 2003;30:927–937. doi: 10.1071/FP03111. [DOI] [PubMed] [Google Scholar]
- Greer DH, Seleznyova AN, Green SR. From controlled environments to field simulations: leaf area dynamics and photosynthesis of kiwifruit vines (Actinidia deliciosa) Functional Plant Biology. 2004;31:169–179. doi: 10.1071/FP03151. [DOI] [PubMed] [Google Scholar]
- Grossman YL, DeJong TM. PEACH: a simulation model of reproductive and vegetative growth in peach trees. Tree Physiology. 1994;14:329–345. doi: 10.1093/treephys/14.4.329. [DOI] [PubMed] [Google Scholar]
- Hallé F, Oldeman R, Tomlinson P. Tropical trees and forests: an architectureal analysis. Berlin: Springer-Verlag; 1978. [Google Scholar]
- Hopping ME. Floral biology, pollination, and fruit set. In: Warrington IJ, Weston GC, editors. Kiwifruit: science and management. Auckland: Ray Richards Publisher and New Zealand Society for Horticultural Science; 1990. pp. 71–96. [Google Scholar]
- Karwowski R, Prusinkiewicz P. Design and implementation of the L + C modeling language. Electronic Notes in Theoretical Computer Science. 2003;86(19 pp) [Google Scholar]
- Lacointe A. Carbon allocation among tree organs: a review of basic processes and representation in functional–structural tree models. Annals of Forest Science. 2000;57:521–533. [Google Scholar]
- Laing WA. Temperature and light response curves for photosynthesis in kiwifruit (Actinida chinensis) cv. Hayward. New Zealand Journal of Agricultural Research. 1985;28:117–124. [Google Scholar]
- Letort V, Cournède PH, Mathieu A, de Reffye P, Constant T. Parametric identification of a functional–structural tree growth model and application to beech trees. Functional Plant Biology. 2008;35:951–968. doi: 10.1071/FP08065. [DOI] [PubMed] [Google Scholar]
- Lindenmayer A. Mathematical models for cellular interaction in development, parts I and II. Journal of Theoretical Biology. 1968;18:280–315. doi: 10.1016/0022-5193(68)90079-9. [DOI] [PubMed] [Google Scholar]
- Lopez G, Favreau R, Smith C, Costes E, Prusinkiewicz P, DeJong T. Integrating simulation of architectural development and source–sink behavior of peach trees by incorporating Markov chains and physiological organ function submodels into L-PEACH. Functional Plant Biology. 2008;35:761–771. doi: 10.1071/FP08039. [DOI] [PubMed] [Google Scholar]
- Mathieu A, Cournède P, Barthélémy D, de Reffye P. Rhythms and alternating patterns in plants as emergent properties of a model of interaction between development and functioning. Annals of Botany. 2008;101:1233–1242. doi: 10.1093/aob/mcm171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Měch R, Prusinkiewicz P. SIGGRAPH ‘96: Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques. New Orleans: ACM; 1996. Visual models of plants interacting with their environment; pp. 397–410. [Google Scholar]
- Miller SA, Broom FD, Thorp TG, Barnett AM. Effects of leader pruning on vine architecture, productivity and fruit quality in kiwifruit (Actinidia deliciosa cv. Hayward) Scientia Horticulturae. 2001;91:189–199. [Google Scholar]
- Minchin PEH, Thorpe MR, Farrar JF. A simple mechanistic model of phloem transport which explains sink priority. Journal of Experimental Botany. 1993;44:947–955. [Google Scholar]
- Minchin PEH, Snelgar WP, Blattmann P, Hall AJ. Competition between fruit and vegetative growth in Hayward kiwifruit. New Zealand Journal of Crop and Horticultural Science. 2010;38:101–112. [Google Scholar]
- Morgan DC, Warrington IJ, Halligan EA. Effect of temperature and photosynthetic photon flux density on vegetative growth of kiwifruit (Actinidia chinensis) New Zealand Journal of Agricultural Research. 1985;28:109–116. [Google Scholar]
- Morgan ER, McNaughton KG. Architecture of a kiwifruit canopy. New Zealand Journal of Crop and Horticultural Science. 1991;19:237–246. [Google Scholar]
- Pallardy S. Physiology of woody plants. Boston, MA: Elsevier; 2008. [Google Scholar]
- Pallas B, Christophe A, Lecoeur J. Are the common assimilate pool and trophic relationships appropriate for dealing with the observed plasticity of grapevine development? Annals of Botany. 2010;105:233–247. doi: 10.1093/aob/mcp278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piller GJ, Meekings JS. The acquisition and utilization of carbon in early spring by kiwifruit shoots. Annals of Botany. 1997;79:573–581. [Google Scholar]
- Piller GJ, Greaves AJ, Meekings JS. Sensitivity of floral shoot growth, fruit set and early fruit size in Actinidia deliciosa to local carbon supply. Annals of Botany. 1998;81:723–728. [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical recipes in C: the art of scientific computing. Cambridge: Cambridge University Press; 1992. [Google Scholar]
- Prusinkiewicz P. Art and science for life: designing and growing virtual plants with L-systems. Acta Horticulturae. 2004;630:15–28. [Google Scholar]
- Prusinkiewicz P, Hanan J, Hammel M, Měch R. L-systems: from the theory to visual models of plants. In: Michalewicz MT, editor. Plants to ecosystems. Advances in computational life sciences. Melbourne: CSIRO Publishing; 1997. pp. 1–27. [Google Scholar]
- Prusinkiewicz P, Karwowski R, Měch R, Hanan J. L-studio/cpfg: a software system for modeling plants. In: Nagl M, Schurr A, Munch M, editors. Applications of graph transformations with industrial relevance. Berlin: Springer-Verlag; 2000. pp. 457–464. [Google Scholar]
- Prusinkiewicz P, Allen M, Escobar-Gutierrez A, DeJong T. Numerical methods for transport-resistance source–sink allocation models. In: Vos J, Marcelis L, De Visser P, Struik P, Evers J, editors. Functional–structural plant modelling in crop production. Dordrecht, The Netherlands: Springer; 2007a. pp. 123–137. [Google Scholar]
- Prusinkiewicz P, Karwowski R, Lane B. The L + C plant-modelling language. In: Vos J, Marcelis L, De Visser P, Struik P, Evers J, editors. Functional–structural plant modelling in crop production. Dordrecht, The Netherlands: Springer; 2007b. pp. 27–42. [Google Scholar]
- Room P, Hanan J, Prusinkiewicz P. Virtual plants: new perspectives for ecologists, pathologists and agricultural scientists. Trends in Plant Science. 1996;1:33–38. [Google Scholar]
- Sale PR, Lyford PB. Cultural, management and harvesting practices for kiwifruit in New Zealand. In: Warrington IJ, Weston GC, editors. Kiwifruit: science and management. Auckland: Ray Richards Publisher and New Zealand Society for Horticultural Science; 1990. pp. 247–296. [Google Scholar]
- Seleznyova AN. Dissecting external effects on logistic-based growth: equations, analytical solutions and applications. Functional Plant Biology. 2008;35:811–822. doi: 10.1071/FP08078. [DOI] [PubMed] [Google Scholar]
- Seleznyova AN, Greer D. Effects of temperature and leaf position on leaf area expansion of kiwifruit (Actinida deliciosa) shoots: development of a modelling framework. Annals of Botany. 2001;88:605–615. [Google Scholar]
- Seleznyova AN, Halligan E. Modelling effect of temperature on area expansion at the leaf, the shoot, and the whole plant level. Acta Horticulturae. 2006;707:167–174. [Google Scholar]
- Seleznyova AN, Thorp TG, Barnett AM, Costes E. Quantitative analysis of shoot development and branching patterns in Actinidia. Annals of Botany. 2002;89:471–482. doi: 10.1093/aob/mcf069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinozaki K, Yoda K, Hozumi K, Kira T. A quantitative analysis of plant form – the pipe model theory. I. Basic analysis. Japanese Journal of Ecology. 1964;14:97–105. [Google Scholar]
- Sievänen R, Nikinmaa E, Nygren P, Ozier-Lafontaine H, Perttunen J, Hakula H. Components of functional–structural tree models. Annals of Forest Science. 2000;57:399–412. [Google Scholar]
- Smith G, Clark C, Boldingh H. Seasonal accumulation of starch by components of the kiwifruit vine. Annals of Botany. 1992;70:19–25. [Google Scholar]
- Snelgar WP, Clearwater M, Walton EF. Flowering of kiwifruit (Actinida deliciosa) is reduced by long photoperiods. New Zealand Journal of Crop and Horticultural Science. 2007;35:33–38. [Google Scholar]
- Snelgar WP, Hall AJ, Ferguson AR, Blattmann P. Temperature influences growth and maturation of fruit on ‘Hayward’ kiwifruit vines. Functional Plant Biology. 2005;32:631–642. doi: 10.1071/FP05062. [DOI] [PubMed] [Google Scholar]
- Snowball AM. Seasonal cycle of shoot development in selected Actinida species. New Zealand Journal of Crop and Horticultural Science. 1997;25:221–231. [Google Scholar]
- Snowball AM, Considine JA. Flowering in kiwifruit (Actinidia deliciosa Liang et Ferguson): Positional effects and development. Acta Horticulturae. 1986;175:85–89. [Google Scholar]
- Taylor H, Karlin S. An introduction to stochastic modeling. Orlando, FL: Academic Press; 1998. [Google Scholar]
- Thornley JHM. Modelling stem height and diameter growth in plants. Annals of Botany. 1999;84:195–205. [Google Scholar]
- Thornley JHM, Johnson IR. Plant and crop modelling. Oxford: Oxford University Press; 1990. [Google Scholar]
- Thorp TG, Barnett AM, Miller SA. Effects of cane size and pruning system on shoot growth, flowering and productivity of ‘Hayward’ kiwifruit vines. Journal of Horticultural Science & Biotechnology. 2003;78:219–224. [Google Scholar]
- Tombesi A, Antognozzi E, Palliotti A. Influence of assimilate availability on translocation and sink strength in kiwifruit. New Zealand Journal of Crop and Horticultural Science. 1993;21:177–182. [Google Scholar]
- Vos J, Marcelis LFM, Evers JB. Functional–structural plant modelling in crop production: adding a dimension. In: Vos J, Marcelis L, De Visser P, Struik P, Evers J, editors. Functional–structural plant modelling in crop production. Dordrecht, The Netherlands: Springer; 2007. pp. 1–12. [Google Scholar]
- Vos J, Evers JB, Buck-Sorlin GH, Andrieu B, Chelle M, de Visser PHB. Functional–structural plant modelling: a new versatile tool in crop science. Journal of Experimental Botany. 2010;61:2101–2115. doi: 10.1093/jxb/erp345. [DOI] [PubMed] [Google Scholar]
- Walton EF. Occurrence of multiple shoots bearing flowers arising from single axillary buds on kiwifruit canes treated with hydrogen cyanamide. New Zealand Journal of Crop and Horticultural Science. 1996;24:95–97. [Google Scholar]
- Walton EF, Fowke PJ. Effect of hydrogen cynamide on kiwifruit shoot flower number and position. Journal of Horticultural Science. 1993;68:529–534. [Google Scholar]
- Walton E, Fowke P. Estimation of the annual cost of kiwifruit vine growth and maintenance. Annals of Botany. 1995;76:617–623. [Google Scholar]
- Walton E, Fowke P, Weis K, McLeay P. Shoot axillary bud morphogenesis in kiwifruit (Actinidia deliciosa) Annals of Botany. 1997;80:13–21. [Google Scholar]
- Wardlaw IF. The control of carbon partitioning in plants. New Phytologist. 1990;116:341–381. doi: 10.1111/j.1469-8137.1990.tb00524.x. [DOI] [PubMed] [Google Scholar]