Characterization of the interactions between architecture and source–sink relationships in winter oilseed rape (Brassica napus) using the GreenLab model

Abstract

Background and Aims

This study aimed to characterize the interaction between architecture and source–sink relationships in winter oilseed rape (WOSR): do the costs of ramification compromise the source–sink ratio during seed filling? The GreenLab model is a good candidate to address this question because it has been already used to describe interactions between source–sink relationships and architecture for other species. However, its adaptation to WOSR is a challenge because of the complexity of its developmental scheme, especially during the reproductive phase.

Methods

Equations were added in GreenLab to compute expansion delays for ramification, flowering of each axis and photosynthesis of pods including the energetic cost of oil synthesis. Experimental field data were used to estimate morphological parameters while source–sink parameters of the model were estimated by adjustment of model outputs to the data. Ecophysiological outputs were used to assess the sources/sink relationships during the whole growth cycle.

Key Results

First results indicated that, at the plant scale, the model correctly simulates the dynamics of organ growth. However, at the organ scale, errors were observed that could be explained either by secondary growth that was not incorporated or by uncertainties in morphological parameters (durations of expansion and life). Ecophysiological outputs highlighted the dramatic negative impact of ramification on the source–sink ratio, as well as the decrease in this ratio during seed filling despite pod envelope photosynthesis that allowed significant biomass production to be maintained.

Conclusions

This work is a promising first step in the construction of a structure–function model for a plant as complex as WOSR. Once tested for other environments and/or genotypes, the model can be used for studies on WOSR architectural plasticity.

INTRODUCTION

Crop yield results from the product of seed weight and number of seeds. These components may vary with genotype and with availability of resources. Achieving maximal yield depends on the plant's capacity to tune resources (offer) to its needs (demand) at each phase of seed development and growth. Regulation of each phase by resource availability results in a trade-off between the different yield components (Peltonen-Sainio and Jauhiainen, 2008; Gambin and Borras, 2010).

Brassica napus is a herbaceous annual plant with indeterminate flowering that lasts at least 1 month and produces a great number of small seeds (70 000–85 000 m⁻² of 4–8 mg; Gambin and Borras, 2010). It is cultivated to produce oil for human nutrition or industrial and energetic uses, and oil production is directly linked to seed biomass production, i.e. to yield. For this species, which has a complex reproductive architecture, yield results from the product of number of ramifications, number of pods per ramification, number of seeds per pod and seed weight. The plant is very plastic, and there may be compensatory mechanisms betweens the different components that are linked to source–sink relationships. For instance, in cultivated monospecific crops, plants compete with other plants thereby reducing resource availability per plant, particularly during plant bolting and ramification. This leads to a trade-off between plant density and number of ramifications per plant (Diepenbrock, 2000), corresponding at the plant scale to the tuning of growth to resource availability.

In addition, there is an important falling off of leaves during pod filling, and although pod envelopes are known to be photosynthetic (Leterme, 1985; Müller and Diepenbrock, 2006), results suggest that pod photosynthesis does not completely compensate for this (Leterme, 1985; Diepenbrock, 2000). This leads to a high rate of abortion in number of ramifications and number of pods per plant, suggesting that demand is higher than offer. Thus, optimization of winter oilseed rape (WOSR) production depends on the efficient tuning of resource availability to plant needs during the reproductive phase, in particular by regulation of ramification growth, which represents an expensive investment in structural tissues and may compromise future capacity to grow seeds. We suggest that this tuning is not optimal under today's growth conditions. To assess this hypothesis, we need to characterize the dynamics of offer/demand during plant growth and its consequences for plant yield. Therefore, we assume that biomass is an integrated indicator of resource availability.

The dynamics of offer and demand in biomass are difficult to calculate because of sequential plant development during the reproductive phase. Indeed, indeterminate flowering and ramification lead to an important heterogeneity in pod age. Thus, each pod will have specific source–sink dynamics according to its date of setting. In the same manner, at each date, each pod will have a different demand according to its age. Thus, to calculate source–sink dynamics, we need to know precisely the plant topology at each date. Therefore, we chose to use a Function Structure Plant Model. Indeed, this kind of model has often been used to study the interactions between plant architecture and functioning (Fournier and Andrieu, 1999; Yan et al., 2004; Mathieu et al., 2009). Regarding WOSR, only two architectural models exist. One, a three-dimensional model (Groer et al., 2007), starts simulation from the end of the rosette period but was not calibrated from experimental data. The other, a GreenLab plant model adapted to WOSR (Jullien et al., 2007), starts from sowing but stops at the end of the rosette stage. We chose to use GreenLab here because it specifically accounts for the interactions between source–sink relationships and architecture. Parameters that control plant morphogenesis are inputs to the model (phyllochrone, duration of expansion and duration of functioning of each organ) while parameters that control the rules of biomass production and allocation (photosynthetic efficiency, parameters of the sink function of each organ) are estimated by adjusting model outputs to experimental data. This model has already been calibrated for numerous plant species and was successfully used to shed light on the impact of source availability on fruit setting and growth (Guo et al., 2003, 2006; Yan et al., 2004; Mathieu et al., 2008). However, the model needs to be extended to the reproductive period of WOSR. Indeed, three specificities need to be adapted in the model to account properly for source–sink relationships for WOSR: the process of ramification, the dynamics of pod appearance and the source–sink functioning of the fruits (which are photosynthetic and oleaginous).

The objective was to evaluate the offer/demand dynamics during the reproductive phase of WOSR using the GreenLab model. Therefore, we established a three-step procedure. First, we adapted the GreenLab model to WOSR specificities by computing ramification expansion, the dynamics of pod appearance, and envelope and seed growth. Secondly, we adjusted model simulations to experimental data to estimate source–sink parameters. And thirdly, we used GreenLab output to characterize source–sink dynamics during WOSR growth cycle.

MATERIALS AND METHODS

The GreenLab model

As the GreenLab model is well described in the literature (Yan et al., 2004; Dong et al., 2008; Mathieu et al., 2009), we focus in this article on the parts of the model that are necessary to reproduce the dynamics of growth and development of WOSR (Brassica napus L.).

The module of organogenesis

A plant can be seen as the combination of elementary units, the phytomers, i.e. an internode and the corresponding node that bears a leaf and occasionally an axillary bud. Plant architecture is the spatial arrangement of these phytomers. Phytomers are grouped into categories based on physiological age (Barthelemy et al., 1997).

In the GreenLab model, plant growth is discretized with a time step based on the rhythm of organ appearance and is called the growth cycle (GC). As WOSR shows continuous growth (Barthelemy and Caraglio, 2007), we chose to compute the time step from the phyllochron (Rickman and Klepper, 1995).

The source–sink module

Plant growth is driven by a source–sink module. At each growth cycle t, the amount of net biomass Q(t) produced by the plant is computed with an empirical function based on the Beer–Lambert law (Vose et al., 1995):

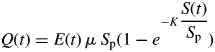(1)

where E(t) is the sum of the daily photosynthetically active radiation during the growth cycle t, μ is similar to the radiation use efficiency, K is the extinction coefficient of the Beer–Lambert law and S_p is similar to the inverse of stand density. S(t) is the plant photosynthetic surface at growth cycle t; it is the sum of green photosynthetic surfaces of the plant. A photosynthetic surface is assumed to stay green and functional during a fixed period of time, termed its life duration. This parameter is fixed from plant observations and varies in relation to leaf rank.

Biomass Q(t) is shared between growing organs according to a proportional model. The sink strength of an organ of type O of chronological age n is the product of a sink strength value p_O and a function of sink strength variations denoted by g_O(n) (see eqn 2). O can be replaced by A, I or F for leaves, internodes and pods, respectively. Total plant demand D(t) is the sum of all the organ sink strengths at GC t.

Variations in organ sink strengths g_O according to the age of the organ are given with beta functions in the classical framework of the GreenLab model (Yin et al., 2003). This function is null when the chronological age exceeds T_O. Otherwise, when 0 ≤ n < T_O, it is given by eqn (2):

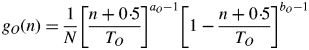(2)

N is a normalization factor and T_O denotes the organ duration of expansion, i.e. the number of growth cycles during which the organ grows. T_O varies with type (leaf, internode or pod) and emergence date of the organ.

Organ masses are computed as the sum of the successive increases in biomass given by the allocation model. At growth cycle t, the mass q_O(n,t) of an organ O of chronological age n is defined by:

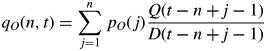(3)

Dimensions are deduced from masses by rules of allometry (Mathieu et al., 2009). Among others, leaf surface area is mass divided by leaf mass per area. See below under ‘Parameter estimation’ for an explanation of the terms a_O, b_O and p_O.

Biomass remobilization

After the end of its expansion, each organ can remobilize part of its biomass that will be added to the common pool. At chronological age n, the biomass q_r,O(n) remobilized from an organ O of chronological age n is calculated according to the time duration (T_e) between the end of organ expansion (T_O) and the beginning of emptying, the speed of remobilization (k), the maximal proportion of biomass (F) that can be mobilized from this organ, and its maximal mass (q_max) reached when n = T_O (Letort, 2008):

(4)

Parameter estimation

There are two kinds of parameters in GreenLab. The first can be computed from the measured data. They help in controlling organogenesis (phyllochron), as well as calculating time of functioning (leaf life span), organ growth (organ duration of expansion) and organ size (specific mass). The second type are hidden parameters that cannot be deduced from the measured data. These parameters help control equations of the source–sink model and are estimated by fitting the model to data of organ biomass using the fitting function of Digiplante software (Cournède et al., 2006). This is the case for parameters a_O, b_O and p_O in eqns (2) and (3). There is one parameterization of the source–sink functions for each physiological age.

Adaptation of GreenLab to WOSR

Ramification process

Ramification needs to be precisely characterized because it will influence both source and sink dynamics. It is complex because expansion of ramification is not synchronous and delayed compared with the main stem. The number of ramifications is pre-determined during organ initiation early in the growth cycle in autumn: the meristem produces leaves, bearing axillary buds that can produce a ramification (Tittonel, 1990; Diepenbrock, 2000). Only 10–15 leaves of the rosette emerge during autumn. These leaves usually never develop ramifications. Expansion stops during the winter and starts again in spring. Following emergence of leaves, internodes of the main stem start elongating while ramification elongation from lateral buds is delayed. This means that a ramification does not start elongating at the same time as its bearing internode even if they have been initiated at the same time. Thus, there is a delay between organ initiation in autumn and expansion in spring, and this delay is variable according to position. These delays need to be estimated to characterize ramification properly. Equations were added to implement the delay between organ initiation and appearance, based on similar works (Kang et al., 2006). We first compute a delay for ramification emergence, from the upper to the bottom ramification. If j is the rank of the internode that bears a branch, φ(j) the emergence delay for this ramification is given by the following equation:

(5)

where M is the last leaf number of the main stem and ⌊x⌋ is the integer part of x. Parameter λ was estimated according to experimental data.

Dynamics of pod setting

Pod setting lasts approximately 1 month and induces sequential growth of a pod that will influence source–sink relationships. To account for this, growth of fruits should be simulated individually. Pods issue from flowers initiated during winter between November and December. Flower initiation starts on the apical meristem (main inflorescence) and propagates basipetally to the lateral inflorescences (Tittonel, 1988, 1990). This means that the basal and oldest ramifications bear the youngest inflorescences. This order of organ initiation will be maintained during pod appearance (Fig. 1) but with a delay due to the delay in ramification expansion. Within a ramification, pod setting remains acropetal.

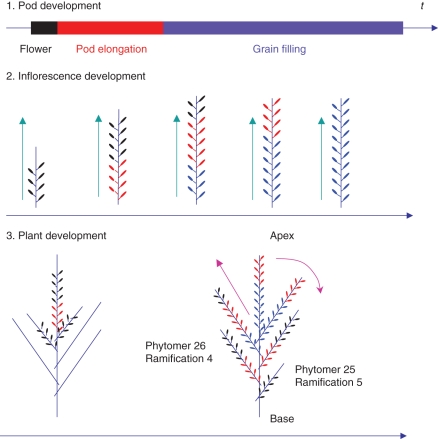
Fig. 1.

Developmental scheme of the inflorescence of winter oilseed rape from Leterme (1985). 1. Pod development: a pod results from flower fecundation, lengthens and enlarges (grain filling). 2. Inflorescence development: flowering and pod setting on the inflorescence occur from bottom up (acropetal). 3. Plant development: flowering starts on the main stem and propagates from top down to ramifications (basipetal). From Jullien et al. (2009b; © IEEE).

With regard to pods, we implemented similar laws of delay that described the progression of pod appearance from the main inflorescence to basal lateral ramifications:

(6)

Parameters m and λ_pod were estimated based on experimental data.

Source–sink functioning of pods

It is clear that specificities of pods that have a photosynthetic envelope and oleaginous seeds should be explicitly defined in the model to account properly for the balance of biomass. However, this is not trivial because information about the ecophysiology of seed in WOSR is scarce. Fruit functioning was well described by Leterme (1985) for the ‘Jet Neuf’ variety. Pods are composed of envelopes and seeds and their development is divided into two phases. The first is termed the ‘heterotrophic phase’ because each pod is supplied mainly by photosynthesis of leaves and stems. The ‘autotrophic phase’ follows, so called because each pod is supplied by its own photosynthesis. The autotrophic phase is also subdivided into two phases, one during which photosynthetic efficiency is maximal and biomass is allocated to envelopes in priority, and one during which photosynthetic efficiency declines and biomass is allocated to seeds in priority. Leterme (1985) explained the decline in photosynthetic efficiency by (1) the senescence of the envelopes, and/or (2) the energetic cost of oil synthesis in seeds. The solution tested here in the model is to implement envelopes as leaves and seeds as fruits with an increased cost of biomass compared with vegetative biomass. Thus, envelopes are characterized by photosynthetic capacity, duration of expansion (T_env) and life span (T_f). Seeds are characterized by duration of expansion. Each also has its specific sink function.

Few data on photosynthetic efficiency of envelopes are available. Existing studies concern only the entire pod including envelopes and seeds. However, Yu et al. (2010) showed that both envelopes and seeds are photosynthetic. Leterme (1985) indicated that the photosynthetic rate of pods first increases until a maximal value (heterotrophic phase), second remains at a maximal value equivalent to that of leaves (autotrophic phase) and third decreases at the end of pod growth due to senescence. By contrast, measurements of gas exchange realized on entire pods (envelopes + seeds) showed that maximal photosynthetic efficiency of pods is approximately two times lower than that of leaves (Gammelvind et al., 1996; Müller and Diepenbrock, 2006). It is thus difficult to conclude properly on pod photosynthetic activity. Thus, for the sake of simplicity, we assume that photosynthetic efficiency of envelopes is equal to that of leaves.

In consequence, in the GreenLab model, a unique photosynthetic efficiency was considered for all photosynthetic surfaces that are summed to calculate biomass production (eqn 1). Pod photosynthesis was considered to be null from birth to the start of autotrophy (T_h), equal to μ from T_h to the end of the autotrophic phase (T_a, see eqn 1 for μ) and null after the end of the autotrophic phase.

To take into account the cost of oil synthesis in seeds, biomass allocated to seeds was multiplied by the ratio between energetic contents of vegetative biomass and of seeds. Therefore, energetic contents were estimated using the energetic content of glucids (4200 cal g⁻¹), proteins (5000 cal g⁻¹) and lipids (9300 cal g⁻¹) given by Varlet-Grancher (1982). Vegetative biomass was assigned to glucids while seed biomass was allocated between glucids, proteins and lipids according to their respective content in seed biomass.

Field trials

Field experiments were conducted at the experimental unit of INRA in Grignon (Yvelines, France, 48·9 °N, 1·9 °E). All the data needed could not be recorded on the same trial. Thus, two trials were used. First trial was conducted in 2004–2005 and focused on pod development and growth with very fine measurements at the seed scale. The second trial was conducted in 2007–2008 and considered the whole plant scale and the whole growth cycle.

First trial: pollen 2004

The objective of this trial was to focus on pod development to validate the model of development and growth proposed by Leterme (1985). The results obtained in this experiment for pollen genotype in 2004 are compared with those obtained by Leterme (1985) for the ‘Jet Neuf’ genotype in 1985. If the results are similar, we assume that the model of pod development is robust and can be used to characterize pod development in GreenLab.

Pollen was sown the 1 September 2004 at a density of 60 plants m⁻². Nitrogen fertilization was carried out three times: 100 kg ha⁻¹ on the 21 September, 40 kg ha⁻¹ on 18 February and 60 kg ha⁻¹ on 17 March.

Once to two times a week, for eight sampling dates between flowering (6 April 2005) and harvest (29 June), 15 plants were randomly harvested at each sampling date. Five median plants were chosen from these 15 plants. On the five plants, on the main stem, numbers of present and aborted pods were counted. On three median plants of the five already selected, on the main stem, we measured length and width on one of every five pods. This corresponded to approx. 15–95 pods per sampling date, 295 pods in total. Pods were placed on a white sheet with a scale of 50 mm and scanned. Images were then analysed using ImageJ software (Abramoff et al., 2004; Rasband, 2009). Two measures of pod length and width were taken and averaged to estimate pod length and width. The scale on the sheet was used to convert measures from pixels into millimetres. On two of the three plants, for one pod out of ten on the main stem, seeds and envelopes were then oven dried at 40 °C, separated and weighted. At the final sampling date, seed samples were used to analyse seed content in nitrogen (Dumas, 1831) and oil (near-infrared spectrometry; Font et al., 2005).

Second trial: pollen 2007

The objective of this trial was to characterize the scheme of plant development and to record the data needed for GreenLab calibration. The crop was sown on the 4 September 2007 at a density of 50 seeds m⁻². Nitrogen fertilization was carried out twice: 40 kg ha⁻¹ on 4 March and 100 kg ha⁻¹ on 18 March.

Non-destructive measurements were carried out to determine the dynamics of ramification expansion, organ appearance and organ development (durations of expansion and life span) during whole plant growth. Three median plants were selected according to their number of emerged leaves among 30 plants selected as seedlings. Position (number of internode), length of each leaf longer than 2 cm and internode length were recorded every week from 12 October on the main stem and from the beginning of April on the ramifications. Measurements were stopped at harvest on 16 June, i.e. after 36 weeks. Only ramifications longer than 2 cm were counted. The number of generated pods and the position of pod abortion were also detailed in April and May on the main stem and ramifications.

Destructive measurements were carried out on eight different dates between 12 November and 19 June, i.e. over 34 weeks, to calibrate the source–sink model of GreenLab and to estimate leaf mass per area and internode mass per length. At each of the harvest dates, five median plants were selected among 20 randomly harvested plants. Different selection criteria of median plants were used before and after bolting. Before bolting, plants were selected according to the number of leaves and diameter at the base of the stem whereas they were selected according to number of ramifications and total height after bolting. Leaves and internodes of the main stem were measured, oven dried at 40 °C and weighed. For lateral axes, leaves and internodes were gathered by axis, oven dried and weighed. Pods were gathered 15 × 15 along an axis, dried and weighted.

Data treatment

Thermal time, expressed in degree-days, was determined cumulatively after plant emergence with a base temperature of 4·5 °C according to previous indications (Morrison et al., 1989; Habekotté, 1997; Miralles et al., 2001). Temperature was recorded at a weather station located 500 m from the field.

Leaf growth was computed from the non-destructive measurements of leaf length. According to the method used by Lemaire et al. (2008), the following logistic function was fitted to the data:

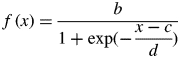(7)

where b is the maximum value of the function, c is the inflection point and b/d is the slope at the inflection point. We assume that leaf surface growth stops simultaneously with leaf length. As a logistic function is symmetrical, the growth duration was computed as 2*(c – D_a), where D_a is the emergence date of the leaf, computed from an arbitrary length of 2 mm.

Fitting of linear relationships and of logistic functions to the data was performed using the least mean square method with the nls function of the R software program (http://www.r-project.org/). Results of fitting are given with 95 % confidence intervals.

The small number of plants in each sample did not allow means and confidence intervals of measures of each sample to be calculated (Siegels and Castellan, 1988; Good and Hardin, 2006). Thus, we considered the median of the three (non-destructive measurements) or five (destructive measurements) plants rather than the average.

To distinguish the order of ramification initiation from the order of flower initiation, ramifications were numbered in two ways: (1) from base to apex according to order of initiation, i.e. to phytomer rank; and (2) from apex to base according to the order of flower initiation, i.e. to ramification number (Fig. 1). Thus, on the median plant of the non-destructive measurements, there are 29 phytomers on the main stem; phytomer 25 corresponds to ramification 5 while phytomer 26 corresponds to ramification 4.

GreenLab outputs used to characterize source–sink relationships

Once the model had been adjusted to the experimental data from the 2007 pollen trial, we analysed the dynamics of four ecophysiological variables calculated by the model. First, we considered the photosynthetic surfaces (leaves and pod envelopes) to evaluate compensation by pod envelopes for leaf fall. Indeed, these surfaces are important because they control the biomass production by photosynthesis. They are calculated from organ biomass using the relationships of allometry between mass and surface calibrated from our data. Green surfaces are divided by the projected surface of the plant (S_p in eqn 1) and the ratio obtained is used to calculate light interception in the model. Thus, the ratio obtained with the leaf surfaces is equivalent to a plant leaf area index (LAI) and will be called leaf projected surface (LPS), while the ratio obtained with the envelope surfaces is an equivalent of the pod area index (PAI) and will be called pod projected surface (PPS). The sum of LPS and PPS is the green projected surface (GPS). Second, we considered the dynamics of organ demand. Demand in GreenLab is unitless and expresses the relative demand of an organ (see ‘The source–sink module’ in the presentation of the model). Third, we analysed the dynamics of biomass production Q expressed in grams per GC (see eqn 1). Fourth, we considered the Q/D ratio where D is the sum of the demands of all organs. The Q/D ratio can be defined as the ‘quantity of biomass in grams available per GC and per unit of demand’ that gives an indication of the relative evolution of the offer/demand ratio: when Q/D decreases the offer/demand ratio becomes less favourable. For the sake of legibility on the graphs presented, time scale in GC will be converted into cumulative °Cd since plant emergence.

RESULTS

Organ setting

Rhythms of organ setting were calculated from data of the Pollen 2007 trial. In this trial, first leaves appeared on the main stem a few days after sowing and the last leaf emerged at the end of March.

Leaves and ramifications

From non-destructive measurements, we displayed the number of emerged phytomers along the main stem according to the thermal time to compute the phyllochron. This revealed a linear piecewise relationship between the number of organs and the thermal time, highlighting a modification of the phyllochron (data not shown; see Jullien et al., 2009b). Statistical adjustments gave a breaking point of about 610 °Cd, i.e. at the middle of January. The inverse of the estimated slope gives an estimate of the phyllochron (Table 1).

Table 1.

Parameters of the dynamics of leaf and pod appearance on the main stem and ramifications

Stem order	Organ	Ramification number	Phytomer rank	Parameter (°Cd)	Value
Main stem	Leaf			Phyllochron, phase 1	28·53 ± 3·2
				Phyllochron, phase 2	11·75 ± 0·6
				Transition date	610 ± 13
	Pod			Podochron	1·87 ± 0·29
				Flat date	1008 ± 20
Ramifications	Pod	4	26	Podochron	2·48 ± 0·26
		3	27	Podochron	2·63 ± 0·28
		2	28	Podochron	2·95 ± 0·48
		1	29	Podochron	3·17 ± 0·12
		1–4	26–29	Podochron	2·79 ± 0·42
		All ramifications	All ramifications	Podochron	3·01 ± 0·48
		4	26	Date of flat	1037 ± 5
		3	27	Date of flat	1049 ± 18
		2	28	Date of flat	1041·5 ± 14
		1	29	Date of flat	1028·44 ± 12
		1–4	26–29	Date of flat	1033 ± 20
		All ramifications	All ramifications	Date of flat	1057 ± 17

The number of ramifications increased from six to 18 between 17 and 31 March and then decreased to 12 ramifications on 5 May. All leaves of a ramification were already present at the time the ramification appeared. Basal ramifications that were initiated first had more leaves than apical ramifications (from zero on the upper ramification to seven on the ninth ramification). Thereafter, for lower ramifications (internodes 18–23), we observed a decrease of two to three leaves per ramification as a result of senescence. For upper internodes (24–29), falling off of leaves on the ramifications was rare (zero to one leaf). In addition, there was variability from different dates, due to the difficulty in counting leaves on those ramifications.

Pods

Pods were set once all the leaves of the main stem had emerged. In our experiment, flowering began on 14 April and ended on 15 May. The results show that the first pods were initiated on the main stem and then on ramifications from apical to basal. The dynamics of pod setting on the main stem was estimated by fitting a linear piecewise relationship to the data. The slope of the linear part of this function was 0·54 ± 0·04 pod (°Cd)⁻¹ while the steady-state date was 1008 ± 20 °Cd. The time between two pod settings, the so-called podochron, was estimated by the inverse of the estimated slope (Table 1). To estimate the progression of pod setting within ramifications, we calculated the time of setting of the first pod on each ramification. The time between first pod setting on two successive ramifications was 15 °Cd. For each ramification, a podochron was estimated with the same method as for the main stem. There was an increase in podochron with rank of the ramification (Table 1).

The number of pods generated per ramification on the median plant tended to increase between the first ramification (internode 29, 55 pods) and the seventh ramification (internode 23, 66 pods). Thereafter, from internode 21 to 18, the number of pods tended to stabilize. However, no significant gradient between ramifications was found.

Field observations also revealed the importance of pod abortions, which varied from 5 to 70 % with ramifications and plants. On the median plant of the non-destructive measurements, pod abortion was 7·4 % for the main stem and approx. 11 % for ramifications.

Organ development and growth

Once emerged, each organ will grow, cease growth and eventually die. The timing of these phases is necessary to characterize the dynamics of plant architecture and was obtained from the non-destructive measurements of the Pollen 2007 trial.

Leaf

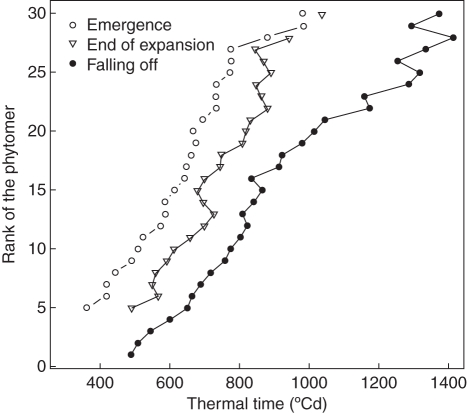
Parameters of the logistic function and D_a were estimated from data of the Pollen 2007 trial. For the main stem, leaf growth and life span were calculated for each leaf rank (Fig. 2). They were highly variable according to rank, possibly due to large variations in the environmental conditions. For leaves of ramifications, average expansion duration for all leaves was 137 °Cd. In addition, no significant falling off of leaves was noted on ramifications during the period of measurements.

Fig. 2.

Leaf development stages expressed in thermal time (T_base = 4·5 °C) according to the rank of the corresponding phytomer. From Jullien et al. (2009b; © IEEE).

Internodes

The dynamics of main stem and ramification elongation presented a linear-flat shape. A linear relationship was fitted to the data to estimate the start and end of elongation of each stem. The main stem started elongating about 70 °Cd before basal ramifications did; all ramifications started elongation between 788 and 800 °Cd. Elongation stopped at 835 °Cd for the main stem, at 847 °Cd for upper ramifications (internodes 28–23) and at 881 °Cd for basal ramifications (internodes 22–20). We thus concluded that elongation of ramifications was synchronous and that differences in ramification lengths were due to differences in numbers of internodes per ramification, growth rates or date of end of elongation.

Pods

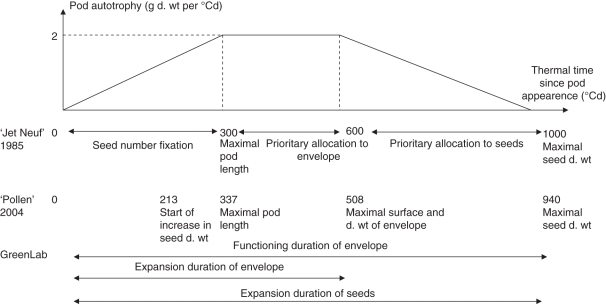
Parameters of the model of pod development were estimated according to experimental data recorded in the Pollen 2004 trial for Pollen variety. Key development stages (appearance, end of elongation, end of enlargement, start of biomass accumulation in seeds, end of seed growth) were estimated using 0 °C as the base temperature to compare them with results obtained for ‘Jet Neuf’ by Leterme (1985) (Fig. 3). Results obtained for the two varieties are consistent. Data from the Pollen 2004 trial were thus used to estimate expansion duration of seeds and envelopes as well as life duration of envelopes with T_base = 0 °C. Values were then converted using T_base = 4·5 °C (Table 2).

Fig. 3.

Pod development stages expressed in thermal time (T_base = 0 °C) for ‘Jet Neuf’ variety (from Leterme, 1985) and ‘Pollen’ variety (from the Pollen 2004 field experiment).

Table 2.

Estimation of the durations of life (DL) and expansion (DE) for envelopes and seeds of an average pod of the Pollen 2004 experiment

Unit	Seed DE	Envelope DE	Envelope DL
Thermal time Tbase = 0 °C	940	508	940
Thermal time Tbase = 4·5 °C	640	325	640
Growth cycle	54	28	54

Estimates were made using different units: thermal time with T_base = 0 °C; thermal time with T_base = 4·5 °C, and GreenLab Growth Cycle (GC).

Estimation of the model parameters of morphogenesis

For WOSR, we consider that the short phytomers of the rosette are of physiological age 1. The long phytomers of the main stem and the ramifications are respectively of physiological age 2 and 3. The phytomers of the main and lateral inflorescences are respectively of physiological age 4 and 5. The latter comprise phytomers with leaves that represent pod envelopes and flowers that become fruits.

Rhythms of organ appearance on each axis

All the above data were used to calculate fixed parameters of the GreenLab model. We converted them from degree-days to number of growth cycles of the model from the results given in Table 1. We based the duration of the growth cycles on the phyllochron of the second phase (phytomers of the main stem, physiological age 2, one growth cycle = one phytomer). The rhythm of phytomer appearance during the first phase (leaves of the main stem, physiological age 1), which is slower, was calculated relative to the second phase: for some growth cycles, no organ will appear. For physiological age 3 (leaves of the ramifications), we considered growth cycles to have the same duration as those of physiological age 2. By contrast, pods are set in place faster than leaves, with a factor of 6 (0·167 GC) for pods of the main stem (physiological age 4), and a factor of 4 (0·25 GC) for pods of ramifications (physiological age 5). In addition, to take into account the importance of pod abortion, a maximal number of pods was fixed equal to the actual number of pods present on the plant for each ramification.

Leaf and internode expansion

For the main stem, expansion duration and life span of leaves depend on the rank of the leaf, and were calculated for each leaf according to the data presented in Fig. 2. Leaf expansion time varies from 7 GC to 13 GC, while leaf life span varies from 17 GC to 40 GC. Leaf mass per area (thickness) increased from sowing to bolting and then decreased for all leaves. However, differences between leaf ranks were also observed (data not shown; see Jullien et al., 2009a). Thus, we attributed to each leaf its individually average specific leaf mass per area. For ramifications, leaf expansion duration and leaf life duration could not be estimated properly because few data were available. Thus, for each leaf of the ramifications we considered its GC of emergence and used the same values for leaf expansion and life durations as the leaf of the main stem appearing at the same GC. Their expansion varies from 5 GC to 10 GC. Expansion duration of internodes was estimated at 12 GC for the main stem and ramifications from field measurements.

Ramification

We considered that all ramifications elongated synchronously. Thus, delay functions for ramification expansion and pod setting compared with the main stem were calibrated with data for the number of organs counted on the median plant. Calibration gave us λ = 0·8, m = 3 and λ_pod = 1 (eqns 4 and 5). M, the maximal number of leaves, was 29. We fixed the number of ramifications to ten, assuming that the next ramifications below these ten are negligible for estimation of yield.

Pod expansion

Durations of life span (envelope) and expansion (seeds and envelopes) were estimated according to data of the Pollen 2004 trial (Table 2 and Fig. 3). Expansion duration of seeds was set equal to envelope duration. We considered that the first 213 °Cd (T_base 0) of seed expansion corresponded to fixation of the number of seeds and that the increase in seed dry weight during this phase was negligible. To account for this delay of increase in seed dry weight in GreenLab, we implemented a primordia from pod apparition to 213 °Cd (T_base 0; equivalent to 125 °Cd T_base 4·5 and to 11 GC). This means that the sink of seeds is considered to be null during primordia duration. This is the case for an average pod of the main stem. However, data on basal ramifications recorded on the same trial but on another variety (‘Capitol’, data not shown) show that the delay between pod setting and the beginning of increase in seed dry weight decreases with the rank of the ramification. Thus, to account for the effect of pod position on the plant, we implemented a decrease in value of the primodia of one GC per rank of ramification.

Pod functioning

Autotrophy of the envelopes starts at T_h = 12 GC, priority of allocation being to envelopes, and autotrophy stops at T_a = T_env = 28 GC. Seed nitrogen and oil content in the Pollen 2004 trial were 18 and 50 %, respectively, corresponding to an energetic content of 7296 cal g⁻¹. The ratio between seed and vegetative biomass energetic content was 0·57. This ratio was applied to biomass allocated to seeds to take into account the cost of oil synthesis.

Remobilization

Biomass data analysis showed a 20 % decrease in internode and leaf biomass at the plant scale. Thus, the remobilization function of GreenLab (eqn 4) was calibrated for these two organs using experimental data. Parameter values were: T_e = 15 GC, k = 0·1 and F = 0·2.

Evaluation of the model simulation of plant topology

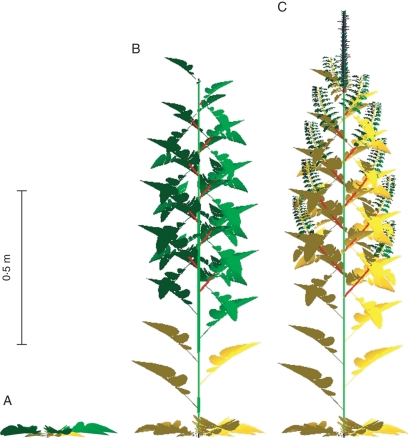
A simulation of the model is shown in Fig. 4 at three different growth cycles. First, leaves with short internodes correspond to the rosette stage. Emergence of ramifications is synchronous and basal ramifications have a greater number of leaves. Apical inflorescences have a larger number of pods because they started flowering first. The plant topology simulated using the parameters of morphogenesis described above is consistent with field observations and general understanding of WOSR development.

Fig. 4.

Realistic visualization of the simulated plant architecture at three different stages of growth: rosette stage, bolting, pod appearance. Dead leaves are in yellow.

Model adjustment and estimation of source–sink parameters

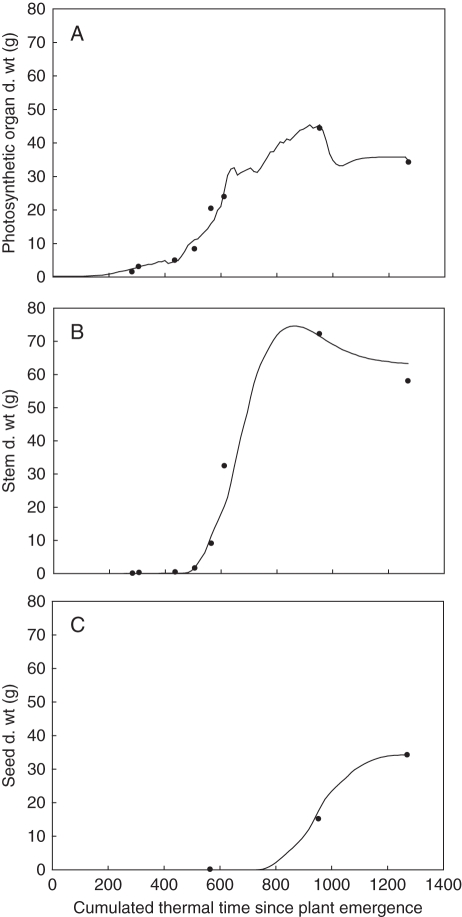
At the plant scale, parameter calibration allowed the dynamics of leaf, internode and fruit masses during the whole growth cycle to be determined (Fig. 5). Root mean square errors (RMSEs) calculated for these three compartments for all the sampling dates were 2·012, 4·76 and 0·81 g per plant, respectively. Regarding leaves, note that the two final points are leaf and envelope dry weights and that the decrease at the end reflects the dramatic falling off of leaves.

Fig. 5.

Comparison of model adjustment to data of cumulated dry weight at the plant scale for photosynthetic organs (A), internodes (B) and seeds (C) for the eight sampling dates of the Pollen 2007 field experiment. Photosynthetic organ dry weight is the sum of leaf and pod envelope dry weight. Lines are model simulations; points are experimental data for the median plant of each sampling date.

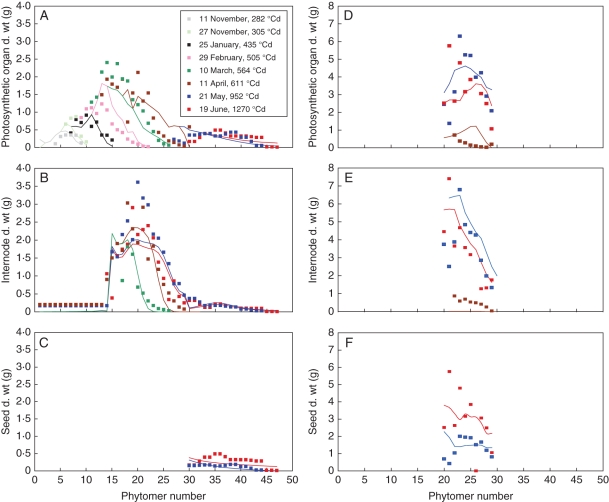
At the organ scale, on the main stem, profiles for the dry weight of photosynthetic organs, internodes and seeds are given in Fig. 6A, B and C for the eight sampling dates. These graphs represent the variations in organ dry weight with the number of phytomers for the median plant of each sampling date. For the photosynthetic organs (Fig. 6A), note that phytomers 1 to 29 correspond to leaves while phytomers 30 to 47 correspond to pod envelopes. For the internodes (Fig. 6B), phytomers 1 to 29 correspond to internodes of the stem while phytomers 30 to 47 correspond to internodes of the inflorescence raceme (stem between two successive pods). The model correctly simulated the dynamics of organ growth and their variations with number of phytomers and age. However, maximal values of leaf and internode dry weight between phytomers 19 and 22, i.e. during plant bolting, were underestimated. By contrast, seed dry weight was dramatically underestimated especially for the last sampling date (Fig. 6C). For the four first dates before plant bolting, RMSE for the leaves varied with sampling dates between 0·14 and 0·36 g, while for the four last dates during ramification and seed filling, RMSE varied with the sampling dates between 0·15 and 0·46 g for leaves, between 0·37 and 0·46 g for internodes, and between 0·07 and 0·16 g for seeds.

Fig. 6.

Comparison of model adjustment to data for the dry weight of photosynthetic organs (A, D), internodes (B, E) and seeds (C, F) for the eight sampling dates of the Pollen 2007 field experiment. Each point represents an individual organ (or six pods for seeds and envelopes) for the main stem (A–C), while organs have been pooled by ramification for the ramifications (D–F). Note that, on the main stem, phytomers 1–29 correspond to leaves and stem internodes, while phytomers 30–47 correspond to pod envelopes and raceme internodes. Lines are model simulations; points are experimental data for the median plant of each sampling date; each colour stands for a sampling date, as indicated.

On the ramifications, data on the graphs represent the pooled dry weight of each organ (Fig. 6D, leaves and pod envelopes; Fig. 6E, internodes of stem and raceme; Fig. 6F, seeds) per ramification for the median plant at each sampling date. Phytomer number indicates the position on the ramification, phytomer 29 corresponding to the upper ramification. Profiles of variation of organ dry weight with the phytomer number were calculated correctly by the model for phytomers 29–23 but not for phytomers 22–20 for which experimental data present erratic variations that the model does not manage to account for. The decrease in leaf and pod envelope dry weight due to falling off of leaves is correctly simulated, as is the decrease in dry weight of internodes and racemes due to remobilisation. RMSE varied with the three sampling dates between 0·61 and 1·3 g for leaves and envelopes, 0·47 and 1·77 g for internodes and racemes, and 0·78 and 1·47 g for seeds.

Corresponding values of source–sink parameters are presented in Table 3. Values of internode sink strengths for different physiological ages are coherent with the increase in internode mass during plant bolting (physiological age 2) and ramification (physiological age 3), and with its decrease during pod growth (internodes of racemes, physiological ages 4 and 5). Sink strength of photosynthetic surfaces is dramatically lower for physiological ages 4 and 5 compared with physiological ages 1–3, possibly due to the difference in surface and dry weight between leaves (physiological ages 1–3) and pod envelopes (physiological ages 4 and 5). The photosynthetic efficiency of green surfaces is 7·04 g MJ⁻¹ m⁻². Regarding the parameters of the sink function (beta function), the value of a_O/(a_O + b_O) is an indication of the shape of the function. When this ratio is close to 0·5, the sink function is symmetric. When it is higher than 0·5, the sink function maximum is shifted on the right (sink increases at the end of organ life), which is the case for leaves, pod envelopes and internodes. When the ratio is lower than 0·5, the sink function maximum is shifted to the left (demand is high at the beginning of organ life), which is the case for seeds. The high value of a for internodes indicates a very sharp function, consistent with the rapid growth of internodes during plant bolting.

Table 3.

Parameters of the model estimated by model adjustment on the experimental data

	Physiological age	Photosynthetic surfaces	Internodes	Seeds
Sink strength	1	1	0·03
	2	0·95	3·13
	3	0·67	3·57
	4	0·10	0·10	0·22
	5	0·17	0·19	0·35
Sink functions	aO/(aO + bO)	0·67	0·62	0·41
	a	2·43	21·71	2·76
Photosynthetic efficiency (g MJ−1 m−2)			7·04

Physiological age 1: rosette stage; physiological age 2: main stem during plant bolting; physiological age 3: ramification; physiological age 4: flowering and pod growth on the main stem; physiological age 5: flowering and pod growth on the ramification. Photosynthetic surfaces during physiological ages 1–3: leaves; during physiological ages 4 and 5: pod envelopes. Internodes during physiological ages 1–3: internodes of the stem; during physiological ages 4 and 5: internodes of the racemes. a and b are parameters of the beta-function (see Materials and Methods).

Characterisation of source–sink relationships

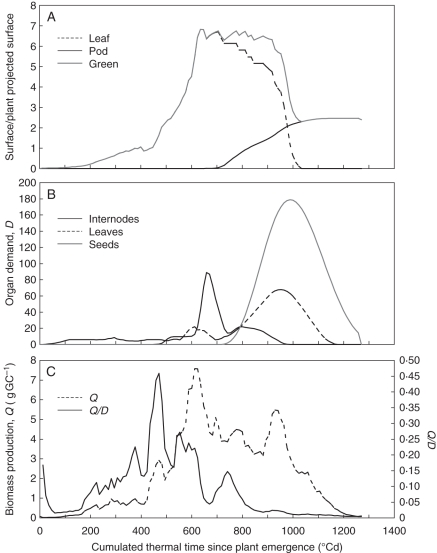
Variations in LPS, PPS, organ demand, Q and Q/D with thermal time are presented in Fig. 7. We do not have measurements to validate the dynamics of LPS and PPS (Fig. 7A) but they are in agreement with values obtained for other experiments conducted in Grignon for which LAI at the crop scale increased until 6 and then decreased during pod growth, while PAI increased up to 2–3 (J.-M. Allirand, unpubl. res.). Values of demand D, biomass production Q and Q/D (Fig. 7B, C) were calculated by the model. Q was highly variable. Part of this variability is due to variation in the environment (data not shown), this is the case of the peak values observed at 482, 611, 693, 788 and 940 °Cd. The other part of the variations of Q is due to the dynamics of GPS that control light interception.

Fig. 7.

Dynamics of some ecophysiological variables calculated via the GreenLab model after adjustment for the experimental data of the Pollen 2007 trial. (A) Dynamics of leaf projected surface, pod projected surface and green projected surface, as indicated. For the calculation of these variables, see Materials and Methods. (B) Dynamics of demand D of internodes, leaves and seeds, as indicated. (C) Dynamics of biomass production Q and of Q/D ratio, as indicated.

Analysis of the dynamics allowed us to identify the principal ontogenic phases of the plant. Five phases could be distinguished.

1. From 0 to 470 °Cd: this is the rosette period. Organ demands are low and Q increases due to rosette leaf emergence and expansion. Thus, Q/D increases from 0·1 to 0·45, the latter being its maximal value on the whole crop cycle.

2. From 470 to 611 °Cd: this phase corresponds to plant bolting. Internode and leaf demands increase, and although Q is still increasing, Q/D decreases from 0·44 to 0·22.

3. From 611 to 670 °Cd: this period corresponds to ramification. Internode demand increases dramatically while Q and LPS reach their maximum value at 623 °Cd (value: 7·57 g) and 635 °Cd (value: 6·82), respectively. At the same time, Q/D decreases dramatically to 0·044 at 670 °Cd, linked to the investment cost of the plant in the ramification.

4. From 670 to 740 °Cd: this is the beginning of flowering. Internode demand decreases while envelope and seed demands begin to increase. LPS decreases while PPS begins to increase, and GPS is stabilized at approximately 6·5. This is a transition phase during which Q/D increases slightly to 0·15.

5. From 740 to 1270 °Cd: this is the period of envelope growth and seed filling. Internode demand increases slightly as a result of growth of the raceme. Envelope demand increases until 952 °Cd and then decreases, and seed demand increases until 988 °Cd. GPS remains stabilized at approx. 6·5 up to 917 °Cd, i.e. just before maximal envelope demand. Then GPS decreases dramatically, indicating that pod envelopes no longer compensate for falling off of leaves. At the time of maximal seed demand, GPS is 3·3. During this phase, Q/D decreases from 0·15 to 0·006.

DISCUSSION

Our experimental results allowed us to validate the developmental scheme proposed in the Introduction for the Pollen genotype, and to quantify all the different processes involved in this developmental scheme.

The apparent complexity of the proposed scheme during the reproductive phase can be discussed under three headings. First, the rhythm of organ emergence (leaves, ramifications) or setting (pods) on a given axis is acropetal and controlled by temperature. Secondly, first-order ramifications appear synchronously with all their leaves being already present in the bud. Thirdly, flowering and pod setting starts from the main stem and sequentially propagates to ramifications in a basipetal order.

This developmental scheme, which is coherent with the literature (Leterme, 1985; Tittonel, 1990), was quantified. Leaf emergence dynamics were found to be bi-phasic with a 2·4-fold lower phyllochrone in the second phase than in the first phase, consistent with the results obtained by Morrison et al. (1989). The transition between the two phases was estimated to 610 °Cd cumulated from sowing, which corresponds to 16 January under the conditions of our experiments. However, the change might be progressive and sampling dates surrounding this date are remote in time (7 and 21 January), not sufficiently refined to get a precise estimation of the transition time. Thus, we can infer from these data merely that the change in phyllochron occurs in January, i.e. before plant bolting. Variations in phyllochron have been observed for other species (Cao and Moss, 1991; Lemaire et al., 2008) but with different patterns: for wheat, variation is similar to that for WOSR with a decrease of phyllochron whereas for sugar-beet the phyllochron increases. Several hypotheses are evoked in the literature to explain these bi-phasic dynamics. For instance, these variations were attributed to variations in the relationship between the air temperature used in the calculation of thermal time and the temperature of the apex during plant growth in height (Jamieson et al., 1995). For WOSR, in our conditions, this explanation is not pertinent because change in the phyllochron occurs before plant bolting. Several studies (Tittonel, 1988; Netzer et al., 1989) demonstrate the role of plant ontogeny, and especially the correlation with flower initiation that occurs between November and January. This hypothesis is consistent with the phyllochron change observed in January in our conditions.

Pod setting on the main stem is six times faster than leaf emergence during the second phase. The thermal time between pod setting of two consecutive ramifications was 15 °Cd. The rhythm of pod setting for ramifications was found to be slower than for the main stem, with an increasing podochron gradient from apical to basal ramifications. Our interpretation is that pod setting on ramifications is subject to higher competition for assimilates than on the main stem because of the internode expansion and pod setting on all ramifications within a short period. Experimental results were used to compute reproductive development of rapeseed in the GreenLab model. A delay in ramification expansion and top-down propagation of flowering were implemented. This modification allowed us to correctly simulate the dynamics of reproductive development described for rapeseed. A delay function for ramification expansion has been already used in GreenLab to simulate structural development of Arabidopsis thaliana (Christophe et al., 2008). However, in their study delay was a function of the source–sink ratio. We did not consider this effect in our model for the sake of simplicity but this could be done in further versions of the model especially if we want to simulate the effect of variety, cultural techniques (density) or pests (for instance florivory) on plant structural development. In the same manner, a more generic function such as that proposed by Kang et al. (2006) could be used.

Source–sink parameters were calculated by fitting model simulations to the experimental data. Positive results from the fitting are that we managed to reproduce the complete dynamics of organ development and growth of WOSR from sowing to harvest. Model adjustment to the experimental data was satisfying at the plant scale: total leaf, internode and seed biomasses were correctly simulated. The model accounted for the decrease in internode dry weight due to biomass demobilization and for the decrease in leaf dry weight due to falling off of leaves during the reproductive phase. Model adjustment at the organ scale presented some defaults showing that biomass repartition within the plant was not completely accounted for. In the example given, regarding internodes of the main stem, we observed that internode dry weight was underestimated for phytomers 19–22, i.e. during plant bolting. This can be explained either by an underestimation of internode sink strength during this period or to the fact that we did not calculate the secondary growth of the internodes in the model. In the same manner, seed dry weight were underestimated on the main stem. This has a weak influence on the total seed weight calculation because seeds of the main stem represent only 15 % of the total seed weight. The underestimation can be due either to an underestimation of seed sink strength or to an error in the model of pod development we used. Indeed, we had little information about pod development and its variation with pod position on the plant. In the same manner, the estimation of pod envelope photosynthesis remains incompletely resolved (Leterme, 1985; Gammelvind et al., 1996; Müller and Diepenbrock, 2006). Further investigations should be done on these points to improve our description of pod development in the model. On the ramifications, error in organ dry weight estimation was more important for basal ramifications than for upper ramifications. This can be explained by the fact that the observed data are more variable for basal ramifications. Our interpretation is that at this position in the canopy, many factors other than source–sink relationships interact and generate crop heterogeneity. In the example given, abortion of a ramification on a neighbouring plant may induce a heterogeneity in light environment that will favour the development of basal ramifications on the studied plant. According to our observations, these events are more frequent at the base of the canopy.

The values obtained for the source–sink parameters after adjustment must be interpreted with care because they correspond to a specific experimental data set, and because they are highly sensitive to the values of measured parameters entered, for which there can be an important uncertainty. For example, regarding phenology, the transition time between the two values of the phyllochron will have an impact on the phenology and source–sink relationships. This is also the case for the duration of life and the expansion duration of leaves, pod envelopes and internodes as well as the leaf mass per area, which are all involved in calculation of the offer and of the demand, and to which the model is applicable. This is especially the case for the ramifications, for which we have very little data to estimate life duration and expansion duration of leaves and internodes. In the same manner, the rate of biomass remobilization from the internodes and the time of beginning of remobilization may influence the source–sink relationships. Internode dry weight decreased by 20 %, within the range of 15–25 % described in the literature as a function of genotypes and growing conditions (Allen and Morgan, 1975; Mendham and Scott, 1975; Tayo and Morgan, 1975). However, in the model average values of these parameters were set for all internodes even if they could also vary with the number of the phytomer and the ramification.

In addition to uncertainty in parameter values, estimation errors may also be due to processes that the model does not account for. This is the case for the secondary growth mentioned above, and also for the root growth. It is possible to introduce a root compartment in the model. However, we chose not to do so for two reasons. First, we measured only the pivot-roots of sampled plants in the experiment, which form only a part of the total root system. Secondly, measurements showed a decrease in pivot-root dry weight during spring and summer of approx. 1 g (data not shown), suggesting that biomass remobilization from root compartment to aerial parts was negligible in our experiment. Thus, we consider that not taking the root compartment into account may have an influence on photosynthetic resistance but would not affect the estimation of offer in biomass and its repartition within aerial parts during the reproductive phase.

All these limits could be improved in a further version of the model. However, before modifying the model with new processes or before refining the estimation of the measured parameters, the first step will be to analyse the sensitivity of the model to identify parameters that should be precisely defined as well as their variations with organ position in the plant, and those that can be estimated by using an average value.

Values of source–sink parameters obtained after model adjustments and source–sink dynamics calculated are consistent with what we know about WOSR ecophysiology. The increase in internode sink during bolting and ramification leads to a dramatic decrease in the source–sink ratio; falling off of leaves of the main stem is compensated for by pod envelope photosynthesis until a certain point, and seed filling takes place at very low Q/D. However, photosynthetic surfaces correspond to a GPS calculated by the model of approx. 3·3. This variable, equivalent to an LAI at the plant scale, can be used to estimate the efficiency of light interception during seed filling. Measurements carried out at the crop scale show that 80 % of the light is intercepted with an LAI of 2, and 90 % with an LAI of 3 (J.-M. Allirand, pers. observ.). This indicates that under the conditions of our experiment, GPS would be sufficient to intercept 80–90 % of the incident light during seed filling. However, this needs to be confirmed by further results because GPS calculated is highly dependent on variations in leaf specific area that we specified in the model, and we know that this parameter is in fact very variable (Jullien et al., 2009a).

Conclusions

This work is a first step towards building and calibrating a structure–function model of WOSR that accounts for variations in dry weight at the organ scale. Improvements are needed concerning the secondary growth of stems, variations of pod development with position in the plant and estimation of growth parameters of the ramifications. Nevertheless, it seems to be a satisfying tool to analyse source/sink relationships within the plant. First results shed light on the important cost of the ramification and its impact on the source–sink ratio; they also confirmed the significant role of pod envelopes in biomass production during seed filling. This should be validated on other data sets recorded under different environments and/or genotypes.

Once validated for other situations, the model could be used to reproduce plant plasticity. Indeed, this model will allow us to simulate ramification or organ pruning due to damage from parasites and that induces modifications in plant architecture and biomass allocation. This is a recent challenge that functional structural plant models deal with (Robert et al., 2008) and we intend to apply it to the interactions between insects and plants based on experimental data (Pinet et al., 2009).