Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2010 Dec 23;107(5):805–815. doi: 10.1093/aob/mcq244

Correlation between dynamic tomato fruit-set and source–sink ratio: a common relationship for different plant densities and seasons?

MengZhen Kang 1, LiLi Yang 2,*, BaoGui Zhang 3, Philippe de Reffye 4,5
PMCID: PMC3077983  PMID: 21183453

Abstract

Background and Aims

It is widely accepted that fruit-set in plants is related to source–sink ratio. Despite its critical importance to yield, prediction of fruit-set remains an ongoing problem in crop models. Functional–structural plant models are potentially able to simulate organ-level plasticity of plants. To predict fruit-set, the quantitative link between source–sink ratio and fruit-set probability is analysed here via a functional–structural plant model, GreenLab.

Methods

Two experiments, each with four plant densities, were carried out in a solar greenhouse during two growth seasons (started in spring and autumn). Dynamic fruit-set probability was estimated by frequent observation on inflorescences. Source and sink parameter values were obtained by fitting GreenLab outputs for the biomass of plant parts (lamina, petiole, internode, fruit), at both organ and plant level, to corresponding destructive measurements at six dates from real plants. The dynamic source–sink ratio was calculated as the ratio between biomass production and plant demand (sum of all organ sink strength) per growth cycle, both being outputs of the model.

Key Results and Conclusions

Most sink parameters were stable over multiple planting densities and seasons. From planting, source–sink ratio increased in the vegetative stage and reached a peak after fruit-set commenced, followed by a decrease of leaf appearance rate. Fruit-set probability was correlated with the source–sink ratio after the appearance of flower buds. The relationship between fruit-set probability and the most correlated source–sink ratio could be quantified by a single regression line for both experiments. The current work paves the way to predicting dynamic fruit-set using a functional structure model.

Keywords: Tomato, Solanum lycopersicum, fruit-set probability, time step, source–sink ratio, sink strength, functional–structural plant model, inverse modelling, plant plasticity

INTRODUCTION

Fruit-set generally refers to the transition of a flower or a flower bud into a fruit of certain size. Fruit-set in tomato influences yield through effects on both fruit number and fruit size (Bertin, 1995). Although it has been claimed that hormones are the regulators of fruit-set (Gillaspy et al., 1993), it is also well recognized that it is highly related to source–sink ratio (Valantin-Morison et al., 2006), which can be varied by changing light levels, plant densities, leaf pruning or genetic background (Stephenson, 1981; Marcelis et al., 2004; Wubs et al., 2009). In pepper, a positive correlation has been observed between the number of fruits successfully ripened and source–sink ratio (Marcelis et al., 2004), and the threshold for fruit-set is cultivar-dependent (Wubs et al., 2009); in tomato, less fruit abortion has been observed when flower number per truss (inflorescence) was limited to three instead of seven (Bertin, 1995). Moreover, fruit-set is a dynamic process that varies according to crop growth stage: cyclical abortions have been observed in sweet pepper (Wubs et al., 2009).

Three types of studies carried out on fruit-set may be distinguished. The first approach is based on direct field or experimental observations, e.g. changing growth conditions (leaf removal, shading, CO2 enrichment) (Pettigrew, 1994; Alkio et al., 2003; Iglesias et al., 2003) or comparing fruit-set between different cultivars (Passam and Khah, 1992). Such an approach provides qualitative knowledge on the influence of various factors on fruit-set with different levels of detail. The second type, which is less common, relies on model-assisted analyses in addition to experimental study to clarify the key determinants (e.g. source–sink ratio) involved in fruit-set and to quantify their relative effects (Bertin, 1995; Wubs et al., 2009). This approach is a necessary preliminary step before building predictive models of fruit-set. The third type of study, of which there are rather few, consists in predicting fruit-set either deterministically (Bertin and Gary, 1993) or stochastically (Wubs et al., 2009). Simulation of fruit abortion is a weak point in crop models (Marcelis et al., 1998). Until now, similar to the weakness of predicting tiller senescence in crop models, simulation of fruit-set has not yet been successful, and it relies to a great extent on the soundness of the second step.

In process-based plant models, attempts have been made to link fruit-set probability to the level of assimilate competition (Jones et al., 1991; Bertin and Gary, 1993; Marcelis and Heuvelink, 1999). However, the data sets used to estimate model parameter values were limited, and the prediction of fruit-set was not accurate (Wubs et al., 2009). In these models, the competition level is defined as the ratio between actual growth of fruits and their potential growth under non-limiting assimilate supply (Bertin and Gary, 1993; Bertin, 1995). The actual growth of fruit is treated separately from the remaining processes, which limits the simulation of the interaction between fruit-set and fruit growth. Potential growth, which is expected to be obtained under ‘optimal’ growth condition, depends actually on developmental stage (Bertin, 1995) or temperature (Marcelis and Heuvelink, 1999); therefore, it is not an effective absolute reference in modelling. When topological information on the modelled plant is not explicitly incorporated in the model, it is difficult to simulate organ-level behaviour, such as competition between individual fruits from the same or from different trusses, and feedback of fruit-set on source–sink balance, which limits the model's ability to adapt to a wide range of environmental and competitiveness conditions.

Functional–structural plant models (FSPMs) are regarded as potential tools for simulating organ-level plant plasticity in a whole plant system (de Reffye et al., 2008; Vos et al., 2009). For example, periodic fruit-set pattern can be simulated in a FSPM when it is controlled by source–sink ratio (Mathieu et al., 2009); tiller breakout in wheat can be modelled according to light interception in the canopy (Evers et al., 2006). Two main components of FSPMs are simulation of organogenesis and organ expansion. Simulation of organogenesis gives the number, position and age of any organ, by the Lindenmayer system (Lindenmayer, 1968) or an automaton (Yan et al., 2004), which are equivalent to each other. Differences among FSPMs exist in simulating organ expansion: organ size is forced from measured data (Evers et al., 2006; Zheng et al., 2008), or resulted from photosynthesis and biomass repartition processes (Guo et al., 2006; Evers et al., 2010). Plant three-dimensional architecture may be used as a support to compute light interception and biomass production in FSPMs (Fournier and Andrieu, 1998), but a simple Beer's law analogue formula is also used to calculate growth rate efficiently (Guo et al., 2006). The gap lies in the means of calibrating the model: models are adjusted at the level of underlying sub-processes (Allen et al., 2005; Eschenbach, 2005) separately or at a global level (Renton et al., 2005; Christophe et al., 2008). Modelling the interaction between organogenesis, biomass production and repartition is at the heart of a FSPM. A few models have achieved these objectives, but fewer have been calibrated for a plant over a longer lifetime.

Fruit-set is an organ-level event that fits the goal of FSPMs. In this paper, a FSPM, GreenLab, is chosen to analyse the relationship between fruit-set and source–sink ratio for wide cultivation conditions (four planting densities in two cultivation periods). In GreenLab, individual organ (including lamina) biomass is the result of sink–source regulation during its lifetime; it can simulate the interaction between fruit-set, biomass production and fruit size. Because of its mathematical formalism, model parameters can be adjusted globally by fitting model outputs to the corresponding measured organ biomass (Christophe et al., 2008). In a previous study, the GreenLab model was used to simulate tomato phenotypic plasticity with regard to biomass production and partitioning induced by three plant spacing arrangements (Dong et al., 2008). To prepare for the prediction of fruit-set, this study focuses on: (1) obtaining source–sink ratios for different cultivation periods and planting densities; and (2) seeking for a quantitative relationship between the dynamic fruit-set probability and source–sink ratio. To compare the model parameters and output for different planting density, here a unified time step is used for the source and sink computation. Fruits inside a truss are set to grow in a sequential rather than simultaneous way as in Dong et al. (2008).

MATERIALS AND METHODS

Experiments and measurement

Two experiments were carried out in a solar greenhouse (a greenhouse where the sun is the only source of energy with a back wall of brick that absorbs heat during the day and releases it at night) at the Chinese Academy of Agricultural Science in Beijing (39·55 °N, 116·25 °E), during spring (2 April to 18 June) and autumn (30 August to 15 November) 2007. Plant material was tomato (Solanum lycopersicum L. ‘ZhongZa 9’). At the start of each experiment, tomato seedlings with five leaves were transplanted to 25-cm pots, filled with a mixture of 60 % peat and 40 % vermiculite. In each experiment, four plant densities were imposed by varying the spacing between pots. These were: 1 plant m−2 (D1), 3 plants m−2 (D2), 6 plants m−2 (D3) and 11 plants m−2 (D4). Thirty replicate pots were established for each planting density with two guard rows between density treatments. Water was supplied manually as required. Side shoots were removed regularly to ensure a single sympodial stem; no fruits were picked. Air temperature, humidity and light intensity were recorded throughout the experiment at a fixed position in the greenhouse. As the distribution of light intensity is uneven along a north–south direction, with the help of a handheld light meter, a calibration coefficient was obtained for calculating local light intensity from the fixed-position meter.

Six destructive measurements were carried out in each experiment: 2 April (at planting), 16 April, 25 April, 7 May, 31 May and 18 June for the spring experiment and 30 August (at planting), 13 September, 25 September, 14 October, 2 November and 25 November for the autumn experiment. The purpose of these measurements was to identify inversely the source and sink parameters required to compute source–sink ratio. At each measurement date, three or four plants per plant density treatment were sampled. When a plant was harvested destructively, it was replaced by a comparable plant to maintain the previous light distribution among the remaining plants. The organ-level data measured included dry weight (d. wt) and the dimensions of individual internodes, laminae, petioles and fruits.

Non-destructive measurements were made on five plants per treatment, twice per week, with observations on the number of leaves, phytomer ranks (internode number counting from the base) of trusses on the main stem, and stage of development (flower bud, flower, a fruit or an abortion) at each flower position. The purpose was to obtain a dynamic fruit-set probability assessment for each treatment. Different kinds of abortion were distinguished. Bud abortion refers to when a flower bud fails at flowering and simply falls off without opening. Flower abortion occurs when a flower opens, closes and then falls with no apparent ovary development. Otherwise it enters into the fruiting stage. Fruit abortion occurs when a fruit falls before reaching 1·0 cm in diameter. Fruit-set probability is defined as the proportion of flower buds that enter the fruiting stage, with or without a delay in fruit growth – considerable delay can occur between fruit-set and the initiation of fruit expansion (Bertin, 1995). Dynamic fruit-set probability is the ratio between the total number of buds at an observation date and the proportion of them that will set as fruit, based on later records. For example, if at time t five buds are observed from all trusses, and four of them eventually develop into fruits then, for this plant, a fruit-set probability of 0·8 is assigned to time t. For each treatment, the dynamic fruit-set probability was the mean of the five plants under observation.

Calculating a common time step and growth rhythm

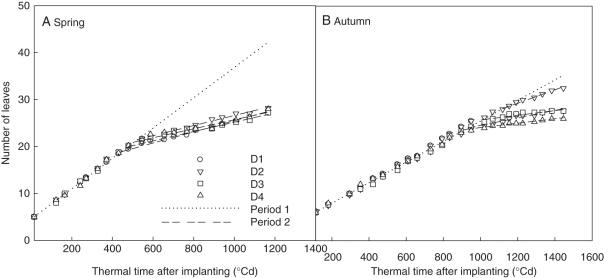
An important step for a discrete model is the choice of time step. Parameter values are incomparable if discrete models are based on different time steps. In the GreenLab model, for crops a time step, or a growth cycle, represents the phyllochron of the main stem, which is the thermal time between the appearance of two successive leaves (Guo et al., 2006). In a previous GreenLab model for tomato (Dong et al., 2008; Kang et al., 2008a), it was approximated that the number of leaves increased linearly with growing thermal time, and each cycle represents a constant phyllochron. In this case, plant age is simply the number of leaves in the main stem, but as a result plants sampled on the same date can have different ages. For the tomato plants under study here, the phyllochron changed with plant density, season and growth stage (Fig. 1), so there is risk of running the model with different time steps inside and between treatments.

Fig. 1.

Fig. 1.

Open in a new tab

Evolution of the leaf appearance rate (LAR) during plant development. LAR decreased at the transition from vegetative stage (regression lines, dotted: y = 0·0323x + 4·53 for A, y = 0·0219x + 3·59 for B) to reproductive stage (regression lines, dashed). D1, 1 plant m−2; D2, 3 plants m−2; D3, 6 plants m−2; D4, 11 plants m−2. Thermal time was expressed in growing degree-days, with a temperature base of 10 °C.

To have a common time step for different planting densities, the shortest phyllochron was chosen as the duration of a cycle in source and sink computation (see below). The recurrent equations for biomass production and partitioning all run on this common time step, so that the model parameters and output are comparable. Using the common time step, the age of the plant at final sampling was 46 cycles for the spring experiments and 37 for the autumn experiments. The number of days per cycle was computed by dividing the shortest phyllochron with the daily temperature. The potential evapotranspiration (PET) per cycle was calculated by accumulating daily PET in a growth cycle.

To simulate organogenesis properly, for periods having longer phyllochrons, a rhythm ratio, or a relative leaf appearance rate, is introduced, which is the ratio between the two leaf appearance rates. For example, if the leaf appearance rate (LAR) under the shortest phyllochron is 0·0323, and another LAR is 0·0219, then the rhythm ratio is 0·0219 ÷ 0·0323 = 0·68. Using the rhythm ratio, periodic sequences of 0 and 1 s can be generated through numerical methods, where 1 represents the appearance of a new leaf, and 0 means a pause at that cycle. For example, if the rhythm ratio is 0·34, the leaf appearance sequence is 0 0 1 0 0 1 0 0 1, which means the appearance of a leaf is followed by two pause cycles. At the pause of new phytomer appearance, the expansion of existing organs continues. Compared with the reference period with shortest phyllochron, whose rhythm ratio is 1, a lower LAR is simulated.

GreenLab model

In a discrete GreenLab model, at growth cycle (GC) i, the biomass increment of an organ o of age j, or its growth rate Δqo(i, j), is dependent on the biomass production from the last cycle and the demand in the current cycle, as in eqn (1).

graphic file with name mcq244eqn1.jpg (1)

where Po is the relative organ sink strength, a dimensionless parameter indicating the strength of a certain type of organ in competing for assimilates from thecommon pool, and o is lamina (b), petiole (p), internode (i) or fruit (f). The sink strength of the lamina was set to 1 as reference (Guo et al., 2006; Dong et al., 2008). The sink strengths of other organs (Pp, Pi, Pf) are not directly measurable, and are thus called ‘hidden’ parameters to be estimated inversely from plant data. As each organ has different needs for biomass during its lifetime; function fo(j) is defined as organ sink variation, described empirically by a discrete Beta function as in eqn (2):

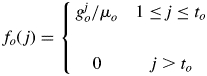graphic file with name mcq244eqn2.jpg (2)

where

graphic file with name mcq244UM1.jpg
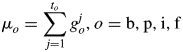graphic file with name mcq244UM2.jpg

This function gives the shape of the organ sink variation curve at constant biomass supply. The product Pofo(j) gives the demand of an organ o at age j in the plant system. Given the expansion duration to and one of the control parameters ao = 2, another control parameter bo was estimated from the plant data for each type of organ. The bigger the value of bo, the faster the expansion. The sum of organ demands gives the total plant demand D(i) in eqn (1), computed as in eqn (3):

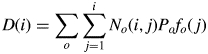graphic file with name mcq244eqn3.jpg (3)

where No(i, j) is the number of organs o of age j at plant age i. In the tomato plants here, for leaves and internodes, this value is 1 or 0 depending on the rhythm ratio and resulting leaf appearance sequence; for fruits there can be zero to several fruits of the same age but borne on different trusses. Naturally, the growth of each fruit suffers from competition both from other fruits in the same truss and also from fruits in other trusses, as claimed by many authors (Bertin, 1995). The effect of phytomer rank of a truss is taken into account (by giving the number and ages of expanding fruits), while the positional effect of each fruit inside the truss (Bangerth and Ho, 1984) is not considered for the moment.

Assimilate supply for the current cycle in eqn (1), Q(i), is computed by the source function defined as in eqn (4):

graphic file with name mcq244eqn4.jpg (4)

where PET(i) (mm GC−1) is the potential evapotranspiration during the ith growth cycle, which is affected by several microclimate conditions (light, temperature, vapour pressure deficit) (Allen et al., 1998). The PET of a growth cycle is summed from daily PET values, the duration depending on daily temperature and phyllochron per cycle. SP (cm2) is the projection area of a plant, closely linked to planting density (Ma et al., 2008). r (mg cm−2 mmPET−1) effectively estimates water use efficiency. S(i) is the total functioning leaf surface at the ith growth cycle, summed from individual leaf areas in the model. Each leaf area is computed from its biomass and a specific leaf weight, the latter being assessed directly from the data. As each leaf biomass is dependent on the global plant demand during its expansion, it can be affected by concurrent events such as fruit-set.

The dynamic ratio Q(i – 1)/D(i), or simply written as Q/D, is called the source–sink ratio, which reflects the competition level in the plant. It is the amount of biomass available per share of plant demand. According to eqn (1), larger Q/D values during the expansion of an organ give a larger final biomass. This ratio can be computed by the model recurrently when all parameter values are known. The model parameters were obtained by the inverse method, i.e. by fitting the model outputs on individual and total organ biomass data per plant. Inverse modelling means estimation of quantities that are directly or indirectly related to the measured quantity. For the GreenLab model, the basic hypothesis is that organ size and biomass are the result of source and sink functions, and thus parameters can be identified from architectural data (Zhan et al., 2003). Let the target data for fitting be vector Z, including plant-level and organ-level organ biomass. Let the corresponding model output be F(θ), θ being a vector of model parameters, including the organ sink strength (Pp, Pi, Pf), parameters controlling organ sink variation (bb, bf, bi, bf) in eqn (2), and two parameters (SP, r) in the source function eqn (4) controlling plant biomass production, as listed in Table 2. The weighted least-square error (weight W being calculated from the variance of the data) as in eqn (5) was minimized by searching best parameter values through the Levenberg–Marquardt algorithm:

graphic file with name mcq244eqn5.jpg (5)

Table 2.

Sink and source parameters identified from measurement data with the inverse method

Parameter Definition Units
Pp, Pi, Pf Organ sink strength (cf. eqn 1) g
bb, bp, bi, bf* Organ sink variation parameter (cf. eqn 2) –
SP Characteristic surface of an individual plant (cf. eqn 4) cm2
r Water use efficiency (cf. eqn 4) mg cm−2 mmPET−1
Open in a new tab

* b, lamina; p, petiole; i, internode; f, fruit.

The mathematical principle of inverse modelling in GreenLab, i.e. estimation of model parameters from measured plant data, has been described in more detail by Zhan et al. (2003). Model computation and model fitting on experimental data were conducted using the open-source GreenScilab software dedicated to tomato (http://liama.ia.ac.cn/greenscilab).

RESULTS

Fruit-set in response to plant density and growing season

There were two periods of linear increase of leaf number with thermal time, and LAR was higher in period 1 (vegetative stage) than in period 2 (reproductive stage) (Fig. 1). The transition of LAR started around 950 °Cd (51 d) in autumn and 545 °Cd (36 d) in spring after planting. Thermal time was in growing degree-days, and the base temperature was 10 °C. Whereas in period 1, all plant densities shared a common LAR (y = 0·0323x + 4·53 for spring, y = 0·0219x + 3·61 for autumn), in period 2, LAR decreased slightly with plant density, and this trend was more obvious in the autumn experiment. The rhythm ratios calculated for each period with reference to period 1 are shown in Table 1. The daily PET was computed from the daily temperature, light intensity and air humidity (Fig. 2), which will be used in eqn (4). The accumulated PET at day 81 was higher in spring (381·7 mm) than in autumn (263·2 mm).

Table 1.

The effect of plant density and growing season on leaf appearance rate (LAR)

Rhythm ratio (period 2)
Season LAR (period 1) Rhythm ratio* (period 1) D1 D2 D3 D4 Transition thermal time†
Spring 0·323 1 0·34 0·34 0·24 0·23 545 °Cd, GC 22
Autumn 0·219 1 0·66 0·37 0·23 0·22 950 °Cd, GC 25
Open in a new tab

* Ratio of LAR for each period to the LAR of period 1.

† For each treatment, there was a point in time that LAR decreased, separating the whole growth period into two sub-periods – period 1 and period 2.

Note: D1, 1 plant m−2; D2, 3 plants m−2; D3, 6 plants m−2; D4, 11 plants m−2.

Fig. 2.

Fig. 2.

Open in a new tab

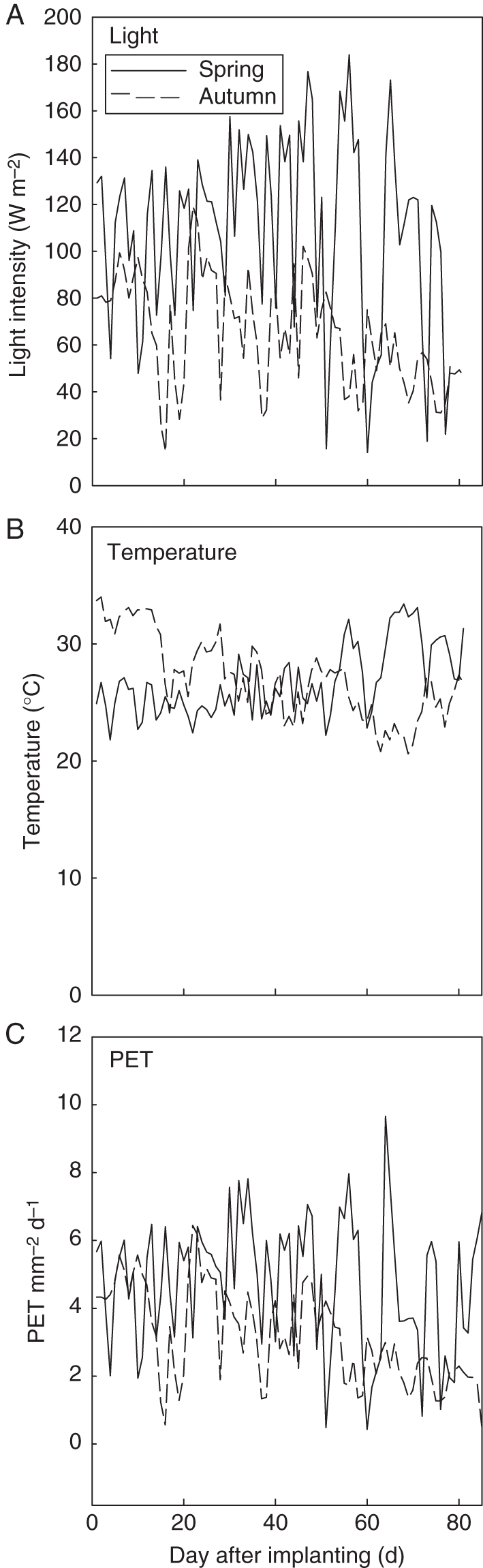
Environmental conditions in the greenhouse: light level (A), temperature (B) and daily potential evapotranspiration (PET, C).

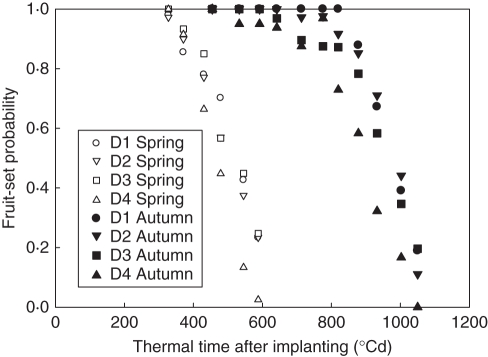
The tomato plant exhibited plasticity in different plant densities and seasons, i.e. change in organ biomass and size, biomass allocation at the plant level, total plant biomass, organ number and position, etc. For biomass production and allocation, the trend was generally found to be in line with previous observations (Dong et al., 2008). For fruit-set, the number of flower buds per truss was independent of plant density or season (P > 0·05). Few flower bud abortions occurred except on trusses 4 and 5 (counting from the base), and flower bud abortion increased with plant density and truss position (P < 0·05). The same trend was observed for flower abortion. As a summed result, total fruit-set probability, being the ratio between total fruit and total flower buds, decreased with plant density (P < 0·05). Fruit-set probability decreased with plant age (Fig. 3). Note that time refers to the moment when flower buds were observed, not the moment when abortion actually occurred. The starting phytomer rank of a truss was higher in autumn (11·63 ± 0·96, mean ± s.d.) than in spring (8·17 ± 0·39). Total fruit dry weight per plant and mean individual fruit dry weight (from the first three fruits in trusses 1 and 2) at final harvest also decreased with plant density (Table 3).

Fig. 3.

Fig. 3.

Open in a new tab

Evolution of fruit-set probability. Fruit-set probability at any given time is the percentage of flower buds appearing at that stage that give rise to a fruit. D1, 1 plant m−2; D2, 3 plants m−2; D3, 6 plants m−2; D4, 11 plants m−2. Thermal time was expressed in growing degree-days, with a temperature base of 10 °C.

Table 3.

Effect of plant density and growing season on fruit number, total fruit weight and mean fruit dry weight per plant

Number of fruits
 Total fruit dry weight (g)
 Mean fruit dry weight (g)
Season D1 D2 D3 D4 D1 D2 D3 D4 D1 D2 D3 D4
Spring 14·3 14·0 13·3 10·3 96·0 84·7 51·9 48·3 8·45a 8·23a 5·23b 5·56b
Autumn 18·7 12·7 12·0 11·0 137·3 87·8 47·9 41·3 9·6a 8·9a 6·29b 6·15b
Open in a new tab

D1, 1 plant m−2; D2, 3 plants m−2; D3, 6 plants m−2; D4: 11 plants m−2.

Different lower-case letters represent significant differences between plant densities at P = 0·05 (Levene's test).

Resolving source and sink function

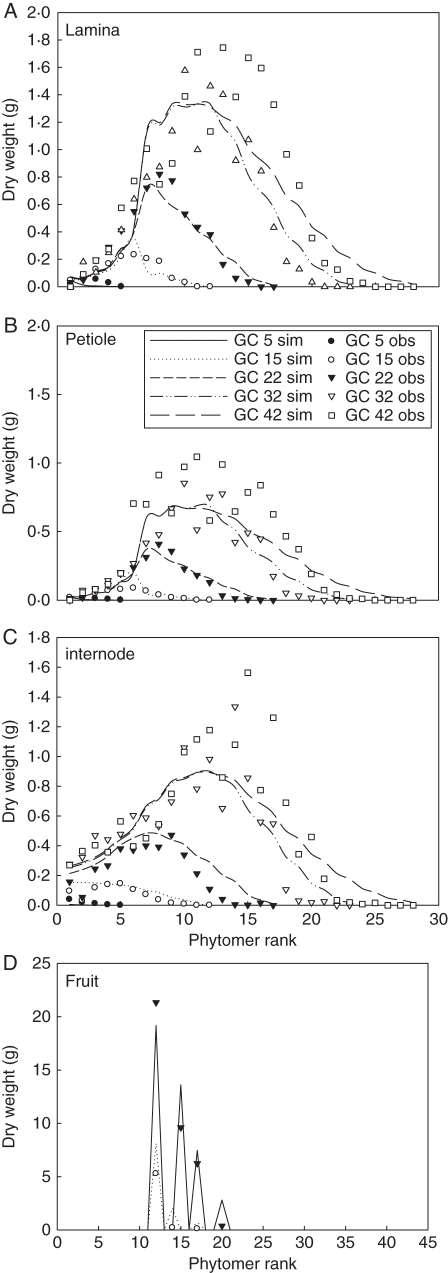
Target data for six plants from different sampling dates were fitted simultaneously, including the dry weights of individual internodes, laminae, petioles, and trusses, and the total dry weight of each component. Following our observations, in spring, the maximum duration of expansion was set to be 12 growth cycles for leaves and internodes, and 25 cycles for fruits (excluding six cycles of flowering time). Although the expansion duration was set to be stable between different densities, leaf functioning time decreased with plant density according to the number of living leaves (data not shown). Such information together with the number of fruits per truss, truss position and specific leaf weight at each sampling date were input parameters for each treatment. An example of fitting results on organ-level data is shown by D3 of the autumn experiment (Fig. 4).

Fig. 4.

Fig. 4.

Open in a new tab

Multi-fitting on plant data from six samplings. All data were fitted simultaneously, including total dry weight of each type of organ (data not shown) and the dry weight of individual laminae (A), petioles (B), internodes (C) and trusses (D), shown with D3 (6 plants m−2) of the autumn experiment.

A set of sink–source parameters was identified for each treatment, as shown in Table 4. Petiole and internode sink strength (Pp and Pi), and sink variation parameters of laminae, petiole and internode (bb, bp and bi) were similar between the two seasons. Regarding planting density, organ sink strength (Pp, Pi and Pf) were stable except for highest planting density (D4). Although sink variation parameters of vegetative organs (bb, bp and bi) decreased with planting density, that of fruit (bf) had the reverse trend, which means faster growth of vegetative organs and delayed growth of fruits at high density. Between seasons, bf was greater in the autumn experiment. Regarding source parameters, as expected, the projection area (SP) decreased with plant density. Light use efficiency (r) was stable in spring but increased with planting density in autumn, compensating for the greater change of SP values.

Table 4.

Parameter values from fitting on measured data from six sampling dates

Spring
 Autumn
Parameter D1 D2 D3 D4 D1 D2 D3 D4
Pp 0·62 (1·3) 0·65 (1·3) 0·67 (1·2) 0·75 (1·3) 0·59 (1·3) 0·52 (0·9) 0·56 (0·9) 0·66 (1·0)
Pi 0·57 (1·2) 0·64 (1·3) 0·61 (1·2) 0·88 (1·2) 0·65 (1·2) 0·73 (1·0) 0·77 (0·9) 0·98 (1·0)
Pf 25·48 (1·4) 38·68 (1·3) 25·88 (1·4) 60·61 (1·2) 39·77 (1·1) 25·76 (0·9) 43·20 (0·8) 115·41 (0·9)
bb 1·67 (1·7) 1·77 (1·7) 2·18 (1·6) 2·71 (3·3) 1·11 (3·0) 1·63 (1·1) 1·62 (1·2) 2·75 (1·4)
bp 1·88 (10·3) 1·41 (11·4) 1·47 (11·3) 1·63 (9·0) 1·58 (13·5) 1·44 (13·1) 1·73 (11·6) 2·96 (10·6)
bi 1·74 (12·2) 1·59 (12·9) 1·43 (13·0) 1·74 (10·4) 1·42 (14·9) 1·81 (14·3) 1·87 (11·5) 2·48 (11·5)
bf 1·73 (22·9) 0·77 (32·0) 0·72 (30·8) 0·25 (37·3) 4·69 (42·2) 3·09 (34·5) 2·11 (36·8) 1·35 (49·6)
SP 1371·8 (15·6) 1622·1(18·9) 1241·6 (19·3) 811·2 (18·1) 6523·7 (35·9) 3090·6 (35·6) 1938·3 (22·7) 877·5 (22·3)
r 0·40 (11·3) 0·41 (11·2) 0·35(12·0) 0·40 (10·5) 0·25 (7·8) 0·32 (9·0) 0·34 (9·1) 0·42 (9·4)
Open in a new tab

See Table 2 for definition of parameters. Note: D1, 1 plant m−2; D2, 3 plants m−2; D3, 6 plants m−2; D4, 11 plants m−2. CV (%) in parentheses.

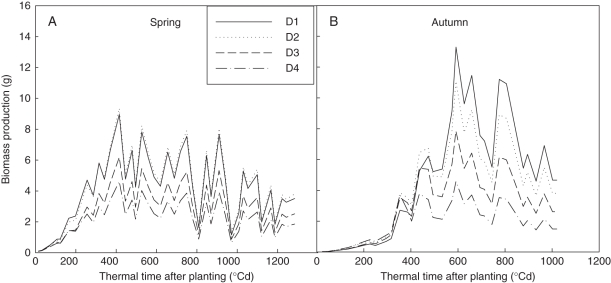
Computing source–sink ratio

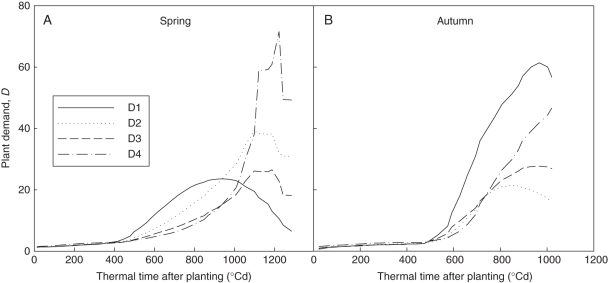
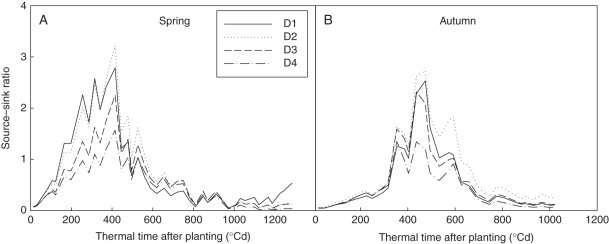
Using these parameter values, plant biomass production (Fig. 5) and plant demand (Fig. 6) of each cycle were computed. The biomass production per cycle (Q) decreased with increasing plant density, as expected. Biomass production was highly sensitive to PET (see eqn 4). Plant demand (Fig. 6) increased more rapidly at lower planting density, corresponding to faster expansion of individual fruits (larger bf). Comparing seasons, the boost of plant demand started later in autumn, caused by higher truss position. The ratio between biomass supply and demand (Q/D) increased during the vegetative stage until fruits began to be the dominant sinks (Fig. 7). The peak values were reached simultaneously for all plant densities, being cycle 18 (thermal time = 479 °Cd) in spring and cycle 19 (thermal time = 862 °Cd) in autumn. Note that although truss position started later in autumn (phytomer rank 11·63 ± 0·96) than in spring (8·17 ± 0·39), as fruit expansion was faster in autumn (larger bf), the Q/D peak was reached at similar growth cycles. Logically, the Q/D peak time arrived before the transition of LAR (GC 22 and 25, Table 1), a phenomenon recognized as a result of high sink load.

Fig. 5.

Fig. 5.

Open in a new tab

Computed evolution of plant biomass production per cycle (Q, cf. eqn 4) in both spring (A) and autumn (B) experiments. D1, 1 plant m−2; D2, 3 plants m−2; D3, 6 plants m−2; D4, 11 plants m−2. Thermal time was expressed in growing degree-days, with a temperature base of 10 °C.

Fig. 6.

Fig. 6.

Open in a new tab

Computed evolution of plant demand per cycle (D, cf. eqn 3). D1, 1 plant m−2; D2, 3 plants m−2; D3, 6 plants m−2; D4, 11 plants m−2. Thermal time was expressed in growing degree-days, with a temperature base of 10 °C.

Fig. 7.

Fig. 7.

Open in a new tab

Evolution of the plant source–sink ratio (Q/D), computed as the ratio between plant biomass production and demand. It increased in the vegetative stage and then decreased when fruit-set began, in both spring (A) and autumn (B) experiments. D1, 1 plant m−2; D2, 3 plants m−2; D3, 6 plants m−2; D4, 11 plants m−2. Thermal time was expressed in growing degree-days, with a temperature base of 10 °C.

Quantitative relationship between fruit abortion rate and source–sink ratio

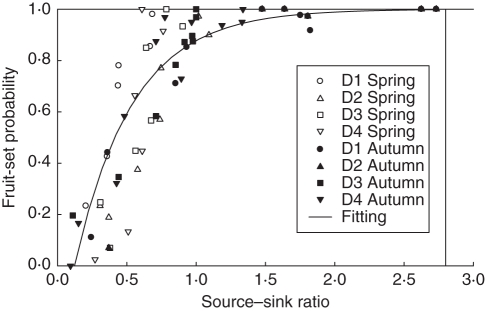
Q/D decreased after their peak values, as did fruit-set probability. To be able to compute fruit-set probability as a function of Q/D, we calculated the correlation coefficient between fruit-set probability and Q/D with different cycle delay to find the most correlated sequence of Q/D. In spring, for flower buds observed at time t, the most correlated Q/D was at time t + 7 for all plant densities, with an average correlation coefficient of 0·93. In autumn, the most correlated Q/D was at time t + 2, with an average correlation coefficient of 0·92. In other words, for a flower bud, the most sensitive time for deciding its fate is two to seven phyllchrons after its appearance. Regression was carried out for all treatments using the function y = 1−e−a(x−b), where y represents fruit-set probability, x represents the most correlated Q/D value, and a and b are two parameters (Fig. 8). Parameter b represents the minimal Q/D level for a non-zero fruit-set probability. A fitting script in Scilab gave parameter values of a = 2·39 and b = 0·12 (R2 = 0·77).

Fig. 8.

Fig. 8.

Open in a new tab

Quantitative relationship between fruit-set probability and source–sink ratio for four plant densities, from spring and autumn experiments, with data (symbols) and regression line: fruit-set probability = 1−e−2·39 (Q/D−0·12), R2 = 0·77.

DISCUSSION

Toward prediction of fruit-set

The aim of the current study was to quantify the link between source–sink ratio and fruit-set probability for tomato plants with different seasons and planting densities. Although previous studies (Passam and Khah, 1992; Wubs et al., 2009) have focused on the genetic differences in fruit-set patterns, we analysed the fruit-set response of a particular cultivar to source–sink ratio for different climatic conditions. Encouragingly, a common regression line fitted well the data from wide planting density conditions, which suggests that a constant mechanism may regulate this behaviour. The shape of the response curve is visually close to that in Bertin (1995), with a saturation trend and a minimum threshold source–sink ratio. This model-assisted analysis result is important for future fruit-set predictions, in that cultivar-specific response curves may be used to predict the number of fruits.

Comparison of the GreenLab model with previous approaches

Although source–sink ratio has been regarded as the principal factor determining fruit-set and organ growth, its definition and the means by which it is calculated variable differ between models. In previous models as represented in Marcelis and Heuvelink (1999), the source and sink strength are computed separately. Source strength, or the amount of assimilate available for plant growth, is simulated from destructively measured leaf area. Sink strength of a plant, or plant demand, is summed from those of the existing fruits under observation, whose potential growth rate was obtained from a standalone experiment with little competition. Source–sink ratio is measured as the ratio of actual to potential growth of a fruit. Vegetative sink strength is regarded as constant. Different components are calibrated separately; for example, plant total biomass is calculated from directly measured leaf area, and potential growth is fit by a Gomperz function. Such a method is perfect for comparing genetic differences or to understand plant responses (Wubs et al., 2009), but can meet obstacles when predicting fruit-set, as interactions between source and sink are not taken into account when computing source–sink ratio.

Here source–sink ratio is defined as the ratio of instant total biomass available for partitioning to total plant demand for this biomass, so it is a measure of the resource availability in the plant, representing the amount of biomass per share of demand. Source and sink modules are integrated in the same system and fitting is achieved at a global level on organ biomass of all types for several ages simultaneously. Source function is still a function of leaf area as with the previous model, but leaf area is the result of biomass partitioning, which is done according to total sink strength of all organs (plant demand) and lamina sink. Feedback of fruit-set on plant growth is naturally simulated. For example, pruning of young fruits in the model will favour growth of leaves and increase Q/D, which in turn gives larger fruits, a phenomena that has been observed experimentally (Gautier et al., 2001). Simulation of the interactions between plant development and growth gives it potential for modelling plant plasticity.

Fruit-set: definition and timing

Generally fruit-set differs from plant to plant, and thus fruit-set percentage or probability can better reflect the variations compared with the number of set fruit. In Wubs et al. (2009), fruit-set percentage of pepper was calculated as the number of fruits set divided by the number of flowers. For tomato, in our study, the number of flower buds was more stable across different plant densities and seasons than the number of flowers, and thus for tomato it is a better denominator to show change of fruit-set probability with growth conditions. The number of flower buds per truss can thus be an input of a model as a cultivar property. Another important aspect is the timing of determining fruit-set. The development of fruit relates to cell division and cell expansion. For tomato, cell division ends about 2 weeks after anthesis, and aborted fruits contain smaller cell numbers compared with set fruits (Bertin et al., 2001). Factors affecting cell division before and after anthesis can bring about a failure of fruit-set. For modelling it is necessary to find the time period that is most sensitive to environmental conditions to determine the fate of a flower. For pepper, this has been done both experimentally (Marcelis et al., 2004) and by statistical criteria (Wubs et al., 2009): about 5 d after flowering. In the present study, the most correlated source–sink ratio to fruit-set for spring and autumn is two and seven phyllochrons, respectively, after the appearance of flower buds, although the correlation coefficient is positive in several neighbouring cycles.

Future work

Defining organ sink strength plays a key role in plant models. Organ sink strength is the ability to attract assimilates and depends both on sink activity and size, linked to cell division and cell expansion events. Stable model parameters are expected by modellers to distinguish between environmental and quantitative trait loci effects, the so called Q × E effect (Dingkuhn et al., 2005). In the field crop maize, which has simple plant architecture, GreenLab sink parameters were stable across different seasons and plant densities (Ma et al., 2008). In the current study, compared with sink strength of vegetative organs, greater variation in fruit sink parameters was observed (Pf, bf, Table 4). Here the fruit sink parameters are a measure of average fruit behaviour, i.e. they do not depend on fruit and flower position. Similarly, for vegetative organs, the same sink function is applied for all individual organs along the stem, and the final organ size (biomass) differs from each other according to the source–sink ratio in its expansion history. This method fits less closely for the organs around truss position (Fig. 4), although fitting of the data on the plant level is good (result not shown). A more mechanistic sink function is expected to simulate organ size better, considering not only factors affecting its expansion, but also factors affecting cell division, which set the boundary for later cell expansion. Attempts to create a new sink function have been started in GreenLab (Zhang et al., 2009), but more knowledge at the cell level is needed to improve the model; for example, how cell number decreases along a truss is unclear. Regarding model calibration, as GreenLab simulates the plant system in a simplified way, parameters for calculating source and sink functions are not directly measurable and have less clear physical meanings compared with process-based models. On the other hand, the link between sink source parameters and the target data is a complex multi-input and multi-output non-linear function. Complex sensitivity analysis (Wu and Cournède, 2009) can help to determine the effect of certain parameters on final yield, and help users to find sets of parameters more easily.

As already mentioned, the current study looked at the relationship between fruit-set and source–sink ratio a posteriori, i.e. after solving the source and sink functions with the numbers of fruits being forced, and fruit-set probability was not integrated into the model in computing the source and sink strengths. Our next goal is prediction of fruit-set using a common function for different environmental conditions. Achieving this aim may need a stochastic model (Kang et al., 2008b) with fruit-set probability linked to sink–source ratio.

Summary

By fitting organ biomass from six sampling dates, a set of sink and source model parameters was estimated to calculate the source–sink ratio, which was defined as the ratio of instant total biomass available for partitioning to total plant demand for this biomass. Their peaks were reached simultaneously for all plant densities, at about 6–10 phyllochrons after the appearance of the first inflorescence, which is followed later by a decreased LAR. A single regression line described well the relationship between dynamic fruit-set and source–sink ratio for four plant densities in the spring and autumn experiments. The quantitative link between fruit-set and within-plant source–sink ratio provides a method for predicting fruit-set, an important aspect of plant plasticity.

ACKNOWLEDGEMENTS

This study was supported by the Hi-Tech Research and Development (863) Program of China (nos. 2006AA10Z229 and 2008AA10Z218), NSFC (no. 60703043) and the Excellent SKL Project of NSFC (no. 60723005). We thank several anonymous reviewers for their valuable comments.

LITERATURE CITED

  1. Alkio M, Schubert A, Diepenbrock W, Grimm E. Effect of source–sink ratio on seed set and filling in sunflower (Helianthus annuus L.) Plant, Cell & Environment. 2003;26:1609–1619. [Google Scholar]
  2. Allen M, Prusinkiewicz P, DeJong T. Using l-systems for modeling source–sink interactions, architecture and physiology of growing trees: the l-peach model. New Phytologist. 2005;166:869–880. doi: 10.1111/j.1469-8137.2005.01348.x. [DOI] [PubMed] [Google Scholar]
  3. Allen RG, Pereira LS, Raes D, Smith M. Crop evapotranspiration. Guidelines for computing crop water requirements. Rome: FAO; 1998. FAO Irrigation and Drainage Paper No. 56. [Google Scholar]
  4. Bangerth F, Ho LC. Fruit position and fruit set sequence in a truss as factors determining final size of tomato fruits. Annals of Botany. 1984;53:315–319. [Google Scholar]
  5. Bertin N. Competition for assimilates and fruit position affect fruit set in indeterminate greenhouse tomato. Annals of Botany. 1995;75:55–65. doi: 10.1016/S0305-7364(05)80009-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bertin N, Gary C. Tomato fruit-set: a case study for validation of the model TOMGRO. Acta Horticulturae. 1993;328:185–193. [Google Scholar]
  7. Bertin N, Gautier H, Roche C. Number of cells in tomato fruit depending on fruit position and source-sink balance during plant development. Plant Growth Regulation. 2001;36:105–112. [Google Scholar]
  8. Chenu K, Rey H, Dauzat J, Lydie G, Lecoeur J. Estimation of light interception in research environments: a joint approach using directional light sensors and 3d virtual plants applied to sunflower (Helianthus annuus) and Arabidopsis thaliana in natural and artificial conditions. Functional Plant Biology. 2008;35:850–866. doi: 10.1071/FP08057. [DOI] [PubMed] [Google Scholar]
  9. Christophe A, Letort V, Hummel I, Cournede PH, de Reffye P, Lecoeur J. A model-based analysis of the dynamics of carbon balance at the whole-plant level in Arabidopsis thaliana. Functional Plant Biology. 2008;35:1147–1162. doi: 10.1071/FP08099. [DOI] [PubMed] [Google Scholar]
  10. Dingkuhn M, Luquet D, Quilot B, de Reffye P. Environmental and genetic control of morphogenesis in crops: towards models simulating phenotypic plasticity. Australian Journal of Agricultural Research. 2005;56:1289–1302. [Google Scholar]
  11. Dong QX, Louarn G, Wang YM, Barczi JF, de Reffye P. Does the Structure-Function Model GREENLAB deal with crop phenotypic plasticity induced by plant spacing? A case study on tomato. Annals of Botany. 2008;101:1195–1206. doi: 10.1093/aob/mcm317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Eschenbach C. Emergent properties modelled with the functional structural tree growth model ALMIS: computer experiments on resource gain and use. Ecological Modelling. 2005;186:470–488. [Google Scholar]
  13. Evers JB, Vos J, Andrieu B, Struik PC. Cessation of tillering in spring wheat in relation to light interception and red : far-red ratio. Annals of Botany. 2006;97:649–658. doi: 10.1093/aob/mcl020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Evers JB, Vos J, Yin X, Romero P, van der Putten PEL, Struik PC. Simulation of wheat growth and development based on organ-level photosynthesis and assimilate allocation. Journal of Experimental Botany. 2010;61:2203–2216. doi: 10.1093/jxb/erq025. [DOI] [PubMed] [Google Scholar]
  15. Fournier C, Andrieu B. A 3D architectural and process-based model of maize development. Annals of Botany. 1998;81:233–250. [Google Scholar]
  16. Gautier HN, Guichard S, Tchamitchian M. Modulation of competition between fruits and leaves by flower pruning and water fogging, and consequences on tomato leaf and fruit growth. Annals of Botany. 2001;88:645–652. [Google Scholar]
  17. Gillaspy G, David HB, Gruissem W. Fruits: a developmental perspective. The Plant Cell. 1993;5:1439–1451. doi: 10.1105/tpc.5.10.1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Guo Y, Ma YT, Zhan ZG, et al. Parameter optimisation and field validation of the functional-structural model GREENLAB for maize. Annals of Botany. 2006;97:217–230. doi: 10.1093/aob/mcj033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Iglesias DJ, Tadeo FR, Primo-Millo E, Talon M. Fruit set dependence on carbohydrate availability in citrus trees. Tree Physiology. 2003;23:199–204. doi: 10.1093/treephys/23.3.199. [DOI] [PubMed] [Google Scholar]
  20. Jones JW, Dayan E, Allen LH, Van Keulen H, Challa H. A dynamic tomato growth and yield model (TomGro) American Society of Agricultural Engineering. 1991;34:663–672. [Google Scholar]
  21. Kang MZ, Evers JB, Vos J, de Reffye P. The derivation of sink functions of wheat organs using the GreenLab model. Annals of Botany. 2008a;101:1099–1108. doi: 10.1093/aob/mcm212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kang MZ, Cournède PH, de Reffye P, Auclair D, Hu BG. Analytical study of a stochastic plant growth model: application to the GreenLab model. Mathematics and Computers in Simulation. 2008b;78:57–75. [Google Scholar]
  23. Lindenmayer A. Mathematical models for cellular interactions in development. Part I and II. Journal of Theoretical Biology. 1968;18:280–299. doi: 10.1016/0022-5193(68)90079-9. 300–315. [DOI] [PubMed] [Google Scholar]
  24. Ma Y, Wen M, Guo Y, Li B, Cournède P-H, de Reffye P. Parameter optimization and field validation of the functional structural model GREENLAB for maize at different population densities. Annals of Botany. 2008;101:1185–1194. doi: 10.1093/aob/mcm233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Marcelis LFM, Heuvelink E. Modelling fruit set, fruit growth and dry matter partitioning. Acta Horticulturae. 1999;499:39–49. [Google Scholar]
  26. Marcelis LFM, Heuvelink E, Goudriaan J. Modelling biomass production and yield of horticultural crops: a review. Scientia Horticulturae. 1998;74:83–111. [Google Scholar]
  27. Marcelis LFM, Heuvelink E, Hofman-Eijer LRB. Flower and fruit abortion in sweet pepper in relation to source and sink strength. Journal of Experimental Botany. 2004;55:2261–2268. doi: 10.1093/jxb/erh245. [DOI] [PubMed] [Google Scholar]
  28. Mathieu A, Cournède PH, Letort V, Barthélémy D, de Reffye P. A dynamic model of plant growth with interactions between development and functional mechanisms to study plant structural plasticity related to trophic competition. Annals of Botany. 2009;103:1173–1186. doi: 10.1093/aob/mcp054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Passam HC, Khah EM. Flowering, fruit set and fruit and seed development in two cultivars of aubergine (Solanum melongena L.) grown under plastic cover. Scientia Horticulturae. 1992;51:179–185. [Google Scholar]
  30. Pettigrew WT. Source-to-sink manipulation effects on cotton lint yields and yield components. Agronomy Journal. 1994;86:731–735. [Google Scholar]
  31. Renton M, Hanan J, Burrage K. Using the canonical modelling approach to simplify the simulation of function in functional–structural plant models. New Phytologist. 2005;166:845–857. doi: 10.1111/j.1469-8137.2005.01330.x. [DOI] [PubMed] [Google Scholar]
  32. de Reffye P, Heuvelink E, Guo Y, Hu BG, Zhang BG. Coupling process-based models and plant architectural models: a key issue for simulating crop production. In: White JW, Cao W, Wang E, editors. Crop Modelling and Decision Support (ISCMDS 2008, April 19–22, Nanjing, China) Springer/Tsinghua University Press; 2008. pp. 130–147. [Google Scholar]
  33. Stephenson AG. Flower and fruit abortion: causes and ultimate functions. Annual Review of Ecological System. 1981;12:253–279. [Google Scholar]
  34. Valantin-Morison M, Vaissière BE, Gary C, Robin P. Source–sink balance affects reproductive development and fruit quality in cantaloupe (Cucumis melo L.) Journal of Horticultural Science & Biotechnology. 2006;81:105–117. [Google Scholar]
  35. Vos J, Evers JB, Buck-Sorlin GH, Andrieu B, Chelle M, de Visser PHB. Functional–structural plant modelling: a new versatile tool in crop science. Journal of Experimental Botany. 2009;61:2101–2115. doi: 10.1093/jxb/erp345. [DOI] [PubMed] [Google Scholar]
  36. Wu Q, Cournède PH. Sensitivity analysis of GreenLab model for maize. In: Li B, Jaeger M, Guo Y, editors. Plant Growth modelling, Simulation, Visualisation and Applications. Proceedings – PMA09. Los Alamitos, CA: IEEE Computer Society; 2009. pp. 311–318. [Google Scholar]
  37. Wubs AM, Ma Y, Heuvelink E, Marcelis LFM. Genetic differences in fruit-set patterns are determined by differences in fruit sink strength and a source : sink threshold for fruit set. Annals of Botany. 2009;104:957–964. doi: 10.1093/aob/mcp181. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Yan HP, Kang MZ, de Reffye Ph, Dingkuhn M. A dynamic, architectural plant model simulating resource- dependent growth. Annals of Botany. 2004;93:591–602. doi: 10.1093/aob/mch078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zhan ZG, de Reffye Ph, Houllier F, Hu BG. Fitting a structural functional model with plant architectural data. In: Hu BG, Jaeger M, editors. Plant Growth Modelling and Applications: 2003 International Symposium on Plant Growth Modelling, Simulation, Visualisation and Their Applications. Beijing: Tsinghua University Press/Springer; 2003. pp. 236–249. [Google Scholar]
  40. Zhang BG, Kang MZ, Letort V, Wang X, de Reffye P. Comparison between empirical or functional sinks of organs – Application on Tomato plant. In: Li B, Jaeger M, Guo Y, editors. Plant Growth modelling, Simulation, Visualisation and Applications. Proceedings – PMA09. Los Alamitos, CA: IEEE Computer Society; 2009. pp. 191–197. [Google Scholar]
  41. Zheng B, Shi L, Ma Y, Deng Q, Li B, Guo Y. Comparison of architecture among different cultivars of hybrid rice using a spatial light model based on 3-d digitizing. Functional Plant Biology. 2008;35:900–910. doi: 10.1071/FP08060. [DOI] [PubMed] [Google Scholar]

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES