Abstract
An acoustic pointing task was used to measure extents of laterality produced by ongoing interaural temporal disparities (ITDs) conveyed by the envelopes of 4-kHz-centered raised-sine stimuli while varying, parametrically, their peakedness, depth of modulation, and frequency of modulation. One purpose of the study was to determine whether such manipulations would produce changes in laterality logically consistent with those found for ITD-discrimination thresholds reported by Bernstein and Trahiotis [J. Acoust. Soc. Am. 125, 3234–3242 (2009)]. The data obtained revealed that they did in that (1) increasing depth of modulation, peakedness, or frequency of modulation between 32 and 128 Hz produced smaller threshold ITDs and greater laterality and (2) increasing frequency of modulation to 256 Hz produced modest increases in threshold ITDs and modest decreases in laterality. The extents of laterality measured were successfully accounted for via an augmentation of the cross-correlation-based “position-variable” modeling approach developed by Stern and Shear [J. Acoust. Soc. Am. 100, 2278–2288 (1996)] to account for ITD-based extents of laterality obtained at low spectral frequencies.
INTRODUCTION
Recent investigations have focused on stimulus manipulations that foster enhancements of the potency of interaural temporal disparities (ITDs) conveyed by the envelopes of high-frequency complex stimuli. The earliest of these (Bernstein and Trahiotis, 2002, 2003) employed “transposed” stimuli of the type originally introduced by van de Par and Kohlrausch (1997), who studied binaural detection at low vs high spectral frequencies. Their study was designed to help explain why ITDs conveyed by low-frequency waveforms were commonly found to be far more potent than ITDs conveyed by the envelopes of high-frequency, complex stimuli. Transposed stimuli were specifically developed to provide high-frequency portions of the auditory periphery with envelope-based neural timing information that would mimic, or approximate, waveform-based neural timing information that occurs naturally in low-frequency portions of the auditory periphery. Bernstein and Trahiotis (2002, 2003) reported that transposed stimuli yielded both lower thresholds for discrimination of changes in ITD and larger extents of laterality produced by a given ITD as compared to “conventional” stimuli such as sinusoidally amplitude modulated (SAM) tones and bands of Gaussian noise. They also reported that, in several instances, performance with high-frequency transposed stimuli approximated that found when the ITDs were conveyed by conventional low-frequency stimuli.
Later experiments focused on attempting to identify which aspect(s) of the envelopes of high-frequency stimuli lead to efficient processing of ongoing ITDs. These experiments capitalized on the use of “raised-sine” stimuli, which were originally described by John et al. (2002). As discussed by Bernstein and Trahiotis (2009), manipulation of the parameters defining raised-sine stimuli allow one to vary independently the frequency of modulation, the depth of modulation, and the relative “peakedness” or “sharpness” of the envelope of the waveform. The use of raised-sine stimuli provides opportunities to manipulate and to control aspects of the envelope that cannot be controlled and varied independently when using SAM tones, Gaussian noises, repeated Gaussian clicks (e.g., McFadden and Pasanen, 1976; Nuetzel and Hafter, 1976; Buell and Hafter, 1988; Stecker and Hafter, 2002), or transposed tones. Using raised-sine stimuli, Bernstein and Trahiotis (2009) found that increases in relative peakedness, depth of modulation, or rate of modulation all generally led to decreases in threshold ITD. In addition, the overall patterning of those improvements in performance was captured well by a model based on the normalized interaural correlation (i.e., the value of the normalized cross-correlation function at a lag of zero) calculated subsequent to stages mimicking peripheral auditory processing. One aspect of the data not accounted for by the model was the relatively low threshold ITDs obtained when a highly peaked envelope was coupled with a low depth of modulation. A more recent experiment verified and extended both the empirical outcomes and the modeling (Bernstein and Trahiotis, 2010). In addition, further theoretical analyses revealed that the overestimations of threshold ITDs found with such stimuli in the original study and its replication were redressed when it was assumed that listeners employ information within “off-frequency” auditory filters centered slightly above the center frequency of the stimuli.
One purpose of the present study was to measure ITD-based extents of laterality of intracranial acoustic images produced by raised-sine stimuli while varying, parametrically, their peakedness, depth of modulation, and frequency of modulation (i.e., stimuli similar to those used in the ITD-discrimination studies described above). Of particular interest was whether the relative potency of ITD found across the stimulus set when discrimination thresholds were measured would also be found when ITD-based laterality was measured. Collecting such data would be informative because evidence suggests that threshold ITDs cannot, for some stimuli and conditions, be predicted quantitatively solely on the basis of measures of extent of laterality and vice versa (Domnitz and Colburn, 1977; Stern and Colburn, 1978; 1985, 25; Heller and Trahiotis, 1996; Trahiotis, et al., 2001). Intuitively, the lack of a direct relation between the two measures can be understood within the context of the cross-correlation function. Consider that the resolution of ITDs is determined by both the magnitude of overall “displacement” of activity along the ITD axis and the underlying variance of that activity. In other words, what determines threshold ITD is a mean-to-sigma change in the pattern of the cross-correlation. In contrast, extent of laterality appears to be determined by the position of the centroid (or, perhaps, the peak) of activity along the ITD axis produced by supra-threshold values of ITD (see Domnitz and Colburn, 1977 for a detailed explication). Thus, within this schema, the variance of activity would influence the ability to discriminate changes in ITD but not the ascribed intracranial position produced by supra-threshold values of ITD. Thus, there are both empirical and theoretical reasons justifying the measurements of both threshold ITDs and extents of laterality for the purpose of determining the relative potency of ITDs conveyed by raised-sine stimuli (and other novel acoustic stimuli, for that matter).
A second purpose of the present study was to attempt to predict, quantitatively, empirical measures of extents of laterality. As is shown below, the patterning of lateralization of envelope-based ITDs conveyed by high-frequency raised-sine stimuli can generally be accounted for by augmenting the low–frequency, cross-correlation-based, “position-variable” modeling approach originally put forth by Stern and Colburn (1978) and as modified by Stern and Shear (1996). This success notwithstanding, several types of theoretical analyses strongly suggest that improving the predictive power of the position-variable model will require additional information regarding similarities∕differences in the processing of ITDs conveyed by low- vs high-frequency signals.
EXPERIMENT
Generation of raised-sine stimuli
The generation of raised-sine stimuli is accomplished by raising a DC-shifted sine-wave to a power (exponent) greater than or equal to 1.0 prior to multiplication with a carrier. The equation used to generate such stimuli was originally described by John et al. (2002) and is:
| (1) |
where fc is the frequency of the carrier, fm is the frequency of the modulator, and m is the index of modulation. The exponent, n (the power to which the DC-shifted modulator is raised), determines the peakedness or sharpness of the individual “lobes” of the envelope. As described in Bernstein and Trahiotis (2010), an equivalent and more compact form of Eq. (1) is:
| (2) |
Examples of raised-sine waveforms generated with m = 1.0 and values of n from 1.0 to 8.0 can be found in Bernstein and Trahiotis (2009).
Procedure
Extents of laterality were measured for raised-sine “targets” while varying, parametrically, their exponent, depth (index) of modulation, and rate of modulation. The values of the exponents (n) were 1.0 (equivalent to a SAM tone), 1.5, or 8.0; the depths of modulation (m) were 0.25, 0.50, 0.75, or 1.00; and the rates of modulation (fm) were 32, 128, and 256 Hz. The rates of modulation employed represent a subset of the values employed by Bernstein and Trahiotis (2002, 2009, 6) and were chosen for empirical reasons. In those studies, a rate of 128 Hz was shown to yield the lowest threshold ITDs, while the values of 32 and 256 Hz represent the endpoints of the range of rates of modulation for which valid measures of threshold ITD were obtained consistently. All 36 raised-sine targets were centered at 4 kHz. They were generated digitally using a sampling rate of 20 kHz (TDT AP2), were low-pass filtered at 8.5 kHz (TDT FLT2), and were presented via Etymotic ER-2 insert earphones at a level of 72 dB SPL. Ongoing ITDs (0, 200, 400, 600, 800, and 1000 μs, left ear leading) were imposed by applying linear phase-shifts to the representation of the targets in the frequency domain, transforming them to the time-domain, and then gating the signals destined for the left and right ears coincidentally.
Extents of laterality were measured for three normal-hearing young adult listeners1 (one male and two females) via an acoustic pointing task in which the listeners varied the interaural intensitive difference (IID) of a 200-Hz-wide band of noise centered at 500 Hz (the pointer) so that it matched the intracranial position of the raised-sine target. This procedure has been used previously in several studies (e.g., Trahiotis and Stern, 1989; Buell et al., 1991; Heller and Trahiotis, 1996; Bernstein and Trahiotis, 2003) and is described fully in Bernstein and Trahiotis (1985a). The pointer was generated digitally in a manner similar to that described above and its overall level, when presented diotically (IID = 0), was 60 dB SPL. Listeners adjusted the intracranial position of the pointer by rotating a knob. Rotation of the knob produced symmetric changes of the IID (in dB) of the pointer (i.e., increases in level at one ear and decreases in level at the other ear). The IID adjusted by the listener served as a metric of the intracranial position of the target. An arbitrary and randomly chosen value of the IID was inserted in the pointer prior to each match. This served to randomize the initial position of the pointer with respect to the absolute position of the knob. Each sequence of stimuli consisted of three presentations of the target (each separated by 150 ms), a pause of 200 ms, three presentations of the pointer (each separated by 150 ms), and a pause of 600 ms. The duration of target and pointer stimuli was 100 ms including 10-ms cos2 rise∕decay ramps. Targets and pointers were repeated until the listeners indicated that they had matched the intracranial positions of the target and pointer. Prior to completing a match, listeners had the option of halting, and then restarting, the sequence in order to check their adjustments after a period of silence.
All of the aforementioned stimulus conditions were visited in random order. Having chosen a particular stimulus condition as the target, a random process was used to select a value of ITD from the set to be tested until the listeners had completed three independent matches for each value of ITD. The magnitude of the mean IID inserted by the listener to match the diotic targets (ITD of 0 μs) was typically less than 3 dB and served as a “correction factor.” That is, it was subtracted from the IIDs resulting from all the matches in the run. Finally, all the stimulus conditions (targets) were re-visited in reverse order. In the event that the correction factor for a particular run of a stimulus condition was ≥5 dB, that run was discarded and was repeated until that criterion was not exceeded. The data reported in the figures represent the mean “corrected” value of IID of the pointer across the six “valid” matches (three from each run) made by each listener for a particular combination of target and ITD.
Results and discussion
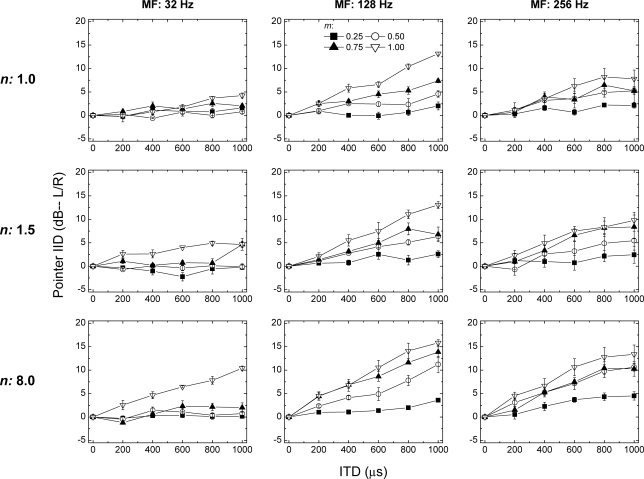
The nine panels of Fig. 1 contain the entire set of data. The panels in the left-most, middle, and right-most columns display the data obtained when the frequency of modulation was 32, 128, or 256 Hz, respectively. The panels along the top, middle, and bottom rows display the data obtained when the exponent of the raised-sine was 1.0, 1.5, or 8.0, respectively. The parameter within each panel is the depth of modulation. Within each panel, the mean IID of the pointer (taken across the three listeners) is plotted as a function of the ITD imposed on the target. Positive values along the ordinate represent values of IID favoring the left ear. Error bars represent ±1 standard error of the mean.
Figure 1.
The panels in the left-most, middle, and right-most columns display the data obtained when the frequency of modulation was 32, 128, or 256 Hz, respectively. The panels along the top, middle, and bottom rows display the data obtained when the exponent of the raised-sine was 1.0, 1.5, or 8.0, respectively. Each panel displays the IID of the pointer (in dB) required to match the intracranial position of the target as a function of the ongoing ITD (left ear leading) imposed on a 200-Hz-wide band of Gaussian noise centered at 500 Hz. Data points represent the mean values computed across the three listeners. The error bars represent ±1 standard error of the mean. The parameter within each plot is the depth of modulation (m).
Depending on the context and for ease of exposition, the data are discussed below in terms of extent of laterality rather than in terms of the IID of the pointer, per se, required to match the target (see Bernstein and Trahiotis, 1985a,b, 2003, 2, 6; Schiano et al., 1986). Beginning with the data in the left-hand column, when the rate of modulation was 32 Hz and the exponent of the raised-sine (n) was 1.0, note that, independent of depth of modulation, ITDs of up to 600 μs were matched by near-zero values of IID of the pointer. This indicates that those stimulus conditions produced virtually no displacement of the intracranial image away from midline. When the value of ITD was increased to 800 or 1000 μs, the raised-sine having a modulation of index of 1.0 was matched by an IID of the pointer of 4–5 dB. This typically corresponds to an intracranial image placed slightly less than half the distance along the lateral axis from midline to the ear (e.g., Watson and Mittler, 1965; Yost, 1981). Increasing the exponent to 1.5 and to 8.0 (middle and bottom panels, respectively) led to substantial increases in extent of laterality at all values of ITD for raised-sines having an index of modulation of 1.0. In fact, when the exponent was 8.0 and the ITD was 1000 μs, the listeners matched the position of the target with an average IID of the pointer of 10.4 dB. This corresponds to an intracranial image quite close to the leading ear. Most of the matches obtained with smaller depths of modulation indicated intracranial images heard near midline, with the exceptions being those obtained with the largest two ITDs when the depth of modulation was 0.75.
Turning to the data obtained when the frequency of modulation was 128 Hz (middle column), note that, in comparison to the data obtained at 32 Hz, extents of laterality were substantially and increasingly larger for depths of modulation of 0.50, 0.75, and 1.00. In fact, for the largest combinations of ITD and depth of modulation, listeners required 10–15 dB of IID of the pointer, thereby indicating intracranial images positioned far toward the leading ear. Once again, however, when the depth of modulation was 0.25, all combinations of values of ITD and exponent produced images heard at, or near, midline. This outcome appears to be consistent with, and perhaps mirrors, earlier reports that threshold ITDs, measured as a function of depth of modulation, increase dramatically for depths of modulation well below 0.50 (McFadden and Pasanen, 1976; Nuetzel and Hafter, 1981; Bernstein and Trahiotis, 1996). The data obtained with a frequency of modulation of 256 Hz (right-most column) generally exhibit the same patterning of extents of laterality found at 128 Hz, albeit with, in general, somewhat smaller extents of laterality.
The data in Fig. 1 were subjected to a four-factor (three frequencies of modulation X, four depths of modulation X, three values of exponent X, and six values of interaural delay), within-subjects analysis of variance (ANOVA). The error terms for the main effects and for the interactions were the interaction of the particular main effect (or the particular interaction) with the subject “factor” (Keppel, 1991). In addition to testing for significant effects, the proportions of variance accounted for (ω2) were determined for each significant main effect and interaction (Hays, 1973).
Overall, the statistical analysis revealed that 84% of the variability in the IIDs of the pointer calculated across the three listeners was accounted for by the stimulus variables. Said differently, only 16% of the variance in the complex patterns of data in Fig. 1 is attributable to experimental “error” which, within this design, includes not only errors of measurement but also differences among the three listeners. Each of the four main effects was significant (assuming an α of 0.05) and, in aggregate, they accounted for 63% of the variance: (1) frequency of modulation [F(2,4) = 6.6, p = 0.05], accounting for 12% of the variance; (2) depth of modulation [F(3,6) = 90.8, p < 0.01], accounting for 18% of the variance; (3) value of exponent [F(2,4) = 21.3, p < 0.01], accounting for 5% of the variance; and (4) value of interaural delay [F(5,10) = 84.5, p < 0.01], accounting for 28% of the variance. Of the 11 interactive effects, 6 were significant and, in aggregate, they accounted for 18% of the variance. Only two of those significant interactions accounted for more than 2% of the variance. One was the interaction between frequency of modulation and interaural delay [F(10,20) = 9.1, p < 0.01] that accounted for 5% of the variance. This interaction is visually apparent in the substantially different patterns of data across the three columns of Fig. 1. The other was the interaction between depth of modulation and interaural delay [F(15,30) = 45.4, p < 0.01] that accounted for 7% of the variance. This interaction is also visually apparent in Fig. 1 in that the slopes relating pointer-IID to ITD differed greatly across the different depths of modulation. The remainder of the 84% of the variance accounted for by the stimulus variables resulted from interactive effects that, individually, were not statistically significant.
ACCOUNTING FOR ITD-BASED EXTENTS OF LATERALITY AT HIGH SPECTRAL FREQUENCIES
Attempts to account, quantitatively, for the extents of laterality displayed in Fig. 1 began with predictions obtained via the interaural-correlation-based “pattern-processing” approach successfully employed by Bernstein and Trahiotis (2003) to account for lateralization of (1) narrow bands of noise centered at low frequencies; the same bands of noise transposed to 4 kHz and (2) narrow bands of noise centered at 4 kHz. That model included stages of peripheral auditory processing (bandpass filtering, envelope compression, half-wave, square-law rectification, and low-pass filtering at 425 Hz) and a stage of low-pass filtering at 150 Hz for stimuli centered at high frequencies, where the envelope rather than the fine-structure conveys the ITD. Lateral position was defined as the position of the peak of the across-frequency averaged cross-correlation function, re-scaled to units of IID of the pointer. Upon applying the model to the stimuli employed in the current study, it quickly became apparent that it could not account, either qualitatively or quantitatively, for the data in Fig. 1. That is, the model did not account for the effects on lateralization produced by varying, parametrically, frequency of modulation, depth of modulation, and exponent of the raised-sine stimuli. Given this negative outcome, it was decided to incorporate the theoretical approach developed, employed, and refined by Stern, Colburn, and their colleagues, that is now commonly referred to as the “position-variable model” (e.g., Stern and Colburn, 1978; 1985, 25; Stern and Shear, 1996; Trahiotis et al., 2001). That model has evolved to the point that it currently provides successful qualitative and quantitative accounts of lateralization based on both ITDs and IIDs and their combination for a wide variety of low–frequency stimuli. To our knowledge, the ability of the position-variable model to account for ITD-based detection and lateralization of high–frequency stimuli has only been assessed, in an unpublished report, and for a very limited set of stimuli (Stern et al., 1988a).
Within the position-variable model, monaural stages of peripheral auditory processing are included to accomplish the bandpass filtering, non-linear half-wave rectification, and low-pass filtering that were included as stages in the general model utilized by Bernstein and Trahiotis (2003). The stimuli as processed serve as inputs to a binaural comparator that computes a cross-correlation “surface” or correlogram, the axes of which are center frequency, interaural delay, and the magnitude of the “cross-products” which, within the model, represents the relative strength of temporally coincident neural activity. The correlogram is then modified by applying a “centrality” function that differentially emphasizes activity within the correlogram that occurs at relatively small delays. The centrality function has often been interpreted as representing greater density of neural elements “tuned” to small interaural delays. For relatively narrowband signals, the decision variable is formed by computing the centroid of activity of the correlogram along the interaural delay axis. For relatively broadband stimuli, the general model has been augmented to capture how the centroid of activity is also affected by integration of activity along the frequency axis (Stern et al., 1988b; Trahiotis and Stern, 1989, 1994, 31).
The form of the position-variable model used to make predictions for the data in Fig. 1 was as follows. Bandpass filtering was accomplished by passing the respective stimuli through a pair of (left∕right) gammatone filter banks (see Patterson et al., 1995) spanning center frequencies of 2000–8000 Hz. The output of each gammatone filter was subjected to half-wave, cube-law rectification and low-pass filtering at 1200 Hz in accord with and as described by Stern and Shear (1996). This was followed by a stage of low-pass filtering at 150 Hz for stimuli centered at high frequencies, where the envelope rather than the fine-structure conveys the ITD. Then, the correlogram was computed for ITDs ranging from −2.0 to +2.0 ms. The correlogram was then modified using Stern and Shear’s frequency-dependent centrality function [p(τ)] (where τ represents internal delay) with the proviso that the “frequency” used to calculate that function be the frequency of the envelope, rather than the 4000-Hz center frequency of the stimulus.2 Finally, the centroid of the across-filter-averaged activity was computed along the ITD axis and linearly scaled in order to convert ITD to IID of the pointer. The predictions, in units of IID (dB), were made assuming that 1 dB of IID of the pointer equals 11.7 μs of ITD along the internal delay axis. That relation was found to maximize the amount of variance accounted for between the predicted and the obtained extents of laterality. The computations were carried out via Dr. Michael Akeroyd’s “Binaural Toolbox” for matlab®. The reformulation described above of Stern and Shear’s model will be referred to as “the position-variable model” within this presentation.
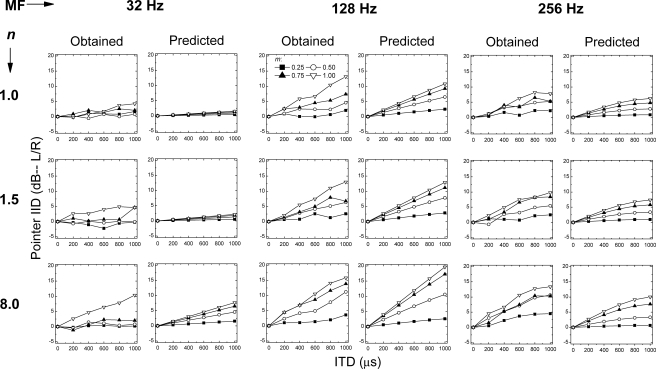
Figure 2 displays, in adjacent pairs of panels, the empirical data re-plotted from Fig. 1 along with the predictions of those data obtained via the model. Visual inspection verifies that the predictions of the model capture, qualitatively, the trends in the data as discussed in Sec. 2 that were found across frequency of modulation, across depth of modulation, and across value of the raised-sine exponent, respectively. One of those trends is the more curvilinear nature of both the empirical data and the predictions obtained when the rate of modulation was 256 Hz as compared to the more linear nature of the data and predictions obtained at the two lower rates of modulation. This difference in the predictions obtained across the three frequencies of modulation results from the operation of the 150-Hz low-pass filter. Overall, the patterning of the predictions of the model appears to capture both the main effects and the interactions that can be observed in Fig. 1 and that were confirmed via the ANOVA conducted on the empirical data themselves. Quantitatively, a statistical analysis revealed that the predictions of the model accounted for 80% of the variability in the behavioral data.3
Figure 2.
Similar to Fig. 1. The empirical data from Fig. 1 and the corresponding predictions from the position-variable model (see text) are plotted as adjacent pairs of panels.
The success of the model is, perhaps, best appreciated by considering the fact that the ANOVA performed on the data (see Sec. 2) revealed that the main effects and their interactions accounted for 84% of the variance. Said differently, 84% of the variation in the lateralization judgments of the listeners was determined by variation of the stimulus variables. Assuming 84% to be the upper limit on the amount of variance in the data for which the model could account, then the conclusion follows that the model accounts for 95% (80∕84) of the variability in the data attributable to the manipulations of the stimuli. Thus, from both quantitative and qualitative perspectives, it appears that the model does an excellent job of accounting for or explaining the data.
SUMMARY AND GENERAL DISCUSSION
One purpose of this study was to obtain measures of extent of laterality using the same raised-sine stimuli centered at 4 kHz that were employed previously in experiments measuring listeners’ abilities to discriminate changes in envelope-based ITD. The general question was whether the manipulations of the same physical variables (frequency of modulation, depth of modulation, and value of the raised-sine exponent) produce commensurate changes in both discrimination and lateralization, thereby reflecting commensurate changes in the potency of ITDs across the two tasks. Comparisons of the lateralization data obtained in this study with the discrimination data obtained by Bernstein and Trahiotis (2009, 2010), 7 reveal that to be the case. Specifically, increasing either depth of modulation or the value of the raised-sine exponent led to both smaller threshold ITDs and larger extents of laterality. In addition, increasing the frequency of modulation from 32 to 128 Hz did likewise. A further increase in the frequency of modulation to 256 Hz led to modest, but consistent, increases in both threshold ITDs and smaller extents of laterality. This latter outcome appears to be a manifestation of, and additional evidence for, the operation of a 150-Hz low-pass filtering of the envelope of high-frequency stimuli found in previous behavioral and physiological experiments (e.g., Kohlrausch et al., 2000; Bernstein and Trahiotis, 2002; Griffin et al., 2005).
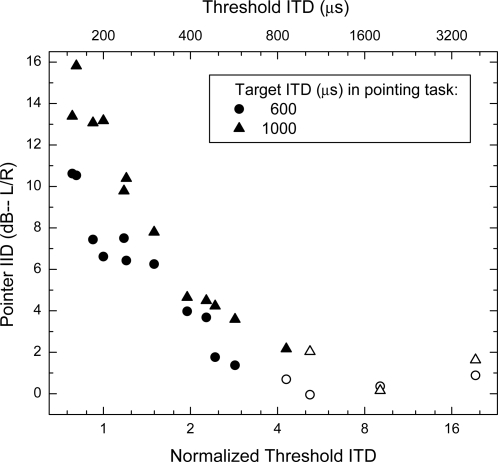
Figure 3 indicates a commensurate relation between extents of laterality obtained in this study and threshold ITDs reported by Bernstein and Trahiotis (2010). The points within Fig. 3 represent conditions across the two studies for which both threshold ITDs and extents of laterality were measured. For raised-sine stimuli having a depth of modulation of 100%, rates of modulation of 32, 128, or 256, and exponents of 1.0, 1.5 or 8.0, the values of threshold ITD were taken from Fig. 1 of Bernstein and Trahiotis. For raised-sine stimuli having a depth of modulation of 25%, rates of modulation of 32, 128, or 256, and exponents of 1.0 or 8.0, the values of threshold ITD were taken from Fig. 4 of Bernstein and Trahiotis.
Figure 3.
IID of the pointer (in dB) required to match the intracranial position of the target as a function of normalized threshold ITD. The parameter of the plot is the ITD of the target imposed in the acoustic pointing task. The upper abscissa reflects the approximate threshold ITD in miocroseconds corresponding to the values of normalized threshold ITD. Open symbols represent data obtained in conditions for which the threshold ITD exceeded the ITD imposed on the target in the acoustic pointing task.
The ordinate of Fig. 3 represents the mean, across listeners, of the IID of the pointer required to match the intracranial of position of targets having an ITD of 600 μs (circles) or an ITD of 1000 μs (triangles). The lower abscissa of Fig. 3 represents the mean threshold ITD normalized to the threshold ITD obtained in the “reference condition” defined by a rate of modulation of 128 Hz, a depth of modulation of 100%, and an exponent of 1.0 [see Bernstein and Trahiotis (2009, p. 3235) for further explanation and justification]. The threshold ITD, averaged across listeners, was approximately 200 μs for the reference condition. The upper abscissa reflects the approximate mean threshold ITD in microseconds corresponding to the values of normalized threshold ITD.
Open symbols within the plot represent data obtained in those conditions for which the threshold ITD exceeded the 600-μs (circles) or 1000-μs (triangles) ITD imposed on the target in the acoustic pointing task. They represent data obtained with raised-sines having a frequency of modulation of 32 Hz, a depth of modulation of 25%, and exponents of either 1.0 or 8.0. In those instances, the IID of the pointer is very small, indicating intracranial images near midline. This outcome is easily understood by considering that ITDs that are detectable less than 71% of the time (the criterion used to define “threshold”) would be expected to produce very small (if any) changes in extent of laterality.
In contrast, visual inspection of the closed symbols in Fig. 3 suggests that, for these stimuli, there exists an inverse linear relation between threshold ITD and extent of laterality. Statistical linear regression analyses support that notion in that the r2 between pointer IID (dB) and the log of normalized threshold ITD was 0.92 when the ITD was 600 μs (closed circles) and was 0.93 when the ITD was 1000 μs (closed triangles). In summary, the relative potency of ITD found across the stimulus set when discrimination thresholds were measured was also found when ITD-based extents of laterality were measured. Thus, for these stimuli, it does appear that one can predict extents of ITD-based laterality on the basis of threshold ITDs and vice versa.
A second purpose of the present study was to evaluate predictions of extent of laterality obtained via an interaural-correlation-function based model that incorporates stages of peripheral auditory processing. Two important outcomes were found while attempting to account for the data. First, a model that was previously successful in accounting for extents of laterality obtained with narrow bands of noise centered at low frequencies, the same bands of noise transposed to 4 kHz, and narrow bands of noise centered at 4 kHz (Bernstein and Trahiotis, 2003) could not account, either qualitatively or quantitatively, for the new data. Second, a model based on the position-variable model of Stern and Shear (1996) was highly successful in accounting for the new data.
The reader is reminded that the two models are somewhat similar in that both include bandpass filtering, rectification, and two stages of low-pass filtering. One stage of low-pass filtering is “peripheral” and its purpose is to account for the loss of neural synchrony to the fine-structure that occurs with increasing center frequency. A second stage of low-pass filtering (which was not included in the earlier versions of the position-variable model) is “more central” and its purpose is to account for the apparent loss of neural synchrony to increasing envelope frequencies.
The two models, however, differ in important ways with regard to specifics concerning both the peripheral and central processes that are assumed to operate. The reader is reminded that, with regard to the periphery, the model employed by Bernstein and Trahiotis (2003) included envelope compression, half-wave square-law rectification, and low-pass “neural synchrony” filtering at 425 Hz. In contrast, the position-variable model employed here and which accounted for the data included half-wave, cube-law rectification and low-pass neural synchrony filtering at 1200 Hz but did not include envelope compression. With regard to central processing, the decision variable of the model employed by Bernstein and Trahiotis (2003) was defined in terms of the position of the peak of activity of the correlogram. As described earlier, the decision variable of the extended position-variable was taken to be the centroid of activity of the correlogram measured subsequent to frequency-dependent centrality weighting.
These differences led us to begin a theoretical exploration with the goal of determining which differences between the models were responsible for the success of the position-variable model in accounting for the data in Fig. 1. First, it was found that adding peripheral envelope compression à la Bernstein and Trahiotis (2002, 2003), 35 to the position-variable model resulted in substantially poorer predictions because adding compression resulted in extremely (and hopelessly) small displacements of the centroid along the ITD axis. Just as important, the patterning of the predictions across parametric variations of the input stimuli did not conform well to the patterning of the empirical data. At this time, we are unable to understand, let alone explain, why the inclusion of compression is so detrimental when incorporated within the position-variable model in order to account for ITD-based extents of laterality at high frequencies, while it seems to be so necessary in order to account for binaural detection data (e.g., Bernstein et al., 1999; Bernstein and Trahiotis, 2002).
Second, it was found that, for both models, using the peak of activity of the correlogram along the ITD axis as the decision variable resulted in highly inaccurate predictions. This occurred principally because changing the frequency of modulation from 32 to 128 to 256 Hz produced essentially the same predicted extent of laterality (in stark contrast to the data in Fig. 1). Therefore (1) the absence of envelope compression and (2) the use of the centroid rather than the peak of the correlogram as the decision variable were both important factors regarding the successful predictions obtained from the position-variable model.
This naturally leads to the question of how well the present version of the position-variable model can account for the extents of laterality reported by Bernstein and Trahiotis (2003). The model correctly predicts that low-frequency Gaussian noises and their counterparts transposed to 4 kHz yield greater extents of laterality than do bands of Gaussian noises centered at 4 kHz. The model incorrectly predicts that extents of laterality obtained with noises centered at low frequencies are somewhat, but consistently, larger than those obtained with their transposed counterparts. In fact, the empirical data indicate that, for a given ITD, both stimuli produce essentially the same extent of laterality. Several computer simulations made while manipulating stages of the model revealed that this disparity comes about essentially entirely as a result of the 150-Hz envelope low-pass filter that affects temporal processing within each “monaural” channel for stimuli centered at high spectral frequencies, but not for stimuli centered at low spectral frequencies for which the fine-structure, rather than the envelope, conveys the ITD. At this time, we cannot offer a clear-cut explanation for this outcome. Because of the paucity of psychophysical data that would inform and∕or constrain the precise nature of the envelope low-pass filter, it remains for future investigations to provide the information necessary to modify the models suitably.
In summary, parametric variations of the depth of modulation, peakedness, and frequency of modulation of 4-kHz-centered raised-sine stimuli produce changes in ITD-based extents of laterality that were logically consistent with threshold ITDs obtained with same stimuli (Bernstein and Trahiotis, 2009). The extents of laterality were successfully accounted for via an augmentation of the cross-correlation-based position-variable modeling approach developed by Stern and Shear (1996) to account for ITD-based extents of laterality obtained at low spectral frequencies.
ACKNOWLEDGMENTS
This research was supported by research grant NIH DC-04147 from the National Institute on Deafness and Other Communication Disorders, National Institutes of Health. The authors thank two anonymous reviewers and the associate editor for comments that were often deemed to be quite helpful.
Footnotes
Data were also obtained from a fourth listener. Those data were excluded from the study because the individual matches that entered into the calculation of the mean for each stimulus condition were characterized by a degree of variability that was both very much larger than that characterizing the data from the other three listeners and very much larger than that typically observed over decades of the use of the acoustic pointing procedure in our laboratory. We concluded that the listener simply could not perform the task reliably.
Our application of a ρ(tau) function to the processing of the envelopes of high-frequency carriers assumes that the function operates similarly at low and high spectral frequencies, where the cross-correlation of the waveform and envelope, respectively, is germane. This assumption does not theoretically or logically force the conclusion that effects attributable to ρ(tau) functions are manifest or realized in the same manner for low vs high spectral frequencies. At this time, our analyses appear to support the hypothesis that similar ρ(tau) functions affect the processing of ITDs conveyed by either low-frequency waveforms or the envelopes of high-frequency waveforms.
The formula used to compute the percentage of the variance for which our predicted values of threshold accounted was , where Oi and Pi represent individual observed and predicted values of threshold, respectively, and represents the mean of the observed values of threshold (e.g., Bernstein and Trahiotis, 1994).
References
- Bernstein, L. R., and Trahiotis, C. (1985a). “Lateralization of low-frequency, complex waveforms: The use of envelope-based temporal disparities,” J. Acoust. Soc. Am. 77, 1868–1880. 10.1121/1.391938 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (1985b). “Lateralization of sinusoidally amplitude-modulated tones: Effects of spectral locus and temporal variation,” J. Acoust. Soc. Am. 78, 514–523. 10.1121/1.392473 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (1994). “Detection of interaural delay in high-frequency SAM tones, two-tone complexes, and bands of noise,” J. Acoust. Soc Am. 95, 3561–3567. 10.1121/1.409973 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (1996). “The normalized correlation: Accounting for binaural detection across center frequency,” J. Acoust. Soc. Am. 100, 3774–3784. 10.1121/1.417237 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2002). “Enhancing sensitivity to interaural delays at high frequencies by using transposed stimuli,” J. Acoust. Soc. Am. 112, 1026–1036. 10.1121/1.1497620 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2003). “Enhancing interaural-delay-based extents of laterality at high frequencies by using ‘transposed stimuli’,” J. Acoust. Soc. Am. 113, 3335–3347. 10.1121/1.1570431 [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2009). “How sensitivity to ongoing interaural temporal disparities is affected by manipulations of temporal features of the envelopes of high-frequency stimuli,” J. Acoust. Soc. Am. 125, 3234–3242. 10.1121/1.3101454 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2010). “Accounting quantitatively for sensitivity to envelope-based interaural temporal disparities at high frequencies,” J. Acoust. Soc. Am. 128, 1224–1234. 10.1121/1.3466877 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein, L. R., Par, S. van de, and Trahiotis, C. (1999). “The normalized correlation: Accounting for NoSπ thresholds obtained with Gaussian and ‘low-noise’ masking noise,” J. Acoust. Soc Am, 106, 870–876. 10.1121/1.428051 [DOI] [PubMed] [Google Scholar]
- Buell, T. N., and Hafter, E. R. (1988). “Discrimination of interaural differences of time in the envelopes of high-frequency signals: Integration times,” J. Acoust. Soc. Am. 84, 2063–2066. 10.1121/1.397050 [DOI] [PubMed] [Google Scholar]
- Buell, T. N., Trahiotis, C., and Bernstein, L. R. (1991). “Lateralization of low-frequency tones: Relative potency of gating and ongoing interaural delay,” J. Acoust. Soc Am. 90, 3077–3085. 10.1121/1.401782 [DOI] [PubMed] [Google Scholar]
- Domnitz, R. H., and Colburn, H. S. (1977). “Lateral position and interaural discrimination,” J. Acoust. Soc. Am. 61, 1586–1598. 10.1121/1.381472 [DOI] [PubMed] [Google Scholar]
- Griffin, S. J., Bernstein, L. R., Ingham, N. J., and McAlpine, D. (2005). “Neural sensitivity to interaural envelope delays in the inferior colliculus of the guinea pig,” J. Neurophysiol. 93, 3463–3478. 10.1152/jn.00794.2004 [DOI] [PubMed] [Google Scholar]
- Hays, W. L. (1973). Statistics for the Social Sciences (Holt, Rinehart, and Winston, New York: ), pp. 417–419. [Google Scholar]
- Heller, L. M., and Trahiotis, C. (1996). “Extents of laterality and binaural interference effects,” J. Acoust. Soc. Am. 99, 3632–3637. 10.1121/1.414961 [DOI] [PubMed] [Google Scholar]
- John, M. S., Dimitrijevic, A., and Picton, T. (2002). “Auditory steady-state responses to exponential modulation envelopes,” Ear Hear. 23, 106–117. 10.1097/00003446-200204000-00004 [DOI] [PubMed] [Google Scholar]
- Keppel, G. (1991). Design and Analysis: A Researchers Handbook (Prentice-Hall, Englewood Cliffs, NJ: ), p. 494. [Google Scholar]
- Kohlrausch, A., Fassel, R., and Dau, T. (2000). “The influence of carrier level and frequency on modulation and beat-detection thresholds for sinusoidal carriers,” J. Acoust. Soc. Am. 108, 723–734. 10.1121/1.429605 [DOI] [PubMed] [Google Scholar]
- McFadden, D., and Pasanen, E. G. (1976). “Lateralization at high frequencies based on interaural time differences,” J. Acoust. Soc. Am. 59, 634–639. 10.1121/1.380913 [DOI] [PubMed] [Google Scholar]
- Nuetzel, J. M., and Hafter, E. R. (1976). “Lateralization of complex waveforms: Effects of fine-structure, amplitude, and duration,” J. Acoust. Soc. Am. 60, 1339–1346. 10.1121/1.381227 [DOI] [PubMed] [Google Scholar]
- Nuetzel, J. M., and Hafter, E. R. (1981). “Discrimination of interaural delays in complex waveforms: Spectral effects,” J. Acoust. Soc. Am. 69, 1112–1118. 10.1121/1.385690 [DOI] [Google Scholar]
- Par, S. van de, and Kohlrausch, A. (1997). “A new approach to comparing binaural masking level differences at low and high frequencies,” J. Acoust. Soc. Am. 101, 1671–1680. 10.1121/1.418151 [DOI] [PubMed] [Google Scholar]
- Patterson, R. D., Allerhand, M. H., and Giguere, C. (1995). “Time-domain modeling of peripheral auditory processing: A modular architecture and a software platform,” J. Acoust. Soc. Am. 98, 1890–1894. 10.1121/1.414456 [DOI] [PubMed] [Google Scholar]
- Schiano, J. L., Trahiotis, C., and Bernstein, L. R. (1986). “Lateralization of low-frequency tones and narrow bands of noise,” J. Acoust. Soc. Am. 79, 1563–1570. 10.1121/1.393683 [DOI] [PubMed] [Google Scholar]
- Stecker, G. C., and Hafter, E. R. (2002). “Temporal weighting in sound localization,” J. Acoust. Soc. Am. 112, 1046–1057. 10.1121/1.1497366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern, R. M., and Colburn, H. S. (1978). “Theory of binaural interaction based on auditory-nerve data. IV. A model for subjective lateral position,” J. Acoust. Soc. Am. 64, 127–140. 10.1121/1.381978 [DOI] [PubMed] [Google Scholar]
- Stern, R. M., and Colburn, H. S. (1985). “Lateral-position-based models of interaural discrimination,” J. Acoust. Soc. Am. 77, 753–755. 10.1121/1.392345 [DOI] [PubMed] [Google Scholar]
- Stern, R. M., and Shear, G. D. (1996). “Lateralization and detection of low-frequency binaural stimuli: Effects of distribution of internal delay,” J. Acoust. Soc. Am. 100, 2278–2288. 10.1121/1.417937 [DOI] [Google Scholar]
- Stern, R. M., Shear, G. D., and Zeppenfeld, T. (1988a). “Lateralization predictions for high-frequency binaural stimuli,” J. Acoust. Soc. Am. 84, S80. 10.1121/1.2026494 [DOI] [Google Scholar]
- Stern, R. M., Zeiberg, A. S., and Trahiotis, C. (1988b). “Lateralization of complex binaural stimuli: A weighted image model,” J. Acoust. Soc. Am. 84, 156–165,. 10.1121/1.396982 [DOI] [PubMed] [Google Scholar]
- Trahiotis, C., Bernstein, L. R., and Akeroyd, M. A. (2001). “Manipulating the “straightness” and “curvature” of patterns of interaural cross-correlation affects listeners’ sensitivity to changes in interaural delay,” J. Acoust. Soc. Am. 109, 321–330. 10.1121/1.1327579 [DOI] [PubMed] [Google Scholar]
- Trahiotis, C., and Stern, R. M. (1989). “Lateralization of bands of noise: Effects of bandwidth and differences of interaural time and phase,” J. Acoust. Soc. Am. 86, 1285–1293. 10.1121/1.398743 [DOI] [PubMed] [Google Scholar]
- Trahiotis, C., and Stern, R. M. (1994) “Across-frequency interaction in lateralization of complex binaural stimuli,” J. Acoust. Soc. Am. 96, 3804–3806. 10.1121/1.410570 [DOI] [PubMed] [Google Scholar]
- Watson, C. S., and Mittler, B. (1965). “Time-intensity equivalence in auditory lateralization: A graphical method,” Psychonomic Sci. 2, 219–220. [Google Scholar]
- Yost, W. A. (1981). “Lateral position of sinusoids presented with interaural intensive and temporal differences,” J. Acoust. Soc. Am. 70, 397–409. 10.1121/1.386775 [DOI] [Google Scholar]