Pressure distributions in a static physical model of the uniform glottis: Entrance and exit coefficients

Abstract

Pressure distributions for the uniform glottis were obtained with a static physical model (M5). Glottal diameters of d = 0.005, 0.0075, 0.01, 0.02, 0.04, 0.08, 0.16, and 0.32 cm were used with a range of phonatory transglottal pressures. At each pressure and diameter, entrance loss and exit coefficients were determined. In general, both coefficients decreased in value as the transglottal pressure or the diameter increased. Entrance loss coefficients ranged from 0.69 to 17.6. Use of these coefficients with the measured flow rates in straightforward equations accurately reproduced the pressure distributions within the glottis and along the inferior vocal fold surface.

INTRODUCTION

Experimental studies of air pressures in static laryngeal models have established a basic understanding of glottal aerodynamics. The experiment of van den Berg et al.1 provided general characteristics of intraglottal pressures, introduced a pressure coefficient of 1.375 to describe energy loss at the glottal entrance, and gave an exit coefficient of 0.5 to describe the effects of pressure recovery. Ishizaka and Matsudaira2 and Ishizaka and Flanagan3 adopted the value of 1.375 for the entrance loss coefficient (in what they termed the “turbulent” flow approach) and used Newton’s second law to derive an exit coefficient that depends on the ratio of the area of the glottal exit to the area of the vocal tract and whose value is substantially smaller than that given by van den Berg et al. In addition, Ishizaka and Matsudaira2 introduced a “laminar” approach that allowed the pressure drop to be defined by the growth of a boundary layer within the glottis. Using laryngeal geometry as an example, Beavers et al.4 have shown that the ratio of the pressure drop between the trachea and a specific cross-section on the inferior vocal fold surface to the kinetic pressure at that location will be 1.0. Downstream of that location the pressure continues to decrease such that the pressure drop at the actual entrance to the (uniform) glottis creates a ratio value greater than 1.0. In this context, the result of van den Berg et al.1 would be considered an increase over the value of 1.0 by 0.375, on average. Since Beavers et al.4 found the location at which the ratio of 1.0 was achieved to have a significant dependence on glottal diameter and driving pressures, one would expect a constant entrance loss coefficient of 1.375 to be too great a simplification for accurate phonatory modeling.

Scherer et al.5 tested the aerodynamic formulas of Ishizaka and Matsudaira2 using two life-size polyester resin models of the larynx (MI and MII) having rectangular glottal shapes and fixed minimal glottal diameters of 0.104 and 0.158 cm, respectively. Results supported the transglottal pressure-flow relations of Ishizaka and Matsudaira2 to an accuracy of about 10% for a wide range of pressures, MI fitting the laminar formula, and MII fitting the turbulent formula. The work by Gauffin et al.6 used a scaled-up larynx model and found exit coefficients consistent with the formula derived by Ishizaka and Matsudaira2 but found the entrance loss coefficients at large Reynolds numbers to be about 20% lower than the 1.375 value. The scaled-up model of Scherer and Titze7 (MIII) had a fixed diverging angle of 42° and allowed variation of the minimal diameter. The average glottal entrance coefficients were 1.067, 1.329, and 1.445 for the three diameters of 0.02, 0.04, and 0.06 cm, respectively, showing a considerable variation with diameter. For the 0.02 cm diameter case, the entrance coefficient decreased as pressure increased but tended to slightly rise with pressure for the other two diameters.

The goal here is to report the pressure distributions for the uniform glottis of M5, give the entrance and exit coefficients (and a general formula for the former), and offer equations that accurately reproduce the pressure distributions. The results should allow researchers whose model calculations8, 9, 10, 11 are based on Bernoulli-like formulas to describe the pressures driving the vocal folds to take an important step toward a more realistic treatment of glottal aerodynamics.

METHODS

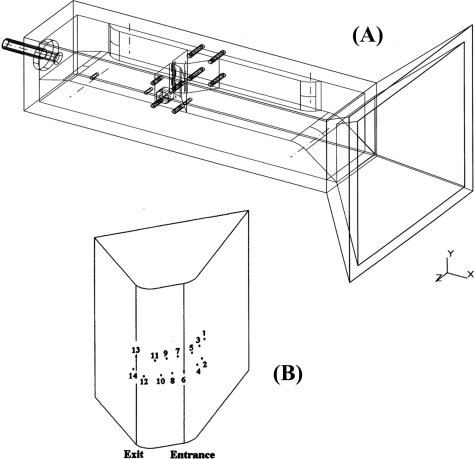
Model M5 is shown in Fig. 1. Air enters from the right side of the figure, passes through a rectangular duct (the trachea), accelerates through the narrow opening between the vocal folds, and then enters another rectangular duct (the vocal tract). The medial surface of one of the vocal folds [Fig. 1B] has 14 pressure taps. In addition, tap 15 is located on the tunnel wall directly past the glottis, tap 16 is located further downstream, and tap 0 gives the reference pressure in the “trachea.” The medial edges of the vocal folds were carefully rounded to give a reasonable representation of the surfaces of the glottis.12 Shims and feeler gauges were placed between one of the vocal folds and the wind tunnel wall to precisely adjust the glottal diameter.

Figure 1.

Schematic diagram (A) of model M5 showing the wind tunnel with vocal fold inserts. The minimal glottal diameter is the smallest separation between the vocal folds. Locations of the 14 pressure taps on one of the plastic inserts (B). Tap 6 lies at the glottal entrance, and tap 13 lies at the glottal exit.

Pressures were obtained using a Validyne DP109 transducer system.12 Each pressure measurement at each tap was repeated four times, the average of which was used. The flows were measured using a Rudolph pneumotach with a Validyne MP45 pressure transducer system.

Pressure distributions were obtained for glottal diameters d = 0.005, 0.0075, 0.01, 0.02, 0.04, 0.08, 0.16, and 0.32 cm (life-size values). The transglottal pressures ranged from 1 to 25 cm H₂O (life-size values). Because the size enlargement was 7.5, flows in the model were 7.5 times life-size and pressures (1∕7.5)² smaller than life-size. There were a total of 35 different pressure distributions.

PRESSURE DISTRIBUTIONS

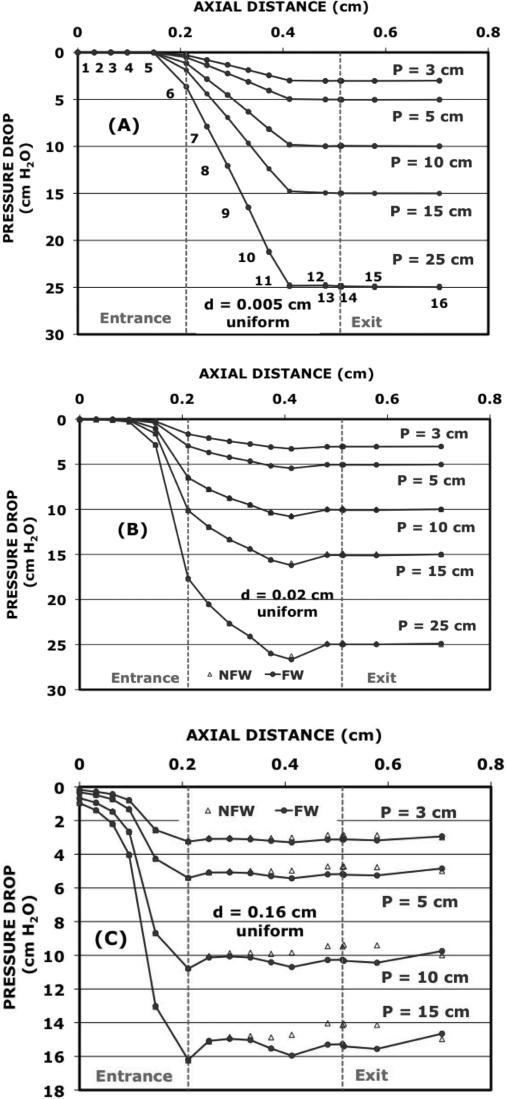
Pressure distributions are shown in Fig. 2 for d = 0.005 cm (A), d = 0.02 cm (B), and d = 0.16 cm (C). The experimental uncertainty13 of data points from taps 6 to 14 were less than 1%, and thus 1% error bars are attached to each data point in Fig. 2A as an upper limit to the uncertainty. Error bars are comparable to the size of the filled circles used to represent the data points and do not show up in most cases.

Figure 2.

(Color online) Pressure distributions collected with model M5 within and near the glottis for minimal glottal diameters of (A) 0.005 cm, (B) 0.02 cm, and (C) 0.16 cm. The glottal entrance is located at an axial distance of 0.211 cm (tap 6) and the glottal exit at 0.511 cm (tap 13). For the two larger diameters, the NFW pressure distributions were taken on the side from which the flow jet has separated, and the FW pressure distributions were taken on the side to which the jet adhered.

The pressure at glottal entrance is lower than that in the trachea due to acceleration of the air along the narrowing subglottal region. The data are conveniently presented as a pressure drop from the tracheal pressure tap location. For the two smaller diameters of Fig. 2, the pressure distributions show an approximately uniform rate of decrease within the straight portion of the glottis (taps 6–11), as expected from viscosity effects in a narrow rectangular channel.14 This feature is also shared by the pressure distributions at d = 0.075 and 0.01 cm (not shown), in a smaller region (taps 7–11) for d = 0.08 cm (not shown), and in Fig. 2 of Ref. 15 for d = 0.04 cm. The slope of the uniform decrease is larger for smaller diameters, consistent with greater viscous effects for narrower channels. After the uniform decrease, pressure recovery near the glottal exit can be seen for d = 0.02 cm (B) and for d = 0.16 cm (C). Pressure recovery occurs in the other distributions, except for the d = 0.005 cm case. These begin at tap 11 where the straight portion of the glottal surface starts to expand to accommodate the rounded portion of the glottal exit.

The short glottal expansion near the glottal exit encourages stable flow skewing to one side [here called the flow wall (FW)] and gives rise to two surface pressure distributions, as shown in Fig. 2C for each transglottal pressure. Pressures on the FW side tend to be lower than those on the nonflow wall (NFW) side due to the greater velocities near the FW. The pressure differences for d = 0.02 cm in Fig. 2B are small, and most of the NFW empty triangle symbols are hidden behind the FW filled circle symbols. For the larger diameters the differences tend to increase as the transglottal pressure increases. At taps 11 and 12, they become as large as 9% of the transglottal pressure for d = 0.16 cm and as large as 12% for d = 0.32 cm. For the coefficients calculated below, pressures at each tap were averaged between the FW and NFW values.

ENTRANCE LOSS COEFFICIENTS

The entrance loss coefficient1, 2, 3, 14k_ent is defined as the difference between the pressure in the trachea (at tap 0) and that at the glottal entrance (at tap 6) divided by the kinetic energy density at the glottal entrance, that is,

$$k_{\text{ent}}=2A_6^2\frac{p_0-p_6}{\rho U_g^2}$$ (1)

where ρ = 0.00121 g∕cm³ is the density of air at room temperature, U_g is the glottal volume flow rate, and A₆ is the glottal area at tap 6. A₆ is the product of the glottal length l_g = 1.2 cm and the glottal diameter d. Table TABLE I. lists the flow rates (first row) and entrance loss coefficients (second row) for all diameters and transglottal pressures. The entrance coefficients16 range from 0.687 for a diameter of 0.32 cm and transglottal pressure of 5 cm H₂O to 17.55 for a diameter of 0.005 cm and transglottal pressure of 3 cm H₂O. The entrance loss coefficients become very large for small diameters and low pressures. The coefficients tend to decrease as the transglottal pressure or the glottal diameter increases. The value 1.375 from van den Berg et al.1 is not an accurate approximation for small or large diameters but is within 10% of the values calculated from the M5 measurements for some intermediate diameters.

Table 1.

Flow rates (in cm³∕s, first row) and entrance loss coefficients (second row) for the uniform glottis using model M5. Boldface indicates the results that were within 10% of 1.375. These occur in specific pressure ranges for diameters 0.02–0.08 cm.

	Pressure (cm H2O)
Diameter (cm)	1	3	5	10	15	25
0.005		1.0	1.9	4.2	6.3	10.5
		17.553	8.578	3.782	2.768	1.927
0.0075		2.3	4.3	9.2	13.8	22.1
		9.624	5.343	3.004	2.373	1.920
0.01		6.1	10.2	19.6	27.3	40.2
		3.862	2.744	2.007	1.790	1.601
0.02		29.7	41.6	64.7	82.8	113
		1.743	1.602	1.447	1.378	1.291
0.04		80.7	106	161	204
		1.337	1.338	1.201	1.134
0.08		180	231	336	416
		1.298	1.320	1.274	1.254
0.16		420	552	826	1055
		1.096	1.058	0.943	0.870
0.32	563	1060	1460
	0.931	0.800	0.687

EXIT COEFFICIENTS

The exit coefficients are a means of representing the effects of pressure recovery2, 3, 8 from glottal exit to the pharyngeal cavity, which begins near tap 11 where the straight glottal wall begins to curve [Fig. 1B]. The exit coefficient can be defined by comparing the pressure at tap 11 with that at tap 16, viz.,

$$k_{\text{ex}}=2A_{11}^2\frac{p_{16}-p_{11}}{\rho U_g^2}$$ (2)

where A₁₁ is the same as A₆ for the uniform glottis, and the sign of the exit coefficient is positive whenever the pressure at tap 16 is above that at tap 11. Again for simplicity, the FW and NFW pressure values were averaged at taps 11 and 16. Coefficients determined in this manner are listed in Table TABLE II.. All of the exit coefficients for d = 0.005 cm and two of those for d = 0.0075 cm are negative because the pressures at tap 11 are above those at tap 16. This suggests that pressure recovery per se does not occur at these diameters. The behavior of the coefficients beginning with d = 0.02 cm is easier to describe, since their values tend to decrease as transglottal pressure increases and to decrease with increasing diameter. The exit coefficient equation derived by Ishizaka and Matsudaira2 takes the form,

$$k_{\text{ex},\text{IM}}=2A_{11}\frac{(1-A_{11}∕A_{\text{vt}})}{A_{\text{vt}}.}$$ (3)

In Eq. 3 the quantity A_vt denotes the area of the vocal tract (2.4 cm² for M5). Equation 3 is not consistent with the M5 empirical results—it does not predict the dependence on the transglottal pressure (Table TABLE II.). Equation 3 also predicts an increase of the exit coefficient with glottal diameter, since A₁₁ increases linearly with glottal diameter, also inconsistent with the trends of Table TABLE II..

Table 2.

Exit coefficients for the uniform glottis.

	Pressure (cm H2O)
Diameter (cm)	1	3	5	10	15	25
0.005		−0.723	−1.103	−0.567	−0.346	−0.077
0.0075		−1.313	−0.397	0.114	0.194	0.228
0.01		0.211	0.279	0.268	0.257	0.218
0.02		0.275	0.219	0.167	0.146	0.111
0.04		0.140	0.108	0.101	0.071
0.08		0.079	0.078	0.066	0.057
0.16		0.064	0.055	0.035	0.028
0.32	0.079	0.061	0.043

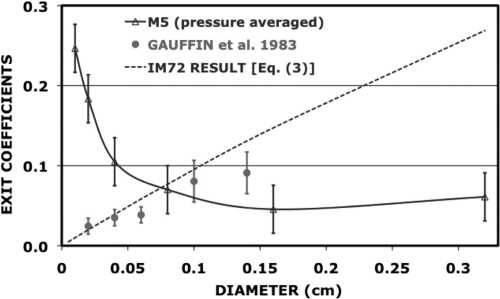
In Fig. 3 exit coefficients derived from the M5 pressure distributions for diameters from 0.01 to 0.32 cm are compared with those calculated with Eq. 3. For a given diameter, the M5 coefficients were averaged over the pressures of Table TABLE II., and the error bars were determined from the standard deviations of the pressure dependence along the rows of Table TABLE II.. The M5 curve decreases monotonically with increasing diameter and does not agree with the trend of the Newton’s law result. For comparison, the exit coefficients measured by Gauffin et al.6 are also shown in Fig. 3, after a rescaling that considers the size of their vocal tract. These data were taken for a range of diameters from d = 0.02 cm to d = 0.14 cm. The error bars are included to indicate the range of exit coefficients measured for different pressures and flows. The error bars at d = 0.10 and 0.14 cm diameters are comparable to the M5 error bars, indicating a similar range of variation of the exit coefficients with transglottal pressure for the two data sets. However, the exit coefficients determined by Gauffin et al. do seem to support the trend predicted by Eq. 3, as they noted, although the size of their coefficients for the larger diameters seems consistent with those derived from M5. The differences between the two data sets are more pronounced for the smaller diameters, but the results near the top of Table TABLE II. suggest that pressure recovery may not be well defined for this range of diameters. The removable ventricles that Gauffin et al. included in their vocal tract and different glottal exit geometry may be responsible for the differences between their coefficients and the M5 coefficients.

Figure 3.

(Color online) Pressure-averaged exit coefficients as functions of glottal diameter.

A PRESSURE ALGORITHM AND THE M5 PRESSURE DISTRIBUTIONS

If one assumes that the entrance loss coefficient embodies essentially all of the important corrections to the Bernoulli equation within the subglottal region bounded laterally by the inferior surface of the vocal folds, then the pressures at the taps within this region are given by

$$P_i=P-k_{\text{ent}}\frac{\rho {(U_g∕A_i)}^2}{2},(i=1,\dots 6),$$ (4)

where A_i is the area of the subglottal channel at the location of the ith tap, and k_ent is the entrance loss coefficient for the given glottal diameter and transglottal pressure. The value of A_i is the product of the glottal length l_g and the transverse distance at the ith tap. The values of k_ent and U_g listed in Table TABLE I. may be used directly for the comparison with the observed M5 pressures. Under similar assumptions, the pressures near the glottal exit are given by

$$P_i=P_{16}-k_{\text{ex}}\frac{\rho {(U_g∕A_i)}^2}{2},(i=11,12,13),$$ (5)

where k_ex is the exit coefficient from Table TABLE II.. Linear interpolation in the axial distance z is employed to estimate the approximate pressure drop in the straight-walled portion of the glottis of model M5, which takes the form,

$$P\left(z\right)=\frac{(z_{11}-z)P_6+(z-z_6)P_{11}}{z_{11}-z_6},$$ (6)

for any value of the axial distance z between tap 6 (0.211 cm) and tap 11 (0.413 cm).

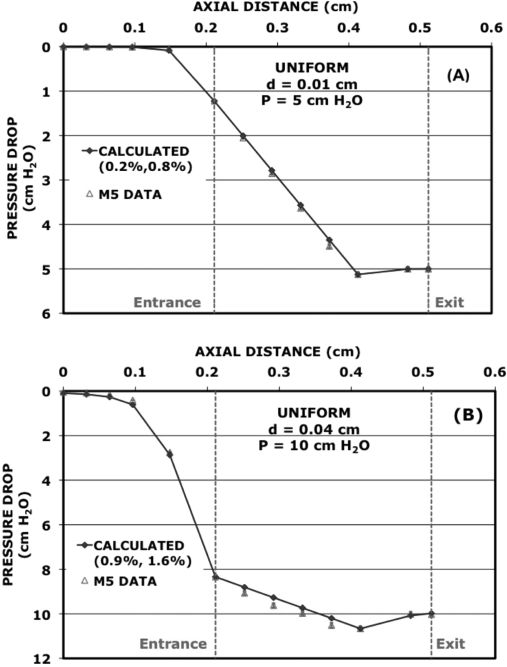
Pressure distributions calculated with Eqs. 4, 5, 6 for representative pressures at d = 0.01 and 0.04 cm are shown in Fig. 4, where they are compared with the corresponding M5 data. The 1% error bars discussed in Sec. 3 are attached to the data points and are barely visible within the open triangles. The agreement of the calculations with the M5 data for these two cases is excellent, although the data have a slight curvature between taps 6 and 11 in Fig. 4B that is not included in the linear interpolation of Eq. 6. The accuracy of the fit may be measured by comparing the difference between the calculated and the measured pressure values at each tap divided by the transglottal pressure for the given distribution. This ratio is translated into a percentage and averaged over the first six taps to evaluate the accuracy of these formulas along the inferior surface of the vocal fold. For the distributions of Figs. 4A, 4B, the average discrepancies along this surface are 0.2% and 0.9%, respectively (first entry in parentheses in Fig. 4). The corresponding average discrepancies within the glottis (taps 6–13) are 0.8% and 1.6% (second entry in parentheses) and reflect the accuracy of the linear interpolation along the straight part of the glottis as well as the accuracy of Eq. 5 in reproducing pressure recovery. For the entire set of pressure distributions, none of the intraglottal discrepancies is as large as 4%, and the average of the intraglottal discrepancies over all the diameters is 1.8%. For diameters of 0.08 cm and smaller, all of the inferior surface discrepancies are less than 3%, and the average for this set of diameters is 1.4%. The average for the inferior surface discrepancies for d = 0.16 cm is 6.6% and those for d = 0.32 cm is 14.4%. The average of the inferior surface discrepancies over all of the diameters is 2.8%.

Figure 4.

(Color online) Comparison of pressure distributions calculated from Eqs. 4 to 6 with the pressure distributions measured at d = 0.01 cm (A) and at d = 0.04 cm (B).

SUMMARY AND CONCLUSIONS

For the uniform glottis, the glottal entrance loss coefficients were found to be large at small diameters and to decrease with increasing pressure and diameter. The glottal exit coefficients were smaller and possessed the same decreasing trends with diameter and transglottal pressure for diameters of 0.02 cm and greater. Moreover, the exit coefficients did not agree with the theoretical result derived by Ishizaka and Matsudaira.2 This may be partly due to the “natural” rounding of the glottal exit of model M5 rather than the abrupt area increase assumed in the momentum derivation of Ishizaka and Matsudaira.

An algorithm for calculating the intraglottal pressures and the pressures along the inferior surface of the vocal fold from the tabulation of glottal flow rates, entrance loss coefficients, and exit coefficients was developed and tested. When combined with linear interpolation within the glottis, the algorithm accurately reproduced the inferior surface pressures and the intraglottal pressures to an accuracy of 3% or better for the set of M5 pressure distributions with diameters of 0.08 cm and smaller. The errors are larger for the 0.16 cm and the 0.32 cm cases, but the errors for the intraglottal pressures were never as large as 4%. The success of the pressure algorithm suggests that the accuracy of modeling pressure distributions relies on valid entrance loss and exit coefficients and that judicious use of the flow rates and coefficients of Tables 1, TABLE II. should lead to a more realistic treatment of the forces that act on the vocal folds in lumped-element models8, 9, 10 or more elaborate models.11