Characterization of microfluidic mixing and reaction in microchannels via analysis of cross-sectional patterns

Abstract

For the diagnosis of biochemical reactions, the investigation of microflow behavior, and the confirmation of simulation results in microfluidics, experimentally quantitative measurements are indispensable. To characterize the mixing and reaction of fluids in microchannel devices, we propose a mixing quality index (M_qi) to quantify the cross-sectional patterns (also called mixing patterns) of fluids, captured with a confocal-fluorescence microscope (CFM). The operating parameters of the CFM for quantification were carefully tested. We analyzed mixing patterns, flow advection, and mass exchange of fluids in the devices with overlapping channels of two kinds. The mixing length of the two devices derived from the analysis of M_qi is demonstrated to be more precise than that estimated with a commonly applied method of blending dye liquors. By means of fluorescence resonance-energy transfer (FRET), we monitored the hybridization of two complementary oligonucleotides (a FRET pair) in the devices. The captured patterns reveal that hybridization is a progressive process along the downstream channel. The FRET reaction and the hybridization period were characterized through quantification of the reaction patterns. This analytical approach is a promising diagnostic tool that is applicable to the real-time analysis of biochemical and chemical reactions such as polymerase chain reaction (PCR), catalytic, or synthetic processes in microfluidic devices.

INTRODUCTION

Microfluidic devices have attracted much attention and are widely applied in analytical chemistry,¹ biomedical diagnosis,^{2, 3, 4} and chemical synthesis.⁵ For these devices, mixing is a vital procedure that has a crucial impact on the products of chemical reactions⁶ and the consequences of biochemical assays;⁷ one can obtain no satisfactory results without effective mixing of samples or reagents. Dozens of micromixers (or microreactors) have thus been devised to achieve rapid mixing in a small space and a small duration. These devices are classified as passive and active units.^{8, 9} A passive unit allows microfluids to mix readily with varied and complicated flow patterns and mechanisms induced by structural designs; an active unit mixes microfluids with a violent flow field generated by a controllably external source such as piezovibration¹⁰ or electrokinetic forces.^{11, 12, 13} The full exploration of a flow field is hence significant.

To characterize the mixing dynamics and efficiency of fluids in microdevices, measuring techniques applicable to the investigation of velocity and concentration fields are urgently required. Although computational fluid dynamics (CFD) is a mature technique to analyze conveniently and even to optimize devices, analysis of a full-scale device is required but rarely achieved with CFD because of the large grids (hardware limitation) and the drawback of numerical diffusion. One currently visualizes the velocity field with microparticle imaging velocimetry (micro-PIV);^{14, 15} this technique is useful to depict the trend and magnitude of the velocity field, but for the reaction and blending of reagents, the most meaningful issue concerns the concentration field and the distribution of component species. A developed measuring technique involving micro-PIV and particle counting was proposed to resolve simultaneously the concentration and flow fields.¹⁶ The flexibility of this technique to resolve the concentration field is partly restricted by the size of seeding particles.

In microfluidic systems, analytical measurements of the concentration field are critical, especially for micromixers and microreactors; the analysis of a concentration field directly reflects the mixing and reaction conditions of reagents and enables appraisal of the performance of devices. Some facile approaches to observe the distributions of species have been developed, including dye-liquor blending,^{17, 18} acid-base test (phenolphthalein),^{19, 20} colorimetry of a redox reaction,^{21, 22} and fluorophore dilution.^{23, 24} With a conventional optical microscope (OM), the observations from a top view in these tests are superimposed, however, on images at various depths along an optical axis, resulting in overestimated mixing results. Moreover, effective devices invariably utilize three-dimensional (3D) flows to boost fluid mixing and reaction. It is unlikely that three-dimensional flow patterns can be analyzed precisely with an OM.

3D-image reconstruction is a promising means to interpret a flow field exactly, so avoiding poor estimates. These techniques include magnetic-resonance imaging (MRI),²⁵ nuclear-magnetic-resonance (NMR) microscopy,^{26, 27, 28} circular-dichroism spectra with synchrotron radiation (CDSR),²⁹ and optical-coherence tomography (OCT),^{30, 31} and the use of a deconvolution microscope,³² laser-sheet illumination microscope,³³ confocal microscope,³⁴ two-photon absorption fluorescence microscope,³⁵ and a coherent anti-Stokes Raman scattering (CARS) microscope.³⁶ They have received much attention in the biological and medical fields, and their application to microfluidics is thriving. One can thereby scrutinize the distribution of species on cross sections of microchannels (streamwise direction) so to define the mixing patterns. MRI, NMR, and CARS techniques are sophisticated and require technical experts for operation; their instruments are costly. CDSR is also a highly complicated technique that requires radiation from a synchrotron. OCT forms a 3D image in a manner similar to ultrasound, but its imaging resolution is greater than that of ultrasound through the use of near-infrared light rather than sound. With regard to molecular biology and medical assay, appropriate biolabeling fluorescent dyes or biomarkers are employed to enable highly selective and sensitive detection. A confocal microscope, relying on its accessibility and its prospective high resolution and large contrast power, provides an alternative way to observe a fluorescent image.

Combining a confocal microscope with fluorescence, confocal-fluorescence microscopy (CFM) has been developed to visualize the mixing pattern of fluids noninvasively in microfluidic systems. Through the use of a powerful laser as source and a pinhole to eliminate noise emanating from beyond the focal plane, a confocal-fluorescence microscope is capable of capturing a highly defined and contrastive image, and facilitates optical slicing for the dissection of 3D samples; these samples are reconstructed on stacking the thin sections from separate depths using image processing. CFM is a practical, convenient, and reliable technique for the examination of 3D microfluids and microstructures in microfluidics and lab-on-a-chip (LOC) systems. Many researchers have adopted a CFM to measure the mixing patterns for qualitative study, whereas the quantitative measurement of a concentration field is most valuable for the exploration of reagent blending and reaction. Stroock et al.³⁴ quantified the mixing patterns based on a concept of the intensity distribution of fluorescence. Preceding workers seldom focused on the detailed procedure for the quantification of fluorescence intensity and the operating parameters of CFM, which are significant for quantification of fluid mixing and reaction.

In this work, we utilized CFM to capture the mixing and reaction patterns of fluids in microdevices with overlapping channels of two kinds. These patterns clearly depicted the flow advection and the mass exchange of fluids. We propose an index, named mixing quality index(M_qi), to represent objectively the mixing quality of fluids in the devices and to express definitively the uniformity of the distribution of species in solutions. We investigated the hybridization of two complementarily labeled oligonucleotides in the devices, applying fluorescence resonance-energy transfer (FRET); the hybridization occurring in the devices was clearly displayed and quantified.

MATERIALS AND METHODS

Device descriptions

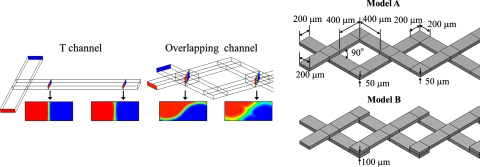
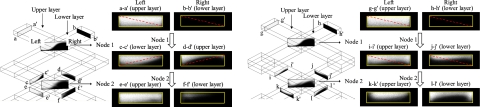
The characteristically small dimensions of microfluidic devices signify that fluids are characterized by a small Reynolds number; the mixing of fluids restricted to molecular diffusion is thus sluggish, and the structural design of channels in these devices is consequently significant to enhance fluid mixing. Through the designed configuration and structure of the channels, a general means to improve microfluidic mixing comprises of mechanisms involving chaotic advection,^{17, 34, 37} split-and-recombination (SAR),^{22, 38, 39} and other actions involving flow instability⁴⁰ and hydrodynamic focusing.⁴¹ Ismagilov et al.⁴² invented a device with overlapping channels as a tunable switch to control the mass exchange between two orthogonal flows based on the aspect ratio of the channels. Wang and Yang⁴³ designed overlapping channels with herringbone grooves to achieve the rapid mixing of fluids. For this purpose, the node (or confluence) of the overlapping channels not only generates a mass exchange of fluids but also induces effects involving SAR and chaotic advection for fluid mixing. The material interface between fluids in overlapping channels is larger than that in a T-shaped channel [Fig. 1a]. The nodes of channels have a major influence on flow mixing. We therefore analyzed the overlapping channels of two kinds—models A and B, which possess diverse overlapping styles. Figure 1b shows their detailed dimensions.

Figure 1.

Device description. (a) Schematic representation of an interface in an overlapping flow. (b) Configuration of the devices, models A and B.

Numerical simulation

Commercial software (CFD-ACE+, CFD Research Corp., USA) was adopted to simulate the steady fluidic system in the devices. To curtail the solving period and to ensure the reliability of the results, we adopted a cubic mesh with length of 5 μm, of which the mesh independence was evaluated. The physical properties of water were assumed to conform to these parameters: densityρ=997 kg m⁻³, diffusivityD=10⁻¹⁰ m² s⁻¹, and viscosityμ=8.55×10⁻⁴ kg m⁻¹ s⁻¹. To minimize numerical diffusion, the second-order scheme combined a central scheme with upwind for spatial differencing based on the work of Yang et al.⁴⁴

Microfabrication

Polydimethyl siloxane (PDMS) microdevices were fabricated according to a procedure described elsewhere.²² In summary, a silicon wafer containing a thick photoresist (SU-8, MicroChem) relief structure complementary to the designed microchannels was manufactured with a standard photolithographic method. The devices were composed of two PDMS layers with the same structural design; the layers were made on casting a mixture (10:1 by mass) of PDMS precursor and curing agent (Sylgard 184, Dow Corning) on a silicon mold and then curing the mixture at 80 °C for at least 2 h; after PDMS layers solidified, they were peeled off from the mold. These layers were activated with an oxygen-plasma treatment and then sealed. During that sealing, the layers were aligned with each other; methanol served as a lubricant to facilitate the assembly of the devices.

Experiments

One inflow was a fluorophore solution containing a 20-mer adenine sequence of oligonucleotide modified with 5′-FAM (6-carboxy-fluorescein, λ_ex|λ_em=495|521 nm) (10 μM, MDBio Inc., Taiwan). The other inflow was a buffer solution (phosphate-buffered saline, pH=7.4). All experiments were conducted with flow driven by pressure generated with a syringe pump (KDS220 syringe pump, KD Scientific, Inc.). The rates of volumetric flow were controlled through the settings of the syringe pump (2 and 10 μl min⁻¹).

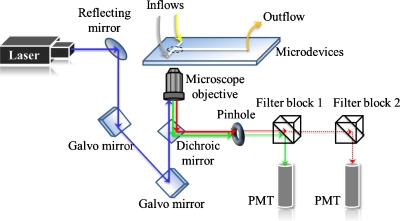
The 3D mixing patterns of fluids in the devices were visualized with a confocal microscope (Nikon A1R). All optical measurements were performed at 23 °C under ambient conditions; an argon ion laser (wavelength: 488 nm) served as the excitation source. A schema of the light path appears in Fig. 2. The excitation light passed an objective lens (Plan Apochromat VC 20×, NA=0.75) to illuminate the sample solution within the channels; the entire emitted light was collected with the same objective lens and then passed a dichroic mirror (405∕488) that excluded light at 488 nm. The emission then passed through a pinhole (diameter: 12.8 μm) to eliminate some stray light, and a filter (band pass: 500–550 nm) was inserted in filter block 1; the refined light was detected eventually with a photomultiplier tube (PMT).

Figure 2.

Schematic diagram of the confocal-fluorescence system.

The 3D images were formed on stacking a series of XY images, each of which was captured in a separate Z location through galvano-scanning. The scanning resolution in the XY plane was 1024×1024 and that in the XZ plane was 1024×100. The resolving power of the XY plane was estimated to be 0.63 μm; the thickness of an optical slice was chosen to be 1.8 μm. All projection of images was processed with a commercial software (NIS-ELEMENTS AR, Nikon, Japan).

QUANTIFICATION OF MIXING

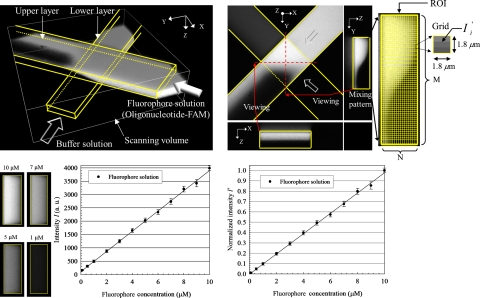
For quantification of mixing of fluids in a microdevice, we tracked a specific solution of a fluorophore (FAM-labeled oligonucleotide) with the confocal-fluorescence microscope. A 3D reconstructed image depicts the flow structure of fluids captured at the first node of the device, as shown in Fig. 3a. A buffer solution was injected into the channel from one inlet; the fluorophore solution was injected from the other inlet. The fluids were compelled to exchange their mass at the node due to the channel structures. Figure 3b shows varied images; the top view is a section image in the middle of the channel depth. The mixing pattern is observed from a side view along the negative X-direction; the quantitative method to determine the mixing patterns is described as follows.

Figure 3.

Scheme for mixing quantification. (a) 3D reconstructed confocal image, (b) method of mixing quantification for mixing patterns, (c) calibration curve of intensity and fluorophore concentration∕μM, and (d) normalized calibration curve.

We initially established a calibration line to correlate the intensity of emitted light with the concentration of the fluorophore solutions, with fixed operating parameters—pinhole size, laser power, and detector gain (parameters were optimized). Fluorophore solutions with varied concentrations (0.1–10 μM) were individually injected into the devices from both inlets. We captured the cross-sectional images and evaluated the corresponding intensity; the cross-sectional images for cases 10, 7, 5, and 1 μM are exhibited in Fig. 3c (left). The calibration curve between intensity and concentration is plotted in Fig. 3c (right); the curve is linear, which facilitates a reliable quantification. Because of the background noise, the minimum value of intensity is not 0 but 100. The calibration curve was normalized according to the following equation [see Fig. 3d]:

$$I^{\prime }=\frac{\overline{I}-I_{\text{min}}}{I_{\text{max}}-I_{\text{min}}},$$ (1)

where I_min indicates the intensity of the background and I_max is the maximum intensity.

We focused our attention on the mixing pattern in a particular region [the region of interest (ROI), see Fig. 3b (right)], which was divided into M×N grids; the grid was a square with length of 1.8 μm. Because the intensity contour of the mixing pattern implies the distribution of species (fluorophore), we can measure the species concentration in each grid in the ROI upon assessing the magnitude of the normalized intensity. For this purpose, we define a mixing quality index, M_qi, to quantify a mixing pattern according to this equation,

$$M_{qi}=1-\frac{{\int }_A\left|I_i^{\prime }-I_{\infty }^{\prime }\right|dA}{{\int }_A\left|I_{\left(0\right)i}^{\prime }-I_{\infty }^{\prime }\right|dA}=1-\frac{\sqrt{\frac{1}{\text{M}\times \text{N}}{\sum }_{i=1}^{\text{M}\times \text{N}}{\left(I_i^{\prime }-I_{\infty }^{\prime }\right)}^2}}{\sqrt{\frac{1}{\text{M}\times \text{N}}{\sum }_{i=1}^{\text{M}\times \text{N}}{\left(I_{\left(0\right)i}^{\prime }-I_{\infty }^{\prime }\right)}^2}},$$ (2)

where $I_i^{\prime }$ is the normalized intensity of grid i in the region of interest of a given mixing pattern, $I_{\infty }^{\prime }$ is the normalized intensity of fully mixed fluids, i.e., the normalized intensity of 5 μM, $I_{\left(0\right)i}^{\prime }$ is the normalized intensity of grid i at the initiation (unmixed status).

RESULTS AND DISCUSSION

Validation using a T-shaped channel

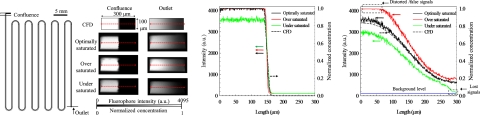
In applying a confocal-fluorescence microscope to a micromixing device, most researchers using this technique achieved only a limited demonstration of the quantitative nature of devices because of a lack of a standard for fluorescence quantification. We explain below the importance of parameter setting for a satisfactory quantification. To validate the reliability of the confocal-fluorescence microscope, we adopted a T-shaped channel as a test object; this channel is known to be a simple model and its simulation results commonly serve as a control. Its configuration (total length of 30 cm, height of 100 μm, and width of 300 μm for cross section) is shown in Fig. 4a (left).

Figure 4.

Validation of a confocal-fluorescence system. (a) Configuration of T-shaped channel (left) and mixing patterns of experimental (confocal) and simulation results at confluence and outlet (right); intensity distributions at the confluence (b) and the outlet (c).

To measure the mixing patterns with high quality and to prevent samples from photobleaching, we maintained a fixed pinhole size and laser power. Varying the detector gain affects the fluorescence signal and further influences the mixing patterns upon quantification. For the detection power of the PMT, each pixel in the 12-bit image was assigned an intensity value between 0 (black) and 4095 (white), which is particularly beneficial for image quantification because of a large gradation (4096 gray levels). We compared the mixing patterns in three cases under varied conditions; specifically, optimally, over-, and undersaturated conditions. The optimally saturated condition signifies that an appropriate setting of the detector gain generates a maximum intensity approximately 4095; the oversaturated condition signifies that an excessive gain induces most intensity to be saturated at 4095; and in the undersaturated condition, a small detector gain would cause a maximum intensity less than 4095. The mixing patterns at the confluence and the outlet for these cases and the CFD results are, respectively, shown in Fig. 4a (right). For all cases, the interface between the two fluids at the cross sections of confluence was distinct without blending. On flowing downstream, the fluids were driven to mix through molecular diffusion.

The intensity curves along the red dotted lines in the mixing patterns are plotted in Figs. 4b, 4c. For the intensity distribution at the confluence [Fig. 4b], the intensity of three cases is distributed mainly in the left-half cross sections, which is analogous to the results of simulation (black dotted line), whereas the undersaturated case displays a small distribution of intensity. In the middle of the cross sections, the sharply decreased intensity proves that the interface between the fluids is clear. The diversity of the intensity curves of the cases at the outlet is evident [Fig. 4c]. A comparison of the experimental curves with CFD results indicates that the curve of the optimally saturated case fits perfectly the CFD results. For the oversaturated case, some regional saturation of the curve emerges to distort the intensity curve [Fig. 4c (upper left)]; these distorted signals are a severe weakness for the quantification. For the undersaturated case, the intensity curve is not distorted but is partly lacking [Fig. 4c (lower right)]. Some signal is as small as the background, precluding identification with the PMT; such a signal might be lost.

The validation test shows that an appropriate setting of parameters of the confocal-fluorescence microscope is significant for the mixing patterns, especially for quantitative analysis. To avoid distortion and loss of signals, the detection range of the PMT must be exploited. We suggest accordingly a criterion to acquire an appropriate mixing pattern.

Mass exchange and flow advection

The mass exchange of fluids in the devices, models A and B, was visualized with the confocal-fluorescence microscope, as shown in Fig. 5. On flowing through the nodes, the fluids in the upper or lower layer were divided into two mass groups with dotted lines (see the cross sections in Fig. 5). The mass group below the dotted line in the upper layer merged with the mass group below that in the lower layer; the mass group above the dotted line in the upper layer merged with the mass group above that in the lower layer.

Figure 5.

Mass exchange of devices: (a) model A and (b) model B.

For model A, the fluids of the upper layer streamed into the left of node 1, while the fluids of the lower layer streamed into the right of node 1; after passing node 1, the fluids of the upper layer were deflected into the right of node 2, while the other fluids of the lower layer were deflected into the left of node 2. For model B, in contrast, the fluids of the upper layer invariably streamed into the left of the nodes; the fluids of the lower layer streamed correspondingly into the right of the nodes. The mass exchange of the fluids at node 1 of models A and B was the same, but differed greatly at node 2; compare the orientation of the dotted lines in cross sections c-c^′, d-d^′, i-i^′, and j-j^′. After the fluids traversed node 2, their interface (see cross sections k-k^′ and l-l^′) was still distorted for model B, but the interface (see cross sections e-e^′ and f-f^′) dissipated for model A. The disparate mass exchange between models A and B resulted from the diverse modes of overlap of the channels. The greater was the duration of the interface of the fluids holding in the devices, the more effective was the mixing of the fluids.

The mixing patterns for models A and B at various nodes are shown in Figs. 6a, 6b, respectively. The mixing patterns recorded with the confocal-fluorescence microscope are nearly identical to those of the CFD results. For model A, the fluids flowing through node 1 appeared to undergo a clockwise rotation, whereas on flowing through the next node (node 2) they appeared to undergo a counterclockwise rotation because of the alternating overlap of the channels [Fig. 6a]. The clockwise rotation was balanced by the counterclockwise rotation so that the mixing patterns, from upstream to downstream, of model A were almost unchanged; the mixing of fluids was driven by diffusion at the interface. In contrast to model A, the fluids flowing through each node in model B displayed a clockwise rotation; a sequence of clockwise rotations effected a rotating flow within the flow field of model B [Fig. 6b]. This rotating flow caused a deformation of the interface involving stretching and twisting; during this deformation, the mixing of fluids was greatly enhanced.

Figure 6.

Flow advection of devices: (a) model A and (b) model B.

Quantification of mixing patterns

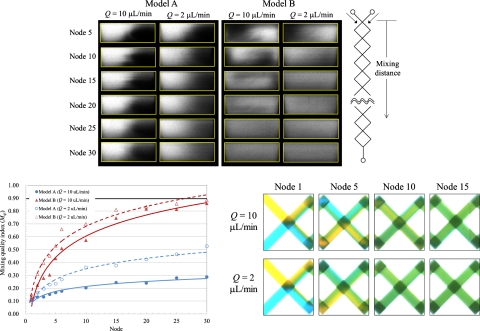
Figure 7a shows various mixing patterns of models A and B for volumetric flow rates Q=10 and 2 μl min⁻¹. The interface between the fluids displays a curved line in model A; the line gradually blurs from the upstream to the downstream channel because of fluid diffusion. At node 30, the mixing patterns show that the fluids were still poorly mixed. For model B, the deformation of the interface between the fluids induced from the rotating flow progressed downstream so that effective mixing of the fluids was achieved rapidly. The fluids reach uniformly mixed at node 25 for Q=10 μl min⁻¹ and at node 30 for Q=2 μl min⁻¹.

Figure 7.

Mixing quantification of the devices at Q=2 and 10 μl∕min. (a) Mixing patterns of the devices at various nodes, (b) relation between the mixing quality index (M_qi) and the mixing distance (node), and (c) dye-liquor blending test in the device, model B.

According to Eqs. 1, 2, we depict the relation between the mixing quality index (M_qi) and the location in Fig. 7b for quantitative analysis. As expected, M_qiincreased with downstream distance for all test cases. The regression lines are drawn for the test points; the values of squared parameter correlation coefficient R² exceed 0.96 in all cases. As a mixing length, we adopted a distance (longitudinal direction) through which the fluids flowed to attainM_qi=0.9. For model A, the mixing lengths cannot be estimated for Q=10 and 2 μl min⁻¹, whereas for model B, the mixing lengths are 24.4 mm for Q=10 μl min⁻¹ and 20.8 mm forQ=2 μl min⁻¹. The mixing quality of the fluids for Q=2 μl min⁻¹ was superior to that for Q=10 μl min⁻¹ for both models A and B, because in the cases of Q=2 and 10 μl min⁻¹, the mixing of fluids was dominated by the diffusion-mixing region; the smaller volumetric rate implies a greater duration for the fluid to pass through the channels. The mixing of the fluids for Q=2 μl min⁻¹ was therefore uniform at a decreased length because of the extended duration.

As the dye-liquor test performed with an OM typically shows a superimposition of two distinct fluids, the mixing quantification of the fluids is accordingly overestimated. Even though the dye-liquor test has widespread use to demonstrate the performance of a device for fluid mixing, it might be suitable for a simple device without a complicated structure but futile for verifying a device with overlapping channels. We therefore performed a test in which the mixing of two fluid streams (distinguished with yellow and blue dye solutions) in the devices was monitored with an OM. The dye solutions were composed of food dye (0.5% by mass) in de-ionized water; the diffusivity is about 10⁻¹⁰ m² s⁻¹; the density is 1 kg l⁻¹. Figure 7c shows the mixing of dye solutions in model B at Q=10 and 2 μl min⁻¹. The Reynolds number (Re) is 25 forQ=10 μl min⁻¹, whereas 5 forQ=2 μl min⁻¹; the Péclet number (Pe) is about 6000 for Q=10 μl min⁻¹ but about 1200 forQ=2 μl min⁻¹. A uniform mixing of the yellow and blue solutions produced a green hue. The mixing lengths of this test were 11.9 mm for Q=10 μl min⁻¹ and 7.6 mm forQ=2 μl min⁻¹, estimated based on the previous research.¹⁸ Because the diffusivity of the dye in de-ionized water is analogous to that of an oligonucleotide in a buffer solution, it is reasonable to compare the mixing lengths of dye solutions with those of fluorophore solutions in a device under the same hydraulic conditions. The mixing length obtained with the confocal-fluorescence microscope is greater than that estimated with the dye-liquor blending test because the confocal-fluorescence microscope does not detect superimposed fluids. The results captured with the confocal-fluorescence microscope are, without doubt, accurate. The relative discrepancy between the dye-liquor blending test and the confocal-fluorescence test in mixing lengths is large—about 100%–150%—because of overlapping flows in the devices; the 3D flow field yields a misleading judgment of the mixing length in the dye-liquor blending test. While a conventional OM is incapable of analyzing quantitatively the overlapping channels, the CFM is demonstrated to be a tool applicable to visualize the complicated and 3D flows in a microdevice.

FRET test

The FRET technique has become popular for assay protein-DNA binding,⁴⁵ to detect bacteria,⁴⁶ to diagnose DNA hybridization,⁴⁷ and to be applied in lab-on-a-chip devices.⁴⁸ FRET involves energy transfer such that an excited donor molecule radiates light that serves to excite an acceptor molecule if these molecules are conjugated, i.e., sufficiently near (typically 2–10 nm). For energy transfer to occur, the fluorescence emission of the donor must overlap the absorption spectrum of the acceptor. In this experiment, FAM (6-carboxy-fluorescein, λ_ex|λ_em=495|521 nm) and TAMRA (tetramethy-6-carboxyrhodamine; λ_ex|λ_em=560|583 nm) were chosen as donor and acceptor, respectively; they constituted a FRET pair. Two complementary oligonucleotides—FRET- DNA₁ and FRET- DNA₂—were adopted to execute the FRET test; FRET- DNA₁ labeled with FAM has a sequence 5′-CAGGTCAGGT-FAM-3′ (5 μM, MDBio Inc., Taiwan); FRET- DNA₂ labeled with TAMRA has a sequence 5′-ACCTGACCTG-TAMRA-3′ (5 μM, MDBio Inc., Taiwan); their melting point is 32 °C.

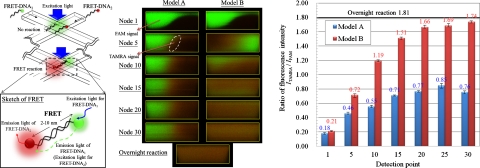
We injected the two solutions containing FRET- DNA₁ and FRET- DNA₂, respectively, into the devices, as shown in Fig. 8a (left). A laser emitting at 488 nm served as the excitation source. The signals were filtered and simultaneously detected with two individual PMT; one PMT received the signal from FAM, the other from TAMRA; the signal of FAM displayed green, while that of TAMRA displayed red. Figure 8a (right) shows cross-sectional images captured in various nodes of the devices. At the first node of the devices, the laser excited mostly the donor and the signal of FAM was thus bright and green; the signal of TAMRA appeared faint. For model A, the signal of TAMRA initially appeared at the interface of the DNA solutions (see the reaction pattern at node 5) and then slowly spread on flowing downstream. The FRET reaction of FRET- DNA₁ and FRET- DNA₂ hence occurred at the interface of the solutions and then tardily progressed downstream based on the diffusion of only the interface; the energy emitted from FAM was partially absorbed by TAMRA, inducing emission from TAMRA. For model B, on flowing downstream, the signal of FAM declined and the signal of TAMRA shone remarkably. The reaction pattern at node 30 shows uniform signals. The two segments of the oligonucleotide thus rapidly blended and reacted because of the rotating flow in model B.

Figure 8.

FRET reaction of two complementary DNA oligonucleotides in the devices. (a) Fluorescence distribution of two oligonucleotides at the various cross sections of the devices(Q=2 μl∕min). (b) Ratio of fluorescence intensity(I_TAMRA∕I_FAM).

The results of FRET between the two fluorochromes were quantified as shown in Fig. 8b. We estimated the ratio I_TAMRA∕I_FAM of fluorescence intensity and composed a relation between the intensity and the detection points. The ratio gradually increased along the downstream channel, which demonstrated that the hybridization of the complementary oligonucleotides progressed and that energy continuously transformed from FAM to TAMRA as the fluids passed through the devices. For model A, the intensity ratio increased from 0.18 at node 1 to 0.76 at node 30, whereas that for model B from 0.21 to 1.74, resulting from the disparate mixing mechanisms of the devices. With regard to model B, the intensity ratio appears to increment in two stages: the first stage involved mixing and reaction that causes the intensity ratio to increase from 0.21 to 1.66 (from node 1 to node 20); the increase of the intensity ratio is hence steep; the second stage showed a gently increased ratio of intensity from 1.66 to 1.74 (from node 20 to node 30). The FRET- DNA₁ and FRET- DNA₂ thus hybridized in a nearly balanced condition; the rate of hybridization is hence large during the first stage but decreases upon approaching the equilibrium point.

We performed also a static hybridization of FRET- DNA₁ and FRET- DNA₂ in a test tube; to ensure their full hybridization, the mixed oligonucleotides in buffer solutions underwent denaturation at a temperature (60 °C) greater than the melting point for 6 h and then reaction overnight and hybridization at 4 °C for 16 h. The solutions containing the fully reacted oligonucleotides were injected into model B and captured as shown in Fig. 8a (right below). We compared the results of DNA solutions reacting in model B with that of the overnight reaction. The intensity ratio for the overnight reaction regarded as a control was 1.81, whereas that for reaction of the DNA solutions at node 30 of model B was 1.74. Even though this difference in the intensity ratios is small, we supposed that FRET- DNA₁ and FRET- DNA₂ at node 30 was almost completely hybridized. With an increased length of the microchannel, we expect that the hybridization of FRET- DNA₁ and FRET- DNA₂ would eventually attain equilibrium. The reaction period of the DNA solutions can be also estimated through this approach. The reaction period (s) is derived from a volume∕m⁻³, which flows through to achieve 90% of the complete reaction (overnight reaction), divided by a volumetric flow rate∕m³ s⁻¹. In this case, the reaction period of the DNA solutions in model B is hence calculated to be 4.5–5.5 s.

These results show that the probability of hybridization of two complementary oligonucleotides in the devices was improved, through the structural effect of the microchannel on the flow motion, so to facilitate the progress of the hybridization and FRET reaction. With this FRET test, we verified that the CFM has the potential to diagnose quantitatively a biochemical reaction occurring in a microchannel device.

CONCLUSION

We developed an approach to quantify the microfluidic mixing in microchannel devices with a CFM. A mixing pattern to represent the mixing quality of fluids was captured at high resolution with this technique. To quantify the mixing patterns satisfactorily, we performed a validation test and so demonstrated the significance of the parameter settings for this technique. An optimized setting of the parameters, called an optimally saturated condition, is required to prevent the detectable signal from being distorted and lost; the utilization of the detection limit of PMT is hence crucially significant. We utilized devices of two kinds with diverse modes of overlapping channels (models A and B); the rotating flows, mass exchange, and mixing patterns of fluids were explored in those devices with the CFM. We propose a mixing quality index (M_qi) to quantify the uniformity of mixing of fluids in the mixing patterns; a mixing length is defined as a distance through which fluids achieveM_qi=0.9. The results demonstrate that the accuracy of the mixing length measured with the CFM is superior to that estimated from a customary method in the dye-liquor blending test; the relative difference in the mixing lengths between the two methods is 100%–150%. We introduced a FRET reaction of two complementary oligonucleotides, one labeled FAM as donor and another labeled TAMRA as acceptor, in solutions in the devices to test this approach. The results show that the ratio I_TAMRA∕I_FAM of fluorescence intensity evaluated with this approach increased with flowing distance, which verifies that energy transfer between the donor and the acceptor continued as the fluids flowed downstream. We estimated the reaction period of hybridization of two complementary oligonucleotides in model B to be about 4.5–5.5 s. This approach is qualified not only to serve for inspection of microfluidic mixing but also to diagnose biochemical reactions and assays on a chip and even to achieve a real-time monitor; this approach will yield unprecedented insight into the quantification of mixing and reaction in microfluidic devices and LOC systems.