Abstract
Purpose: The purpose of this work is twofold: First, to characterize the artifacts occurring in helical 4D-CT imaging; second, to propose a method that can automatically identify the artifacts in 4D-CT images. The authors have designed a process that can automatically identify the artifacts in 4D-CT images, which may be invaluable in quantifying the quality of 4D-CT images and reducing the artifacts from the reconstructed images on a large dataset.
Methods: Given two adjacent stacks obtained from the same respiration phase, the authors determine if there are artifacts between them. The proposed method uses a “bridge” stack strategy to connect the two stacks. Using normalized cross correlation convolution (NCCC), the two stacks are mapped to the bridge stack and the best matching positions can be located. Using this position information, the authors can then determine if there are artifacts between the two stacks. By combining the matching positions with NCCC values, the performance can be improved.
Results: To validate the method, three expert observers independently labeled over 600 stacks on five patients. The results confirmed that high performance was obtained using the proposed method. The average sensitivity was about 0.87 and the average specificity was 0.82. The proposed method also outperformed the method of using respiratory signal (sensitivity increased from 0.50 to 0.87 and specificity increased from 0.70 to 0.82).
Conclusions: This study shows that the spatial artifacts during 4D-CT imaging are characterized and can be located automatically by the proposed method. The method is relatively simple but effective. It provides a way to evaluate the artifacts more objectively and accurately. The reported approach has promising potential for automatically identifying the types and frequency of artifacts on large scale 4D-CT image dataset.
Keywords: 4D-CT, artifacts, normalized cross correlation convolution
INTRODUCTION
The spatial accuracy of reconstructed medical images is critically important in radiation therapy, both for tumors and for the surrounding normal tissue. Respiratory motion can be a major source of positional and temporal uncertainty in the thorax and abdomen, causing a miss with significant dosimetric consequences. Four dimensional computed tomography (4D-CT) provides a way of reducing the uncertainties caused by respiratory motion. With 4D-CT images, one can assess the three dimensional (3D) position of the tumor and avoidance structures at the specified phases of the respiratory cycle and directly incorporate that information into treatment planning.1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17
4D-CT image sets are a sequence of 3D-CT datasets indexed by respiratory phase, acquired using sorting based on the respiration amplitude or the phase of fan- or cone-beam images.18, 19 Such methods can be acquired for sequential table positions, also termed the cine acquisition method,20, 21, 22 or by “helical” scanning, also called spiral acquisition,23, 24, 25, 26, 27 and the differences between these two methods is well-documented.21 Approaches to 4D-CT gating include retrospective gating17, 20, 24, 26, 28, 29 and prospective gating30 and commonly applied acquisition methods include phase-4, 24, 26, 28, 31 and amplitude-based sorting.29, 32, 33, 34 However, all the current 4D-CT acquisition and reconstruction methods require multiple cycles of patient respiration, which frequently lead to spatial artifacts. A recent study showed these artifacts occurred with an alarmingly high frequency and spatial magnitude.9
Furthermore, there were several important studies on strategies for improving 4D-CT including (1) using breathing training to improve the respiratory regularity that could reduce the artifacts,35, 36, 37 (2) improved sorting,6, 32, 33, 38, 39, 40, 41 (3) using internal anatomical features instead of external surrogates to improve the image quality,42, 43 and (4) postscan image processing.44, 45, 46, 47, 48, 49 Although these methods propose to reduce artifacts in 4D-CT image data, no tool currently exists to allow clinicians to efficiently evaluate the integrity of the 4D-CT scans or researchers to compare the effectiveness of corrective strategies. To date, this has been accomplished by human observation only,9 which is subjective and variable, making the evaluation of large numbers of datasets unfeasible. There were several methods used to evaluate the quality of 4D-CT artifacts.46, 47 One method used the mean squared gray value difference between two adjacent slices as a metric to measure the magnitude of artifacts.46 Another method first predicted the slices between two adjacent stacks. The discontinuity measure was computed as the distance between the predictions and the actual slices from the adjacent stack.47 However, both methods identified the artifacts poorly because their metrics can be affected by artifacts and also by anatomical changes. Additionally, both methods were proposed to measure discontinuity and were not intended as a tool to identify the artifacts.
Since artifacts in 4D-CT have a high frequency,9 automatically identifying them in 4D-CT images is very useful, especially when using a large scale dataset. Furthermore, accurate identification of spatial artifacts is a prerequisite for correcting aberrant sections of a dataset. Based on this reasoning, we present a method to automatically identify and evaluate the spatial artifacts within 4D-CT scans, providing indicators for correction strategies as well as establishing a clinical means to quantify the quality of the reconstructed 4D-CT images.
MATERIALS AND METHOD
Definition of terms
4D-CT image data consists of a series of multiple 3D-CT volume datasets acquired at different respiratory phases. Each phase-specific 3D-CT dataset is made of several groups of 2D images (stacks), where each stack is reconstructed from each cycle of respiration during acquisition. For the purpose of this study, we define the following terms:
Slice: A 2D CT image denoted as I. The pixel value at location (x,y) is denoted as I(x,y).
Stack: Sequence slices acquired at one respiratory cycle occurring at a certain respiratory phase denoted as S(i,j), where i is the respiratory phase index and j is the respiratory cycle index. A 2D slice in S(i,j) is denoted as I[p], i.e., I[p]∊S(i,j), where p denotes the pth slice in S(i,j).
3D-CT: Sequence stacks that cover the full imaged patient anatomy at a certain respiratory phase denoted as{S(i,1),S(i,2),…,S(i,N−1),S(i,N)}, where N is the number of respiratory cycles.
4D-CT: Series of 3D-CT volume datasets acquired at different respiratory phases, which can be denoted as {{S(1,1),S(1,2),…,S(1,N−1),S(1,N)},{S(2,1), S(2,2),…,S(2,N−1),S(2,N)},…,{S(K,1), S(K,2),…,S(K,N−1),S(K,N)}} , where K is the number of respiratory phases and N denotes the number of respiratory cycles.
The number of stacks required at each respiratory phase to construct the 3D-CT volume is equivalent to the number of respiratory cycles needed. This is a function of the anatomical length of the scan, the patient’s respiratory rate, and the translation speed of the imaging couch. Each stack S(i,j) is indexed by its respiratory phase i and the respiratory cycle j. Two consecutive stacks of the same phase [i.e., S(i,j) and S(i,j+1)] have continuous couch positions produced by adjacent respiratory cycles.
Image acquisition
All patients were imaged in accordance with a clinical trail approved by the Institutional Review Board. Patients were scanned using a 40-slice CT scanner (Siemens Biograph, Hoffman Estate, IL) operating in helical mode. Imaging parameters were 120 kVp, 2.0 mm slice thickness, 1.2 mm collimator, and B30F medium smooth kernel reconstruction filter. Acquisition occurred with a pitch of 0.1 and either a tube rotation speed of 500 ms∕rotation (requiring each respiratory cycle to not exceed 5 s) or 1000 ms∕rotation (for respiratory cycles to not exceed 10 s). Since each image was reconstructed with 180° rotation, the temporal resolutions of the two tube rotation speed scans were 250 and 500 ms, respectively. The amplitude of the respiratory motion was monitored using a strain gauge belt with a pressure sensor (Anzai, Tokyo, Japan). The respiratory phase at each time point was computed by the scanner console software via renormalization of each respiratory cycle by the cycle-specific maxima and minima. The patients were allowed to breathe freely while listening to musical-audio instruction. The pace of the musical-audio instruction was determined for each patient during a 10 min respiratory training session that preceded the 4D-CT scan.
Characterization of 4D-CT artifacts
Siemens BIOGRAPH 40 software was used to sort raw 4D-CT images into respiratory phase-based bins of 4D-CT images. The Anzai strain gauge belt utilizes a pressure sensor to measure changes in strain during respiration. The amplitude of the strain signal is adjusted for each data point relative to the maximum and minimum inflection points for each cycle of respiration. The system then calculates a relative amplitude-based phase at each point of a respiratory trace, where 0% corresponds to end expiration and 100% corresponds to peak inspiration. The application reads raw 4D-CT projection data as well as the normalized respiration trace and assigns a phase to each CT slice according to the temporal correlation between the trace and CT data acquisition. The reconstructed CT slices are sorted into a dataset corresponding to their amplitude-based respiratory phase: Either 0%, 100%, or one of a series of four phases during the inhale and exhale sides of the respiratory trace (20%, 40%, 60%, and 80%).
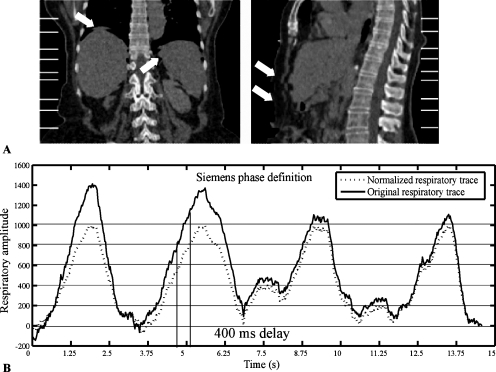
Image artifacts caused by irregular breathing are possible during helical 4D respiratory-gated CT acquisition; an example is shown in Fig. 1a. Obvious changes occur with the large variations in patient respiration shown in Fig. 1b, although even subtle changes can create a phase shift following the normalization process, as shown in Fig. 1b. These artifacts compromise image quality and introduce spatial distortions that reduce the spatial accuracy of the reconstructed image, resulting in inaccurate radiation treatment planning. For this study, we utilized ten phases for each respiration cycle consistent with the vendor’s nomenclature—inhalation: 20%, 40%, 60%, 80%, and 100%; exhalation: 80%, 60%, 40%, 20%, and 0%.
Figure 1.
Image artifacts due to the irregular breathing. (a) The white lines show the stack locations and the arrows show the artifacts. (b) Respiratory cycle-specific normalization (dashed line) and original (solid line) respiratory trace. There are about 400 ms delay between the original respiratory trace and the normalized respiratory trace, which may cause large artifacts due to anatomy motion.
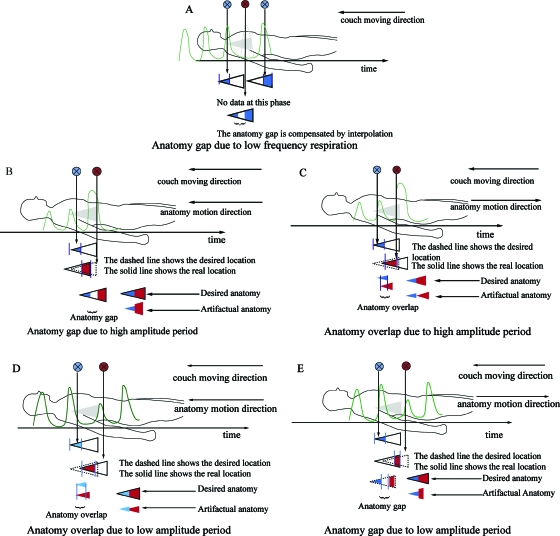
Our method is designed to identify spatial distortions within each CT dataset. Even with contiguous couch positions, anatomical structures that move with respiration may have artifacts, particularly when variations in respiration occur during image acquisition. We have categorized three types of artifact sources: Low frequency respiration, high amplitude cycle, and low amplitude cycle. Low frequency respiration means longer respiration cycles, which result in the absence of some respiration phases. If the respiration cycles are longer than the collimator width divided by the table speed, objects that pass through the collimator field of view will not be imaged at every phase. In this instance an anatomical loss in the dataset will occur, as shown in Fig. 2a. The anatomical loss resulting from the missing data is compensated for by interpolation, which leads to “blurring.” If the amplitude cycle is too low or too high, either an anatomy gap or an anatomy overlap may occur. The anatomy gap is different from the anatomy loss caused by low frequency respiration in that images are acquired during the specified phase, but the mobile anatomy is not within the collimator field of view due to the high∕low amplitude cycle. The anatomy overlap is similar to the anatomy gap, but caused when the mobile anatomy reappears within the colli-mator field of view due to the high∕low amplitude cycle. Figure 2 provides a graphical rendition. The main factors under consideration here are the irregular respiratory cycles and the different respiratory motion directions.
Figure 2.
Example of the problems due to irregular respiration during 4D-CT imaging. (a) Anatomy gap due to low frequency respiration. In this case, the anatomy gap is not imaged and the missing data is compensated by interpolation. (b) Anatomy gap under high respiration cycle. The couch and anatomy motion are the same. (c) Anatomy overlap under high respiration cycle. The couch moving direction is opposite to the anatomy motion. (d) Anatomy overlap under low respiration cycle. The couch and anatomy motion are the same. (e) Anatomy gap under low respiration cycle. The couch moving direction is opposite to the anatomy motion.
The oversampling of anatomy during the 4D acquisition process produces image stacks from consecutive cycles with slices that overlie each other. The number of overlying slices depends on the pitch and the patient’s respiration frequency; the vendor application removes slices of duplicated table positions(z). As a result, the total length Wj of the image stack corresponding to the respiration cycle j is always smaller than the maximum length Wmax, which can potentially be reconstructed from the available raw data. The total length is typically the distance L traveled by the couch table between the two consecutive cycles, while the maximum length Wmax is close to the total nominal detector length D (the exact value is slightly less and depends on the spiral interpolation algorithm used for image reconstruction). Therefore, the length of each stack, Wj=pitch×D×cycle time∕rot time. Clinically, when the patient’s respiration pattern (cycle time) varies, the value of Wj will vary but remain below Wmax as long as lengthy pauses in respiration do not occur.
Description of the bridge stack method
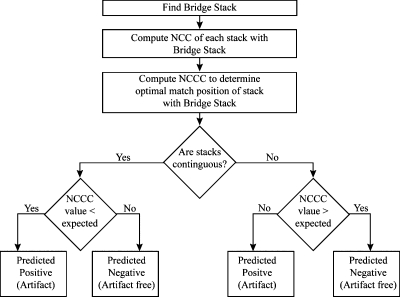
The proposed method identifies artifacts between two stacks S(i,j) and S(i,j+1) using a “bridge stack.” The bridge stack comes from a different phase (i) but contains slices in common with both stacks S(i,j) andS(i,j+1). The quality of each stack’s alignment with the bridge stack is quantified by normalized cross correlation (NCC) for each possible alignment position. The optimal matching positions are determined using normalized cross correlation convolution (NCCC) and used to identify the artifacts between two stacks. Finally, the algorithm determines the presence of an artifact based on evaluating both the (1) proximity of the matching positions on the bridge stack for S(i,j) and S(i,j+1) and (2) any deviation of NCCC values from those expected. A flow diagram detailing the process is provided in Fig. 3, while each element of the proposed method is described below.
Figure 3.
The flow diagram for the proposed algorithm to predict the presence of image artifacts within 4D-CT scanned images.
Bridge stacks to benchmark
Two consecutive stacks S(i,j) and S(i,j+1) are continuous in terms of their couch positions, but they may have artifacts (overlaps, gaps, or blurring). To identify the presence of spatial distortions between the stacks, a single stack that contains slices from both stacks (a bridge stack Sb) is needed. A bridge stack Sb(k,t) is selected to connect two stacks S(i,j) and S(i,j+1) and the bridge stack should have overlaps with S(i,j) and S(i,j+1). If the stack that has the largest number of overlapping slices with both S(i,j) and S(i,j+1) is to be selected as the bridge stack, it will occur at half the time between j and j+1. Supposing S(i,j) is acquired at time T(i,j) and S(i,j+1) is acquired at time T(i,j+1), we should choose the bridge stack, which is acquired at T(i,j)+(T(i,j+1)−T(i,j))∕2. Because human respiratory patterns are irregular and asymmetric, the stack acquired at the time nearest to T(i,j)+(T(i,j+1)−T(i,j))∕2 is selected. Then, let S(i,j) and S(i,j+1) come from the ith phase, the phase k and cycle t of the bridge stack are computed as
| (1) |
Finding the best position on bridge stack by normalized cross correlation
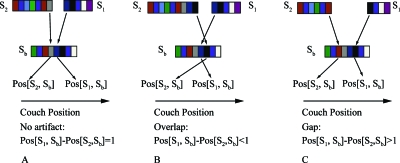
The second step of our method is to compare how well the image slices I(x,y) of stacks S(i,j) and S(i,j+1) match up with those from the bridge stack Sb(k,t), as shown conceptually in Fig. 4. At each position, we compute the average NCC value on the overlapping slices. The best position for a stack corresponds to the one with the largest value. Since this process is similar to the signal convolution, we call it NCCC.
Figure 4.
The use of a bridge stack Sb to connect image stacks S1 and S2. (a) No artifacts are present when S1 is matched to Sb contiguous with the position where S2 is matched to Sb. (b) Overlap between slices of S1 and S2 produces artifacts, as do (c) gaps between S1 and S2.
The NCC value between two 2D image slices is defined as
| (2) |
where μI=(1∕N)∑x,yI(x,y), μI′=(1∕N)∑x,yI′(x,y), and N is the number of pixels in I and I′. The NCC value varies between a value of 0.0 and 1.0, where a value of 1.0 corresponds to perfect image similarity.
Supposing S(i,j) consists of m 2D image slices, S(i,j+1)consists of n 2D image slices, and Sb(k,t) consists of l 2D image slices. The NCCC between S(i,j) and Sb(k,t) [S(i,j+1) and Sb(k,t)] is defined as the vector of length m+l−1 (n+l−1), whose pth element is computed using
| 3 |
| 4 |
The NCCC value also varies between a value of 0.0 and 1.0, where a value of 1.0 corresponds to the perfect image similarity. The position corresponding to the largest NCCC value is the best matching position. Since the best position locates the last slice of S(i,j) or S(i,j+1), we need to move it to the first slice position for S(i,j). The best position between S(i,j) and Sb(k,t), S(i,j+1) and Sb(k,t) is computed as follows:
| (5) |
| (6) |
If the two stacks are beyond one slice of being contiguous, there is a strong probability they contain an artifact, that is,
| (7) |
When the two stacks are contiguous [e.g., Pos[S1,Sb]−Pos[S2,Sb]=1, as shown in Fig. 4a], the images are likely artifact-free. If the two stacks overlap, then Pos[S1,Sb]−Pos[S2,Sb]<1 [as shown in Fig. 4b], and if there are gaps, then Pos[S1,Sb]−Pos[S2,Sb]>1 [as shown in Fig. 4c].
Evaluate optimal NCCC value
Stacks with no artifact will produce larger NCCC values than those with artifacts. Therefore, we utilize the NCCC values as an additional parameter to reduce false positive (FP) and false negative (FN) results. A true positive (TP) event exists when there are artifacts between two stacks S(i,j) and S(i,j+1), while a true negative (TN) event exists when no geometric distortions are present.
Our algorithm classifies a positive result from Eq. 7 as either TP or FP, where a FP has larger NCCC values than a TP due to greater similarity between the stacks. Conversely, a negative result from Eq. 7 is classified as either TN or FN, where a TN has higher NCCC values than a FN, again due to the greater similarity between the stacks. Practically, we established the NCCC cutoff between true and false by training two parameters, λPP and λPN. One is used to classify TP and FP and another is used to classify TN and FN.
First, 80 pairs of stacks for which ground truth had been established (Sec. 2F) were selected as training sets. For each pair of stacks S(i,j) and S(i,j+1), we obtained two NCCC values denoted as NCCC(S(i,j),Sb(k,t)) and NCCC(S(i,j+1),Sb(k,t)), which correspond to the best positions when matching the two stacks to the bridge stack. Second, stacks were grouped as predicted positive (PP) or predictive negative (PN) based on the matching positions described above [Eq. 7, Sec. 2D2], the mean μPP, μPN and the standard deviation σPP, σPN were obtained from all computed NCCC values in PP and PN groups. Finally, the parameters λPP and λPN were selected to maximize the product of the sensitivity and specificity based on the ground truth, where Eq. 8 was used if S(i,j+1) and Sb(k,t) were in PP and Eq. 9 was used if S(i,j+1) and Sb(k,t) were in PN.
For the remaining 544 stacks, we use these optimized values of λPP and λPN in Eqs. 8, 9 to identify the artifacts. This way, both the matching positions and the NCCC values are used to improve the algorithm’s performance,
| (8) |
| (9) |
The method of using respiratory signal
For the purpose of comparison with our method, we evaluated the correlation of artifacts with the amplitude of the patient’s respiration trace. Specifically, in each respiratory cycle, each stack S(i,j) is assigned a respiration amplitude denoted as v(i,j), where i is the respiratory phase index and j is the respiratory cycle index. We compute the mean μ(i) and standard deviation σ(i) for all the stacks from the same respiratory phase, where i is the respiratory phase index. Then, we use Eq. 10 to identify the artifacts, where w is a parameter to balance the sensitivity and specificity. We compared our method to this direct method in the following sections,
| (10) |
Evaluation
4D-CT datasets from five patients with known image artifacts were used in our experiments. Datasets were reconstructed for ten phases, details of the acquired data are presented in Table 1. Expert observers reviewed all of the images and identified stacks containing artifacts. The final ground truth was determined by consensus among the three observers and used to compute the sensitivity and specificity of the competing methods to identify artifacts.
Table 1.
Patients’ data statistics. For each patient, the number of respiration phases, the number of respiration cycles, the total number of stacks and the average respiration cycle (mean) and standard deviation (std) are given.
| Total No. of respiration phases | Total No. of respiration cycles | Total No. of stacks | Respiration cycle mean±std (s) | |
|---|---|---|---|---|
| Patient 1 | 10 | 10 | 100 | 4.5±1.3 |
| Patient 2 | 10 | 20 | 200 | 4.0±2.0 |
| Patient 3 | 8 | 18 | 144 | 3,6±0.9 |
| Patient 4 | 10 | 11 | 110 | 4.6±0.8 |
| Patient 5 | 10 | 7 | 70 | 9.1±2.5 |
RESULTS
Ability of NCCC to characterize 4D-CT artifacts
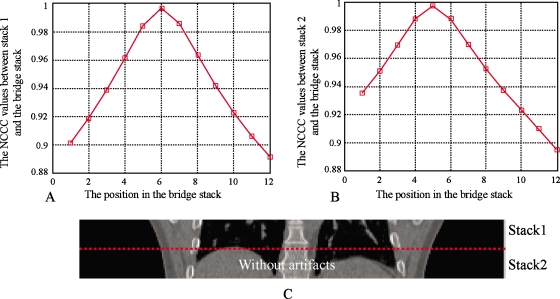
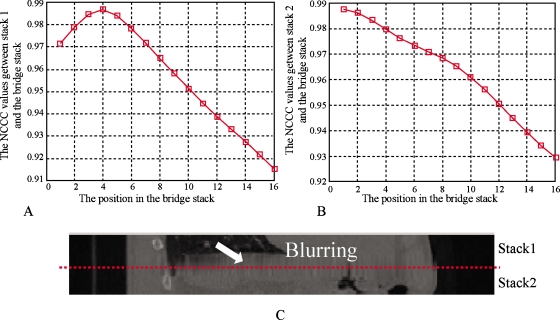
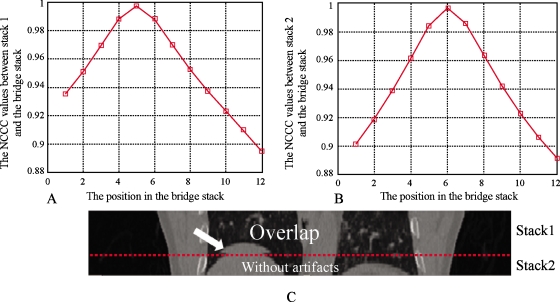
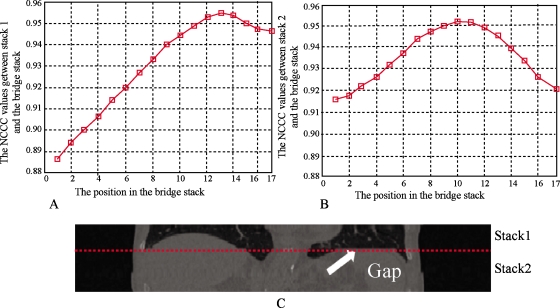
Figure 5 shows the behavior of the NCCC parameter between two stacks for which no artifact is present. The stacks evaluated were from 100% inhalation phase; the NCCC values at different positions are shown in Fig. 5a for stack 1 and Fig. 5b for stack 2, where the bridge stack comes from 0% exhalation. The alignment of the adjacent stacks can be appreciated visually in Fig. 5c, showing the coronal view. The couch positions of the slices in stack 1 range from 144 to 160 mm. The couch positions of slices in stack 2 range from 126 to 142 mm. The couch positions of slices in the bridge stack range from 134 to 156 mm. As seen in Fig. 5, when stack 1 is matched to the bridge stack, the best position (highest NCCC value) is at slice 6, which corresponds to the couch position of 144 mm. Similarly, stack 2 is matched to the position of slice 5, which corresponds to a couch position of 142 mm. In this case, the CT slices are 2 mm thick, so there are no artifacts between stack 1 and stack 2 and Pos[S1,Sb]−Pos[S2,Sb]=1. For both stacks, the NCCC values increase monotonically until a clear maximum is reached. Figure 6 shows another case where there are artifacts between the two stacks. Stack 1 and stack 2 come from phase 80% inhalation and the bridge stack comes from phase 60% exhalation. The couch positions in stack 1 range from 16 to 50 mm and the couch positions in stack 2 are from −18 to 14 mm. The couch positions in the bridge stack range from 10 to 40 mm. The NCCC values between stack 1 and the bridge stack first increase and then decrease. However, because of the blurring and deformations, the NCCC values between stack 2 and the bridge stack decrease monotonously for all overlapping positions. In this example, Pos[S1,Sb]−Pos[S2,Sb]=4−1=3, which means there is a space between the two stacks resulting in the blurring artifact seen in Fig. 6c. Figures 78 show the overlapping case and gapping case using the same method. In Fig. 7, stack 1 is matched to Sb and the best matching position is Pos[S1,Sb]=5. Stack 2 is matched to Sb and the best matching position is Pos[S2,Sb]=6. Since Pos[S1,Sb]−Pos[S2,Sb]=−1, it means that there are overlapping artifacts. In Fig. 8, Pos[S1,Sb]−Pos[S2,Sb]=3, which corresponds to gapping artifacts.
Figure 5.
Without artifacts. (a) The NCCC values at each position on Sb when S1 is matched to Sb. The best position is Pos[S1,Sb]=6. (b) The NCCC values at each position on Sb when S2 is matched to Sb. The best position is Pos[S2,Sb]=5. (c) Stack 1 and stack 2. The dashed line shows the adjacent location. In this example, Pos[S1,Sb]−Pos[S2,Sb]=1, which indicates that there is no artifact between S1 and S2.
Figure 6.
Blurring artifacts due to gap caused by low frequency respiration. (a) The NCCC values at each position on Sb when S1 is matched to Sb. The best position is Pos[S1,Sb]=4. (b) The NCCC values at each position on Sb when S2 is matched to Sb. The best position is Pos[S2,Sb]=1. (c) Stack 1 and stack 2. The dashed line shows the adjacent location. In this example, blurring occurs because of low frequency respiration. Pos[S1,Sb]−Pos[S2,Sb]=3 shows that gaps occur.
Figure 7.
Overlapping artifacts. (a) The NCCC values at each position on Sb when S1 is matched to Sb. The best position is Pos[S1,Sb]=5. (b) The NCCC values at each position on Sb when S2 is matched to Sb. The best position is Pos[S2,Sb]=6. (c) Stack 1 and stack 2. The dashed line shows the adjacent location. Since Pos[S1,Sb]−Pos[S2,Sb]=−1, it indicates that the overlapping artifacts occur.
Figure 8.
Gapping artifacts. (a) The NCCC values at each position on Sb when S1 is matched to Sb. The best position is Pos[S1,Sb]=13. (b) The NCCC values at each position on Sb when S2 is matched to Sb. The best position is Pos[S2,Sb]=10. (c) Stack 1 and stack 2. There is an obvious flat region around the adjacent location, which is shown with a dashed line. Pos[S1,Sb]−Pos[S2,Sb]=3 indicates that gapping artifacts occur.
In Table 2, we showed the results for identifying the artifacts types. We showed the numbers for no artifacts, gapping artifacts, and overlapping artifacts, where gapping artifacts included the blurring artifacts caused by low frequency respiration and the gapping artifacts caused by high amplitude cycle or low amplitude cycle. For patient 1, the proposed method identified 56 no artifacts and 44 artifacts, in which 20 gapping artifacts and 24 overlapping artifacts. For patient 2, the proposed method identified 162 no artifacts and 38 artifacts, in which 29 gapping artifacts and 9 overlapping artifacts. For patient 3, the proposed method identified 109 no artifacts, 20 gapping artifacts, and 15 overlapping artifacts. For patient 4, the proposed method identified 73 no artifacts, 21 gapping artifacts, and 16 overlapping artifacts. Finally, the proposed method can identify 27 no artifacts, 30 gapping artifacts, and 13 overlapping for patient 5.
Table 2.
Results on identifying artifacts types using the proposed method. We showed the numbers for no artifacts, gapping artifacts, and overlapping artifacts, where gapping artifacts included the blurring artifacts caused by low frequency respiration and the gapping artifacts caused by high amplitude cycle or low amplitude cycle. The ground truth is shown in brackets.
| No artifacts | Gapping artifacts | Overlapping artifacts | |
|---|---|---|---|
| Patient 1 | 56 (65) | 20 (16) | 24 (19) |
| Patient 2 | 162 (163) | 29 (28) | 9 (9) |
| Patient 3 | 109 (121) | 20 (13) | 15 (10) |
| Patient 4 | 73 (73) | 21 (20) | 16 (17) |
| Patient 5 | 27(46) | 30 (18) | 13 (6) |
Results on identification 4D-CT artifacts
Sensitivity and specificity of the proposed method
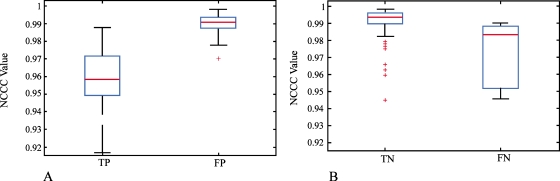
In Table 3, we show the results using our method when applied to all 624 stacks from ten phases acquired for five patients (note that patient 3 has eight phases). λPP and λPN were trained on 80 pairs of stacks that were randomly selected. We showed our results with three different λPP and λPN values. The optimal λPP=0.5 and λPN=−2.9 were used in our experiments. The corresponding average sensitivity was 0.87 and the average specificity was 0.82. The results indicate that around 87% of artifacts could be correctly identified using the proposed method, while about 82% artifact-free stacks could be correctly identified. In Fig. 9, we showed the statistical analysis of the NCCC values in the PP and PN samples by only using matching positions information (see Fig. 9). It is evident that FP has higher NCCC values than TP [Fig. 9a] and that TN has higher NCCC values than FN [Fig. 9b]. This proved our assumption in Sec. 2D3, i.e., by combining matching positions and NCCC values, performance could be improved.
Table 3.
Results of the proposed method. For each patient, TP, TN, FP, and FN are given, respectively. For each patient, we tried three different λPP and λPN values and gave the average results. The last row was computed based on the results obtained by λPP=0.5 and λPN=−2.9, which were shown in bold.
| λPP | λPN | TP | TN | FP | FN | Sensitivity | Specificity | Sensitivity×specificity | |
|---|---|---|---|---|---|---|---|---|---|
| Patient 1 | 0.3 | −2.5 | 29 | 55 | 10 | 6 | 0.83 | 0.85 | 0.71 |
| 0.5 | −2.9 | 32 | 53 | 12 | 3 | 0.91 | 0.82 | 0.75 | |
| 0.8 | −3.3 | 33 | 50 | 15 | 2 | 0.94 | 0.77 | 0.72 | |
| Avg | 0.53 | −2.9 | 31.3 | 52.7 | 12.3 | 3.7 | 0.89 | 0.81 | 0.72 |
| Patient 2 | 0.3 | −2.5 | 30 | 159 | 4 | 7 | 0.81 | 0.98 | 0.79 |
| 0.5 | −2.9 | 34 | 159 | 4 | 3 | 0.92 | 0.98 | 0.90 | |
| 0.8 | −3.3 | 35 | 156 | 7 | 2 | 0.95 | 0.96 | 0.91 | |
| Avg | 0.53 | −2.9 | 33 | 158 | 5 | 4 | 0.89 | 0.97 | 0.86 |
| Patient 3 | 0.3 | −2.5 | 17 | 106 | 15 | 6 | 0.76 | 0.88 | 0.67 |
| 0.5 | −2.9 | 19 | 105 | 16 | 4 | 0.83 | 0.87 | 0.72 | |
| 0.8 | −3.3 | 19 | 102 | 19 | 4 | 0.83 | 0.84 | 0.70 | |
| Avg | 0.53 | −2.9 | 18.3 | 104.3 | 16.7 | 4.7 | 0.81 | 0.86 | 0.70 |
| Patient 4 | 0.3 | −2.5 | 31 | 68 | 5 | 6 | 0.84 | 0.93 | 0.78 |
| 0.5 | −2.9 | 32 | 68 | 5 | 5 | 0.86 | 0.93 | 0.80 | |
| 0.8 | −3.3 | 33 | 62 | 11 | 4 | 0.89 | 0.85 | 0.76 | |
| Avg | 0.53 | −2.9 | 32 | 66 | 7 | 5 | 0.86 | 0.90 | 0.78 |
| Patient 5 | 0.3 | −2.5 | 17 | 35 | 11 | 7 | 0.71 | 0.76 | 0.54 |
| 0.5 | −2.9 | 20 | 23 | 23 | 4 | 0.83 | 0.50 | 0.42 | |
| 0.8 | −3.3 | 20 | 19 | 27 | 4 | 0.83 | 0.42 | 0.35 | |
| Avg | 0.53 | −2.9 | 19 | 25.7 | 20.3 | 5 | 0.79 | 0.56 | 0.44 |
| Avg | λPP=0.5 | λPN=−2.9 | 27.4 | 81.6 | 12 | 3.8 | 0.87 | 0.82 | 0.72 |
Figure 9.
Statistical analysis of the NCCC values for TP, FP, TN, and FN. (a) Comparisons between TP and FP for all PP samples. (b) Comparisons between TN and FN for all PN samples.
Comparison of the proposed method with the method of using respiratory signal
The intuitive way to identify the 4D-CT artifacts is to directly use the respiratory signal. Table 4 displays the results of three different w values that we tested with this method. From Eq. 10, we know w is inversely proportional to sensitivity and proportional to specificity. The three different w values used were 0.5, 0.75, and 1. The average sensitivity and specificity were 0.50 and 0.70 when w was set to 0.75. The results showed that simply using the amplitude of the respiratory signal can only correctly identify about 50% of the artifact stacks, while correctly identifying 70% artifact-free stacks.
Table 4.
Results by the method of using respiratory signal. For each patient, we tried three different w values (0.5, 0.75, and 1) and gave the average results. The last row was computed based on the results obtained by w=0.75, which were shown in bold.
| w | TP | TN | FP | FN | Sensitivity | Specificity | Sensitivity×specificity | |
|---|---|---|---|---|---|---|---|---|
| Patient 1 | 0.5 | 26 | 30 | 35 | 9 | 0.74 | 0.46 | 0.34 |
| 0.75 | 20 | 41 | 24 | 15 | 0.57 | 0.63 | 0.36 | |
| 1 | 17 | 50 | 15 | 18 | 0.49 | 0.77 | 0.36 | |
| Avg | 0.75 | 21 | 40.3 | 24.7 | 14 | 0.6 | 0.62 | 0.37 |
| Patient 2 | 0.5 | 26 | 123 | 40 | 11 | 0.70 | 0.75 | 0.52 |
| 0.75 | 21 | 149 | 14 | 16 | 0.57 | 0.91 | 0.52 | |
| 1 | 18 | 156 | 7 | 19 | 0.49 | 0.96 | 0.47 | |
| Avg | 0.75 | 21.7 | 142.7 | 20.3 | 15.3 | 0.59 | 0.87 | 0.51 |
| Patient 3 | 0.5 | 15 | 67 | 54 | 8 | 0.65 | 0.55 | 0.29 |
| 0.75 | 9 | 87 | 34 | 14 | 0.39 | 0.72 | 0.28 | |
| 1 | 8 | 100 | 21 | 15 | 0.35 | 0.83 | 0.29 | |
| Avg | 0.75 | 10.7 | 84.7 | 36.3 | 12.3 | 0.46 | 0.7 | 0.32 |
| Patient 4 | 0.5 | 25 | 47 | 26 | 12 | 0.68 | 0.64 | 0.44 |
| 0.75 | 13 | 50 | 23 | 24 | 0.35 | 0.68 | 0.24 | |
| 1 | 10 | 56 | 17 | 27 | 0.27 | 0.77 | 0.21 | |
| Avg | 0.75 | 16 | 51 | 22 | 21 | 0.43 | 0.70 | 0.30 |
| Patient 5 | 0. 5 | 15 | 18 | 28 | 9 | 0.63 | 0.39 | 0.24 |
| 0.75 | 14 | 24 | 22 | 10 | 0.58 | 0.52 | 0.30 | |
| 1 | 8 | 31 | 15 | 16 | 0.33 | 0.67 | 0.22 | |
| Avg | 0.75 | 12.3 | 24.3 | 21.7 | 11.7 | 0.51 | 0.53 | 0.27 |
| Avg | w=0.75 | 15.4 | 70.2 | 23.4 | 15.8 | 0.50 | 0.70 | 0.35 |
From Tables 3, 4, we can see that the proposed method clearly outperformed the method of using respiratory signal in all the experiments. With all five patients’ data, sensitivity increased from 0.50 to 0.87. Specificity increased from 0.70 to 0.82. If we fixed the specificity around 0.8, the sensitivity was about 0.87 using the proposed method, while its value was about 0.3 using the method of using respiratory signal, which is a significant improvement (Tables 3, 4). Similarly, if we fixed sensitivity around 0.9, the specificity was about 0.80 and 0.2 using the proposed method and the method of using respiratory signal, respectively. The comparisons supported the validity of the proposed method.
DISCUSSION
Performance analysis
First, we discuss the characteristics of the NCCC values to thoroughly analyze the performance of the proposed method. When computing NCCC values between S(i,j) and Sb(k,t), we obtain m+l−1 NCCC values at each position on Sb(k,t), where m and l are the number of slices in S(i,j) and Sb(k,t), respectively. Plotting m+l−1 values, we produce a curve called the NCCC value curve. We used four main shape types in our experiments to describe the NCCC value curve. Type 1: The curve first increases and then decreases with a single maximum value. Type 2: The curve first increases and then decreases with several maximum values. Type 3: The curve decreases monotonously. Type 4: The curve increases monotonously. Our ideal case shape is type 1 and most TN belongs to this category. If there are no overlaps, type 3 and type 4 curves may occur, which means there may be artifacts. We found type 2 to be the most problematic. The reason is that there are several maximum values which may lead to misclassification due to very similar maximum values. We viewed 624 stacks and gave a static distribution for the four types of curves (see Table 5). The results showed that the number of stacks with type 2 in FN+FP was 25+10=35 (20, 12, and 12 for types 1, 3, and 4), which was larger than the other three types. While using only the matching position information may lead to errors, we noticed that we can combine the matching positions with NCCC values to improve performance, which has been validated in Sec. 3B1.
Table 5.
The proportion of the four types of NCCC value curve shape in TP, TN, FP, and FN. Type 1: The curve first increases and then decreases with a single maximum value. Type 2: The curve first increases and then decreases with several maximum values. Type 3: The curve decreases monotonously. Type 4: The curve increases monotonously.
| Type 1 | Type 2 | Type 3 | Type 4 | |
|---|---|---|---|---|
| TP(total=137) | 43 | 39 | 28 | 27 |
| TN(total=408) | 301 | 65 | 19 | 23 |
| FP(total=60) | 12 | 25 | 11 | 12 |
| FN(total=19) | 8 | 10 | 1 | 0 |
We also tested the proposed method by only using the matching positions, i.e., without combining the NCCC values to show the usefulness of combing optimal NCCC values. Let S(i,j) and S(i,j+1) be matched to Sb(k,t) at Pos[S(i,j),Sb(k,t)] and Pos[S(i,j+1),Sb(k,t)], respectively. If |Pos[S(i,j),Sb(k,t)]−Pos[S(i,j+1),Sb(k,t)]−1|>threshold, it is identified as a positive sample, otherwise the sample is a negative sample. Tuning the threshold can achieve a balance between sensitivity and specificity, i.e., a larger threshold getting a higher specificity and a smaller threshold getting a higher sensitivity. We investigated two types of thresholds, threshold=0and threshold=1. Theoretically, the threshold should be chosen as threshold=0 (denoted as T1) to get the best sensitivity value. Because of the deformations, we can relax it to threshold=1 (denoted as T2) to improve the specificity value. The results showed that by using T2, the specificity is 0.96; however, the sensitivity was only 0.35, which means fewer artifacts were identified. Using T1, we can achieve a balance between the two metrics on our dataset. The average sensitivity and specificity were 0.77 and 0.80 with T1. Compared to the results in Table 3, it is clearly shown that the sensitivity was improved by 13% (from 0.77 to 0.87) and the specificity was improved 3% (from 0.80 to 0.82) by combining NCCC values. Note that the sensitivity was much improved, which meant more artifacts were being identified. We have used a simple search method to find parameters to improve performance but more research is needed to improve this technique; specifically which method should be used to find the parameters and how many samples should be used for training.
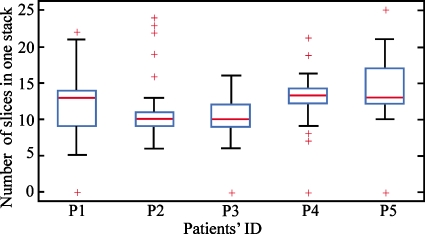
Second, we discuss the relations between the patients’ respiratory cycle, the stack length, and the spatial distortion artifacts. The number of slices in one stack may vary due to the irregular respiration cycles and helical data acquisition method. The irregular respiration cycles lead to different lengths of stacks and spatial distortion artifacts. The box plot seen in Fig. 10 shows the variation in the stack length (the number of slices in one stack) from five patients’ image datasets. The maximum stack length for these five patients would be 22, yet that length was rarely accomplished in any case. More importantly, these data showed the substantial range in stack length, indicating patients had significant variations in their respiratory rate during image acquisition. Patient 5 showed the largest variation, while the distribution of stack lengths for patient 2 was far more consistent, implying they may have fewer respiration-induced spatial distortion artifacts. The relatively high respiratory rate in these patients resulted in stack lengths reconstructed by the system being much less than the maximum amount of the slices per stack that could be reconstructed from the acquired raw projection data.
Figure 10.
The variation in the stack length (the number of slices in one stack) for different patients. Large variation indicates that patients had significant changes in their respiratory rate during the image acquisition. Therefore, the patients with larger variation may have more artifacts.
Third, the outlier patient is of interest. During the method evaluation study, we observed that all the patients showed good results, except for patient 5. After analyzing the data, we observed that the motion inside this patient was great, which meant that the respiration of this patient was very erratic. Consequently, the bridge stacks may not be correctly selected due to the irregular breathing. We were able to use the bridge stack to correctly connect the measured stacks. One way to avoid selecting the wrong bridge stack is to directly recover the overlapping slices from the raw data, which is currently removed by the vendor supplied software.
Finally, the performance of the different methods is worth discussing. The proposed methods were an improvement over the method of using respiratory signal. One possible reason is that the artifacts have correlations with irregular respiration; however, there is no exact function to show the correlations between the occurrence of the artifacts and the shapes of the respiratory signal. Thus, simply using respiratory signals cannot attain satisfactory results. The proposed method provided a fundamental solution to the identification of 4D-CT artifacts. A good method should be easy to understand and to implement in the clinical process. From this point of view, NCCC is simple but effective and is a good choice in our study. For the metrics we used in this paper, sensitivity is more useful than specificity because we are more concerned that the 4D-CT artifacts are evaluated by sensitivity. Thus, as described in the Abstract, the increase in sensitivity from 0.50 to 0.87 is significant.
Comparisons of the automated method with the manual method
The manual method has been used in the past.9 In their study, at each position, the observers searched for the coronal view where the artifacts are most prominent. Then, the observers scrolled all the phases to record the artifacts types, location, and the corresponding phase information. Compared to our automated method, the manual method9 only recorded the large artifacts (larger than 4.4 mm). Artifacts of smaller magnitude than the minimum one found in their analysis (i.e., 4.4 mm) almost certainly exist and were present in the image but were not found by their method. The possible reason is that it is difficult to identify smaller artifacts by the observers. This is not difficult for the automated method. On one hand, the manual method would allow us to identify the types, locations, and magnitude of larger artifacts more accurate than the automated method. On the other hand, the automated method would allow us to identify the artifacts more objectively than the manual method. Additionally, the automated method could save more time than the manual method. Thus, it could be used on a large dataset.
Potential usage for improving 4D-CT image
As we addressed in the previous sections, our method can help improve the quality of 4D-CT image. In order to get an artifact-reduced 4D-CT image, we can first use our method to automatically identify the location of the artifacts. Thus, only the problematic slices need to be reconstructed or repaired and not all slices have to be rejected. After we get an artifact-reduced image, we could use the proposed method to measure whether we have reduced the artifacts. Thus, our method can prelocate the artifacts and validate 4D-CT image quality. Both of these will be benefit for improving the 4D-CT image.
Limitations and future work
One of the limitations of our method is that it requires a bridge stack. The bridge stack should contain slices in common with both measured stacks, otherwise we cannot link the measured stacks. Thus, if the patients have large irregular breathing pattern, the bridge stacks may not be correctly selected. Another limitation is that the NCCC cannot efficiently differentiate the rigid and nonrigid anatomy deformation. Both the bridge stack and the nonrigid anatomy deformation could affect the residual uncertainties. Additionally, more accurate ground truth may benefit for improving the residual uncertainties. The future work includes (1) training the parameters on a large dataset and (2) quantitatively analyzing the helical 4D-CT artifacts using the proposed method on a large dataset.
CONCLUSION
Automatically identifying artifacts is essential to quantitatively analyzing the 4D-CT images. Current clinical demands in 4D-CT image guided radiation therapy show that it can be very useful to automatically identify the artifacts, a subject that is not well addressed in the current literature. In this paper, we first characterized the spatial artifacts during 4D-CT imaging, summarized three types of artifact sources, and analyzed the resulting artifacts. Based on our analysis, we proposed a method of automatically identifying the artifacts between two consecutive stacks acquired using the helical mode 4D-CT imaging technique; that is, using the bridge stack to connect two consecutive stacks. The method can also be used for any two stacks if a bridge stack can be selected. Freed from the constraints of changing machine configurations, the method is applicable to those clinical centers that hope to directly use the reconstruction image to identify the artifacts.
ACKNOWLEDGMENT
This paper was funded in part by NIH Grant No. R01 EB 004640.
References
- Colgan R. et al. , “Planning lung radiotherapy using 4D CT data and a motion model,” Phys. Med. Biol. 53, 5815–5830 (2008). 10.1088/0031-9155/53/20/017 [DOI] [PubMed] [Google Scholar]
- El Naqa I., Low D. A., Deasy J. O., Amini A., and Parikh P. M. N., “Automated breathing motion tracking for 4D computed tomography,” IEEE Nuclear Science Symposium, pp. 3219–3122, 2003. (unpublished).
- Endo M., Tsunoo T., Kandatsu S., Tanada S., Aradate H., and Saito Y., “Four-dimensional computed tomography (4D CT)—Concepts and preliminary development,” Radiat. Med. 21, 17–22 (2003). [PubMed] [Google Scholar]
- Keall P., “4-dimensional computed tomography imaging and treatment planning,” Semin. Radiat. Oncol. 14, 81–90 (2004). 10.1053/j.semradonc.2003.10.006 [DOI] [PubMed] [Google Scholar]
- Low D. A. et al. , “Novel breathing motion model for radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 63, 921–929 (2005). 10.1016/j.ijrobp.2005.03.070 [DOI] [PubMed] [Google Scholar]
- Rietzel E., Pan T., and Chen G. T., “Four-dimensional computed tomography: Image formation and clinical protocol,” Med. Phys. 32, 874–889 (2005). 10.1118/1.1869852 [DOI] [PubMed] [Google Scholar]
- Sharp G. C., Jiang S. B., Shimizu S., and Shirato H., “Prediction of respiratory tumour motion for real-time image-guided radiotherapy,” Phys. Med. Biol. 49, 425–440 (2004). 10.1088/0031-9155/49/3/006 [DOI] [PubMed] [Google Scholar]
- Webb S., “Motion effects in (intensity modulated) radiation therapy: A review,” Phys. Med. Biol. 51, R403–R425 (2006). 10.1088/0031-9155/51/13/R23 [DOI] [PubMed] [Google Scholar]
- Yamamoto T., Langner U., B. W.Loo, Jr., Shen J., and Keall P. J., “Retrospective analysis of artifacts in four-dimensional CT images of 50 abdominal and thoracic radiotherapy patients,” Int. J. Radiat. Oncol., Biol., Phys. 72, 1250–1258 (2008). 10.1016/j.ijrobp.2008.06.1937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boldea V., Sharp G. C., Jiang S. B., and Sarrut D., “4D-CT lung motion estimation with deformable registration: Quantification of motion nonlinearity and hysteresis,” Med. Phys. 35, 1008–1018 (2008). 10.1118/1.2839103 [DOI] [PubMed] [Google Scholar]
- Carnes G., Gaede S., Yu E., Van Dyk J., Battista J., and Lee T. Y., “A fully automated non-external marker 4D-CT sorting algorithm using a serial cine scanning protocol,” Phys. Med. Biol. 54, 2049–2066 (2009). 10.1088/0031-9155/54/7/013 [DOI] [PubMed] [Google Scholar]
- Wolthaus J. W. et al. , “Mid-ventilation CT scan construction from four-dimensional respiration-correlated CT scans for radiotherapy planning of lung cancer patients,” Int. J. Radiat. Oncol., Biol., Phys. 65, 1560–1571 (2006). 10.1016/j.ijrobp.2006.04.031 [DOI] [PubMed] [Google Scholar]
- Yang D., Lu W., Low D. A., Deasy J. O., Hope A. J., and El Naqa I., “4D-CT motion estimation using deformable image registration and 5D respiratory motion modeling,” Med. Phys. 35, 4577–4590 (2008). 10.1118/1.2977828 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keall P. J., Joshi S., Vedam S. S., Siebers J. V., Kini V. R., and Mohan R., “Four-dimensional radiotherapy planning for DMLC-based respiratory motion tracking,” Med. Phys. 32, 942–951 (2005). 10.1118/1.1879152 [DOI] [PubMed] [Google Scholar]
- Liang Y., Xu H., Yao J., Li Z., and Chen W., “Four-dimensional intensity-modulated radiotherapy planning for dynamic multileaf collimator tracking radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 74, 266–274 (2009). 10.1016/j.ijrobp.2008.10.088 [DOI] [PubMed] [Google Scholar]
- Nehmeh S. A. et al. , “Four-dimensional (4D) PET∕CT imaging of the thorax,” Med. Phys. 31, 3179–3186 (2004). 10.1118/1.1809778 [DOI] [PubMed] [Google Scholar]
- Lu W. et al. , “Quantitation of the reconstruction quality of a four-dimensional computed tomography process for lung cancer patients,” Med. Phys. 32, 890–901 (2005). 10.1118/1.1870152 [DOI] [PubMed] [Google Scholar]
- Defrise M. and Gullberg G. T., “Image reconstruction,” Phys. Med. Biol. 51, R139–R154 (2006). 10.1088/0031-9155/51/13/R09 [DOI] [PubMed] [Google Scholar]
- Kalender W. A., “X-ray computed tomography,” Phys. Med. Biol. 51, R29–R43 (2006). 10.1088/0031-9155/51/13/R03 [DOI] [PubMed] [Google Scholar]
- Low D. A. et al. , “A method for the reconstruction of four-dimensional synchronized CT scans acquired during free breathing,” Med. Phys. 30, 1254–1263 (2003). 10.1118/1.1576230 [DOI] [PubMed] [Google Scholar]
- Pan T., “Comparison of helical and cine acquisitions for 4D-CT imaging with multislice CT,” Med. Phys. 32, 627–634 (2005). 10.1118/1.1855013 [DOI] [PubMed] [Google Scholar]
- Tazawa S., Gotoh Y., Takahashi S., Zuguchi M., and Maruoka S., “Cine viewing of abdominal CT,” Comput. Methods Programs Biomed. 66, 105–110 (2001). 10.1016/S0169-2607(01)00143-2 [DOI] [PubMed] [Google Scholar]
- Dinkel J. et al. , “Four-dimensional multislice helical CT of the lung: Qualitative comparison of retrospectively gated and static images in an ex-vivo system,” Radiother. Oncol. 85, 215–222 (2007). 10.1016/j.radonc.2007.09.003 [DOI] [PubMed] [Google Scholar]
- Ford E. C., Mageras G. S., Yorke E., and Ling C. C., “Respiration-correlated spiral CT: A method of measuring respiratory-induced anatomic motion for radiation treatment planning,” Med. Phys. 30, 88–97 (2003). 10.1118/1.1531177 [DOI] [PubMed] [Google Scholar]
- Hu H., “Multi-slice helical CT: Scan and reconstruction,” Med. Phys. 26, 5–18 (1999). 10.1118/1.598470 [DOI] [PubMed] [Google Scholar]
- Vedam S. S., Keall P. J., Kini V. R., Mostafavi H., Shukla H. P., and Mohan R., “Acquiring a four-dimensional computed tomography dataset using an external respiratory signal,” Phys. Med. Biol. 48, 45–62 (2003). 10.1088/0031-9155/48/1/304 [DOI] [PubMed] [Google Scholar]
- Wang G. and Vannier M. W., “The effect of pitch in multislice spiral∕helical CT,” Med. Phys. 26, 2648–2653 (1999). 10.1118/1.598804 [DOI] [PubMed] [Google Scholar]
- Pan T., Lee T. Y., Rietzel E., and Chen G. T., “4D-CT imaging of a volume influenced by respiratory motion on multi-slice CT,” Med. Phys. 31, 333–340 (2004). 10.1118/1.1639993 [DOI] [PubMed] [Google Scholar]
- Wink N., Panknin C., and Solberg T. D., “Phase versus amplitude sorting of 4D-CT data,” J. Appl. Clin. Med. Phys. 7, 77–85 (2006). 10.1120/jacmp.2027.25373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mageras G. S. et al. , “Fluoroscopic evaluation of diaphragmatic motion reduction with a respiratory gated radiotherapy system,” J. Appl. Clin. Med. Phys. 2, 191–200 (2001). 10.1120/1.1409235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mageras G. S. et al. , “Measurement of lung tumor motion using respiration-correlated CT,” Int. J. Radiat. Oncol., Biol., Phys. 60, 933–941 (2004). 10.1016/j.ijrobp.2004.06.021 [DOI] [PubMed] [Google Scholar]
- Fitzpatrick M. J. et al. , “Displacement-based binning of time-dependent computed tomography image data sets,” Med. Phys. 33, 235–246 (2006). 10.1118/1.2044427 [DOI] [PubMed] [Google Scholar]
- Lu W., Parikh P. J., Hubenschmidt J. P., Bradley J. D., and Low D. A., “A comparison between amplitude sorting and phase-angle sorting using external respiratory measurement for 4D CT,” Med. Phys. 33, 2964–2974 (2006). 10.1118/1.2219772 [DOI] [PubMed] [Google Scholar]
- Wang J., Byrne J., Franquiz J., and McGoron A., “Evaluation of amplitude-based sorting algorithm to reduce lung tumor blurring in PET images using 4D NCAT phantom,” Comput. Methods Programs Biomed. 87, 112–122 (2007). 10.1016/j.cmpb.2007.05.004 [DOI] [PubMed] [Google Scholar]
- George R. et al. , “Audio-visual biofeedback for respiratory-gated radiotherapy: Impact of audio instruction and audio-visual biofeedback on respiratory-gated radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 65, 924–933 (2006). 10.1016/j.ijrobp.2006.02.035 [DOI] [PubMed] [Google Scholar]
- Neicu T., Berbeco R., Wolfgang J., and Jiang S. B., “Synchronized moving aperture radiation therapy (SMART): Improvement of breathing pattern reproducibility using respiratory coaching,” Phys. Med. Biol. 51, 617–636 (2006). 10.1088/0031-9155/51/3/010 [DOI] [PubMed] [Google Scholar]
- Venkat R. B., Sawant A., Suh Y. L., George R., and Keall P. J., “Development and preliminary evaluation of a prototype audiovisual biofeedback device incorporating a patient-specific guiding waveform,” Phys. Med. Biol. 53, N197–N208 (2008). 10.1088/0031-9155/53/11/N01 [DOI] [PubMed] [Google Scholar]
- Rietzel E. and Chen G. T., “Improving retrospective sorting of 4D computed tomography data,” Med. Phys. 33, 377–379 (2006). 10.1118/1.2150780 [DOI] [PubMed] [Google Scholar]
- Mutaf Y. D., Antolak J. A., and Brinkmann D. H., “The impact of temporal inaccuracies on 4DCT image quality,” Med. Phys. 34, 1615–1622 (2007). 10.1118/1.2717404 [DOI] [PubMed] [Google Scholar]
- Pan T., Sun X., and Luo D., “Improvement of the cine-CT based 4D-CT imaging,” Med. Phys. 34, 4499–4503 (2007). 10.1118/1.2794225 [DOI] [PubMed] [Google Scholar]
- Abdelnour A. F. et al. , “Phase and amplitude binning for 4D-CT imaging,” Phys. Med. Biol. 52, 3515–3529 (2007). 10.1088/0031-9155/52/12/012 [DOI] [PubMed] [Google Scholar]
- Zeng R., Fessler J. A., Balter J. M., and Balter P. A., “Iterative sorting for four-dimensional CT images based on internal anatomy motion,” Med. Phys. 35, 917–926 (2008). 10.1118/1.2837286 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R., Lewis J. H., Cervino L. I., and Jiang S. B., “4D CT sorting based on patient internal anatomy,” Phys. Med. Biol. 54, 4821–4833 (2009). 10.1088/0031-9155/54/15/012 [DOI] [PubMed] [Google Scholar]
- Schreibmann E., Chen G. T. Y., and Xing L., “Image interpolation in 4D CT using a BSpline deformable registration model,” Int. J. Radiat. Oncol., Biol., Phys. 64, 1537–1550 (2006). 10.1016/j.ijrobp.2005.11.018 [DOI] [PubMed] [Google Scholar]
- Schreibmann E., Yang Y., Boyer A., Li T., and Xing L., “SU-FF-J-21: Image interpolation in 4D CT using a BSpline deformable registration model,” Med. Phys. 32, 1924 (2005). 10.1118/1.1997567 [DOI] [PubMed] [Google Scholar]
- Ehrhardt J. et al. , “An optical flow based method for improved reconstruction of 4D CT data sets acquired during free breathing,” Med. Phys. 34, 711–721 (2007). 10.1118/1.2431245 [DOI] [PubMed] [Google Scholar]
- Georg M., Souvenir R., Hope A. J., and Pless R., “Manifold learning for 4D CT reconstruction of the lung,” IEEE Computer Society Workshop on Mathematical Methods in Biomedical Image Analysis (MMBIA, CVPR Workshop), pp. 1–8, 2008. (unpublished).
- Werner R. et al. , “Motion artifact reducing reconstruction of 4D CT image data for the analysis of respiratory dynamics,” Methods Inf. Med. 46, 254–260 (2007). [DOI] [PubMed] [Google Scholar]
- Han D., Bayouth J., Bhatia S., Sonka M., and Wu X., “Motion artifact reduction in 4D helical CT: Graph-based structure alignment,” in Medical Computer Vision: Recognition Techniques and Applications in Medical Imaging. Proceedings of MICCAI MCV 2010, Beijing, China, Lecture Notes in Computer Science Vol. 6533, edited by Menze B. H. L. G., Tu Z., and Criminisi A. (Springer, Heidelberg, 2010).