Abstract
Purpose: Implanted markers are commonly used in radiotherapy for x-ray based target localization. The projected marker position in a series of cone-beam CT (CBCT) projections can be used to estimate the three dimensional (3D) target trajectory during the CBCT acquisition. This has important applications in tumor motion management such as motion inclusive, gating, and tumor tracking strategies. However, for irregularly shaped markers, reliable segmentation is challenged by large variations in the marker shape with projection angle. The purpose of this study was to develop a semiautomated method for robust and reliable segmentation of arbitrarily shaped radiopaque markers in CBCT projections.
Methods: The segmentation method involved the following three steps: (1) Threshold based segmentation of the marker in three to six selected projections with large angular separation, good marker contrast, and uniform background; (2) construction of a 3D marker model by coalignment and backprojection of the threshold-based segmentations; and (3) construction of marker templates at all imaging angles by projection of the 3D model and use of these templates for template-based segmentation. The versatility of the segmentation method was demonstrated by segmentation of the following structures in the projections from two clinical CBCT scans: (1) Three linear fiducial markers (Visicoil) implanted in or near a lung tumor and (2) an artificial cardiac valve in a lung cancer patient.
Results: Automatic marker segmentation was obtained in more than 99.9% of the cases. The segmentation failed in a few cases where the marker was either close to a structure of similar appearance or hidden behind a dense structure (data cable).
Conclusions: A robust template-based method for segmentation of arbitrarily shaped radiopaque markers in CBCT projections was developed.
Keywords: image-guided radiotherapy, organ motion, marker segmentation
INTRODUCTION
Modern linear accelerators for radiotherapy are often equipped with a gantry-mounted x-ray system that allows cone-beam CT (CBCT) acquisition. For patients with implanted tumor markers, the CBCT projections provide the target trajectory projected into a 2D rotating coordinate system. The projected trajectory can be used to estimate the three dimensional (3D) target trajectory either retrospectively for tumor motion analysis1 or—at a modest cost of accuracy—in real time for tumor motion tracking.2, 3 It requires reliable marker segmentation in the CBCT projections.
A substantial amount of work has been carried out on automatic segmentation of tumor markers in kV or MV images, but most work has focused on the detection of spherical or cylindrical fiducial markers imaged at a static imager angle.4, 5, 6, 7, 8, 9 For CBCT projections, the imager angle changes continuously. Furthermore, markers with more irregular shapes are often used for tumor visualization in radiotherapy. One example is linear fiducial markers (Visicoil, IBA, Bartlett, TN) that may have fewer CT artifacts and reduced migration risk as compared to cylindrical gold markers. These markers may keep their linear shape or curl up after implantation. Another example is metallic stents that allow insertion into tubelike anatomical structures such as the urethra10 or the bronchial system.11 In these cases, there may be little or no a priori knowledge of the marker shape and it can only be determined through imaging methods after implantation.
For such irregularly shaped markers, the segmentation in CBCT projections is complicated by large variations in the projected marker shape with the projection angle. Often streak artifacts and limited resolution hinder the use of a CT scan to determine the projected marker shape with sufficient resolution for reliable template-based segmentation. Furthermore, the segmentation in each CBCT projection image should refer to the same unique point within the 3D marker structure, e.g., the center of mass. This requirement can be difficult to ensure when the projections extend over a large area and change appearance with the projection angle.
In this paper, we present a simple semiautomatic method for reliable segmentation of arbitrarily shaped markers in CBCT projections. The versatility of the method is demonstrated in a feasibility study by segmentation of two different marker types in two clinical CBCT scans.
METHODS AND MATERIALS
Segmentation method
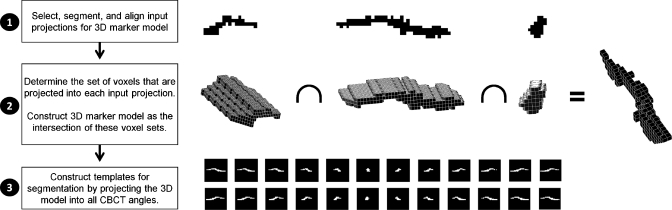
The segmentation procedure consisted of three steps, as summarized in Fig. 1. In the first step, a few CBCT projections (between 3 and 6) with large angular separation and good marker contrast on a uniform background were selected. As the exact projection angle is not critical, it is often possible to select projections without any disturbing background variations due to, e.g., bony anatomy or structures from the treatment couch or immobilization devices. For each selected projection, a binary image of the projected marker shape was generated by threshold-based segmentation. The binary images were aligned to each other in both directions to account for marker motion between the image acquisitions. The alignment was performed such that the central pixel in all binary segmentations coincided.
Figure 1.
Overview of the segmentation method.
In the second step, the binary images were used as input to construct a 3D model of the marker. For each input image, ray tracing was used to determine the set of voxels that projected into the segmented marker. The voxels in these sets were candidates for being part of the 3D marker. The 3D marker model was constructed as the intersection of all candidate voxel sets, i.e., a voxel was assumed to be part of the 3D marker if it was projected into the segmented marker in all input images. This requirement could be relaxed to, e.g., all input images but one in CBCT scans with large uncertainties in the initial threshold-based marker segmentation. We used a voxel side length equal to the pixel side length, which was 0.26 mm when scaled to the isocenter distance. For simplicity, beam divergence was not accounted for in the ray tracing, i.e., all rays were assumed to be parallel to the x-ray central axis.
In the third step, a marker template was constructed for each CBCT projection by projection of the 3D marker model. Again, parallel rays were assumed for simplicity. The templates were smoothed by convolution with a Gaussian function and used for template-based segmentation. Here, the marker position was determined as the position with the highest normalized cross correlation between the template and the projection image. This position was found with a resolution of 1 pixel within a region of typically 40×40 pixels centered at the segmented marker position of the preceding CBCT projection.
For markers offset from the isocenter of the CBCT system, the magnification factor in the CBCT projections depended on the projection angle. This was accounted for by scaling the input images to the 3D model (in step 1 above) and the output templates from the 3D model (in step 3 above) according to a rough estimate of 3D mean marker position. This position estimation was made by a previously described method1 from the projected marker position in the input images of step 1.
Segmentation examples
As summarized in Table 1, the segmentation method was applied for two clinical CBCT scans acquired with an on-board imager system on a Trilogy linear accelerator (Varian Medical Systems, Palo Alto, CA). In the first example, segmentation was performed for three gold linear fiducial markers (Visicoil: 10 mm length, 0.35 mm diameter) implanted in or near the tumor of a non small cell lung cancer (NSCLC) patient treated at the Virginia Commonwealth University, Richmond, VA. One of the Visicoil markers (shown in Fig. 1) maintained its linear shape after implantation, while the other two markers curled up to more compact structures. The CBCT scan was acquired according to an adaptive protocol designed to sample approximately 120 breathing cycles with 20 projection images per breathing cycle during a 360° gantry rotation.12 In the second CBCT scan, segmentation was performed for an artificial cardiac valve of approximately 25 mm diameter in a NSCLC patient at Aarhus University Hospital, Denmark.
Table 1.
CBCT scans.
| CBCT scan | Patient diagnosis | Segmented structure | Projections | Duration (s) | CBCT type |
|---|---|---|---|---|---|
| 1 | NSCLC | 3 Visicoil markers | 2509 | 504 | Half fan |
| 2 | NSCLC | Artificial cardiac valve | 652 | 59 | Half fan |
For each CBCT scan, the proposed segmentation method was applied in all projection images that included the investigated marker entirely. No segmentation was attempted in projections where the marker moved partly or completely outside the imager frame. After segmentation, visual inspection was used to determine the number of projections for which the segmentation had succeeded. The criterion for successful segmentation was an error in the segmented centroid position of the marker projection of 1 mm (4 pixels) or less. After manual correction of the failed segmentations, the resulting projected marker trajectory was used to estimate the 3D marker trajectory.1 Finally, the normalized cross correlation between the template and the CBCT projection was analyzed for all segmentations in order to investigate if a low cross correlation could be used for segmentation failure detection.
RESULTS
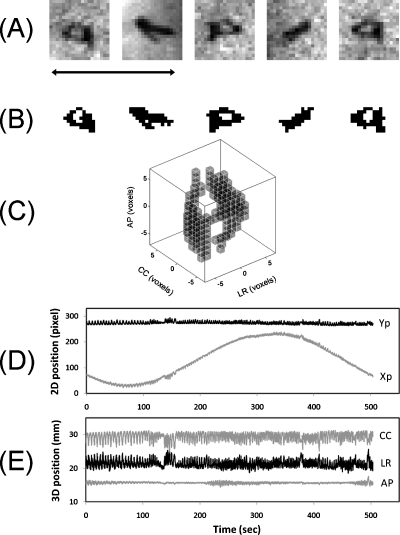
Figure 2 summarizes the segmentation for one of the three Visicoil markers. For this marker, five input projections [Figs. 2a, 2b] were used for the 3D marker model [Fig. 2c]. The automatic segmentation failed in 3 out of 2509 projections either because the marker overlapped with a data cable for an audiovisual biofeedback system (two frames) or because a nearby anatomical structure was mistaken for the marker by the template match (one frame). This marker was implanted close to the aorta and had two motion components induced by respiratory motion (12–15 cycles per minute) and cardiac motion (90 cycles per minute). The peak-to-peak motion was approximately 4 mm in the left-right (LR), 3 mm in the cranio-caudal (CC), and 2 mm in the anterior-posterior (AP) direction. As summarized in Table 2, the other two Visicoil markers in this patient were not visible in all CBCT projections as this was a so-called ‘half fan” scan with the imager shifted 14.8 cm laterally in order to obtain a larger field of view of the reconstructed 3D volume. For Visicoil markers 2 and 3, the automatic segmentation failed in 2 out of 2070 and 0 out of 1734 frames, respectively (Table 2).
Figure 2.
(a) Five CBCT projections of a Visicoil marker. (b) Threshold based segmentations used for construction of the 3D marker model in (c). (d) Segmented 2D trajectory used for estimation of the 3D trajectory shown in (e). The black arrow in (a) indicates 1 cm.
Table 2.
Segmentation results.
| Example | Segmented structure | Projections with marker | Failed segmentations | Failure rate (%) |
|---|---|---|---|---|
| 1.1 | Visicoil marker 1 | 2509 | 3 | 0.12 |
| 1.2 | Visicoil marker 2 | 2070 | 2 | 0.10 |
| 1.3 | Visicoil marker 3 | 1734 | 0 | 0 |
| 2 | Artificial cardiac valve | 368 | 0 | 0 |
Figure 3 shows the segmentation of the artificial cardiac valve. As this marker was relatively large with a nonuniform background, the threshold-based segmentations for the 3D model [shown in Fig. 3b] were manually edited to remove foreign structures such as the suture wire in the two left images in Fig. 3a. The automatic segmentation succeeded in all 368 projections that included the entire cardiac valve (Table 2). The marker motion [Figs. 3d, 3e] was dominated by cardiac motion and had a frequency of 63 cycles per minute and peak-to-peak motion of approximately 7 mm in the LR direction and 5 mm in the CC and AP directions.
Figure 3.
(a) Six CBCT projections of the artificial cardiac valve. (b) Threshold based segmentations used the construction of the 3D marker model in (c). (d) Segmented 2D trajectory used for estimation of the 3D trajectory shown in (e). The black arrow in (a) indicates 1 cm.
Figure 4 shows the normalized cross correlation between the template and the projection image for all template-based segmentations. As indicated by arrows, the segmentation failures were associated with local minima in the cross correlation. The failed segmentations for Visicoil marker 1 around projection 1000 [Fig. 4a] and for Visicoil marker 2 around projection 2300 [Fig. 4b] occurred because the marker passed a data cable. All three Visicoil markers had local cross correlation minima as they passed the data cable near projection 1000 and projection 2300 (see Fig. 4), but in most cases the segmentation was still correct.
Figure 4.
Maximum normalized cross correlation between the template and the projection image in the search area. The arrows for Visicoil markers 1 and 2 in (a) and (b) indicate the projections with failed automatic segmentation.
For Visicoil marker 1, the three failures occurred for the three projections with the lowest, the 4th lowest, and the 18th lowest values of the cross correlation (out of 2509 projections). For Visicoil marker 2, the two failures occurred for the two projections with the third lowest and the fourth lowest values of the cross correlation (out of 2070 projections). In other words, the segmentation failures were limited to the 0.7% and the 0.2% projections with the lowest cross correlation for marker 1 and marker 2, respectively. This suggests that a low cross correlation value is a good indicator for a higher risk of segmentation failure.
As seen in Fig. 4d, the cross correlation for the artificial cardiac valve was generally much lower than for the Visicoil makers because of its larger size covering large background variations in the projections. Despite the lower cross correlation values, the automatic segmentation succeeded in all projections. This illustrates that a cross correlation threshold separating potential failures from successful segmentations must be adapted to the individual case.
DISCUSSION
A robust method for segmentation of arbitrarily shaped radiopaque structures in CBCT projections was proposed. The segmentation succeeded in more than 99.9% of the cases for the Visicoil markers and in all cases for the artificial cardiac valve. The method requires a few projections where the marker is clearly visible with good contrast. This is most often possible to find in clinical CBCT scans where there are typically several hundred projections available. Although the segmentation itself is automatic, the method requires user input in the selection of and threshold-based segmentation of input images for the 3D marker model and in visual inspection of templates generated from the 3D marker model.
At the time of projection selection to create the 3D marker model, no phase information was known. Therefore, it appears that such information is not necessary. However, this information could potentially be used in the future for further improvements. Also, if multiple CBCT scans of a patient are taken throughout a treatment course, the 3D marker model from one scan may be useable for the subsequent scans. This would potentially allow for a fully automatic procedure that could be used for real-time guidance. Here, values of the normalized cross correlation could be very useful for segmentation failure detection.
When more than one marker is implanted, the markers will overlap in some CBCT projections if they are implanted in the same axial plane. In this case, separate 3D marker models can still be constructed for each individual marker by choosing appropriate nonoverlapping projections as input for the 3D model. This would allow construction of joint templates that encompass the overlapping markers and enable segmentation and separation of the markers from each other in the projection images.
While the current segmentation method is robust to translational marker motion during the CBCT acquisition, the method still assumes that no rotation or deformation of the marker occurs during the scan. Further improvements in the successful segmentation fraction may be possible if these additional degrees of freedom were included in the method. Another assumption used for this study was the use of nondivergent beams for the ray tracing, which made the alignment of input projections from different directions straightforward. Although magnification factor variations with imaging angle are still accounted for by scaling, the use of nondivergent beams does not account for the different appearance of large radiopaque structures when imaged from two opposite directions. Including divergent beams in the ray tracing may further increase the successful segmentation fraction. Further potential improvements include the use of increased voxel resolution in the 3D marker model and grayscale (rather than binary) representation of the 2D input projections and the 3D marker model.
In conclusion, a simple and efficient method for robust segmentation of arbitrarily shaped radiopaque structures in CBCT projections was proposed and tested for three linear fiducial markers and an artificial cardiac valve in two clinical CBCT scans. Depending on the marker, automatic segmentation succeeded in 99.9% or more of the projections.
ACKNOWLEDGMENTS
This work was supported by research grants from NIH∕NCI (Grant No. P01 CA116602), Varian Medical Systems, The Danish Cancer Council, CIRRO (The Lundbeck Foundation Center for Interventional Research in Radiation Oncology), and The Danish Council for Strategic Research. The authors would like to thank Julie Baz, the University of Sydney, for reviewing this paper.
Conflict of interest notification: This work was partially supported by Varian Medical Systems.
References
- Poulsen P. R., Cho B., and Keall P. J., “A method to estimate mean position, motion magnitude, motion correlation, and trajectory of a tumor from cone-beam CT projections for image-guided radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 72, 1587–1596 (2008). 10.1016/j.ijrobp.2008.07.037 [DOI] [PubMed] [Google Scholar]
- Poulsen P. R., Cho B., and Keall P. J., “Real-time prostate trajectory estimation with a single imager in arc radiotherapy: A simulation study,” Phys. Med. Biol. 54, 4019–4035 (2009). 10.1088/0031-9155/54/13/005 [DOI] [PubMed] [Google Scholar]
- Poulsen P. R., Cho B., Sawant A., and Keall P. J., “Implementation of a new method for dynamic multileaf collimator tracking of prostate motion in arc radiotherapy using a single kV imager,” Int. J. Radiat. Oncol., Biol., Phys. 76, 914–923 (2010). 10.1016/j.ijrobp.2009.06.073 [DOI] [PubMed] [Google Scholar]
- Nederveen A. J., Lagendijk J. J., and Hofman P., “Feasibility of automatic marker detection with an a-Si flat-panel imager,” Phys. Med. Biol. 46, 1219–1230 (2001). 10.1088/0031-9155/46/4/321 [DOI] [PubMed] [Google Scholar]
- Aubin S., Beaulieu L., Pouliot S., Pouliot J., Roy R., Girouard L. M., Martel-Brisson N., Vigneault E., and Laverdiere J., “Robustness and precision of an automatic marker detection algorithm for online prostate daily targeting using a standard V-EPID,” Med. Phys. 30, 1825–1832 (2003). 10.1118/1.1584041 [DOI] [PubMed] [Google Scholar]
- Buck D., Alber M., and Nusslin F., “Potential and limitations of the automatic detection of fiducial markers using an amorphous silicon flat-panel imager,” Phys. Med. Biol. 48, 763–774 (2003). 10.1088/0031-9155/48/6/305 [DOI] [PubMed] [Google Scholar]
- Mao W., Wiersma R. D., and Xing L., “Fast internal marker tracking algorithm for onboard MV and kV imaging systems,” Med. Phys. 35, 1942–1949 (2008). 10.1118/1.2905225 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S. J., Ionascu D., Hacker F., Mamon H., and Berbeco R., “Automatic marker detection and 3D position reconstruction using cine EPID images for SBRT verification,” Med. Phys. 36, 4536–4546 (2009). 10.1118/1.3218845 [DOI] [PubMed] [Google Scholar]
- Slagmolen P., Hermans J., Maes F., Budiharto T., Haustermans K., and van den Heuvel F., “Fast, accurate, and robust automatic marker detection for motion correction based on oblique kV or MV projection image pairs,” Med. Phys. 37, 1554–1564 (2010). 10.1118/1.3355871 [DOI] [PubMed] [Google Scholar]
- Carl J., Lund B., Larsen E. H., and Nielsen J., “Feasibility study using a Ni-Ti stent and electronic portal imaging to localize the prostate during radiotherapy,” Radiother. Oncol. 78, 199–206 (2006). 10.1016/j.radonc.2005.11.015 [DOI] [PubMed] [Google Scholar]
- Carl J., Jensen H. K., Nielsen J., Nielsen M. S., Schmid M., and Loeschke S., “A new fiducial marker for gated radiotherapy in the lung: A feasibility study of bronchoscopy based insertion and removal in Göttingen Minipig,” Scandinavian Journal of Laboratory Animal Science (accepted).
- Lu J., Guerrore T. M., Munro P., Jeung A., Chi P. M., Balter P., Zhu R., Mohan R., and Pan T., “Four-dimensional cone beam CT with adaptive gantry rotation and adaptive data sampling,” Med. Phys. 34, 3520–3529 (2007). 10.1118/1.2767145 [DOI] [PubMed] [Google Scholar]