Analytical treatment of biased diffusion in tubes with periodic dead ends

Abstract

Effective mobility and diffusion coefficient of a particle in a tube with identical periodic dead ends characterize the motion on large time scale, when the particle displacement significantly exceeds the tube period. We derive formulas that show how these transport coefficients depend on the driving force and the geometric parameters of the system. Numerical tests show that values of the transport coefficients obtained from Brownian dynamics simulations are in excellent agreement with our theoretical predictions.

INTRODUCTION

Effect of dead ends on diffusive transport has been discussed in different contexts. Examples include transport in dendrites,¹ extra-cellular diffusion in brain tissue,² intra-tissue diffusion of water and other substances in muscles,³ diffusive transport in soil,⁴ and linear porous media.^{5, 6, 7} The present paper deals with biased diffusion in tubes with periodic dead ends schematically shown in Fig. 1. Because of the complex geometry of the tube, the problem is too complicated to be solved by conventional methods of the mathematical physics.⁶ In the present paper we suggest a new approach that allows us to overcome the difficulties and to derive approximate formulas for the effective mobility and diffusion coefficient of a point particle, Eqs. 2.2, 2.3. The formulas show how these transport coefficients depend on the driving force and geometric parameters of the tube. To test the accuracy of our approximate theory we compare its predictions with the results obtained from Brownian dynamics simulations finding excellent agreement between the two. This study is an extension of our recent works on unbiased diffusion in tubes with periodic dead ends.⁷

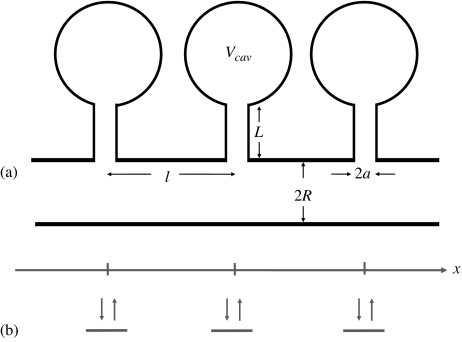
Figure 1.

A tube with identical periodic dead ends [panel (a)] and its one-dimensional model [panel (b)].

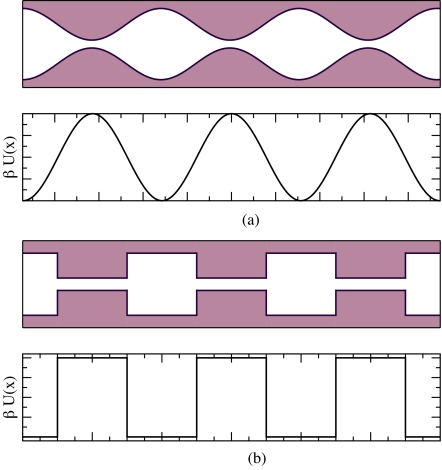
Such tubes represent a special case of linear porous media with periodically varying geometry. Transport in such systems has been actively studied for the last few years.^{6, 7, 8, 9, 10, 11, 12, 13} Varying geometry of the system creates periodic entropy potential along the tube axis. This potential can be smooth or change abruptly as shown in Fig. 2. The entropy potentials created by periodic dead ends can be considered as a periodic set of entropy traps since a particle entering a dead end interrupts its motion along the tube axis (Fig. 1).

Figure 2.

Tubes of periodically varying geometry and corresponding entropy potentials. Variations of the geometry can be smooth [panel (a)] or abrupt [panel (b)].

When developing a theory of transport in such systems, the key step is to reformulate the problem in terms of a one-dimensional description. Such a description depends on the type of the system. For example, unbiased diffusion in tubes of smoothly varying geometry can be analyzed using the reduction to the generalized Fick-Jacobs equation^{14, 15, 16, 17} and successive application of the Lifson–Jackson formula¹⁸ for the effective diffusion coefficient. This approach fails when the tube geometry changes abruptly such as in the tube shown in Fig. 2b. Here one can use a different one-dimensional description. In this description a contact of two segments of the tube, which have different radii, is considered as a partially absorbing boundary.^{19, 20} The effective trapping rate for such a boundary can be found by means of boundary homogenization. Based on this description, one can find the effective diffusion coefficient in a tube of alternating diameter in the absence of the driving force.

An alternative approach is required to analyze unbiased diffusion in tubes with periodic dead ends.⁷ In this approach the focus is on the particle lifetime in the tube between its successive trappings by the dead ends, and on the particle residence time in the dead end. Here we generalize this approach and use it to derive the formulas for the effective mobility and diffusion coefficient in the presence of an external driving force acting on the particle, Eqs. 2.2, 2.3. The outline of the present paper is as follows. In Sec. 2 we (i) discuss the model, (ii) give the formulas for μ_eff(F) and D_eff(F), and (iii) present the results of the numerical tests. Derivations of the formulas are given in Sec. 3. Section 4 contains concluding remarks.

MODEL, RESULTS, NUMERICAL TESTS

Consider a point Brownian particle in a tube of radius R with identical periodic dead ends separated by period l, schematically shown in Fig. 1. In our model the dead end is formed by a cavity of volume V_cav that is connected to the tube by a cylindrical channel of radius a and length L. It is assumed that a ≪ R, l, while L and V_cav can be arbitrary. The particle motion in such a system in the presence of an external driving force F can be characterized by effective drift velocity, v_eff(F), or effective mobility, μ_eff(F) = v_eff(F)∕F, and effective diffusion coefficient, D_eff(F). The goal of the theory is to find these functions. Diffusion coefficient and mobility of the particle in the absence of constraints are denoted by D₀ and μ₀, μ₀ = βD₀, where β = 1∕(k_BT) with the standard notations k_B and T for the Boltzmann constant and absolute temperature.

Results

The effective diffusion coefficient of the particle in the absence of the driving force, D_eff(0), is given by a simple formula⁷

$$D_{\mathrm{eff}}\left(0\right)=D_0\frac{V_{\mathrm{tube}}}{V_{\mathrm{tube}}+V_{\mathrm{de}}},$$ (2.1)

where V_tube and V_de are the volumes of the cylindrical part of the tube of length l and the dead end, V_tube = πR²l, V_de = V_ch + V_cav, and V_ch = πa²L is the volume of the connecting channel. One can use D_eff(0) to find μ_eff(0) by the Einstein relation, μ_eff(0) = βD_eff(0).

As shown in Sec. 3, the effective mobility is independent of the driving force. Thus, we have

$${\mu }_{\mathrm{eff}}\left(F\right)={\mu }_{\mathrm{eff}}\left(0\right)=\beta D_{\mathrm{eff}}\left(0\right)={\mu }_0\frac{V_{\mathrm{tube}}}{V_{\mathrm{tube}}+V_{\mathrm{de}}}.$$ (2.2)

The formula for D_eff(F) is more complex. In Sec. 3, we derive the following formula for the ratio D_eff(F)∕D_eff(0),

$$\begin{array}{ccc}\hfill \frac{D_{\mathrm{eff}}\left(F\right)}{D_{\mathrm{eff}}\left(0\right)}& =& 1+\frac{V_{\mathrm{de}}^2}{{\left(V_{\mathrm{tube}}+V_{\mathrm{de}}\right)}^2}\left[\frac{\tilde{F}∕2}{\tanh \left(\tilde{F}∕2\right)}-1\right.\hfill \\ & & \left.+\frac{\pi R^2〈{\tau }_{\mathrm{de}}^2〉}{8al{⟨{\tau }_{\mathrm{de}}⟩}^2}{\tilde{F}}^2\right],\hfill \end{array}$$ (2.3)

where $\tilde{F}=\beta Fl$, while 〈τ_de〉 and $⟨{\tau }_{\mathrm{de}}^2⟩$ are the first and second moments of the particle lifetime in the dead end. These moments have been found in Ref. 7, where it is shown that the ratio $⟨{\tau }_{\mathrm{de}}^2⟩∕{⟨{\tau }_{\mathrm{de}}⟩}^2$ entering into Eq. 2.3 can be expressed in terms of the geometric parameters of the dead end,

$$\frac{〈{\tau }_{\mathrm{de}}^2〉}{2{⟨{\tau }_{\mathrm{de}}⟩}^2}=1+{\left(\frac{V_{\mathrm{cav}}}{V_{\mathrm{de}}}\right)}^2+\frac{4L}{\pi a}\left[\frac{V_{\mathrm{cav}}}{V_{\mathrm{de}}}+\frac{1}{3}{\left(\frac{V_{\mathrm{ch}}}{V_{\mathrm{de}}}\right)}^2\right].$$ (2.4)

While μ_eff(F) is independent of F, D_eff(F) monotonically increases with the driving force approaching its large-F asymptotic behavior, D_eff(F)∝F² as F → ∞.

Formulas for the effective mobility and diffusion coefficient, Eqs. 2.2, 2.3, are main results of the present paper.

Numerical tests

To check the accuracy of our results, Eqs. 2.2, 2.3, we compare theoretically predicted effective drift velocity, v_eff(F) = μ_eff(F)F, and diffusion coefficient, D_eff(F), with those obtained from Brownian dynamics simulations. The comparison is made assuming that there are no connecting channels, i.e., L = 0. In this case the ratio $⟨{\tau }_{\mathrm{de}}^2⟩∕{⟨{\tau }_{\mathrm{de}}⟩}^2$, Eq. 2.4, is equal to four, and Eq. 2.3 takes the form

$$\begin{array}{c}\hfill \frac{D_{\mathrm{eff}}\left(F\right)}{D_{\mathrm{eff}}\left(0\right)}=1+\frac{V_{\mathrm{de}}^2}{{\left(V_{\mathrm{tube}}+V_{\mathrm{de}}\right)}^2}\left[\frac{\tilde{F}∕2}{\tanh \left(\tilde{F}∕2\right)}-1+\frac{\pi R^2}{2al}{\tilde{F}}^2\right].\end{array}$$ (2.5)

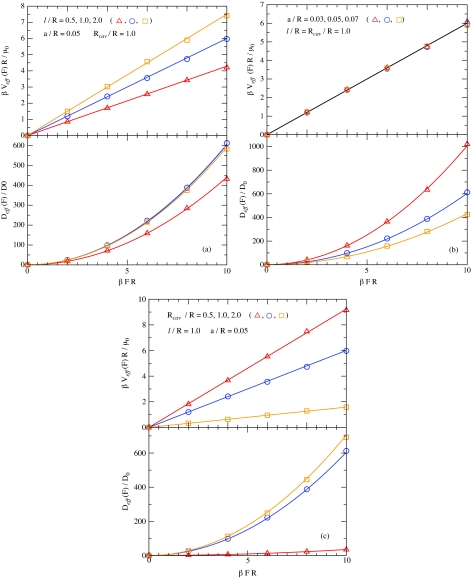
In Fig. 3 we show v_eff(F) and D_eff(F) obtained numerically by circles while solid lines show theoretically predicted dependences.

Figure 3.

Dependences v_eff(F) and D_eff(F) at different values of the geometric parameters of the tube: l∕R = 0.5, 1.0, 2.0, a∕R = 0.05, and R_cav∕R = 1.0 in panel (a); l∕R = 1.0, a∕R = 0.03, 0.05, 0.07, and R_cav∕R = 1.0 in panel (b); l∕R = 1.0, a∕R = 0.05, and R_cav∕R = 0.5, 1.0, 2.0 in panel (c). Solid lines are drawn using the theoretical predictions, Eqs. 2.5, 2.6; symbols represent results obtained from Brownian dynamics simulations.

According to Eq. 2.2, the effective mobility is independent of the driving force. As a consequence, the effective drift velocity is proportional to the driving force (Ohm’s law) and given by

$$v_{\mathrm{eff}}\left(F\right)={\mu }_0\frac{V_{\mathrm{tube}}}{V_{\mathrm{tube}}+V_{\mathrm{de}}}F.$$ (2.6)

We will assume that the dead end cavities are spheres of radius R_cav connected to the cylindrical part of the tube by small apertures of radius a, a ≪ R_cav. Thus, the system geometry is characterized by four-dimensional parameters: R, l, a, and R_cav, and, hence, three-dimensionless parameters: l∕R, a∕R, and R_cav∕R.

Panel (a) in Fig. 3 shows v_eff(F) and D_eff(F) at different values of the tube period, l∕R = 0.5, 1.0, and 2.0, at a∕R = 0.05 and R_cav∕R = 1.0. Panel (b) shows the results at different sizes of the connecting aperture, a∕R = 0.03, 0.05, and 0.07, at l∕R = R_cav∕R = 1.0. Panel (c) shows the results at different values of the cavity radius, R_cav∕R = 0.5, 1.0, and 2.0, at l∕R = 1.0 and a∕R = 0.05. One can see excellent agreement between the theoretically predicted and numerically obtained results.

DERIVATION

In this section we derive the formulas for the effective mobility and diffusion coefficient. First, we map the particle motion onto a random walk. Then we find the random walk propagator and use it to obtain the desired results.

Random walk

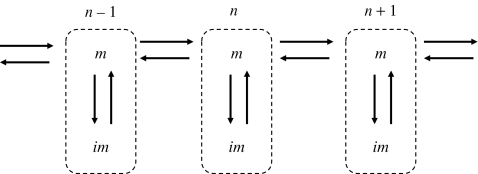
Let us label each dead end with number n, n = 0, ±1, ±2, .... These numbers enumerate the sites of the random walk, each site of which contains mobile and immobile states (Fig. 4). Consider a particle that starts from the tube cross section containing the entrance to the dead end with n = 0. We will assume that the random walk is in the discrete mobile state of the site with n = 0 until the particle enters the dead end or touches for the first time one of the cross sections containing entrances into the neighboring dead ends with n = ±1. We consider the particle entrance into the dead end as a transition of the random walk from the mobile to immobile state of the same site. The first particle touch of one of the cross sections containing entrances into neighboring dead ends, we consider as a transition of the random walk between mobile states of the neighboring sites. Repeating this procedure we can map the particle motion onto the random walk as shown in Fig. 4. The random walk can jump between neighboring sites only when it is in a mobile state, from which it can also jump to the immobile state of the same site.

Figure 4.

Random walk equivalent to the particle motion in a tube with identical periodic dead ends.

The random walk is described by a two-component propagator, P_{n, α}(t), α = m,  im, which is the probability of finding the random walk on site n in state α at time t. The components of the propagator satisfy,

$$P_{n,\alpha }\left(t\right)={\int }_0^t{S}_{\alpha }(t-t^{\prime })J_{n,\alpha }\left(t^{\prime }\right)d{t}^{\prime },$$ (3.1)

where S_α(t) is the survival probability of the random walk in state α for time t, and J_{n, α}(t) is the probability flux entering the state (n, α) at time t. Transitions among the states (Fig. 5) are described by splitting probabilities W_± and W₀, W₊ + W₋ + W₀ = 1, and probability densities of the waiting time distributions φ_±(t), φ₀(t), and φ_im(t), normalized to unity. The splitting probabilities W_± and W₀ are probabilities that the random walk starting from state (n, m) makes a step to states (n ± 1, m) and (n, im), respectively. Introducing the probability fluxes escaping from the mobile state of a site at time t on condition that the random walk enters this state at t = 0, w_±(t) = W_±φ_±(t) and w₀(t) = W₀φ₀(t), we can write the survival probability in this state as

$$S_{\mathrm{m}}\left(t\right)=1-{\int }_0^t\left[w_{+}\left(t^{\prime }\right)+w_{-}\left(t^{\prime }\right)+w_0\left(t^{\prime }\right)\right]d{t}^{\prime }.$$ (3.2)

Respectively, the survival probability in the immobile state is

$$S_{\mathrm{im}}\left(t\right)=1-{\int }_0^t{\varphi }_{\mathrm{im}}\left(t^{\prime }\right)d{t}^{\prime }.$$ (3.3)

The fluxes J_{n, α}(t) satisfy balance equations,

$$\begin{array}{ccc}\hfill J_{n,\mathrm{m}}\left(t\right)& =& {\delta }_{n,0}\delta \left(t\right)+{\int }_0^t\left[w_{+}(t-t^{\prime })J_{n-1,\mathrm{m}}\left(t^{\prime }\right)\right.\hfill \\ & & \left.+w_{-}(t-t^{\prime })J_{n+1,\mathrm{m}}\left(t\right)+{\varphi }_{\mathrm{im}}(t-t^{\prime })J_{n,\mathrm{im}}\left(t^{\prime }\right)\right]d{t}^{\prime },\hfill \end{array}$$ (3.4)

$$J_{n,\mathrm{im}}\left(t\right)={\int }_0^t{w}_0(t-t^{\prime })J_{n,\mathrm{m}}\left(t^{\prime }\right)d{t}^{\prime },$$ (3.5)

where the first term on the right-hand side of Eq. 3.4 is due to the initial condition according to which the random walk starts from the mobile state of the site with n = 0 at t = 0.

Figure 5.

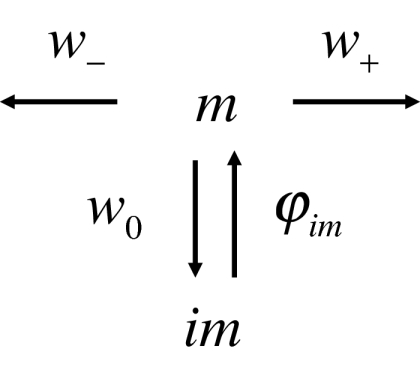
Possible transitions of the random walk.

The Laplace transforms of the probability fluxes w_±(t) and w₀(t) as well as the splitting probabilities W_± and W₀ are derived in Appendix A. The results are (the Laplace transform of function f(t) is defined by $\widehat{f}\left(s\right)={\int }_0^{\infty }{e}^{-st}f\left(t\right)dt$),

$${\displaystyle W_{\pm }=\frac{{\displaystyle \frac{1}{2}\exp \left({\displaystyle \pm \frac{\beta Fl}{2}}\right)}}{{\displaystyle \cosh \left({\displaystyle \frac{\beta Fl}{2}}\right)+\frac{\kappa }{\beta F{D}_0}\sinh \left({\displaystyle \frac{\beta Fl}{2}}\right)}},}$$ (3.6)

$${\displaystyle W_0=\frac{1}{{\displaystyle 1+\frac{\beta F{D}_0}{\kappa }\coth \left({\displaystyle \frac{\beta Fl}{2}}\right)}},}$$ (3.7)

$${\displaystyle {\widehat{w}}_{+}\left(s\right)=\frac{\sqrt{{\displaystyle \frac{s}{D_0}+{\left({\displaystyle \frac{\beta F}{2}}\right)}^2}}\exp \left({\displaystyle \frac{\beta Fl}{2}}\right)}{{\displaystyle \frac{\kappa }{D_0}\sinh \left(l\sqrt{{\displaystyle \frac{s}{D_0}+{\left({\displaystyle \frac{\beta F}{2}}\right)}^2}}\right)+2\sqrt{{\displaystyle \frac{s}{D_0}+{\left({\displaystyle \frac{\beta F}{2}}\right)}^2}}\cosh \left(l\sqrt{{\displaystyle \frac{s}{D_0}+{\left(\frac{\beta F}{2}\right)}^2}}\right)}},}$$ (3.8)

$${\widehat{w}}_{-}\left(s\right)=\exp \left(-\beta Fl\right){\widehat{w}}_{+}\left(s\right),$$ (3.9)

$$\begin{array}{c}\hfill {\displaystyle {\widehat{w}}_0\left(s\right)=\frac{1}{{\displaystyle 1+\frac{2D_0}{\kappa }\sqrt{\frac{s}{D_0}+{\left({\displaystyle \frac{\beta F}{2}}\right)}^2}\coth \left(l\sqrt{{\displaystyle \frac{s}{D_0}+{\left({\displaystyle \frac{\beta F}{2}}\right)}^2}}\right)}},}\end{array}$$ (3.10)

where κ is given by κ = 4D₀a∕(πR²). The expressions above show that the ratio of probabilities W₊ and W₋, W₋∕W₊ = exp (βFl), is independent of the presence of the dead ends since it depends only on the tube period l. One can also find the Laplace transforms of the probability densities φ_±(t), ${\widehat{\varphi }}_{\pm }\left(s\right)={\widehat{w}}_{\pm }\left(s\right)∕W_{\pm }$. Then one can check that these Laplace transforms are identical ${\widehat{\varphi }}_{+}\left(s\right)={\widehat{\varphi }}_{-}\left(s\right)$ and, hence, φ₊(t) = φ₋(t). Although these might seem unexpected, in fact, they are straightforward consequences of the results obtained in Ref. 21.

In addition, we will use the Laplace transform of the probability density of the particle lifetime in the dead end, φ_im(t), which can be found in Ref. 7,

$${\displaystyle {\widehat{\varphi }}_{\mathrm{im}}\left(s\right)=\frac{{\displaystyle (s+k_{\mathrm{cav}})\cosh \left(L\sqrt{{\displaystyle \frac{s}{D_0}}}\right)+{\kappa }_{\mathrm{ch}}\sqrt{{\displaystyle \frac{s}{D_0}}}\sinh \left(L\sqrt{{\displaystyle \frac{s}{D_0}}}\right)}}{{\displaystyle (2s+k_{\mathrm{cav}})\cosh \left(L\sqrt{{\displaystyle \frac{s}{D_0}}}\right)+\left({\displaystyle {\kappa }_{\mathrm{ch}}\sqrt{{\displaystyle \frac{s}{D_0}}}+\frac{\sqrt{s{D}_0}}{{\kappa }_{\mathrm{ch}}}(s+k_{\mathrm{cav}})}\right)\sinh \left(L\sqrt{{\displaystyle \frac{s}{D_0}}}\right)}},}$$ (3.11)

where k_cav and κ_ch are k_cav = 4D₀a∕V_cav and κ_ch = 4D₀∕(πa).

Solution for the propagator

After the Laplace transformation, Eqs. 3.4, 3.5 take the form:

$$\begin{array}{ccc}\hfill {\widehat{J}}_{n,\mathrm{m}}\left(s\right)& =& {\delta }_{n,0}+{\widehat{w}}_{+}\left(s\right){\widehat{J}}_{n-1,\mathrm{m}}\left(s\right)\hfill \\ & & +{\widehat{w}}_{-}\left(s\right){\widehat{J}}_{n+1,\mathrm{m}}\left(s\right)+{\widehat{\varphi }}_{\mathrm{im}}\left(s\right){\widehat{J}}_{n,\mathrm{im}}\left(s\right),\hfill \end{array}$$ (3.12)

$${\widehat{J}}_{n,\mathrm{im}}\left(s\right)={\widehat{w}}_0\left(s\right){\widehat{J}}_{n,\mathrm{m}}\left(s\right).$$ (3.13)

Substituting ${\widehat{J}}_{n,\mathrm{im}}\left(s\right)$ in Eq. 3.13 into Eq. 3.12 and introducing the notation,

$${\widehat{u}}_{\pm }\left(s\right)=\frac{{\widehat{w}}_{\pm }\left(s\right)}{1-{\widehat{w}}_0\left(s\right){\widehat{\varphi }}_{\mathrm{im}}\left(s\right)}.$$ (3.14)

we can write a closed-form equation for the Laplace transforms of ${\widehat{J}}_{n,\mathrm{m}}\left(s\right)$,

$$\begin{array}{ccc}\hfill {\widehat{J}}_{n,\mathrm{m}}\left(s\right)& =& \frac{1}{1-{\widehat{w}}_0\left(s\right){\widehat{\varphi }}_{\mathrm{im}}\left(s\right)}{\delta }_{n,0}\hfill \\ & & +{\widehat{u}}_{+}{\widehat{J}}_{n-1,\mathrm{m}}\left(s\right)+{\widehat{u}}_{-}{\widehat{J}}_{n+1,\mathrm{m}}\left(s\right).\hfill \end{array}$$ (3.15)

This equation can be solved by means of the generating functions. The solution obtained in Appendix B has the form

$$\begin{array}{ccc}\hfill {\widehat{J}}_{n,\mathrm{m}}\left(s\right)& =& \frac{1}{1-{\widehat{w}}_0\left(s\right){\widehat{\varphi }}_{\mathrm{im}}\left(s\right)}{\left(\frac{{\widehat{u}}_{+}\left(s\right)}{{\widehat{u}}_{-}\left(s\right)}\right)}^{n∕2}\hfill \\ & & \times \frac{1}{\widehat{K}\left(s\right)-1}{\left(\frac{2\sqrt{{\widehat{u}}_{+}\left(s\right){\widehat{u}}_{-}\left(s\right)}}{\widehat{K}\left(s\right)}\right)}^{\left|n\right|},\hfill \end{array}$$ (3.16)

where $\widehat{K}\left(s\right)$ is $\widehat{K}\left(s\right)=1+\sqrt{1-4{\widehat{u}}_{+}\left(s\right){\widehat{u}}_{-}\left(s\right)}$. Respectively, according to Eq. 3.13${\widehat{J}}_{n,\mathrm{im}}\left(s\right)$ is given by

$${\widehat{J}}_{n,\mathrm{im}}\left(s\right)={\widehat{w}}_0\left(s\right){\widehat{J}}_{n,\mathrm{m}}\left(s\right).$$ (3.17)

Next we can find the Laplace transforms of the two components of the propagator. According to Eqs. 3.1, 3.2, 3.3 they are given by

$$\begin{array}{ccc}\hfill {\widehat{P}}_{n,\mathrm{m}}\left(s\right)& =& {\widehat{S}}_{\mathrm{m}}\left(s\right){\widehat{J}}_{n,\mathrm{m}}\left(s\right)\hfill \\ & =& \frac{1-{\widehat{w}}_{+}\left(s\right)-{\widehat{w}}_{-}\left(s\right)-{\widehat{w}}_0\left(s\right)}{s}{\widehat{J}}_{n,\mathrm{m}}\left(s\right)\hfill \end{array}$$ (3.18)

and

$$\begin{array}{ccc}\hfill {\widehat{P}}_{n,\mathrm{im}}\left(s\right)& =& {\widehat{S}}_{\mathrm{im}}\left(s\right){\widehat{J}}_{n,\mathrm{im}}\left(s\right)\hfill \\ & =& \frac{{\widehat{w}}_0\left(s\right)\left(1-{\widehat{\varphi }}_{\mathrm{im}}\left(s\right)\right)}{s}{\widehat{J}}_{n,\mathrm{m}}\left(s\right).\hfill \end{array}$$ (3.19)

The ratio ${\widehat{P}}_{n,\alpha }\left(s\right)∕{\widehat{P}}_{-n,\alpha }\left(s\right)$ is independent of α and given by

$$\begin{array}{c}\hfill \frac{{\widehat{P}}_{n,\alpha }\left(s\right)}{{\widehat{P}}_{-n,\alpha }\left(s\right)}=\frac{{\widehat{J}}_{n,\mathrm{m}}\left(s\right)}{{\widehat{J}}_{-n,\mathrm{m}}\left(s\right)}={\left(\frac{{\widehat{u}}_{+}\left(s\right)}{{\widehat{u}}_{-}\left(s\right)}\right)}^n={\left(\frac{W_{+}{\widehat{\varphi }}_{+}\left(s\right)}{W_{-}{\widehat{\varphi }}_{-}\left(s\right)}\right)}^n.\end{array}$$ (3.20)

As has been mentioned above, ${\widehat{\varphi }}_{+}\left(s\right)={\widehat{\varphi }}_{-}\left(s\right)$ and W₋ = W₊exp ( − βFl). As a consequence, we arrive at the relation,

$$\frac{{\widehat{P}}_{n,\alpha }\left(s\right)}{{\widehat{P}}_{-n,\alpha }\left(s\right)}=\frac{P_{n,\alpha }\left(t\right)}{P_{-n,\alpha }\left(t\right)}=\exp \left(n\beta Fl\right),$$ (3.21)

that is the fluctuation theorem for biased diffusion in tubes with periodic dead ends.

Effective mobility

Having in hand the two-component propagator, we can find the long-time asymptotic behavior of the mean particle displacement along the tube axis, 〈Δx(t)〉 = 〈x(t)〉 − x(0), where x(t) is the particle coordinate along this axis at time t. Then we can find the effective drift velocity,

$$v_{\mathrm{eff}}\left(F\right)=\underset{t\to \infty }{lim}\frac{d⟨\Delta x\left(t\right)⟩}{dt},$$ (3.22)

and the effective mobility, μ_eff(F) = v_eff(F)∕F. For this purpose we define P_n(t) as a sum of the components of the propagator,

$$P_n\left(t\right)=P_{n,\mathrm{m}}\left(t\right)+P_{n,\mathrm{im}}\left(t\right).$$ (3.23)

Evidently P_n(t) satisfies the normalization condition:

$$\sum _{n=-\infty }^{\infty }{P}_n\left(t\right)=1.$$ (3.24)

Using P_n(t) we can find the mean displacement of the random walk in time t,

$$⟨n\left(t\right)⟩=\sum _{n=-\infty }^{\infty }n{P}_n\left(t\right).$$ (3.25)

Since at large t 〈Δx(t)〉 = l〈n(t)〉, we can write v_eff (F) as

$$v_{\mathrm{eff}}\left(F\right)=l\underset{t\to \infty }{lim}\frac{d⟨n\left(t\right)⟩}{dt}.$$ (3.26)

To find the long-time asymptotic behavior of 〈n(t)〉 we use the small-s expansion of the Laplace transform of this function. This Laplace transform, $⟨\widehat{n}\left(s\right)⟩$, can be found using the relations in Eqs. 3.16, 3.18, 3.19. The result is

$$⟨\widehat{n}\left(s\right)⟩=\frac{{\widehat{w}}_{+}\left(s\right)-{\widehat{w}}_{-}\left(s\right)}{s\left(1-{\widehat{w}}_{+}\left(s\right)-{\widehat{w}}_{-}\left(s\right)-{\widehat{w}}_0\left(s\right){\widehat{\varphi }}_{\mathrm{im}}\left(s\right)\right)}.$$ (3.27)

Using the relations in Eqs. 3.8, 3.9, 3.10, 3.11 we find that as s → 0,

$$⟨\widehat{n}\left(s\right)⟩\to \frac{\pi R^2{D}_0\beta F}{s^2\left(V_{\mathrm{tube}}+V_{\mathrm{de}}\right)}.$$ (3.28)

This implies that the large-t asymptotic behavior of the mean displacement of the random walk is given by

$$⟨n\left(t\right)⟩=\frac{\pi R^2{D}_0\beta F}{\left(V_{\mathrm{tube}}+V_{\mathrm{de}}\right)}t.$$ (3.29)

Substituting this into Eq. 3.26 and dividing the result by F we arrive at the expression for the effective mobility in Eq. 2.2.

The expression in Eq. 2.2 can be alternatively obtained from consideration of the probabilities of finding the particle in mobile and immobile states at time t. These probabilities are defined as

$$P_{\alpha }\left(t\right)=\sum _{n=-\infty }^{\infty }{P}_{n,\alpha }\left(t\right),\alpha =\mathrm{m},\mathrm{im}.$$ (3.30)

Using the relations in Eqs. 3.16, 3.18, 3.19 we find that the ratio of the Laplace transforms of P_α(t) is given by

$$\frac{{\widehat{P}}_{\mathrm{m}}\left(s\right)}{{\widehat{P}}_{\mathrm{im}}\left(s\right)}=\frac{1-{\widehat{w}}_{+}\left(s\right)-{\widehat{w}}_{-}\left(s\right)-{\widehat{w}}_0\left(s\right)}{{\widehat{w}}_0\left(s\right)\left(1-{\widehat{\varphi }}_{\mathrm{im}}\left(s\right)\right)}.$$ (3.31)

As s → 0 this ratio tends to a constant,

$$\underset{s\to 0}{lim}\frac{{\widehat{P}}_{\mathrm{m}}\left(s\right)}{{\widehat{P}}_{\mathrm{im}}\left(s\right)}=\frac{V_{\mathrm{tube}}}{V_{\mathrm{de}}}.$$ (3.32)

This implies that time spent in the mobile state by the particle observed for sufficiently long time t is equal to tV_tube∕(V_tube + V_de). During this time particle’s mobility is μ₀, so that its displacement is given byμ₀FtV _tube ∕(V _tube +V _de ). The fact that this displacement must be identical to v_eff(F)t leads to the expression for the effective mobility in Eq. 2.2.

The second derivation shed some light on the reason why the effective mobility in tubes with periodic dead ends is independent of the driving force. This independence is a consequence of the fact that the fractions of time spent by the particle in the cylindrical part of the tube and in the dead ends are independent of the driving force. As follows from Eq. 3.32 these fractions, respectively, are V_tube∕(V_tube + V_de) and V_de∕(V_tube + V_de).

Effective diffusion coefficient

The effective diffusion coefficient is defined as

$$D_{\mathrm{eff}}\left(F\right)=\frac{1}{2}\underset{t\to \infty }{lim}\frac{d}{dt}\left[⟨\Delta x{\left(t\right)}^2⟩-{⟨\Delta x\left(t\right)⟩}^2\right],$$ (3.33)

where 〈Δx(t)²〉 is the mean squared displacement of the particle in time t. At large t 〈Δx(t)²〉 is simply related to the second moment of the displacement of the random walk, 〈Δx(t)²〉 = l²〈n²(t)〉. Since at large t 〈Δx(t)〉 = l〈n(t)〉, we have

$$D_{\mathrm{eff}}\left(F\right)=\frac{l^2}{2}\underset{t\to \infty }{lim}\frac{d}{dt}\left[⟨n^2\left(t\right)⟩-{⟨n\left(t\right)⟩}^2\right].$$ (3.34)

The long-time behavior of 〈n(t)〉 can be found from the small-s expansion of $⟨\widehat{n}\left(s\right)⟩$ in Eq. 3.27. To find the long-time behavior of 〈n²(t)〉 we first find the Laplace transform $⟨{\widehat{n}}^2\left(s\right)⟩$ and then obtain the desired asymptotic behavior using the small-s expansion of $⟨{\widehat{n}}^2\left(s\right)⟩$.

The mean squared displacement of the random walk is defined as

$$⟨n^2\left(t\right)⟩=\sum _{n=-\infty }^{\infty }{n}^2{P}_n\left(t\right).$$ (3.35)

Its Laplace transform,

$$⟨{\widehat{n}}^2\left(s\right)⟩=\sum _{n=-\infty }^{\infty }{n}^2{\widehat{P}}_n\left(s\right),$$ (3.36)

can be found using the relations in Eqs. 3.16, 3.18, 3.19. The result is

$${\displaystyle ⟨{\widehat{n}}^2\left(s\right)⟩=\frac{\left({\widehat{w}}_{+}\left(s\right)+{\widehat{w}}_{-}\left(s\right)\right)\left(1-{\widehat{w}}_0\left(s\right){\widehat{\varphi }}_{im}\left(s\right)\right)+{\widehat{w}}_{+}{\left(s\right)}^2+{\widehat{w}}_{-}{\left(s\right)}^2-6{\widehat{w}}_{+}\left(s\right){\widehat{w}}_{-}\left(s\right)}{s{\left(1-{\widehat{w}}_{+}\left(s\right)-{\widehat{w}}_{-}\left(s\right)-{\widehat{w}}_0\left(s\right){\widehat{\varphi }}_{im}\left(s\right)\right)}^2}.}$$ (3.37)

One can find the small-s expansions of $⟨\widehat{n}\left(s\right)⟩$ and $⟨{\widehat{n}}^2\left(s\right)⟩$ using the relations in Eqs. 3.8, 3.9, 3.10, 3.11. Inverting these expansions one can find the leading terms of the large-t behavior of 〈n(t)〉 and 〈n²(t)〉, and then D_eff(F) by means of Eq. 3.34. Eventually, this leads to the formula for D_eff(F) given in Eq. 2.3.

CONCLUDING REMARKS

While unbiased diffusion in linear systems of periodically varying geometry has been studied both analytically and numerically, biased diffusion has been studied mainly numerically. The focus of such studies is on the dependences of the effective mobility, μ_eff(F), and diffusion coefficient, D_eff(F), on the driving force, F, and the system geometry. It has been found that in systems of different types these dependences are qualitatively different. In systems of smoothly varying geometry μ_eff(F) monotonically increases from μ_eff(0) ≪ μ₀ to μ_eff(∞) = μ₀. When the geometry changes abruptly μ_eff(F) monotonically decreases from μ_eff(0) ≪ μ₀ to μ_eff(∞) < μ_eff(0). Effective diffusion coefficient at finite F is larger than its value at F = 0, D_eff(0) < D_eff(F), in both cases. When the tube geometry changes abruptly D_eff(F) monotonically increases with the driving force. Its large-F asymptotic behavior is given by D_eff(F)∝F². In the case of smoothly changing geometry dependence D_eff(F) is nonmonotonic: D_eff(F) first increases with F, reaches its maximum, and then decreases approaching its asymptotic value D_eff(F) = D₀.

Tubes with periodic dead ends have a specific feature, namely, in such tubes it is possible to develop an analytical theory of biased diffusion. This is done in the present paper, in which we derive approximate formulas for μ_eff(F) and D_eff(F), Eqs. 2.2, 2.3. The theory predicts that the particle effective mobility is independent of the driving force and given by μ_eff(F) = μ_eff(0) = βD_eff(0). The independence of the effective mobility of the driving force is sharply in contrast with the dependences μ_eff(F) mentioned above. At the same time, dependence D_eff(F) in tubes with periodic dead ends is similar to that in periodic systems with abruptly changing geometry: the effective diffusion coefficient monotonically increases with the driving force approaching its asymptotic behavior D_eff(F)∝F² as F → ∞. The theoretically predicted dependences μ_eff(F) and D_eff(F) are in excellent agreement with the results obtained from Brownian dynamics simulations.

APPENDIX A: LAPLACE TRANSFORMS OF FLUXES w_±(t), w₀(t) AND SPLITTING PROBABILITIES W_±, W₀

To find the Laplace transforms of fluxes w_±(t) and w₀(t), ${\widehat{w}}_{\pm }\left(s\right)$ and ${\widehat{w}}_0\left(s\right)$, as well as splitting probabilities W_±, W₀, we describe the particle motion in the tube as one-dimensional biased diffusion along the tube axis on the interval of length 2l terminated by absorbing end points at x = ±l. The particle starts from the tube cross section located at x = 0 (center of the interval) that contains the entrance into the dead end with n = 0. We describe the particle entrance into the dead end as trapping by a δ-function sink of strength κ located at x = 0. Justification for this can be found in Ref. 7. The sink strength is determined by the particle diffusion coefficient, the tube radius, and the radius of the aperture, κ = 4D₀a∕(πR²).

Let G(x, t) be the particle propagator or the Green function that satisfies

$$\begin{array}{ccc}\hfill \frac{\partial G}{\partial t}& =& D_0\frac{\partial }{\partial x}\left\{e^{\beta Fx}\frac{\partial }{\partial x}\left[e^{-\beta Fx}G\right]\right\}-\kappa \delta \left(x\right)G,-l<x<l,\hfill \end{array}$$ (A.1)

with the initial condition G(x, 0) = δ(x) and boundary conditions G( − l, t) = G(l, t) = 0. After the Laplace transformation, the equation takes the form

$$\begin{array}{ccc}\hfill s\widehat{G}& =& D_0\frac{d}{dx}\left\{e^{\beta Fx}\frac{d}{dx}\left[e^{-\beta Fx}\widehat{G}\right]\right\}+\left(1-\kappa \widehat{G}\right)\delta \left(x\right),\hfill \\ & & -l<x<l,\hfill \end{array}$$ (A.2)

where $\widehat{G}(x,s)$ is the Laplace transform of the propagator. Solving this equation with the boundary conditions $\widehat{G}(-l,s)=\widehat{G}(l,s)=0$ we obtain

$$\begin{array}{ccc}\hfill \widehat{G}(x,s)& =& e^{\beta Fx∕2}A\{\sinh \left[\sigma (l+x)\right]H(-x)\hfill \\ & & +\sinh \left[\sigma (l-x)\right]H\left(x\right)\},-l<x<l,\hfill \end{array}$$ (A.3)

where H(x) is the Heaviside step function, σ² = s∕D₀ + (βF∕2)², and

$$A=\frac{1}{\kappa \sinh \left(\sigma l\right)+2D_0\sigma \cosh \left(\sigma l\right)}.$$ (A.4)

Flux w₀(t) from the mobile to immobile state of the site is defined as w₀(t) = κG(0, t). Using the solution for the Laplace transform of the propagator, Eq. A.3, we obtain the expression for the Laplace transform of w₀(t) given in Eq. 3.10. The probability W₀ of the particle entrance into the dead end is given by

$$W_0={\int }_0^{\infty }{w}_0\left(t\right)dt={\widehat{w}}_0\left(0\right).$$ (A.5)

Using this relation we obtain W₀ in Eq. 3.7 from ${\widehat{w}}_0\left(s\right)$ in Eq. 3.10.

Flux w₊(t) is defined as w₊(t) = −D₀∂G(x, t)∕∂x|_{x = l}. Respectively, the Laplace transform of this flux is given by ${\widehat{w}}_{+}\left(s\right)=-D_{0}d\widehat{G}{(x,s)∕dx|}_{x=l}$. Substituting here the Laplace transform of the propagator, Eq. A.3, we obtain the expression for ${\widehat{w}}_{+}\left(s\right)$ given in Eq. 3.8. The probability W₊ is given by

$$W_{+}={\int }_0^{\infty }{w}_{+}\left(t\right)dt={\widehat{w}}_{+}\left(0\right).$$ (A.6)

Using this relation we obtain W₊ in Eq. 3.6 from ${\widehat{w}}_{+}\left(s\right)$ in Eq. 3.8.

Flux w₋(t) is defined as w₋(t) = D₀∂G(x, t)∕∂x|_{x = −l}. Respectively, the Laplace transform of this flux is given by ${\widehat{w}}_{-}\left(s\right)=-D_{0}d\widehat{G}{(x,s)∕dx|}_{x=-l}$. Using Eq. A.3 we find that the Laplace transforms ${\widehat{w}}_{+}\left(s\right)$ and ${\widehat{w}}_{-}\left(s\right)$ satisfy the relation

$${\widehat{w}}_{-}\left(s\right)={\widehat{w}}_{+}\left(s\right)\exp (-\beta Fl).$$ (A.7)

As a consequence, similar relation is fulfilled for the fluxes w₊(t) and w₋(t):

$$w_{-}\left(t\right)=w_{+}\left(t\right)\exp (-\beta Fl).$$ (A.8)

The probability W₋ is given by

$$W_{-}={\int }_0^{\infty }{w}_{-}\left(t\right)dt={\widehat{w}}_{-}\left(0\right).$$ (A.9)

As a consequence of Eqs. A.7, A.8, probabilities W₊ and W₋ also satisfy similar relation:

$$W_{-}=W_{+}\exp (-\beta Fl),$$ (A.10)

from which it follows that the probability W₋ is given by Eq. 3.6.

APPENDIX B: SOLUTION TO EQ. 3.15

Let F(θ) be the generating function defined as

$$F\left(\theta \right)=\sum _{n=-\infty }^{\infty }{e}^{in\theta }{\widehat{J}}_{n,m}\left(s\right).$$ (B.1)

Using Eq. 3.15 we find that F(θ) satisfies

$$\begin{array}{ccc}\hfill F\left(\theta \right)& =& \frac{1}{1-{\widehat{w}}_0\left(s\right){\widehat{\varphi }}_{im}\left(s\right)}\hfill \\ & & +\left({\widehat{u}}_{+}\left(s\right)e^{i\theta }+{\widehat{u}}_{-}\left(s\right)e^{-i\theta }\right)F\left(\theta \right).\hfill \end{array}$$ (B.2)

Solving this equation we obtain

$$\begin{array}{c}\hfill F\left(\theta \right)=\frac{1}{\left(1-{\widehat{w}}_0\left(s\right){\widehat{\varphi }}_{im}\left(s\right)\right)\left(1-{\widehat{u}}_{+}\left(s\right)e^{i\theta }-{\widehat{u}}_{-}\left(s\right)e^{-i\theta }\right)}.\end{array}$$ (B.3)

We use this solution for the generating function to find ${\widehat{J}}_{n,m}\left(s\right)$,

$${\widehat{J}}_{n,m}\left(s\right)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{e}^{-in\theta }F\left(\theta \right)d\theta .$$ (B.4)

Carrying out the integration we arrive at the formula for ${\widehat{J}}_{n,m}\left(s\right)$ given in Eq. 3.16.