Quantum mechanical theory of dynamic nuclear polarization in solid dielectrics

Abstract

Microwave driven dynamic nuclear polarization (DNP) is a process in which the large polarization present in an electron spin reservoir is transferred to nuclei, thereby enhancing NMR signal intensities. In solid dielectrics there are three mechanisms that mediate this transfer—the solid effect (SE), the cross effect (CE), and thermal mixing (TM). Historically these mechanisms have been discussed theoretically using thermodynamic parameters and average spin interactions. However, the SE and the CE can also be modeled quantum mechanically with a system consisting of a small number of spins and the results provide a foundation for the calculations involving TM. In the case of the SE, a single electron–nuclear spin pair is sufficient to explain the polarization mechanism, while the CE requires participation of two electrons and a nuclear spin, and can be used to understand the improved DNP enhancements observed using biradical polarizing agents. Calculations establish the relations among the electron paramagnetic resonance (EPR) and nuclear magnetic resonance (NMR) frequencies and the microwave irradiation frequency that must be satisfied for polarization transfer via the SE or the CE. In particular, if δ, Δ < ω_0I, where δ and Δ are the homogeneous linewidth and inhomogeneous breadth of the EPR spectrum, respectively, we verify that the SE occurs when ω_M = ω_0S ± ω_0I, where ω_M, ω_0S and ω_0I are, respectively, the microwave, and the EPR and NMR frequencies. Alternatively, when Δ > ω_0I > δ, the CE dominates the polarization transfer. This two-electron process is optimized when ω_0S1−ω_0S2=ω_0I and ω_M∼ω_0S1 orω_0S2, where ω_0S1 and ω_0S2 are the EPR Larmor frequencies of the two electrons. Using these matching conditions, we calculate the evolution of the density operator from electron Zeeman order to nuclear Zeeman order for both the SE and the CE. The results provide insights into the influence of the microwave irradiation field, the external magnetic field, and the electron−electron and electron−nuclear interactions on DNP enhancements.

INTRODUCTION

In the past two decades high frequency dynamic nuclear polarization (DNP) has been utilized extensively to improve the sensitivity in high resolution magic angle spinning (MAS) experiments at magnetic fields used in contemporary NMR spectroscopy.^{1, 2, 3, 4, 5, 6, 7} The significant signal enhancements demonstrated in these experiments (currently in the range of ∼50–300)^{8, 9} have been utilized in the study of many biological systems including membranes and membrane proteins,^{10, 11, 12, 13, 14} amyloid fibrils,¹⁵ nanocrystals,¹⁶ phage particles,¹⁷ and more recently extended to applications including quadrupolar nuclei¹⁸ and surface catalysis.¹⁹ The enhancements in sensitivity demonstrated in these applications suggest that the size of molecular structures determined with MAS experiments or their precision could be extended or improved, respectively. Thus, DNP enhanced MAS experiments on biological macromolecules and on materials¹⁹ are poised to make a significant contribution to our knowledge of the structure–function relationships in these types of systems. For similar reasons DNP is also impacting magnetic resonance imaging.^{20, 21}

DNP experiments involve microwave excitation near the electron Larmor frequency, ω_0S, and generally low experimental temperatures^{17, 22, 23} to increase the spin lattice relaxation times and improve spin diffusion. In addition, an efficient polarizing agent is essential for successful high-field DNP experiments. For the first 50 years of DNP experiments, monoradicals were used for this purpose, but, recently, we demonstrated that biradicals²⁴—in particular two TEMPO molecules tethered by a short molecular linker—improve the enhancements by a factor of 3–4.^{8, 9, 24, 25} The larger electron−electron dipolar coupling in these molecules (∼20–30 MHz in the case of the biradicals TOTAPOL (Ref. ⁸) and bTbk (Ref. ⁹) versus 0.3 MHz in a 10 mM solution of TEMPO)^{8, 24} facilitates the cross effect polarization mechanism. Thus, one of the primary aims of this paper is to present a formalism that will enable the understanding of these larger enhancements and provide a basis for the improvement of DNP experiments at high magnetic fields.

In the existing literature, DNP processes are usually treated using equations of motion that relate macroscopic quantities that are averaged over an ensemble of spins.^{26, 27, 28, 29} These quantities describe thermodynamic reservoirs including the electron Zeeman, the nuclear Zeeman, and the electron–electron baths that are characterized either by measurable or estimated parameters. In most treatments the electron–electron reservoir is assumed to be homogeneously coupled via the dipolar interaction, but, at high fields and low radical concentrations, the g-anisotropy is large, the electron–electron coupling is relatively small, and therefore, the electron spin reservoir is inhomogeneously broadened. In this situation, a microscopic description of polarization transfer between the paramagnetic polarizing agent and coupled nuclei potentially provides more insight into the mechanism whereby a chosen biradical improves the observed DNP enhancement factors. Such a microscopic picture can be derived from the quantum dynamics calculations presented here.

Polarizing mechanisms for DNP in solid dielectrics include the solid effect (SE),²⁶ the cross effect (CE),^{30, 31, 32, 33, 34, 35} and thermal mixing (TM).^{28, 29} However, to simplify the framework of our description of DNP, we focus in Secs. 2, 3, 4 on the SE and the CE, which together provide an interesting comparison of the difference in efficiency between single- and two-electron polarizing agents. From an experimental perspective, they are distinguished first by comparing the relative size of three parameters: (1) the homogeneous EPR linewidth, δ, of the paramagnetic polarizing species, (2) the nuclear Larmor frequency, ω_0I, and (3) the inhomogeneous breadth, Δ, due to the g-anisotropy. When δ, Δ < ω_0I, the SE dominates the polarization process, and the enhancement maximum and minimum are observed with the microwave irradiation frequencies at ω_0S ± ω_0I. In the opposite limit, when the breadth of the EPR spectrum, Δ, is large compared to the nuclear Larmor frequency, Δ > ω_0I, then there exist two electron resonance frequencies ω_0S1 and ω_0S2 that can be separated by ω_0I, and the CE or TM emerges as the dominant mechanism. These two mechanisms are further differentiated by whether the EPR spectrum is either inhomogeneously (Δ > δ) or homogeneously (Δ ≈ δ) broadened, respectively. With respect to the microscopic physics, the number of electrons involved in a polarizing mechanism—one, two, or multiple electrons—characterizes the SE, the CE, or TM. For example, the two unpaired electrons associated with the two radical moieties of a biradical correspond to the two electrons required for the CE.²⁴ Thus, the spin dynamics of an electron–electron–nuclear system can be used to understand the function of a biradical in DNP. Furthermore, in the limit that the two electron transitions are degenerate and the spectrum is narrow, then the three-spin system reduces to the SE, which requires only a single electron–nuclear spin interaction. Finally, TM depends on the presence of a strongly coupled, multiple electron spin bath that can be viewed as an extension of the three-spin system.

Elegant quantum mechanical descriptions of an electron–nuclear system^{36, 37, 38} and an electron–electron–nuclear system³⁹ have appeared previously, the latter in connection with a description of spin correlated radical pairs and CIDNP experiments.^{40, 41} However, that discussion was concerned primarily with effects at low magnetic fields, and the effect of larger nuclear Zeeman interactions on DNP was not emphasized. The treatment of the two-spin Hamiltonian was used to understand microwave-excited electron–nuclear transitions that lead to enhancements of nuclear polarization via the SE.³⁶ Furthermore, calculations with a three-spin Hamiltonian provided an understanding of the generation of nuclear coherences with spin-correlated radical pairs and also illustrated how DNP was possible from the transient electron polarization.⁴² In contrast, in this paper we examine an alternative and systematic approach that focuses on DNP phenomena occurring with microwave irradiation at high magnetic fields and low radical concentrations.

Our presentation is aimed at clarifying the frequency matching conditions for the SE and the CE, and at evaluating the time-dependent growth of the nuclear polarization during microwave irradiation. In practice, the polarization mechanisms in DNP experiments involve an ensemble of electron and nuclear spins. Nevertheless, a simplified spin system for discussion of polarization transfers is feasible. In Sec. 2A, we describe a localized spin system that is isolated from the bulk nuclear spin system with dilute electron concentrations and containing one or two electron spins and a single nuclear spin. In Secs. II B and II C, we calculate the evolution of the density matrix in a diagonalized frame for an electron–nuclear two-spin system and an electron–electron–nuclear three-spin system. The DNP phenomenon is in fact an evolution of the electron Zeeman order to nuclear Zeeman order. Thus, we describe the systematic analytical diagonalization of multispin Hamiltonians and the following extraction of the effective microwave operators that transfer the electron Zeeman operators to the nuclear Zeeman operator. In Sec. 3, we present experimental data that illustrates the frequency matching conditions discussed above, and in Sec. 4 we summarize and compare the influence of the microwave field and the external magnetic field on the SE and the CE.

THEORY

Polarization transfer in electron–nuclear spin systems

DNP involves polarization transfer processes between the electron and nuclear spin systems that are in contact with a lattice and are governed by the following generalized Hamiltonian:

$$\begin{array}{ccc}\hfill H& =& H_S+H_I+H_{SS}+H_{IS}+H_{II}\hfill \\ & & +H_M+H_{SL}+H_{IL}+H_L,\hfill \end{array}$$ (1)

where H_S and H_I are the Zeeman Hamiltonians of the electron spins S and nuclear spins I, H_SS, H_IS, and H_II describe the electron–electron, the electron–nuclear, and nuclear–nuclear couplings, H_M accounts for the microwave excitation, H_SL and H_IL are the spin–lattice interactions, and H_L is a generalized lattice interaction. The important terms in the Hamiltonian for DNP are H_S, H_I, H_IS, and in cases considered here, H_SS. Further, in situations with diluted electron concentrations, H_II mediates the propagation of enhanced nuclear polarization throughout the bulk nuclei. Concurrently, the coupling of the electron and nuclear relaxation due to H_SL, H_IL, and H_L regulates the efficiency of polarization transfer in DNP. To simplify the quantum mechanical calculations, we limit the size of the spin system, and discuss the approximations required for focusing on polarization transfers involving the terms H_S, H_I, H_SS, and H_IS that are combined into H₀ in the following derivations.

Figure 1 is a schematic representation of polarization transfer in a DNP experiment. The electron spin polarization initially propagates to coupled nuclei residing outside a “diffusion barrier” (Region A) and subsequently throughout the bulk nuclei (Region B) via homonuclear spin diffusion. Note that nuclear spins inside the barrier, which experiments suggest has a typical radius of ≤3 Å for a paramagnetic metal ion,⁴³ are effectively isolated from the bulk nuclear spin diffusion by the strong electron–nuclear coupling. In particular, the electron−nuclear couplings shift the resonances of the near neighbor nuclei^{43, 44} so that they interact weakly with the bulk. Thus, the DNP process involves electron spins and nuclear spins immediately outside Region A. However, in the case of bulky organic radicals such as TOTAPOL,⁸ bTbk,⁹ BDPA (Ref. ⁴⁵) or trityl,⁴⁶ which are commonly used in contemporary DNP experiments, the spin density is distributed over part or the whole molecule. Thus, the barrier between regions A and B is probably less well-defined, and, accordingly, the polarization and subsequent spin diffusion steps are likely to be more complex than the simplified picture depicted in Fig. 1.

Figure 1.

A schematic representation of polarization transfer in DNP experiments. Region B represents the observable bulk nuclei. Region A represents the paramagnetic center and nuclei within the diffusion barrier. The electron polarization is transferred to a nuclear spin with a strong hyperfine interaction but residing outside region A. The enhanced polarization then propagates throughout the bulk nuclei via homonuclear spin diffusion.

The microwave-excited electron–nuclear transitions responsible for the steady-state enhancement ɛ_SS can be discussed in the eigenbasis set of the Hamiltonian H₀ of a spin system composed of electron spins with S_i = 1/2 and a nuclear spin with I = 1/2. Specifically, H₀ is

$$\begin{array}{ccc}\hfill H_0& =& \sum _i{\omega }_{0S_i}{S}_{iz}+\sum _{i,j>i}[d_{ij}(3S_{iz}{S}_{jz}-{\mathrm{S}}_i·{\mathrm{S}}_j)-2J_{ij}{\mathrm{S}}_i·{\mathrm{S}}_j]\hfill \\ & & -{\omega }_{0I}{I}_z+\sum _i(A_i{S}_{iz}{I}_z+B_i{S}_{iz}{I}_x),\hfill \end{array}$$ (2)

where ω_0Si and ω_0I are the Larmor frequencies of the electrons and the nucleus, d_ij and J_ij are the dipolar interaction and exchange integral, respectively, between electron spins i and j, A_i and B_i are the coefficients of the secular and nonsecular terms of the hyperfine interactions, respectively. Note that both the electron−electron and electron−nuclear dipolar interactions are truncated by the high EPR frequency, and that J_ij is an isotropic quantity whereas d_ij depends on the orientation of the dipolar vector. The S_izI_x term is sufficient to describe the nonsecular hyperfine interaction after a rotation of the spin operator along S_izI_z, and A_i and B_i can be treated as average quantities for a randomly oriented powder sample. In addition, the Hamiltonian of the microwave field, H_M, for DNP is defined as

$$H_M\equiv 2{\omega }_{1S}\cos \left({\omega }_{M}t\right)\sum _i{S}_{ix},$$ (3)

where ω_M and ω_1S are the frequency and amplitude of the microwave irradiation, respectively.

The evolution of the electron–nuclear (or the three spin electron–electron–nuclear) spin system in the presence of a microwave field is conveniently described in the eigen basis-sets (EBS) of H₀. The unitary transformation(s) discussed below can be used to transform the spin operator of H_M into the EBS, rendering new spin operator terms. The importance of each spin operator term is singled out by matching ω_M with the energy difference between the eigenstates coupled by the appropriately selected operator denoted as ${\tilde{H}}_M^{\mathrm{eff}*}$.

Taking ℏ = 1, the density operator evolves according to the Liouville–von Neumann equation

$$\frac{d}{dt}{\tilde{\rho }}^{*}=-i\left[{\tilde{H}}_M^{\mathrm{eff}*},{\tilde{\rho }}^{*}\right],$$ (4)

where ${\tilde{\rho }}^{*}$ and ${\tilde{H}}_M^{\mathrm{eff}*}$ are the density operator and the effective microwave Hamiltonian, respectively, in the eigen basis-sets (tilde) and the interaction frame (asterisk) that is defined by ω_M. The time-independent ${\tilde{H}}_M^{\mathrm{eff}*}$ leads to time-evolution of ${\tilde{\rho }}^{*}$ in the usual manner

$${\tilde{\rho }}^{*}\left(t\right)=\exp \left(-i{\tilde{H}}_M^{\mathrm{eff}*}t\right){\tilde{\rho }}_0^{*}\exp \left(i{\tilde{H}}_M^{\mathrm{eff}*}t\right).$$ (5)

As mentioned above the DNP mechanisms operative in solid dielectrics are distinguished by the number of electrons involved in Eq. 2 and describe polarization transfer from single (SE), a pair (CE) and multiple (TM) electron spins, respectively, to the dipolar coupled nuclear spin. This is shown in Fig. 2 where the energy level diagrams appropriate for the S_i = I = 1/2 basis functions |_αSi⟩,|_βSi⟩,|α_I⟩,|β_I⟩ are illustrated. The SE arises from a single electron−nuclear interaction, and the DNP and electron−nuclear double resonance transitions excited by the microwave field [indicated as dashed arrows in Fig. 2a] are partially allowed due to the mixing of states |1〉 and |3〉 and the mixing of states |2〉 and |4〉 by terms in the electron–nuclear dipole Hamiltonian of the form S_zI_±. Note that double-quantum (flip-flip) and zero-quantum (flip-flop) transitions occur between states |1〉 and |4〉, and |2〉 and |3〉. Applying first order perturbation theory leads to a mixing coefficient that governs the probabilities of the above transitions and is proportional to ${\omega }_{0I}^{-2}$. Thus, the efficiency of the SE scales with ${\omega }_{0I}^{-2}$, where ω_0I is the nuclear Larmor frequency.²⁶

Figure 2.

Quantum mechanical picture of the electron–nuclear transitions (dashed arrows) in (a) the SE, (b) the CE and (c) TM mechanisms, which involve one, two or multiple electron spins, respectively. Note that the probabilities of electron–nuclear transitions are always small in the SE but could be large in the CE and TM when degeneracy exists between the states with alternating nuclear spin quantum numbers.

In the case of the CE [Fig. 2b] there are two participating electrons—S₁ and S₂—and a single nuclear spin I, and there are now eight energy levels to consider. Microwave transitions occur between the levels connected with the dashed lines and result from the mixing of states |2〉 and |7〉, or the mixing of states |3〉 and |6〉 if γ_I < 0. The mixing results from electron−electron and electron−nuclear interactions and becomes important when the degeneracy is provided by the frequency matching condition|ω_0S1−ω_0S2|=ω_0I. The frequency matching mentioned here implies electron−electron dipole couplings (∼25 MHz) that are smaller than the EPR frequency separation arising from inhomogeneous interactions such as g- and hyperfine anisotropies (≥600 MHz at 5 T). However, stronger electron−electron interactions are possible and lead to a different regime of frequency matching, in which the dipolar or hyperfine couplings approximate ω_0I. We briefly discuss this strong electron–electron coupling regime for the CE in the Appendix.

TM shares many features with the CE but is due to the coupling of multiple, rather than two, electrons in the paramagnetic center. Weak couplings among those electrons produce the manifolds of states illustrated in Fig. 2c. Similar to the frequency matching condition in the CE, the energy overlap between manifolds is required for maximizing the probabilities of electron−nuclear transitions. Since the TM is related to the CE, our calculations are focused on the SE and the CE and are aimed at understanding the important parameters that can be controlled to improve DNP at high magnetic fields.

The SE in an electron–nuclear spin system

The SE is based on the polarization transfer between a single electron and a nuclear spin described by the time-independent Hamiltonian [simplified from Eq. 2]

$$H_0^{\mathit{IS}}={\omega }_{0S_1}{S}_{1z}-{\omega }_{0I}{I}_z+A_1{S}_{1z}{I}_z+B_1{S}_{1z}{I}_x$$ (6)

that can be represented in the product spin basis (PSB) as shown in Fig. 3. Note that $H_0^{\mathit{IS}}$ is used to describe the static electron–nuclear Hamiltonian, which contains contributions from the terms H_S, H_I and H_IS in Eq. 1.

Figure 3.

A level diagram of an electron–nuclear system. Transition energies of EPR/NMR and couplings between product spin states are calculated to the first order. The DNP transitions leading to positive and negative enhancements are indicated by the solid and dashed arrows, respectively. Note that E_ij = E_i− E_j and H_ij = 〈i|H|j〉.

Diagonalization of a two-spin Hamiltonian

The diagonalization of an electron–nuclear spin Hamiltonian is relatively straightforward and examples can be found in the literature.³⁷ Here, we outline the procedure for completeness and as a basis for our discussion of the diagonalization of the CE Hamiltonian (see Sec. 2C). The diagonalization of $H_0^{\mathit{IS}}$ to ${\tilde{H}}_0^{\mathit{IS}}$ is achieved by the following unitary transformation:

$${\tilde{H}}_0^{\mathit{IS}}=U_{\eta }{H}_0^{\mathit{IS}}{U}_{\eta }^{-1}.$$ (7)

In order to take advantage of the block diagonal structure of the Hamiltonian, it is easier to rewrite $H_0^{\mathit{IS}}$ and the propagator U_η using the polarization operators $S_1^{\alpha }$ and $S_1^{\beta }$. These operators correspond to the two subspaces in the PSB (Fig. 3) and can be defined as

$$\begin{array}{cc}\hfill S_1^{\alpha }\equiv \frac{1}{2}E+S_{1z},& \hfill \text{for}\text{the}\text{subspace}\left\{|1⟩,|3⟩\right\},\\ \hfill S_1^{\beta }\equiv \frac{1}{2}E-S_{1z},& \hfill \text{for}\text{the}\text{subspace}\left\{|2⟩,|4⟩\right\}.\end{array}$$ (8)

In this representation, the propagator U_η has the form

$$U_{\eta }=\exp \left[i\left({\eta }_{\alpha }{S}_1^{\alpha }{I}_y+{\eta }_{\beta }{S}_1^{\beta }{I}_y\right)\right],$$ (9)

where the scalar coefficients [−π/2 < (η_α and η_β) < π/2] satisfy the following relations:

$$\tan {\eta }_{\alpha }=\frac{B_1}{A_1-2{\omega }_{0I}},\tan {\eta }_{\beta }=\frac{B_1}{A_1+2{\omega }_{0I}}.$$ (10)

The angles η_α and η_β define the directions of the effective frequency vectors ω_α and ω_β with respect to B₀ (Fig. 4), where each vector describes the effective magnetic field experienced by the nuclear spins in the α (|1〉, |3〉) or β (|2〉, |4〉) subspace.

Figure 4.

Effective frequency vectors in the α and β subspaces of the PSB representation. A₁, B₁, and ω_0I are assumed to be positive.

Using Eq. 6, 7, 9, we obtain the Hamiltonian ${\tilde{H}}_0^{\mathit{IS}}$:

$$\begin{array}{ccc}\hfill {\tilde{H}}_0^{\mathit{IS}}& =& {\omega }_{0S_1}{S}_{1z}+S_1^{\alpha }\left[\left(-{\omega }_{0I}+\frac{1}{2}{A}_1\right)\left(I_z\cos {\eta }_{\alpha }-I_x\sin {\eta }_{\alpha }\right)+\frac{1}{2}{B}_1\left(I_x\cos {\eta }_{\alpha }+I_z\sin {\eta }_{\alpha }\right)\right]\hfill \\ & & +S_1^{\beta }\left[\left(-{\omega }_{0I}-\frac{1}{2}{A}_1\right)\left(I_z\cos {\eta }_{\beta }-I_x\sin {\eta }_{\beta }\right)-\frac{1}{2}{B}_1\left(I_x\cos {\eta }_{\beta }+I_z\sin {\eta }_{\beta }\right)\right].\hfill \end{array}$$ (11)

The values for the coefficients η_α and η_β illustrated in Fig. 4 and Eq. 10 ensure that the off-diagonal terms in ${\tilde{H}}_0^{\mathit{IS}}$ disappear, so that ${\tilde{H}}_0^{\mathit{IS}}$ is now diagonal and can therefore be expressed in its EBS representation. Furthermore, the diagonal terms in ${\tilde{H}}_0^{\mathit{IS}}$ can be rearranged, so that the Hamiltonian adopts the more familiar form

$${\tilde{H}}_0^{\mathit{IS}}={\omega }_{0S_1}{S}_{1z}-{\tilde{\omega }}_{0I}{I}_z+{\tilde{A}}_1{S}_{1z}{I}_z,$$ (12)

where the coefficients are

$$\begin{array}{ccc}\hfill {\tilde{\omega }}_{0I}& =& \frac{1}{2}{\omega }_{0I}(\cos {\eta }_{\alpha }+\cos {\eta }_{\beta })-\frac{1}{4}{A}_1(\cos {\eta }_{\alpha }-\cos {\eta }_{\beta })\hfill \\ & & -\frac{1}{4}{B}_1(\sin {\eta }_{\alpha }-\sin {\eta }_{\beta }),\hfill \end{array}$$ (13)

$$\begin{array}{ccc}\hfill {\tilde{A}}_1& =& -{\omega }_{0I}(\cos {\eta }_{\alpha }-\cos {\eta }_{\beta })+\frac{1}{2}{A}_1(\cos {\eta }_{\alpha }+\cos {\eta }_{\beta })\hfill \\ & & +\frac{1}{2}{B}_1(\sin {\eta }_{\alpha }+\sin {\eta }_{\beta }).\hfill \end{array}$$ (14)

The microwave Hamiltonian in the EBS

The microwave Hamiltonian in the PSB and the laboratory frame is given by

$$H_M=2{\omega }_{1S}{S}_{1x}\cos \left({\omega }_{M}t\right),$$ (15)

H_M should be transformed from the PSB to the EBS by the same propagator U_η [Eq. 9] using the expression

$${\tilde{H}}_M=2{\omega }_{1S}\cos \left({\omega }_{M}t\right)U_{\eta }{S}_{1x}{U}_{\eta }^{-1}.$$ (16)

In this case it is easier to keep the product operators S_1z and E (identity) in the equation for the propagator U_η instead of the polarization operators $S_1^{\alpha }$ and $S_1^{\beta }$:

$$U_{\eta }=\exp [i\left({\eta }_{\alpha }-{\eta }_{\beta }\right)S_{1z}{I}_y+\frac{i}{2}\left({\eta }_{\alpha }+{\eta }_{\beta }\right)I_y].$$ (17)

Using Eqs. 16, 17, and substituting the raising and lowering operators for S_1x, S_1y, and I_y, yields the following expression for ${\tilde{H}}_M$:

$$\begin{array}{ccc}\hfill {\tilde{H}}_M& =& 2{\omega }_{1S}\cos \left({\omega }_{M}t\right)\{S_{1x}\cos \frac{{\eta }_{\alpha }-{\eta }_{\beta }}{2}\hfill \\ & & -\frac{1}{2}(S_1^{+}{I}^{-}+S_1^{-}{I}^{+})\sin \frac{{\eta }_{\alpha }-{\eta }_{\beta }}{2}\hfill \\ & & +\frac{1}{2}(S_1^{+}{I}^{+}+S_1^{-}{I}^{-})\sin \frac{{\eta }_{\alpha }-{\eta }_{\beta }}{2}\}.\hfill \end{array}$$ (18)

In Eq. 18, either the zero quantum term, $S_1^{+}{I}^{-}+S_1^{-}{I}^{+}$, or the double quantum term, $S_1^{+}{I}^{+}+S_1^{-}{I}^{-}$, of ${\tilde{H}}_M$ mediates the DNP process. The selection of those terms is made by matching the microwave frequency ω_M to the oscillation frequency of each term of ${\tilde{H}}_M$ in the interaction frame of ${\tilde{H}}_0^{\mathit{IS}}$ [see Eq. 12]. For this purpose, the following transformations are useful:

$$\begin{array}{ccc}& & e^{i{\tilde{H}}_0^{\mathit{IS}}t}\frac{1}{2}(S_1^{+}{I}^{-}+S_1^{-}{I}^{+})e^{-i{\tilde{H}}_0^{\mathit{IS}}t}\hfill \\ & & =\frac{1}{2}{S}_1^{+}{I}^{-}\exp \left[i({\omega }_{0S_1}+{\tilde{\omega }}_{0I})t\right]+\frac{1}{2}{S}_1^{-}{I}^{+}\mathrm{c}.\mathrm{c}.,\hfill \end{array}$$ (19)

$$\begin{array}{ccc}& & e^{i{\tilde{H}}_0^{\mathit{IS}}t}\frac{1}{2}(S_1^{+}{I}^{+}+S_1^{-}{I}^{-})e^{-i{\tilde{H}}_0^{\mathit{IS}}t}\hfill \\ & & =\frac{1}{2}{S}_1^{+}{I}^{+}\exp \left[i({\omega }_{0S_1}-{\tilde{\omega }}_{0I})t\right]+\frac{1}{2}{S}_1^{-}{I}^{-}\mathrm{c}.\mathrm{c}.,\hfill \end{array}$$ (20)

where c.c. denotes the complex conjugate of the exponentials.

Polarization transfer during microwave excitation

As indicated in Fig. 3, a positive enhancement of the nuclear polarization is observed following the onset of microwave irradiation atω_M∼ω_0S1−ω_0I. Specifically, according to Eq. 20, the $S_1^{+}{I}^{+}+S_1^{-}{I}^{-}$ term is selected when ${\omega }_M={\omega }_{0S_1}-{\tilde{\omega }}_{0I}$, and drives the polarization transfer. In this case, the effective Hamiltonian in the interaction frame contains the double quantum terms and has the following form:

$${\tilde{H}}_M^{\mathrm{eff}*}={\omega }_{1S}\sin \frac{{\eta }_{\alpha }-{\eta }_{\beta }}{2}\frac{1}{2}(S_1^{+}{I}^{+}+S_1^{-}{I}^{-}).$$ (21)

Under the condition thatω_0S1≫ω_0I, the initial density operator is

$${\tilde{\rho }}_0^{*}={\tilde{\rho }}_0\approx -\frac{1}{Z}\frac{\hslash }{k_{B}T}{\omega }_{0S_1}{S}_{1z},$$ (22)

where T is the temperature and ℏ, k_B are the Planck (ℏ = h/2π) and Boltzmann constants, while Z is the spin system's partition function. Note that the nuclear Zeeman order is excluded from ${\tilde{\rho }}_0$, since the initial nuclear polarization is much smaller than the nuclear polarization generated by DNP. Namely, the enhancement factor can be defined as

$$\varepsilon \equiv \frac{⟨P_I⟩\left(t\right)}{{⟨P_I⟩}_{\mathrm{eq}}},$$ (23)

where 〈P_I〉_eq is the thermal equilibrium nuclear polarization

$${⟨P_I⟩}_{\mathrm{eq}}=Tr\left(I_z·\frac{-\hslash }{Z{k}_{B}T}{H}_0^{\mathit{IS}}\right)\approx \frac{\hslash {\omega }_{0I}}{Z{k}_{B}T},$$ (24)

while the nuclear polarization at any time t during DNP is

$$⟨P_I⟩\left(t\right)=Tr\left({\tilde{P}}_I^{*}{\tilde{\rho }}^{*}\right).$$ (25)

Note that in Eq. 25 the nuclear polarization operator in the appropriate frame is

$$\begin{array}{ccc}\hfill {\tilde{P}}_I^{*}& =& e^{i{\tilde{H}}_0^{\mathit{IS}}t}{U}_{\eta }{I}_z{U}_{\eta }^{-1}{e}^{-i{\tilde{H}}_0^{\mathit{IS}}t}\hfill \\ & =& \frac{\cos {\eta }_{\alpha }+\cos {\eta }_{\beta }}{2}{I}_z-\frac{\sin {\eta }_{\alpha }+\sin {\eta }_{\beta }}{4}\hfill \\ & & \times \left\{I^{+}{e}^{i(-{\tilde{\omega }}_{0I}+{\tilde{A}}_1{S}_{1z})t}+I^{-}\mathrm{c}.\mathrm{c}.\right\}\hfill \\ & & +(\cos {\eta }_{\alpha }-\cos {\eta }_{\beta })S_{1z}{I}_z-(\sin {\eta }_{\alpha }-\sin {\eta }_{\beta })S_{1z}\hfill \\ & & \times \frac{1}{2}\left\{I^{+}{e}^{i(-{\tilde{\omega }}_{0I}+{\tilde{A}}_1{S}_{1z})t}+I^{-}\mathrm{c}.\mathrm{c}.\right\};\hfill \end{array}$$ (26)

and following Eq. 5 the time-dependent density operator is

$$\begin{array}{ccc}\hfill {\tilde{\rho }}^{*}\left(t\right)& =& \exp \left(-i{\tilde{H}}_M^{\mathrm{eff}*}t\right){\tilde{\rho }}_0^{*}\exp \left(i{\tilde{H}}_M^{\mathrm{eff}*}t\right)\hfill \\ & =& \frac{\hslash }{Z{k}_{B}T}\frac{-{\omega }_{0S_1}}{2}\left[\phantom{\left(\frac{{\eta }_{\alpha }-{\eta }_{\beta }}{2}\right)}(S_{1z}-I_z)+(S_{1z}+I_z)\right.\hfill \\ & & \times \cos \left(2\sin \left(\frac{{\eta }_{\alpha }-{\eta }_{\beta }}{2}\right){\omega }_{1S}t\right)+i(S_1^{+}{I}^{+}-S_1^{-}{I}^{-})\hfill \\ & & \left.\times \sin \left(2\sin \left(\frac{{\eta }_{\alpha }-{\eta }_{\beta }}{2}\right){\omega }_{1S}t\right)\right].\hfill \end{array}$$ (27)

Therefore, the gain of nuclear polarization due to DNP is [using Eq. 25]

$$\begin{array}{ccc}\hfill ⟨P_I⟩\left(t\right)& =& \frac{\hslash }{Z{k}_{B}T}\frac{-{\omega }_{0S_1}}{2}\frac{\cos {\eta }_{\alpha }+\cos {\eta }_{\beta }}{2}\hfill \\ & & \times \left[-1+\cos \left(2\sin \left(\frac{{\eta }_{\alpha }-{\eta }_{\beta }}{2}\right){\omega }_{1S}t\right)\right].\hfill \end{array}$$ (28)

Note that when η_α and η_β are small, then $\left(\frac{\cos {\eta }_{\alpha }+\cos {\eta }_{\beta }}{2}\right)$ is close to unity. In addition, Eq. 28 is a statement that the polarization of the electron can be transferred to the nucleus. Inserting the expressions for 〈P_I〉(t) and 〈P_I〉_eq from Eqs. 28, 24 respectively, into Eq. 23 yields an expression for the theoretical enhancement of the nuclear polarization that is |γ_S/γ_I|. In the case of a ¹H nuclear spin, this ratio is ∼660, for ¹³C ∼2600 and for ¹⁵N ∼6500.

The CE in an electron–electron–nuclear spin system

Our initial experiments using TEMPO as a polarizing agent^{3, 10, 17, 47, 48, 49} demonstrated that the CE is a more efficient approach to performing DNP at high fields than is the SE. In particular, since the SE is mediated by forbidden transitions, it exhibits a ${\omega }_{0I}^{-2}$ dependence. In contrast, as we will see below, the CE enhancements scale as ${\omega }_{0I}^{-1}$ because the number of spin packets that satisfy the CE matching condition, ω_0S1−ω_0S2=ω_0I, decreases linearly with ω_0I. This field dependence has been verified experimentally by recording spectra of the same standard sample at both 140 GHz/5 T and 250 GHz/9 T and observing that the enhancement scales as (140/250).^{22, 25}

Since the CE is a polarization transfer mechanism involving three spins—two coupled electrons and one nucleus—the time-independent Hamiltonian for this spin system is derived from Eq. 2 and can be represented schematically in the PSB as shown in Fig. 5.

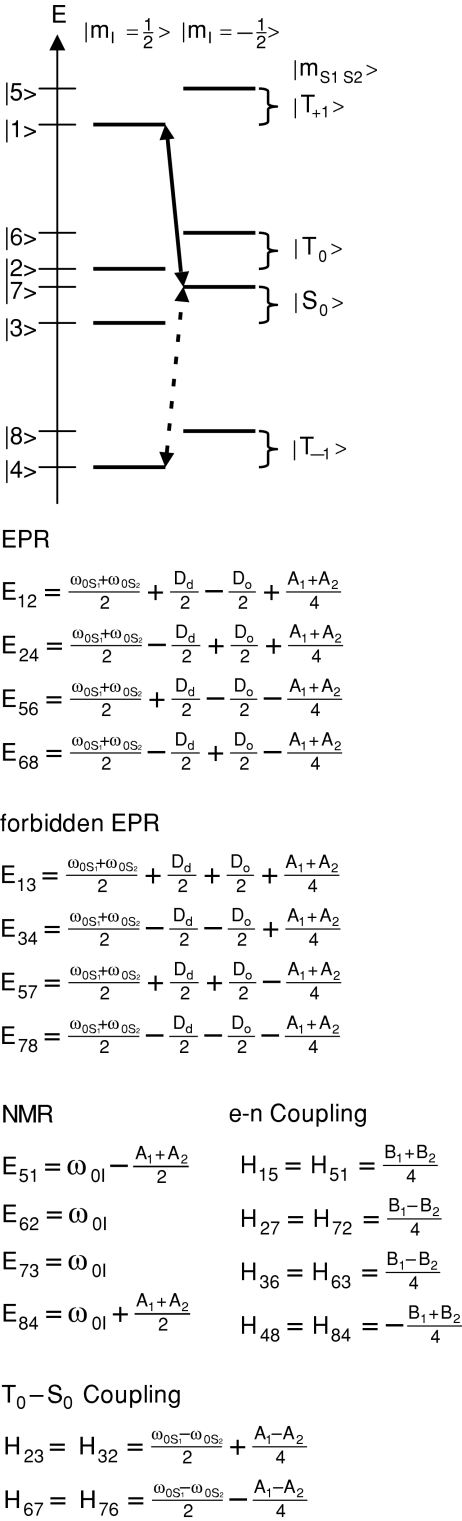
Figure 5.

A diagram of a three-spin electron–electron–nuclear system showing the energy levels associated with the various spin states. The diagonal and off-diagonal Hamiltonian terms correspond to the EPR/NMR transitions and the couplings between states, respectively. DNP transitions leading to positive and negative enhancements are indicated by the solid and dashed arrows, respectively. Note that D_d ≡ 2(d − J), and D_o ≡ −d−2J.

Diagonalization of a three-spin Hamiltonian

$$\begin{array}{ccc}\hfill H_0^{ISS}& =& {\omega }_{0S_1}{S}_{1z}+{\omega }_{0S_2}{S}_{2z}-{\omega }_{0I}{I}_z+(A_1{S}_{1z}+A_2{S}_{2z})I_z\hfill \\ & & +(B_1{S}_{1z}+B_2{S}_{2z})I_x+d(3S_{1z}{S}_{2z}-{\genfrac{}{}{0pt}{}{\rightharpoonup }{S}}_1·{\genfrac{}{}{0pt}{}{\rightharpoonup }{S}}_2)\hfill \\ & & -2J{\genfrac{}{}{0pt}{}{\rightharpoonup }{S}}_1·{\genfrac{}{}{0pt}{}{\rightharpoonup }{S}}_2,\hfill \end{array}$$ (29)

$H_0^{\mathit{ISS}}$, describing the interaction of the two electrons and a nuclear spin, is block diagonal with two 2 × 2 blocks (corresponding to {|1 〉, |5 〉} and {|4 〉, |8 〉} and one 4 × 4 block (corresponding to {|2 〉, |3 〉, |6 〉, |7 〉}). The interesting DNP phenomena are related to the mixing of states in the 4 × 4 block. Separation of the different subspaces in $H_0^{\mathit{ISS}}$ can be achieved by rewriting Eq. 29 in the following form:

$$\begin{array}{ccc}\hfill H_0^{\mathit{ISS}}& =& {\omega }_{\Sigma }{S}_{\Sigma z}+{\omega }_{\Delta }{S}_{\Delta z}-{\omega }_{0I}{I}_z+(A_{\Sigma }{S}_{\Sigma z}+A_{\Delta }{S}_{\Delta z})I_z\hfill \\ & & +D_d{S}_{1z}{S}_{2z}+(B_{\Sigma }{S}_{\Sigma z}+B_{\Delta }{S}_{\Delta z})I_x+D_o{S}_{\Delta x}.\hfill \end{array}$$ (30)

Note that the form of $H_0^{\mathit{ISS}}$ in Eq. 30 uses the sum (S_Σ) and difference (S_Δ) operators, defined in Table 1, and the following coefficients:

$$\begin{array}{ccc}& {\omega }_{\Sigma }={\omega }_{0S_1}+{\omega }_{0S_2},{\omega }_{\Delta }={\omega }_{0S_1}-{\omega }_{0S_2},& \hfill \\ & A_{\Sigma }=A_1+A_2,A_{\Delta }=A_1-A_2,& \hfill \\ & B_{\Sigma }=B_1+B_2,B_{\Delta }=B_1-B_2,& \hfill \\ & D_d=2(d-J),D_o=-(d+2J).\end{array}$$ (31)

Table 1.

Definitions of the operators used in the diagonalization of the CE Hamiltonian [Eqs. 30, 42, 47].

Reference	Definition	Subspace
Equation 30	$\begin{array}{c}{S}_{\Sigma z}=\frac{1}{2}(S_{1z}+S_{2z}),S_{\Sigma x}=\frac{1}{2}(S_1^{+}{S}_2^{+}+S_1^{-}{S}_2^{-}),S_{\Sigma y}=\frac{1}{2i}(S_1^{+}{S}_2^{+}-S_1^{-}{S}_2^{-}),\hfill \end{array}$	|1〉, |4〉, |5〉, |8〉
Equation 42	$\begin{array}{c}{E}_{S\Sigma }=4S_{\Sigma z}^2,S_{\Sigma }^{\alpha }=\frac{1}{2}{E}_{S\Sigma }+S_{\Sigma z},S_{\Sigma }^{\beta }=\frac{1}{2}{E}_{S\Sigma }-S_{\Sigma z},S_{\Sigma }^{+}=S_{\Sigma x}+i{S}_{\Sigma y},S_{\Sigma }^{-}=S_{\Sigma x}-i{S}_{\Sigma y}\hfill \end{array}$
Figure 5	$\begin{array}{c}{S}_{\Delta z}=\frac{1}{2}(S_{1z}-S_{2z}),S_{\Delta x}=\frac{1}{2}(S_1^{+}{S}_2^{-}+S_1^{-}{S}_2^{+}),S_{\Delta y}=\frac{1}{2i}(S_1^{+}{S}_2^{-}-S_1^{-}{S}_2^{+}),\hfill \end{array}$	|2〉, |3〉, |6〉, |7〉
	$\begin{array}{c}{E}_{S\Delta }=4S_{\Delta z}^2,S_{\Delta }^{\alpha }=\frac{1}{2}{E}_{S\Delta }+S_{\Delta z},S_{\Delta }^{\beta }=\frac{1}{2}{E}_{S\Delta }-S_{\Delta z},S_{\Delta }^{+}=S_{\Delta x}+i{S}_{\Delta y},S_{\Delta }^{-}=S_{\Delta x}-i{S}_{\Delta y}\hfill \end{array}$
Equation 47	$\begin{array}{c}{M}_{\Sigma z}=\frac{1}{2}(S_{\Delta z}+E_{S\Delta }{I}_z),M_{\Sigma x}=\frac{1}{2}(S_{\Delta }^{+}{I}^{+}+S_{\Delta }^{-}{I}^{-}),M_{\Sigma y}=\frac{1}{2i}(S_{\Delta }^{+}{I}^{+}-S_{\Delta }^{-}{I}^{-}),\hfill \end{array}$	$|\tilde{2}⟩,|\tilde{7}⟩$
Figure 6	$\begin{array}{c}{E}_{M\Sigma }=4M_{\Sigma z}^2,M_{\Sigma }^{\alpha }=\frac{1}{2}{E}_{M\Sigma }+M_{\Sigma z},M_{\Sigma }^{\beta }=\frac{1}{2}{E}_{M\Sigma }-M_{\Sigma z}\hfill \end{array}$
	$\begin{array}{c}{M}_{\Delta z}=\frac{1}{2}(S_{\Delta z}-E_{S\Delta }{I}_z),M_{\Delta x}=\frac{1}{2}(S_{\Delta }^{+}{I}^{-}+S_{\Delta }^{-}{I}^{+}),M_{\Delta y}=\frac{1}{2i}(S_{\Delta }^{+}{I}^{-}-S_{\Delta }^{-}{I}^{+}),\hfill \\ E_{M\Delta }=4M_{\Delta z}^2,M_{\Delta }^{\alpha }=\frac{1}{2}{E}_{M\Delta }+M_{\Delta z},M_{\Delta }^{\beta }=\frac{1}{2}{E}_{M\Delta }-M_{\Delta z}\hfill \end{array}$	$|\tilde{3}⟩,|\tilde{6}⟩$

For biradical polarizing agents such as BT2E,^{24, 25} TOTAPOL (Ref. ⁸) or bTbk,⁹ the electron−electron interactions are ∼20–30 MHz and are larger than the electron−nuclear dipolar interaction (<1 MHz), so that

$$\frac{D_o}{{\omega }_{\Delta }}>\frac{B_{\Sigma }}{{\omega }_{0I}},\frac{B_{\Delta }}{{\omega }_{0I}}.$$ (32)

The first step in diagonalizing $H_0^{\mathit{ISS}}$ is to eliminate the coefficient of the D₀S_Δx term in Eq. 30, which can be performed by the propagator

$$U_{\zeta }=\exp [i{\zeta }_{\alpha }{S}_{\Delta y}{I}^{\alpha }+i{\zeta }_{\beta }{S}_{\Delta y}{I}^{\beta }],$$ (33)

where the nuclear spin operators and the scalar coefficients [−π/2 < (ζ_α and ζ_β) < π/2] are

$$I^{\alpha }=\frac{1}{2}+I_z,I^{\beta }=\frac{1}{2}-I_z,$$ (34)

$$\tan {\zeta }_{\alpha }=\frac{D_o}{\frac{A_{\Delta }}{2}+{\omega }_{\Delta }},\tan {\zeta }_{\beta }=\frac{D_o}{-\frac{A_{\Delta }}{2}+{\omega }_{\Delta }}.$$ (35)

The result of this unitary transformation can be written as the sum of diagonal and off-diagonal elements:

$${\tilde{H}}_0^{\mathit{ISS}}\equiv U_{\zeta }{H}_0^{\mathit{ISS}}{U}_{\zeta }^{-1}={\tilde{H}}_{00}^{\mathit{ISS}}+{\tilde{H}}_{01}^{\mathit{ISS}},$$ (36)

${\tilde{H}}_{00}^{\mathit{ISS}}$ is the sum of diagonal terms and has the following form:

$$\begin{array}{ccc}\hfill {\tilde{H}}_{00}^{\mathit{ISS}}& =& {\omega }_{\Sigma }{S}_{\Sigma z}+{\tilde{\omega }}_{\Delta }{S}_{\Delta z}-{\omega }_{0I}{I}_z\hfill \\ & & +(A_{\Sigma }{S}_{\Sigma z}+{\tilde{A}}_{\Delta }{S}_{\Delta z})I_z+D_d{S}_{1z}{S}_{2z},\hfill \end{array}$$ (37)

where the new coefficients are

$$\begin{array}{ccc}\hfill {\tilde{\omega }}_{\Delta }& =& \frac{1}{2}{\omega }_{\Delta }(\cos {\zeta }_{\alpha }+\cos {\zeta }_{\beta })+\frac{1}{2}{D}_o(\sin {\zeta }_{\alpha }+\sin {\zeta }_{\beta })\hfill \\ & & +\frac{1}{4}{A}_{\Delta }(\cos {\zeta }_{\alpha }-\cos {\zeta }_{\beta }),\hfill \end{array}$$ (38)

$$\begin{array}{ccc}\hfill {\tilde{A}}_{\Delta }& =& {\omega }_{\Delta }(\cos {\zeta }_{\alpha }-\cos {\zeta }_{\beta })+D_o(\sin {\zeta }_{\alpha }-\sin {\zeta }_{\beta })\hfill \\ & & +\frac{1}{2}{A}_{\Delta }(\cos {\zeta }_{\alpha }+\cos {\zeta }_{\beta }).\hfill \end{array}$$ (39)

Concurrently, ${\tilde{H}}_{01}^{\mathit{ISS}}$ is the off-diagonal part, which can be simplified as

$${\tilde{H}}_{01}^{\mathit{ISS}}=(B_{\Sigma }{S}_{\Sigma z}+{\tilde{B}}_{\Delta }{S}_{\Delta z}+\tilde{K}{S}_{\Delta x})I_x,$$ (40)

with coefficients

$${\tilde{B}}_{\Delta }=B_{\Delta }\cos \frac{{\zeta }_{\alpha }+{\zeta }_{\beta }}{2},\tilde{K}=-B_{\Delta }\sin \frac{{\zeta }_{\alpha }+{\zeta }_{\beta }}{2}.$$ (41)

The first two terms in the parenthesis of Eq. 40 contribute to SE DNP processes that occur concurrently with the CE. However, for the moment they are not interesting since our goal is to derive expressions for the more efficient CE polarization mechanism, which involves the last term. Note that the last term in Eq. 40 affects only the $\left\{\right|\tilde{6}⟩,|\tilde{2}⟩,|\tilde{7}⟩,|\tilde{3}⟩\}$ subspace as illustrated in Fig. 6 and provides an effective coupling for the CE mechanism. This coupling is not large due to the small size of ζ_α and ζ_β, but can lead to the mixing of degenerate states if the matching condition among the EPR and NMR frequencies is satisfied.

Figure 6.

The subspace of the electron–electron–nuclear spin system relevant for the CE mechanism. The tilde indicates the intermediate states that are different from the PSB.

The second step of the diagonalization process involves the transformation of ${\tilde{H}}_{01}^{\mathit{ISS}}$ into the interaction frame of ${\tilde{H}}_{00}^{\mathit{ISS}}$, similar to Eqs. 19, 20:

$$\begin{array}{c}\hfill \begin{array}{ccc}{e}^{i{\tilde{H}}_{00}^{\mathit{ISS}}t}{\tilde{H}}_{01}^{\mathit{ISS}}{e}^{-i{\tilde{H}}_{00}^{\mathit{ISS}}t}\hfill & =& \frac{1}{4}{B}_{\Sigma }\left\{S_{\Sigma }^{\alpha }(I^{+}{e}^{i(-{\omega }_{0I}+\frac{1}{2}{A}_{\Sigma })t}+I^{-}\mathrm{c}.\mathrm{c}.)-S_{\Sigma }^{\beta }(I^{+}{e}^{i(-{\omega }_{0I}-\frac{1}{2}{A}_{\Sigma })t}+I^{-}\mathrm{c}.\mathrm{c})\right\}\hfill \\ & & +\frac{1}{4}{\tilde{B}}_{\Delta }\left\{S_{\Delta }^{\alpha }(I^{+}{e}^{i(-{\omega }_{0I}+\frac{1}{2}{\tilde{A}}_{\Delta })t}+I^{-}\mathrm{c}.\mathrm{c}.)-S_{\Delta }^{\beta }(I^{+}{e}^{i(-{\omega }_{0I}-\frac{1}{2}{\tilde{A}}_{\Delta })t}+I^{-}\mathrm{c}.\mathrm{c})\right\}\hfill \\ & & +\frac{1}{4}\tilde{K}[S_{\Delta }^{+}{I}^{+}{e}^{i({\tilde{\omega }}_{\Delta }-{\omega }_{0I})t}+S_{\Delta }^{-}{I}^{-}\mathrm{c}.\mathrm{c}.]\hfill \\ & & +\frac{1}{4}\tilde{K}[S_{\Delta }^{+}{I}^{-}{e}^{i({\tilde{\omega }}_{\Delta }+{\omega }_{0I})t}+S_{\Delta }^{-}{I}^{+}\mathrm{c}.\mathrm{c}.].\hfill \end{array}\end{array}$$ (42)

The operators $S_{\Delta }^{+}$ and $S_{\Delta }^{-}$ are defined in Table 1. The first and second terms in Eq. 42 oscillate at ω_0I, which is much larger than the electron−nuclear dipolar interactions at high magnetic fields, so these terms average to zero. However, frequency matching can arise from the third or the fourth term in Eq. 42 when

$${\tilde{\omega }}_{\Delta }=\pm {\omega }_{0I}.$$ (43)

In this case, the exponential vanishes, leaving a form of ${\tilde{H}}_{01}^{\mathit{ISS}}$ consisting of non-oscillating terms. For example, the condition ${\tilde{\omega }}_{\Delta }\approx -{\omega }_{0I}$ selects the term $\frac{1}{4}\tilde{K}(S_{\Delta }^{+}{I}^{-}+S_{\Delta }^{-}{I}^{+})$. Taking advantage of this condition, we can now rewrite ${\tilde{H}}_0^{\mathit{ISS}}$ [Eq. 36] in its “truncated” form with new spin operators as defined in Table 1.

$$\begin{array}{ccc}\hfill {\tilde{H}}_{0,\mathrm{truncated}}^{\mathit{ISS}}& =& {\omega }_{\Sigma }{S}_{\Sigma z}-{\omega }_{0I}{E}_{S\Sigma }{I}_z+({\tilde{\omega }}_{\Delta }-{\omega }_{0I})M_{\Sigma z}\hfill \\ & & +({\tilde{\omega }}_{\Delta }+{\omega }_{0I})M_{\Delta z}+(A_{\Sigma }{S}_{\Sigma z}+{\tilde{A}}_{\Delta }{S}_{\Delta z})I_z\hfill \\ & & +D_d{S}_{1z}{S}_{2z}+\frac{1}{2}\tilde{K}{M}_{\Delta x}.\hfill \end{array}$$ (44)

Note that M_Δx in Eq. 44 commutes with S_ΔzI_z, S_1zS_2z, S_Σz, E_SΣI_z, M_Σz and S_ΣzI_z (see Supporting Information II).⁵⁰ The only noncommuting term remaining in Eq. 44 contains M_Δz, which means that another unitary transformation ${\tilde{H}}_0^{\mathit{ISS}}=U_{\xi }{\tilde{H}}_{0,\mathrm{truncated}}^{\mathit{ISS}}{U}_{\xi }^{-1}$ with respect to M_Δx is required for completing the diagonalization. The propagator for this transformation is

$$U_{\xi }=\exp \left[i\xi M_{\Delta y}\right],$$ (45)

where the scalar coefficient (−π/2 < ξ < π/2) satisfies

$$\tan \xi =\frac{\tilde{K}}{2({\tilde{\omega }}_{\Delta }+{\omega }_{0I})}.$$ (46)

The result of this transformation is

$$\begin{array}{ccc}\hfill {\tilde{\tilde{H}}}_0^{\mathit{ISS}}& =& {\omega }_{\Sigma }{S}_{\Sigma z}-{\omega }_{0I}{E}_{S\Sigma }{I}_z+({\tilde{\omega }}_{\Delta }-{\omega }_{0I})M_{\Sigma z}\hfill \\ & & +(A_{\Sigma }{S}_{\Sigma z}+{\tilde{A}}_{\Delta }{S}_{\Delta z})I_z+D_d{S}_{1z}{S}_{2z}+\tilde{\tilde{\Omega }}{M}_{\Delta z},\hfill \end{array}$$ (47)

with the new coefficient

$$\tilde{\tilde{\Omega }}=({\tilde{\omega }}_{\Delta }+{\omega }_{0I})\cos \xi +\frac{1}{2}\tilde{K}\sin \xi .$$ (48)

Using the operators defined in Table 1, the diagonalized electron−electron−nuclear Hamiltonian [Eq. 47] can be described by the conventional spin operators and a set of new coefficients:

$$\begin{array}{ccc}\hfill {\tilde{\tilde{H}}}_0^{\mathit{ISS}}& =& {\tilde{\tilde{\omega }}}_{0S_1}{S}_{1z}+{\tilde{\tilde{\omega }}}_{0S_2}{S}_{2z}-{\tilde{\tilde{\omega }}}_{0I}{I}_z+D_d{S}_{1z}{S}_{2z}+{\tilde{\tilde{A}}}_1{S}_{1z}{I}_z\hfill \\ & & +{\tilde{\tilde{A}}}_2{S}_{2z}{I}_z+\tilde{\tilde{V}}{S}_{1z}{S}_{2z}{I}_z,\hfill \end{array}$$ (49)

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\omega }}}_{0S_1}& =& \frac{1}{2}{\omega }_{\Sigma }+\frac{1}{4}({\tilde{\omega }}_{\Delta }-{\omega }_{0I})+\frac{1}{4}\tilde{\tilde{\Omega }},\hfill \\ \hfill {\tilde{\tilde{\omega }}}_{0S_2}& =& \frac{1}{2}{\omega }_{\Sigma }-\frac{1}{4}({\tilde{\omega }}_{\Delta }-{\omega }_{0I})-\frac{1}{4}\tilde{\tilde{\Omega }},\hfill \\ \hfill {\tilde{\tilde{\omega }}}_{0I}& =& \frac{1}{2}{\omega }_{0I}-\frac{1}{4}({\tilde{\omega }}_{\Delta }-{\omega }_{0I})+\frac{1}{4}\tilde{\tilde{\Omega }},\hfill \\ \hfill {\tilde{\tilde{A}}}_1& =& \frac{1}{2}(A_{\Sigma }+{\tilde{A}}_{\Delta }),\hfill \\ \hfill {\tilde{\tilde{A}}}_2& =& \frac{1}{2}(A_{\Sigma }-{\tilde{A}}_{\Delta }),\hfill \\ \hfill \tilde{\tilde{V}}& =& -({\omega }_{0I}+{\tilde{\omega }}_{\Delta })+\tilde{\tilde{\Omega }}.\hfill \end{array}$$ (50)

The microwave Hamiltonian in the EBS

To obtain the effective microwave excitations for DNP, the microwave Hamiltonian H_M = 2ω_1S(S_1x + S_2x)cos (ω_Mt) for the two electrons needs to be transformed from the PSB to the EBS using the unitary transformations U_ζ [Eq. 33] and U_ξ [Eq. 45]:

$${\tilde{\tilde{H}}}_M=2{\omega }_{1S}\cos \left({\omega }_{M}t\right)·U_{\xi }{U}_{\zeta }(S_{1x}+S_{2x})U_{\zeta }^{-1}{U}_{\xi }^{-1}.$$ (51)

The technical details necessary to perform these transformations are given in supporting information Sec. 3.⁵⁰ Here, we restrict ourselves to outlining the major steps and results necessary to pinpoint the terms in ${\tilde{\tilde{H}}}_M$ that are important for DNP. First, applying the transformation U_ζ produces the intermediary Hamiltonian ${\tilde{H}}_M$ containing the following coefficients:

$$\begin{array}{ccc}\hfill {\tilde{H}}_M& =& U_{\zeta }(S_{1x}+S_{2x})U_{\zeta }^{-1}\hfill \\ & =& S_{1x}\left(I^{\alpha }\cos \frac{{\zeta }_{\alpha }}{2}+I^{\beta }\cos \frac{{\zeta }_{\beta }}{2}\right)\hfill \\ & & +2S_{1z}{S}_{2x}\left(I^{\alpha }\sin \frac{{\zeta }_{\alpha }}{2}+I^{\beta }\sin \frac{{\zeta }_{\beta }}{2}\right)\hfill \\ & & +S_{2x}\left(I^{\alpha }\cos \frac{{\zeta }_{\alpha }}{2}+I^{\beta }\cos \frac{{\zeta }_{\beta }}{2}\right)\hfill \\ & & -2S_{1x}{S}_{2z}\left(I^{\alpha }\sin \frac{{\zeta }_{\alpha }}{2}+I^{\beta }\sin \frac{{\zeta }_{\beta }}{2}\right)\hfill \\ & =& \frac{1}{2}(S_{1x}+S_{2x})(c_{\alpha }+c_{\beta })+(S_{1x}+S_{2x})I_z(c_{\alpha }-c_{\beta })\hfill \\ & & +(S_{1z}{S}_{2x}-S_{1x}{S}_{2z})(s_{\alpha }+s_{\beta })\hfill \\ & & +2(S_{1z}{S}_{2x}-S_{1x}{S}_{2z})I_z(s_{\alpha }-s_{\beta }),\hfill \end{array}$$ (52)

$$\begin{array}{ccc}\hfill c_{\alpha }& =& \cos \frac{{\zeta }_{\alpha }}{2},c_{\beta }=\cos \frac{{\zeta }_{\beta }}{2},\hfill \\ \hfill s_{\alpha }& =& \sin \frac{{\zeta }_{\alpha }}{2},s_{\beta }=\sin \frac{{\zeta }_{\beta }}{2}.\hfill \end{array}$$ (53)

In order to apply the second unitary transformation U_ξ, it is convenient to rewrite Eq. 52 to take advantage of the following commutator relations:

$$\begin{array}{ccc}\hfill [M_{\Delta y},S_{1z}{I}_z]& =& [M_{\Delta y},S_{1z}{S}_{2z}]=[M_{\Delta y},S_{2z}{I}_z]=0,\hfill \\ \hfill S_{1x}& =& -2i{S}_{1y}{S}_{1z},S_{2x}=-2i{S}_{2y}{S}_{2z}.\hfill \end{array}$$ (54)

The new, more convenient form of ${\tilde{H}}_M$ is given below, followed by the result of the second unitary transformation:

$$\begin{array}{ccc}\hfill {\tilde{H}}_M& =& \frac{1}{2}(c_{\alpha }+c_{\beta })(S_{1x}+S_{2x})\hfill \\ & & -2i(c_{\alpha }-c_{\beta })(S_{1y}{S}_{1z}{I}_z+S_{2y}{S}_{2z}{I}_z)\hfill \\ & & +2i(s_{\alpha }+s_{\beta })(S_{1y}-S_{2y})S_{1z}{S}_{2z}\hfill \\ & & -2(s_{\alpha }-s_{\beta })(S_{1x}{S}_{2z}{I}_z-S_{2x}{S}_{1z}{I}_z).\hfill \end{array}$$ (55)

$$\begin{array}{ccc}\hfill U_{\xi }{\tilde{H}}_M{U}_{\xi }^{-1}& =& (c_{\alpha }+c_{\beta })\{\frac{1}{4}(S_{1x}+S_{2x})-(S_{1x}{S}_{2z}-S_{1z}{S}_{2x})I_z\hfill \\ & & +\left[\frac{1}{4}(S_{1x}+S_{2x})+(S_{1x}{S}_{2z}-S_{1z}{S}_{2x})I_z\right]\cos \frac{\xi }{2}\hfill \\ & & +\frac{1}{2}\left[S_{1z}(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})-(S_1^{+}{I}^{-}+S_1^{-}{I}^{+})S_{2z}\right]\sin \frac{\xi }{2}\}\hfill \\ & & +\frac{1}{2}(c_{\alpha }-c_{\beta })\{(S_{1x}+S_{2x})I_z-(S_{1x}{S}_{2z}-S_{1z}{S}_{2x})\hfill \\ & & +[(S_{1x}+S_{2x})I_z+(S_{1x}{S}_{2z}-S_{1z}{S}_{2x})]\cos \frac{\xi }{2}\hfill \\ & & +\frac{1}{2}(S_2^{+}{I}^{+}+S_2^{-}{I}^{-}+S_1^{+}{I}^{-}+S_1^{-}{I}^{+})\sin \frac{\xi }{2}\}\hfill \\ & & +\frac{1}{2}(s_{\alpha }+s_{\beta })\{(S_{1x}+S_{2x})I_z-(S_{1x}{S}_{2z}-S_{1z}{S}_{2x})\hfill \\ & & -[(S_{1x}+S_{2x})I_z+(S_{1x}{S}_{2z}-S_{1z}{S}_{2x})]\cos \frac{\xi }{2}\hfill \\ & & -\frac{1}{2}(S_2^{+}{I}^{+}+S_2^{-}{I}^{-}+S_1^{+}{I}^{-}+S_1^{-}{I}^{+})\sin \frac{\xi }{2}\}\hfill \\ & & +(s_{\alpha }-s_{\beta })\{\frac{1}{4}(S_{1x}+S_{2x})-(S_{1x}{S}_{2z}-S_{1z}{S}_{2x})I_z\hfill \\ & & -\left[\frac{1}{4}(S_{1x}+S_{2x})+(S_{1x}{S}_{2z}-S_{1z}{S}_{2x})I_z\right]\cos \frac{\xi }{2}\hfill \\ & & -\frac{1}{2}[S_{1z}(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})\hfill \\ & & -(S_1^{+}{I}^{-}+S_1^{-}{I}^{+})S_{2z}]\sin \frac{\xi }{2}\}.\hfill \end{array}$$ (56)

For book-keeping purposes, the operators in ${\tilde{\tilde{H}}}_M$ can be grouped into six terms where each term is defined in supporting information Sec. 3:⁵⁰

$$\begin{array}{ccc}\hfill {\tilde{\tilde{H}}}_M& =& 2{\omega }_{1S}\cos \left({\omega }_{M}t\right)\hfill \\ & & \times \left({\tilde{\tilde{H}}}_M^1+{\tilde{\tilde{H}}}_M^2+{\tilde{\tilde{H}}}_M^3+{\tilde{\tilde{H}}}_M^4+{\tilde{\tilde{H}}}_M^5+{\tilde{\tilde{H}}}_M^6\right).\hfill \end{array}$$ (57)

Only some of the terms in Eq. 57 lead to polarization transfer for DNP; the remaining terms are associated with EPR transitions. We can now delineate the selection rules for microwave excitation, which can be identified within the interaction frame with respect to the Hamiltonian ${\tilde{\tilde{H}}}_0^{\mathit{ISS}}$. Specifically, it is necessary to calculate

$${\tilde{\tilde{H}}}_M^{n*}=e^{i{\tilde{\tilde{H}}}_0^{\mathit{ISS}}t}{\tilde{\tilde{H}}}_M^n{e}^{-i{\tilde{\tilde{H}}}_0^{\mathit{ISS}}t}.$$ (58)

For example, for ${\tilde{\tilde{H}}}_M^1$ (n = 1) the following result is obtained:

$$\begin{array}{ccc}\hfill {\tilde{\tilde{H}}}_M^{1*}& =& {\tilde{\tilde{h}}}_1{e}^{i{\tilde{\tilde{H}}}_0^{\mathit{ISS}}t}(S_{1x}+S_{2x})e^{-i{\tilde{\tilde{H}}}_0^{\mathit{ISS}}t}\hfill \\ & =& \frac{1}{2}{\tilde{\tilde{h}}}_1[S_1^{+}{e}^{i({\tilde{\tilde{\omega }}}_{0S_1}+D_d{S}_{2z}+{\tilde{\tilde{A}}}_1{I}_z+\tilde{\tilde{V}}{S}_{2z}{I}_z)t}\hfill \\ & & +S_1^{-}\mathrm{c}.\mathrm{c}.+S_2^{+}{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}+D_d{S}_{1z}+{\tilde{\tilde{A}}}_2{I}_z+\tilde{\tilde{V}}{S}_{1z}{I}_z)t}+S_2^{-}\mathrm{c}.\mathrm{c}.],\hfill \end{array}$$ (59)

which can be further expanded to

$$\begin{array}{ccc}\hfill {\tilde{\tilde{H}}}_M^{1*}& =& \frac{1}{2}{\tilde{\tilde{h}}}_1\{S_1^{+}{S}_2^{\alpha }{I}^{\alpha }{e}^{i({\tilde{\tilde{\omega }}}_{0S_1}+\frac{D_d}{2}+\frac{{\tilde{\tilde{A}}}_1}{2}+\frac{\tilde{\tilde{V}}}{4})t}\hfill \\ & & +S_1^{-}{S}_2^{\alpha }{I}^{\alpha }\mathrm{c}.\mathrm{c}.+S_2^{+}{S}_1^{\alpha }{I}^{\alpha }{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}+\frac{D_d}{2}+\frac{{\tilde{\tilde{A}}}_2}{2}+\frac{\tilde{\tilde{V}}}{4})t}\hfill \\ & & +S_2^{-}{S}_1^{\alpha }{I}^{\alpha }\mathrm{c}.\mathrm{c}.+S_1^{+}{S}_2^{\alpha }{I}^{\beta }{e}^{i({\tilde{\tilde{\omega }}}_{0S_1}+\frac{D_d}{2}-\frac{{\tilde{\tilde{A}}}_1}{2}-\frac{\tilde{\tilde{V}}}{4})t}\hfill \\ & & +S_1^{-}{S}_2^{\alpha }{I}^{\beta }\mathrm{c}.\mathrm{c}.+S_2^{+}{S}_1^{\alpha }{I}^{\beta }{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}+\frac{D_d}{2}-\frac{{\tilde{\tilde{A}}}_2}{2}-\frac{\tilde{\tilde{V}}}{4})t}\hfill \\ & & +S_2^{-}{S}_1^{\alpha }{I}^{\beta }\mathrm{c}.\mathrm{c}.+S_1^{+}{S}_2^{\beta }{I}^{\alpha }{e}^{i({\tilde{\tilde{\omega }}}_{0S_1}-\frac{D_d}{2}+\frac{{\tilde{\tilde{A}}}_1}{2}-\frac{\tilde{\tilde{V}}}{4})t}\hfill \\ & & +S_1^{-}{S}_2^{\beta }{I}^{\alpha }\mathrm{c}.\mathrm{c}.+S_2^{+}{S}_1^{\beta }{I}^{\alpha }{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}-\frac{D_d}{2}+\frac{{\tilde{\tilde{A}}}_2}{2}-\frac{\tilde{\tilde{V}}}{4})t}\hfill \\ & & +S_2^{-}{S}_1^{\beta }{I}^{\alpha }\mathrm{c}.\mathrm{c}.+S_1^{+}{S}_2^{\beta }{I}^{\beta }{e}^{i({\tilde{\tilde{\omega }}}_{0S_1}-\frac{D_d}{2}-\frac{{\tilde{\tilde{A}}}_1}{2}+\frac{\tilde{\tilde{V}}}{4})t}\hfill \\ & & +S_1^{-}{S}_2^{\beta }{I}^{\beta }\mathrm{c}.\mathrm{c}.+S_2^{+}{S}_1^{\beta }{I}^{\beta }{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}-\frac{D_d}{2}-\frac{{\tilde{\tilde{A}}}_2}{2}+\frac{\tilde{\tilde{V}}}{4})t}\hfill \\ & & +S_2^{-}{S}_1^{\beta }{I}^{\beta }\mathrm{c}.\mathrm{c}.\}.\hfill \end{array}$$ (60)

The corresponding expressions for n = 2 to 6 in Eq. 57 are summarized in supporting information Sec. 4,⁵⁰ while the transformed Hamiltonian can be written as

$$\begin{array}{ccc}\hfill {\tilde{\tilde{H}}}_M^{*}& =& 2{\omega }_{1S}\cos \left({\omega }_{M}t\right)\hfill \\ & & \times \left({\tilde{\tilde{H}}}_M^{1*}+{\tilde{\tilde{H}}}_M^{2*}+{\tilde{\tilde{H}}}_M^{3*}+{\tilde{\tilde{H}}}_M^{4*}+{\tilde{\tilde{H}}}_M^{5*}+{\tilde{\tilde{H}}}_M^{6*}\right).\hfill \end{array}$$ (61)

Furthermore, the six terms can be divided into two groups depending on the nature of the coefficients:

$$\begin{array}{ccc}& & {\tilde{\tilde{H}}}_M^{1*}+{\tilde{\tilde{H}}}_M^{2*}+{\tilde{\tilde{H}}}_M^{3*}+{\tilde{\tilde{H}}}_M^{4*}\hfill \\ & & =\frac{1}{2}(c_{\alpha }-s_{\alpha })\cos \frac{\xi }{2}\left[S_1^{+}{S}_2^{\alpha }{I}^{\alpha }{e}^{i({\tilde{\tilde{\omega }}}_{0S_1}+\frac{D_d}{2}+\frac{{\tilde{\tilde{A}}}_1}{2}+\frac{\tilde{\tilde{V}}}{4})t}+S_1^{-}{S}_2^{\alpha }{I}^{\alpha }\mathrm{c}.\mathrm{c}.\right]+\frac{1}{2}(c_{\beta }-s_{\beta })\left[S_1^{+}{S}_2^{\alpha }{I}^{\beta }{e}^{i({\tilde{\tilde{\omega }}}_{0S_1}+\frac{D_d}{2}-\frac{{\tilde{\tilde{A}}}_1}{2}-\frac{\tilde{\tilde{V}}}{4})t}+S_1^{-}{S}_2^{\alpha }{I}^{\beta }\mathrm{c}.\mathrm{c}.\right]\hfill \\ & & +\frac{1}{2}(c_{\alpha }+s_{\alpha })\left[S_1^{+}{S}_2^{\beta }{I}^{\alpha }{e}^{i({\tilde{\tilde{\omega }}}_{0S_1}-\frac{D_d}{2}+\frac{{\tilde{\tilde{A}}}_1}{2}-\frac{\tilde{\tilde{V}}}{4})t}+S_1^{-}{S}_2^{\beta }{I}^{\alpha }\mathrm{c}.\mathrm{c}.\right]+\frac{1}{2}(c_{\beta }+s_{\beta })\cos \frac{\xi }{2}\left[S_1^{+}{S}_2^{\beta }{I}^{\beta }{e}^{i({\tilde{\tilde{\omega }}}_{0S_1}-\frac{D_d}{2}-\frac{{\tilde{\tilde{A}}}_1}{2}+\frac{\tilde{\tilde{V}}}{4})t}+S_1^{-}{S}_2^{\beta }{I}^{\beta }\mathrm{c}.\mathrm{c}.\right]\hfill \\ & & +\frac{1}{2}(c_{\alpha }+s_{\alpha })\left[S_2^{+}{S}_1^{\alpha }{I}^{\alpha }{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}+\frac{D_d}{2}+\frac{{\tilde{\tilde{A}}}_2}{2}+\frac{\tilde{\tilde{V}}}{4})t}+S_2^{-}{S}_1^{\alpha }{I}^{\alpha }\mathrm{c}.\mathrm{c}.\right]+\frac{1}{2}(c_{\beta }+s_{\beta })\cos \frac{\xi }{2}[S_2^{+}{S}_2^{+}+S_1^{\alpha }{I}^{\beta }{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}+\frac{D_d}{2}-\frac{{\tilde{\tilde{A}}}_2}{2}-\frac{\tilde{\tilde{V}}}{4})t}\hfill \\ & & +S_2^{-}{S}_1^{\alpha }{I}^{\beta }\mathrm{c}.\mathrm{c}.]+\frac{1}{2}(c_{\alpha }-s_{\alpha })\cos \frac{\xi }{2}\left[S_2^{+}{S}_1^{\beta }{I}^{\alpha }{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}-\frac{D_d}{2}+\frac{{\tilde{\tilde{A}}}_2}{2}-\frac{\tilde{\tilde{V}}}{4})t}+S_2^{-}{S}_1^{\beta }{I}^{\alpha }\mathrm{c}.\mathrm{c}.\right]\hfill \\ & & +\frac{1}{2}(c_{\beta }-s_{\beta })\left[S_2^{+}{S}_1^{\beta }{I}^{\beta }{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}-\frac{D_d}{2}-\frac{{\tilde{\tilde{A}}}_2}{2}+\frac{\tilde{\tilde{V}}}{4})t}+S_2^{-}{S}_1^{\beta }{I}^{\beta }\mathrm{c}.\mathrm{c}.\right],\hfill \end{array}$$ (62)

$$\begin{array}{ccc}\hfill {\tilde{\tilde{H}}}_M^{5*}+{\tilde{\tilde{H}}}_M^{6*}& =& \frac{1}{2}(c_{\alpha }-s_{\alpha })\sin \frac{\xi }{2}\left[S_2^{+}{I}^{+}{S}_1^{\alpha }{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}+\frac{D_d}{2}-{\tilde{\tilde{\omega }}}_{0I}+\frac{{\tilde{\tilde{A}}}_1}{2})t}+S_2^{-}{I}^{-}{S}_1^{\alpha }\mathrm{c}.\mathrm{c}.\right]\hfill \\ & & -\frac{1}{2}(c_{\beta }+s_{\beta })\sin \frac{\xi }{2}\left[S_2^{+}{I}^{+}{S}_1^{\beta }{e}^{i({\tilde{\tilde{\omega }}}_{0S_2}-\frac{D_d}{2}-{\tilde{\tilde{\omega }}}_{0I}-\frac{{\tilde{\tilde{A}}}_1}{2})t}+S_2^{-}{I}^{-}{S}_1^{\beta }\mathrm{c}.\mathrm{c}.\right]\hfill \\ & & -\frac{1}{2}(c_{\beta }+s_{\beta })\sin \frac{\xi }{2}\left[S_1^{+}{I}^{-}{S}_2^{\alpha }{e}^{i({\tilde{\tilde{\omega }}}_{0S_1}+\frac{D_d}{2}+{\tilde{\tilde{\omega }}}_{0I}-\frac{{\tilde{\tilde{A}}}_2}{2})t}+S_1^{-}{I}^{+}{S}_2^{\alpha }\mathrm{c}.\mathrm{c}.\right]\hfill \\ & & +\frac{1}{2}(c_{\alpha }-s_{\alpha })\sin \frac{\xi }{2}\left[S_1^{+}{I}^{-}{S}_2^{\beta }{e}^{i({\tilde{\tilde{\omega }}}_{{}^{0S_1}}-\frac{D_d}{2}+{\tilde{\tilde{\omega }}}_{0I}+\frac{{\tilde{\tilde{A}}}_2}{2})t}+S_1^{-}{I}^{+}{S}_2^{\beta }\mathrm{c}.\mathrm{c}.\right].\hfill \end{array}$$ (63)

Polarization transfer by the effective microwave excitation

The oscillations in the terms in Eqs. 62, 63 can be canceled by an appropriately chosen value of the microwave frequency ω_M that selects the effective microwave operators with coefficients proportional to the microwave field strength ω_1S. The selected effective microwave operator has to be expressed in the interaction frame of ${\tilde{\tilde{H}}}_0^{\mathit{ISS}}$ and interacts with the density operator according to Eqs. 4, 5. The initial value of the density operator is given by the following equation:

$${\tilde{\tilde{\rho }}}_0^{*}={\tilde{\tilde{\rho }}}_0=-\frac{\hslash }{Z{k}_{B}T}{\tilde{\tilde{H}}}_0^{\mathit{ISS}}\approx \frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}(S_{1z}+S_{2z}).$$ (64)

Since the initial nuclear polarization is much smaller than the nuclear polarization generated by DNP, the nuclear Zeeman term is not included in Eq. 64. Thus, the resulting enhancement factor still follows Eq. 23, which is based on the thermal equilibrium nuclear polarization 〈P_I〉_eq:

$${⟨P_I⟩}_{\mathrm{eq}}\equiv tr\left(I_z·\frac{-\hslash }{Z{k}_{B}T}{H}_0^{\mathit{ISS}}\right)\sim \frac{2\hslash {\omega }_{0I}}{Z{k}_{B}T}.$$ (65)

The nuclear polarization at any time t during DNP can be calculated by following Eq. 66, while the nuclear polarization operator ${\tilde{\tilde{P}}}_I^{*}$ is given in Eq. 67 [similar to the procedure described in supporting information Sec. 3, Eqs. (S12)–(S29)].⁵⁰

$$⟨P_I⟩\left(t\right)=tr\left({\tilde{\tilde{P}}}_I^{*}{\tilde{\tilde{\rho }}}^{*}\right),$$ (66)

$$\begin{array}{ccc}\hfill {\tilde{\tilde{P}}}_I^{*}& =& e^{i{\tilde{\tilde{H}}}_0^{\mathit{ISS}}t}{U}_{\xi }{U}_{\zeta }{I}_z{U}_{\zeta }^{-1}{U}_{\xi }^{-1}{e}^{-i{\tilde{\tilde{H}}}_0^{\mathit{ISS}}t}\hfill \\ & =& \frac{3}{4}{I}_z+\frac{1}{4}{S}_{1z}-\frac{1}{4}{S}_{2z}+S_{1z}{S}_{2z}{I}_z\hfill \\ & & -(\frac{1}{4}{S}_{1z}-\frac{1}{4}{S}_{2z}-\frac{1}{4}{I}_z+S_{1z}{S}_{2z}{I}_z)\cos \xi \hfill \\ & & +\frac{1}{2}(S_1^{+}{S}_2^{-}{I}^{-}{e}^{i\tilde{\tilde{\Omega }}t}+S_1^{-}{S}_2^{+}{I}^{+}{e}^{-i\tilde{\tilde{\Omega }}t})\sin \xi .\hfill \end{array}$$ (67)

Recall that any term of ${\tilde{\tilde{H}}}_M^{*}$ [Eqs. 62, 63] that has a coefficient dependent on ξ will enhance the nuclear polarization. We will demonstrate the generation of positive DNP enhancements from combinations of four possible transitions whenω_M∼ω_0S1. Although these transitions— $S_{1x}{S}_2^{\alpha }{I}^{\alpha },S_{1x}{S}_2^{\beta }{I}^{\beta },\frac{1}{2}{S}_1^{\alpha }(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})$ and $-\frac{1}{2}{S}_1^{\beta }(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})$—occur at different microwave frequencies nearω_0S1, they can be excited simultaneously by a sufficiently intense ω_1S and a broad frequency distribution of ω_M. The following examples illustrate the calculation of the enhanced nuclear polarization in several of these cases.

Example 1

When ω_M matches the oscillation frequency of the first term in Eq. 62, i.e.,

$${\omega }_M={\tilde{\tilde{\omega }}}_{0S_1}+\frac{1}{2}{D}_d+\frac{1}{2}{\tilde{\tilde{A}}}_1+\frac{1}{4}\tilde{\tilde{V}},$$ (68)

the effective microwave Hamiltonian [from Eq. 57 and the first line of Eq. 62] becomes

$${\tilde{\tilde{H}}}_M^{\mathrm{eff}*}={\tilde{\tilde{\omega }}}_1^{*}{S}_{1x}{S}_2^{\alpha }{I}^{\alpha }.$$ (69)

Here, ${\tilde{\tilde{\omega }}}_1^{*}={\omega }_{1S}(c_{\alpha }-s_{\alpha })\cos \frac{\xi }{2}$. Since the effective Hamiltonian only affects S_1z, the time-dependent density operator can be readily calculated following Eqs. 4, 5:

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\rho }}}^{*}& =& \frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}\{S_{2z}+S_{1z}\left(E-S_2^{\alpha }{I}^{\alpha }\right)\hfill \\ & & +S_{1z}{S}_2^{\alpha }{I}^{\alpha }\cos {\tilde{\tilde{\omega }}}_1^{*}t-S_{1y}{S}_2^{\alpha }{I}^{\alpha }\sin {\tilde{\tilde{\omega }}}_1^{*}t\}.\hfill \end{array}$$ (70)

Furthermore, according to Eqs. 66, 67, the time-dependent nuclear polarization is

$$⟨P_I⟩\left(t\right)=\frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}\frac{1}{4}(1-\cos \xi )(\cos {\tilde{\tilde{\omega }}}_1^{*}t-1).$$ (71)

Comparing Eq. 71 to the initial nuclear polarization in Eq. 65, suggests that the maximum NMR enhancement is 1/4|γ_S/γ_I| with ξ = 90°, since −90° ⩽ ξ ⩽ 90° [see Eq. 46 for the exact frequency matching]. Note, this result is valid only in the absence of relaxation. When ${\omega }_M={\tilde{\tilde{\omega }}}_{0S_1}-\frac{1}{2}{D}_d-\frac{1}{2}{\tilde{\tilde{A}}}_1+\frac{1}{4}\tilde{\tilde{V}}$, the selected term is $S_{1x}{S}_2^{\beta }{I}^{\beta }$ [from Eqs. 62, 63], which yields the same maximal DNP enhancement as above. We will discuss the significance of this example further in Sec. 4C.

Example 2

In this case, we let ω_M match the oscillation frequency of the first term in Eq. 63, which gives the following effective microwave Hamiltonian:

$${\omega }_M={\tilde{\tilde{\omega }}}_{0S_2}-{\tilde{\tilde{\omega }}}_{0I}+\frac{1}{2}{D}_d+\frac{1}{2}{\tilde{\tilde{A}}}_1,$$ (72)

$${\tilde{\tilde{H}}}_M^{\mathrm{eff}*}={\tilde{\tilde{\omega }}}_2^{*}\frac{1}{2}(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})S_1^{\alpha }.$$ (73)

Here, ${\tilde{\tilde{\omega }}}_2^{*}={\omega }_{1S}(c_{\alpha }-s_{\alpha })\sin \frac{\xi }{2}$. Again, the effective Hamiltonian interacts with the density operator according to the Liouville–von Neumann equation [Eqs. 4, 5]. To simplify the calculation of the evolution, we need the following definitions:

$$\begin{array}{ccc}& & I_{2\Sigma z}=\frac{1}{2}(S_{2z}+I_z),E_{I2\Sigma }=4I_{2\Sigma z}^2,\hfill \\ & & I_{2\Sigma }^{+}=S_2^{+}{I}^{+},I_{2\Sigma }^{-}=S_2^{-}{I}^{-},\hfill \\ & & I_{2\Sigma x}=\frac{1}{2}(I_{2\Sigma }^{+}+I_{2\Sigma }^{-}),I_{2\Sigma y}=\frac{1}{2i}(I_{2\Sigma }^{+}-I_{2\Sigma }^{-}),\hfill \\ & & I_{2\Delta z}=\frac{1}{2}(S_{2z}-I_z),E_{I2\Delta }=4I_{2\Delta z}^2,\hfill \\ & & I_{2\Delta }^{+}=S_2^{+}{I}^{-},I_{2\Delta }^{-}=S_2^{-}{I}^{+},\hfill \\ & & I_{2\Delta x}=\frac{1}{2}(I_{2\Delta }^{+}+I_{2\Delta }^{-}),I_{2\Delta y}=\frac{1}{2i}(I_{2\Delta }^{+}-I_{2\Delta }^{-}).\hfill \end{array}$$ (74)

The relevant part of the evolving density operator results from the following derivation (θ is an arbitrary angle)

$$\begin{array}{ccc}& & e^{-i\theta \frac{1}{2}(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})S_1^{\alpha }}(S_{1z}+S_{2z})\mathrm{c}.\mathrm{c}.\hfill \\ & & =e^{-i\theta I_{2\Sigma x}{S}_1^{\alpha }}(S_{1z}+I_{2\Sigma z}+I_{2\Delta z})\mathrm{c}.\mathrm{c}.\hfill \\ & & =S_{1z}+I_{2\Delta z}+S_1^{\beta }{I}_{2\Sigma z}+S_1^{\alpha }(I_{2\Sigma z}\cos \theta -I_{2\Sigma y}\sin \theta )\hfill \\ & & =S_{1z}+\frac{1}{2}(S_{2z}-I_z)+\frac{1}{2}{S}_1^{\beta }(S_{2z}+I_z)\hfill \\ & & +\frac{1}{2}{S}_1^{\alpha }[(S_{2z}+I_z)\cos \theta +i(S_2^{+}{I}^{+}-S_2^{-}{I}^{-})\sin \theta ].\hfill \end{array}$$ (75)

Thus, the time-dependent density operator and the time-dependent nuclear polarization during DNP [Eqs. 66, 67] are given by the following equations:

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\rho }}}^{*}& =& \frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}\{S_{1z}+\frac{1}{2}(S_{2z}-I_z)\hfill \\ & & +\frac{1}{2}{S}_1^{\beta }(S_{2z}+I_z)+\frac{1}{2}{S}_1^{\alpha }(S_{2z}+I_z)\cos {\tilde{\tilde{\omega }}}_2^{*}t\hfill \\ & & +\frac{i}{2}{S}_1^{\alpha }(S_2^{+}{I}^{+}-S_2^{-}{I}^{-})\sin {\tilde{\tilde{\omega }}}_2^{*}t\}.\hfill \end{array}$$ (76)

$$⟨P_I⟩\left(t\right)=\frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}\frac{1}{4}(1+\cos \xi )(\cos {\tilde{\tilde{\omega }}}_2^{*}t-1),$$ (77)

Comparing Eq. 77 with Eq. 65 indicates that the enhancement at the matching condition is $\frac{1}{4}\left|\frac{{\gamma }_S}{{\gamma }_I}\right|$, the same result as in Eq. 71 when ξ = 90°. Similarly, when ${\omega }_M={\tilde{\tilde{\omega }}}_{0S_2}-{\tilde{\tilde{\omega }}}_{0I}-\frac{1}{2}{D}_d-\frac{1}{2}{\tilde{\tilde{A}}}_1$, the selected $\frac{1}{2}(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})S_1^{\beta }$ term yields the same expression for the enhancement.

Example 3

In this example, we assume that the microwave field is stronger than the difference of the frequencies selected in Examples 1 and 2 [Eqs. 68, 72] such that

$${\tilde{\tilde{\omega }}}_1^{*}or{\tilde{\tilde{\omega }}}_2^{*}>\left|{\tilde{\tilde{\omega }}}_{0S_1}+\frac{1}{4}\tilde{\tilde{V}}-{\tilde{\tilde{\omega }}}_{0S_2}+{\tilde{\tilde{\omega }}}_{0I}\right|=\left|\tilde{\tilde{\Omega }}\right|.$$ (78)

In this case, both the $S_{1x}{S}_2^{\alpha }{I}^{\alpha }$ and the $\frac{1}{2}(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})S_1^{\alpha }$ terms are excited. In fact, $\tilde{\tilde{\Omega }}$ is usually small compared to ω_1S because it originates from the second order effect of the dipolar interactions. Using the condition in Eq. 78 and ξ = 90° (exact frequency matching), the effective microwave Hamiltonian becomes

$${\tilde{\tilde{H}}}_M^{\mathrm{eff}*}={\tilde{\tilde{\omega }}}_3^{*}\left[S_{1x}{S}_2^{\alpha }{I}^{\alpha }+\frac{1}{2}(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})S_1^{\alpha }\right],$$ (79)

where ${\tilde{\tilde{\omega }}}_3^{*}=\frac{1}{\sqrt{2}}{\omega }_{1S}(c_{\alpha }-s_{\alpha })$. The propagation of the density operator can be simplified by rewriting the microwave Hamiltonian and using the following recursive commutation relations (supporting information Sec. 5):⁵⁰

$$\begin{array}{c}\hfill {\tilde{\tilde{H}}}_{M3}^{\mathrm{eff}*}=S_{1x}{S}_2^{\alpha }{I}^{\alpha }+\frac{1}{2}{S}_1^{\alpha }(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})=S_{1x}{I}_{2\Sigma }^{\alpha }+S_1^{\alpha }{I}_{2\Sigma x},\end{array}$$ (80)

$$\begin{array}{ccc}& & \left[{\tilde{\tilde{H}}}_{M3}^{\mathrm{eff}*},S_{1z}+S_{2z}\right]\hfill \\ & & =-i{S}_{1y}{S}_2^{\alpha }{I}^{\alpha }-\frac{1}{2}{S}_1^{\alpha }(S_2^{+}{I}^{+}-S_2^{-}{I}^{-}),\hfill \end{array}$$ (81)

$$\begin{array}{ccc}& & \left[{\tilde{\tilde{H}}}_{M3}^{\mathrm{eff}*},\left[{\tilde{\tilde{H}}}_{M3}^{\mathrm{eff}*},S_{1z}+S_{2z}\right]\right]\hfill \\ & & =-S_1^{\alpha }{S}_2^{\alpha }{I}^{\alpha }+\frac{1}{2}{S}_1^{\beta }{S}_2^{\alpha }{I}^{\alpha }\hfill \\ & & +\frac{1}{2}{S}_1^{\alpha }{S}_2^{\beta }{I}^{\beta }+\frac{1}{2}(S_1^{+}{S}_2^{-}{I}^{-}+S_1^{-}{S}_2^{+}{I}^{+}),\hfill \end{array}$$ (82)

$$\begin{array}{ccc}& & \left[{\tilde{\tilde{H}}}_{M3}^{\mathrm{eff}*},\left[{\tilde{\tilde{H}}}_{M3}^{\mathrm{eff}*},\left[{\tilde{\tilde{H}}}_{M3}^{\mathrm{eff}*},S_{1z}+S_{2z}\right]\right]\right]\hfill \\ & & =2\left[i{S}_{1y}{S}_2^{\alpha }{I}^{\alpha }+\frac{1}{2}{S}_1^{\alpha }(S_2^{+}{I}^{+}-S_2^{-}{I}^{-})\right].\hfill \end{array}$$ (83)

The time-dependent density operator can be obtained by combining the relations in Eqs. 81, 82, 83

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\rho }}}^{*}& =& \frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}\{S_{1z}+S_{2z}\hfill \\ & & +[-\frac{1}{2}{S}_1^{\alpha }{S}_2^{\alpha }{I}^{\alpha }+\frac{1}{4}{S}_1^{\beta }{S}_2^{\alpha }{I}^{\alpha }+\frac{1}{4}{S}_1^{\alpha }{S}_2^{\beta }{I}^{\beta }\hfill \\ & & +\frac{1}{4}(S_1^{-}{S}_2^{+}{I}^{+}+S_1^{+}{S}_2^{-}{I}^{-})][1-\cos \sqrt{2}{\tilde{\tilde{\omega }}}_3^{*}t]\hfill \\ & & +\frac{1}{\sqrt{2}}[S_{1y}{S}_2^{\alpha }{I}^{\alpha }+\frac{1}{2i}{S}_1^{\alpha }(S_2^{+}{I}^{+}-S_2^{-}{I}^{-})]\sin \sqrt{2}{\tilde{\tilde{\omega }}}_3^{*}t\}.\hfill \end{array}$$ (84)

Since ξ = 90°, the nuclear polarization operator is simplified to

$$\begin{array}{ccc}\hfill {\tilde{\tilde{P}}}_I^{*}& =& \frac{3}{4}{I}_z+\frac{1}{4}{S}_{1z}-\frac{1}{4}{S}_{2z}+S_{1z}{S}_{2z}{I}_z\hfill \\ & & +\frac{1}{2}(S_1^{+}{S}_2^{-}{I}^{-}{e}^{i\tilde{\tilde{\Omega }}t}+S_1^{-}{S}_2^{+}{I}^{+}{e}^{-i\tilde{\tilde{\Omega }}t}).\hfill \end{array}$$ (85)

Therefore, the time-dependent nuclear polarization is

$$\begin{array}{ccc}\hfill ⟨P_I⟩\left(t\right)& =& tr\left({\tilde{\tilde{P}}}_I^{*}{\tilde{\tilde{\rho }}}^{*}\right)\hfill \\ & =& \frac{\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}{\sin }^2\left(\frac{1}{2}\tilde{\tilde{\Omega }}t\right){\sin }^2\left(\frac{\sqrt{2}}{2}{\tilde{\tilde{\omega }}}_3^{*}t\right).\hfill \end{array}$$ (86)

This expression implies that the polarization transfer rate is determined by the smaller of the terms $\frac{1}{2}\tilde{\tilde{\Omega }}\mathrm{and}\frac{\sqrt{2}}{2}{\tilde{\tilde{\omega }}}_3^{*}$. Comparing Eqs. 86, 65, we find that the maximum enhancement of nuclear polarization is equal to $\frac{1}{2}\left|\frac{{\gamma }_S}{{\gamma }_I}\right|$.

Example 4

As in Example 3, we assume that the microwave irradiation is sufficiently broadband to cover two frequencies (differing by $D_d+{\tilde{\tilde{A}}}_1-\tilde{\tilde{\Omega }}$ due to dipolar interactions):

$$\begin{array}{c}\hfill {\tilde{\tilde{\omega }}}_{0S_2}+\frac{1}{2}{D}_d-{\tilde{\tilde{\omega }}}_{0I}+\frac{1}{2}{\tilde{\tilde{A}}}_1\mathrm{and}{\tilde{\tilde{\omega }}}_{0S_1}-\frac{1}{2}{D}_d-\frac{1}{2}{\tilde{\tilde{A}}}_1+\frac{1}{4}\tilde{\tilde{V}},\end{array}$$ (87)

In this example, the terms $\frac{1}{2}(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})S_1^{\alpha }$ and $S_{1x}{S}_2^{\beta }{I}^{\beta }$ are selected. With additional assumptions that s_α is small, and ξ = 90° (exact frequency matching), the effective microwave Hamiltonian becomes

$${\tilde{\tilde{H}}}_M^{\mathrm{eff}*}={\tilde{\tilde{\omega }}}_4^{*}\left[\frac{1}{2}{S}_1^{\alpha }(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})+S_{1x}{S}_2^{\beta }{I}^{\beta }\right],$$ (88)

where ${\tilde{\tilde{\omega }}}_4^{*}=\frac{1}{\sqrt{2}}{\omega }_{1S}$. Similarly for Example 3, the time-dependent density operator can be calculated by taking advantage of the following relations (see supporting information Sec. VI for the details):⁵⁰

$${\tilde{\tilde{H}}}_{M4}^{\mathrm{eff}*}=S_{1x}{S}_2^{\beta }{I}^{\beta }+\frac{1}{2}{S}_1^{\alpha }(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})=S_{1x}{I}_{2\Sigma }^{\beta }+S_1^{\alpha }{I}_{2\Sigma x},$$ (89)

$$\begin{array}{ccc}& & \left[{\tilde{\tilde{H}}}_{M4}^{\mathrm{eff}*},S_{1z}+S_{2z}\right]\hfill \\ & & =-i{S}_{1y}{S}_2^{\beta }{I}^{\beta }-\frac{1}{2}{S}_1^{\alpha }(S_2^{+}{I}^{+}-S_2^{-}{I}^{-}),\hfill \end{array}$$ (90)

$$\begin{array}{ccc}& & \left[{\tilde{\tilde{H}}}_{M4}^{\mathrm{eff}*},\left[{\tilde{\tilde{H}}}_{M4}^{\mathrm{eff}*},S_{1z}+S_{2z}\right]\right]\hfill \\ & & =-S_{1z}{S}_2^{\beta }{I}^{\beta }-\frac{1}{2}{S}_1^{\alpha }(S_2^{\alpha }{I}^{\alpha }-S_2^{\beta }{I}^{\beta }),\hfill \end{array}$$ (91)

$$\begin{array}{ccc}& & \left[{\tilde{\tilde{H}}}_{M4}^{\mathrm{eff}*},\left[{\tilde{\tilde{H}}}_{M4}^{\mathrm{eff}*},\left[{\tilde{\tilde{H}}}_{M4}^{\mathrm{eff}*},S_{1z}+S_{2z}\right]\right]\right]\hfill \\ & & =-\frac{i}{2}{S}_{1y}{S}_2^{\beta }{I}^{\beta }-\frac{1}{4}{S}_1^{\alpha }(S_2^{+}{I}^{+}-S_2^{-}{I}^{-}).\hfill \end{array}$$ (92)

Again, the time-dependent density operator is obtained by combining the recursive relations in Eqs. 90, 91, 92, and the time-dependent nuclear polarization can be calculated from Eqs. 66, 67:

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\rho }}}^{*}& =& \frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}\{(S_{1z}+S_{2z})-2[S_{1z}{S}_2^{\beta }{I}^{\beta }\hfill \\ & & +\frac{1}{2}{S}_1^{\alpha }\left(S_2^{\alpha }{I}^{\alpha }-S_2^{\beta }{I}^{\beta }\right)]\left[1-\cos \left(\frac{1}{\sqrt{2}}{\tilde{\tilde{\omega }}}_4^{*}t\right)\right]\hfill \\ & & -\sqrt{2}\left[S_{1y}{S}_2^{\beta }{I}^{\beta }+\frac{1}{2i}{S}_1^{\alpha }(S_2^{+}{I}^{+}-S_2^{-}{I}^{-})\right]\sin \left(\frac{1}{\sqrt{2}}{\tilde{\tilde{\omega }}}_4^{*}t\right)\}.\hfill \end{array}$$ (93)

$$⟨P_I⟩\left(t\right)=\frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}\left[-1+\cos \left(\frac{1}{\sqrt{2}}{\tilde{\tilde{\omega }}}_4^{*}t\right)\right].$$ (94)

Comparing this expression to the initial nuclear polarization [Eq. 65] implies a maximum DNP enhancement of |γ_S/γ_I|.

Example 5

In this example, we assume that the microwave frequency is broadband and the irradiation amplitude is strong. Therefore, all four of the transitions mentioned earlier are excited— $S_{1x}{S}_2^{\alpha }{I}^{\alpha },S_{1x}{S}_2^{\beta }{I}^{\beta },\frac{1}{2}{S}_1^{\alpha }(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})$ and $-\frac{1}{2}{S}_1^{\beta }(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})$. Assuming that s_α and s_β are small, and ξ = 90°, the effective microwave Hamiltonian is the sum of all four transitions. This effective Hamiltonian can be simplified further [using the definitions in Eq. 74]

$${\tilde{\tilde{H}}}_M^{\mathrm{eff}*}={\tilde{\tilde{\omega }}}_5^{*}(S_{1x}{E}_{I2\Sigma }+2S_{1z}{I}_{2\Sigma x}),$$ (95)

where ${\tilde{\tilde{\omega }}}_5^{*}=\frac{1}{\sqrt{2}}{\omega }_{1S}$. To simplify the propagation of the density operator according to Eqs. 4, 5, one needs to rewrite the initial density operator [Eq. 64] as

$${\tilde{\tilde{\rho }}}_0^{*}=\frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}(S_{1z}{E}_{I2\Sigma }+S_{1z}{E}_{I2\Delta }+I_{2\Sigma z}+I_{2\Delta z}).$$ (96)

An inspection of the definitions given in Eq. 74 and the commutation relations among them reveals that the S_1xE_I2Σ and S_1zI_2Σx terms of the effective microwave Hamiltonian affect only the S_1zE_I2Σ and I_2Σz terms in the density operator, respectively. Therefore, the time-dependent density operator and the time-dependent nuclear polarization can be obtained as follows:

$$\begin{array}{ccc}\hfill {\tilde{\tilde{\rho }}}^{*}& =& \frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}\{(S_{1z}+S_{2z})\hfill \\ & & +\frac{1}{2}(S_{1z}{E}_{I2\Sigma }-2S_{1y}{I}_{2\Sigma y}-2S_{1x}{I}_{2\Sigma x}+I_{2\Sigma z})\hfill \\ & & \times [\cos \left(\sqrt{2}{\tilde{\tilde{\omega }}}_5^{*}t\right)-1]\hfill \\ & & -\frac{1}{\sqrt{2}}(S_{1y}{E}_{I2\Sigma }+2S_{1z}{I}_{2\Sigma y})\sin \left(\sqrt{2}{\tilde{\tilde{\omega }}}_5^{*}t\right)\},\hfill \end{array}$$ (97)

$$⟨P_I⟩\left(t\right)=\frac{-\hslash }{Z{k}_{B}T}\frac{{\omega }_{0S_1}+{\omega }_{0S_2}}{2}\left(-2{\sin }^2\frac{\tilde{\tilde{\Omega }}t}{2}{\sin }^2\frac{{\tilde{\tilde{\omega }}}_5^{*}t}{\sqrt{2}}\right).$$ (98)

The maximum DNP enhancement can now be obtained based on Eqs. 65, 23, and it is |γ_S/γ_I|. The maximum DNP enhancements and the time-dependence of the nuclear polarization from examples 1 to 5 for microwave irradiation frequency near ω_0S1are summarized in Table 2.

Table 2.

The effective excitation Hamiltonians and the corresponding microwave frequencies that produce positive DNP enhancements are listed. The selection of excitation depends on the microwave bandwidth and amplitude. The maximum enhancement and the Rabi oscillation characterize the time dependence of the nuclear polarization. The results are based on small ζ_α and ζ_β (moderate electron–electron dipolar interaction) and ξ = 90 ° (full three-spin mixing). The asterisks denote the effective excitation selected by ω_M.

Effective excitation ${\tilde{H}}_M^{\mathrm{eff}*}$	Microwave frequency ωM	Excitation selected by ωM
$S_{1x}{S}_2^{\alpha }{I}^{\alpha }$	${\tilde{\tilde{\omega }}}_{0S_1}+\frac{1}{2}{D}_d+\frac{1}{2}{\tilde{\tilde{A}}}_1+\frac{1}{4}\tilde{\tilde{V}}$	*		*		*
$\frac{1}{2}{S}_1^{\alpha }(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})$	${\tilde{\tilde{\omega }}}_{0S_2}+\frac{1}{2}{D}_d-{\tilde{\tilde{\omega }}}_{0I}+\frac{1}{2}{\tilde{\tilde{A}}}_1$		*	*	*	*
$S_{1x}{S}_2^{\beta }{I}^{\beta }$	${\tilde{\tilde{\omega }}}_{0S_1}-\frac{1}{2}{D}_d-\frac{1}{2}{\tilde{\tilde{A}}}_1+\frac{1}{4}\tilde{\tilde{V}}$				*	*
$-\frac{1}{2}{S}_1^{\beta }(S_2^{+}{I}^{+}+S_2^{-}{I}^{-})$	${\tilde{\tilde{\omega }}}_{0S_2}-\frac{1}{2}{D}_d-{\tilde{\tilde{\omega }}}_{0I}-\frac{1}{2}{\tilde{\tilde{A}}}_1$					*
Maximum enhancement of		$\frac{1}{4}\left|\frac{{\gamma }_S}{{\gamma }_I}\right|$	$\frac{1}{4}\left|\frac{{\gamma }_S}{{\gamma }_I}\right|$	$\frac{1}{2}\left|\frac{{\gamma }_S}{{\gamma }_I}\right|$	$\left|\frac{{\gamma }_S}{{\gamma }_I}\right|$	$\left|\frac{{\gamma }_S}{{\gamma }_I}\right|$
nuclear polarization
Oscillation between the electron		$\frac{1}{2}(1-\cos \frac{{\omega }_{1S}t}{\sqrt{2}})$	$\frac{1}{2}(1-\cos \frac{{\omega }_{1S}t}{\sqrt{2}})$	${\sin }^2\frac{\tilde{\tilde{\Omega }}t}{2}{\sin }^2\frac{{\omega }_{1S}t}{2}$	$\frac{1}{2}(1-\cos \frac{{\omega }_{1S}t}{\sqrt{2}})$	${\sin }^2\frac{\tilde{\tilde{\Omega }}t}{2}{\sin }^2\frac{{\omega }_{1S}t}{2}$
and nuclear polarizations

EXPERIMENTAL DNP RESULTS

A typical DNP experiment is recorded with continuous-wave microwave irradiation as illustrated in Fig. 7a and the DNP mechanism that leads to enhanced ¹H polarization depends on the concentration of radical present, the breadth of its EPR spectrum, and whether it is in the form of a monoradical or biradical. The enhanced ¹H polarization is then usually transferred to the ¹³C nuclei in the sample via cross-polarization.⁵¹ A train of saturating pulses at the beginning of the sequence ensures that the measured enhancement results only from the DNP process. Note that while in this case the ¹³C nuclei are observed, the enhancement reflects the ¹H polarization.

Figure 7.

(a) A typical DNP–MAS experimental pulse sequence. Continuous microwave irradiation is used to saturate the electrons in the sample, and the enhanced ¹H polarization is transferred via a CP-MAS experiment to the ¹³C nuclei for observation. A train of saturating pulses on the ¹H channel is used to ensure that all of the nuclear polarization arises from DNP. (b) ¹³C-urea spectra obtained from a sample doped with the biradical BT2E at a concentration of 5 mM (or 10 mM electrons), 90 K, ω_r/2π = 3.5 kHz. The top row shows the enhanced signal (with microwave irradiation on) as a function of the irradiation time τ_DNP. The bottom row shows the ¹³C-urea signal in the absence of DNP (microwave irradiation off). The observed enhancement is 175 ± 25. (c) Buildup curve of the enhanced nuclear polarization (filled circles) with a time constant of 5 s, coinciding with the ¹H T₁ curve, measured without microwave irradiation (empty circles).

Figure 7b shows a series of DNP enhanced spectra of a ¹³C-urea sample, doped with the biradical BT2E. In this case the CE leads to an enhancement of 172 ± 25, measured by comparing the ¹³C signal with microwave irradiation on and off. The signal dependence on the microwave irradiation time (τ_DNP) is plotted in Fig. 7c. It has a time constant of 5 s, similar to the ¹H spin–lattice relaxation time obtained by using the same pulse sequence in the absence of microwave irradiation. This important experimental observation regarding the CE will be discussed in Sec. 4C.

The validity of the analytical results discussed above regarding the frequency matching conditions for the SE and the CE can be demonstrated experimentally by recording DNP enhancement profiles as a function of the magnetic field and comparing them to the corresponding radical EPR spectrum (Fig. 8). This has been possible in our current DNP and EPR instruments where we have been able to record both high-field MAS NMR and EPR spectra at 5 T (211 MHz ¹H Larmor frequency, 140 GHz EPR frequency).^{1, 52, 53, 54} By changing the static magnetic field with a superconducting sweep coil in our NMR magnet and recording an enhanced ¹H MAS NMR spectrum at each field point, a field profile of the enhancement spanning several hundred Gauss can be obtained.

Figure 8.

Experimental ¹H DNP enhancement profiles for the SE and the CE mechanisms showing the positions of positive and negative enhancement and their dependence on ω_0S and ω_0I. (a) A typical SE enhancement profile obtained with 40 mM trityl. (b) A CE enhancement profile obtained with 10 mM TOTAPOL (20 mM electrons). Samples were prepared as described in the supporting information, and the position of the EPR spectrum of each radical is shown on the top. The lines connecting the data points are to guide the eye.

The profile for the SE [Fig. 8a] was recorded using 40 mM trityl radical,⁴⁶ whose EPR spectra have relatively narrow inhomogeneous linewidth (Δ = 42 MHz at 5 T).⁵⁵ The positive and negative enhancements corresponding to the DQ and ZQ SE transitions are clearly resolved and can be found at ± 75 Gauss (ω_0I = ± 211 MHz) from the center of the EPR spectrum (ω_0S). Note that the enhancements in this case are ɛ = +15 and −13.

The CE polarization transfer mechanism relies on the presence of two electrons that have a relatively large dipolar coupling to each other and small dipolar couplings to other electrons in the sample. The optimal polarizing agent in such a case is a biradical, e.g., the nitroxide-based biradical TOTAPOL (∼22 MHz electron–electron dipolar coupling).^{8, 24}

Nitroxide radicals in general exhibit EPR spectra dominated by inhomogeneous broadening with Δ ≈ 600 MHz at 5 T,²⁵ and therefore can satisfy the matching condition for the CE, i.e., there are electrons with EPR frequencies ω_0S1and ω_0S2separated by ω_0I (211 MHz in this case). This situation is illustrated in Fig. 8b. The transitions giving rise to the experimental profiles in Fig. 8 are, of course, much broader than the sharp frequency matching conditions described above. This is due to the breadth of the g-tensor of the EPR spectrum where each field position leads to a unique set of electron pairs that satisfy the matching condition.

The observed enhancement factors are also worth noting. In contrast to the SE, the CE mechanism produces enhancements on the order of 172. This is due to the more favorable ω₀ dependence of the CE, discussed in more detail below. It should also be noted that the field profile is asymmetric with a larger enhancement observed on the high field side. This is a reflection of the fact that the largest number of electrons/gauss that meet the matching condition occurs on the low field side of the EPR spectrum at B₀ ∼ 49 680 G. Therefore, irradiating on the high field side of the spectrum at 49 800 G then produces the larger enhancement. Interestingly when ω_0I is smaller, as is the case for ¹³C, then the asymmetry in the field profile is more pronounced since the matching condition now requires that ω_0S1and ω_0S2only differ by 53 MHz (at 5 T).⁵⁶ Therefore, irradiating on the left side of the spectrum not only targets more electrons but also leads to contributions from their paired electrons, which are on the same side of the spectrum, thus producing larger enhancements on this low-field side. In the case where ²H is polarized, ω_0I is even smaller and trityl radical becomes the polarizing agent of choice.⁵⁷ Improvements in the experimental apparatus, such as using more efficient MW transmission lines,⁵⁸ can increase the microwave B₁ field delivered to the sample. This has a dramatic effect on the enhancements observed for the SE mechanism and will be discussed in a future publication.

DISCUSSION

In Secs. 1, 2, we have shown the systematic diagonalization of the two or three-spin Hamiltonian necessary to describe the SE or the CE, respectively. In each case, we have derived the effective microwave irradiation Hamiltonian that leads to the evolution of the electron Zeeman order into the nuclear Zeeman order and yields DNP. Here, we discuss further the frequency matching conditions for the SE and the CE polarization transfer mechanisms and compare the influence of the microwave irradiation field strength ω_1S and the static magnetic field B₀. We hope that this discussion will further clarify the advantages of the CE over the SE at high magnetic fields.

Frequency matching conditions for DNP

While the frequency matching requirements for both the SE and CE have been discussed in the literature, the exact EPR and microwave frequencies, which depend on the specific electron−electron and electron−nuclear interactions, have been ignored due to the presence of relaxation in realistic spin systems. Nonetheless, the exact nature of these frequencies becomes important as we attempt to understand the mechanisms of polarization transfer using quantum dynamics of ideal spin systems. According to Eqs. 19, 20, 13 the exact frequency matching for the SE is ${\omega }_M={\omega }_{0S_1}\pm {\tilde{\omega }}_{0I}$. A Taylor expansion of the cosine and sine terms in Eq. 13 shows that

$${\tilde{\omega }}_{0I}\approx {\omega }_{0I}+\frac{B_1^2}{4{\omega }_{0I}}.$$ (99)

This expression is consistent with a second order perturbation of the semisecular hyperfine interaction B₁. Since B₁ is usually small and thus $B_1^2\ll {\omega }_{0I}$, the matching condition generally equalsω_0S1±ω_0I. Without relaxation, the frequency matching allows the nuclear polarization to be enhanced through an oscillation of the polarization between the electron and nuclear spin systems. The maximum enhancement due to this oscillation is |γ_S/γ_I|.

Efficient microwave excitation for the CE relies on the full mixing of states, which requires ${\tilde{\omega }}_{\Delta }=\pm {\omega }_{0I}$ according to Eqs. 43, 38. Taylor expansion of the cosine and sine terms in Eq. 38 yields

$${\tilde{\omega }}_{\Delta }\approx {\omega }_{\Delta }+\frac{D_o^2}{{\omega }_{\Delta }},$$ (100)

whereω_Δ=ω_0S1−ω_0S2. This result is again consistent with a second order perturbation of the off-diagonal electron−electron interaction D_o. It is obvious that electron−electron interactions affect the matching condition for the EPR frequency separation. While the discussion of the CE in Secs. 1, 2 is primarily based on moderate electron−electron interactions, the frequency matching for the CE in the region of strong electron−electron interactions is discussed in the Appendix.

Furthermore, the microwave transitions for the CE are excited by microwave irradiation at ω_M∼ω_0S1orω_M∼ω_0S2. These transitions can be divided into two groups of four as shown in Eqs. 62, 63. Without relaxation, the correct EPR and microwave frequencies allow the nuclear polarization to be enhanced through various oscillation mechanisms depending on the selected transitions:

1. When the microwave irradiation is narrowband and weak, thus choosing only one of the four transitions, the oscillation between the electron and nuclear polarization contains one frequency, namely, ∼${\omega }_{1S}∕\sqrt{2}$ and leads to a maximum nuclear polarization enhancement of |γ_S/γ_I|/4 in the absence of relaxation.

2. When the microwave irradiation is narrowband and strong, two of the four transitions can be selected. The selected transitions are separated by $\tilde{\tilde{\Omega }}$, which is usually small due to a second-order effect of the spin–spin interactions [See Eq. 48]. In this case, the oscillation between the electron and nuclear polarization contains two frequencies, $\tilde{\tilde{\Omega }}∕2$ and ∼ ω_1S∕2, and leads to a maximum nuclear polarization enhancement of |γ_S/γ_I|/2.

3. In the case of broadband but weak microwave irradiation, only the two transitions separated by $D_d+{\tilde{\tilde{A}}}_1-\tilde{\tilde{\Omega }}$ (usually large due to the first-order electron−electron interactions) are selected. The oscillation between the electron and nuclear polarization contains only one frequency, ∼${\omega }_{1S}∕\sqrt{2}$, and leads to a maximum nuclear polarization enhancement of |γ_S/γ_I|.

4. In the last example, when the microwave irradiation is broadband and strong, all four transitions are selected despite their separation in excitation frequency. The oscillation between the electron and nuclear polarization contains two frequencies, $\tilde{\tilde{\Omega }}∕2$ and ∼ ω_1S∕2, which leads to a maximum nuclear polarization enhancement of |γ_S/γ_I|.

The frequency matching conditions derived in this paper appear to be independent of the microwave field strength ω_1S. The reason is that we generally assume weak microwave field perturbations given that ω_1S leaves the eigenstates unaffected. However, in practical DNP experiments it is often the case that strong microwave field strengths are available; thus the matching condition would break down, the couplings between the mixed states would become less effective, and the polarization transfer would be attenuated. This ω_1S disturbance to the frequency matching is more serious in the CE, where the effective couplings for state-mixing result from the second order effect of the spin–spin interactions, as opposed to the first order interaction in the SE. Nevertheless, in reality, the frequency matching range for DNP can be broadened by relaxation and in the case of CE can be increased further by strong electron−electron interactions.

Influence of the microwave field strength and the static magnetic field on DNP

According to Fermi's golden rule, the polarization rate approximates the initial slope of the involved oscillation between the electron and nuclear polarizations. In the SE, the polarization rate approximates the first term of the Taylor expansion of Eq. 28, which is ∼ (B₁ω_1S/ω_0I)² under the assumption that A₁ ≪ ω_0I (note that A₁ and B₁ represent the secular and nonsecular hyperfine interactions). This result indicates that the efficiency of the SE is proportional to$P{B}_0^{-2}$, where P is the microwave power ($P\propto {\omega }_{1S}^2$), and B₀ is the external magnetic field.

In the CE, the time-dependent nuclear polarization oscillates in a more complicated manner. For positive DNP enhancement, the strong microwave irradiation excites all four transitions mentioned previously, and the smaller of the frequencies $\tilde{\tilde{\Omega }}∕2$ or ω_1S∕2 determines the oscillating envelope of the DNP enhancement. Therefore, the initial slope of the oscillation is either ${\left(\tilde{\tilde{\Omega }}∕2\right)}^2$ or(ω_1S∕2)². Thus, when ${\omega }_{1S}\ll \tilde{\tilde{\Omega }}$, the polarization rate is proportional to ${\omega }_{1S}^2$ or P and so is the DNP enhancement. When ${\omega }_{1S}\sim \tilde{\tilde{\Omega }}$, the DNP efficiency becomes independent of the microwave power, and a saturation of the DNP enhancement by the microwave power is reached.

The magnetic field effect on a single CE process is reflected by $\tilde{\tilde{\Omega }}$ which is a second-order effect with respect to the electron–electron dipolar, hyperfine, and nuclear Zeeman interactions. However, typical DNP enhancements result from many polarization processes and the involved dipolar interactions can compensate for the effect of B₀. Hence B₀ does not explicitly affect the CE through $\tilde{\tilde{\Omega }}$, especially when the oscillation of enhanced nuclear polarization is controlled by ω_1S. In fact, external magnetic fields affect the CE through frequency matching that requires the correct EPR frequency separation. When the desirable frequency separation is obtained from a broad EPR lineshape, the probability of frequency matching is linearly decreased by the linewidth. If the line broadening is primarily due to g-anisotropy which scales with B₀, then the overall DNP enhancement through the CE is proportional to B₀⁻¹. This magnetic field dependence is common for DNP experiments relying on the use of nitroxide radicals, which exhibit relatively well resolved g-anisotropies at high magnetic fields.

The efficiency of the CE can in principle be improved dramatically by increasing significantly the number of electrons with isotropic g values at ω_0S1andω_0S2. In an ideal case, the EPR spectrum then will consist of two lines, separated by ω_0I. While at the moment we are not aware of radicals that satisfy this condition, it has been demonstrated that by using a mixture of a narrow line radical such as trityl and a nitroxide radical such as TEMPO, one can obtain greater enhancements.⁵⁵ Greater enhancements can also be obtained by using more rigid biradicals, such as bTbk where a rigid tether locks the two TEMPO moieties in a more favorable orientation.⁹ Enhancements up to 250 have been observed in this system under identical conditions as the ones reported for TOTAPOL in this work.

Implications of quantum mechanical treatments on macroscopic rate equations

In the absence of relaxation, a single electron–nuclear or electron–electron–nuclear system could allow one to monitor the oscillation frequencies and amplitudes derived here. Similar to the observation of Rabi oscillations at the beginning of a saturation pulse on the electron, the oscillation of the nuclear polarization might be observable in a simplified electron–nuclear spin system, e.g., in a single crystal sample. This requires that the rate of the electron T₂ relaxation has to be slower than the Rabi oscillation frequency and the oscillation depth would depend on the level of state mixing. However, most DNP experiments involve much larger quantum mechanical systems, with a range of couplings, Larmor frequencies, and relaxation. Thus, when observing NMR intensities, a monoexponential polarization buildup curve, such as the one shown in Fig. 7c, is obtained for most DNP experiments, making it difficult to observe the microscopic behavior. However, the response of the DNP time constant to microwave irradiation can provide information about the mechanism of DNP involved.

The solid effect can be modeled macroscopically using Eq. 101, where N_I/N_S is the ratio of nuclei to electrons, T_1I and T_1S are the nuclear and electronic relaxation times, and k_SE is the solid effect DNP rate constant.^{26, 34, 59, 60}

$$\begin{array}{ccc}\hfill \frac{d{P}_S}{dt}& =& \frac{N_I}{N_S}{k}_{\mathrm{SE}}\left(P_S-P_I\right)-\frac{1}{T_{1S}}\left(P_S-P_{S,\mathrm{eq}}\right),\hfill \\ \hfill \frac{d{P}_I}{dt}& =& k_{\mathrm{SE}}\left(P_S-P_I\right)-\frac{1}{T_{1I}}\left(P_I-P_{I,\mathrm{eq}}\right).\hfill \end{array}$$ (101)

In Eq. 21, we see that microwave irradiation introduces mixing of the electron–nuclear states, which then manifests itself in Eq. 101 as electron–nuclear polarization transfer parameterized by k_SE. The DNP time constant can be obtained from Eq. 101 by assuming a fast equilibrium of the electrons and setting dP_S/dt = 0.

$$\frac{1}{T_{\mathrm{DNP}}}=\frac{1}{T_{1I}}+\frac{k_{\mathrm{SE}}}{1+\frac{N_I}{N_S}{k}_{\mathrm{SE}}{T}_{1S}}.$$ (102)

Because the DNP rate constant adds to the nuclear relaxation rate constant, larger DNP enhancements due to the solid effect are accompanied by a decrease in the DNP time constant.³⁴

Equation 103 is commonly used to describe macroscopic polarization transfer due to the cross effect, where the parameters are as before, except we have introduced k_CE as the cross effect DNP rate constant and k₀ as the rate constant driving saturation of S₁.^{30, 31, 32, 33, 34}

$$\begin{array}{ccc}\hfill \frac{d{P}_{S_1}}{dt}& =& -k_0{P}_{S_1}+\frac{N_S}{N_I}\left(2k_{\mathrm{CE}}\right)\left[\left(P_{S_2}-P_{S_1}\right)-P_I\right]\hfill \\ & & -\frac{1}{T_{1S_1}}\left(P_{S_1}-P_{S_1,\mathrm{eq}}\right),\hfill \\ \hfill \frac{d{P}_{S_2}}{dt}& =& -\frac{N_S}{N_I}\left(2k_{\mathrm{CE}}\right)\left[\left(P_{S_2}-P_{S_1}\right)-P_I\right]\hfill \\ & & -\frac{1}{T_{1S_2}}\left(P_{S_1}-P_{S_1,\mathrm{eq}}\right),\hfill \\ \hfill \frac{d{P}_I}{dt}& =& k_{\mathrm{CE}}\left[\left(P_{S_2}-P_{S_1}\right)-P_I\right]-\frac{1}{T_{1I}}\left(P_I-P_{I,\mathrm{eq}}\right).\hfill \end{array}$$ (103)

In Eq. 103, we take the assumption that k_CE results from mixing of the electron and nuclear states via the static Hamiltonian, and not from the microwave field, whereas k₀ does result from the applied field and saturates S₁. The difference in polarization of the two electrons then allows polarization transfer to the nuclei. One can show that since the rate constants governing the nuclear polarization buildup do not change for different microwave fields, the DNP time constant will also remain constant when 2N_IT_1S/N_ST_1I ≪ 1, whereas the enhancement will depend strongly on the microwave field. We note that the microwave Hamiltonian in Eq. 69 brings about this behavior. In the presence of relaxation, the single quantum excitation of S₁($S_{1x}{S}_2^{\alpha }{I}^{\alpha }$) will lead to saturation of S₁[k₀ in Eq. 103]. Because of the mixing of states brought about by ${\tilde{\tilde{H}}}_0^{\mathit{ISS}}$[k_CE in Eq. 103], this saturation of S₁ then leads to a gain in nuclear polarization. It is important to note that this mixing of states exists even in the absence of the microwave field. It is for this reason that one can assume k_CE in Eq. 103 remains constant in the presence of a microwave field.

In contrast to Eq. 69, the microwave Hamiltonians in Eqs. 73, 79, 88, 95 include double quantum electron–nuclear transitions. Therefore, the microwave Hamiltonian will increase the mixing between states. This will manifest itself as an increase in the rate constant governing the DNP transfer, much like the solid effect. Therefore, like the solid effect, the DNP rate constant will be decreased.

Figure 7c demonstrates that for the CE the DNP time constant and T_1I are the same. This is consistent with Eq. 103, where we assume that mixing of electron and nuclear states is unaffected by the microwave field and so the DNP time constant does not differ from T_1I. Therefore, it is the Hamiltonian in Eq. 69 that is the most consistent with this result. While perhaps surprising at first, this observation can be explained by the fact that most electron pairs will not exactly satisfy the matching condition ${\tilde{\omega }}_{\Delta }=-{\omega }_{0I}$, and with only small hyperfine couplings, most values for ξ will be much closer to 0° than to 90°. Thus, the rate of the double-quantum transitions in Eq. 73 will be very slow for weak microwave fields since ${\tilde{\tilde{\omega }}}_2^{*}={\omega }_{1S}(c_{\alpha }-s_{\alpha })\sin \frac{\xi }{2}$, but fast for the single-quantum transitions since ${\tilde{\tilde{\omega }}}_1^{*}={\omega }_{1S}(c_{\alpha }-s_{\alpha })\cos \frac{\xi }{2}$. This suggests that with stronger microwave fields, it should be possible not only to saturate S₁ more completely, but also to gain additional sensitivity by improving the electron–nuclear mixing via double quantum excitation and therefore decreasing the DNP time constant.

CONCLUSIONS

The enhanced nuclear polarization in the SE and CE DNP mechanisms has been described quantum mechanically using an electron–nuclear or an electron–electron–nuclear spin system under microwave irradiation. Our calculations verify the frequency matching conditions for each mechanism, namely ω_M = ω_0S ± ω_0I for the SE and ω_0S1−ω_0S2=ω_0I for the CE. Based on our theory, the effects of the microwave field strength and the external magnetic field on DNP are consistent with the conclusions of classical theories established on spin thermodynamics. Although stringent frequency matching conditions are inferred by our analytical approach, they can be eased when relaxation effects are incorporated into the calculations. Simulations of DNP in electron−electron−nuclear spin systems with relaxation are in progress and will be reported in a future article.

APPENDIX: STRONG ELECTRON−ELECTRON INTERACTIONS IN A THREE-SPIN SYSTEM

Although the analytical approach to describing an electron−electron−nuclear system includes the possibility of stronger electron−electron interactions, the overall discussion so far has implied that such interactions are much smaller than the nuclear Larmor frequency. Thus, the required frequency separation in the EPR spectrum has mainly been provided by the electron Zeeman interaction. However, dipolar splittings can also contribute to the EPR frequency separation. Specifically, in the case when the differences in the g-values are small, the triplet-singlet basis-sets are more relevant to the discussion of frequency matching for the CE than the spin-pair basis set. For example, if the electron−electron interaction terms d and J in Eq. 29 are larger than|ω_0S2−ω_0S1|, it is appropriate to represent the spin Hamiltonian in the electron triplet-singlet basis set. The transformation from electron spin-pair basis set to triplet-singlet basis set involves the following energy levels, also shown in Fig. 9:

$$\begin{array}{ccc}\hfill |T_1⟩& =& |\alpha \alpha ⟩,|T_{-1}⟩=|\beta \beta ⟩,|T_0⟩=\frac{1}{\sqrt{2}}\left(\right|\alpha \beta ⟩+|\beta \alpha ⟩),\hfill \\ \hfill |S_0⟩& =& \frac{1}{\sqrt{2}}\left(\right|\alpha \beta ⟩-|\beta \alpha ⟩).\hfill \end{array}$$ (A1)

Figure 9.

A level diagram for a triplet-singlet-nuclear spin system. The variables used in the expressions of the transitions and the coupling energies are defined in Sec. 2. Because of the forbidden EPR transitions associated with the singlet state, only half of the DNP transitions are allowed. They are marked by the solid and dashed arrows for positive and negative DNP enhancement, respectively.

If |D_o| ∼ |ω_0I|, levels |2〉 and |7〉 become approximately degenerate and are fully mixed into |2^′〉 and |7^′〉 by H₂₇. According to the selection rules involving the triplet-singlet basis set, the transitions |2^′〉 ↔ |1〉 and |7^′〉 ↔ |4〉 are excited by microwave irradiation near E₁₂ and E₂₄ and lead to positive and negative DNP enhancements, respectively. Note that the two EPR peaks in this case are separated by E₁₂ − E₂₄ = |D_d −D₀| since the EPR transitions are near E₁₂ and E₂₄. With negligible J, the definition in Table 2 suggests that the two EPR peaks are separated by 3ω_0I and the matching condition requires d ∼ ω_0I.