Measuring Disparities: Bias in the SF-36v2 among Spanish-speaking Medical Patients

Abstract

Background

Many national surveys have found substantial differences in self-reported overall health (SROH) between Spanish-speaking Hispanics and other racial/ethnic groups. However, because cultural and language differences may create measurement bias, it is unclear whether observed differences in SROH reflect true differences in health.

Objectives

This study uses a cross-sectional survey to investigate psychometric properties of the SF-36v2 for subjects across four racial/ethnic and language groups. Multi-group latent variable modeling was used to test increasingly stringent criteria for measurement equivalence.

Subjects

Our sample (N = 1281) included 383 non-Hispanic whites, 368 non-Hispanic blacks, 206 Hispanics interviewed in English and 324 Hispanics interviewed in Spanish recruited from outpatient medical clinics in two large urban areas.

Results

We found weak factorial invariance across the four groups. However, there was no strong factorial invariance. The overall fit of the model was substantially worse (change in CFI > .02, RMSEA change > .003) after requiring equal intercepts across all groups. Further comparisons established that the equality constraints on the intercepts for Spanish-speaking Hispanics were responsible for the decrement to model fit.

Conclusions

Observed differences between SF-36v2 scores for Spanish speaking Hispanics are systematically biased relative to the other three groups. The lack of strong invariance suggests the need for caution when comparing SF-36v2 mean scores of Spanish-speaking Hispanics with those of other groups. However, measurement equivalence testing for this study supports correlational or multivariate latent variable analyses of SF-36v2 responses across all four subgroups, since these analyses require only weak factorial invariance.

INTRODUCTION

Health policy decisions are informed by comparisons of the health care needs and outcomes of specific populations. Nationally representative health surveys are particularly useful in gathering relevant information about the general population and variations among specific subpopulations. Such surveys rely heavily on subjective self reports. Self-rated health assessments are commonly used as key outcomes in randomized trials. For example, a recent systematic review identified 52 trials in 2005 alone that made use of some version of the SF-36 as an outcome measure.¹

If self-reported health measures are to be used to fuel decision-making regarding racial or ethnic health inequality, it is important to verify the measurement equivalence/invariance of such measures.² Bias in self-reported health measures could lead to overestimates or underestimates of some subpopulations’ true health needs with the potential to mislead health practitioners, researchers and policy makers.

This potential measurement bias is of particular importance to researchers studying the health of Hispanic populations. The Hispanic population is extraordinarily heterogeneous in socioeconomic status, culture, and acculturation level. Such heterogeneity may introduce systematic bias into survey responses and subjective health measures gleaned from these responses for Hispanics collectively, or across Hispanic sub-populations. Providing adequate translations of survey questions does not by itself address the issues of “potential cultural differences in the interpretation of questions and in response styles [that] may limit direct comparisons between members of different racial/ethnic groups.”³ Several studies challenge the validity of subjective health as indicators of health, health care need, and satisfaction with care when comparing Hispanics to non-Hispanic whites.^4–8

Determining that a subjectively assessed scale has good reliability and validity properties within specific populations (e.g., whites, blacks, English-speaking and Spanish-speaking Hispanics) does not guarantee measurement equivalence across populations. Perceived health depends on cultural norms of health and illness, and cross-cultural differences could mean that two individuals with the same objective levels of physical and mental health would nonetheless report differently about their health. In particular, the same mean scores for whites and Spanish-speaking Hispanics on a subjective measure might not reflect the same objective status on a particular health domain. Health disparities researchers rely on the ability to compare scale scores between racial/ethnic groups. However, any examination and interpretation of group differences in health is premature without first establishing that health status measures are invariant across groups.^9–12

Without measurement equivalence, SF-36 scores cannot be used to make valid inferences about racial/ethnic group differences; such differences might be due to item response bias rather than true differences in self reported health.¹³ Non-equivalence can occur when differences in values, attitudes, language and overall worldview cause respondents to respond to survey questions differently, leading to differential item functioning.¹⁴ As an example, comparing racial/ethnic groups in terms of mean SF-36 scores would be problematic if factorial invariance in the scales did not hold, in which case differences in mean scale scores would fail to reflect “true” differences in health between groups.^2,12,15–17

While a previous study investigated measurement equivalence of the SF-36 across a regional sample of English and Spanish-language respondents,¹⁸ our study expands on that work in several important ways. First, Hays et al tested only for differences between language groups (Spanish and English). We test for differences across race/ethnicity and language, assessing measurement equivalence between whites, blacks, English-speaking Hispanics and Spanish-speaking Hispanics. Second, Hays et al ended their investigation after finding evidence for weak invariance (invariance of factor loadings). We test for weak, strong (invariance of item intercepts) and strict (invariance of measurement errors/residuals) invariance. Although weak invariance is sufficient for understanding cross-group associations between latent variables, strong invariance is a necessary prerequisite to the group comparison of SF-36 latent means.^2,17 A lack of strong invariance (intercept differences) may lead to the over or underestimation of group differences in health.² While some researchers do not view testing for strict invariance as a necessary step, we follow the more conservative approach advocated by Meredith and Teresi⁹ and Lubke and Dolan¹⁹; our study further evaluates constraints on error/residual variances and covariances to determine whether comparison of observed means (SF-36v2 composite scores) are defensible. Finally, our study investigates these measurement invariance issues using the more recent Short-Form 36 version 2 (SF-36v2).

METHODS

We conducted a cross-sectional multigroup comparison of responses to the SF-36v2. Our sample (N=1281) included 383 non-Hispanic whites, 368 non-Hispanic blacks, 206 Hispanics interviewed in English and 324 Hispanics interviewed in Spanish. Adult patients aged 45–64 were recruited from outpatient medical clinics in two academic general internal medicine practices and two community health clinics in Chicago, Illinois and Cleveland, Ohio.

Study design and population

Patients were recruited by several methods, including “live” recruiting while waiting for appointments, telephone calls made to patients scheduled for clinic appointment, mailings, and advertisements (i.e., posters and flyers) in community centers and hospital/clinic areas. When possible, potential subjects were screened for eligibility prior to their arrival at the research sites; exclusions included being non-ambulatory, having a body mass index >35.0 kg/m², or not speaking English or Spanish. Upon arrival, research associates obtained formal consent and completed exclusion assessments. Patients were also excluded if their resting heart rate was <56 or >90, resting respiratory rate was >17, or resting blood pressure was >160/100.

Face-to-face interviews were conducted in English or Spanish based on patient preference. The survey questionnaire was computer-assisted and interviewer-administered.

Measures

Self-reported health was measured using the SF-36v2 health survey. We classified Hispanics as English-speaking and Spanish-speaking based on the subject’s expressed preference at interview. Socioeconomic status variables included: 1) educational level (number of years; < 9 years, 9–11 years, HS graduate, some college, college graduate); 2) yearly household income (<$10,000, 10–20,000, 20–50,000 and 50,000 or more); and 3) an indicator of health insurance. Chronic conditions were measured by a count of seven self-reported conditions: hypertension, diabetes, heart disease, cancer, arthritis, lung disease, and stroke. Health behaviors included smoking status (current, past, and never) and body mass index <25 kg/m² (referent), ≥ 25 but <30 kg/m², and ≥ 30 kg/m² but >35 kg/m².

Data Analysis

Assessing measurement equivalence can be done using either item response theory (IRT) and/or confirmatory factor analysis (CFA) methods, which share several common aims.^20–21 However, most IRT-based tests for measurement equivalence and differential item functioning (DIF) carry a unidimensionality assumption that is not satisfied by the SF-36.²² Additionally, the Multiple-Indicator-Multiple-Cause Model (MIMIC) has been used to investigate DIF in the SF-12,²³ however this approach assumes factor loadings are the same in different subgroups, an assumption tested directly in our analysis. CFA is useful for testing invariance because it is capable of directly modeling the multidimensional structure of the SF-36. Models using CFA to test measurement equivalence (in particular testing for invariance of item intercepts) can detect and describe systematic bias that causes members of a particular group to respond differently to items in a scale or subscale. (See November 2006 Medical Care Special Issue Volume 44, Number 11, Suppl 3 devoted to invariance testing for a complete discussion of terms, theory and methods).

Several studies have evaluated the measurement structure of the SF-36 using exploratory and confirmatory factor analysis.^24–28 Our analysis uses the eight factor measurement structure from the ten country International Quality of Life Assessment (IQOLA) project.²⁵ We used multi-group confirmatory factor analysis to test increasingly stringent criteria for measurement equivalence. All analyses were conducted using AMOS statistical software version 16 (Chicago, IL: SPSS). Our approach to testing for measurement equivalence was adapted from Byrne’s “Logically Organized” strategy ^29–30 and the more detailed approach described by Vandenberg and Lance¹⁷:

1. Test for invariance of 1^st order factor loadings (weak invariance)

2. Test for invariance of 2^nd order factor loadings (2^nd order weak invariance)

3. Test for invariance of all factor loadings and intercepts (strong invariance)

4. Test for invariance of all factor loadings and intercepts using subsets of racial and ethnic groups (partial invariance)

5. Test for invariance of measurement errors/residuals (strict invariance)

Following multiple previous studies of the SF-36, all CFA models were tested using maximum likelihood estimation, which is fairly robust to departure from normality.^18,25,26 Because the data from the SF-36v2 ordinal measures were expected to exhibit some amount of non-normality, the bootstrap procedure (in AMOS) was also used; bootstrapped estimates are less biased in the presence of non-normality.^30–33

Identification of models in CFA testing for invariance requires that factors be assigned a scale. The most common practice is to use a unit loading constraint (ULI) in which one unstandardized factor loading per factor is constrained to 1.0.³⁴ However, when testing for measurement equivalence there is no way to examine group differences in the items with a ULI (these items are assumed to perform equally well in all groups). We addressed this problem by re-analyzing the data using two alternate approaches: 1) constraining the factor variances to 1.0 (i.e., standardizing the factors) and allowing the factor loadings to be freely estimated and 2) testing several additional models in which the second item in each subscale is constrained for identification, the third item, and so forth. Model fit in these alternate models was sufficiently similar to our original model and did not alter study results or conclusions.

Five correlated measurement errors (residuals) were specified a priori as indicated by past studies ^25,26 and supported by a sensible theoretical explanation in which items shared especially similar wording and content: walking “one flight of stairs” with “several flights of stairs” (r=.27), walking “100 yards” with “several 100 yards” (r=.57), walking “100 yards” with “1 mile” (r=.36), “several 100 yards” with “1 mile” (r=.68), and in the vitality subscale “worn out” with “tired” (r=.50). The correlated errors between these items indicate the potential for sub-factors explaining the item covariances (e.g., a walking sub-factor within physical functioning). In lieu of modeling this “factor-within-a-factor” we chose to simply retain the correlated errors in all of our models. Post hoc examination of modification indices did not lead us to specify any additional correlated errors.

To examine whether there was significant clustering within clinic sites we estimated the intraclass correlation coefficient (ICC) for each the SF-36v2 subscales. ICC’s ranged in magnitude from .01 to .09 and none were statistically significant.

“Goodness of Fit” Measures

A pivotal and often contentious issue in CFA studies of measurement invariance is the criteria used for evaluating the fit of the incremental models. Many past studies rely on comparisons of chi-square values which are overly sensitive when sample size is large resulting in the false rejection of invariant models.^35,36 In evaluating overall model fit of the unconstrained CFA model, our approach is informed by Hu and Bentler³⁷ as summarized by Brown³⁸ and clarified by Byrne³⁰ where models with Standardized Root Mean Residual (SRMR) values ≤ .09, Root Mean Square Error of Approximation (RMSEA) values ≤ .06 and CFI values ≥ .95 are considered to fit acceptably. In iterative (nested) model testing, we use cutoff points for the RMSEA and the Comparative Fit Index (CFI) as recommended by simulation studies of model fit comparisons.^13,36 For all tests, a decrease in CFI greater than 0.01 and an increase in RMSEA exceeding 0.01 suggest non-invariance and lead us to reject the model.^13,36 When the CFI and RMSEA results are different we followed CFI results because RMSEA results have been demonstrated to be less stable across changes in sample size and model complexity.²⁹ The iterative approach focusing on changes in CFI and RMSEA has been described as the most theoretically and empirically justifiable approach to model selection for invariance testing that we have available ³⁹ and has been the favored approach in at least one published empirical study.⁴⁰

It should be noted that none of these goodness of fit guidelines--whether the Hu and Bentler ³⁷ combination rules or the newer guidelines designed specifically for invariance testing ^13,36--should be taken as “universal golden rules, absolute cutoff values, or highly rigid criteria that [are] universally appropriate”.⁴¹ Authors have long cautioned that the use of rigid fit rules as sole criterion for model section is an impediment to scientific progress.⁴² The plausibility of a model relies on the judgment of a researcher taking into account theoretical and practical considerations as well as statistical ones.³⁰

RESULTS

Study population characteristics

Our sample included 383 non-Hispanic whites, 368 non-Hispanic blacks, 206 Hispanics interviewed in English and 324 Hispanics interviewed in Spanish (Table 1). Compared to whites, all three racial/ethnic groups were slightly younger and less educated. The percentage of white and black females were comparable (48.9% and 53.8%), while both English and Spanish-speaking Hispanic groups had larger percentages of women (58.3% and 66.4%, respectively). Household income levels were lower for blacks and Spanish-speaking Hispanics compared to whites, but higher for English-speaking Hispanics. Blacks and Spanish-speaking Hispanics had lower rates of insurance, while English-speaking Hispanics had higher insurance rates as compared to whites.

Table 1.

Study Population Characteristics by Race/Ethnicity (N=1281)

Characteristic	Whites N=383	Blacks N=368	Hispanic/English N=206	Hispanic/Spanish N=324
Age, mean years (SD)	54.4 (5.9)	52.2‡ (5.3)	51.2‡ (5.1)	53.2* (5.3)
Female, %(‡)	53.8	48.9	58.3	66.4
Education, mean years (SD)	14.6 (3.0)	12.9‡ (2.2)	13.5‡ (3.0)	9.3‡ (4.0)
Education Level, %(‡)
Less than 9 years	1.6	2.2	5.3	43.5
9–11 years	8.9	17.4	10.2	16.7
High school graduate	21.7	34.5	26.2	21.2
Some college	21.4	32.1	28.2	12.7
College graduate or more	46.5	13.9	30.1	5.3
Household Income level, %(‡)
<$10,000	26.1	45.9	13.6	35.5
$10,000–20,000	14.1	19.0	12.1	33.3
$20,000–50,000	19.3	21.2	23.3	27.2
$50,000 and more	40.5	13.9	51.0	4.0
Has health insurance, %(‡)	71.3	60.1	87.9	63.9
Self-reported Chronic Condition Count, mean (SD)	1.2 (1.2)	1.3 (1.2)	1.0 (1.0)	1.5† (1.2)
Smoking Status, %(‡)
Current	32.6	53.0	19.4	21.7
Past	29.5	24.2	40.3	31.1
Never Smoked	37.9	22.8	40.3	47.3
BMI, %(‡)
<25.0 kg/m2	40.5	35.9	18.5	17.6
25.0–29.9 kg/m2	38.1	34.2	45.2	41.4
30–34.9 kg/m2	21.4	29.9	36.4	41.2
SF-36v2 Physical Component Summary Score (PCS), mean (SD)	48.9 (9.7)	49.7 (8.8)	51.3 (8.5)	48.1 (9.4)
SF-36v2 Mental Component Summary Score (MCS), mean (SD)	50.2 (11.1)	49.7 (11.8)	50.2 (11.8)	44.0 (14.7)
Self Reported Overall Health, distribution(‡)
Excellent	13.8	6.8	9.7	10.8
Very Good	37.3	26.4	31.1	11.1
Good	31.3	44.6	38.8	38.6
Fair	14.1	19.6	18.0	33.6
Poor	3.4	2.7	2.4	5.9

Notes: SD=standard deviation. Significance tests for categorical variables are based on the Pearson χ² statistic and tests for continuous variables are based on the F statistic for overall significance and the Bonferroni-adjusted statistic for comparisons across the groups compared to whites. For categorical/nominal variables statistical significance is across all values of the variables. For continuous variables statistical significance comparisons are relative to whites.

^*p<0.05

^†p<0.01

^‡p<0.001

Spanish-speaking Hispanics were the only group reporting more chronic conditions as compared to whites (1.5 versus 1.2, on average). Blacks reported higher rates of smoking (53.0%) and the English and Spanish-speaking Hispanic groups reported lower rates of smoking (19.4% and 21.7%, respectively) compared to whites (32.6%). All three minority groups had elevated BMI rates in the “30 and more” category (29.9%, 36.4% and 41.2% of blacks, English, and Spanish-speaking Hispanics) compared to whites (21.4%). Whites reported the lowest levels of fair/poor health (17.5%) followed by English-speaking Hispanics (20.4%), blacks (22.3%) and finally Spanish-speaking Hispanics at 39.5%.

Figure 1 displays the best fitting measurement model tested on the full (i.e., pooled) sample, based upon the eight factor model described by Keller et al ²⁵ which includes all of the SF-36v2 items, eight subscales, three 2^nd order factors (physical and mental health functioning and general well-being) and a single 3^rd order factor (overall health related quality of life) and which we label SF-36v2 (CFI= .94; RMSEA= .028, 90% CI .028-.030; chi square= 4358 and df = 2152). The model in Figure 1 also fit best in our sample when compared to measurement models described by Ware et al ²⁴ and Reed and Moore.²⁶ Consistent with other studies of SF-36 factor structure, eigenvalues from the first two factors in a single-level exploratory factor analysis using polychoric correlations explain approximately 70% of the total variance (see Table A1 for further detail).^24–26

Figure 1.

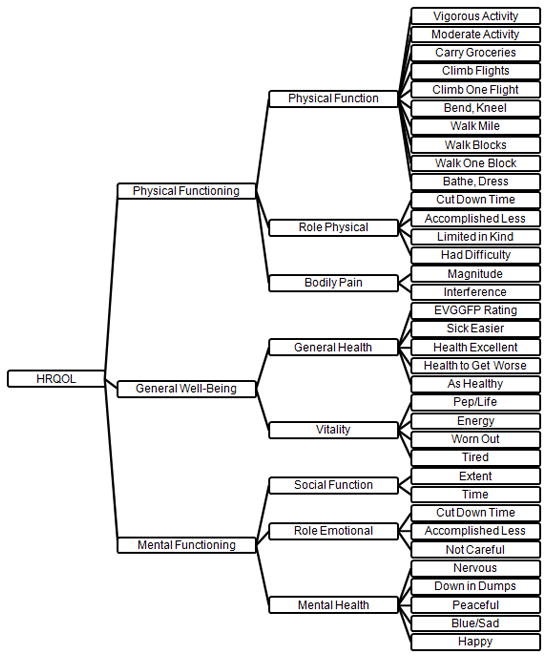
Measurement Model of the SF-36v2²⁵

Multi-group Modeling Results

Table 2 presents model fit statistics for seven successive multi-group models. The multi-group CFA began with the unconstrained measurement model of the SF-36v2 as depicted in Figure 1 above (Model 1 in Table 2) and proceeded to test for weak invariance (Models 2 and 3), strong invariance (Model 4), selected three-group strong invariance (Models 5 and 6) and strict invariance (Model 7).

Table 2.

Goodness of Fit for SF36 Multigroup Factorial Invariance Testing

Model	Description	RMSEA (90% CI)	SRMR	CFI	χ2	df	p*	Ref	ΔRMSEA	ΔCFI	Δχ2	Δdf	p* for Δχ2
1	Unconstrained Model	0.028 (.027–.030)	0.059	0.937	4358	2152	0.001
2	Weak Invariance (1st Order Factor Weights)	0.029 (.028–.030)	0.057	0.931	4664	2248	0.001	1	0.001	−0.006	306	96	0.000
3	Weak Invariance (1st & 2nd Order Factor Weights)**	0.029 (.028–.030)	0.058	0.929	4731	2265	0.001	2	0.000	−0.002	67	17	0.000
4	Strong Invariance (Intercepts)	0.032 (.031–.033)	0.057	0.909	5526	2370	0.001	3	0.003	−0.020	795	105	0.000
5	3 Group Strong Invariance (B=W=HS not HE)	0.032 (.031–.033)	0.058	0.911	5422	2335	0.001	3	0.003	−0.018	691	70	0.000
6	3 Group Strong Invariance (B=W=HE not HS)	0.030 (.029–.031)	0.058	0.923	5029	2335	0.001	3	0.001	−0.006	298	70	0.000
7	Error Variances/Covariances(B=W=HE not HS)†	0.031 (.030–.032)	0.060	0.915	5362	2415	0.001	6	0.001	−0.008	333	80	0.000

Notes:

^*The bootstrapped Bollen – Stine p-value is reported because of significant (p<.01) multivariate non-normality.

^**Factor weights/covariances are constrained equal for Blacks, Whites and Hispanic English (Hispanic Spanish are unconstrained).

^†Also termed strict invariance.

Model 1 is the unconstrained model in which intercepts, factor loadings and covariances are all allowed to be freely estimated. This model allows variation in the relationship (factor loading) of each survey item to its latent variable across each racial/ethnic group in the study. The complete table of unstandardized factor loadings is presented in the Appendix (Table A2).

Model 2 tests for weak invariance (1^st order factor loadings constrained to be equal) across the four racial/ethnic groups. The constrained model still fits the data well. Changes in RMSEA (.001) and CFI (−.006) are small. Weak invariance of the SF-36v2 across the four racial/ethnic groups was supported. Model 3 tests for 2^nd order weak invariance (1^st and 2^nd order factor loadings constrained to be equal) across the four racial/ethnic groups. This model with 1^st and 2^nd order factor loadings constrained is supported. For all four racial and ethnic groups the correlations between second order factors are: mental with physical = .65, mental with general well-being = .78, and physical with general well-being = .78.

Model 4 tests for strong invariance (factor loadings and intercepts constrained to be equal across all four racial/ethnic groups). The added constraints on the intercepts result in a decrease in model fit. Although the overall model fit remains acceptable (RMSEA=.032, CFI=.909, SRMR=.057) and the increase in RMSEA is small (.003), the decrease in CFI (−.020) is beyond accepted limits for model fit increments.^13,36 Strong invariance across all four racial/ethnic groups is not fully supported in this analysis.

Model 5 in Table 2 presents the fit statistics and change in fit when allowing intercepts to vary for English-speaking Hispanics and constrains intercepts for whites, blacks and Spanish-speaking Hispanics to be equal. As compared to the weak invariant model (Model 3), Model 5 results show an increase in RMSEA (.003) and a decrease in CFI (−.018). This is similar to the decrement to model fit observed when comparing Model 4 to Model 3 and suggests that three-group invariance is not supported when constraining the intercepts for Spanish-speaking Hispanics to be equal to those for blacks and whites and allowing the intercepts for English-speaking Hispanics to be freely estimated.

Model 6 presents the fit statistics and change in fit when allowing intercepts to vary for Spanish-speaking Hispanics while constraining intercepts for whites, blacks and English-speaking Hispanics to be equal. According to the logically organized strategy of cumulatively retaining invariant parameters, Model 6 is compared to Model 3 in order to determine whether invariance is supported when allowing intercepts for Spanish-speaking Hispanics to be freely estimated. Model 6 fits the data moderately well. The change in RMSEA (.001) is trivial and change in CFI (−.006) is acceptable. This suggests that strong invariance of the SF-36v2 is supported for blacks, whites and English-speaking Hispanics, but not supported for Spanish-speaking Hispanics.

Model 7 tests for strict invariance by constraining the error variances and error covariances to be equal for blacks, whites and English-speaking Hispanics, but not for Spanish-speaking Hispanics. Model 7 is compared to Model 6 and the change in model fit (ΔRMSEA=.001 and ΔCFI=−.008) is low enough to accept the model with strict invariance for blacks, whites and English-speaking Hispanics.

Kline points out that where strong invariance does not hold (as in Model 4), it is important to examine the estimates of the intercepts across groups.³⁴ The magnitude of the SF-36v2 item intercepts for Spanish speaking Hispanics as compared to whites, blacks and English speaking Hispanics are compared here to determine whether there are differences in the intercepts for specific items and subscales or whether there is an overall trend across all of the intercepts.

Figure 2 presents percent differences between intercepts as estimated in Model 6, by subtracting the constrained common intercepts (for whites, blacks and English-speaking Hispanics) from the intercepts for Spanish-speaking Hispanics and dividing by the respective common intercepts. Comparison of unconstrained intercepts for all items in all groups (Model 3) is available in the supplemental appendix (Table A3). There is a notable trend in Figure 2: Spanish-speaking Hispanics have intercepts that are nearly uniformly lower than the other three racial/ethnic groups. The lower intercepts for Spanish-speaking Hispanics persist across all eight sub-dimensions of the SF-36v2. Items from the mental health sub-dimension have the greatest intercept differences. For example, the intercept for the “depressed” item for Spanish-speaking Hispanics (57.7) is 27.9% lower than the common “depressed” item intercept for the other three racial/ethnic groups (80.1). Only four of the SF-36v2 survey item intercepts were not lowest for Spanish-speaking Hispanics: “walking 100 yards”, “full of life”, “lots of energy”, “peaceful”. Of these four items, three are reverse-worded.

Figure 2.

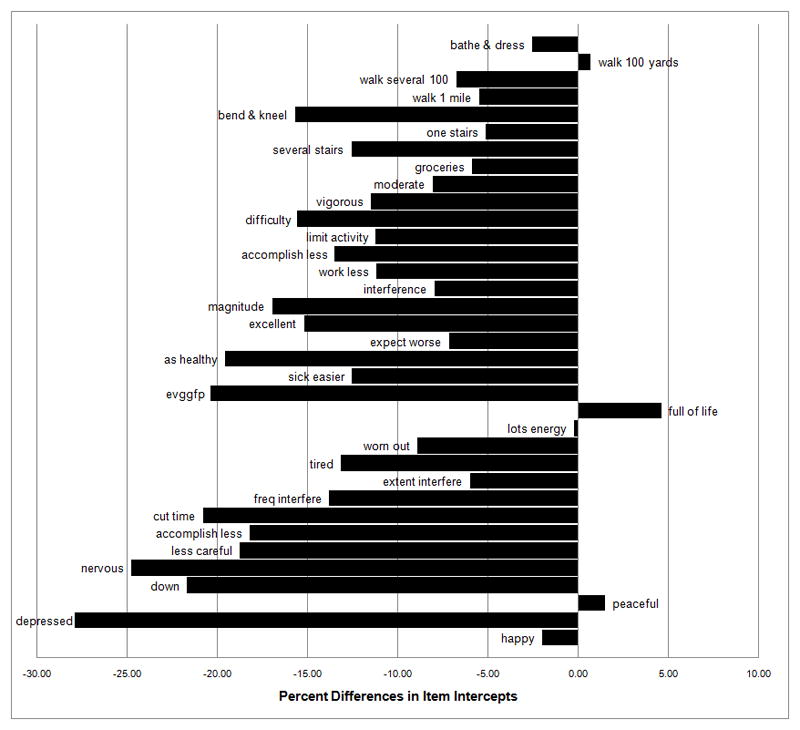
Percent Differences in Item Intercepts between Spanish-speaking Hispanics and Common Intercepts for Whites, Blacks and English-speaking Hispanics

DISCUSSION

Our results suggest that correlational or multivariate latent variable analyses of SF-36v2 responses can be done across whites, blacks, English-speaking Hispanics, and Spanish-speaking Hispanics, since these analytic methods require only weak factorial invariance, as was found in this study. For example, multiple regression analysis (stratified by race/ethnicity/language) with MCS or PCS as the dependent variable does not present a problem in terms of measurement equivalence. However, the lack of strong invariance seen in our study suggests the need for caution when comparing SF-36v2 mean scores of Spanish-speaking Hispanics with those of other groups. The pattern of differences in item intercepts (Figure 2) suggests a systematic linguistic/translational or cultural (values and beliefs) bias regarding Spanish-speaking Hispanics for most of the SF-36v2 items. Further analysis found that strict invariance was confirmed for whites, blacks and English-speaking Hispanics.

Our findings agree with the weak (metric) invariance analysis conducted by Hays, Revicki and Coyne who also found support for weak invariance across both English-and Spanish-speaking Hispanics using the SF-36 version 1.¹⁸ However, they did not conduct tests for strong or strict invariance. Our results extend this previous body of research and provide contrasting findings of a lack of strong invariance for most SF-36v2 items for Spanish-speaking Hispanics.

The lack of strong invariance should not be that surprising to Hispanic health researchers given the findings of prior studies. Bzostek et al ⁴ presented evidence suggesting that lack of measurement invariance could result from the difficulties in translation and the lack of linguistic equivalence for some words in English and Spanish. They suggest that the single self-rated health question (“Would you say your health in general is excellent, very good, good, fair or poor?”) when translated into Spanish with response options of excellente, muy buena, buena, regular and mala creates a language-based measurement artifact. They explain:

“Regular” can mean “okay” or “fine” (but also “so-so”), whereas in English, “fair” clearly connotes subpar health. Angel and Guarnaccia (1989) also suggest that there may be language-related differences in “anchoring”, e.g., buena or regular may be used to describe normal health in Spanish…while excellent and very good may imply having no health problems—i.e., normal—health in English (or in the United States)” (p. 992)

Our results are consistent with these suggestions regarding the single self-rated health item as we noted in the results section. But this translational issue cannot explain the pattern of lower intercepts on most items for Spanish-speakers because no other items in the SF-36v2 use the same response options.

Several potential explanations of bias in the responses of Spanish-speaking Hispanics have been suggested in prior research.^4,8,43,44 Differences in how Spanish-speaking Hispanics respond to particular SF-36v2 items could result from cultural differences in what is acceptable to say about one’s health. For example, it may be socially unacceptable to express optimism or boast about one’s health.⁴ Alternatively, Hispanics in general may be more likely to choose responses at scale endpoints rather than those in the middle. ⁴⁵ Our study results are consistent with both of these explanations for Spanish-speaking Hispanics.

As a counter point, Morales, Diamant and Hays⁴⁶ performed an analysis of the SF-12 version 1 in a U.S. population of English and Spanish-speaking persons and also found weak invariance. A test for strong invariance found differential item functioning (i.e., different intercepts) for only two items (general health status and “downhearted and blue”). They suggest one can establish psychometric equivalence with only weak invariance and that partial strong invariance is acceptable. Part of the lack of congruence between our study and that of Morales et al may be due to the differences in response options between the two versions supporting the notion that modifications of response categories—even when they are designed to improve scale properties--can often lead to unintended consequences. For example, the dichotomous responses for 4 items in the SF-12 version 1 (2 role physical and 2 role emotional) were changed to 5 category response scales in version 2—and all 4 of these exhibited differential item functioning in our study while no difference was reported in the Morales et al study.⁴⁶ Additionally, demographic differences in the study populations such as age, sex, national origin for those speaking Spanish and education may have contributed to the differences in our findings but these data were not available for comparison. However, both samples were clinic based and drawn mainly from major urban public hospital systems and therefore clinical differences should have had little effect on our differential findings.

Limitations

Our analysis has several limitations. First, the age of participants was 45–64 years and hence results cannot be generalized to other age groups. Second, this is a clinical population and hence the results may not be generalized to community dwelling populations. Third, the majority (85%) of our Spanish-speaking respondents self-identified their ethnicity as Puerto-Rican (53%) or Mexican (32%). We were concerned about combining these two major Hispanic subgroups in the analysis for two reasons. They have very different cultural histories, and most of the analyses conducted on English and Spanish-language differences in self-reported health status have been among Mexican ancestry participants. However, results among Spanish-speaking Puerto Ricans living in the Commonwealth of Puerto Rico in the Behavioral Risk Factor Surveillance System (BRFSS) suggest that responses to the single-item general health status question are consistent with those seen among Mexican ancestry Spanish-speaking Hispanics. For example, over the past decade the percentage of residents of Puerto Rico reporting fair or poor health has consistently been approximately 32% (the national average for residents of other U.S. states is approximately 14.5%). Again, this mirrors the results of our study, as well as those of Bzoctek et al⁴ and others who focused on Mexican Spanish-speakers. Hence we believe this lends support to the linguistic/translational explanation for some of the differences we have found and that it applies to both Mexican and Puerto Rican Spanish-speaking subgroups.

A fourth limitation is the significant educational differences between the Spanish-speakers and the other three racial/ethnic groups. As a partial test of this limitation, we replicated our multi-group analysis excluding those with less than a high school education. The results of this supplemental analysis were nearly identical to that of the full sample across the models, and showed a similar pattern of differences in intercepts (see Appendix Figure A1).

Fifth, the Spanish-speaking group was disproportionately female (66.4%) compared to whites (53.8%), blacks (48.9%), and English-speaking Hispanics (58.3%) and that may have induced bias in an unknown direction in our results. Sample size and power limitations precluded a multi-group analysis stratified by sex; future studies would benefit from larger samples and a more equal sex distribution. However, cross-tabulation of self-reported overall health status by race/ethnicity and language group revealed a similar distribution of responses by sex. Hence we believe that at least for this single item the linguistic/translational explanation holds across the sexes.

Sixth, while we have conducted a comprehensive set of analyses and the approaches we have employed in this study are growing in acceptance (i.e., our use of specific goodness-of-fit measures and cutoff points and the use of delta tests), it still remains an area of controversy and debate and these approaches are not universally accepted.

Finally, a limitation of all purely psychometric approaches to invariance testing using self-reports of health and physical functioning among language groups is the inability to distinguish between linguistic/translational and cultural influences and actual objective physical health status. In short, we cannot definitively say whether or not the Spanish-language differences we observed would be replicated if we were to compare against “gold standard” objective measures of health and physical functioning. Future studies would benefit from including performance based measures of physical functioning and other clinically based measures of health status.

In closing, our findings suggest the need for caution when using self-reported health measures to compare the health status and health care needs of Spanish-speaking Hispanic populations with white, Black, or English-speaking Hispanic groups. Policy makers, public health officials, and health providers should be aware that SF-36v2 mean scores for Spanish-speakers may not be directly equivalent to those of English-speakers using current items, response options, and analytic methods. Future studies are needed to establish procedures for accurately comparing the self-reported health of Spanish-speakers with that of English-speakers, such as the use of numerical visual-analogue scales instead of Likert scales with response options that may lack true linguistic equivalents. Additionally, qualitative studies (including focus groups, cognitive interviewing and in-depth interviews) are needed to better understand the cultural origins and meanings attached to questions of health and how these artifacts, attitudes and orientations to health influence perceptions of physical, emotional and social well-being.

Supplementary Material

4

Figure A1. Percent Differences in Item Intercepts between Spanish-speaking Hispanics and Common Intercepts for Whites, Blacks and English-speaking Hispanics Excluding Subjects with Less than High School Education.