Timescale-dependent shaping of correlation by olfactory bulb lateral inhibition

Abstract

Neurons respond to sensory stimuli by altering the rate and temporal pattern of action potentials. These spike trains both encode and propagate information that guides behavior. Local inhibitory networks can affect the information encoded and propagated by neurons by altering correlations between different spike trains. Correlations introduce redundancy that can reduce encoding but also facilitate propagation of activity to downstream targets. Given this trade-off, how can networks maximize both encoding and propagation efficacy? Here, we examine this problem by measuring the effects of olfactory bulb inhibition on the pairwise statistics of mitral cell spiking. We evoked spiking activity in the olfactory bulb in vitro and measured how lateral inhibition shapes correlations across timescales. We show that inhibitory circuits simultaneously increase fast correlation (i.e., synchrony increases) and decrease slow correlation (i.e., firing rates become less similar). Further, we use computational models to show the benefits of fast correlation/slow decorrelation in the context of odor coding. Olfactory bulb inhibition enhances population-level discrimination of similar inputs, while improving propagation of mitral cell activity to cortex. Our findings represent a targeted strategy by which a network can optimize the correlation structure of its output in a dynamic, activity-dependent manner. This trade-off is not specific to the olfactory system, but rather our work highlights mechanisms by which neurons can simultaneously accomplish multiple, and sometimes competing, aspects of sensory processing.

Neurons respond to stimuli by emitting action potentials. These action potentials are the sole means of both encoding information and propagating activity to downstream neurons. Inhibitory circuits shape stimulus-evoked activity and facilitate sensory-guided behavior in many systems (1–5), including the olfactory system (6–8). These circuits alter the patterns and rates of postsynaptic action potentials, including the correlation of spiking across neurons (9). Lateral inhibition can promote competition between neurons (10), resulting in decorrelation of spike trains (11) or stimulus-evoked patterns (12, 13). In other situations, inhibition correlates spiking across pairs of neurons (14–19). Inhibitory inputs can change rates and correlations differentially, suggesting that some circuits may be capable of encoding stimulus information at multiple timescales (20–24). Thus, inhibition can influence population activity in a variety of ways according to the details of the circuitry and the patterns of population activity.

The relationship between changes in correlation and sensory processing remains controversial. Correlation may be helpful or harmful depending on stimulus statistics, noise statistics, population size, and decoding mechanisms (25–31). Here we focus on how correlations influence two primary functions of spike trains: encoding information and propagating activity to downstream neurons. Imagine hearing a group of people talking simultaneously. A trade-off arises between the quality and the quantity of communicated messages; a single phrase chanted in unison is loud, but simple. Conversely, each person saying a different phrase is informative, but no single message is loud enough to be understood. Neurons face a conceptually similar problem. Correlated spiking facilitates propagation (30, 32–34). However, these correlations reduce the available repertoire of population activity patterns (31, 35, 36), thereby potentially impairing sensory discriminations (27). Because correlations can impact propagation and encoding in opposing ways, how do networks structure their correlations? And how should they? We investigate this problem here in the specific case of inhibitory circuits of the olfactory bulb.

The mouse olfactory bulb provides an excellent model system to study the effects of inhibitory circuits on pairwise properties of spike trains. Mitral (and the related tufted) cells receive direct input from sensory neurons and provide the only output projections from the olfactory bulb (37). Because they function as an obligatory processing stage, the ∼100,000 mitral cells must effectively propagate activity to millions of neurons in areas such as cortex and amygdala. Moreover, mitral cell odor coding must minimize redundancy because these cells are few in number compared with the number of sensory neurons that provide their inputs (∼10 million/mouse) (37). Connections between mitral cells are dominated by disynaptic inhibition mediated by a granule cells—a large population of local circuit GABAergic interneurons (37). Olfactory bulb inhibition improves the discriminability of structurally and psychophysically similar odors (6, 7). Therefore, inhibition-evoked changes to mitral cell correlations are an attractive model for studying the effects of correlations on propagation and encoding, but also represent a behaviorally relevant component of stimulus processing in this circuit.

Here we use paired whole-cell recordings of mitral cells to examine the effects of inhibition on spike train correlations and on stimulus-evoked population activity patterns. We measured correlations at small and large time windows and explored how the observed changes affected propagation and encoding. Using experimental and computational approaches, we show that minimal activation of inhibitory circuits in the olfactory bulb mediates simultaneous fast correlation (i.e., synchrony increases) and slow decorrelation (i.e., firing rates become less similar). We argue that the combination of fast correlation and slow decorrelation enhances population level discrimination of similar inputs, while promoting propagation of mitral cell activity to cortex. Thus, inhibition in olfactory circuits is structured to take advantage of the encoding and propagation benefits that correlation can confer, while mitigating the deleterious aspects of the propagation/encoding trade-off.

Results

Timescale-Dependent Correlation Changes in Pairs of Active Mitral Cells.

We first directly measured how the inhibition recruited by two active mitral cells changed correlations between the two mitral cell spike trains. We performed simultaneous whole-cell voltage recordings from pairs of nearby mitral cells in slices of mouse olfactory bulb (SI Materials and Methods). Firing was evoked via somatic direct current (DC) injection. We first examined pairs of spike trains that were recorded simultaneously (Fig. 1 A and B, orange box). We hypothesized that the recruited inhibition would influence both cells in the pair, altering pairwise correlations. Notably, we expect these interactions to be nearly exclusively inhibitory as mitral cells are disynaptically coupled via interneurons and lack direct excitatory connections [although excitatory coupling has been observed in homotypic mitral cells (mitral cells terminating in the same glomerulus)] (38–41). Because we recorded mitral cells terminating in different glomeruli, we do not expect excitatory interactions due to gap junction coupling or glutamate spillover (Fig. S1).

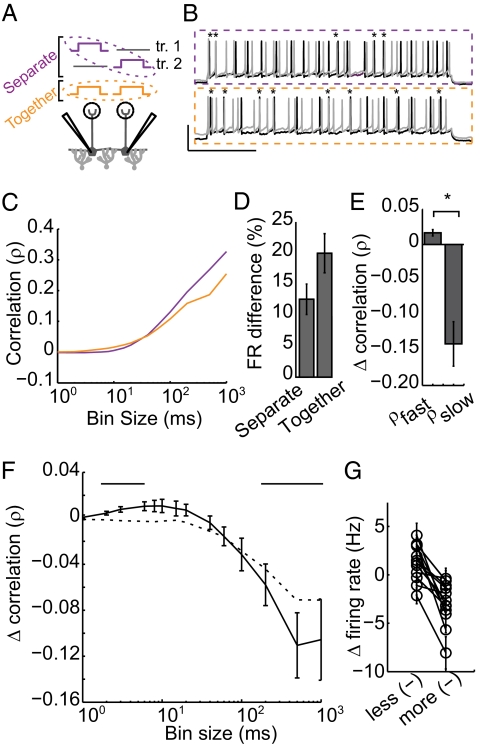
Fig. 1.

Physiological recruitment of inhibition results in fast timescale correlation and slow timescale decorrelation. (A) Experimental setup: Pairs of mitral cells were depolarized via DC current injection. Pairwise correlation was measured in the presence (recorded together; orange) and absence (recorded on separate trials; purple) of shared inhibition. (B) Example voltage traces for the no shared inhibition (purple) and shared inhibition (orange) conditions. (Scale bar, 50 mV, 500 ms.) Synchronous spikes are denoted with asterisks. (C) Pearson correlation was calculated across fast and slow timescales (bin sizes, 1–1,000 ms) for pairs recorded in the separate (purple) and together (orange) conditions. (D) Firing rate difference between the two cells in each recording condition. (E) Average peak fast correlation and peak slow decorrelation. (F) Shared inhibition-induced change in correlation across timescales (solid black line). Bars, above, mark bins with significant correlation change. Shuffled data are shown by a dotted black line. (G) Inhibition-induced rate change for the less reduced and the more reduced cell for each recorded pair. (n = 13 pairs for C–E, error bars indicate SE.)

Correlations in simultaneously recorded spike trains arise from several sources. We wanted to isolate changes in correlation that arise due to trial-to-trial shared synaptic input. To eliminate trial-locked sources of correlation (e.g., those that that arise from the transients induced by somatic current injection or repeated input patterns) we compared the correlations of simultaneously recorded spike trains to those produced by cells recorded on interleaved trials (i.e., cell 1, sweep 1 is compared with cell 2, sweep 2; Fig. 1 A and B, purple box). This comparison provides a useful internal control because all traces include the same sources of spurious, trial-locked correlations (transients and repeated input patterns; Fig. S2) whereas only the cells recorded simultaneously receive the shared inputs that are of interest to us.

To quantify spike train correlation (ρ) across timescales, we constructed histograms of each cell's activity for bin sizes ranging from 1 to 1,000 ms (Fig. S3A) and calculated Pearson's correlation coefficient (Fig. 1C). Thus, for each bin size we calculate spike count correlation with and without shared inhibition, allowing us to measure the effects of the simplest lateral inhibitory circuit at a variety of timescales. We observed modest but significant timescale-dependent changes in correlation in the simultaneously recorded spike trains (Fig. 1F; P < 0.05 in bins marked with bars, n = 12 mitral cell pairs, nine animals).

When the trials were shuffled (Fig. 1F, dotted line), fast correlation was abolished (P < 0.05 bins < 100 ms) whereas slow decorrelation was largely preserved (Δρ_slow = −0.07 ± 0.005, P < 0.05 all bins ≥ 100 ms). Thus, the specific timing of correlating inhibition was variable from trial to trial, whereas decorrelation was replicable across trials. Mechanistically, this result suggests that slow timescale decorrelation relies on a competitive mechanism. Consistent with this result, the difference in firing rate between the pair increased in the together condition (Fig. 1D). Firing rate reduction is consistently larger for one cell in a pair (Fig. 1G; P < 0.05), suggesting that there is a “winner” and a “loser” with respect to firing rate. The fact that the identity of the winner is conserved across trials suggests that slow competition relies on features of the circuit that are conserved across trials (for example, differences in connectivity that determine a cell's ability to recruit lateral inhibition). Whereas the observed slow decorrelation is significant, average firing rate changes were quite small (3.1%).

The bin size of maximum correlation changes varies across pairs, because each pair is influenced by a unique inhibitory network. Given this variability, averaging inhibition-induced changes across pairs (as shown in Fig. 1F) shows smaller peak changes than are achieved by individual pairs. For this reason, peak correlation changes were identified in each pair for small (bin size <30 ms, average Δρ_fast = 0.016 ± 0.005; P < 0.05) and large bin sizes (bin size >100 ms, average Δρ_slow = −0.14 ± 0.03; P < 0.05; Fig. 1E).

Timescale-Dependent Correlation Changes Require Fast, Shared, Activity-Dependent Inhibition.

Given our experimental results, we sought a mechanistic understanding of timescale-dependent correlation changes. Which features of inhibition were responsible for fast and slow timescale changes, respectively? First, we hypothesized that fast correlation arose from shared inhibition with rapid kinetics (14, 15). Such inputs have been observed from GABAergic granule cells (6, 16, 18) and may synchronize mitral cell firing via a mechanism dubbed “stochastic synchronization” (14). Second, we hypothesized that slow decorrelation arose from long latency, competitive recruitment of these same granule cells (11, 12, 42, 43), giving rise to lateral inhibition whereby more active cells suppress firing of less active cells (11). We predicted that our experimental results might be explained by these known features of olfactory bulb inhibition.

To understand the requisite features of inhibition, we constructed a highly simplified model consisting of two leaky integrate-and-fire (LIF) neurons (simulated mitral cells) that received inhibitory inputs (Fig. 2A₂). Each cell received shared inhibition as well as inhibition independent to each cell. Inhibitory firing was generated using an inhomogeneous Poisson process driven by excitatory firing (SI Materials and Methods). We selected this simplified representation of the olfactory circuit because it allowed us to isolate the features of inhibition that are necessary and sufficient to mediate cross-timescale correlation changes between a single pair of neurons. We generated pairs of model spike trains and calculated correlation across timescales as described above. For comparison, we generated spike trains with inhibition removed from the model (Fig. 2A₁). Shared, activity-dependent inhibition reduced firing rate (Δ_FR = −27.8 ± 0.03%, P < 0.05; Fig. 2B). Further, synchrony increased (Δρ_{bin size=10 ms} = 0.07 ± 0.01) whereas slow timescale correlation decreased (Δρ_{bin size=1,000 ms} = −0.04 ± 0.015; Fig. 2C; P < 0.05 for all points). Thus, this simple circuit is sufficient to generate the simultaneous fast correlation and slow decorrelation observed in slice experiments.

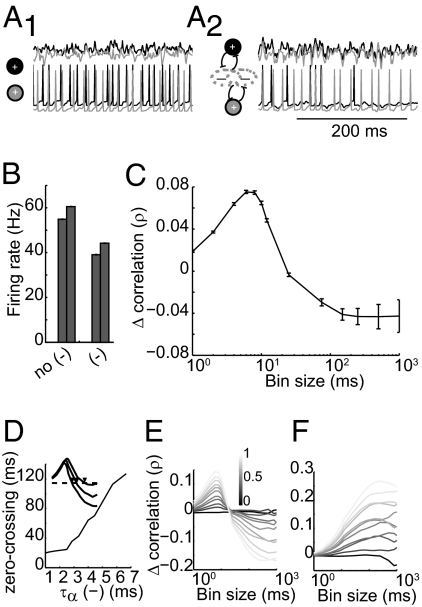
Fig. 2.

Simple two-cell model replicates timescale-dependent correlation changes. (A) Model schematic and raw traces. The model contains two excitatory LIF neurons coupled by activity-dependent Poisson inhibition (A₂). A portion of the inhibition is shared by the pair (constant, c; gray overlap) and a portion is independent to each cell (constant, 1 − c; nonoverlapping gray). Firing in this model is compared with firing with inhibitory coupling removed (A₁). (Upper) Currents received by each cell. (Lower) Membrane voltages of the pair. (B) Firing rate for each cell with and without inhibitory coupling. (C) Inhibition-evoked change in correlation across timescales. Error bars indicate SE. (D) IPSC kinetics shift the zero-crossing point of cross-timescale changes. (Inset) Example of correlation changes for three values of τ_α, with zero-crossing points marked with arrowheads. (E) Varying c (portion of shared inhibition) alters the magnitude of timescale-dependent correlation changes. The color bar denotes the value of c. (F) Removing activity dependence of inhibition preserves inhibition-induced correlation increases (with changes in c) but removes slow timescale decorrelation. Error bars indicate SE.

We next manipulated the kinetics, correlation, and activity dependence of evoked inhibition in our model to observe the contribution of each in timescale-dependent changes. We first altered the kinetics of inhibition by varying the parameter τ_α [which controls the rise and decay times of individual inhibitory postsynaptic currents (IPSCs).] For very fast inhibition (τ_α = 1), the zero-crossing point (timescale at which inhibition shifts from being correlating to decorrelating, shown by arrowheads in Fig. 2D, Inset) occurred at small bin sizes (Fig. 2D). As inhibition became slower (τ_α = 6), the zero-crossing point shifted to larger bin sizes, suggesting that IPSC kinetics determine the upper range of correlating timescales (Fig. S4).

Next, we varied the fraction of shared inhibition (c) to alter the portion of shared inhibitory inputs while keeping the total amount of inhibition constant. As c increases, fast correlation increases (P < 0.05) and slow correlation decreases (Fig. 2E; P < 0.05 for c > 0.3). Notably, timescale-dependent correlation changes were observed when 100% of inhibition was shared, indicating that a single inhibitory population is capable of mediating correlation changes at both timescales.

Finally, we eliminated the activity dependence of recruited inhibition and instead generated IPSCs with a fixed Poisson rate. Increasing c in this condition increased correlation (due to increased coincident inputs; Fig. 2F). However, this increase extended into long timescales, with no slow decorrelation observed as seen in the activity-dependent case. Thus, when inhibition was evoked by an external source rather than the local circuit, common inputs were correlating at all timescales because there was no asymmetry of one cell recruiting inhibition more effectively. Taken together, these results indicate that rapid, shared, activity-dependent inhibition provides a simple and biologically plausible mechanism of timescale-dependent correlation changes.

Timescale-Dependent Correlation Changes Improve Both Propagation and Encoding.

Two kinds of correlations are often considered in analyzing sensory processing (13): channel correlations (within-trial correlations between pairs of neurons) and pattern correlations (across-trial correlations between the population activity evoked by different stimuli). Above, we considered channel correlations between pairs of mitral cell spike trains. Because changes to channel correlations may contribute to pattern decorrelation in the olfactory system, we developed an expanded model to investigate these changes at the network level. We constructed an olfactory bulb model with 100 excitatory cells reciprocally connected to 800 inhibitory interneurons (SI Materials and Methods). This model allowed us to ask two important questions related to our experimental results. First, do inhibitory circuits enact timescale-dependent correlation changes in this network model? And second, how do changes in correlation influence the propagation/encoding trade-off during a simulated detection/discrimination task?

To answer the first question, we activated inputs to all excitatory cells in the network and recorded their spike trains. For comparison, we removed all synaptic coupling and again recorded spike trains from excitatory cells. We measured cross-timescale correlation for all pairwise combinations of excitatory cells in both conditions. This model olfactory bulb network replicates the timescale-dependent correlation changes observed experimentally (Fig. 3A; Δρ_fast = 0.10 ± 0.01, Δρ_slow = −0.10 ± 0.02, P < 0.05).

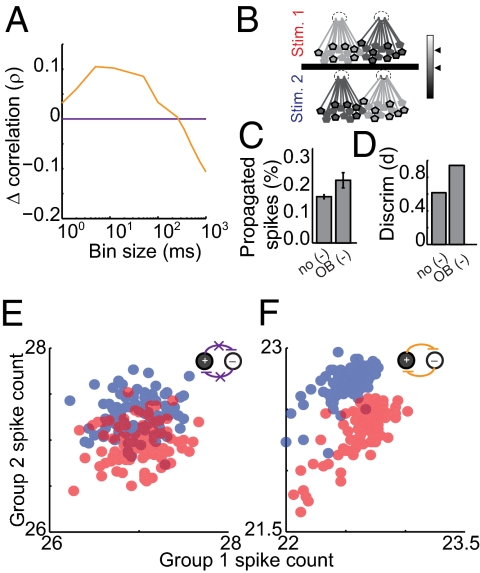
Fig. 3.

The olfactory bulb model replicates timescale-dependent correlation changes, which improves both propagation and encoding. (A) Cross-timescale correlation changes for the olfactory bulb model (orange) and the model with no inhibitory coupling (purple). (B) Stimulus generation: For stimulus 1 (Upper) one subpopulation received higher-magnitude DC stimulation (Left, light gray shading) whereas the other subpopulation received lower-magnitude DC stimulation (Right, dark gray shading). Stimulus 2 (Lower) reversed which subpopulation received the higher- and lower-magnitude stimulation, respectively. The mean activity of two randomly selected groups—group 1 (black outlines) and group 2 (no outlines)—was monitored. (C) Percentage of propagated spikes and (D) stimulus discriminability for both model variants are shown. (E and F) Average firing rate in group 1 (x axis) and group 2 (y axis) during stimulus 1 (red) and stimulus 2 (blue). Each point represents mean firing rates over 500 ms in groups 1 and 2 for a single trial in the no-coupling model (E) and the olfactory bulb model (F).

Olfactory bulb inhibition is important for behavioral discriminations, particularly between highly similar stimuli that elicit overlapping patterns of activity (6, 7, 12, 44) (for example, two mixtures containing the same odorants at slightly different ratios). A mixture containing 55% odor A and 45% odor B might activate one glomerulus at a higher intensity and a second glomerulus at a lower intensity whereas a 45/55% mixture would do the opposite (44). To implement this olfaction-inspired scenario in our model, excitatory cells were randomly divided into two groups shown schematically in Fig. 3B: group A (stimulated at a particular intensity; Upper, light gray) and group B (stimulated at an intensity ∼10% less than group A; Upper, dark gray). To generate a second, highly similar stimulus, we simply reversed the stimulation intensities applied to groups A and B (Fig. 3B, Lower). Thus, a particular cell stimulated at higher intensity for stimulus 1 received lower-intensity stimulation for stimulus 2.

We evaluated our model's propagation efficacy and stimulus discriminability, with and without inhibitory coupling. To test propagation efficacy, we created a second layer of decoding neurons, each of which received input from 20 layer 1 mitral cells. Thresholds were set so that activation of layer 2 cells required roughly 12 coincident inputs. We calculated the portion of layer 1 spikes that elicited a postsynaptic spike in layer 2. In the network with coupling absent, 0.17 ± 0.01% of layer 1 spikes are successfully propagated to layer 2 (Fig. 3C, P < 0.05). In the olfactory bulb-like model, propagation is increased to 0.23 ± 0.03% (P < 0.05). These results suggest that timescale-dependent correlation changes can maintain propagation even when average firing rate is reduced (Fig. 4C; Δ_FR = −19 ± 3%, P < 0.05).

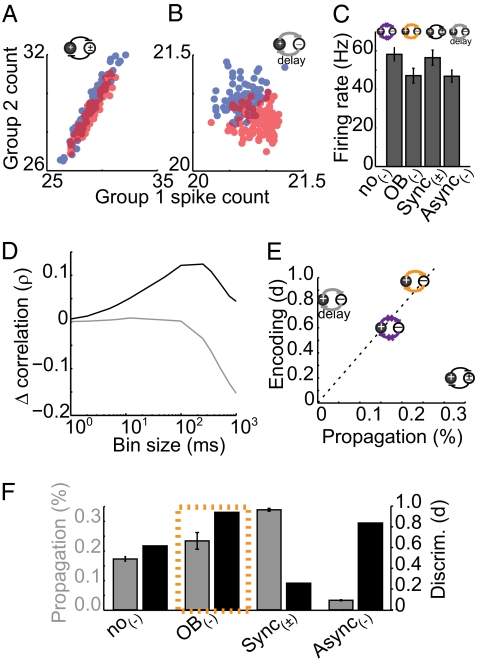
Fig. 4.

Timescale-dependent correlation changes maximally benefit both encoding and propagation: illustration from model variants. Evoked responses to stimuli 1 and 2 in sync_(±) (A) and async₍₋₎ (B) models are shown. (C) Mean firing rates for all four model variants. (D) Cross-timescale interneuron-induced change in correlation for async₍₋₎ (gray) and sync_(±) (black) variants. (E) Propagation/encoding trade-off: async₍₋₎ facilitates encoding at the expense of propagation (gray, left), whereas sync_(±) facilitates propagation at the expense of encoding (black, right). Timescale-dependent correlation changes simultaneously improve both propagation and encoding (orange, top). (F) Propagation efficacy and discriminability for each model variant. Error bars denote SE.

Next, we measured discriminability in layer 1 by measuring the correlation between the two stimulus-evoked patterns. To obtain a simple quantification of the network's output patterns, we randomly divided excitatory cells into two observation groups (Fig. 3B, group 1, black outlines; group 2, no outlines; see Fig. S5 for alternate analysis). For each stimulus, we compared the average firing rate in groups 1 and 2. We applied stimulus 1 to the no-coupling network 150 times, giving us an estimate of the mean and variance of the stimulus 1-evoked pattern (Fig. 3E, center and spread of red representation). Next, we again monitored the evoked mean and distribution of the pattern evoked by stimulus 2 (Fig. 3E, shown in blue). For nonoverlapping stimulus-evoked distributions, it is clear which stimulus was presented for any single observation of evoked firing patterns. However, when two distributions overlap (as in Fig. 3E), there is a range of observed patterns for which the presented stimulus is ambiguous to a downstream decoder. Encoding performance was quantified using a 2D linear discriminant analysis, using a receiver operator characteristic. Without interneuron-mediated coupling, pattern overlap is sizable [d = 0.6, where d is proportional to area under the receiver–operator characteristic (ROC); SI Materials and Methods and Fig. 3D]. The two stimuli were next applied to the olfactory bulb model, which greatly reduced pattern overlap (Fig. 3F; d = 0.97). Mechanistically, excitatory cells cooperatively recruit inhibitory interneurons, resulting in competitive interactions between the two excitatory neurons of the pair. Like the electrophysiological results shown in Fig. 1D, this competition causes a separation of the firing rates between subpopulations. At the population level, competition alters average firing rates such that that overlap in the stimulus-evoked patterns is reduced. Thus, inhibition-mediated timescale-dependent changes in channel correlation persist at the network level, and these changes improve both the propagation efficacy and discriminability of applied stimuli.

Fast Correlation and Slow Decorrelation Contribute Synergistically to Avoid Propagation/Encoding Trade-Off.

Thus far, we have seen that interneuron coupling can achieve simultaneous fast correlation and slow decorrelation, which can benefit both propagation and encoding. We wondered whether the observed improvements to propagation and encoding were truly specific to a timescale-dependent correlation strategy (observed in the olfactory bulb), or whether they could be achieved via correlation changes at a single timescale. Our two-cell model shown in Fig. 2 suggests that shared, competitively recruited input is required for fast correlation/slow decorrelation. Because these mechanistic components can be isolated in our network model, we manipulated properties governing inhibitory synapses to investigate how fast correlation and slow decorrelation independently affect encoding and propagation.

To isolate fast correlation changes, we modified interneuron polarity so that interneuron output had equal probability of being excitatory or inhibitory [sync_(±) model]. Although not biologically realistic, this simple manipulation preserved shared fast fluctuations while eliminating slower inhibitory influences on firing rate (Fig. 4 C and D, black). The opposing model variant isolated slow decorrelation by disrupting the timing of GABAergic inhibition (Fig. 4C, async₍₋₎, gray). This disruption was accomplished by introducing a random lag (0–50 ms) before each postsynaptic cell received inhibitory current, keeping the total amount of inhibition constant and activity dependent, while eliminating shared fast fluctuations. These manipulations effectively isolated correlation changes at the timescales of interest (Fig. 4D, sync_(±) Δρ = 0.12 ± 0.02; async₍₋₎ Δρ = −0.15 ± 0.01, P < 0.05) while matching firing rates to the no-coupling and olfactory bulb variants (Fig. S6).

In the sync_(±) variant, propagation is increased to 0.34 ± 0.05%. However, discriminability is severely hindered in this case because increased spike covariance stretches response patterns along the diagonal axis (Fig. 4 A and F, d = 0.2). Conversely, in the async₍₋₎ variant, pattern overlap is reduced because the more active group suppresses firing rate in the less active group, stretching the two distributions along the antidiagonal (Fig. 4 B and F, d = 0.82). However, the decrease in firing rate reduces propagation to 0.03 ± 0.004%. Notably, even though the olfactory-like model combines the timescale-specific correlation changes represented in the sync_(±) and async₍₋₎ variants, it outperforms the propagation and encoding predicted by the mean of these models. These models further highlight the benefits of the olfactory bulb-like inhibition with respect to the propagation/encoding trade-off. Without any interneuron-mediated coupling, the model performs poorly with respect to both propagation and encoding (Fig. 4E, purple). Although the sync_(±) (Fig. 4E, black) and async₍₋₎ (Fig. 4E, gray) variants improve one aspect of processing, they do so at the expense of the other function. Only the olfactory-like timescale-dependent correlation model (Fig. 4E, orange) improves both propagation and encoding simultaneously.

Discussion

Our results show that interneuron-mediated coupling between pairs of active principal neurons can modulate pairwise spike train correlations in a timescale-dependent manner. Simultaneous fast and slow correlation changes depend on two general features of interneuron recruitment. First, granule cells provide GABA_A inhibition to subsets of mitral cells that synchronize spike timing (14–16, 18, 20). Second, inhibition is recruited competitively, resulting in slow decorrelation between mitral cells (11, 12, 45). That is, more active mitral cells are more effective at recruiting lateral inhibition that suppresses the firing rate of less-active mitral cells. Downstream neurons may be sensitive to coincident inputs due to short membrane time constants, high firing thresholds, or feedback inhibition. For these neurons (e.g., pyramidal cells in olfactory cortex) (46, 47) increased correlation of input spike trains increases propagation efficacy.

Like the recently described “synchrony by competition” (20) mechanism, timescale-dependent correlation changes rely on competitively recruited synchronizing inhibition. Our study provides a unique perspective on correlation by considering effects on correlation at multiple timescales and directly assessing their impact on both propagation and encoding. Although the impact of correlation changes on sensory coding has been extensively discussed (18, 27, 32–35, 48–50), few studies have measured spike train correlation across timescales (51). Our work shows that influencing spike train correlations at different timescales in opposing directions facilitates improvements to both activity propagation and stimulus encoding. Our report of timescale-dependent correlation changes in a real biological circuit demonstrates not only that this effect arises naturally from recruitment of local inhibitory circuits, but also that it can be accomplished in a minimal circuit (two excitatory cells and the shared inhibitory interneurons) to study pairwise correlation. These measurements of the effects of such minimal and well-defined circuits provide valuable data for understanding the circuit mechanisms that generate spike train correlations.

Whereas the increase in fast timescale correlation is highly significant, the magnitude of this change observed between mitral cell pairs in slice is small, due both to physiological and to analytic causes. Physiologically, we expect this change to be small because it is induced by the inhibitory circuits recruited by a single pair of mitral cells. Because odor stimuli recruit tens to hundreds of neurons in vivo, this observed change likely represents a small fraction of the changes that would be seen in vivo. Analytically, spike count correlation will always approach zero as bin size is reduced (52). Given these limitations, we found it quite striking that significant changes in correlation were observed in these experiments.

Numerous studies have investigated the role of olfactory bulb inhibition in shaping behavior. In honey bees, selective disruption of inhibition-induced synchrony impairs behavioral performance only for difficult olfactory discriminations (6). Similar effects have also been observed in mice whose GABAergic signaling has been reduced genetically (7). Conversely, genetic enhancement of GABAergic transmission improves performance on difficult olfactory discrimination tasks (7, 53). Despite the clear behavioral improvements conferred by olfactory inhibition, their relationship to correlating (14, 15, 18) or decorrelating (11–13, 54) inhibition has remained unclear. Our results suggest that a single mechanism can account for increases and decreases in correlation and that these changes result in improvements in signal propagation and encoding.

Given that several features of inhibition discussed here are unique to the olfactory bulb, inhibition-mediated timescale-dependent correlation changes may be particularly well suited for this system. Unlike purely center-surround lateral inhibitory circuits (such as the retina) (55), olfactory bulb lateral inhibition is less topographically confined (11, 56, 57) and mitral cells can laterally influence distant cells (37, 58–60). Further, the reciprocal nature of dendrodendritic synapses in the olfactory bulb may facilitate the generation and activation of shared inputs. However, inhibition-mediated cross-timescale correlation changes can in principle be accomplished without these specific anatomical features (51). As discussed in Fig. 2, timescale-dependent correlation changes require inhibition that is fast, shared, and activity dependent, features that are quite general to neural circuits. Further, timescale-dependent correlation changes were observed over a broad range of parameter changes as long as these requisite features remained intact. We believe that our described mechanism could be efficacious for a wide variety of networks and tasks, given that population coding and incomplete propagation (i.e., <100%) are general features of many circuits. For example, attention can result in frequency-dependent changes in coherence between local field potentials and spikes (61–63) that might be explained by a related mechanism.

We present a unique perspective of lateral inhibition within the context of sensory coding. Examining correlations across different timescales reveals that inhibition shapes spike train correlations between principal cells in a highly specialized fashion. This mechanism integrates the traditional view of lateral inhibition (pattern decorrelation) (55, 64) with more recent studies detailing fast-timescale correlation changes (6, 14, 15, 18, 53). This perspective views spike timing and rate information not as opposing coding strategies, but rather as features that can be modulated semi-independently. This view represents a targeted strategy by which a network can optimize the correlation structure of its output in a dynamic, activity-dependent manner. For example, networks may have an optimal correlation structure, given their inputs and processing demands (65). Thus, timescales of increased and decreased correlation may be shaped by biological features such as time constants of downstream neurons, kinetics of neurotransmitter release, or particular stimulus statistics.

Materials and Methods

A detailed description of the methods is provided in SI Materials and Methods. Briefly, slices were obtained from P13–P20 mouse olfactory bulb. We performed whole-cell current-clamp recordings of mitral cells during somatic current injection. Granule cell excitability was increased either by reducing Mg²⁺ concentration in solution or by adding the mGluR agonist (S)-3,5-dihydroxyphenylglycine (DHPG). Spiking activity was recorded over 2-s stimulus epochs repeated 20–80 times. All P values noted were calculated using a t test. Cross-timescale correlation was calculated by binning spike times and calculating Pearson's correlation coefficient:

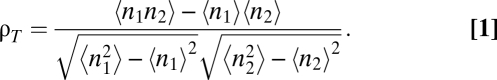All simulations were performed in Matlab. Both the two-cell and the network models consisted of leaky integrate-and-fire neurons with inhibitory coupling. Voltages were calculated using a standard Euler integration scheme.