A competitive network theory of species diversity

Abstract

Nonhierarchical competition between species has been proposed as a potential mechanism for biodiversity maintenance, but theoretical and empirical research has thus far concentrated on systems composed of relatively few species. Here we develop a theory of biodiversity based on a network representation of competition for systems with large numbers of competitors. All species pairs are connected by an arrow from the inferior to the superior. Using game theory, we show how the equilibrium density of all species can be derived from the structure of the network. We show that when species are limited by multiple factors, the coexistence of a large number of species is the most probable outcome and that habitat heterogeneity interacts with network structure to favor diversity.

Ecologists have long sought to explain how a wide diversity of species coexists in nature (1). Coexistence is a conundrum because if two species share the same niche, the competitive exclusion principle predicts the extinction of the inferior competitor (2). This foundational principle continues to motivate advances in niche and neutral theories (3–5) of coexistence, which use niche differences and species equivalence, respectively, to avoid competitive exclusion. However, each theory suffers shortcomings. Field evidence that classic resource-based niche differences are essential for coexistence is rare (6–8), whereas the species equivalence assumption of neutral theory is hard to reconcile with nature. These shortcomings justify the quantitative exploration of less conventional niche mechanisms of coexistence.

Here, we ask how embedding pairs of superior and inferior species in a network of competitors alters the outcome of competition and influences patterns of relative abundance. We find that although the competitive exclusion principle certainly holds for any pair of competitors, when multiple factors determine the outcome of competition and species are embedded in competitive networks, a large number of species can coexist. The coexistence relies on the stabilizing effect of intransitivities (9–12) that emerge in these networks rather than more traditional pairwise niche differences. By combining a game theoretical framework with graph theory and dynamical systems (13, 14), we show how the equilibrium abundance of all species can be determined from the competitive network, how species diversity relates to the number of limiting factors, and how spatial heterogeneity combines with intransitivity to interactively favor diversity maintenance.

Model

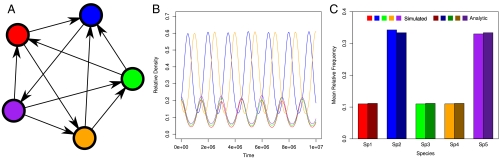
The pairwise competitive relationships between species in a community can be expressed as a network, or more formally, a tournament, in which species are the nodes and arrows connect the competitive inferior to the superior competitor (Fig. 1A). In the simplest case, where all species in a system compete for a single limiting resource, their competitive abilities should be transitive: Species A beats all others, B beats all but A, C beats all but A and B, and so on. We therefore expect a single winner; the best competitor will drive all others extinct. By contrast, when at least one pair of species competes for a resource different than the other pairs, we might observe intransitive competitive relationships: In pairwise interactions, species A excludes B, B excludes C, but C excludes A. This forms the familiar “rock-paper-scissor” dynamic, which has been studied extensively, as it can lead to the indefinite coexistence of the three species (10–12) and facilitate the coexistence of many more species with the appropriate consumer resource interactions (9, 15). In the tournament representation of this very same problem, intransitive relationships between competitors generate cycles (Fig. 1B).

Fig. 1.

(A) Species’ competitive abilities can be represented in a tournament in which we draw an arrow from the inferior to the superior competitor for all species pairs. A tournament is a directed graph composed by n nodes (the species) connected by n(n - 1)/2 edges (arrows). (B) Simulations of the dynamics for the tournament. The simulation begins with 25,000 individuals assigned to species at random (with equal probability per species). At each time step, we pick two individuals at random and allow the superior to replace the individual of the inferior. We repeat these competitions 10⁷ times, which generates relative species abundances that oscillate around a characteristic value (SI Text). (C) The average simulated density of each species from B (shown in lighter bars) almost exactly matches the analytic result obtained using linear programming (shown in darker bars).

Which type of competitive networks should we expect in nature? Empirical work over the last several decades has shown that multiple factors regulate the outcome of plant species interactions, causing different plant species to compete for different resources (16, 17) and limit one another via shared pathogens and consumers (18). With such a diversity of mechanisms controlling the interaction between competitors, a simple transitive hierarchy is highly unlikely. However, the prevalence of intransitivities will depend on whether superior competitors for one resource tend to be superior for others. Because the empirical literature is not clear on this matter (16, 19, 20), we initially assume that species’ competitive ranks for different limiting factors are uncorrelated, an assumption we later relax.

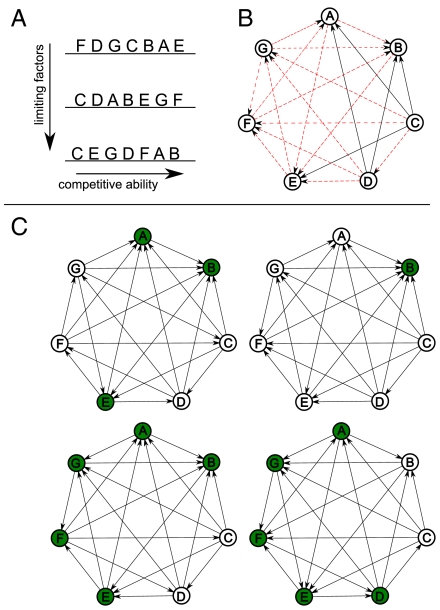
To investigate the relationship among intransitivity, coexistence, and the number of limiting factors, we begin with the following scenario: Suppose we have three limiting factors and seven species are ranked at random for each factor (Fig. 2A). For each pair of species, there are two possible competitive relationships: (i) One species is the superior for all factors (Fig. 2B, in black) or (ii) one species is better for two of three factors (Fig. 2B, in red). For the second case, we might expect the better competitor in each pair to win in two-thirds of the tournaments. From this “master tournament” (Fig. 2B) describing the ranking of the n species for f factors, we can derive multiple possible networks. For example, in Fig. 2C we report four tournaments generated from the ranking of the species illustrated in Fig. 2A. More generally, we draw an arrow from A to B with probability N_AB/f, where N_AB is the number of factors in which A is worse than B and f is the number of factors (SI Text). We therefore assume each factor is equally likely to determine the dominant in pairwise competition. For a given network (e.g., one of those in Fig. 2C), we consider a system in which large numbers of individuals interact and compete with one another at random, leading to the loss of the inferior individual after each bout of competition.

Fig. 2.

(A) The competitive abilities of species A–G are ranked at random for three limiting factors. (B) Two possible competitive relationships can emerge: (i) The inferior species is ranked lower than its competitor for all three factors (e.g., C versus B, black arrows) or (ii) the inferior species is ranked lower than its competitor for two factors (e.g., A and B, red arrows). (C) We can use this information to “draw” tournaments: We draw an arrow from node i to j with a probability equal to the proportion of factors for which species i is ranked below j. For example, we draw the arrow A → B with probability 2/3, whereas B → A with probability 1/3. In this way we can generate several tournaments from the same set of competitive relationships in A. For each tournament, we can find the equilibrium solution, and those species with nonzero equilibrium densities coexist (in green), though the equilibrium is neutrally stable.

Results

Under the assumption of zero-sum dynamics (gains by one species require losses by others) and mass-action interactions (the interaction rate is proportional to species’ densities), we find that the dynamics for a system composed of n competing species are characterized by a unique equilibrium point (13, 14) (shown by the lighter bars in Fig. 1C) and that the dynamics around the equilibrium are linearly neutrally stable (SI Text). Therefore, after a transient phase in which some species may go extinct, the surviving species fluctuate with regular cycles (Fig. 1B). Moreover, we can show that the average density of each species is that it would attain at equilibrium. Thus, although the initial conditions determine the amplitude of the cycles around the equilibrium, the average densities of the species eventually equal their equilibrium value. In this respect, coexistence via intransitive competition is a stabilizing niche mechanism—one that generates an advantage when rare (21). Indeed, if a focal species is perturbed to low density, compositional shifts among the remaining competitors tend to favor an increase in the focal species, albeit with cycles (SI Text).

Using a game theoretical framework, we can find the equilibrium values for all species in an efficient way using linear programming (13) (i.e., we can predict the average relative abundances of the species without having to run the dynamical system, Fig. 1C). For any tournament expressing the dominance relationships between pairs of competitors, we can find the predicted average density for each species when embedded in the competitive network (SI Text). Using these techniques, we can show, for example, that only a subset of species (shown in green) would coexist for any given tournament in Fig. 2C. Note that all species coexisting after the initial exclusions are part of intransitive cycles, but membership in a cycle need not lead to persistence. For example, species G, C, D, and F form an intransitive cycle in the top-left tournament in Fig. 2C, but all fail to persist at equilibrium.

To examine how the number of limiting factors influences the number of coexisting species, we repeat the same procedure used to develop the network in Fig. 2, but for a larger number of species and with varying numbers of limiting factors (for which species rank is still randomly assigned). As in classic niche theory, we find that an increasing number of limiting factors allows an increasing number of species to coexist (Fig. 3A). In contrast to traditional niche theory, however, species do not coexist because each species in a pair is limited by a different factor (all pairs have a clear competitive rank). Instead, they coexist because multiple limiting factors generate competitive intransitivities that counter the outcome of each pairwise interaction in isolation.

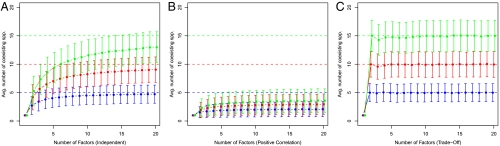
Fig. 3.

Average number of species coexisting (± 1 SD) when we perform the simulations described in the main text for a variable number of limiting factors (x axis) and size of the species pool (colors). The blue line is for a 10 species pool, the red line for 20 species, and the green line for 30 species. Dashed lines mark the theoretical expectation for an infinite number of factors. (Left to Right) (A) results obtained drawing the ranking for the species independently; (B) positive correlation among factors; (C) trade-off among factors. Details are reported in SI Text.

When the number of limiting factors goes to infinity in our competitive network framework, the probability of drawing an arrow from species A to B is the same of that of drawing the arrow from B to A (i.e., the probability of either species being the dominant competitor is the same). This scenario defines a random tournament, a limiting case that is particularly interesting because one can derive several predictions analytically. For example, it can be shown (13, 14) that in a random tournament composed of n species, the probability of observing k number of coexisting species at equilibrium is

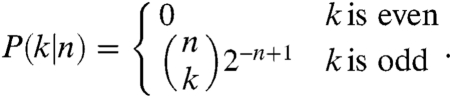This formula yields a nontrivial result: In the most basic competitive network framework presented here, one can never observe an even number of coexisting species. This means that without any pairwise niche differences, a system with an even number of species will always collapse to a smaller one formed by an odd number of species. In fact, for any tournament composed of an even number of species, we can find a subtournament composed of an odd number of species that collectively wins against each of the remaining species more often than it loses, eventually driving the other species extinct. At the low diversity extreme, this finding reiterates the competitive exclusion principle; a two species system collapses to one species. Another constraint is that the proportional abundance of the dominant species is either 1 (complete dominance) or less than or equal to 1/3. Abundances in between are not possible in this most basic model (SI Text).

Another important finding from random tournaments is that due to the symmetry granted by the binomial coefficient, the probability of finding very few coexisting species is exactly that of finding all but very few species coexisting. The most likely outcome is the co-occurrence of half of the species pool (i.e., the species in the master tournament). More formally, from this equation, the expected number of coexisting species for a random tournament composed by n species (13) E[k|n] = n/2 and the variance Var[k|n] = n/4 (SI Text). Therefore, in this theory, with a large number of limiting factors, species diversity is bounded only by the size of the species pool; half of the members of the species pool coexist independent of n.

Given the simplicity of the results for random tournaments, we asked how many factors are necessary to closely approximate these results. Specifically, we ask how many factors are needed to attain the same level of coexistence we would observe in random tournaments? As shown in Fig. 3A, when we increase the number of factors, we rapidly increase the average number of coexisting species: For one factor we have a single winner, but with just two factors, an average of 4.17 of the initial 20 species coexist. The fraction of coexisting species grows rapidly and then saturates around the expected value for random tournaments (50% of the species pool persisting). Importantly, just a handful of limiting factors can generate the coexistence of many species, a feature of intransitive networks (9, 15).

Clearly, this analysis assumes that species’ competitive ranks for the various factors are independent, yet the correlation between these ranks is likely to influence dynamics (15). To explore this influence, we first examined the coexistence resulting when species ranks for the different factors are positively correlated (SI Text). We find that such correlations reduce the number of “effective factors,” such that we need many more limiting factors to have the same level of coexistence as with uncorrelated ranks (Fig. 3B). To explore the influence of a negative correlation between factors, we examined a case where each species has a limited amount of resource to allocate to various functions, so that high competitive rank for one factor means lower competitive rank for other factors (SI Text). Results show that such trade-offs increase the number of effective factors, such that only a handful of factors is required to generate the coexistence that would be found in a tournament with uncorrelated ranks among numerous factors (Fig. 3C). A particularly interesting case is where we have just two limiting factors, and a trade-off between them (SI Text). This generates a random tournament where half of the species in the regional pool coexist on just two factors (Fig. 3C).

Finally, we show how classic niche processes can combine with intransitive competition to regulate the number of coexisting species. Our model thus far has examined tournaments in spatially uniform resource environments. To explore how spatial niches combine with intransitive competitive interactions, we simulated a system of 100 species ranked at random for five factors. The species compete in many patches, each of which is limited by a randomly assigned combination of up to five factors. All species are initially present in all patches, but due to between patch differences in the limiting factors, different tournaments arise in different patches (following the logic outlined in Fig. 2 for each patch). We assume no dispersal between patches, thereby allowing us to use our analytical approach for estimating relative abundance at the patch scale. The total relative abundance for all species in the system is the average over all patches. See SI Text for methodological details and other parameter combinations.

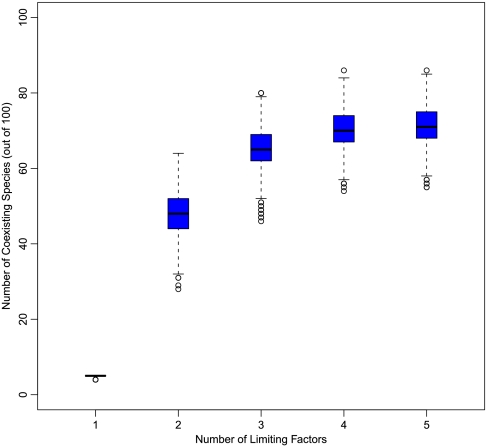
Results show that when just one factor is limiting in each patch, we obtain no more coexisting species than limiting factors (five, Fig. 4), reproducing a classic result (1, 2). However, with up to two of five factors limiting each patch, thereby allowing intransitive competitive networks to develop, we find around 50 coexisting species (half the total species pool), demonstrating the large additional contribution of intransitive competition in spatially heterogeneous systems. Another important result is that even though each individual patch still supports only an odd number of species, summing abundances over all patches often gives an even number of coexisting species in the system as a whole (SI Text). In addition, the dominant competitors can obtain relative abundances greater than 1/3 of the community, eliminating a second constraint of the more simple version of the model. Additional flexibility in the relative abundance patterns and the identity of the dominant species can be achieved by allowing different patches to have different area or allowing ties between species (SI Text).

Fig. 4.

The number of coexisting species as a function of the number of limiting factors in spatially heterogeneous systems. The simulated systems contain a pool of 100 species, competing in numerous patches, each of which is limited by a combination of up to k factors of five total factors. For example, the far left box shows the number of coexisting species in the system when each patch is limited by only one of the five factors (SI Text).

Discussion

Ecologists have long appreciated that resource competitors can indirectly benefit one another via the suppression of shared competitors (22, 23). And more recent studies have demonstrated that intransitivity in competitive networks can maintain diversity (9, 10, 11, 15). However, in past work, very specific requirements were necessary for intransitive networks to emerge, and in turn, stabilize the interaction between competitors. This has given the potentially false impression that such mechanisms might be confined to a small number of natural systems (24). Here, by contrast, we have shown that intransitive competitive networks are the most likely outcome in systems with multiple limiting factors, suggesting broad generality of the mechanism. In addition, by showing how game theory, graph theory, and dynamical systems allow one to move between the network structure and the relative abundance of species, we open previously undescribed lines of empirical inquiry into this mechanism of diversity maintenance. Finally, our analytical approach allowed us to prove the potential for unlimited coexistence, as well as demonstrate the limitations of diversity maintenance via competitive intransitivity. The requirement for an odd number of species, for example, would have been difficult to notice, let alone prove, using simulations.

In our model, the abundances of the coexisting species are characterized by a neutrally stable equilibrium. If the system is perturbed away from the equilibrium, species cycle with a temporal average density equal to their equilibrium value. The coexistence resulting from intransitive competitive networks is stabilized in the sense that species’ densities averaged over the cycle period converge to their equilibrium value (SI Text). Focal species perturbed to low density tend to recover because the composition of competitors shifts in a way that favors the growth of the focal species. Meanwhile those perturbed toward monodominance tend to decline. The intransitivities that stabilize this coexistence depend on different factors determining dominance between different pairs of competitors. These factors may correspond to different resources, such as light or nitrogen, but will also include factors determining dominance in apparent competition such as predators and pathogens.

One of the more striking results of our analysis is that for random tournaments in spatially homogeneous environments, the most likely number of coexisting species is n/2, half the size of the species pool. Coexistence is therefore unbounded in that increases in the size of the species pool are not accompanied by a leveling off of local diversity (25, 26). This leveling off, or “saturation,” of local communities is commonly predicted by more traditional coexistence mechanisms, where exogenous niche structure (e.g., resource heterogeneity) allows only so many species to share a habitat. In our model, by contrast, the niche structure is itself a function of the competitors’ relationships with one another, and a larger species pool creates opportunities for more species to coexist. As in other studies, the species pool in our model is best considered to include all species dispersing into a focal habitat. This follows from our finding that species’ equilibrium relative abundances are independent of their initial densities, provided that these densities are nonzero.

Our model makes several empirical predictions that can be evaluated with field data. First, it predicts that with enough limiting factors, local richness should be a constant fraction of the total species pool. This is consistent with many empirical datasets showing linear relationships between local and regional species richness (25, 26). Second, we can ask how well an empirical relative abundance pattern is described by the best fitting tournament. As we show in SI Text, our model provides very good fits to abundance data from tropical forest tree assemblages and marine faunal communities in kelp holdfasts. The general agreement between the theory and common community patterns suggests that the abundance and diversity patterns generated by our model are not so inconsistent with nature to justify its rejection. But this leaves unanswered the key question of whether intransitive networks of competitive ability stabilize coexistence in real communities.

Although several cases of rock-paper-scissor dynamics among sessile organisms are well documented (27–29), it is difficult to assess the true prevalence of these interactions. This question can be partially answered by studies that compete all possible pairs of plant species from a defined community. Although prior reviews of such studies have emphasized that certain species tend to win in competition and others tend to lose (30, 31), these studies often show that some poorly ranked competitors (those that tend to lose to other species) beat some species of generally higher rank (those that tend to win), and sometimes of much higher rank (32, 33). Importantly, these empirical results likely underestimate the frequency of intransitive competitive relationships because they are almost always conducted in greenhouse pot experiments. Such settings artificially favor limitation by a single resource, which in turn disfavors intransitivities (Fig. 3).

The strongest empirical tests of our model follow from its ability to predict species’ relative abundances from the tournament structure. Specifically, one can first quantify the pairwise interactions between all competitors in a community, and thereby document the tournament structure. Second, the relative abundance of each species predicted by the tournament structure can be compared to their observed relative abundance in a natural community. We attempted such an analysis with published data, but were stymied by the rarity of studies combining unambiguous competitive dominance results for a wide diversity of taxa with natural patterns of relative abundance. A reasonable way forward for quantifying competitive dominance might involve using field data to parameterize mathematical models of competitive interactions, such as Beverton–Holt or Ricker formulations (7). Alternatively, the outcome of pairwise competition can be directly observed for species with clear patterns of overgrowth, such as many marine invertebrates (27) or species with very short generation times. With this latter group in mind, protist microcosm systems might provide a starting point for testing model predictions.

One of the broader challenges in exploring the importance of intransitive competition to coexistence in natural communities is that more traditional niche mechanisms almost certainly operate alongside competitive intransitivities, and the two can be difficult to disentangle. For example, spatial variability in the identity of limiting factors establishes different tournaments in different locations, allowing many more species to coexist than would be found in an environment without intransitive competition. Although overcoming this methodological hurdle will require innovative empirical approaches, we expect that competitive networks may provide a better starting point for understanding diversity maintenance than the simple two species competitive exclusion principle.