Modification of deeply buried hydrophobic interfaces by ionic surfactants

Abstract

Hydrophobicity, the spontaneous segregation of oil and water, can be modified by surfactants. The way this modification occurs is studied at the oil–water interface for a range of alkanes and two ionic surfactants. A liquid interfacial monolayer, consisting of a mixture of alkane molecules and surfactant tails, is found. Upon cooling, it freezes at T_s, well above the alkane’s bulk freezing temperature, T_b. The monolayer’s phase diagram, derived by surface tensiometry, is accounted for by a mixtures-based theory. The monolayer’s structure is measured by high-energy X-ray reflectivity above and below T_s. A solid–solid transition in the frozen monolayer, occurring approximately 3 °C below T_s, is discovered and tentatively suggested to be a rotator-to-crystal transition.

Hydrophobicity (1) is abundant in nature and in technology (2). It plays a dominant role in fields ranging from the structure of living matter, like cell membrane stabilization and protein folding, to microemulsion-mediated nanoparticle and quantum dot formation (1, 3–7). Although the macroscopic phenomenology of hydrophobicity is well studied, its theoretical understanding, particularly on a molecular level, is still incomplete (1, 8). Recent progress in X-ray scattering from buried interfaces allowed determination of the structure of hydrophobic interfaces (including the oil–water one) with near-atomic resolution, leading to an animated debate on the molecular-scale origin and manifestations of the hydrophobic interaction (9–13). Surfactants are often used to modify the hydrophobic interactions in a manner that reduces the interfacial free energy. However, the microscopic structure of surfactant-modified bulk oil–water interfaces, the subject of the present study, has been studied by X-ray methods only for nonionic alkanol surfactants (14, 15). X-ray measurements for oil–water interfaces modified by ionic surfactants are not available in the literature. Macroscopic optical measurements have uncovered intriguing interface structure modifications (16), indicating that these more widely used and more complex electrically charged surfactants, which also have bulkier headgroups, may modify the interface differently from the nonionic ones. Thus, a key ingredient in the fundamental understanding of the relation between ionic surfactants and the hydrophobic interaction is still missing.

Using X-ray reflectivity (XR) and surface tensiometry, we measured the atomic-resolution structure and thermodynamics of oil–water interfaces decorated by ionic surfactants (see Fig. 1A). Two different interfacial phases are observed. At high temperatures, a liquid interfacial monolayer is found; upon cooling, a frozen monolayer forms at the interface, separating the bulk liquid oil and aqueous phases. We measured the interfacial phase diagram and offer a simple thermodynamic model which fully accounts for the interfacial freezing (IF). At a lower temperature, the frozen monolayer is found to undergo an additional transition to full crystallinity where the molecular plane’s rotational degree of freedom is frozen out.

Fig. 1.

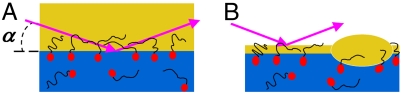
The interfaces studied. (A) The l/l interface between a bulk alkane and an aqueous surfactant solution. (B) An alkane monolayer at the same solution’s l/v interface. Note the alkane droplet-alkane monolayer coexistence (18). Arrows denote the X-ray reflectivity geometry.

Results

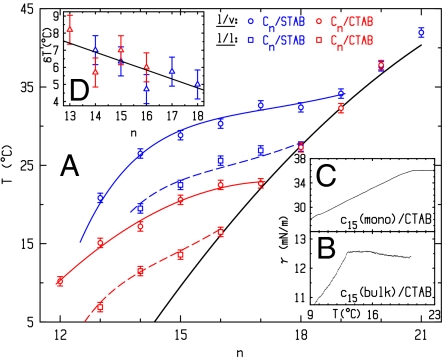
The surfactant-decorated oil–water interfaces that we study form a mixed surfactant–alkane interfacial layer between a bulk phase of submillimolar aqueous solution of alkyl-trimethylammonium bromide [H(CH₂)_mN(CH₃)₃Br] surfactant, with m = 16 (CTAB) or m = 18 (STAB), and a bulk phase of alkane [H(CH₂)_nH, denoted C_n, n = 12–21]. The thermodynamics are conveniently probed by temperature-dependent interfacial tension measurements, γ(T), which is the difference per unit area between a molecule’s free energy at the surface and in the bulk: γ(T) = (ε_s - ε_b) - T(S_s - S_b). S, ε, b, and s denote entropy, energy, bulk, and surface, respectively. For liquids S_s > S_b, and thus dγ/dT is negative. If interfacial freezing occurs, S_s drops below S_b, rendering dγ/dT > 0 (17). Shown in Fig. 2B for the liquid–liquid (l/l) interface of C₁₅ alkane and a CTAB solution, γ(T) is measured by the Wilhelmy plate method. At high T, the slope is negative, indicating a disordered interface. Upon cooling, an abrupt slope change occurs, similar to that observed (18) for mixed CTAB/alkane monolayers [called Langmuir–Gibbs films (LGFs)] at the surfactant solution–vapor (l/v) interface (see Fig. 1). These LGFs freeze at T_s into an ordered solid monolayer. The slope change dγ/dT_T<Ts - dγ/dT_T>Ts = S_s,T<Ts - S_s,T>Ts = ΔS_s is the entropy loss upon monolayer freezing. ΔS_s measured at the l/l interface is very close to that measured for LGFs at the l/v interface, suggesting that the l/l interface also exhibits IF. Measured at the l/v interface for an LGF of components identical to those of Fig. 2B, γ(T) is shown in Fig. 2C. The curves at the two interfaces exhibit similar breaks and slopes, though the IF ranges of existence, ΔT = T_s - T_b, are different. ΔT is also observed in Fig. 2A to decrease with increasing n at both the l/l and the l/v interfaces, due to the fast increasing T_b (bold line), which eventually preempts IF at an n depending on m and the interface type: l/v or l/l.

Fig. 2.

(A) Measured (symbols) and theory-fitted T_s(n) (see text) for the l/v (solid lines) and l/l (dashed lines) interfaces of CTAB (red) and STAB (blue). T_b (bold line) averages over the odd-even variations with n. (B and C) Measured γ(T) at the l/l (“bulk”) and l/v (“mono”) interfaces. The curves terminate at T_b ≈ 9.5 °C. (D) Measured (symbols) and fitted (line) δT = T_s(l/v) - T_s(l/l) for CTAB (red) and STAB (blue).

To confirm that the observed kink in γ(T) (Fig. 2B) is not an artifact (e.g., an abrupt T-dependent surface adsorption of impurities) T_s is measured for a wide range of alkanes for both CTAB and STAB. The systematic and gradual variation of T_s with both n and m (Fig. 2A, squares) which follows the general trends (Fig. 2D) of the same-alkane LGFs appears to rule out impurities, suggesting that the measured ΔS_s can be attributed to IF at the l/l interface. However, as macroscopic γ(T) measurements are unable to resolve the microscopic structural details of the transition, direct X-ray structure determination is used to verify this conclusion.

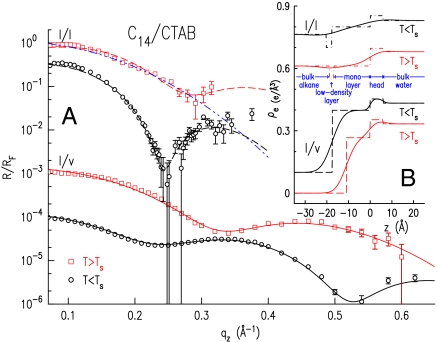
To this end, we have measured the X-ray reflectivity from the interface (19, 20), R(q_z), vs. grazing incidence angle α (see Fig. 1), where q_z = (4π/λ) sin α. The interface’s structural information resides in the deviations of R(q_z) from the theoretical Fresnel XR of an ideally flat and abrupt interface, R_F(q_z). Fig. 3A (symbols) shows R(q_z)/R_F(q_z), which emphasizes these deviations, for the C₁₄/0.6 mM CTAB solution interface. For the l/l interface (top two curves), a sharp dip is observed for T < T_s, and a shallow one for T > T_s within the limited measurable q_z range. These are indicative of a structured interface, exhibiting a nonmonotonic interface-normal density profile ρ_e(z) (21–23).

Fig. 3.

(A) Measured (symbols) and model-fitted (lines) XR curves, for the indicated interfaces. The bottom three curves are downshifted by 3, 1,000, and 10,000 for clarity. The fit by a model without a low-density layer (blue dash-dot-dot line) is discussed in the text. (B) Fit-obtained electron density profiles with (solid lines) and without (dashed lines) capillary wave smearing. The top three curves are upshifted by 0.1, 0.35, and 0.5.

Constructing a model for ρ_e(z) and fitting its Fourier transform to the measured R(q_z)/R_F(q_z) yields ρ_e(z) (24). A simple two-box model of the interface, with one box representing the monolayer’s alkyl chains, and a second the surfactants’ headgroups, reproduces well the R/R_F curves measured both above and below T_s. However, without explicitly including a third box to represent the low-density CH₃ endgroups of the interfacial monolayer, this model is unphysical. The low-density layer is expected because of the (up to twofold) larger volume of the solvated CH₃ moiety as compared to that of CH₂ one (25, 26). Such low-density layers were demonstrated to be essential to obtain physically acceptable models for interfaces between a solid layer of alkyl chains and a liquid alkyl bulk (24, 27). Moreover, the best fit of this two-box model to the R/RF curve measured at T < T_S curve yields a frozen monolayer thickness significantly shorter than the extended molecular length, in contrast with the results obtained by ellipsometry for the l/l interface (16), and by both ellipsometry (28) and X-rays (18) for the corresponding l/v interface, where the layer thickness is equal to the extended molecular length. Also, for T > T_s, the two-box model invariably yields a monolayer density significantly larger than that of the overlying liquid bulk alkane. However, because the monolayer is liquid at T > T_s, as shown by the γ(T)-derived negative slope, ellipsometry (16), and the corresponding phase at the l/v interface (18), it should have a very similar density to that of the overlying bulk. A two-box model with equal monolayer and alkane bulk densities cannot reproduce the dip observed in all R/RF curves measured at T < T_S (e.g., top curves in Figs. 3A and 4A), as demonstrated by the best fit of such a model to the measured data, the blue dash-dot-dot line in Fig. 3A. A third, low-density, box must be included in the model to reproduce the dip in the T > T_s-measured R/R_F curves.

Fig. 4.

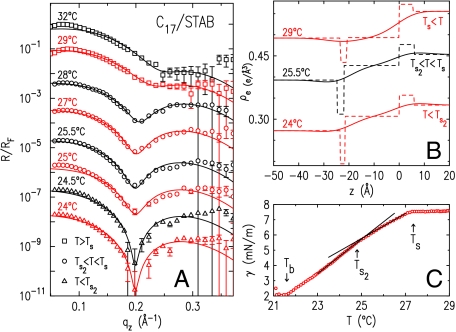
(A) Measured (symbols) and model-fitted (lines) XR curves of the l/l interface of C₁₇ and 0.16 mM STAB solution. (B) Best-fit electron density profiles with (solid lines) and without (dashed lines) capillary wave smearing. (C) Measured (symbols) γ(T). Fitted lines show the slope change at T_s2.

A three-box model incorporating such a low-density layer (LDL) (Fig. 3B, Top) indeed reproduces the measured R/R_F well both below and above T_s (Fig. 3A, dashed lines). For T < T_s (Fig. 3A, second from top), a solid monolayer of thickness (17.9 ± 0.6) Å is obtained, equal to the length of an extended C₁₄ molecule, and thus implying a near interface-normal molecular alignment. The LDL is clearly observed in the corresponding density profile in Fig. 3B, Top, where the strong smearing by roughness due to the interfacial capillary waves (29) is also observed. For T > T_s, the monolayer’s density was kept fixed at the nominal 0.264 e/ų of the C₁₄ bulk, and only its thickness and the LDL’s parameters were fitted. The three-box ρ_e(z) model (Fig. 3B) fits well the measured R/R_F (Fig. 3A, top curve), yielding an approximately 16.5-Å-thick monolayer, which is further discussed in the next paragraph.

To gain a deeper insight, we compare the l/l interface results discussed above with those measured for an LGF of the same alkane and surfactant at the l/v interface (Fig. 3A, Bottom). The modulated R/R_F indicate the presence of a monolayer, yet the exact form is different from that at the l/l interface. Here a two-box model is sufficient to reproduce well the measured reflectivity (18), because the low density of the alkanes’ end groups is absorbed into the overall density decrease upon moving from the monolayer into the overlying vapor. Above T_s (squares) the two-box model fit (line) yields an 11-Å-thick liquid layer (Fig. 3B), approximately 5-Å smaller than that at the l/l interface. It is, however, important to note that the T > T_s layer thickness at the l/l interface is poorly defined by the short range of the measured R. Simulations indicate that a more detailed modeling of the headgroup region (e.g., by including an additional low-density box to represent the water-adjacent methyls of the monolayer’s alkanes) could reproduce well the measured R(q_z) of the l/l interface with a total layer thickness 3–4-Å shorter, bringing it close to that at the l/v interface. However, the measured R(q_z) has insufficient q_z range to support an unbiased, uncorrelated, extraction of fit parameters for this more complex model. On the other hand, the different upper phases at the two interfaces may induce a real difference in the monolayers’ thickness, even though it cannot be resolved with confidence from our data. For example, the solubility of the mixed monolayer’s chains in an overlying alkane phase are greater than their solubility in an overlying vapor phase (30). Also, the compressive Casimir force between the monolayer’s two interfaces at the l/v interface (28) is greatly reduced at the l/l one. Both effects drive for a thicker liquid monolayer at the l/l interface than at the l/v one (28, 30, 31).

Below T_s, the fit to the l/v data (Fig. 3A, circles) yields the same density profile and fit values as at the l/l interface, indicating a solid monolayer of surface-normal molecules. Grazing incidence X-ray diffraction (GID) at the l/v interface support this conclusion, revealing a lateral hexagonally packed rotator phase (24), also found for C₁₆ LGFs at the l/v CTAB solution interface (18).

It is instructive to calculate the integrated depletion, Γ = δρ_e × δd of the LDL at the l/l interface. Here, the density depletion is 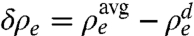. The average bulk density, and the LDL’s density and thickness are 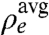, , 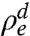and δd (9, 24). The T < T_s solid monolayer’s Γ = 0.20 e/Ų exceeds Γ = 0.15 e/Ų of the T > T_s liquid monolayer. Both are smaller than Γ = 0.33 e/Ų found for surface-frozen alkane monolayers floating on their own liquid bulk (24). The smaller Γ is indeed expected in our system, because our LDLs include higher-density methylenes from the different-length interdigitated alkanes and STAB, not just methyls, as is the case for surface-frozen layers of the alkane melt.

Finally, a second transition, at a temperature T_s2 < T_s, was also found in the frozen monolayer at the C₁₇–STAB interface (Fig. 4). For T > T_s ≈ 28 °C, the shallow dip in R/R_F is due, as above, to an LDL, separating a liquid monolayer (approximately 1.5-Å thinner than the extended molecular length, 21.6 Å) from the overlying alkane bulk. For T < T_s, a sharper dip appears in R/R_F at a lower q_z. The fit reveals that this sharpening is caused by an increase in Γ (0.27 vs. 0.14 e/Ų) and ρ_e [(0.30 ± 0.008) vs. the nominal 0.27 e/ų] upon IF. These increases can be observed by comparing the monolayer and LDL regions in Fig. 4B at 25.5 and 29 °C. The layer thickness at T < T_s, (21.5 ± 0.5) Å, equals the extended molecular length of C₁₇. Thus, C₁₇ follows the general behavior found for C₁₄. However, a second phase transition at T_s2 ≈ 24.5 °C is manifested by an abrupt dip sharpening but no q_z shift, implying the same thickness and a better-ordered monolayer at T < T_s2.

To elucidate the nature of this transition, we fit all R/R_F for T ≤ 28 °C, varying only the LDL box and interface roughness, keeping the densities and widths of the monolayer and headgroups’ boxes fixed at 0.30 e/ų, 0.35 e/ų, 21.5 Å, and 6 Å, respectively. The fits (Fig. 4A, lines) agree well with the data and yield Γ(T < T_s2) = 0.19 e/Ų, intermediate between the sub- and supra-T_s values, but close to that of C₁₄ described above. Although δρ remained practically unchanged, a somewhat smaller δd was found to be favored below T_s2 than above it. Above T_s2, the greater number of gauche configurations at the terminus of the monolayer is likely due to the slight length mismatch between fully stretched STAB and C₁₇ chains which leaves the terminal methyl groups of the two in slightly different planes. This interpretation is supported by our γ(T) measurements, Fig. 4C, where the two transitions are observed as slope changes in γ(T). ΔS_s = (0.3 ± 0.01) mJ/(m² K) obtained from the slope change at T_s2 agrees well with the 0.32 mJ/(m² K) measured for the bulk rotator-crystal transition (32). We suggest, therefore, that the T = T_s2 transition is a rotator-to-crystal transition, which explains the higher chain end order, and thus also the thinner LDL region. Regrettably, GID measurements, probing directly the monolayer’s lateral structure, are prohibited at our l/l interface by the high diffuse background from the liquid bulks. We also note that no such transition was detected in the frozen monolayer at the l/v interface (18).

Discussion

To account for the thermodynamics of our system, we propose a model based on mixtures’ theory (18, 33) and compare it with the measured phase diagram, Fig. 2A. The liquid interfacial monolayer at T > T_s is an ideal mixture of alkanes and surfactant tails. Its free energy includes only those of the pure components and the mixing entropy (34, 35). The frozen monolayer at T < T_s is a strictly regular mixture of close-packed extended alkanes and surfactant tails. Their free energy includes also a surfactant–alkane interaction term, ω (34). Equating the chemical potentials of the two phases at T_s for each component yields (18, 33)

T_b(n) and ΔS_n are the published (17, 25) values for pure bulk C_n alkanes, with the values of even-n alkanes (which freeze into a crystalline phase) interpolated from those of odd-n alkanes (which freeze into a rotator phase) to avoid odd–even effects (25). Also, ϕ (∼0.4; ref. 36) and x are the surfactant concentrations in the liquid and solid monolayer, and ΔS_C = ΔS_Cm is the surfactant’s entropy loss upon freezing (25), taken as that of an equal-length alkane, C_m. The interchange energy, 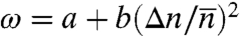, includes the mismatch (Δn) (18, 33) and average (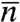) of the surfactant tail and alkane lengths, and a constant interaction term a of the surfactant’s positively charged headgroup with the alkane (18). Thus, in this model, the surfactant m differs thermodynamically from a C_m molecule only by the headgroup interaction energy a. Note that at both l/l and l/v interfaces replacing the C₁₆-alkyl CTAB by the C₁₈-alkyl STAB shifts by two the n at which bulk freezing preempts IF, further supporting the Δn dependence of ω. Fitting these equations to the measured T_s yields ω.

The theory (lines) measurement (symbols) agreement (Fig. 2A) is remarkably good for all four interfaces studied. The chain–chain interaction values, b = (27 ± 1)k_BT, are all within 4% of each other, as expected. The a values, all negative, reveal an effective headgroup–alkane attraction, in contrast with alkane mixtures (33), where ω > 0 and unlike molecules invariably repel each other. The additional van der Waals interaction due to replacing the vapor by an alkane bulk reduces significantly this attraction, from a = -(1.75 ± 0.05)k_BT for the l/v interfaces to a = -(0.35 ± 0.15)k_BT for the l/l ones. The x values obtained vary in all cases studied here from approximately 0.65 (n ≈ 12–14) to approximately 0.4 (n ≈ 17–19), in agreement with a limiting surface area of approximately 34 Å² per cation (37) and the results obtained for the l/v interface of the CTAB solution (18).

The results obtained here for ionic surfactants differ significantly from those reported for the nonionic alkanol surfactants (14, 15), where a different transition is found: adsorption/desorption of alkanols at the interface, rather than the freezing transition in a preexisting liquid layer observed here. The almost-pure alkanol layer formed below T_s in that transition in the nonionic alkanol surfactant systems (14, 15) is a monolayer for Δn > 6 only, and a multilayer for Δn < 6. In contrast, we observe a mixed surfactant–alkane monolayer for all Δn and T. The monolayer’s structure at T < T_s also differs greatly in the two systems, comprising partly disordered chains for alkanols (14, 15) and extended chains here. A detailed elucidation of the origin of these differences will have to await the availability of a broader set of similar studies for other systems. At present, we suggest that the differences originate in the different sizes of, and interactions among, the surfactants’s various moieties. The surfactants have different hydration shells, alkane and water solvation properties, interfacial anchoring strengths, and headgroup–headgroup interactions. For example, the surfactants’ headgroup cross-sections equal (alkanols), and much exceed (CTAB), that of the alkyl tail. These factors differently promote, or prohibit, close packing of surfactant tails and alkane interdigitation, and thus the interface layer’s ordering.

In conclusion, this study provides a molecular-resolution view of the structure of the ionic surfactant-modified hydrophobic oil–water interface, of its temperature variation, and of the interfacial thermodynamics. Preliminary additional measurements show that macroscopic hydrophobicity cannot only be tuned, but even eliminated altogether by reducing the interfacial tension to zero over a range of temperatures and surfactant concentrations. We hope that these experimental results will provide a basis for a deeper theoretical insight into the molecular level causes and characteristics of the hydrophobic interaction.

Materials and Methods

Highest purity commercially available materials were purchased and further purified using standard methods. Alkyl-trimethylammonium bromide [H(CH₂)_mN(CH₃)₃Br] surfactants, with m = 16 (CTAB) or m = 18 (STAB), were purchased from Sigma-Aldrich-Fluka with nominal purities of ≥99% and ≥98%, respectively, and recrystallized thrice from a methanol–acetone solution. The water used was Millipore Ultrapure 18.2 MΩ-cm resistivity. Normal-Alkanes [H(CH₂)_nH, n = 12–21] of nominal purities 99% or better were also purchased from Sigma-Aldrich-Fluka and percolated thrice through activated alumina columns to remove polar components.

The Wilhelmy plate method, well documented in the literature (17, 24, 38), was used for surface tension measurements with a glass Wilhelmy plate of 41-mm circumference. The method of X-ray reflectivity from surfaces is also well documented (21–23, 39). Our X-ray reflectivity measurements were carried out at the high-energy (wavelength λ = 0.177 Å), high-intensity (5 × 10¹¹ photons/s), microfocus (5 × 20 μm², height × width) beamline ID15A at the European Synchrotron Radiation Facility. The beamline’s high-energy microdiffraction diffractometer (HEMD) (19) was operated in the liquid mode (20), which allows measuring the X-ray reflectivity R(q_z) vs. wavevector transfer q_z = (4π/λ) sin α (where α is the grazing angle of incidence of the incoming beam onto the surface, see Fig. 1) without moving the sample. The fixed position avoids perturbing the fragile liquid interface by motion-induced vibrations and flows, and greatly enhances the stability of the ultraaccurate sample positioning dictated by the beam’s high energy and small size. To extract the interface-normal density profile from the measured R(q_z) we use the so-called multislab model (23, 24, 40). Here a physically motivated model is constructed for the profile, using a minimal number of constant-density layers. This model is then Fourier transformed to yield an expression for the X-ray reflectivity. This expression is least-squares fitted to the measured R(q_z) to yield the values of the model-defining parameters: density, thickness, and interfacial roughness of each slab.