How frequency and intensity shape diversity–disturbance relationships

Abstract

Understanding the relationship between disturbance regimes and species diversity has been of central interest to ecologists for decades. For example, the intermediate disturbance hypothesis proposes that diversity will be highest at intermediate levels of disturbance. Although peaked (hump-shaped) diversity–disturbance relationships (DDRs) have been documented in nature, many other DDRs have been reported as well. Here, we begin to theoretically unify these diverse empirical findings by showing how a single simple model can generate several different DDRs, depending on the aspect of disturbance that is considered. Additionally, we elucidate the competition-mediated mechanism underlying our results. Our findings have the potential to reconcile apparently conflicting empirical results on the effects of disturbance on diversity.

The effects of disturbance on species diversity have been studied for decades (1–5), but no clear consensus has been reached. Understanding how different disturbance regimes affect competitive outcomes is important, because disturbance regimes in many locations are changing rapidly, and these changes can have potentially profound effects on ecosystems (6–8). Moreover, human control of disturbances such as mowing, burning, grazing, and flooding can be a useful tool for conservation and management efforts (9). The lack of a clear predictive understanding of the effects of disturbance has even led some to question whether disturbance actually plays a strong role in structuring communities (10). We provide here a conceptual framework that helps to reconcile many of the diverse perspectives and research findings on disturbance and diversity.

Many different patterns of variation in community diversity across disturbance gradients have been observed in nature. The effects of disturbance on species diversity can be described graphically with diversity–disturbance relationships (DDRs), which plot a measure of species diversity (e.g., richness) against a dependent variable that is a quantity related to disturbance (e.g., intensity). Mackey and Currie (10) conducted a meta-analysis of empirical disturbance studies and found that increasing, decreasing, and U-shaped DDRs can all be found in nature. Moreover, they found no trend among the studies for any specific shape to be more common than the others. This finding is ostensibly in contrast to the pattern predicted by the well-known intermediate disturbance hypothesis (IDH), which suggests a tendency for peaked, unimodal DDRs to be the most common.

Connell influentially summarized the IDH by the claim that “diversity is higher when disturbances are intermediate on the scales of frequency and intensity” (2), though similar ideas had been presented previously (e.g., in refs. 1, 11, and 12). Indeed, if predation is included in the definition of disturbance (3), then the work of Paine (13) can be seen as an important early step in understanding how disturbance can affect diversity. In light of this variety of modeling and descriptive approaches, we view the IDH as essentially a heuristic model: Low rates of disturbance lead to a low-diversity community of competitive-dominant species, and high rates of disturbance lead to extinction of all but the most disturbance-adapted ruderal species (14). Thus, the central idea of the IDH can be stated as the claim that DDRs will be peaked. Theoretical models have shown that the IDH can be used to describe several distinct community processes: Peaked DDRs can be generated by “within-patch” models of local temporal variation, as well as “between-patch” models of regional spatially explicit dynamics (15). Moreover, the peaked DDRs predicted by the IDH can result from distinct mathematical mechanisms of coexistence (15). Because the IDH can describe the patterns generated by such disparate phenomena, we view it as an umbrella concept that encompasses a wide variety of community characteristics.

The IDH can be explained as the result of disturbance acting to reduce the effects of competitive dominance, and this explanation has recently been investigated experimentally (16). The results of these experiments show that competition can regulate species richness over a broad range of disturbance regimes, and that competitive exclusion can be hastened by disturbance. These findings are consistent with some of the theory of disturbance (17), though the mostly negative DDRs found by Violle et al. (16) may be related to the fact that only intensity of the disturbance regime was manipulated. The authors conclude “more attention should thus be focused on examining other candidate mechanisms that may potentially contribute to IDH patterns” (16), and we take this as an impetus for our theoretical investigation of the effects of different disturbance regimes on competitive coexistence.

The base entities in our disturbance framework are concrete individual disturbance events. We use the definition of Pickett and White (5), that a disturbance is “…any relatively discrete event in time that disrupts ecosystem, community, or population structure and changes resources, substrate availability, or the physical environment.” Part of the confusion surrounding the effects of disturbance on communities can be traced to the (often implicit) terminologies and ontologies (i.e., conceptual framework and relations) that underlie experiment and model design. Formal ontologies are becoming increasingly important for ecologists (18), and disturbance ecology specifically can benefit from the development of a common system of nomenclature and concepts.

Each disturbance event has a cause (e.g., lightning) and an effect (e.g., combustion), which triggers a species response (e.g., resprouting). In particular, it is the species responses that directly affect ecological processes, so care should be taken to separate physical effects from biological responses, because species may respond differently to the same physical effects of disturbance.

Each disturbance event has several aspects that can be measured. There are five key aspects of particular importance for ecological studies: intensity, timing, duration, extent, and disturbance interval. For example, a flood has a maximum depth (intensity), a date of onset (timing), inundation period (duration), a maximum area inundated (extent), and the time since the last flood occurred (disturbance interval).

For a given set of disturbance events, one can then construct a sample distribution of the quantified aspects. We use this distribution to define the disturbance regime. In this manner, we define frequency and predictability as the mean and variance of the reciprocal of time since last disturbance, respectively. This framework for describing disturbance events and regimes in terms of individual aspects proves useful for understanding the different DDRs found in nature.

Though diversity can be discussed in terms of species turnover via colonization, speciation, and extinction, we are interested in the maintenance of diversity via mechanisms of stable coexistence (19). Because disturbance contributes to environmental heterogeneity, there has been interest in describing the effects of disturbance in terms of general theory of coexistence in variable environments (15, 17, 20–24).

Here, we present a model of two competing plant species subject to disturbance, and show how different intensities and frequencies of the disturbance regime lead to different competitive outcomes. Though many theoretical and graphical models of disturbance describe peaked patterns of diversity consistent with IDH, theoretical literature explaining other DDRs is depauperate. Our model gives a theoretical basis for U-shaped, increasing, and decreasing DDRs, and also shows how IDH patterns are generated for certain disturbance aspects. In short, our model indicates that DDRs will depend very strongly on which aspect of disturbance is used to construct them.

Although diversity can be affected by other types of species interaction (both direct and indirect), our model includes only competition and disturbance, with the hope of understanding the basic case before further complicating factors are added. Many species can coexist in our model (15), but for clarity we focus on a simple two-species case that illustrates our findings concisely. Our findings highlight how the shapes of DDRs depend on which aspect of disturbance is being studied and outline an inclusive understanding of the effects of disturbance on community diversity. Thus, we propose that, although the IDH is intuitive and useful, considering additional aspects of disturbance can explain the variety of DDRs found in natural communities.

Results

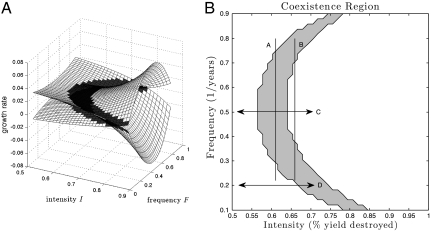
Our model shows how changing the aspects of frequency or intensity of a disturbance regime can have very different effects on associated DDRs. In particular, we examine how the frequency and intensity of a disturbance regime affect competitive outcomes, and hence DDRs. In our two-species model, species richness is always 1 or 2. Surfaces representing each species’ long-term low-density growth rates are plotted in Fig. 1A. When each species has a positive mean growth rate while “invading” an established resident, then both species can persist indefinitely in stable coexistence (20). This procedure is known as invasion analysis (unrelated to invasive species) and allows us to construct the region of disturbance regime parameters that will lead to stable coexistence (coexistence region), shown in Fig. 1B.

Fig. 1.

Coexistence region in the frequency-intensity plane. (A) Growth rate 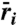for each species as a surface. Surfaces are shaded gray where both species have positive growth rates, which leads to stable coexistence. (B) Projection of coexistence region where 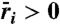for each species. Vertical lines indicate how different frequency DDRs [peaked on left (line A) and U-shaped on right (line B)] result from changing disturbance intensity. Horizontal arrows mark different intensity DDRs [peaked on top (C) and increasing on bottom (D)] that result from changing disturbance frequency. For clarity, we present a pair of species with symmetric life-history traits, which generate a symmetric coexistence region. Life-history parameters for (dominant, inferior) species: seed yield Y = (0.9,1.1), seedbank survival s = (0.4,0.6), germination rate G = (0.6,0.4), competition α = (1.1,0.9).

An important feature of our framework is that all possible combinations of frequency and intensity of a disturbance regime are contained in the compact unit square. Though the “intermediacy” of disturbance described by the IDH is understood to depend on the life-history of the organisms composing the community (e.g., longevity) (23), our method facilitates comparisons between systems by measuring intensity in terms of the mortality response of species.

One advantage of this framework is that it is easy to see how a DDR generated from the frequency of the disturbance regime is affected by the intensity. The vertical lines in Fig. 1B show that changing intensity of disturbance can radically change the shape of the DDR for frequency. Lower intensity (line A) leads to a peaked DDR, as predicted by the IDH, meaning that, along line A, intermediate frequencies lie inside the shaded coexistence region (i.e., richness = 2) whereas extremal frequencies lead to exclusion (richness = 1). Higher intensity (line B) reverses this pattern, and results in a U-shaped DDR, with lowest richness at intermediate frequencies. Frequency also has a strong effect on intensity DDRs. Horizontal arrows in Fig. 1B show that at low frequency (arrow D), over a given range of intensity the DDR is increasing, whereas at higher frequency (arrow C), the same range of intensity leads to a peaked DDR (i.e., single species at extremal intensities, two species at intermediate levels). In both cases, the range of intensities examined is the same. This highlights the need to measure (and present) multiple aspects of disturbance, even if constructing a DDR in terms of only one quantity.

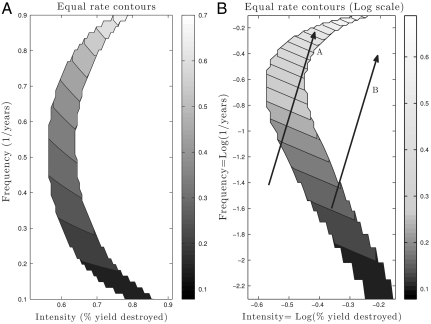
Many empirical studies use rates of disturbance to quantify the effect of a regime (10, 25). Of particular interest is the disturbance rate defined by percent individuals destroyed per year (i.e., frequency × intensity), perhaps due to the original wording of Connell in describing the IDH (2). Fig. 2A shows the coexistence region from Fig. 1B, shaded by the rate of disturbance. This image illustrates both that coexistence can occur across a range of rates and that rate alone cannot be used to predict coexistence. On a log–log scale, curves of equal rate are straight lines (25). We show this log transformation of the coexistence region in Fig. 2B. The arrows in Fig. 2B illustrate how gradients that span the same range of rates can also lead to different DDRs. Across a given gradient of disturbance rates (arrow A), increasing rate of the regime leads to higher diversity. However, the same range of rates can be derived from different component frequencies and intensities. Arrow B shows a situation in which increasing disturbance rate decreases diversity. Because DDRs based upon rate can be increasing or decreasing for the same range, care must be taken when interpreting the effect of disturbance rate on community diversity.

Fig. 2.

Coexistence regions shaded by rate (R) of disturbance, R = F·I; i.e., percent individuals destroyed per year. Coexistence occurs across a range of rates, but rate alone does not determine coexistence. This illustrates the interactive properties of frequency and intensity. (A) On a linear scale, isoclines of constant rate are hyperbolic segments. (B) On a log–log scale, rate isoclines are straight lines. Arrows demarcate rate gradients of equal range. The top left arrow A corresponds to an increasing DDR, and the bottom right arrow B corresponds to a decreasing DDR. In this example, the arrows could not be distinguished if only rate were recorded. This highlights the need to measure multiple aspects of disturbance. Life-history parameters for (dominant, inferior) species: seed yield Y = (0.9,1.1), seedbank survival s = (0.4,0.6), germination rate G = (0.6,0.4), competition α = (1.1,0.9).

As well as demonstrating the possibility of different DDRs arising from the same model, we also show the utility of determining the underlying mechanism of coexistence. The mechanism that drives coexistence in our model can explain why frequency DDRs shift from peaked to U-shaped as intensity is increased. In this model, competitive coexistence is not possible in a constant environment, unless intraspecific competition is stronger than interspecific competition (26). Because of this dependence on environmental variation, the mechanism of coexistence is classified as a variation-dependent mechanism. Following the methods of Chesson (20), we partition species’ growth rates into contributions from fitness differences in a constant environment and the variation-dependent mechanism known as relative nonlinearity of competition. Briefly, this mechanism describes how fluctuation in competition (due to disturbance in our model) can promote coexistence by increasing the growth rate of a competitive inferior (relative to a constant environment) while decreasing the growth rate of the competitive dominant.

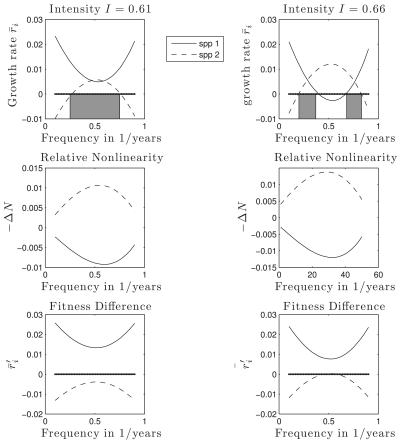
Fig. 3 shows a graphical representation of the mechanistic partitioning of growth rates for different levels of disturbance intensity. The Bottom row shows that the competitive dominant always excludes the inferior in a constant environment. However, when disturbance is present in the system, contributions to the growth rate from relative nonlinearity (ΔN) can result in positive growth rates for both species. Note that in this model, the magnitude of ΔN is proportional to the variance of the resident population at its stationary distribution. Thus, the strongest effects of relative nonlinearity are found at intermediate frequencies of disturbance, which generate the most variation in resident density. When intensity is increased, this also increases the magnitude of relative nonlinearity, which acts to suppress the competitive dominant. This can result in the competitive “inferior” excluding the dominant at intermediate frequencies, leading to the transition from peaked to U-shaped DDRs. The DDRs are indicated by the shaded rectangles in Fig. 3. At lower intensity (Left panels), higher diversity (coexistence) occurs at intermediate frequency, which generates a peaked DDR. At higher intensity (Right panels), intermediate frequency results in competitive exclusion, and extremal frequencies lead to coexistence.

Fig. 3.

Long-term low-density growth rates (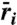) as sum of relative nonlinearity (ΔN) and fluctuation-independent term (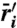). (Left) Mechanisms for a fixed intensity I = 0.61, corresponding to Fig. 1B line A. Coexistence occurs where 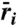is positive for both species, indicated by shaded regions. At intermediate frequencies, relative nonlinearity ΔN has the largest magnitude. (Right) At higher intensity (I = 0.66, corresponding to Fig. 1B line B), relative nonlinearity increases in magnitude, which disadvantages the competitive dominant at intermediate frequencies. Note the coexistence region (shaded rectangles) is split into disconnected components, and represents a U-shaped DDR. Life-history parameters for (dominant, inferior) species: seed yield Y = (0.9,1.1), seedbank survival s = (0.4,0.6), germination rate G = (0.6,0.4), competition α = (1.1,0.9).

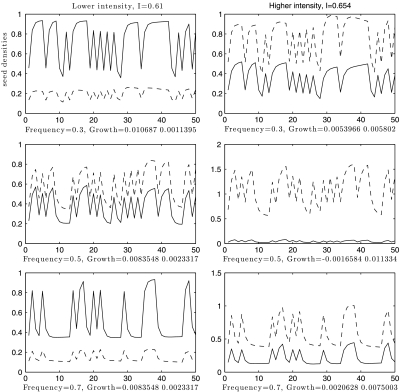
Representative population densities corresponding to the regimes shown in Fig. 3 are plotted in Fig. 4. These illustrate how the disturbance regime can also change relative population densities. Under lower intensity, the competitive superior attains higher mean density for low and high frequency, but has its density reduced at intermediate frequency. At higher intensity, relative nonlinearity further suppresses the superior’s growth rates, leading to lower density at low and high frequency, and extinction at intermediate frequency.

Fig. 4.

Density plots for a range of frequency and intensity parameters (F,I). (Left) (corresponding to line A in Fig. 1B) Coexistence occurs at all three frequencies. Note that species 2 has higher mean density at extremal frequencies. (Right) (corresponding to line B in Fig. 1B) Species 1 is forced to extinction (slowly) at intermediate frequencies, because the stronger negative effect of relative nonlinearity forces a negative growth rate (), as shown in Top Right of Fig. 3. Life-history parameters for (dominant, inferior) species: seed yield Y = (0.9,1.1), seedbank survival s = (0.4,0.6), germination rate G = (0.6,0.4), competition α = (1.1,0.9).

Discussion

Disturbance is inherently a multidimensional and multifaceted phenomenon, and we have demonstrated how considering multiple aspects of disturbance can potentially reconcile apparently contradictory results on the effects of disturbance in natural communities summarized by Mackey and Currie (10). Though we have used a two-species model to illustrate these concepts clearly, it is known that relative nonlinearity due to disturbance can support multispecies coexistence (15). Moreover, additional or alternate mechanisms of coexistence such as the storage effect can operate in similar models (15, 20, 24). Thus, though the specific quantitative results shown here are not expected to apply generally to models with multiple species and mechanisms, we do generally expect that the shapes of DDRs will depend strongly on which aspect is used to construct the DDR, as well as the magnitude of other aspects of disturbance.

A better understanding of how different aspects of disturbance affect community diversity will be helpful in assessing the ecological effects of climate change. In particular, fire, drought, and hurricane regimes are predicted to change in their timing, frequency, and intensity in the coming decades (27, 28), and our framework for quantifying mechanisms of coexistence in terms of specific aspects of disturbance will help researchers to determine how communities will respond to changing climate. Additionally, disturbance is implicated as an important factor in species invasion (29), and our methods can be adapted to specifically investigate how different aspects of disturbance affect invasion success.

In principle, our theoretical findings can be investigated empirically; for example, using techniques such as those described by Violle et al. (16) or Angert et al. (30). In particular, the experimental method in ref. 16 has several advantages, including low space requirements and fast generation times of species. Though Violle et al. (16) found only decreasing DDRs in their experiment, the present work allows us to predict that other patterns could be found if frequency were to be independently manipulated in their design.

Our results can also inform general practice for disturbance research. In simplest terms, we have shown that DDRs found in nature depend very strongly upon how one constructs them. Regardless of the specific focus of research, as many aspects as possible should be measured and presented. This can help resolve findings that seem contradictory: If two researchers sampled disturbance gradients analogous to arrows A and B in Fig. 2B, they would get different resulting DDRs. These differences are due to the fact that different combinations of frequency and intensity can yield the same rate, but a reader would be unable to discern the differences in the disturbance gradients unless frequency and intensity were individually reported.

We have given an example of how multiple aspects of disturbance can act and interact to determine competitive outcomes. However, the quantitative information contained in DDRs will also depend on life-history traits of community members. Though beyond the scope of this work, analysis of how life-history strategies can effect DDRs will be a fruitful area of future research.

Though disturbance regimes can have many effects on community diversity, these effects can only be understood by studying the different aspects of disturbance. Our framework can describe how a single system can generate both the peaked DDR patterns predicted by the IDH, as well as the many other possible shapes that have been documented in natural systems (10). With appropriate extensions, our concepts and methods can potentially be applied to a wide variety of ecological communities, and can be used to inform experimental design for the investigation of complex diversity–disturbance responses.

Materials and Methods

Plant Dynamics and Life History.

To investigate interactions between frequency and intensity, we employ an annual plant model that incorporates the reciprocal yield law for reduction of seed yield due to competition (15, 26).

Our model is a system of stochastic finite-difference equations, based upon similar models used by refs. 15 and 26. Let X_jt be equal to the number of seeds of species j at time t. We specify the model via the finite rate of increase λ. The finite rate of increase is the multiplicative growth rate of a species, that is, X_j,t+1 = λ_jtX_jt. We define λ in terms of the life-history parameters: germination G, seedbank survival s, and seed yield Y:

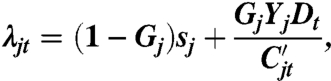[1]

The disturbance process D_t represents the decrease of seed yield due to disturbance, with details explained below. Competition 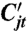is defined by

[2]

which is the total number of seeds that germinate in a given year, weighted by the competitive effect α_jk. Thus, an individual plant’s potential yield Y is reduced by the reciprocal of total density of competitors 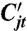. More detail on the behavior of the model and mechanism of coexistence is given in SI Appendix.

Disturbance Model.

Disturbance enters into the model via the term D_t, which represents the modification of yield by disturbance. We consider a two-parameter disturbance regime, controlled by frequency F and intensity I. Although there are several ways of measuring F and I, we consider both as proportions: F indicates the proportion of years in which a disturbance occurs, and I indicates what proportion of seed yield is destroyed by disturbance. In this manner, both F and I are contained in the unit interval, which removes any possible ambiguity resulting from different measurement scales.

Occurrence of disturbance is an independent, identically distributed Bernoulli process with probability of success (disturbance) equal to F. When disturbance occurs in a given year T, we set D_T = (1 - I) so that yield is reduced by I percent. In nondisturbed years K, there is no effect from disturbance, and we set D_K = 1.

The term “disturbance rate” is often used in studies of disturbance, but it is not always well-defined. One definition of the rate of disturbance is the total area affected by disturbance per year; i.e., extent times frequency (31). Following ref. 31, we define the rate of disturbance as the proportion of seed yield destroyed per year. In this manner, very different disturbance regimes can be described by the same rate.