History Can Matter: Non-Markovian Behavior of Ancestral Lineages

Abstract

Although most of the important evolutionary events in the history of biology can only be studied via interspecific comparisons, it is challenging to apply the rich body of population genetic theory to the study of interspecific genetic variation. Probabilistic modeling of the substitution process would ideally be derived from first principles of population genetics, allowing a quantitative connection to be made between the parameters describing mutation, selection, drift, and the patterns of interspecific variation. There has been progress in reconciling population genetics and interspecific evolution for the case where mutation rates are sufficiently low, but when mutation rates are higher, reconciliation has been hampered due to complications from how the loss or fixation of new mutations can be influenced by linked nonneutral polymorphisms (i.e., the Hill–Robertson effect). To investigate the generation of interspecific genetic variation when concurrent fitness-affecting polymorphisms are common and the Hill–Robertson effect is thereby potentially strong, we used the Wright–Fisher model of population genetics to simulate very many generations of mutation, natural selection, and genetic drift. This was done so that the chronological history of advantageous, deleterious, and neutral substitutions could be traced over time along the ancestral lineage. Our simulations show that the process by which a nonrecombining sequence changes over time can markedly deviate from the Markov assumption that is ubiquitous in molecular phylogenetics. In particular, we find tendencies for advantageous substitutions to be followed by deleterious ones and for deleterious substitutions to be followed by advantageous ones. Such non-Markovian patterns reflect the fact that the fate of the ancestral lineage depends not only on its current allelic state but also on gene copies not belonging to the ancestral lineage. Although our simulations describe nonrecombining sequences, we conclude by discussing how non-Markovian behavior of the ancestral lineage is plausible even when recombination rates are not low. As a result, we believe that increased attention needs to be devoted to the robustness of evolutionary inference procedures that rely upon the Markov assumption.

Statistician George Box famously wrote “all models are wrong but some models are useful” (e.g., Box and Draper 2007, p. 414), which has become a common mantra for scientists who advocate the elegance of simpler models. But one must also remember biochemist and author Isaac Asimov (1989), who wrote “if you think that thinking the earth is spherical is just as wrong as thinking the earth is flat, then your view is wronger than both of them put together.” So although simple models may be easier to use, they run the risk of being less accurate. Thus, it is imperative to identify possible limitations of existing models and explore alternatives that may be more complex but offer increased accuracy.

Here, we explore some properties that should be possessed by phylogenetic models of sequence change if they are to be reconciled with the population-genetic origin of interspecific sequence variation. Unfortunately, a population-genetic basis for the elaborate probabilistic models of phylogenetics is often absent or unclear. This disconnect hampers population genetics as well as phylogenetics because population genetics seeks to understand how mutation, natural selection, and genetic drift have interacted during evolutionary history, and interspecific comparisons are the only way to study all but the most recent evolutionary history. It is undeniably more difficult to make accurate population-genetic inferences from interspecific data than from intraspecific data. However, it is also undeniably important to reconcile interspecific data and phylogenetics with population-genetic theory.

Substantial progress has been made for the case where all genetic variation is neutral so that the neutral coalescent process of population genetics can be employed to disentangle gene trees and species trees (Takahata 1989; Rosenberg 2002; Yang 2002; Rannala and Yang 2003; Hobolth et al. 2007; Dutheil et al. 2009; Liu et al. 2009; see also Ané et al. 2007). All this work relies on the assumption of essentially neutral mutation to conveniently uncouple the branching process from the mutation/substitution process. Accordingly, the main focus of the aforementioned work is the consequences of incomplete lineage sorting, for example, the potential discrepancy between gene and species trees and between coalescence times and species divergence dates.

Extending these ideas to account for natural selection appears to be extremely complex, as selection introduces a nontrivial coupling between the coalescence process and the substitution process. The ancestral selection graph (Krone and Neuhauser 1997, Wakeley 2008) and its extension further into the past, the ancestral lineage (Fearnhead 2002, Baake and Bialowons 2008), appear to be the theoretically most satisfying approaches. However, this direction poses computational challenges because the complexity of ancestral selection graphs grows with the strength of natural selection. To lessen computational demands, much of the work on ancestral selection graphs has relied upon the biologically implausible assumption that a new mutant allele is independent of the type of allele from which it was derived.

Our interest here is to explore the consequences of natural selection on the substitution process while avoiding the assumption of parent-independent mutation. We also ignore the potential additional issue of incomplete lineage sorting. Our focus is therefore most relevant to situations where species are not closely related and where there is only one sequence sampled per locus per species; such situations are probably not that uncommon in phylogenetic analyses. In this context, we would like to better understand how the observed substitution process can be understood in terms of the underlying population genetic mechanisms, for example, in terms of mutation, selection, and drift.

In this direction, a further limiting case can be derived. With a sufficiently low mutation rate, the possibility of interactions between simultaneous genetic polymorphisms is negligible, so that each new mutation appearing in the population will either get lost or fixed before the next one occurs. In this context, the substitution rate is simply equal to the product of the mutation rate and the fixation probability. Given a fitness function and a mutation model, it is then possible to derive a substitution process that will be Markovian (Halpern and Bruno 1998). When fitted with empirical (interspecific) data, such models allow one to estimate mutation parameters as well as the product of effective population size and relative fitness difference between sequences. Later studies followed similar approaches for interpreting phylogenetic parameters in terms of population-genetic parameters (Nielsen and Yang 2003, Berg et al. 2004, Mustonen and Lässig 2005, Sella and Hirsh 2005, Thorne et al. 2007, Choi et al. 2008, Yang and Nielsen 2008, Rodrigue et al. 2010).

One shortcoming of the Halpern–Bruno strategy is that it requires a population to be mutation limited such that the new mutant allele is either fixed or lost prior to the occurrence of additional mutations that affect fitness. This low mutation rate condition is important for the fixation probability formula of Kimura (1962) or the modification suggested by Sella and Hirsh (2005) to be applicable, as these fixation probabilities assume only two alleles (ancestral and mutant) in the population. The Kimura and Sella–Hirsh approximations thus ignore the possibility of interference between multiple fitness-affecting polymorphisms. Another important parameter here is the recombination rate, which determines the typical number of loci that are linked during a fixation event. Due to the possibility of interference between linked nonneutral polymorphisms, the Kimura and Sella–Hirsh fixation probability approximations are likely to break down under low recombination, high per locus mutation, or both. The way that linkage disequilibrium dissipates the effectiveness of natural selection is known as the Hill–Robertson effect (Hill and Robertson 1966, Felsenstein 1974, Li and Tanimura 1987, Comeron et al. 2008). Although Hill–Robertson complexities can be neglected when mutation rates are sufficiently low, it is unclear how low the mutation rate should be in order for the fixation approximations to be valid and it is unclear how often mutation rates in real biological systems are in the valid range. A variety of previous studies have already investigated how the Hill–Robertson effect influences intraspecific polymorphism. Of particular relevance is the work of McVean and Charlesworth (2000), who demonstrated both that genotypes become less adapted due to the Hill–Robertson effect and that the impact of the Hill–Robertson effect is not solely attributable to a reduction in effective population size (see also Comeron and Kreitman 2002).

The consequences of interference between fitness-affecting polymorphisms on interspecific genetic variation remain undercharacterized. Our aim is to make progress in this direction. Due to the absence of a general analytical theory for the influences on interspecific genetic variation of mutation, natural selection, and genetic drift, we elected to do simulations. One goal was to reveal features that should be incorporated into the phylogenetic models for the substitution process. Another was to contrast low mutation analytical results about interspecific genetic variation with simulation results for higher mutation rates.

We were particularly motivated to evaluate the assumption that the substitution process is Markovian with respect to time. This assumption pervades the substitution models that are employed in phylogenetics. Halpern and Bruno (1998) examined one scenario where the Markov property is reasonable but, given its ubiquity in phylogenetics, we think a closer examination is warranted.

SIMULATIONS

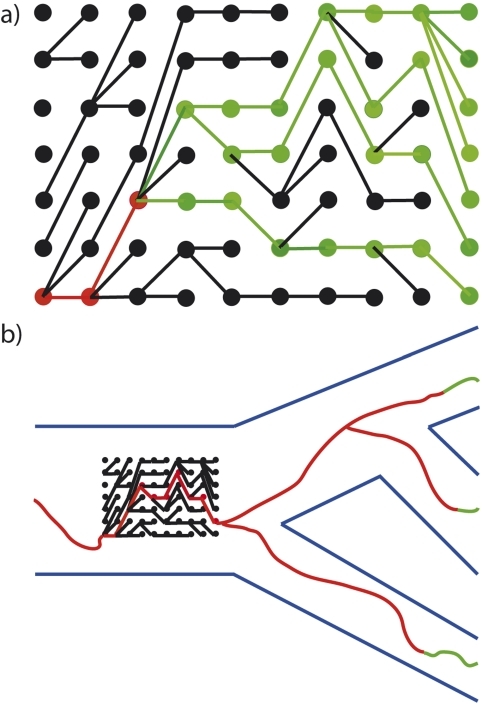
We simulated the ancestral lineage, which we define as the historical series of fixed sequences in a population. To describe the ancestral lineage, it is perhaps easiest to think about moving backward through time (i.e., from present to past). For simplicity, we consider a particular gene and ignore recombination as well as insertion and deletion. In the present, a haploid species has N copies of the gene. If we trace the ancestry of these N copies backward in time, they will eventually have a most recent common ancestor. We can then take this most recent common ancestor's allele and follow it back even further in time. The evolutionary lineage that results is referred to as the ancestral lineage. For each generation, the gene copy that is in the ancestral lineage is the one from which all gene copies starting at some future generation will be descended (see Fig. 1). This means that every gene copy in the ancestral lineage is eventually fixed. Sequence changes in the ancestral lineage are therefore exclusively fixed.

FIGURE 1.

Representations of ancestral lineages. a) An ancestral lineage. A haploid population of constant size N = 7 is represented. Each column corresponds to a specific generation. The most recent generation is the rightmost column. Each circle represents a specific gene copy in a specific generation. Line segments connect gene copies and their parents. Red segments connect the gene copies that are in the ancestral lineage. Black segments are not in the ancestral lineage because they relate gene copies that eventually have no descendants. Green segments may or may not be in the ancestral lineage, depending on what happens to their descendants in future generations. b) Ancestral lineages relating three species. The phylogeny relating three species is depicted in blue and the ancestral lineage of (a) predates the most recent common ancestor of the three species. One gene copy is sampled from each species and the histories of these three sampled copies are colored as above according to ancestral lineage membership.

By fixation, we mean that all gene copies in some future generation will be descended from that gene copy. We do not imply that all gene copies in some future generation will necessarily be identical in sequence to the allele of the ancestral lineage. Our definition of ancestral lineage is similar to the “common ancestor process” of Fearnhead (2002) and Baake and Bialowons (2008), except that our process excludes the lineage from a sampled allele to the most recent common ancestor of the population. In practice, this means that the final generations of each of our simulations are discarded.

When we compare sequences from species that are not closely related, we expect that the evolutionary history separating them consists almost exclusively of events that occurred on ancestral lineages. Study of the ancestral lineage is clearly in the realm of phylogenetics. Ideally, it should even be at the core of its underlying conceptual framework—the substitution process along the lineages of a phylogenetic tree being nothing else than a branched ancestral lineage. Yet only now, with some of the most innovative recent work in population genetics (e.g., Fearnhead 2002, Baake and Bialowons 2008) are researchers beginning to investigate how population genetic parameters influence the ancestral lineage. Unfortunately, much of this impressive and quickly developing population-genetic theory rests on the assumption that the result of a mutation does not depend on the allele that is mutated. This parent-independent mutation assumption is usually not well advised, in particular, when following the history of DNA sequences rather than individual DNA sites.

We considered simulating via the ancestral selection graph technique (Krone and Neuhauser 1997, Baake and Bialowons 2008, Wakeley 2008). However, we chose less sophisticated simulations that are easier to implement. Specifically, we performed brute-force simulation of the Wright–Fisher model with mutation and selection for very many generations. From our simulations, we could determine which allele in each generation is in the ancestral lineage. This permits investigation of how the ancestral lineage changes over time.

Our Wright–Fisher simulations employ discrete generations and describe a haploid population with N individuals. Each individual has a nonrecombining gene sequence with L positions. At each sequence position, one of the four possible nucleotide types is optimal. The remaining three types are equally suboptimal. All sites are equally likely to experience mutations, and the mutation rate per site per generation will be denoted as μ. If a mutation occurs at a site, the nucleotide type is equally likely to change to any of the three others. The model therefore permits advantageous mutations (a mutation from suboptimal to optimal type), deleterious mutations (a change from the optimal type to one of the three suboptimal ones), and selectively neutral mutations (a change from a suboptimal type to another). With our mutation process, the possibility of multiple simultaneous substitutions affecting the ancestral lineage allele in some generation is negligible. To avoid such very rare but complicating cases, mutant sequences in our simulations can only differ by one site from their parents.

Our multiplicative fitness scheme sets the relative fitness of a sequence to w_k = (1 − s)^k, where k is the number of deleterious sites. The selection coefficient, s, is kept constant throughout the simulation. By performing the Wright–Fisher simulations for a very large number of generations and by tracking the parent–offspring relationships in successive generations, we can identify the ancestral lineage and examine how it changes over time. By ignoring a large number of generations that constitute the beginning of the simulation, we can lessen sensitivity to initial simulation conditions. We also discard the generations at the very end of the simulation for which the ancestral lineage is undetermined. For example, we would not know which gene copy in the final generation of the Wright–Fisher simulation would be in the ancestral lineage because the ancestral lineage in a generation is determined by what happens in future generations.

Our primary goal with these simulations was to identify patterns in ancestral lineage evolution when there is a high probability of multiple nonneutral polymorphisms in a population at the same time. Accordingly, we chose parameter values—a high per sequence mutation rate, long sequences not subject to recombination, and a moderate selection coefficient—so as to obtain and investigate such phenomena. These parameter values in themselves are not meant to precisely describe any actual genetic locus, although they bear some qualitative resemblance to animal mitochondrial genomes. In addition to animal mitochondria, our simulations have potential relevance to taxa that reproduce asexually. Other situations for which our simulations seem relevant include the fourth chromosome of Drosophila melanogaster and nonrecombining sex chromosomes.

We focused on simulations using N = 50,000, L = 10,000, s = 10 ^{− 4}, and μ = 10 ^{− 8}. We will refer to this set of parameter values as our “core” set. These core values were not selected arbitrarily nor were they the result of an extensive search. Instead, we did preliminary simulations with a few different sets of parameter values that seem biologically plausible and that we anticipated might lead to numerous concurrent nonneutral polymorphisms. We then did substantially more simulations with the parameters listed above because of the interesting behavior of the ancestral lineage that they generated. These parameters (θ = 2NLμ = 10 and σ = 2Ns = 10) are consistent with a region identified by Wakeley (2008) that produces complex ancestral selection graphs because nonneutral polymorphisms are maintained in the population. The choice of μ = 10 ^{− 8} was motivated by recent estimates that include 1.3×10 ^{− 8} (Lynch 2010) and 1.1×10 ^{− 8} (Roach et al. 2010) for humans, 0.7×10 ^{− 8} for Arabidopsis thaliana (Ossowski et al. 2010), and 6.2×10 ^{− 8} for D. melanogaster (Haag-Liautard et al. 2008).

For the core set of parameter values and also for other sets explored below, we did a series of pilot simulations prior to the ones summarized here. For each parameter set, the pilot simulations were used to obtain a preliminary approximation of the stationary distribution for the number of deleterious sites in the ancestral lineage. We sampled from the approximate stationary distribution and then had the initial state of the simulations be a population that was monomorphic for the sampled number of deleterious sites. For the core parameter set, we ran 10 independent simulations of 5 billion generations each. We performed multiple runs because the ancestral lineage status in different generations within a run are not independent observations. The variability among runs sheds light on how accurately our simulations describes ancestral lineage behavior. To lessen the dependence on the initial simulation conditions, we paralleled the conventional treatment of Markov chain Monte Carlo output by discarding the earliest of the simulated generations from each run. By applying a variety of diagnostic procedures, we concluded that a “burn-in” of 500 million generations (i.e., 10%) was sufficient to neglect dependence of the latter 4.5 billion generations on the initial simulation conditions. The average number of generations at the end of a simulation run for which the ancestral lineage could not be determined was less than 50,000. As a result, the 10 simulation runs for the core parameter set yielded a total of almost 45 billion generations of ancestral lineage.

Simulation data associated with study can be found at http://scit.us/∼reed/noindex/anclin-data.tar.bz2. Code for producing and interpreting the simulation output can be checked out from a subversion repository at svn://scit.us/klineage/current/.

RESULTS

Failure of Low Mutation Approximation

When mutation rates are sufficiently low, the population-genetic scheme studied here is a special case of one used by Sella (2009). At stationarity, the low mutation approximation of Sella shows that the number of deleterious sites per sequence in the ancestral lineage has a binomial distribution

(1)

where k is the number of deleterious sites and q = 3(1 − s)^{2(N − 1)}. The mutation rate, μ, does not appear in Equation 1 because our mutation process makes all point mutations equally likely and because Equation 1 is derived for the case where each mutation is fixed or lost before the next appears. When mutation rates are sufficiently low for this to almost always be the case, populations will be monomorphic during most of their history. This means that the fixation probabilities of new mutations, and therefore the stationary distribution of the ancestral lineage, will not be functions of μ.

Applying our core parameter values of N = 50,000 and L = 10,000 and s = 10 ^{− 4} to the binomial distribution of Equation 1, the expected value and standard deviation of k are, respectively, about 1.36 and 1.17 deleterious sites. In contrast, we find from our simulations that setting μ to its core value of 10 ^{− 8} yields a stationary distribution for the ancestral lineage with a mean that is more than two orders of magnitude higher than predicted by Equation 1. The simulations suggest that the stationary distribution of the ancestral lineage has a mean of about 449.6 deleterious sites and a standard deviation of about 18.6 deleterious sites. Likewise, the most probable state according to the low mutation approximation is one deleterious site per sequence, whereas the mode for our simulations was 455 deleterious sites. If we separately estimate the mean number of deleterious sites per sequence for each of the 10 runs, we find that our estimates have a sample standard deviation of about 3.38 deleterious sites. By adding and subtracting 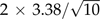, a crude 95% confidence interval of (447.4,451.8) is obtained for the mean of the stationary distribution.

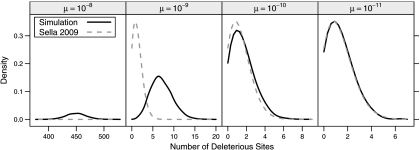
We believe that the disparity between the simulations and Equation 1 can be attributed to μ = 10 ^{− 8} being higher than can accurately be handled by the low mutation assumption. Our simulations with values of μ that are lower than 10 ^{− 8} yield results that are closer to Equation 1. Figure 2 displays simulations results when μ is 10 ^{− 9}, 10 ^{− 10}, and 10 ^{− 11}, as well as 10 ^{− 8}. Simulations for these lower values of μ were done in the same fashion as for μ = 10 ^{− 8} except that lengths of simulation runs and burn-in periods were inversely proportional to the value of μ. For example, each of the 10 simulations for μ = 10 ^{− 11} continued for 5 trillion generations rather than for the 5 billion generations of μ = 10 ^{− 8}. Although values of μ that are 10 ^{− 9} and 10 ^{− 10} gave results somewhat closer to the low mutation approximation, Equation 1 is not accurate for these mutation rates either. Our simulations had a mean of about 7.06 deleterious sites and a standard deviation of about 2.65 with μ = 10 ^{− 9} and a mean of 1.63 and a standard deviation of 1.31 with μ = 10 ^{− 10}. For μ = 10 ^{− 11}, the mean and standard deviation of the number of deleterious sites in the ancestral lineage were about 1.39 and 1.15. These are not too far from the values of 1.36 and 1.17 that are predicted by Equation 1. The approximate 95% confidence intervals for the means of the stationary distributions are (6.85,7.27) for μ = 10 ^{− 9}, (1.51,1.75) for μ = 10 ^{− 10}, and (1.34,1.44) for μ = 10 ^{− 11}.

FIGURE 2.

Stationary distributions of simulated ancestral lineages. Each panel contains the stationary distribution of simulated ancestral lineages (solid lines) under a specific mutation rate. The dashed lines are low mutation expectations derived in Sella (2009). To emphasize differences, discrete distributions are plotted as continuous lines.

The low mutation approximation also leads to an underestimation of the rate of substitution. From Equation 1, the stationary probability that a site in the ancestral lineage is deleterious is π₀ = q/(1 + q) and that a site is advantageous is π₁ = 1/(1 + q). The total rate of ancestral lineage change, Q, will depend on the values of π₀ and π₁ as well as on the neutral substitution rate Q₀₀, the advantageous rate Q₀₁, and the deleterious rate Q₁₀. Thus, we have

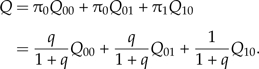Because substitution rates are the products of mutation rates and fixation probabilities,

(2)

where P₀₁ is the fixation probability of a new advantageous mutations and P₁₀ is the fixation probability of a new deleterious mutation. The fixation probability approximation of Sella and Hirsh (2005) gives 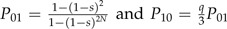. Substituting these into Equation 2 and simplifying, we get

(3)

For μ = 10 ^{− 8}, Equation 3 gives a rate of about 9.98×10 ^{− 8} changes per ancestral lineage sequence per generation. In contrast, our simulations with μ = 10 ^{− 8} yield a rate estimate of 1.84×10 ^{− 5}, which is more than 2 orders of magnitude higher than the predicted rate. Likewise, the low mutation approximation is too low by a factor of about 5 for μ = 10 ^{− 9} (4.75×10 ^{− 8} vs. 9.98×10 ^{− 9}) and about 1.2 for μ = 10 ^{− 10} (1.21×10 ^{− 9} vs. 9.98×10 ^{− 10}). As in the case of the mean number of deleterious mutations at stationarity, the approximation and the simulated values are very close for μ = 10 ^{− 11}(9.95×10 ^{− 11} vs. 9.98×10 ^{− 11}).

One can often equate the behavior of a population of some census size in terms of the behavior of an idealized population with some different effective size. In particular, the Hill–Robertson effect of interference due to linkage, which is at the core of the present observation, is usually accounted for by reducing the effective size (but see McVean and Charlesworth 2000, Comeron and Kreitman 2002). One possibility is that our simulation results with μ = 10 ^{− 8} and census population size N = 50,000 would be consistent with the low mutation approximation of Equation 1 for some other value of N (i.e., for some effective population size). Because Equation 1 is a binomial distribution, we compared the distribution that we simulated for μ = 10 ^{− 8} to a binomial with the same mean. A binomial distribution with L = 10,000 and a mean of 449.6 would correspond according to Equation 1 to an effective population size of about 20,773. However, the binomial distribution should then have a variance of about 429.4. In contrast, the variance of our simulated distribution was about 344.1 with an approximate 95% confidence interval of (311.6,376.6). The difference in variances implies that it is not sufficient to attribute the disparity between the low mutation approximation and our μ = 10 ^{− 8} simulations solely to a difference between census and effective population size, as the binomial distribution and thus the independence of sites also no longer hold. Interestingly, the lower variance of the simulation is reminiscent of a sequence with fewer sites than those simulated. Table 1 includes effective population size estimates for the mutation rates lower than 10 ^{− 8}. For these lower mutation rates, disparity between simulation results and Equation 1 could be explained relatively well simply by differences between census and effective population sizes.

TABLE 1.

Effective population size estimates from simulation data

μ	Deleterious sitesa	Ne(Δ)b	Qc	Ne(Q)d
10−8	449.6	20, 772	1.84 × 10−5	19, 731
10−9	7.06	41, 768	4.75 × 10−8	41, 343
10−10	1.63	49, 100	1.21 × 10−9	48, 946
10−11	1.39	49, 896	9.95 × 10−11	50, 019

^aThe mean number of deleterious sites per ancestral lineage sequence estimated from the simulations.

^bEffective population size estimates obtained by equating the mean of the binomial distribution in Equation 1 to the mean number of deleterious sites per ancestral lineage sequence inferred from the simulations.

^cEstimated rates of ancestral lineage change per sequence per generation.

^dEffective population size estimates obtained by using Equation 3 and the values of Q estimated from the simulations.

Another way to obtain effective population size estimates relies upon equating the rate of ancestral lineage change per generation as estimated from the simulations to the rate expected from the low mutation assumption. The true values of μ, L, and s along with value of Q that is inferred from simulations can be employed to numerically solve for the value of N that satisfies Equation 3. Effective population size estimates derived in this way are not too different from those obtained by equating the mean of the binomial distribution of Equation 1 to the means inferred from simulations (Table 1).

Failure of Markov Assumption

The simulations produced intriguing results that have relevance to phylogenetics and to other tasks of evolutionary inference from interspecific sequence data. Virtually all probabilistic models for molecular evolution assume a Markovian substitution process: the rate at which a sequence changes depends only on the current sequence and not on the specific evolutionary path that led to it. When mutation rates are sufficiently low, fixation of a new sequence variant v_{t + 1} nearly always takes place in a population otherwise monomorphic for the sequence v_t. This implies that any memory about previous allelic states along the ancestral lineage (v_{t − 1},v_{t − 2},…) has then been lost and therefore that the Markov assumption holds. Our simulations can be used to explore how close to a Markov process is evolution of the ancestral lineage under higher mutation rates.

With a Markov process, the time from which a sequence changes until it changes again (waiting time) should have a geometric distribution if time is measured in discrete generations or an exponential distribution if time is treated as continuous. With the mutation and relative fitness scheme of our simulations, a Markov process would have the waiting time until the next ancestral lineage change be a function of the number of deleterious sites in the ancestral lineage. Because 455 deleterious sites was the most frequent ancestral lineage state visited by our simulations for μ = 10 ^{− 8}, we assessed the distribution of waiting times in state k = 455 deleterious sites. This situation occurred 18,083 times in our simulations; they started when the 455-creating mutations originated and stopped at the occurrence of the following substitution in the ancestral lineage, whether it was neutral, advantageous, or deleterious.

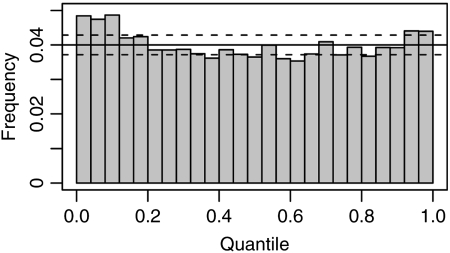
The mean of the 18,083 times was about 54,286.12 generations. We then compared our simulated distribution of times to a geometric distribution with mean set equal to the mean from the simulations. We find that the simulated distribution has a higher variance than the geometric distribution (Fig. 3) with a noticeable excess of short times and with a surplus of long times.

FIGURE 3.

A comparison between the simulated distribution of interevent times and a geometric distribution with the same mean. When μ = 10⁻⁸, our simulations had 18, 083 cases of entering and then exiting the ancestral lineage state of 455 deleterious sites. These interevent times were compared with a geometric distribution with an identical mean. Quantiles were determined to specify 25 bins that are equiprobable according to the geometric distribution. The histogram depicts the proportion of the 18, 083 simulated times that fall into each of these 25 bins. The solid line is the expected proportion in each bin according to the geometric distribution. The dashed lines indicate the 95% confidence interval for the proportion falling into a bin if the 18, 083 times had actually been sampled from the geometric distribution.

Motivated by this departure between the geometric distribution and our simulations, we reasoned that one strategy for modeling molecular evolution might be to describe the waiting times as a mixture of geometric distributions. Via the expectation maximization algorithm, we fitted the waiting times in Figure 3 to a mixture of geometric distributions. We found that a mixture of two geometric distributions provided a substantially better fit than a single distribution and that a mixture of three geometric distributions provided little improvement beyond the mixture of two geometric distributions. Our mixture of two geometrics had 94.2% of the probability associated with a geometric of mean 57,162 generations and the other 5.8% of the probability with a geometric of mean 7594 generations.

When investigating the time series of the ancestral lineage, we noticed the tendency for consecutive fitness-affecting substitutions to alternate sign (Table 2). For example, if the ancestral lineage has 455 deleterious sites in some generation, then it must have entered that state in a previous generation from either 454 or 456 deleterious sites. Likewise, if the ancestral lineage has 455 deleterious sites, it will exit that state in a future generation to either 454 or 456 deleterious sites. If the state of the ancestral lineage changes according to a Markov chain, then the state prior to 455 (i.e., 454 or 456) should be independent of the state following 455. The entries in Table 2 emphatically demonstrate that this is not the case for μ = 10 ^{− 8} (Fisher's exact test, P < 3.15×10 ^{− 65}).

TABLE 2.

Behavior of ancestral lineage when k = 455^a

	455→454	455→456
454→455	4346	3238
456→455	3235	4217

^aRows specify whether the ancestral lineage has 454 or 456 deleterious sites immediately prior to it having 455. Columns show whether the ancestral lineage had 454 or 456 deleterious sites immediately after having 455. Entries are the total number of times that each case was observed over 10 separate simulations.

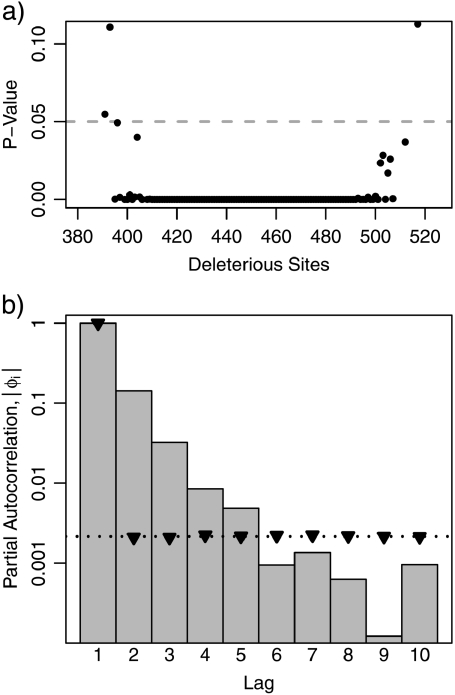
We concentrate upon the non-Markovian behavior for the ancestral lineage state of 455 deleterious sites simply because this state occurs more often in the simulated ancestral lineages than any other state. Other states also exhibit non-Markovian behavior. We repeated the Fisher's exact test for all other ancestral lineage states visited by the core parameter simulations. In Figure 4a, we plot the P values of these tests. Except for the infrequently observed states at the tails of the stationary distribution of the ancestral lineage, there is strong evidence throughout the distribution of nonindependence of consecutive fitness-affecting substitutions.

FIGURE 4.

Non-Markovian nature of the ancestral lineage. Results derive from simulations with core parameter values as described in the text. Neutral changes to the ancestral lineage are disregarded for the jump chain analyses presented here. a) The P values of Fisher's exact tests for independence between consecutive substitutions that enter and exit each ancestral lineage state are plotted on the y-axis. The ancestral lineage state is plotted on the x-axis. b) The absolute values of partial autocorrelations ϕ_i for i ∈ {1, …, 10} estimated from the jump chain of the ancestral lineage. The dotted line at 0.00216 shows one critical value for testing the null hypothesis that ϕ_i = 0 at significance level α = 0.05. The other critical value would be at – 0.00216. The triangles mark the 95^th percentile of ϕ_i estimates obtained from parametric bootstrapping with a first-order Markov model. (See text for details.)

Partial Autocorrelation in the Ancestral Lineage

Partial autocorrelations (Wei 1994) are an alternative summary of the dependence between successive nonneutral substitutions. Autocorrelation measures the correlation between samples in a time series separated by specific lag, whereas partial autocorrelation measures the correlation at specific lags that is not explained by autocorrelations at lower lags. We calculated the partial autocorrelation function of the jump chain of the μ = 10 ^{− 8} simulations for lags 1–10 (denoted here by φ₁–φ₁₀). The absolute values of the partial autocorrelation functions (|φ_i|) are plotted in Figure 4b on the log scale; note that φ₉ is originally negative.

For white-noise processes, the true value of φ_i is 0 for all lags. Furthermore, the approximate sampling distribution for estimates of φ_i has a simple form when data are generated by a white-noise process. Specifically, the sampling distribution is approximately normal with mean 0 and variance that is approximately the inverse of the sample size (Wei 1994). If our ancestral lineage data had actually been generated by a white-noise process, the standard deviation would be approximately 0.0011. White-noise processes therefore serve as useful null models for testing whether a given φ_i from a time series of interest is 0. For each φ_i estimate from our data, we calculated a P value for the null hypothesis that φ_i = 0. Even when correcting for multiple tests via the method of Holm (1979), lags 1–5 had significant nonzero partial autocorrelations at α = 0.05 (Figure 4b).

Beyond testing for significantly nonzero partial autocorrelation values, we also compared our sampled values against a best-fitting Markov model. We fit a first-order Markov model to the 825,973 jumps in our simulated jump chains and used parametric bootstrapping to generate 1000 series of equal length from this model. We calculated the φ_i estimates for each of these replicates. For each lag from 1 through 10, the 95th percentile of the absolute values of our φ_i estimates is plotted as a triangle in Figure 4b. Because the parametric bootstrap replicates were generated according to a Markov model of order 1, the triangle for lag 1 is well within the rejection region for testing the null hypothesis that φ₁ = 0 at a significance level of 0.05, whereas the triangles for the other lags are (as expected) very close to the critical values for the φ_i = 0 hypothesis test (Fig. 4b). In agreement with the white-noise tests, the φ_i estimates from the ancestral lineage jump chains for lags 2–5 are well within the rejection region established by parametric bootstrapping. This suggests that a fifth-order Markov model might be an effective statistical description of the simulated jump chains.

Correlation between Ancestral Excess and Evolutionary Rates

The higher order dependencies in the ancestral lineage that were demonstrated in the last section could stem from the dynamics of the ancestral lineage depending on how its fitness compares with the mean fitness of the rest of the population. However, because the rest of the population also stems from earlier ancestors along the ancestral lineage, the population has an allelic composition and therefore an average fitness that reflects prior events in the ancestral lineage. Taken together, this suggests that the behavior of the ancestral lineage is not solely a function of its current state.

To illustrate this phenomenon, we consider the number of deleterious sites in the ancestral lineage allele and subtract from this the average number of deleterious sites among all alleles in the population. We refer to this difference as the “ancestral excess.” In keeping with the conjecture by Donnelly and Kurtz (1999) that was confirmed for special cases by Slade (2000) and Fearnhead (2002), we expect ancestral excess to be negative because the allele that eventually gets fixed should tend to be comparatively fit.

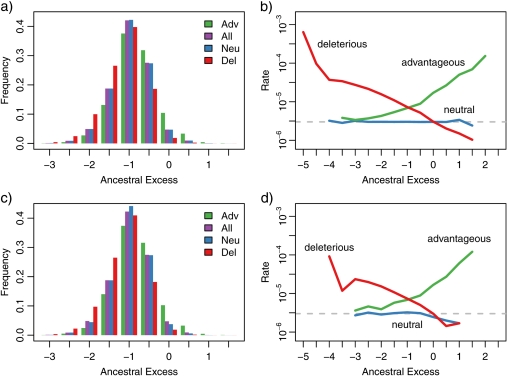
As expected, the allelic state of the ancestral lineage is nearly always more fit than the population average. The ancestral excess bin of − 1 is the one most often visited during our simulations. In Figure 5a, we depict the proportions of time that the ancestral lineage occupied each bin, and we compare these proportions to those for generations that immediately preceded neutral, advantageous, or deleterious bins. In Figure 5b, we show neutral, advantageous, and deleterious rates that are separately estimated for each bin. These rates are measured in terms of expected number of changes per sequence per generation. In keeping with intuition, we see that the neutral rate is independent of ancestral excess. In contrast, rates of deleterious substitutions are positively correlated with ancestral excess and rates of advantageous substitutions are negatively correlated with ancestral excess.

FIGURE 5.

Ancestral excess and substitution rates. For each generation, ancestral excess measures the difference between number of deleterious sites in the ancestral lineage allele and the population average. Negative values indicate that the ancestral lineage was more fit than the population average, and positive values indicate that it was less fit. For these plots, ancestral excess values are categorized according to bins of width 1/2. For example, the bin centered at – 1.5 represents generations in which the ancestral excess is between – 1.75 and – 1.25. a) Proportion of ancestral excess bin occupancy overall and for generations that immediately preceded neutral, advantageous, and deleterious changes. b) Neutral, advantageous, and deleterious substitution rates calculated for each ancestral excess bin. The dashed line shows the expected rate of neutral mutations per sequence per generation for the average ancestral lineage allele. This is obtained by multiplying the average number of deleterious sites in the ancestral lineage (449.6) by the mutation rate per site per generation (10⁻⁸) and by the proportion of mutations to a deleterious site that are expected to yield another deleterious nucleotide (2/3). (c) and (d) are similar to (a) and (b) but are limited to results for generations when there are 455 deleterious sites in the ancestral lineage.

The results in Figure 5a,b group all counts of deleterious sites together. Conceivably, the strong correlations between bin membership and nonneutral rates could be a by-product of other correlations. Specifically, this scenario would have the number of deleterious sites per sequence be correlated with bin membership and it would also have the number of deleterious sites per sequence be correlated with the advantageous and deleterious transition rates. To exclude this possibility, an analysis was done that does not group all counts of deleterious sites together. Figure 5c,d replicate Figure 5a,b but are exclusively based on generations when the ancestral lineage had 455 deleterious sites.

Comparison of Simple Statistical Models for Ancestral Lineage Change

Rodrigue (2007) has made the illuminating distinction between mechanistic and phenomenological models of sequence evolution (see also Rodrigue and Philippe 2010). The parameters of a mechanistic model are attached to clear biological interpretations. The meanings might pertain to the mapping of genotype to phenotype, the mapping of phenotype to fitness, mutation, or population structure. There is often a tension between models that provide good statistical fits to data and models with clear biological interpretations. When phenomenological models are constructed, the highest priority is statistical fit. Phenomenological models have diverse applications and have been very influential as a basis for phylogeny inference.

Although much of our interest in the ancestral lineage is motivated by the goal of studying evolution via inference with mechanistic models, we recognize that the phenomenological perspective also has value. Regarding the task of constructing a phenomenological model to describe change in ancestral lineages, we envision inference proceeding by Markov chain Monte Carlo sampling among ancestral histories that are consistent with observed data. To deal with the non-Markovian behavior of the ancestral lineages, we describe below what we term “tagged” models. Another approach builds upon the modeling idea of Tuffley and Steel (1998) by having rates depend on the value of a hidden state as well as on the number of deleterious sites per sequence. When the number of deleterious sites changes, the initial value of the hidden state would be determined by whether the change was advantageous or deleterious. Subsequent events would let only the hidden state change or would let both the hidden state and the number of deleterious sites change. We have not yet carefully assessed the performance of this Tuffley–Steel approach. Careful parameterization with the Tuffley–Steel idea could capture the pattern seen in Figure 3 so that the model has times between substitution events being a mixture of a distribution with short average waiting times and a distribution with long average waiting times.

We have studied tagged models in more detail. These models classify alleles in the ancestral lineage based on the previous history of the ancestral lineage. For instance, in a second-order tagged model, the same allele can be considered either “hot” or “cold” based on whether it originated through an advantageous or a deleterious mutation, and distinct transition probabilities can be calculated for the hot and cold variants. Additionally, tagging is straightforward to extend to higher orders; a fifth-order tagged model has only 16 different hot–cold patterns. A first-order tagged model is no different than a first-order Markov model, whereas a zeroth-order tagged model completely ignores the state of the ancestral lineage.

We estimated several tagged models from our simulated ancestral lineages and then calculated the likelihood of our ancestral lineage from the models. For the results presented here, neutral changes were ignored so that the kth-order tagged models only describe change in time of the number of deleterious sites per ancestral lineage sequence. Two variants of tagged models were considered. With one, the assumption is that for each possible tag, there is a rate per generation per site of deleterious states changing to advantageous ones and a rate of advantageous states changing to deleterious ones. This means two free parameters are estimated for each tag. The other variant has more parameters because the rates per site per generation for a tag are also allowed to be a function of the total number of deleterious positions per sequence. With this variant, there are two free parameters for each combination of tag and number of deleterious sites per sequence. We refer to this variant as heterogeneously tagged (HeT) models, whereas the other variant is referred to as homogeneously tagged (HoT) models. For the HeT models, a minimum and maximum number of deleterious sites per sequence are incorporated as additional parameters in order to lessen the total number of parameters to be inferred. We note that homogeneous and heterogeneous are employed to refer to whether the rates of change at individual sequence sites are or are not a function of the states at other sequence positions. Both HeT and HoT model variants can be classified as homogeneous Markov processes because the rates among states do not vary over time.

We fit models of each variant from our simulated ancestral lineages for the core parameter set (μ = 10 ^{− 8}) and also for the case where the core parameter set is altered by having μ = 10 ^{− 11}. We considered tags ranging from first order to fifth order for each of these mutation rates. The log likelihood of a simulated ancestral lineage is calculated from the stationary distribution and transition probabilities for both the HeT and the HoT models. For HeT, the transition probabilities and the joint stationary distribution of tags and number of deleterious sites (including its minimum and maximum values) are estimated directly from the simulated data. For HoT, the probabilities per generation of a deleterious site changing into an advantageous site and an advantageous changing into a deleterious site are estimated directly from the simulated data and are then used to calculate the joint stationary distribution and transition probabilities.

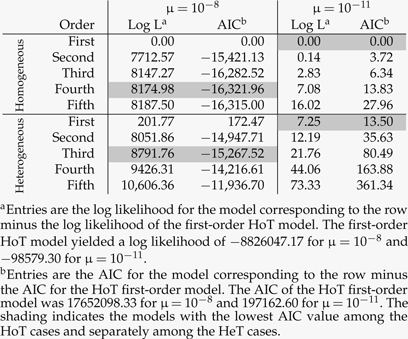
We separately compared Akaike information criterion (AIC) values for the HeT and HoT models. The AIC values are a function of the number of free parameters in a model (Akaike 1973). For the HeT models, the total number of free parameters depends on the range induced by the parameters specifying the minimum and maximum number of deleterious sites per sequence. The AIC scores can be employed to find the range for a specific HeT model order and can then be employed again to compare model orders.

For μ = 10 ^{− 8}, the AIC selects fourth order as the best HoT model among those considered and third order among HeT orders (Table 3). In contrast, first-order models are selected for both the HoT and HeT variants when μ = 10 ^{− 11}. We believe that these particular model selection results need to be interpreted very cautiously. Our main point is that the ancestral lineage is well approximated by a first-order Markov process when μ = 10 ^{− 11} but not when μ = 10 ^{− 8}. Phylogenetic techniques that incorporate higher order information via tags or other approaches may improve model fit and thereby benefit phylogeny inference, but we suggest that directly incorporating population genetics into interspecific evolutionary models may be a more promising research direction for the long term.

TABLE 3.

Model comparisons

DISCUSSION

The simulation results that we find most noteworthy are 1) The non-Markovian behavior of the ancestral lineage and especially the tendency for successive nonneutral substitutions to alternate between advantageous and disadvantageous; 2) The underestimation by low mutation approximations of the expected number of deleterious sites in the ancestral lineage; and 3) The strong correlation between ancestral excess and rates of nonneutral change. Although aspects of these three phenomena are previously described in the literature, we think that they are undercharacterized. We discuss their relevance below.

Non-Markovian Behavior of the Ancestral Lineage due to the Hill–Robertson Effect

One reason that change in the ancestral lineage may be non-Markovian is that fixation probabilities of new mutations depend on more than the fitnesses and frequencies of the new and mutated allele types. Fixation probabilities also depend on the fitnesses and frequencies of other alleles in the population. The history of the ancestral lineage provides some of this additional information upon which fixation probabilities depend. Theoretical population geneticists appreciate the lack of Markovian behavior of ancestral lineages. This has motivated some promising recent work (e.g., Fearnhead 2002, Taylor 2007, Baake and Bialowons 2008). However, we are unaware of previous attention to the tendency for fitness-affecting substitutions to alternate between advantageous and disadvantageous.

The non-Markovian behavior is potentially highly relevant to phylogenetics. The model-based phylogeny literature is huge, and the assumption that sequence change is Markovian with respect to time is ubiquitous within this literature. Although phylogenetic methods might turn out to be robust to violations of the Markov property, it will nevertheless be important to investigate in more detail how general are the deviations from Markovian behavior and what impact these deviations may have on the accuracy of phylogenetic reconstructions.

We suspect that non-Markovian behavior of the ancestral lineage might sometimes impact divergence time estimation. For Bayesian inference of divergence times from molecular sequence data and fossil evidence, it is important to have good estimates of the uncertainty associated with branch length estimates. As pointed out by Cutler (2000), underestimates of branch length uncertainty can lead to overestimates of the amount of evolutionary rate variation over time. If the amount of rate variation over time is overestimated, this could mean that the amount of rate autocorrelation over time is underestimated. This possibility could explain findings that rate autocorrelation over time is small (e.g., Drummond et al. 2006; but see Lepage et al. 2007).

The tendency for alternation between advantageous and deleterious changes can be intuitively explained. If one notes that the ancestral excess statistic is likely to be an indicator of recent nonneutral changes to the ancestral lineage, the same intuitive reasoning would explain the pattern in Figure 5 of strong correlations between ancestral excess and nonneutral rates but lack of correlation between ancestral excess and neutral rates. The explanation relies upon the fact that to belong to an ancestral lineage, an allele must eventually get fixed. Fixation of a deleterious mutation is more probable if the mutation changes an allele that happens to be particularly fit relative to the rest of the population. These comparatively fit alleles are likely to be the result of a recent advantageous mutation. This is because advantageous mutations that were introduced long ago and that were not lost are likely to have risen to a high frequency so that the average gene copy with the advantageous mutation might not be much more fit than the average gene in the population.

A similar explanation can be given if it is the deleterious mutation that happens first. If a deleterious mutation creates a new allele, the resulting allele will tend to have a fitness deficit relative to the rest of the population and will therefore tend to be eliminated from the population. However, membership of a new mutant in the ancestral lineage means conditioning upon survival of descendants of the deleterious mutant. Deleterious mutations that do persist will be enriched for those that occurred on an otherwise highly fit allele or those that were not eliminated prior to the occurrence of advantageous mutations on descendant sequences. Therefore, the deleterious and advantageous changes that get incorporated into the ancestral lineage are likely to be clustered in time with respect to each other—advantageous mutations followed by tolerable deleterious mutations and deleterious mutations followed by compensatory advantageous mutations.

This alternation between advantageous and deleterious mutations is associated with dependent change among sequence positions. For example, the alternating fitness pattern means that different codons may evolve in a dependent fashion even if they have independent effects on phenotype and if the amino acids they encode have no physical interaction. Instead, the dependence is induced by linkage and fitness. We see from our simulations that the tendency can be strong for changes to the ancestral lineage to alternate their fitness effects, but we do not know whether this tendency is strong for a wide range of biologically plausible population genetic scenarios.

Low Mutation Approximation and the Hill–Robertson Effect

The most interesting patterns in our simulations would all be lessened or eliminated with recombination. Most obviously, recombination would hinder the formation of linkage disequilibrium, and it is linkage disequilibrium that reduces the effectiveness of natural selection and causes the number of deleterious sites in our simulated ancestral lineages to greatly exceed what would be expected from the low mutation approximation.

We found that the stationary distribution of the ancestral lineage had a smaller variance of the number of deleterious sites than can be explained by simply adjusting population size in the low mutation approximation of Equation 1. This is consistent with previous findings that the Hill–Robertson effect does not simply make effective population sizes smaller than census population sizes (McVean and Charlesworth 2000). Comeron and Kreitman (2002) have done thorough simulation studies on the impact of the Hill–Robertson effect on intraspecific genetic variation. Although not nearly as thorough as the work by Comeron and Kreitman (2002), this study is somewhat complementary in that our focus can largely be summarized as the consequence of the Hill–Robertson effect on interspecific genetic variation.

Our overall impression is that two phenomena are responsible for the departure between our simulations and the low mutation approximation of Equation 1. For μ = 10 ^{− 9} and μ = 10 ^{− 10}, the reason that the census population size of 50,000 exceeds the estimates in Table 1 is likely to be mainly due to background selection (Charlesworth et al. 1993). Specifically, deleterious mutations may linger in a population for a long time while still being unlikely to fix. This means that the number of gene copies with a higher chance to be incorporated into the ancestral lineage might be substantially smaller than the census population size. For μ = 10 ^{− 8}, the behavior of the ancestral lineage cannot simply be explained by a difference between the census and effective population size. Instead, the Hill–Robertson effect needs to be invoked.

Low Mutation Approximation and Scaled Selection Coefficients

Building upon the Halpern–Bruno idea, a variety of studies have employed interspecific sequence data and the low mutation assumption to estimate the product of effective population size and the difference in relative fitnesses of the two sequences (Nielsen and Yang 2003, Mustonen and Lässig 2005, Thorne et al. 2007, Choi et al. 2008, Yang and Nielsen 2008). Following Nielsen and Yang (2003), we refer to this product as the scaled selection coefficient. We use the convention that deleterious mutations correspond to negative values for the scaled selection coefficients and advantageous mutations correspond to positive values. Selectively neutral mutations yield a scaled selection coefficient near zero.

We can consider all possible mutations that can alter a gene belonging to an ancestral lineage. The distribution of scaled selection coefficients that results from these mutations is of interest. Previous studies (e.g., Nielsen and Yang 2003, Thorne et al. 2007, Choi et al. 2008, Yang and Nielsen 2008) have inferred these distributions and investigated their nature except that the inferred distributions represented possible mutations to observed sequences rather than possible mutations to ancestral lineage sequences. The distinction between observed sequences and ancestral lineage sequences is important, but determination of the ancestral lineage status of a sequence is typically impractical. We assume that both observed and ancestral lineage sequences would yield qualitatively similar inferred distributions of scaled selection coefficients.

Although the details differ between the studies that have leveraged the Halpern–Bruno idea to estimate the distribution of scaled selection coefficients among possible changes to an observed sequence, a common thread that unites the inferred distributions is that all are biologically implausible. Specifically, the inferred probability distributions are missing lower tails that represent extremely deleterious mutations. These tails should be present for functionally important genes because some mutations to these genes should be highly deleterious or even lethal. The absence of highly deleterious scaled selection coefficients probably has multiple causes. One cause may stem from the inability to accurately predict phenotype from genotype because this results in an inability to accurately predict relative fitness from genotype.

Another explanation for the lack of highly deleterious scaled selection coefficients is inadequacy of the low mutation approximation. Our simulations with the core parameter set showed that the ancestral lineage had many more deleterious sites than would be predicted with the low mutation approximation. If the number of deleterious sites was used to estimate the scaled selection coefficient Ns, the low mutation approximation would produce underestimates of Ns. Representing the mean of the binomial distribution of Equation 1 by E[k] and then solving for Ns in terms of E[k], we get

(4)

after approximating q as 3e ^{− 2Ns}. By substituting the core parameter value L = 10,000 and replacing E[k] with the mean of 449.6 from our simulations, Equation 4 yields about 2.1 for Ns and this is about 40% of the true value of 5.

Underestimation of s or Ns produces inferred distributions of scaled selection coefficients that are too concentrated around zero. This underestimation could be partially responsible for why previously inferred distributions of scaled selection coefficients have lacked the lower tail that corresponds to extremely deleterious mutations. However, we still believe that the primary reason for the missing lower tail is inability to accurately predict phenotype from genotype.

Recombination and non-Markovian Behavior of the Ancestral Lineage

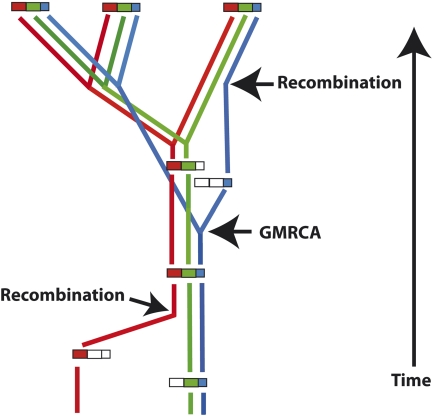
Although recombination will reduce or eliminate the strong Hill–Robertson effects that are responsible for the non-Markovian patterns of our simulations, non-Markovian behavior of the ancestral lineage can also occur via mechanisms that do not rely on extremely low recombination rates. Recombination means that the ancestral lineage of one sequence site will not always pass through the same gene copies as other sequence sites (Fig. 6).

FIGURE 6.

Recombination can cause the ancestral lineage to pass through different gene copies in different sites. Three gene copies are sampled from a population and their history is indicated. The red, green, and blue colors indicate sequence regions that have different histories. Tracing backward through time, the history of the blue region becomes distinct from the histories of the red and green regions at the recombination event indicated on the right side of the figure. The histories of the different regions are again shared at the time marked GMRCA (grand most recent common ancestor, see Griffiths and Marjoram 1996). The recombination event indicated on the left side of the figure delineates where the history of the red region separates from the histories of the green and blue regions.

The possibility of the ancestral lineage passing through different gene copies for different sequence sites is especially relevant to ancestral lineage change when the fitness of a sequence is influenced by interactions between the residues at other sites. For example, the rate of compensatory substitution in helices of RNA secondary structure is negatively correlated with the separation of the interacting sites along the sequence (Piskol and Stephan 2008). If paired sites in a helix always evolved by having mutations at one site get fixed before the occurrence and eventual fixation of a complementarity-restoring mutation at the other site, substitution rates at paired sites should be uncorrelated with sequence separation (i.e., recombination opportunity). The Piskol and Stephan (2008) finding suggests that the sites involved in compensatory substitution are simultaneously polymorphic prior to fixation (see also Meer et al. 2010). Beyond the residue type that occupies one of the two-paired sites in some ancestral lineage generation, the history preceding that generation provides information about the population frequencies of additional residue types at that site. This additional information is pertinent to the linkage disequilibrium that might be generated by a new mutation at the other of the paired helix sites. In contrast to the actual process of ancestral lineage change where haplotype proportions presumably affect the probability of fixation by a new mutation, first-order Markov models consider only the state of the ancestral lineage and neglect allele frequencies.

Even for the extreme case where two interacting sites segregate independently, the recent history of the ancestral lineage provides information about the joint distribution of these sites within the population. This joint information goes beyond the state in some generation of the ancestral lineage at the two sites. It is relevant to fixation probabilities and therefore violates the assumption that ancestral lineage change over time is Markovian. The general problem of including recombination in an ancestral lineage framework appears to represent a formidable challenge, as differing loci should have differing, albeit mutually correlated, ancestral histories. On the other hand, a nonrecombining model may be an acceptable approximation for describing the local behavior of recombining sequences.

Future Directions

In reality, genotype and environment combine to determine phenotype, and phenotype is the intermediary between genotype and fitness. For simplicity, our simulations ignore phenotype and environment and have fitness directly determined by genotype. Our ultimate goal is to make accurate population genetic inferences from interspecific data. Although parameter-rich descriptions are accompanied by a suite of inferential challenges, we believe that the most promising strategy for achieving this goal is to explicitly incorporate genotype–phenotype relationships into evolutionary inference and to additionally model phenotype-fitness links. Previous work has explicitly incorporated genotype–phenotype relationships into interspecific models of sequence change (e.g., Robinson et al. 2003, Rodrigue et al. 2005, Rodrigue et al. 2006, Rodrigue et al. 2009, Yu and Thorne 2006), but these previous studies have assumed that the ancestral lineage evolves in a Markovian fashion and have employed Markov chain Monte Carlo techniques to sample ancestral lineage histories according to their probabilities.

The Wright–Fisher model is a Markov process that determines the counts of offspring genotypes and the parentage of these genotypes by the counts of parental genotypes and parameters like mutation rates and genotypic fitnesses. The ancestral lineage can be viewed as an incomplete summary of a particular Wright–Fisher realization, but the ancestral lineage is not sufficient to reconstruct all details of a particular Wright–Fisher realization. Therefore, there is no guarantee that change in the ancestral lineage is Markovian even though the ancestral lineage represents one way to summarize the outcome of a Markovian inheritance system such as the Wright–Fisher model. Halpern and Bruno (1998) described one important situation for which change in the ancestral lineage is approximately Markovian, but the extent to which the Markov assumption is violated by actual biological systems is unresolved.

For situations where population-genetic parameters cause the ancestral lineage to be poorly described by a Markov model, one possibility will be to adopt the ancestral selection graph approach of Krone and Neuhauser (1997) or some hybrid of ancestral selection graphs and ancestral recombination graphs (see Hein et al. 2005). Work by O'Fallon et al. (2010) on the coalescent with natural selection also appears promising. A slightly different possibility would be to augment the ancestral lineage with summary statistics such as the combination in each generation of ancestral excess and frequency of the ancestral lineage allele. The idea would be that the ancestral lineage and summary statistics together would jointly change in fashion that is well approximated by a Markovian process. Ideally, sufficient statistics rather than summary statistics would be employed, but well-chosen summary statistics can potentially be used to accurately describe the dynamics of fixation in a population without the complications that sufficient statistics might entail (e.g., Rouzine et al. 2003).

Evolutionary biology is faced with a variety of interconnected challenges that need to be addressed. The onslaught of automated techniques for collection of phenotypic and genetic data suggests that mapping genotype and environment to phenotype should become increasingly accurate. The conversion of phenotype into relative fitness is not straightforward but will become much more amenable to study as the relationship between genotype and phenotype is elucidated. As we emphasized here, even if relative fitness can be perfectly predicted from genotype and even if mutation rates and population characteristics are known, patterns of change along the ancestral lineage are not necessarily simple. This potentially complicates inference of phylogeny and population-genetic parameters from interspecific data. The extent of such complication remains unclear. This should be a focus of future research efforts as should be the exploration of the robustness of evolutionary inference techniques to violations of the Markov assumption.

FUNDING

Support for this research was provided by the National Institute of Health (NIH) grant GM070806, NIH grant LM010009 to D. Graur and G. Landan, NIH grant GM090201, and start-up funds for N.L. from the Université de Montréal.