Modeling Type 1 and type 2 diabetes mellitus incidence in youth: an application of Bayesian hierarchical regression for sparse small area data

Abstract

Sparse count data violate assumptions of traditional Poisson models due to the excessive amount of zeros, and modeling sparse data becomes challenging. However, since aggregation to reduce sparseness may result in biased estimates of risk, solutions need to be found at the level of disaggregated data. We investigated different statistical approaches within a Bayesian hierarchical framework for modeling sparse data without aggregation of data. We compared our proposed models with the traditional Poisson model and the zero-inflated model based on simulated data. We applied statistical models to type 1 and type 2 diabetes in youth 10 to 19 years known as rare diseases, and compared models using the inference results and various model diagnostic tools. We showed that one of the models we proposed, a sparse Poisson convolution model, performed better than other models in the simulation and application based on the deviance information criterion (DIC) and the mean squared prediction error.

1. INTRODUCTION

Sparse data is often encountered in epidemiologic studies. For instance, even though diabetes mellitus ranks as the third most common chronic disease among youths, it is still a very rare disease with an estimated incidence of 24.3 per 100,000 person-years at risk (Dabelea et al., 2007). One common solution for modeling sparse data is to aggregate data to a larger spatial or temporal unit, and then model the aggregated data. Previous studies of diabetes mellitus in youth have frequently employed temporal aggregation, basing spatial analyses on ten or more years of incidence data (Pattern and Waugh, 1992; Samuelsson et al., 2004; Feltbower et al., 2003; Staines et al., 1997; Schober et al., 2003; Waldhor et al., 2003; Rytkonen et al., 2003). While in the past most spatial analyses of diabetes incidence relied on describing incidence rates by region (Patterson and Waugh, 1992; Samuelsson et al., 2004; Feltbower et al., 2003), more recently standard Poisson convolution models have been applied in a Bayesian framework (Schober et al., 2003; Waldhor et al., 2003; Cardwell et al., 2006). However, it is well known that spatial or temporal aggregation of data often causes ecological bias (Piantadosi et al., 1988; Greenland and Robins, 1994; Wakefield, 2004; Lawson, 2006). The ecological fallacy (Firebaugh, 2001; Freedman, 2001) occurs when inferences are made about individual level associations based on aggregate data. Another effect is that aggregation increases the spatial correlation between observation units. Thus, there is a need to identify methods suitable for dealing with sparse data at lower levels of aggregation.

The log linear Poisson model which is typically applied to aggregated count data (Lawson, 2006; Besag and Kooperberg, 1995) cannot, however, be applied successfully to sparse or disaggregated data. In sparse data, overdispersion is common when the variance is larger than the mean due to the excess amount of zeros.

In the widely used zero inflated Poisson (ZIP) model (Cheung, 2002; Martin et al., 2005; Lawson, 2008), zero observed counts are divided into excess zero counts and nonexcess zero counts. Excess zero counts are regarded as zero counts which are observed in the process excessively and cannot be modeled by the Poisson distribution; while nonexcess zero counts are zero counts which are derived from a Poisson distribution. While the traditional ZIP models do not model the excess zero counts based on the Poisson model, we may suggest a more sophisticated approach which models the excess zero counts as well as nonexcess zero counts using a special form of the Poisson model for better inference.

We investigate different statistical approaches within a Bayesian hierarchical framework for modeling sparse data without aggregation of data. We modify the ZIP model, and suggest several new statistical models. The Bayesian approach is regarded as a flexible modeling approach compared to the frequentist approach in that it combines both data information and prior information in inference through prior distributions of each parameter, and it enables the building of a complex model by using a hierarchical structure. We compare our proposed models with the traditional Poisson convolution model and the ZIP model through simulation studies, and apply our statistical models to data on the incidence of type 1 and type 2 diabetes mellitus in youth aged 10 to 19 years in South Carolina (SC) as part of a project on the spatial epidemiology of diabetes in youth (Liese et al., 2010). Model evaluation is conducted based on model diagnostic tools such as the deviance information criterion (DIC) and the mean squared prediction error (MSPE) (Lawson, 2008; Banergee et al., 2006).

2. STATISTICAL MODELS

Observed counts are typically fitted by the Poisson model with a log link which establishes a log linear relationship between the mean of the Poisson model and covariates. In the log linear Poisson model, we include log expected counts as an offset to model the relative risk of disease, and also add other covariates to capture confounding effects and random effects to explain the additional variation that cannot be captured by covariates. Let y_i =1, ···, n be the observed count of the i th region. The standard Poisson regression model for modeling count data is defined as,

$$\begin{array}{l}{y}_i\sim \mathit{Pois}({\lambda }_i)=\frac{exp(-{\lambda }_i){\lambda }_i^{y_i}}{y_i!}\\ [log({\lambda }_i)]=log(E_i)+\alpha +X_i\beta +u_i+v_i\end{array}$$

where E_i is an expected count, α is an intercept, X_i is a matrix of covariates, β is a vector of parameters associated with individual covariates, and u_i and v_i are spatially correlated and uncorrelated random effects respectively. This is the classic convolution model with covariates first proposed by Besag, et al (1991).

In the presence of an excess amount of zeros in data, the Poisson model is not a suitable model to apply to data because the key model assumption of the equality of the mean and the variance of the Poisson model is not met. The ZIP model is a frequently suggested model, where a mixture model of a proportion 1-p of excess zeros, and a proportion p of nonexcess zero and nonzero counts is assumed. Excess zero counts are zero counts that are not derived from a Poisson distribution, and nonexcess zero counts are natural zero counts which are derived from a Poisson distribution. In the ZIP model, the Poisson model is fitted by utilizing only a proportion of nonexcess zeros and total nonzero counts. The ZIP model is defined as,

$$\begin{array}{l}{y}_i\sim \mathit{Pois}({\lambda }_i)\\ {\lambda }_i=I_i\ast {\mu }_i\\ log({\mu }_i)log(E_i)+\alpha +X_i\beta +u_i+v_i\\ I_i\sim \mathit{Bernoulli}(p)\\ P\sim \mathit{beta}(1,1)\end{array}$$

where I is the indicator to distinguish excess zero counts and nonexcess zero or nonzero counts (I=0 for excess zero counts, and I=1 for nonexcess zero or nonzero counts) and p is the probability of nonexcess zero counts. A review of zip models can be found in Ghosh, et al (2006).

2.1. Novel models

Here, we propose several models which use the information from expected counts in modeling the proportion of excess zeros, and refer to them as extended ZIP (EZIP) models. In EZIP1, we model the probability of excess zero counts 1− p_i as a function of expected counts E_i: p_i = E_i/(δ + E_i) where δ is a threshold to distinguish excess zeros due to the low values of expected counts from nonexcess zero counts. If we observe an expected count in a region which is larger than δ, p_i becomes close to 1 which indicates that the probability of observing an excess zero count in a region becomes small. On the other hand, for an expected count smaller than δ, we have more probability of observing excess zero counts. The threshold can be chosen to a fixed particular value or it can be estimated within the model. The EZIP1 is defined as,

$$\begin{array}{l}{y}_i\sim \mathit{Pois}({\lambda }_i)\\ {\lambda }_i=I_i\ast {\mu }_i\\ log({\mu }_i)=log(E_i)+\alpha +X_i\beta +u_i+v_i\\ I_i\sim \mathit{Bernoulli}(p)\\ P\sim \frac{E_i}{(\delta +E_i)}\end{array}$$

In addition to the EZIP1 model we also examined two other models that are variants of this model: EZIP2 and EZIP3. The EZIP2 model adopts the information on expected counts directly in modeling the Poisson distribution as well as the proportion of excess zero counts. While the ZIP model uses the expected counts as an offset for nonexcess zero counts and nonzero counts, and excludes information on excess zero counts in modeling, the EZIP2 includes the information on the excess zero counts by using the expected counts in the modeling of the mean of the Poisson distribution: λ_i = [(1 − I_i)] * E_i + I_i * μ_i where λ_i is the mean of the Poisson distribution and I_i is an binary indicator which is 0 if the observed zero count is an excess zero count and 1 otherwise in the ith region. Similar to the previous model, I_i is modeled by the Bernoulli distribution with probability p_i = E_i/(δ + E_i) to assign more probability of excess zeros for a region of low expected counts. The mean of the Poisson model of non excess zero counts and nonzero counts μ_i is modeled by the offset, other covariates and random effects through a log link.

The EZIP3 model is a variant of EZIP2 where a mean mixture is assumed for excess and non-excess zero counts. While the EZIP2 includes expected counts to model excess zero counts in the model, the EZIP3 models another Poisson distribution for excess zero counts, and combines two Poisson distributions based on the proportion of excess zero counts: λ_i = [(1 − I_i)] * μ_1i + I_i * μ_2i where μ_1i and μ_2i are the mean of the Poisson distributions for excess zero counts and nonexcess zero or nonzero counts. The binary indicator I_i is modeled by the Bernoulli distribution with p_i = E_i/(δ + E_i).

Finally, we suggest a sparse Poisson convolution (SPC) model. The main difference between this model and the ZIP model is that while the ZIP model is a mixture model of excess zeros and a Poisson distribution, the SPC approach is a mixture of two Poisson distributions of zero counts and nonzero counts. We define a binary factor j for indicating zero or nonzero observed counts (j=1 if y_i = 0 and j=2 if y_i >0), and include factored intercepts α(j) for modeling zero and nonzero counts:

$$\begin{array}{l}{y}_i\sim \mathit{Pois}({\lambda }_i)\\ log({\lambda }_i)=log(E_i)+\alpha (j)+X_i\beta +u_i+v_i,j=1,2\end{array}$$

In our models, we include spatially correlated and uncorrelated random effects to explain the possibly spatially correlated variation and heterogeneous patterns in the residuals. The spatially correlated random effects are modeled by the conditional autoregressive (CAR) model (Besag and Kooperberg, 1995; Besag et al., 1991) which estimates random effect of the i th region (u_i) based on the sum of the weighted neighborhood values. While neighborhoods can be defined in various ways, widely used criteria are based on shared boundaries and distance between two regions. We use common boundary adjacencies to model spatial association. Adjacency gives a unit weight to each neighbor pair. The uncorrelated random effects v_i are modeled by a zero-mean Gaussian distribution with variance ${\sigma }_v^2(v_i\sim N(0,{\sigma }_v^2))$.

2.2. Multivariate extension

We extended our work to multivariate models for the analysis of multivariate outcomes by adopting the multivariate CAR (MCAR) model (Gelfand and Vounatsou, 2003). The main advantage of the MCAR is that we can construct correlations between spatially correlated random effects of multivariate outcomes, which allow borrowing of information on other outcomes for the inference on a particular univariate outcome. Hence, the MCAR model might improve inference by borrowing information on neighboring areas as well as other multivariate outcomes (Jin et al., 2005; Kim et al., 2001). Similar to the univariate CAR model, M multivariate spatially correlated random effects in the ith region (U_i = (u_i1, ···, u_iM)) are determined by the weighted multivariate neighborhood values.

We apply the MCAR model to the SPC, and develop the sparse Poisson MCAR (SPMCAR) model for analyzing multivariate outcomes. Let us consider M multivariate outcomes and define Y_i = (y_i1, ···, y_iM) as a vector of multivariate outcomes in the ith region. The multivariate outcome Y_i follows a Poisson distribution with the mean μ_i where μ_i is a vector of the mean of the Poisson distribution of the multivariate health outcome (μ_i= (μ_i1, ···, μ_iM)). Using the log link, the mean of the Poisson distribution is expressed as a vector of factored intercepts (α(j)= (α₁(j), ···, α_M(j))), a vector of covariates (X_i = (X_i1, ···, X_iM)) and spatially correlated (U_i) and uncorrelated random effects (V_i):

$$\begin{array}{l}{y}_i\sim \mathit{Pois}({\lambda }_i)\\ log({\lambda }_i)=log(E_i)+\alpha (j)+X_i\beta +U_i+V_i,j=1,2\end{array}$$

In our models, we measure excess risk regions based on the relative risk (RR) estimates which are defined as,

$${RR}_i=exp(\alpha (j)+u_i+v_i)$$

for the SPC model, and

$${\mathbf{RR}}_i=exp(\mathbf{\alpha }(j)+U_i+V_i)$$

for the SPMCAR model. If a RR is greater than 1, the disease is more likely to occur than expected, and a RR less than 1 represents that the disease is less likely to occur than expected.

2.3 Computation

Our models are implemented in a Bayesian framework to utilize the prior information of parameters. Bayesian inference for estimation of parameters is based on the posterior distribution which is obtained by multiplying the likelihood and prior distributions of parameters. Samples are generated from the posterior distribution using several MCMC sampling algorithms such as Gibbs sampling and adaptive rejection sampling. Normal prior distributions (N(0,1000)) are assigned to α, β, and uniform prior distributions are assigned to σ_u, σ_v and δ(σ_u, σ_v ~ Unif(0,10), δ ~ Unif(0,1)) (Gelman, 2006).

We compare our proposed models based on the Deviance Information Criterion (DIC) (Spiegelhalter et al., 2002; Celeux et al., 2006), and the mean squared prediction error (MSPE). The DIC is a criterion to measure the overall goodness of fit by combining the deviance between predicted and observed values and the number of effective parameters which measures a model complexity, and the MSPE evaluates models only in terms of prediction capability.

3. RESULTS

3.1 Simulation

We conducted a simulation study to explore the performance of the four univariate statistical models. The purpose of this simulation study was to compare previously suggested statistical models with the Poisson and the ZIP models in terms of the goodness of fit and the prediction capability under the situations of varying proportions of observed zero counts. Simulated counts of disease y_i over region i were generated from a Poisson model with expected counts E_i and relative risk ζ_i, y_i ~ Poisson(E_iζ_i). For simplicity, we assumed no excess risk situation for all regions (ζ_i =1) and no covariates were considered. The regions with excess zero counts were randomly selected based on the proportion of regions of zero counts (p). We generated a random number r_i ~ U(0,1) for all regions, and select a zero count if r_i < p, and for r_i ≥ p generate a count from Poisson (E_i). Expected count E_i in the ith region was generated from the two different gamma distributions, Gamma (0.1,1) for excess zero observed counts, and Gamma (2,1) for nonexcess zero or non zero observed counts to simulate small values of expected counts for excess zero counts and large values of expected counts for nonexcess zero or non zero counts. For the geographic study region, we used South Carolina, which consists of 46 county units. We fixed p to various values such as 0.3, 0.5, 0.7 and 0.9 to investigate the effects of different proportion of regions with zero counts on the performance of models, and compared the SPC with the Poisson and the ZIP models based on the DIC and the MSPE.

Table 1 shows the average DIC and the average MSPE of all 6 models at various values of p based on 500 simulations fitted using WinBUGS software. Based on the average DIC, we obtained the lowest average DIC from the SPC model for all values of p. However, the average MSPE from the ZIP model was lower than the other models. Our results show that the SPC model fit better than the other models in terms of the DIC, while the ZIP model show better prediction capability. We also compared our models using the separate MSPE of nonzero counts and zero counts (Table 2). The results show that the Poisson and the EZIP2 predict more accurately the nonzero counts than any other model. However, for zero counts, the SPC was the best model and the second best model was the ZIP model. Finally, we present the estimated proportion of excess zero in the Table 3. The EZIP1 estimated quite accurately the proportion of excess zero counts compared to the other models, while the ZIP model showed the most inaccurate estimates of the proportion of excess zero counts. However, from the results of the MSPE, we noticed that the accurate parameter estimates of the proportion of excess zero counts did not guarantee the smallest MSPE since the MSPE were mainly determined by the prediction capability of non-excess zero and nonzero counts which were not good for the EZIP1 compared to the other models. Summarizing our simulation results, the Poisson model and the EZIP2 show better prediction capability than other models for modeling nonzero counts. However, when data have excess zero counts, the SPC and the ZIP model are better than the other models.

Table 1.

DIC and MSPE Comparison of Performance Under Simulation of Various Spatial Models at Different Level of Sparseness.

Proportion of zero counts	Model	DIC		MSPE
		Mean	SD	Mean	SD
30%	Pois	55.44	10.80	0.80	0.25
	ZIP	50.66	11.14	0.78	0.25
	EZIP1	56.93	12.27	0.80	0.25
	EZIP2	54.21	12.95	0.68	0.26
	EZIP3	57.16	10.99	0.79	0.24
	SPC	46.39	10.83	0.79	0.25
50%	Pois	84.60	13.08	1.34	0.30
	ZIP	81.46	13.80	1.33	0.30
	EZIP1	86.52	14.37	1.35	0.30
	EZIP2	88.28	14.37	1.17	0.29
	EZIP3	85.15	11.93	1.30	0.30
	SPC	77.79	12.38	1.34	0.29
70%	Pois	56.27	11.62	0.81	0.26
	ZIP	51.68	11.90	0.79	0.25
	EZIP1	57.92	13.18	0.81	0.25
	EZIP2	55.55	13.87	0.67	0.26
	EZIP3	57.91	11.77	0.80	0.25
	SPC	47.58	11.51	0.80	0.25
90%	Pois	56.39	11.61	0.81	0.25
	ZIP	51.84	11.89	0.79	0.25
	EZIP1	57.98	12.97	0.81	0.25
	EZIP2	55.45	13.48	0.67	0.25
	EZIP3	58.17	11.82	0.79	0.25
	SPC	47.64	11.33	0.80	0.25

Abbreviations: DIC, Deviance Information Criterion; EZIP, Extended ZIP model; MSPE, Mean Squared Prediction Error; Pois, Poisson model; ZIP, Zero inflated Poisson model; SPC, Sparse Poisson Convolution model.

Table 2.

Parameter Estimates of Proportion of Excess Zero and Separate MSPE Comparison of Nonzero and Zero Counts Under Simulation of Various Spatial Models at Different Level of Sparseness.

Proportion of excess zero counts	Model	Parameter estimates of the proportion of excess zero		MSPE of nonzero counts		MSPE of zero counts
		Mean	SD	Mean	SD	Mean	SD
30%	Pois			2.264	0.492	0.368	0.110
	ZIP	0.426	0.104	2.387	0.503	0.090	0.026
	EZIP1	0.326	0.043	2.311	0.491	0.259	0.065
	EZIP2	0.453	0.027	2.259	0.488	0.356	0.100
	EZIP3	0.364	0.03	2.292	0.488	0.287	0.071
	SPC			2.448	0.473	0.003	0.001
50%	Pois			1.619	0.440	0.262	0.083
	ZIP	0.45	0.094	1.708	0.457	0.076	0.022
	EZIP1	0.502	0.042	1.669	0.448	0.170	0.048
	EZIP2	0.591	0.030	1.624	0.442	0.249	0.079
	EZIP3	0.525	0.031	1.656	0.443	0.190	0.053
	SPC			1.770	0.428	0.003	0.001
70%	Pois			0.981	0.279	0.169	0.058
	ZIP	0.473	0.081	1.020	0.286	0.061	0.021
	EZIP1	0.651	0.026	1.011	0.283	0.105	0.034
	EZIP2	0.728		0.989	0.293	0.127	0.043
	EZIP3	0.662		1.009	0.284	0.115	0.036
	SPC			1.081	0.286	0.003	0.001
90%	Pois			0.388	0.189	0.053	0.021
	ZIP	0.494	0.051	0.361	0.182	0.043	0.013
	EZIP1	0.825	0.024	0.406	0.200	0.035	0.012
	EZIP2	0.856	0.024	0.359	0.201	0.061	0.014
	EZIP3	0.827	0.025	0.451	0.279	0.036	0.013
	SPC			0.406	0.189	0.003	0.001

Table 3.

Proportion of South Carolina Counties and Tracts With Zero and Nonzero Counts of Type 1 and Type 2 Diabetes in Youth, 2002–2003.

Diabetes type	County		Tract
	Zero counts N(%)	Nonzero counts N(%)	Zero counts N(%)	Nonzero counts N(%)
Type 1 diabetes	33 (72%)	13 (28%)	725 (84%)	142 (16%)
Type 2 diabetes	34 (74%)	12 (26%)	761 (88%)	106 (12%)

3.2. Application to small area analysis of diabetes incidence

We applied our models to incidence data on type 1 and type 2 diabetes in youth 10 to 19 years of age in South Carolina originally collected in the context of the SEARCH for Diabetes in Youth Study (SEARCH Study Group, 2004; Dabelea, et al., 2007). Diabetes is one of the most common chronic diseases in youth and most cases of diabetes were type 1 diabetes. However, in the last 2 decades, type 2 diabetes has increased among U.S. youth. SEARCH is a multi-center surveillance study of diabetes mellitus which ascertains all incident cases of diabetes mellitus in defined populations including the state of South Carolina from 2002 onward (SEARCH Study Group, 2004). The total population in youth aged 10–19 in 2000 in the South Carolina is 585,856, and the type1 and the type 2 cases in 2002–2003 for youth of that same age group are 170 and 130, respectively (Liese et al., 2010). Information collected on all cases included date of birth, date of diagnosis, gender, race, diabetes type information and contact or residential address. Address was geocoded using TIGER 2000 Road Network File complemented with Zip Code Tabulation Areas (ZCTA) data (U.S. Census, 2000) in Arc GIS 9.3 software (ArcGIS, 2008). Because type 2 diabetes is extremely rare under the age of 10, the age range was limited to 10–19 year olds because we planned to investigate one statistical model (SPMCAR) that combines data on type 1 and type 2 diabetes concurrently. Age groups were categorized into 2 groups (10–14 year, 15–19 year). Gender groups included males and females, and race groups were categorized into 5 race groups (Non-Hispanic white, African American, Hispanic, Asian/Pacific Islander, and American Indian).

The expected number of cases for each age, gender and race group was calculated by multiplying published age, gender, race specific incidence rates (Dabelea et al., 2007) with the population estimates obtained from census 2000 (Census, 2000). The expected total counts of total youth aged 10 to 19 were obtained by the summation of expected counts of age, gender and race groups. To arrive at the number of expected counts for a 2-year period, and we multiplied the expected total counts by the factor two.

Table 3 shows the number and the percentage of counties and Census tracts in South Carolina with zero and nonzero counts of type 1 and type 2 diabetes in youth. The percentage of zero counts increased as we disaggregated the spatial unit from the county level to the tract level. For the county level, approximately 70 % of counties in South Carolina showed zero counts (i.e. had no case), while in the tract level, the percentage of zero counts increased up to 88 %. Comparing type 1 and type 2 diabetes, we noticed a slightly higher number of zero counts for type 2 than type 1 diabetes.

We fitted a range of univariate and multi-variate models to the type 1 and type 2 diabetes data using WinBUGS. The prior distributions assumed for the parameters were relatively non-informative with zero-mean Gaussian distributions for the uncorrelated effects and uniform prior distributions for the standard deviations. Convergence was checked using the Brooks-Gelman-Rubin diagnostic (Brooks and Gelman, 1998). We used a 2,000 sample size to summarize the posterior estimates.

Table 4 shows the model diagnostics in terms of the DIC and the MSPE at the county level and the tract level. The SPC demonstrated the lowest DIC for both type 1 and type 2 diabetes. None of the extended ZIP models showed lower DIC values than the ZIP model. Since lower DIC values indicate better fit, here results suggest that the SPC model fit better than any other model, and the extended ZIP models did not improve the fit of models compared to the ZIP model. We also compared the univariate models and the multivariate SPMCAR model by comparing the summed DIC of type 1 and type 2 of univariate models with the DIC obtained from the SPMCAR model. Since the summed DIC of the univariate SPC was lower than values of the SPMCAR model, we concluded that the MCAR model did not improve models in terms of the overall model fit. In the MSPE results, we also noticed that the MSPE values of the SPC were smaller than the other models except type 2 tract level analysis where the SPMCAR model showed the lowest MSPE, which indicates that the SPC and the SPMCAR model showed better predictions than other models. Table 5 presents the parameter estimates of the proportion of the excess zero counts using the type 1 diabetes data at the tract level. We noticed similar results of simulation. Although the EZIP1 estimated most accurately the proportion of the excess zero counts, the MSPE of the EZIP1 was larger than the other models due to the poor capability of prediction of non-excess zero and nonzero counts. For nonzero counts, the ZIP model showed lower MSPE than other models, while the SPC performed the best prediction of zero counts.

Table 4.

Comparison of Performance of Various Spatial Models Applied to Type 1 and Type 2 Diabetes in Youth in South Carolina.

Spatial units	Models	Type 1 diabetes		Type 2 diabetes		Type 1 and Type 2 diabetes
		DIC	MSPE	DIC	MSPE	SUM DIC
County	Pois	158.06	6.04	162.00	5.59	320.06
	ZIP	143.65	5.95	162.61	5.69	306.27
	EZIP1	163.69	5.97	180.59	5.61	344.27
	EZIP2	161.79	6.18	174.52	5.41	336.31
	EZIP3	179.30	6.01	177.25	5.53	347.55
	SPC	131.87	5.89	141.01	5.59	272.88
	SPMCAR		6.00		6.70	279.00
Tract	Pois	869.33	0.39	687.62	0.29	1556.95
	ZIP	729.09	0.35	589.92	0.27	1319.02
	EZIP1	1182.39	0.37	984.08	0.29	2166.47
	EZIP2	1075.49	0.38	847.32	0.29	1922.81
	EZIP3	1215.80	0.38	994.09	0.28	2209.89
	SPC	350.30	0.26	268.63	0.20	618.93
	SPMCAR		0.31		0.19	630.93

Abbreviations: DIC, Deviance Information Criterion; EZIP, Extended ZIP model; SPC, Sparse Poisson Convolution model; MSPE, Mean Squared Prediction Error; Pois, Poisson model; ZIP, Zero inflated Poisson model; SUM DIC, sum of the DIC of type 1 and type 2 diabetes; SPMCAR, Sparse Poisson MCAR model

Table 5.

Parameter estimates of proportion of excess and Separate MSPE Comparison of Nonzero and Zero Counts Applied to Type 1 Diabetes in Youth in South Carolina at the tract level.

	Parameter estimates of the proportion of excess zero	MSPE of nonzero counts	MSPE of zero counts
Pois		0.198	0.191
ZIP	0.503	0.188	0.159
EZIP1	0.820	0.195	0.185
EZIP2	0.768	0.191	0.179
EZIP3	0.679	0.193	0.178
SPC		0.272	0.00012

We also compare the relative risk estimators based on our models. Although the standardized incidence ratio (SIR) is a crude estimator of relative risk, it captures the pattern of the data adjusted for expectation. Hence, the SIR might be a suitable estimator as a base to compare other relative risk estimators obtained from various models. Figure 1 shows the histograms of the SIR and relative risk estimators of type 1 statistical models. The SIR histogram (a) shows that most values are 0 due to the large proportion of zero observed counts, and we also observe high values of the SIR. In the Poisson model (b), EZIP1 (d), and EZIP3 (e), estimators are ranged between 0.5 and 1, while more relative risk estimators less than 0.5 are noticed in the ZIP and EZIP2 model. Overall, the Poisson, the ZIP, the EZIP2, and the EZIP3 tend to smooth relative risk estimators around 1, and the EZIP1 around 0.5, and relative risk estimators of the SPC and the SPMCAR model are binomially distributed depending on the zero and nonzero observed counts, which captures the binomial distributed pattern of data.

Figure 1.

Histograms of census tract specific estimates of (a) standard incidence ratio (SIR), relative risk estimators of (b) Poisson, (c) ZIP, (d) EZIP1, (e) EZIP2, (f) EZIP3 and (g) SPC model for type 1 diabetes mellitus.

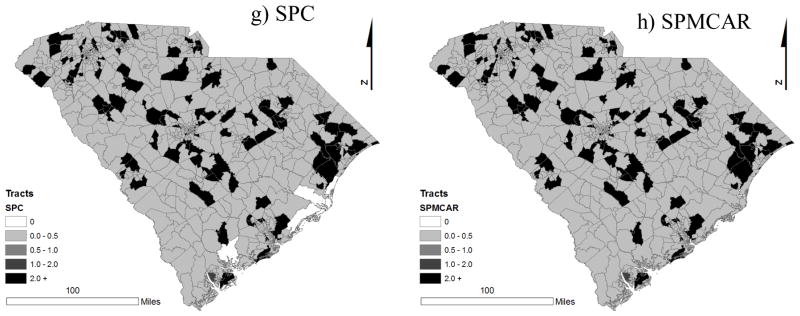
We compare our relative risk estimators using spatial maps to investigate geographic patterns of different relative risk estimators. Figure 2 displays the map of the standardized incidence ratio (SIR) and relative risk estimators of type 1 obtained from various models. In the SIR map (Figure 2(a)), we observe many 0 values due to no observations, and in some regions, we observe high SIR values because of low expected counts. The Poisson model, EZIP1 and EZIP3 yielded similar patterns of relative risk estimators in which most relative risk estimators ranged between 0.5 and 1, and some regions with large SIR’s showed large relative risk estimators. In the Poisson model, the ZIP model, and the extended ZIP models, the relative risks of tracts with no incidence were estimated excessively high due to the smoothing effects. On the other hand, in the SPC and SPMCAR model, we obtained very small values of relative risk estimators in the tracts with no incidence due to different intercepts for zero and nonzero counts, which reduced the shrinkage effects that we found in the other models. Comparing the spatial pattern of relative risk estimators, we noticed that the spatial pattern of the relative risk estimators obtained from the SPC and SPMCAR model displayed similar patterns of the SIR, while the other models showed a very smoothed spatial patterns of the relative risk estimators in the maps.

Figure 2.

Maps of census tract specific estimates of (a) standard incidence ratio (SIR), relative risk estimators of (b) Poisson, (c) ZIP, (d) EZIP1, (e) EZIP2, (f) EZIP3, (g) SPC and (h) SPMCAR model for type 1 diabetes mellitus.

4. DISCUSSION

There have not been many investigations of statistical models appropriate for analyzing sparse data, likely because of the commonly used temporal or spatial aggregation approaches (Patterson and Waugh, 1992; Samuelsson et al., 2004). While the number of studies using Bayesian methods in spatial diabetes epidemiology has lately been increasing (Schober et al., 2003; Waldhor et al., 2003), to the best of our knowledge, our paper is the first to directly address the issue of data sparseness in a Bayesian framework.

Both our simulation study and our application to empirical type 1 diabetes data at both county and census tract level demonstrate that the SPC model performed better than any of the other models in terms of the overall model fit as assessed by DIC. Our comparison models also included the traditionally used Poisson convolution model which has been applied in other studies of diabetes incidence (Schober et al., 2003; Waldhor et al., 2003; Cardwell et al., 2006). To the best of our knowledge, neither the traditional ZIP model nor any of its extensions have been applied or evaluated in spatial analyses of diabetes in youth. As our data show extreme data sparseness – between 70% and 90% of areas with zero case counts – can be expected for type 1 and type 2 diabetes in youth when using only two years of incidence. Regardless of the level of sparseness, the SPC model showed the best fit.

We also compared our models using the relative risk estimators. We found that the traditional Poisson convolution model, the ZIP and the EZIP models tended to over-smooth the relative risk estimators and produced shrunken relative risks around 1 or 0.5. As a result, the relative risk estimators of regions with zero counts tended to be overestimated and the relative risk estimators of regions with nonzero counts tended to be underestimated due to the shrinkage effects. On the other hand, the SPC and SPMCAR models did not allow over-smoothing in relative risk estimators by using different intercepts for zero and nonzero counts, and reduced biases in RR estimators caused by the excessive smoothing.

Our work was conducted in the context of a study that evaluated geographical variation in diabetes incidence, also referred to as studying small area variation, or regional small area analysis (Liese et al., 2010). The aim was entirely descriptive with the goal of identifying the best fitting statistical models. In terms of the overarching purpose, our study is directly comparable to an investigation conducted in Finland using Bayesian methods (Rytkonen, 2001; Ranta and Penttinen, 2000) and other descriptive studies using simpler analytical tools such as the Knox test. Our results indicate that for our purposes, the SPC model seems to perform better than any other model including the traditionally used Poisson convolution model.

The aforementioned studies including our own are however distinct from ecological studies that have aimed to explain regional or geographic variation in diabetes by including other sources of information such as data on population density (Feltbower et al. 2005; Parslow et al. 2001), urbanicity (Rytkonen et al. 2003), overcrowding (Staines et al., 1997), population mixing (Feltbower et al. 2005; Parslow et al. 2001), deprivation (Cardwell et al., 2006; Feltbower et al. 2005), and remoteness (Cardwell et al., 2006), infant mortality and employment type (Schober et al., 2003). For ecologic explorations, it is very possible that the SPC model is not ideal because the inclusion of factored intercepts for modeling zero and non-zero counts leads to aliasing with the neighborhood level variables of interest, rendering the ecologic analysis unfeasible.

Our study has a number of limitations. Our simulation study was limited, and so for further study, we might investigate the biases of parameter estimates based on more extensive simulation studies. In addition we did not examine multivariate models, although we did apply these in our study.

Conclusions

Our study suggests novel ways to address data sparseness when modeling geographic variation in rare diseases. The SPC and SPMCAR models may provide alternative ways to model sparse data avoiding over-smoothing thereby yielding unbiased estimates of relative risk. Our model fitting results showed different relative risk estimators depending on our models, which suggested a careful selection of models for sparse data is necessary.

Abbreviations

ZIP

zero inflated Poisson

SC

South Carolina

DIC

deviance information criterion

MSPE

mean squared prediction error

EZIP

extended ZIP

SPC

sparse Poission convolution

CAR

conditional autoregressive

MCAR

multivariate CAR

SPMCAR

sparse Poisson MCAR

RR

relative risk

Appendix

1. CAR

The spatially correlated random effects are modeled by the conditional autoregressive (CAR) model (Besag and Kooperberg, 1995 and Besag et al. 1991) which estimates the random effect of the ith region (u_i) based on the sum of the weighted neighborhood values

$$\begin{array}{l}(\sum _{j\ne i}\frac{-b_{ij}{u}_j}{b_{ii}}),\\ u_i\mid u_{-i}\sim N(\sum _{j\ne i}\frac{-b_{ij}{u}_j}{b_{ii}},\frac{1}{b_{ii}}),\end{array}$$

where u_i is a set of spatially correlated random effects excluding u_i(u_−i = (u₁, ···, u_i−1, u_i+1, ···, u_n)), and $\frac{-b_{ij}}{b_{ii}}$ is a weight of the jth neighborhood value which controls the strength of the association of random effects between i and j regions.

b_ij is the element of the dispersion matrix B, which is determined by the adjacency matrix C and variance matrix M,

$$B=M^{-1}(I-C)$$

where M is a n× n diagonal matrix with variance ${\sigma }_{u_i}^2$ and I is a n× n identity matrix. The adjacency matrix C satisfies the symmetric condition of the dispersion matrix ( $c_{ij}{\sigma }_{u_j}^2=c_{ji}{\sigma }_{u_i}^2$) and is determined by the neighborhood and its weights.

2. MCAR

The M multivariate spatially correlated random effects in the ith region (U_i = (u_i1, ···, u_iM)) is determined by the weighted multivariate neighborhood values,

$$U_i\mid U_{-i}\sim N(\sum _{j\ne i}\frac{-B_{ij}{U}_j}{B_{ii}},\frac{1}{B_{ii}}),$$

where U_−i is a set of vectors of spatially correlated random effects excluding U_i and $\frac{-B_{ij}}{B_{ii}}$ is a m×1 vector of the weighted neighboring values. B_ij is the ijth m× m block of the symmetric positive definite matrix B which is defined by the adjacency matrix C and variance matrix Σ,

$$B={\mathrm{\sum }}^{-1}(I-C),$$

where Σ⁻¹ and C are nm×nm matrices which satisfy the condition $C_{ij}{\mathrm{\sum }}_j={\mathrm{\sum }}_i{C}_{ji}^T$.

3. Winbugs program for the SPC model

model{

for(i in 1:N){

o[i] ~ dpois(mu[i])

pred[i]~dpois(mu[i])

diff2[i]<-(o[i]-pred[i])*(o[i]-pred[i])

log(mu[i])<- log(e[i]) + alpha0[sp[i]]+ b[i] + v[i]

RR[i] <- exp(alpha0[sp[i]]+ b[i] + v[i])

v[i]~dnorm(0,tau.v[1])

CIND[i]<-step(RR[i]-2)

}

b[1:N]~car.normal(adj[],weights[],num[],tau)

for(k in 1:sumNumNeigh){

weights[k] <-1

}

beta~dnorm(0,0.001)

mspe<-mean(diff2[])

alpha0[1]~dnorm(0,0.001)

alpha0[2]~dnorm(0,0.001)

tau<-1/pow(s6,2)

s6 ~ dunif(0, 1)

tau.v[1]<-1/pow(s7[1],2)

s7[1] ~ dunif(0, 1)

tau.v[2]<-1/pow(s7[2],2)

s7[2] ~ dunif(0, 1)

mrr<-mean(RR[])

sdrr<-sd(RR[])}