Kinetic Isolation and Characterization of the Radical Rearrangement Step in Coenzyme B₁₂-Dependent Ethanolamine Ammonia-Lyase

Abstract

The transient decay reaction kinetics of the 1,1,2,2-²H₄-aminoethanol generated Co^II-substrate radical pair catalytic intermediate in ethanolamine ammonia-lyase (EAL) from Salmonella typhimurium have been measured by using time-resolved, full-spectrum X-band continuous-wave electron paramagnetic resonance (EPR) spectroscopy in frozen aqueous solution over the temperature range of 190-207 K. The decay reaction involves sequential passage through the rearrangement step [substrate radical → product radical], and the step [product radical → diamagnetic product] that involves hydrogen atom transfer (HT) from carbon C5′ of the adenosine moiety of the cofactor to the product radical C2 center. As found for the ¹H-substrate radical, the decay kinetics for the ²H-substrate radical over 190-207 K represent two non-interacting populations (fast decay population: normalized amplitude=0.44 ±0.07; observed rate constant, k_obs,f=5.3×10⁻⁵ – 1.1×10⁻³ s⁻¹; slow decay population: k_obs,s=6.1×10⁻⁶ – 2.9×10⁻⁴ s⁻¹). The ¹H/²H isotope effects (IE) for the fast and slow decay reactions are 1.4 ±0.2 and 0.79 ±0.11, respectively. The IE on the fast phase is uniform over the temperature interval, and the value is consistent with an α-secondary hydrogen kinetic IE, which arises from changes in the force constants of the C-H bonds in the substrate radical structure, upon passing from the substrate radical state to the rearrangement transition state. Therefore, we propose that k_obs,f represents the rate constant for the radical rearrangement, and that this step is the rate determining step in substrate radical decay. The Arrhenius activation energy for the ¹H-substrate radical rearrangement (13.5 ±0.4 kcal/mol) is consistent with values from quantum chemical calculations performed on simple models. The results show that the core, radical rearrangement reaction is culled from the catalytic cycle in the low temperature system, thus establishing the system for detailed transient kinetic and spectroscopic analysis of protein structural and dynamic contributions to EAL catalysis.

Introduction

The interior reactions in a multi-step enzyme catalysis involve the pivotal bond-making/bond-breaking events in substrate transformation. Yet, these reactions are usually not accessible to study by informative single step, transient kinetics meaurements. The short time-scale creation of unstable intermediate states by photolysis^1,2 and γ-irradiation-induced reduction^3,4 in metalloproteins at cryogenic temperatures, followed by annealing, have been developed to study single, or short sequences of, interior reaction steps. The cryotrapping of unstable intermediates,⁵ followed by annealing, has also been performed. We have recently reported that the cryotrapped Co^II-substrate radical pair intermediate in the coenzyme B₁₂ (adenosylcobalamin)-dependent ethanolamine ammonia-lyase (EAL) [EC 4.3.1.7; cobalamin (vitamin B₁₂)-dependent enzyme superfamily]^6,7 from Salmonella typhimurium ^8-10 reacts to form diamagnetic products during annealing, over the temperature range of 190 to 217 K.¹¹ The reaction of the substrate radical is monitored by using time-resolved, full-spectrum electron paramagnetic resonance (EPR) spectroscopy.¹¹ The real-time EPR experiment is made possible by the slow time scale of the reaction in the low temperature range (τ~10³-10⁵ s), relative to the instrument deadtime and the spectrum acquisition periods (≤6×10¹ s). Here, we have examined the ¹H/²H hydrogen isotope effect (IE) on the low temperature decay reaction of the Co^II-substrate radical pair intermediate, with the aim of gaining insight into the rate-determining step(s) and mechanisms.

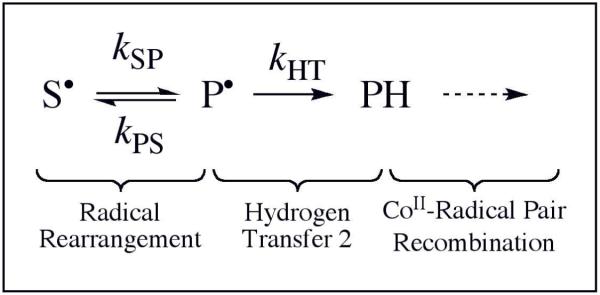
Figure 1 shows the position of the Co^II-substrate radical pair state in the minimal mechanism for the catalytic cycle of EAL.^8,9 The Co^II-substrate radical pair accumulates as the only detectable paramagnetic intermediate during room temperature, steady-state turnover of aminoethanol by EAL.^11-13 As shown in Figure 1, the Co^II-substrate radical pair reacts in the forward direction to form the Co^II-product radical pair. The structure of the product radical is unknown, but a carbinolamine radical is favored by analogy with the demonstrated¹⁴ gem-diol product radical intermediate in the mechanistically similar coenzyme B₁₂-dependent enzyme, diol dehydratase, and by theoretical studies.^15,16 The product radical abstracts a hydrogen atom from the C5′-methyl group of 5′-deoxyadenosine (second hydrogen atom transfer step, HT2), which produces a diamagnetic product species and reforms the 5′-deoxyadenosyl radical. Following the HT2 step, the 5′-deoxyadenosyl radical recombines with Co^II to regenerate the intact coenzyme,¹⁷ and products acetaldehyde and ammonia are released.¹⁸

Figure 1.

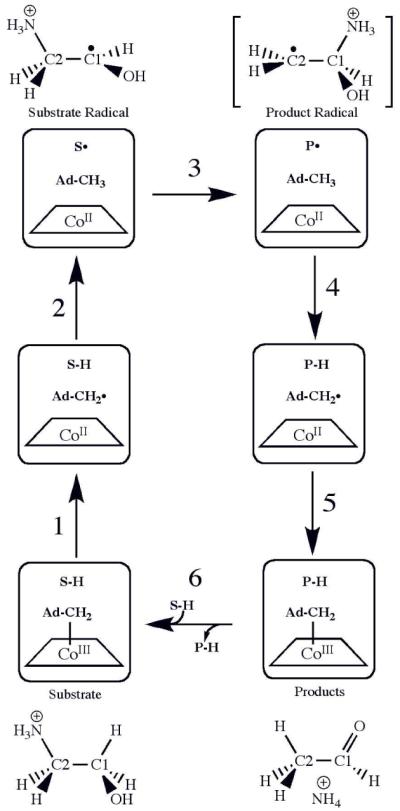
Minimal mechanism of catalysis for coenzyme B₁₂-dependent ethanolamine ammonialyase (EAL) and structures of substrate, intermediates and product.⁸,⁹ The forward direction of reaction is indicated by arrows. The steps are as follows: (1) radical pair separation, (2) first hydrogen atom transfer (HT1), (3) radical rearrangement, (4) second hydrogen atom transfer (HT2), (5) radical pair recombination and (6) product release/substrate binding. Substrate-derived species are designated S-H (bound substrate), S^• (substrate radical), P^• (product radical; brackets indicate proposed structure), and PH (diamagnetic products). The brackets around the product radical indicate that the structure of this intermediate is not known, although the carbinolamine is favored. The 5′-deoxyadenosyl β-axial ligand is represented as Ad-CH₂- in the intact coenzyme, and as Ad-CH₂^• (5′-deoxyadenosyl radical) or Ad-CH₃ (5′-deoxyadenosine) following cobalt-carbon bond cleavage. The cobalt ion and its formal oxidation states are depicted, but the corrin ring and the dimethylbenzimidazole α-axial ligand of the coenzyme ⁴³,⁴⁴ are not shown for clarity.

The accumulation of the Co^II-substrate radical pair as the only EPR-detectable paramagnetic intermediate during steady-state turnover on ¹H-aminoethanol led to the suggestion that the rearrangement step, represents a significant barrier in the overall reaction.¹² Consistent with this observation, the ¹H-aminoethanol substrate ¹⁴N/¹⁵N steady-state kinetic IE on V/K_M (V, maximum velocity; K_M, Michaelis constant) and V was proposed to arise from C2-N bond cleavage in the rearrangement step.^12,19 However, the relatively low value of the ¹⁵N-kinetic IE led to the proposal that hydrogen atom transfer was largely rate limiting in the steady-state reaction of ¹H-aminoethanol substrate.²⁰ The following hydrogen isotope effects suggested that hydrogen transfer, and specifically HT2, contributes to rate determination of steady-state turnover: (a) a steady-state ¹H/²H isotope effect on k_cat (or equivalently, the maximum velocity, V) of 7.4²¹ or 7.5,²² (b) a ¹H/²H IE of 7.3 on transfer of hydrogen from the adenosyl C5′-methyl group to the product radical,²¹ and (c) a ¹H/³H IE of 100 on hydrogen transfer from C5′ to the product radical.^8,21 Here, we use the substrate ²H/¹H IE as a method to assess the contributions of radical rearrangement and HT2 to the low temperature decay reaction of the cryotrapped Co^II-substrate radical pair.

The low temperature decay reaction of the Co^II-substrate radical pair allows a direct, transient kinetic assessment of the reaction sequence that follows the substrate radical state, in the absence of enzyme turnover. As shown previously,¹¹ the decay of the ¹H-substrate radical in EAL displays three regions of kinetic behavior as a function of temperature. Over the range, 190≤T≤207 K, the decay is biexponential, with constant fast phase and slow phase amplitudes and fast and slow observed rate constants (k_obs,f and k_obs,s) that differ by approximately 10-fold. The temperature dependence is characterized by single sets of Arrhenius prefactor (A) and activation energy (E_a) parameters for the slow and fast phases, which correspond to two separate, non-interconverting populations of substrate radicals.¹¹ With increasing temperature over the range, 207<T<210 K, the normalized amplitude of the fast phase increases to unity, while the amplitude of the slow phase decreases to zero. The narrow, <4 K temperature range of this change suggests an origin in a protein dynamical transition.¹¹ At T≥210 K, the decay is monoexponential, with A and E_a parameters that match those for the fast phase decay component at 190-207 K. In order to address the molecular mechanisms of the decay and the emergence of the slow phase at T<207 K, the step(s) represented by k_obs,f and k_obs,s must be identified.

We have cryotrapped the Co^II-substrate radical pair formed during turnover of EAL on 1,1,2,2-²H₄-aminoethanol, and measured the kinetics of the fast and slow decay populations after temperature step to 190-207 K. Turnover on the ²H₄-aminoethanol incorporates ²H into all catalytically exchangeable hydrogen sites after two enyzme turnovers.²² Prior to cryotrapping, the ²H–aminoethanol substrate samples execute >20 turnovers. Therefore, in the starting state for the low temperature decay, the C1-methylene, C2-methylene, and C5′-methyl hydrogen sites are all ²H-labeled in the ²H-substrate radical state, and HT2 proceeds by deuteron transfer. The first-order decay rate constants for the ²H-substrate radical are compared with the previously measured¹¹ first-order decay rate constants obtained for the natural abundance, ¹H-substrate radical over the temperature range of 190-207 K. If HT2 participates in rate limitation, then a primary kinetic IE that is significantly greater than unity is expected. We observe modest, constant IE’s for each kinetic phase from 190 to 207 K, which are not consistent with rate determination by HT2, and conclude that k_obs,f represents the rate constant for radical rearrangement.

Materials and Methods

Enzyme Preparation

Enzyme was purified from the Escherichia coli overexpression strain incorporating the cloned S. typhimurium EAL coding sequence ²³ essentially as described,²⁴ with the exceptions that the enzyme was dialyzed against buffer containing 100 mM HEPES (pH 7.5), 10 mM potassium chloride, 5 mM dithiothreitol, and 10% glycerol,²⁵ and neither Triton X-100 nor urea were used during the purification. Enzyme activity was determined as described²⁶ by using the coupled assay with alcohol dehydrogenase/NADH. The specific activity of the purified enzyme with aminoethanol as substrate was 20-30 μmol/min/mg.

Sample Preparation

Adenosylcobalamin (Sigma Chemical Co.), 1,1,2,2-²H₄ aminoethanol (Cambridge Isotope Laboratories, Inc.), and natural abundance aminoethanol (Aldrich Chemical Co.) were purchased from commercial sources. The reactions were performed in air-saturated buffer containing 10 mM potassium phosphate (pH 7.5). The kinetic parameters were identical in anaerobic samples. All manipulations were carried out on ice under dim red safe-lighting. The final concentration of enzyme was 10-15 mg/ml, which is equivalent to 20-30 μM for a holoenzyme molecular mass of 500,000 g/mol,²⁴ and an active site concentration of 120-180 μM, based on an active site/holoenzyme stoichiometry of 6:1.^27,28 Adenosylcobalamin was added to 240-360 μM (2-fold excess over active sites).

The Co^II-substrate radical pair samples were prepared by using a procedure for fast cryotrapping of steady-state intermediate states in EAL.¹³ Briefly, following manual mixing of the holoenzyme solution with the substrate solution (both prepared in 10 mM potassium phosphate buffer, pH=7.5), the sample was loaded into a 4 mm outer diameter EPR tube, and the tube was plunged into liquid nitrogen-chilled isopentane (T≈150 K) to trap the Co^II-substrate radical pair state. The total elapsed time from mixing to isopentane immersion was 15 s. The Co^II-substrate radical pair to active site ratio is 0.2.^13,14

Continuous-Wave EPR Spectroscopy

EPR spectra were obtained by using a Bruker E500 ElexSys EPR spectrometer equipped with a Bruker ER4123 SHQE cavity. Temperature was controlled with a Bruker ER4131VT liquid nitrogen/gas flow cryostat system, with ER4121VT-1011 evaporator/transfer line, ER4121VT-1013 heater/thermocouple, and 26 liter liquid nitrogen reservoir. For the decay experiments, this temperature control system allowed rapid temperature step changes, relative to the more slowly responding Oxford ESR900 cryostat, and run times of up to 2-3×10⁴ s, depending upon flow rate. Measurements were performed under dim light and with the EPR tubes inserted into the EPR resonator, which shielded the samples from direct exposure to light. Under these conditions with frozen samples, sample degradation owing to coenzyme photolysis is negligible.

Time-Resolved EPR Measurements

EPR samples were held at a staging temperature of 160 K or 180 K in the ER4131VT cryostat system in the Bruker E560 spectrometer, and the microwave bridge was tuned. Temperature steps from 160 K or 180 K to the decay measurement temperatures of 190, 193, 197, 200, 203, or 207 K were initiated by changing the E4131VT temperature set-point. Once the sample temperature stabilized at the set-point, the pre-set auto-tune/auto-scan mode of the spectrometer was triggered, and the sample was auto-tuned at the high temperature set point, followed immediately by continuous spectrum acquisition. The time from initiation of the temperature step to the start of acquisition of the first spectrum was 3.0-6.0×10¹ s. The zero time of the decay was marked at the first collected EPR spectrum. The EPR spectra were acquired with a 24 s sweep time (2.56 ms time constant). The reported temperatures represent the temperature at the sample, which was determined prior to each decay run by using an Oxford Instruments ITC503 temperature controller with a calibrated model 19180 4-wire RTD probe, which has ±0.3 K accuracy over the decay measurement temperature range. For measurements over the temperature range, 190-207 K, the ER4131VT cryostat/controller system provided a temperature stability of ±0.5 K over the length of the EPR sample cavity, as measured by using a thermocouple probe that was translated along the EPR tube axis to achieve different heights within a solution sample. The temperature was therefore stable to ±0.5 K during each run.

Kinetic Analysis

EPR spectra acquired continuously during the decay were used directly in the kinetic analysis, or were averaged in blocks of 2 to 20 spectra to increase the signal-to-noise ratio (SNR), and the acquisition time was calculated as the average time for the block. For each EPR spectrum, the amplitude of Co^II was obtained from the difference between the baseline and the peak feature at g≈2.3, and the substrate radical amplitude was obtained from the difference between peak and trough amplitudes of the derivative feature around g≈2.0. All data processing programs were written in Matlab (Mathworks, Natick, MA). The observed decays were fitted to biexponential (Eq. 1, N=2) functions by using the following expression,

$$\frac{A\left(t\right)}{A\left(0\right)}=\sum _{i=1}^N{A}_i{e}^{-k_{i}t}$$ (1)

where $\frac{A\left(t\right)}{A\left(0\right)}$ is the normalized total amplitude, A_i is the normalized component amplitude $(\underset{i=1}{\overset{N}{\Sigma }}{A}_i=1\mathrm{at}t=0)$, and k_i is the first-order rate constant. The fitting of the data was performed by using Origin (OriginLab, Natick, MA).

Temperature-Dependence of the First-Order Rate Constant

The temperature dependence of the first-order rate constant, k, is given by the Arrhenius expression, as follows:²⁹

$$k\left(T\right)=A{e}^{\frac{-E_a}{RT}}$$ (2)

where E_a is the activation energy, R is the gas constant, and A is a prefactor that represents the value of k as T→∞. In a plot of lnk versus T⁻¹ (Arrhenius plot), the intercept of the linear relation is given by lnA and the slope is given by -E_a/R.

RESULTS

²H₄-Aminoethanol-Generated Co^II-Substrate Radical Pair EPR Spectrum

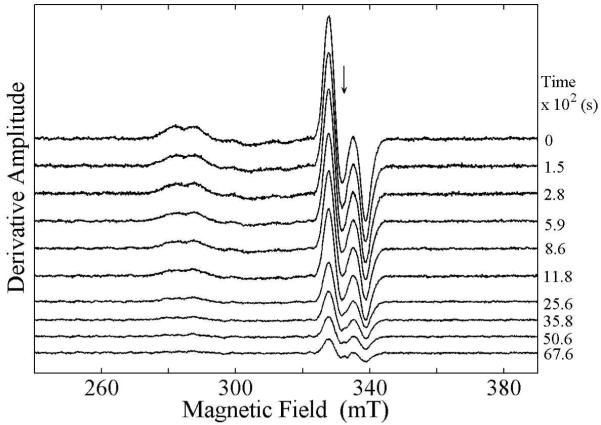
Figure 2 shows the zero-time EPR spectrum of the ²H₄-aminoethanol-derived Co^II-substrate radical pair at the representative annealing temperature of 207 K. The Co^II EPR signal intensity is most prominent in the region around 285 mT, which is near to the g_⊥=2.26 value in the EPR spectrum of isolated cob(II)alamin.³⁰ The Co^II features in the radical pair spectrum are broadened, relative to isolated cob(II)alamin, by the interaction with the unpaired electron localized on C1 of the substrate radical.³¹ The substrate radical line shape extends from approximately 325 to 345 mT. The partially resolved doublet splitting and inhomogeneous broadening is caused by the interaction with the unpaired electron spin on Co^II.^13,31 All of the features of the Co^II-substate radical pair spectrum can be accounted for by EPR simulations.^32,33

Figure 2.

Dependence of the EPR spectrum of the ²H₄-aminoethanol generated Co^II-substrate radical pair state in EAL on time at T=207 K after temperature-step reaction initiation. The free electron resonance position at g=2.0 is shown by the arrow. Experimental Conditions: microwave frequency, 9.3434 GHz; microwave power, 20.25 mW; magnetic field modulation, 1.0 mT; modulation frequency, 100 kHz; scan rate: 6.52 mT/s; time constant, 2.56 ms.

Time-Resolved Measurements of EPR Spectra During the ²H₄-Aminoethanol Substrate Radical Decay Reaction

Figure 2 shows a stack plot of a selection of 11 of the 300 total EPR spectra that were collected during the course of a representative decay of the ²H₄-aminoethanol-generated Co^II-substrate radical pair at 207 K. Decay data were collected for temperatures of 190, 193, 197, 200, 203, and 207 K. The Co^II and substrate radical EPR signals decay in synchrony and no EPR signals from paramagnetic species, other than the Co^II-substrate radical pair, were detected at a signal-to-noise ratio of 10² for the peak-to-trough amplitude of the substrate radical, as found for the decay of the ¹H₄-aminoethanol-generated Co^II-substrate radical pair.¹¹

Time and Temperature Dependence of the ²H₄-Aminoethanol Substrate Radical Decay Reaction

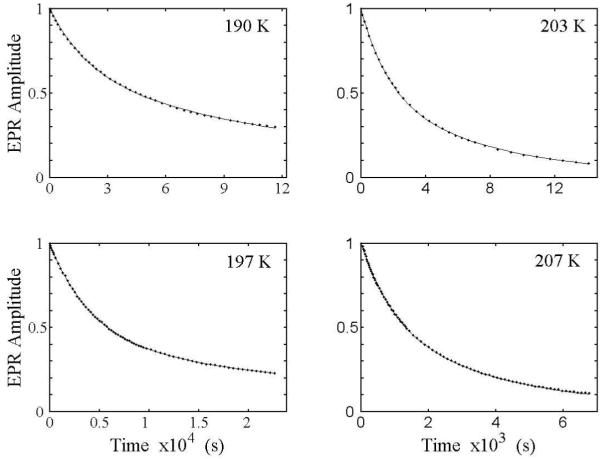
Figure 3 shows representative decays of the substrate radical EPR signal as a function of time at temperatures of 190, 197, 203, and 207 K. The theoretical curves in Figure 3 represent fits of the data to a biexponential function (Eq. 1, N=2). The biexponential function provides an excellent fit to the decay at all of the temperatures examined from 190 to 207 K. The rate constants, k_obs,f and k_obs,s, and normalized amplitude coefficients, A_obs,f and A_obs,s, for the fast and slow phases of the biexponential fitting functions for each temperature are presented in Table 1. Table 1 shows that A_obs,f and A_obs,s remain comparable as the rate constants increase with increasing temperature, with mean values and standard deviations as follows: A_obs,f=0.46 ±0.10 and A_obs,s=0.54 ±0.10. The kinetic fitting results are consistent with complete decay at all temperatures. The complete decay of the substrate radical EPR amplitude indicates that at least one step in the recombination process is irreversible.

Figure 3.

Decay of the amplitude of the ²H₄-aminoethanol generated substrate radical as a function of time at selected temperatures from 190-207 K, and overlaid best-fit biexponential (red). The EPR experimental conditions are as described in the legend to Figure 2. The simulation parameters are presented in Table 1.

Table 1.

Observed first-order rate constants and normalized amplitude parameters for fits of the biexponential function to the decay kinetics of the ²H-substrate radical state, and ¹H/²H hydrogen isotope effects (IE) at different temperatures. The standard deviations for the k_obs and A_obs parameters represent at least three separate determinations at each temperature. The ¹H-substrate radical k_obs values used to calculate IE_f and IE_s were determined previously.¹¹

T (K)	kobs,f (s−1)	Aobs,fa	kobs,s (s−1)	Aobs,sb	R2c	IEf	IEs
207	1.1±0.3 ×10−3	0.53±0.05	2.9±0. 6 ×10−4	0.47±0.05	0.9997	1.4±0. 2	1.00±0.22
203	5.7±0.8 ×10−4	0.52±0.06	1.1±0. 1 ×10−4	0.48±0.06	0.9999	1.5±0. 1	0.73±0.05
200	4.4±1.2 ×10−4	0.41±0.09	7.7±1.8 ×10−5	0.59±0.09	0.9997	1.3±0. 1	0.61±0.04
197	2.6±0.2 ×10−4	0.44 ±0.11	3.6±0.8 ×10−5	0.56±0.11	0.9998	1.4±0.1	0.67±0.07
193	1.2±0.2 ×10−4	0.37±0.02	1.5±0. 3 ×10−5	0.63±0.02	0.9995	1.2±0.3	0.87±0.08
190	5.3±0.5 ×10−5	0.38±0.02	6.1±0. 1 ×10−6	0.62±0.02	0.9995	1.4±0.1	0.85±0.03

^aThe relative fitted amplitude for the fast phase, normalized to the sum, A_obs,f+A_obs,s.

^bThe relative fitted amplitude for the slow phase, normalized to the sum, A_obs,f+A_obs,s.

^cR is Pearson’s correlation coefficient.

DISCUSSION

Isotope Effect on the Fast Phase of the Substrate Radical Decay Reaction

Table 1 shows the values of the ¹H/²H IE for the rate constants, k_obs,s and k_obs,f, at each temperature from 190 to 207 K. The IE values were calculated by using the ratio of the k_obs value for the ¹H-substrate radical (k_obs,s,H, k_obs,f,H) reported previously,¹¹ and the corresponding k_obs values for the ²H-substrate radical (k_obs,s,D, k_obs,f,D), which are presented in Table 1. The mean IE for k_obs,f over the temperature range of 190-207 K is 1.4 ±0.2. The standard deviation of 0.2 represents the error propagation of the standard deviations of the measurements at each temperature. The value of 1.4 is lower than the steady-state ¹H/²H isotope effects on k_cat (or equivalently, the maximum velocity, V) of 7.4²¹ or 7.5,²² lower than the ¹H/²H IE of 7.3 on transfer of hydrogen from the C5′-methyl group of the cofactor to the product radical,²¹ and also lower than the ¹H/²H IE of 17 on hydrogen transfer from C5′ to product radical, which is predicted from the ¹H/³H IE,²¹ by using classical theory.⁸ These results show that the ¹H/²H IE on the reaction of the substrate radical decreases with decreasing temperature, and therefore, that the contribution of the HT2 step to determination of the rate of the substrate radical decay reaction decreases with decreasing temperature.

Table 1 shows that the IE of 1.4 ±0.2 is maintained over the temperature range of 190-207 K. This indicates that the decrease in the rate-determining contribution of the HT2 step occurs at T>207 K, and suggests that the residual, constant IE of 1.4 over the temperature range of 190-207 K arises from a different source. A minimal kinetic model for the irreversible substrate radical decay through the rearrangement and HT2 steps is presented in Figure 4. The following general expression for k_obs,f is derived from this model:²⁹

$$k_{obs,f}=\frac{k_{SP}{k}_{HT}}{k_{PS}+k_{HT}}$$ (3)

The absence of a contribution of k_HT to k_obs,f is consistent with Eq. 3, if the condition, k_PS<<k_HT, holds. In this case, k_obs,f=k_SP, and the hydrogen IE on k_obs,f corresponds to $\frac{k_{SP,H}}{k_{SP,D}}$. The IE of 1.4 on k_obs,f suggests an α-secondary kinetic IE, which arises from changes in the force constants of the C-H bonds in the substrate radical structure, upon passing from the substrate radical state to the rearrangement transition state.^34,35 The α-secondary kinetic IE for the change of hybridization of carbon from sp³ to sp² is typically 1.1-1.2, and the theoretical maximum value has been calculated to be 1.4.³⁶ Therefore, we propose that the fast phase of decay of the substrate radical is rate-determined by the radical rearrangement step for both ¹H- and ²H-substrate, and that k_obs,f represents the first-order rate constant for this step.

Figure 4.

Simple kinetic model for the decay reaction of the cryotrapped substrate radical at 190-207 K. The states are designated, as follows: S^•, substrate radical; P^•, product radical; PH, diamagnetic product.

Isotope Effect on the Slow Phase of the Substrate Radical Decay Reaction

The mean IE for k_obs,s over the temperature range of 190-207 K is 0.79 ±0.11. This inverse IE on k_obs,s indicates that a normal primary kinetic IE from HT2 also does not contribute significantly to rate-determination of the slow phase of the substrate radical decay reaction. The origin of the inverse IE on k_obs,s is not clear, at present. The differences in the values of k_obs,s and k_obs,f, which have been attributed to a difference in protein structure, dynamics, or both,¹¹ and the different IE on k_obs,s and k_obs,f, indicate that different microscopic events are rate determining for the fast and slow decays. For example, if the protein influence shifts the transition state for rearrangement to a later position on the N-migration coordinate, then the development of significant sp²-hybridization at both C1 and C2 in an associative, cyclopropyl transition state,³⁷ or in a dissociative allyloxy transition state,^38,39 may lead to an inverse α-secondary kinetic isotope effect. Additional substrate hydrogen IE studies, performed with substrate labeled specifically at C1 or C2, and with rapid trapping to minimize label scrambling among the substrate and C5′ C-H sites, may identify the origin of the inverse IE.

Temperature Dependence of the Observed Fast-Phase Rate Constants

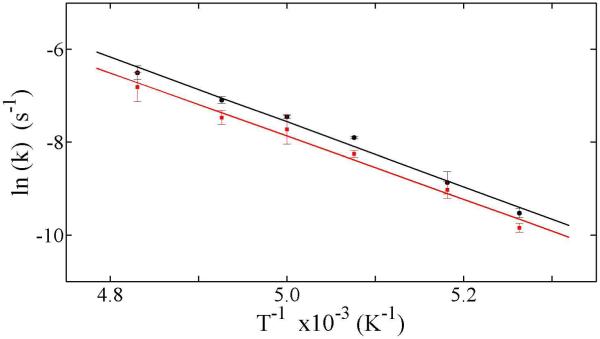
Figure 5 shows plots of the natural logarithms of k_obs,f as a function of inverse absolute temperature for the reaction of the ¹H-substrate and ²H-substrate radicals, and linear fits of Eq. 3 to the two sets of data points. As concluded in the previous section, the k_obs,f values represent the rearrangement reaction step. Therefore, application of the Arrhenius analysis of the first-order rate constant is appropriate. Table 2 shows that the logarithms of the Arrhenius prefactors, A_f,H and A_f,D and activation energies, E_af,H and E_af,D, for the ¹H- and ²H-substrate radical reactions are pairwise the same, to within one standard deviation. The absence of a significant hydrogen IE on the Arrhenius parameters agrees with the absence of a large primary hydrogen kinetic IE.

Figure 5.

Arrhenius plots of the observed first-order rate rate constants for the fast phase of decay of the Co^II-substrate radical pair states, which were generated by using natural abundance (¹H-aminoethanol) substrate. Data from Table 1 for the ¹H-substrate radical k_obs,f (black solid circles) and for the ²H-substrate radical k_obs,f (red solid squares) are shown. The linear fits of the Arrhenius expression for the ¹H-substrate radical (black lines) and for the ²H-substrate radical (red lines) are overlaid on the data. The A and E_a values derived from the fitting parameters are collected in Table 2.

Table 2.

Arrhenius parameters for the fast phase of the ²H- and ¹H-substrate radical decay kinetics for the temperature range, 190-207 K

Substrate	Log[A (s−1)]	Ea (kcal mol−1)	R2a
2H-Aminoethanol	11.4 ±0.9	13.5 ±0.4	0.9920
1H- Aminoethanol	11.9 ±0.9	13.9 ±0.4	0.9935

^aR is Pearson’s correlation coefficient.

The experimental fast phase activation energies of 13.5 ±0.4 kcal/mol (¹H) and 13.9 ±0.4 kcal/mol (²H) (Table 2) are the first directly measured E_a values for a radical rearrangement step in a coenzyme B₁₂-dependent enzyme. The values of the Arrhenius prefactors of 2.5×10¹¹ to 7.9×10¹¹ s⁻¹ differ by less than 17-fold from $\frac{k_{B}T}{h}=4.2\times {10}^{12}{\mathrm{s}}^{-1}$ for T=200 K, which indicates that the rate determinining events in rearrangement are accompanied by relatively small activation entropy contributions (<5.6 cal/mol/K). Therefore, comparisons of the experimental E_a values with values obtained by high-level quantum chemical calculations on restricted-atom models are appropriate. Values of 16 kcal/mol¹⁵ and 12-15 kcal/mol⁴⁰ were obtained from ab initio calculations for the rearrangement reaction in EAL. The calculations were based on models that included the aminoethanol substrate, and different associated molecules, which represented putative active site amino acid side chains.^15,40 The auxilliary molecules assisted the nitrogen migration through the formation of hydrogen bonds with the ammonium group (“push” catalyst)⁴¹ or the substrate hydroxyl oxygen (“pull” catalyst).⁴¹ The calculations suggested that the lowest energy rearrangement pathway proceeds by an associative mechanism.^15,40 Active site arginine and glutamate side chains have been identified as substrate hydrogen bonding partners in the structural proteomics model for the EutB protein of EAL.^7,42 The protein structure and experimental E_a values are thus consistent with the proposed “retro push-pull” hydrogen bonding mechanism⁴¹ of radical rearrangement catalysis in EAL.^15,41

Comparison of Fast-Phase Substrate Radical Decay at 190-207 K and Steady-State Turnover at 298 K

The accumulation of the Co^II-aminoethanol substrate radical pair as the only paramagnetic intermediate under steady-state turnover conditions,¹² and the substrate ¹⁴N/¹⁵N IE on V/K_M and V,^12,19 indicate that the rearrangement step presents a significant barrier to the overall steady-state reaction sequence, for the ¹H-aminoethanol substrate,¹² but the relatively small value of the ¹⁵N-kinetic IE (0.17%)¹⁹ led to the proposal that hydrogen transfer is largely rate limiting for the steady-state reaction at room temperature.²⁰ In contrast, the results and interpretation, presented here, establish that the radical rearrangement is the dominant rate-determining step in the decay reaction of the cryotrapped substrate radical at 190-207 K. The low temperature results lead to the prediction that the rate constant for the HT2 step is temperature dependent (k_HT decreases with decreasing temperature), because the rate constant for radical rearrangement is relatively temperature independent (small activation entropy). The relation of the mechanism for the low and high temperature regimes, in the context of the model presented in Figure 4, will be further addressed, by studying the kinetics of the ¹H- and ²H-substrate radical decay reactions over a more extensive range of temperatures.