Computer-aided classification of centroblast cells in follicular lymphoma

Abstract

Objective

In this paper, we develop a novel automated method to distinguish centroblast (CB) cells from non-centroblast (non-CB) cells in follicular lymphoma cases and measure its performance on cases obtained by a consensus of six pathologists.

Study Design

Geometric and color texture features were used in the training and testing of the supervised quadratic discriminant analysis (QDA) classifier. The technique was trained and tested on a data set composed of 218 CB images and 218 non-CB images. Computer performance was tested by measuring sensitivity and specificity among cells classified as centroblasts and non-centroblasts by consensus of six board-certified hematopathologists.

Results and Conclusion

Automated classification distinguished centroblast cells (CB) from non-centroblast cells (Non-CB) with a classification accuracy of 82.56% and sensitivity and specificity were 86.67% and 86.96%, respectively, when the approach was tested. The novelty of our approach is the identification of the CB cells with prior information, and the introduction of the principal component analysis (PCA) in the spectral domain to extract texture color features.

I. Introduction

In the United States, Follicular Lymphoma (FL) accounts for 20–25% of non-Hodgkin lymphomas.¹ FL affects mostly adults, particularly the middle-aged and elderly. This disease is characterized by a partial follicular or nodular pattern and is composed of lymphoid cells of follicular center origin, including small-cleaved cells (centrocytes), and larger non-cleaved cells (centroblasts). Grading of FL is crucial for patient risk stratification, prognosis and treatment and is based on the average number of centroblasts in ten representative high power fields (40x) in representative neoplastic follicles. This method of grading is fraught with inter- and intra-observer variability leading to poor reproducibility and prompting the search for a more accurate and efficient method of quantifying centroblasts and more reproducible grading schema. In this paper, pathological biopsies and their diagnostic and prognostic indicators for follicular lymphoma are considered and the stand-alone accuracy of the computer was analyzed using centroblast and non-centroblast cell images from two whole-slide H&E-stained follicular lymphoma images.

Computer applications are increasingly used in medicine to help with detection, diagnosis and prognosis of diseases.^2,3 In a Computer Aided Diagnosis (CAD) system, image processing, image analysis, and pattern recognition techniques are applied to extract quantitative data. Precise features extracted from these data are then used for further image analysis and classification discriminant techniques, such as parametric and non-parametric statistical classifiers, are employed to classify the images or objects of interest in these images. Selection of image processing techniques and classification strategies are important for successful implementation of any machine vision system. Several statistical, structural and spectral texture approaches for grayscale images have been suggested. ^4,5,6,7,8,9

Our goal is to develop a new method that improves pathologist accuracy when grading FL using novel texture features, color-space decomposition, and by extracting morphological characteristics of objects. In our previous work, we have used color and texture features and model-based intermediate representations for the grading of follicular lymphoma. ^{10,11,12,13,14,15,16} A multivariate image analysis technique using principal component analysis (PCA) in the spectral domain is investigated. Instead of gray scale images, information from color spaces is utilized, and RGB, Lab, HSI color spaces are explored.

This paper is organized as follows. In section 2, we describe the proposed method. Experimental results are presented in section 3. Finally, a conclusion is offered in section 4.

II. DESCRIPTION OF THE TECHNIQUE

Our method is based on a training features vector composed of a mixture of color texture features and morphological (geometrical) features. The training and testing rules are achieved using a supervised classifier, which is well known as a quadratic discriminate analysis classifier (QDA). ^17,18 The color features are extracted from several color spaces namely R, G, B, H, S, I, L, a, and b respectively.

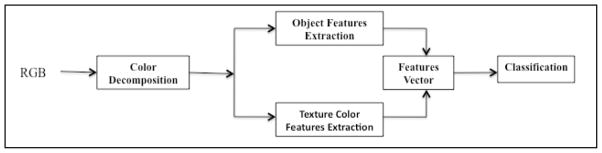
Pathologists discriminate CB cells from non-CB cells by observing specific quantifiable cellular structures. They compare cell size and pick the cells that are larger when compared to other cells. For example, pathologists often compare cells of interest to blood cells. Here, we discuss the geometric characteristics of large cells when image textures are taken into consideration. Figure 1 exhibits the different steps of our technique. Only H&E stained images were used in this study.

Figure 1.

Shows different steps of the proposed method

II.1- Object feature extraction

To extract the geometric features of each image of the data set, we have developed a method that takes into consideration a succession of operations such as thresholding, morphological filtering, and area identification. Next, we give a brief overview of these steps:

1. The RGB image is converted into the Lab space. The Lab space is recognized to be more perceptually uniform with respect to RGB space and presents a better overall contrast. The L channel representing the luminance factor of the Lab space is kept for further processing to extract the object.

2. The Otsu parametric thresholding technique ¹⁹ is then applied to the image obtained from step 1.

3. Opening and closing morphology operations are used on the complement of the binary image obtained in step 2 to recover the shape of objects. A labeling morphology operation is computed on the resulting binary image to identify each object in the image. The connectivity is chosen to be equal to eight.

4. Area measurement is then calculated for each labeled object. The greatest area, which corresponds to the largest object in the image, is then identified. Figure 2 illustrates the different steps of object extraction.

Figure 2.

(a) original image, (b) thresholding operation of image in (a), (c) labeling operation of image in (b), (d) identification operation

The area and the perimeter of the cell are computed and represent the geometrical features. These are combined with the color features to form the feature vector used to train the QDA classifier.

II.2- Texture color features extraction

Pathologists describe the CB cells as containing several dark nucleoli surrounded by bright uniform cytoplasm and non-CB cells as homogenous, dense structure. The color is also another pathological criteria for grading. These criteria were considered when designing our technique. Our method is organized around analyzing the inner color texture of the cells. Therefore, we suggest quantifying texture features extracted from several color spaces: R, G, B, H, S, I, L, a, and b separately.

Several definitions of the image texture have been suggested in the literature. ^{3,4,5,6,7,8,9} Others define texture as a function of roughness, coarseness, directionality, homogeneity, spatial frequency, etc. There is no general agreement on one definition. The best definition depends on the particular application.

For example, in ^8,9, the authors use an auto-regression function derived from the analysis of time sequences in order to derive or create textures. A six dimensional stochastic differential equation describes the correlation of random values (gray values), which are modified by associated coefficients.

Our interest lies within the statistical analysis of texture in the Fourier domain. The variation of the power spectrum along the frequency scale can be a good image textural descriptor. A statistical analysis based on PCA is proposed to first reduce the dimensionality of the texture features space and second to quantify the frequency variations, which characterize the texture in the image. The variance of the first order eigenvector is calculated from the PCA of the power spectrum. This mode is suggested to carry most of the texture variations in the image compared to the rest of the modes. We are limiting the quantification to the first mode in order to filter out the noise from the texture. This feature is extracted for each color of the spaces specified above.

PCA transforms the data into a new orthogonal coordinate system such that the greatest variance by any projection of the data comes to lie on the first coordinate axis (called the first principal component), the second greatest variance on the second coordinate axis, and so on. PCA is theoretically the optimum transform in least squares terms. ⁶

The eigenvectors e_i and the corresponding eigenvalues λ_i are the solutions of the equation:

$$\begin{array}{l}{C}_x{e}_i={\lambda }_i,\\ i=1,\dots \mathrm{..},n\end{array}$$ (1)

In our case, the covariance matrix C_x is defined in the spectral domain as follows:

$$C_x=E\left[(S-{\mu }_p){(S-{\mu }_p)}^T\right],$$ (2)

where S is the power spectrum matrix, and μ_p is the mean of the matrix S. S is defined as follows:

$$S(u,v)=\mathit{sqrt}\left(\mathit{real}{(F(u,v))}^2+\mathit{imag}{(F(u,v))}^2\right)$$ (3)

Where F (u, v) is the Fourier transform (FFT) of the image. The variables u and v are horizontal and vertical frequencies defined in the polar axis respectively. The functions real and imag are the real and the imaginary parts of the FFT respectively.

We assume that the eigenvalues λ_i are distinct. These values can be found by solving the following equation:

$$\mid C_x-\lambda I\mid =0$$ (4)

Where I is the identity matrix having the same order as C_x and |.| denotes the determinant of the matrix.

The variance of the first component is calculated to quantify the statistical dispersion of these variations. It is defined as follows:

$$\begin{array}{l}\mathit{Var}(X)=E\left[{(X-\mu )}^2\right]\\ \mu =E(X)\end{array}$$ (5)

Where X is the first eigenvector and μ is the mean of the same vector.

The variance is proposed as the quantification parameter of the texture color feature. This value is calculated in each proposed space and used as a feature in the training process. Table 1 gives a general overview of the computation of the texture for each color space:

Table 1.

Overview of the computation of the texture for each color space

Color space	R	G	B	L	a	b	H	S	I
Texture	Var(XR)	Var(XG)	Var(XB)	Var(XL)	Var(Xa)	Var(Xb)	Var(XH)	Var(XS)	Var(XI)

X_R, X_G, X_B, X_L, X_a, X_b, X_H, X_s, and X_I are the first eigenvectors of the PCA of the power spectrum of R, G, B, L, a, b, H, S, and I color channels respectively. Var () is the variance of the same cited vectors.

The union of the geometrical features vector and texture color features vector defines the final features vector and is defined as follows:

$$V=V_g\cup V_c$$ (6)

Where V_g and V_c are the geometrical features vector of the cell and the color texture features vector.

III. Experimental Results

To classify CB versus non-CB cells, using a QDA supervised classifier; we collected a data set of two populations. The images in the first set were graded by two board-certified pathologists as CB and none of the images in the second set was graded by either pathologist as CB. The final data set consisted of 218 CB and 218 non-CB H&E images coming from two different patients. The H&E images were sectioned, stained according to the standards of the Ohio State University Department of Pathology, and the images were digitized according to the standard operating procedures. The quality of the images has been visually assessed by two pathologists and considered as very good quality images. The original slides have been scanned using Aperio high-resolution scanner, which is one of the most commonly used digitizers. According to the World Health Organization (WHO) criteria, the FL grading is based on the H&E-stained tissues. While immunohistochemistry and genetic studies have identified potential prognostic variables for FL, they are not used in clinical practice; and this study aims at improving the current standard as accepted by the WHO. By recognizing CB cells from non-CB cells, this method can add significant improvement to the grading of FL. The counting of CB cells can be made more accurate and efficient, with the potential to impact the accurate distinction between low grade and high grade FL classification, which is the new grading system introduced by WHO in 2008. It is critical to note that the ground truth data are not manually annotated and the contours of the cells are not marked. Figure 3 illustrates an example of CB and non-CB images. One can notice that the CB image contains more objects/cells and higher texture compared to the non-CB image. The morphology of the central object and the color texture of the image are considered to classify CB versus non-CB cells.

Figure 3.

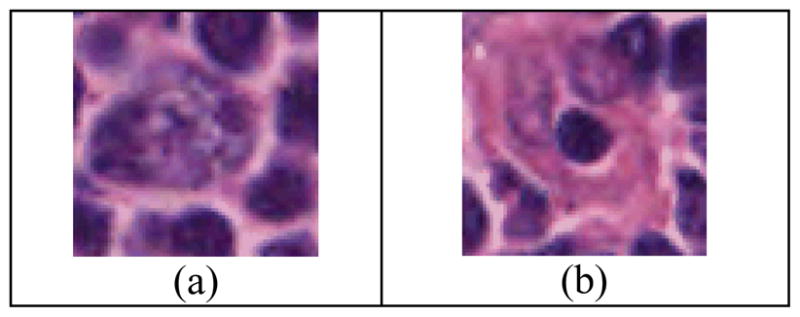
Examples of (a) a typical CB cell, and in (b) a typical non-CB cell.

We randomly divided CB and non-CB data into training and testing sets using an 80%-20% ratio (174 CB images, 174 non-CB images were used for training, and 44 CB images and 44 non-CB images were used testing). The 80% of CB and non-CB images allocated for training were divided again into 90% for training and 10% for testing using the K fold cross-validation¹⁵ approach (empirically, K is set to 10). This operation was repeated ten times to select the best training set. The training set producing the best performance was picked as the final training set. The final set from the 90%-10% split producing the best performance was then applied to the testing set obtained from initial 80%-20% allocation. Table 2 shows the 90%-10% training rule using the supervised QDA classifier. The same rule was used for training and testing operations. In this example, the training set corresponding to the highest classification rate of the classifier was identified as set 6. Its accuracy was equal to 88% in classifying CB and non-CB images. This set was then selected as the training set for further testing of the classifier. The QDA classifier was then applied to the 88 images in the original testing set and the average classification rate was 82.56%. We chose the QDA classifier for our analysis because it showed a higher classification rate compared to the classical supervised classifiers such as linear discriminant analysis (LDA) and K-nearest neighbor classifiers.

Table 2.

Results from 90%-10% training methodology.

Set	Accuracy (classification rate)
1	70%
2	62%
3	85%
4	71%
5	76%
6	88%
7	62%
8	71%
9	79%
10	85%

To analyze the performance of our system with a much more conservative ground truth process, we enlisted six experienced board-certified hematopathologists to complete another ground truthing experiment. In the experiment, these six board-certified hematopathologists graded the images using the graphical user interface (GUI) we developed (see figure 4a). The pathologists were presented with all the cell images in a random fashion and they clicked on the images that they considered to be CBs. This information was recorded and used in the performance analysis.

Figure 4.

The pathologists are shown the CB and non-CB images in (a), when they click on the images that they consider as CB the boundaries of that cell turns black (b) and this information is recorded.

III.1 Statistical analysis

To emphasize the usefulness of the CAD grading, we performed an extensive statistical analysis. Accuracy was quantified in terms of sensitivity and specificity. Sensitivity (Sn) was defined as

$$Sn=\frac{TP}{(TP+FN)},$$ (7)

where TP and FN are the number of true positive and false negative results, respectively. Specificity (Sp) was defined as

$$Sp=\frac{TN}{(TN+FP)},$$ (8)

where TN and FP are the number of true negative and false positive results, respectively. In this study, the sensitivity quantifies the proportion of actual positives correctly identified as CB cells and the specificity measures the proportion of negatives correctly identified as non-CB cells.

In Table 3, the sensitivity and specificity of the CAD are presented based on the ground truth from two pathologists. The results show that the CAD system classification is sensitive to the detection of both true negative (non-CB cells) and true positive (CB cells), respectively.

Table 3.

Overall accuracy of the CAD (44 centroblasts and non-centroblasts)

Sensitivity	Specificity
81.8%	86.4%

Table 4 shows the number of cases from the 88 cases in the testing set (44 CB and 44 non- CB) where 4 or more of the six pathologists agreed in the manual grading of the CB cells and the non-CB cells and the computer’s diagnosis of these cases. The sensitivity and specificity of the stand-alone computer grading are also presented. Based on the results presented in Table 4, the stand-alone grading demonstrates very promising results in terms of sensitivity and sensitivity with this new consensus truth. The values of these measurements are 86.67% and 86.96%, respectively.

Table 4.

Sensitivity and specificity of the CAD system on consensus (≥ 4 pathologist agreement) cases

	Computer diagnosis
Consensus	CB Cell	Non-CB Cell	Performance:
CB Cell	13	2	Sensitivity: 86.67%
Non-CB Cell	3	20	Specificity: 86.96%

IV. Conclusion

In this paper, we have demonstrated a new quantitative methodology to diagnosis CB and non-CB cells in follicular lymphoma using geometric and color texture features in the spectral domain. A statistical analysis has been performed to evaluate the stand-alone accuracy of a CAD system on centroblast and non-centroblast cell grading. The results of our analysis are encouraging. Further investigation of certain parameters in the algorithm is needed and will likely improve the system’s accuracy. Some limitations still exist in recognizing CB cells from non-CB cells, which are caused mainly by the variation in the morphology of the cells and the lack of contextual information. Visual evaluation of the false-positives indicate that these are mostly large centrocytes and follicular dendric cells while the false negatives are mainly caused by small centroblast cells. The segmentation algorithm should be improved by taking into account the variations in staining and by using other color/texture features to improve the overall the system accuracy. In addition, a larger study involving more patients and pathologists is underway to improve generalizability of the results and to assess the impact of CAD on inter- and intra-reader variability. The biological variation between patients will be further studied to demonstrate the inter – and intra- patient variability introduced during the readings.