A Nonlinear Thin-Wall Model for Vein Buckling

Abstract

Tortuous or twisted veins are often seen in the retina, cerebrum, and legs (varicose veins) of one-third of the aged population, but the underlying mechanisms are poorly understood. While the collapse of veins under external pressure has been well documented, the bent buckling of long vein segments has not been studied. The objectives of this study were to develop a biomechanical model of vein buckling under internal pressure and to predict the critical pressure. Veins were modeled as thin-walled nonlinear elastic tubes with the Fung exponential strain energy function. Our results demonstrated that veins buckle due to high blood pressure or low axial tension. High axial tension stabilized veins under internal pressure. Our buckling model estimated the critical pressure accurately compared to the experimental measurements. The buckling equation provides a useful tool for studying the development of tortuous veins.

Introduction

Tortuous or twisted veins are found in one third of the aged population and are often seen in the retina, cerebrum, and lower legs.^{3–5,16,24,26} Venous tortuosity affects blood flow and the wall remodeling process, both of which are associated with venous diseases.^15,17,20,27 It has been shown that deep vein tortuosity may lead to thrombosis.^16,20,28 Tortuous or varicose veins, which cause pain, blood clots, or ulcers, are often associated with aging, diabetic mellitus, hypertension, or pregnancy,^{1,3,4,6,16,18,26} but the underlying mechanisms are unclear. Therefore, it is of clinical interest to unveil the mechanism of vein twisting and tortuosity.

We have previously shown that arteries buckle due to reduced axial tension or hypertensive pressure.^9,10 Our recent work demonstrated that veins buckle similarly when the lumen pressure exceeds a critical level.^21,22 In that study, the wall stiffness of the veins was determined based on either a linear average or a one-dimensional exponential fitting of the axial elongation of the veins under internal pressure. Using these data values, the model overestimated the critical pressure compared to the experimental measurements. An improved model is needed for more accurate predictions. Since veins are thin walled structures, it is necessary to establish a two-dimensional thin-walled model that better represents the vein wall structure for vein buckling analysis.

The objectives of this study were to establish a biomechanics model of vein buckling under internal pressure using the two dimensional Fung strain energy function and to test its predictive value.

Methods

Experimental Measurements of Vein Properties and Buckling Pressure

We used a pressurized inflation test to determine the mechanical properties of porcine jugular veins and then measured their buckling pressure under a series of axial stretch ratios. A detailed description of the experimental methodology was published previously.²² Briefly, porcine jugular veins were pressure inflated with physiological buffered saline (PBS) with one end of the veins left free to expand. So the veins were free to elongate while being inflated under a slowly increasing lumen pressure. After preconditioning, the inflation process was recorded for pressure and dimension (diameter and axial length) measurements. These values were later used for the stress strain calculations.

For the bucking test, veins were connected to cannulae at both ends and stretched to given stretch ratios. The cannulae were fixed to provide fixed end support for the veins during the test. The lumen pressure was then slowly increased to generate vein buckling and continued until a large deflection was reached. The deformation and pressure were recorded and the pressure at which the veins started to deflect (deflection became detectable at ∼0.5 mm from the initial baseline) was measured as the critical pressure.²²

Two-Dimensional Thin-Walled Cylindrical Vein Model

Veins are considered as thin-walled cylindrical tubular vessels. The wall material is assumed to be homogenous and orthotropic, and is characterized by a Fung two-dimensional (2D) strain energy function.⁷

$$w=\frac{1}{2}{b}_0{e}^Q,Q=b_1{E}_{\theta }^2+b_2{E}_z^2+2b_4{E}_{\theta }{E}_z$$ (1)

wherein b₀, b₁, b₂, and b₄ are material constants and E_θ and E_z are the circumferential and longitudinal Green strains.

Let's designate the inner radius, wall thickness, and length of the vein to be R, T, and L at the initial unloaded state (ignoring the residual stress) and r, t, and l at the loaded state, respectively. Veins are under lumen pressure and significant axial strain in vivo.¹³ For veins under lumen pressure p and axial tension N (with an axial stretch ratio ${\lambda }_z^0$ accordingly), we have

$$\begin{array}{c}r=r(R,p,N)\hfill \\ l={\lambda }_z^{0}L.\hfill \end{array}$$ (2)

And the incompressibility of the wall yields

$$t=\frac{R}{{\lambda }_z^{0}r}T.$$ (3)

The Green strains in the circumferential and longitudinal directions are

$$\begin{array}{c}\hfill E_{\theta }=\frac{1}{2}({\lambda }_{\theta }^2-1),E_z=\frac{1}{2}({\lambda }_z^2-1),\\ \hfill \text{with}{\lambda }_{\theta }=\frac{r}{R},{\lambda }_z={\lambda }_z^0=\frac{l}{L}.\end{array}$$ (4)

It is seen that all strain components are axisymmetric and uniform across the vein wall. From the Fung strain energy function, the Cauchy stresses are

$$\begin{array}{c}{\sigma }_{\theta }=(1+2E_{\theta })(b_1{E}_{\theta }+b_4{E}_z)b_0{e}^Q\\ {\sigma }_z=(1+2E_z)(b_2{E}_z+b_4{E}_{\theta })b_0{e}^Q.\end{array}$$ (5)

On the other hand, the circumferential stress in thin-walled veins can be determined using Laplace's law:

$${\sigma }_{\theta }=\frac{pr}{t}.$$ (6)

The axial stress is determined by

$${\sigma }_z=\frac{N}{2\pi rt}.$$ (7)

Combining Eqs. (5), (6), and (7) yields

$$p=\left(\frac{rt}{R^2}\right)(b_1{E}_{\theta }+b_4{E}_z)b_0{e}^Q$$ (8)

$$N=2\pi rt{\left({\lambda }_z^0\right)}^2(b_2{E}_z+b_4{E}_{\theta })b_0{e}^Q.$$ (9)

Therefore the deformed radius r can be determined for given pressures.

Determination of Material Constants of Veins

For veins with one end free to expand under internal pressure, the axial force generated by the internal pressure is

$$N=p\pi r^2.$$ (10)

Taking Eq. (10) into Eq. (7) yields

$${\sigma }_z=\frac{pr}{2t}.$$ (11)

Therefore, with the experimental measurements of the vessel diameter and length at each given pressure, the corresponding stresses and strains were determined using Eqs. (4), (6), and (11) as reported in our previous studies.²² The material constants were then determined by fitting the experimental data with Eq. (5) using Matlab.

Buckling Equation for Veins

The buckling equation was derived using a similar approach as described in our previous studies.^9–11 Since veins will deform into sinusoidal shapes when buckling occurs,¹² we assumed a buckling mode shape

$$u_c=C\cdot sin\left(\frac{n\pi z}{l}\right),n=1,2,3,4,5,\dots$$ (12)

where C is a small-value constant and z is the axial coordinate of the central axis before buckling.

Accordingly, the deformed coordinates for a point on the vein wall are

$$\begin{array}{c}\rho =r(R,p,N)+C\cdot cos\mathrm{\Theta }sin\left(\frac{n\pi z}{l}\right)\hfill \\ \theta =\mathrm{\Theta }-\frac{C}{r}\cdot sin\mathrm{\Theta }sin\left(\frac{n\pi z}{l}\right)\hfill \\ \zeta =z-\frac{n\pi r}{l}C\cdot cos\mathrm{\Theta }cos\left(\frac{n\pi z}{l}\right)\hfill \end{array}$$ (13)

where (r, Θ, z) are the pre-buckling coordinates of a material point (R, Θ, Z) in the no-load state.

Thus, the circumferential and axial stretch ratios in the vessel wall of the bent buckled vessel are:

$$\begin{array}{c}{\lambda }_{\theta }=\frac{\rho }{R}\frac{\partial \theta }{\partial \mathrm{\Theta }}=\frac{r}{R}\left[1-\left(\frac{C}{r}cos\mathrm{\Theta }sin{\left(\frac{n\pi z}{l}\right)}^2\right)\right]\hfill \\ {\lambda }_z=\frac{\partial \zeta }{\partial Z}={\lambda }_z^0\left[1+{\left(\frac{n\pi }{l}\right)}^{2}rC\cdot cos\mathrm{\Theta }sin\left(\frac{n\pi z}{l}\right)\right]\hfill \end{array}$$ (14)

Neglecting the high order terms of small C, the only non-zero incremental strain is

$$\mathrm{\Delta }{E}_z={\left(\frac{n\pi }{L}\right)}^{2}rCcos\mathrm{\Theta }sin\left(\frac{n\pi z}{l}\right)$$ (15)

It is seen that the axial strain becomes non-axisymmetric after buckling (though symmetric to the plane of Θ = 180°). Accordingly, the bending moment M(z) in the vessel can be obtained by integrating the moment generated by the incremental axial stress Δσ_z over the cross-sectional area A of the arterial wall

$$\begin{array}{cc}M(z)\hfill & =\underset{A}{\int }(\mathrm{\Delta }{\sigma }_z)(dA)(rcos\mathrm{\Theta })\hfill \\ \hfill & =r^{2}t\underset{0}{\overset{2\pi }{\int }}\left(\frac{\partial {\sigma }_z}{\partial E_z}\mathrm{\Delta }{E}_z\right)(cos\mathrm{\Theta })d\mathrm{\Theta }.\hfill \end{array}$$ (16)

Taking Eqs. (15) and (5) into Eq. (16) and integrating with respect to Θ leads to

$$M(z)=H_n\cdot C\cdot sin\left(\frac{n\pi z}{l}\right)$$ (17)

where H_n is the “bending force” at buckling.

$$H_n={\left(\frac{n\pi }{L}\right)}^2\pi r^{3}t\left[2(b_2{E}_z+b_4{E}_{\theta })+(1+2E_z)b_2+2(1+2E_z){(b_2{E}_z+b_4{E}_{\theta })}^2\right]b_0{e}^Q.$$ (18)

On the other hand, the internal pressure generates a lateral load q(z), in buckled vessels, due to the uneven size on the concave and convex sides of the vessels^9,11

$$q(z)=p\pi r^2{\left(\frac{n\pi }{l}\right)}^{2}C\cdot sin\left(\frac{n\pi z}{l}\right).$$ (19)

Based on the equations of equilibrium, the bending moment M(z) generated by q(z) is

$$M(z)=(-N+p\pi r^2)C\cdot sin\left(\frac{n\pi z}{l}\right).$$ (20)

Combing Eqs. (20) and (17) gives the critical pressure

$$p\frac{N+H_n}{\pi r^2}.$$ (21)

Taking Eqs. (9) and (18) into Eq. (21) yields

$$p={\left(\frac{n\pi }{L}\right)}^{2}rt\left[2(b_2{E}_z+b_4{E}_{\theta })+{\left({\lambda }_z^0\right)}^2{b}_2+2{\left({\lambda }_z^0\right)}^2{(b_2{E}_z+b_4{E}_{\theta })}^2\right]b_0{e}^Q+2\left(\frac{t}{r}\right){\left({\lambda }_z^0\right)}^2(b_2{E}_z+b_4{E}_{\theta })b_0{e}^Q.$$ (22)

At a given axial stretch ratio, the circumferential strain and radius are functions of pressure. Thus the critical pressure can be determined using Eqs. (8) and (22).

Model Prediction and Simulations

For each vein tested in our previous study, the material constants in the Fung strain energy function were determined by fitting experimental data as described above. Using these material constants, the critical pressure of each vein was estimated using the buckling equation for various axial stretch ratios. Specifically, for each vein at each given axial stretch ratio, the vessel dimensions and strains were determined for each incremental radius step. The lumen pressure was determined using Eq. (8), and the corresponding “buckling pressure” was determined using Eq. (22). The critical pressure was determined as the pressure that satisfies both Eqs. (8) and (22). In addition, a parametric study was performed to investigate the effects of vessel dimensions on the critical pressure using the thin-walled vessel buckling model.

Results

Material Constants for Porcine Jugular Veins

The circumferential and axial Green strains and Cauchy stresses were determined from the experimental data using Eqs. (4), (6), and (11). While we previously fitted the axial stress–strain data with a one dimensional (1D) exponential stress–strain relationship,²² here we used the Fung two-dimensional (2D) strain energy function. For comparison, the strain energy function was first fitted to only the axial stress–strain data and then fitted to both the axial and circumferential stress–strain data simultaneously (Fig. 1). It is seen that the Fung 2D strain energy function achieved an accurate fitting to the experimental data (with R = 0.984 on average). The corresponding material constants b₀, b₁, b₂, and b₄ obtained from the fittings are summarized in Table 1.

FIGURE 1.

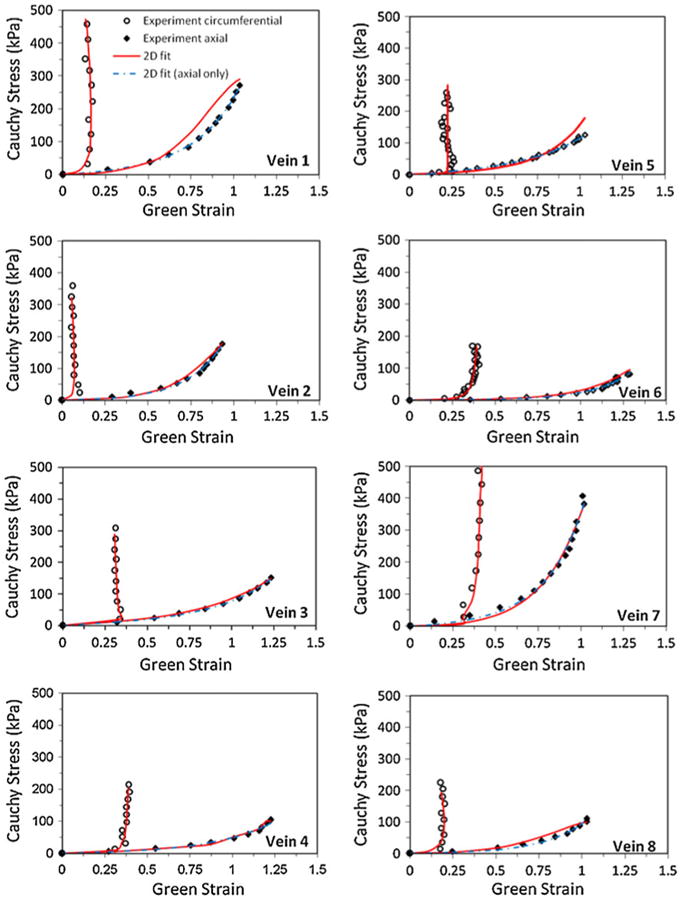
Comparison of the experimental stress and strain data with the fitting curves obtained using the Fung two dimensional (2D) strain energy function. The open circles and the closed diamonds represent the experimental circumferential and axial results respectively. The solid line (2D fit) represents the fitting curves from simultaneous fitting of the axial and circumferential data. The dot-dashed line (2D fit, axial only) represents the fitting curves from fitting the axial stress strain data only.

TABLE 1. Material constants b₀, b₁, b₂, and b₄ determined from vein inflation experiments²².

	Fitting axial stress–strain data only				Fitting axial and circumferential stress–strain data simultaneously
	b0	b1	b2	b4	b0	b1	b2	b4
Vein 1	74.83	0.001	1.039	0.001	54.871	0.001	0.795	6.382
Vein 2	33.430	13.930	1.730	0.002	27.700	0.001	1.586	10.110
Vein 3	38.028	34.648	0.856	0.207	42.250	2.000	0.095	2.910
Vein 4	30.775	0.001	0.218	1.626	30.800	3.150	0.136	1.965
Vein 5	39.900	26.890	0.519	0.260	6.540	2.060	0.530	4.980
Vein 6	5.060	0.001	1.240	0.001	5.520	0.993	0.001	2.870
Vein 7	89.070	0.001	1.384	0.018	87.520	4.000	0.190	2.990
Vein 8	14.370	0.222	1.295	0.002	29.390	0.001	0.276	4.537

The material constants were determined by fitting Eq. (5) with the experimental data using Matlab.

Model Predicted Critical Pressures

The critical pressures of the veins, at given axial stretch ratios, were estimated using the buckling equation and each vein's own material constants as listed in Table 1. The results showed that the critical pressure increased nonlinearly with an increase in the axial stretch ratio and that the predicted critical pressures fit the experimental data well (Fig. 2). The estimations based on the 1D stress strain relationship from our previous studies^21,22 are also given in Fig. 2 for comparison. It is seen that in all but one vein, the 2D model generated better predictive results than the 1D model.

FIGURE 2.

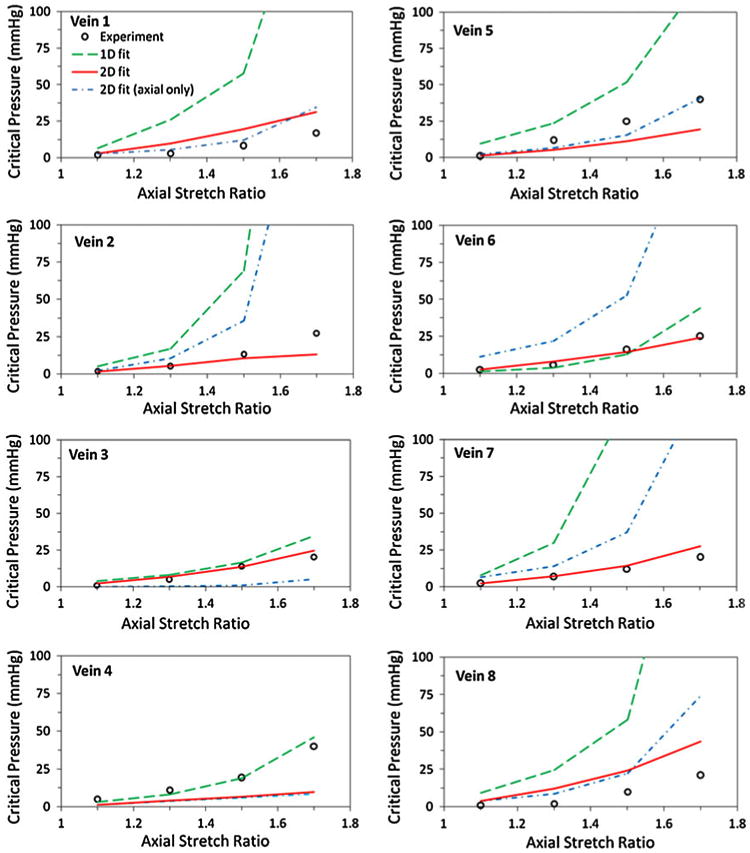
Comparison of experimental and model predicted buckling pressures plotted as functions of the axial stretch ratio. The open circles represent the experimental buckling results.²² The solid line (2D fit) represents the buckling pressure predicted using the material constants obtained from simultaneous fitting of the circumferential and axial data. The dot-dashed line (2D fit, axial only) represents the buckling pressure predicted using the material constants from fitting the axial data only. These 2D material constants are listed in Table 1. The dashed line (1D fit) represents the 1D model predictions given in our previous paper.²²

In addition, the effect of vein dimensions on the buckling pressure was examined through numerical simulations (Fig. 3). The material constants of vein #1 were used in these simulations. The range of slenderness ratio (length to radius ratio, L/r_i) and wall thickness to radius ratio (t/r_i) used in the simulations were based on the range of our experimental measurement of the jugular veins (L/r_i = 7.83–14.36 and t/r_i = 0.06–0.14),²² but a wider range of variations were included for the dimensional parameters to cover different veins. Our results showed that the vessel slenderness ratio (L/r_i) and wall thickness to radius ration (t/r_i) have a significant effect on the critical pressure as previously demonstrated for linear models.⁹ Specifically, an increased vessel length reduced the critical pressure and thinner walls reduced the critical pressure as well. Thus, long, thin vein segments are more prone to buckling than short, thick ones. This trend is similar to the results demonstrated in the linear model for arteries.⁹

FIGURE 3.

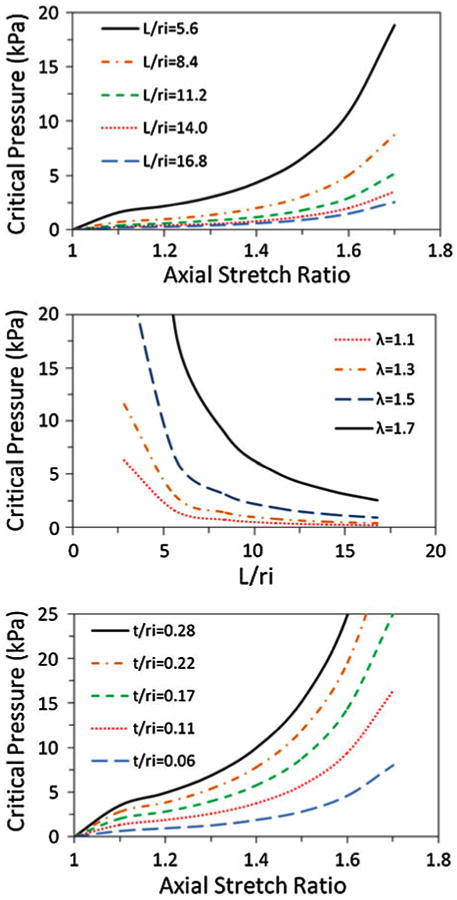
Effect of length and wall thickness on critical pressure. Top: critical pressure vs. axial stretch ratios at different slenderness ratios L/r_i. Middle: critical pressure vs. slenderness ratio L/r_i at four axial stretch ratios. Bottom: critical pressure vs. axial stretch ratios at five different t/r_i ratios.

Discussion

In this study, we developed a buckling equation for veins using a nonlinear elastic thin-walled cylindrical model. Our results demonstrated that veins buckle when the internal pressure exceeded a critical value, which depended upon the axial stretch ratio and wall stiffness. The 2D thin-walled model predicted the critical pressure with good accuracy.

Previously, we used a simple one-dimensional (1D) model to estimate the critical pressure and found that the 1D model largely overestimated the critical pressure of the veins.²² Our current results showed that the 2D models yielded a much better prediction of the experimental critical pressure than our previous 1D model. Though the 2D data did under predict the critical pressure for two veins, it demonstrated much better predictions than the 1D model overall. This advantage may be due to the fact that while the 1D model was based on the arterial wall properties in only one direction (the axial stress–strain data), the 2D material model was based on the properties in two directions (both the axial and circumferential stress and strain data), which took into account the interactions between the axial and circumferential directions. Therefore, the 2D model provides a much better estimation than the 1D model.

An interesting observation was that although the vein diameter initially increased with pressure, it actually decreased slightly as the pressure increased. We have used additional veins to measure the diameters with much higher resolution images and the results confirmed this trend. We think there were two possible reasons for this phenomenon. First, the pressure vs. diameter test was done with veins free to extend axially. The elongation in the axial direction would reduce the diameter of the veins due to the incompressibility of the wall. In contrast, the commonly observed diameter increase under increasing inflation pressure reported in the literature was obtained with vessels fixed on both ends thus had no axial elongation. Secondly, the measurements were of the outer diameter of the wall. The outer diameter of the wall may decrease even if lumen diameter increases under lumen pressure due to wall thinning.

Model Limitations and Applications

The model equations were derived for a thin-walled vein model using the adjacent equilibrium approach.^11,12 The ends of the vessel were fixed in the buckling tests and thus in the subsequent model simulations; the effect of contiguous tissue tethering was ignored in the current model. While the effect of tissue tethering has been discussed in one of our previous reports,¹¹ the rationale for this simplification was to match the conditions used in our previous experimental study to validate the model.²² While these limitations exist, the model generally fits well with the experimental data. The main conclusions from the current nonlinear thin-walled model agree with our previous results for arteries.^9,10 As discussed previously, the current model equations can be easily extended to other boundary conditions such as different end supports and surrounding tissue supports.^11,12

There are multiple factors that may have contributed to the differences between the model prediction and the experimental measurements. First, the model was based on the assumption of an ideal cylindrical shape and homogenous wall, but the geometry of veins demonstrated variations in the wall from the ideal model. Secondly, vein walls are very thin and therefore the imperfections in wall dimension and material properties would have a significant effect on the critical pressure.

Clinical Relevance

The normal physiological pressure of jugular veins is in the range of 3–13 mmHg and the normal axial stretch ratio in jugular veins is in the range of 1.7–1.8.^2,22 Thus veins are very stable under normal venous pressure in vivo. However, buckling is possible under certain conditions as demonstrated by our previous work²² and the current study.

Our model equations clearly demonstrated that the axial stretch ratio in veins plays a significant role in maintaining the stability of veins. Veins are under significant axial strain in vivo.¹³ However, hypertensive venous pressure and reduced axial strain associated with venous hypertension and aging could reduce the critical pressure and cause veins to buckle. Pressure build-up in leg veins due to valve malfunction could lead to vein buckling in addition to vein enlargement.

Another example is vein grafting. Veins are subject to high arterial pressures after being grafted to blocked or damaged arteries. Vein grafts may buckle under arterial pressure when not properly placed, especially when the vein segments are too long.^13,14 The buckling could potentially compromise the normal functioning of the vein grafts. The critical pressure and axial tension that lead to vein buckling are thus very important parameters for surgical consideration. The current model provides a useful tool for determining these parameters.

We have shown that veins buckle with reduced stretch ratios and increased pressure. Vein buckling could alter the blood flow and wall stress that leads to wall remodeling.^8,19,23,25 In addition to biological factors, mechanical buckling could be a possible cause of tortuous veins, such as varicose veins, in human legs. Further studies of tortuous veins, including varicose veins, are needed to better understand this phenomenon. The current model provides a useful tool for experimental designs to produce or prevent tortuous veins.