Aging and the Shape of Cognitive Change Before Death: Terminal Decline Or Terminal Drop?

Abstract

Objectives.

Relative to typical age-related cognitive decrements, the terms “terminal decline” and “terminal drop” refer to the phenomenon of increased cognitive decline in proximity to death. Given that these terms are not necessarily synonymous, we examined the important theoretical distinction between the two alternative trajectories or shapes of changes they imply.

Methods.

We used 12-year (5-wave) data from the Victoria Longitudinal Study to directly test whether pre-death cognitive decrements follow a terminal decline (generally gradual) or a terminal drop (more abrupt) shape. Pre-death trajectories of cognitive decline for n = 265 decedents (M_age = 72.67 years, SD = 6.44) were examined separately for 5 key cognitive constructs (verbal speed, working memory, episodic memory, semantic memory, and crystallized ability).

Results.

Several classes of linear mixed models evaluated whether cognitive decline increased per additional year closer to death. Findings indicated that the shape of pre-death cognitive change was predominantly characterized by decline that is steeper as compared with typical aging-related change, but still best described as slow and steady decline, especially as compared with precipitous drop.

Discussion.

The present findings suggest that terminal decline and terminal drop trajectories may not be mutually exclusive but could rather reflect distinct developmental trajectories within the same individual.

CONSISTENT with the early and conventional terminal decline hypotheses (e.g., Riegel & Riegel, 1972), subsequent research has indicated that accelerated cognitive decline in older adults is not only a function of neurodegenerative disease processes (e.g., leading to dementia) but also related to broader biological decline in proximity to death. An association between cognitive functioning and impending mortality has critical implications for determining the shape and identifying the sources of normal cognitive decline with aging. Arguably, just as the presence of identified cognitively impaired or dementia patients in a study sample can lead to overestimation of normative adult age differences, so can the undiagnosed presence of conditions associated with impending mortality (Kleemeier, 1962). A plausible scenario is that, in the absence of neuropathogenic cognitive decline, most people may maintain stable or slightly declining functions into old age, with more marked decline indicating biological compromise (e.g., cardiovascular disease) associated with impending mortality. Although the source of theoretical confusion and the subject of empirical debate, it is not yet settled whether the predominant shape and magnitude of cognitive decline trajectories preceding death follow a relatively steady linear decline function (i.e., “terminal decline”) or a more accelerated curvilinear function (i.e., “terminal drop”; Palmore & Cleveland, 1976; Siegler, 1975).

Although terminal decline and terminal drop are often used as synonyms, observers (e.g., Berg, 1996) have cautioned that the different shapes implied by these terms may carry distinct theoretical and clinical implications. Theoretically, a curvilinear shape to change characterized by an abrupt drop before death may be attributable to an underlying disease or near-clinical status (e.g., engulfing presence of comorbidities, severe neurobiological compromise, impending death). For example, there is some evidence to suggest that the effect of impending death on cognition is modulated by one or more specific disease processes, including organ failure, cancer, dementia, diabetes, and respiratory and vascular conditions (e.g., Anstey, Mack, & von Sanden, 2006; Hassing et al., 2002; Laukka, MacDonald, & Bäckman, 2006). Whereas certain causes of death (e.g., neoplasms) may be linked to relatively protracted preterminal periods characterized by slow-but-steady decline, other causes of death (e.g., vascular diseases such as stroke and heart attack) are known to diminish cognitive performance and exacerbate cognitive decline, likely reflecting the relatively acute nature of vascular causes of death and corresponding abrupt influence on cognition (see Wilson, Beck, Bienias, & Bennett, 2007). Thus, decline versus drop differences in the shape of mortality-related cognitive trajectories may have both theoretical importance (in modulating observed age differences and aging changes) and clinical significance (reflecting distinct underlying causes of death).

Methodologically, the literature has developed to a point that some of the previously intractable challenges of analyzing, evaluating, and comparing terminal decline versus drop trajectories can be addressed, given appropriate research design and measurement conditions. For example, new approaches have been proposed for indexing developmental time, addressing confounds in sample composition, and applying sensitive statistical analyses to change data (e.g., Sliwinski & Mogle, 2008). To date, however, evidence from these most recent studies is mixed, with results interpreted to support both trajectories. Regarding the terminal drop trajectory, Wilson, Beckett, Bienias, Evans, and Bennett (2003) used change-point models to estimate how long prior to death that cognitive decline exhibited acceleration, as well as the rates of decline prior to and following this change point. With such models, evidence for a terminal drop trajectory should reflect particularly pronounced decline within close proximity to death (i.e., accelerated decline post-change point, with the inflection point of change occurring in close proximity to the death event). Accelerated decline was observed across numerous cognitive constructs (e.g., episodic memory, working memory, perceptual speed) and associated indicators within 3–6 years of death. Within 3.5 years of death, decline for an index of global cognition accelerated more than sixfold relative to the period preceding the change point, a pattern consistent with terminal drop. Similarly, Thorvaldsson, Hofer, Berg, and Johansson (2006) examined terminal decline for a single cognitive outcome (perceptual speed). They observed mortality-related cognitive decline as a function of both chronological age and proximity to death, with the latter providing a better model fit. Moreover, significant quadratic decline (deemed consistent with terminal drop) was observed per additional year closer to death.

Regarding the gradual terminal decline trajectory, other research supports the view that the pre-death decline function is linear and not curvilinear. For example, Sliwinski and colleagues (2006) used a change-point approach to examine mortality-related episodic memory decline as a function of both age and time to death. Although increased terminal decline was identified 8.4 years prior to death (a rate twice that observed as a function of chronological age), no evidence for abrupt terminal drop was observed. Accordingly, Sliwinski and colleagues surmised that reports of terminal drop may reflect a confounding of rates of change for decedents and survivors. Similarly, in their joint analysis of longitudinal and survival data, Ghisletta, McArdle, and Lindenberger (2006) found that only one of eight cognitive outcomes exhibited quadratic change, thereby providing little support for the terminal drop interpretation. The authors emphasized that, because developmental time was modeled as a function of chronological age (time since birth), their models were not optimally suited for testing the terminal drop hypothesis. Notably, time to death may represent a more sensitive developmental index for modeling abrupt drops in cognitive performance (MacDonald, Hultsch, & Dixon, 2008; Sliwinski, Hofer, Hall, Buschke, & Lipton, 2003).

The present goal is to directly test whether (and, if so, under what conditions) terminal drop can be identified and differentiated from terminal decline. We use data from the Victoria Longitudinal Study (VLS; Dixon & de Frias, 2004). The VLS provides several important methodological advantages for conducting such analyses: (a) multiple measurement waves (up to five), (b) well-characterized parent samples (c) available large samples of decedents, (d) a multidimensional cognitive battery, and (e) relatively short retest intervals (3 years). These features permit a formal examination of alternative trajectories associated with terminal decline versus terminal drop. We focus on three main research questions. First, is the mortality–cognition association limited to a narrow interval preceding death? Second, do decedents closer to death show exacerbated cognitive decline characteristic of terminal drop? Third, are terminal drop trajectories (if present) similar across cognitive domains?

Operationally, the answers to these questions determine whether an interpretation of terminal drop (over and above terminal decline) would be justified. Specifically, our criteria required that the following three conditions be met. Specifically, given that conventional terminal decline would be observed, terminal drop would be indicated if the decline (a) can be detected a number of years preceding death, (b) accelerates in proximity to the death event, and (c) is manifested robustly across a range of cognitive outcomes. As a novel feature of this study, we test these conditions by examining cognitive change in relation to number of years to death, a more sensitive and process-based parameterization of time relative to wave or chronological age (e.g., Sliwinski & Mogle, 2008). Whereas many previous studies have performed cross-sectional analyses of longitudinal data (e.g., survival analysis) or longitudinal analyses using repeated measures analysis of variance, the present study employs multilevel modeling to examine across-time covariation between cognitive decline and actual time to death for decedents. Two plausible sets of statistical models for differentiating terminal cognitive decline from drop are evaluated. The first set includes “linear plus quadratic decline models,” for which a significant quadratic effect has been interpreted as evidence for terminal drop (cf. Ghisletta et al., 2006). The second are “change-point models,” for which inflection points differentiating preterminal from terminal cognitive decline are interpreted as reflecting a sensitive test of terminal drop (cf. Sliwinski et al., 2006; see Figure 1). Furthermore, given that previous researchers have argued persuasively that the terminal drop phenomenon may at least partially reflect the conflation of rates of change for samples that include survivors and decedents, the present investigation focuses exclusively on participants who died during the course of the study (cf. Rabbitt, Lunn, & Wong, 2008; Sliwinski et al., 2006). Finally, given the possibility that the shape of pre-death cognitive decline may vary by cognitive domain, we test these models across five theoretically important domains of functioning.

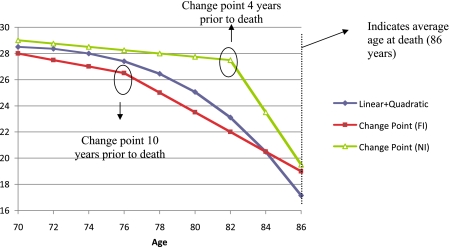
Figure 1.

The figure displays the mapping between theoretical implications of terminal decline versus drop and choice of statistical model for evaluating the distinction. Although often considered as evidence for terminal drop, a linear plus quadratic slope model is not necessarily the definitive choice for differentiating terminal decline from terminal drop. As shown in the figure, the significant linear plus quadratic trend may reflect a steadily accelerating, but nonetheless gradual, terminal decline spanning a period of years prior to death. Similarly, a linear spline model with an inflection point far from death (change point far inflection, or FI) may indicate increased decline following the change point, but similar to the displayed linear plus quadratic model, this decline is manifest in a more gradual fashion many years preceding death (10 years in the hypothetical example). However, a change-point model with an inflection point near death (change point near inflection, or NI) represents a reasonable statistical instantiation of terminal drop, with abrupt cognitive change occurring in close proximity to the death event (4 years in the example). A change trajectory characterized by a larger magnitude quadratic effect (not displayed) could also approximate the change point NI trajectory, consistent with terminal drop.

Methods

Participants

At intake, VLS participants are community-dwelling adults between 55 and 85 years of age with no serious health conditions. They are followed at 3-year retest intervals or waves (for details, see Dixon & de Frias, 2004; Hultsch, Hertzog, Dixon, & Small, 1998). We assembled data from VLS Sample 1 (Waves 1–5; 12 years) and VLS Sample 2 (Waves 1–3; 6 years). Of the 1,014 baseline participants, 265 confirmed decedents were identified by the censoring date (i.e., the date of last systematic search through vital status records). Decedents’ average age was 72.67 years (SD = 6.44) and 75.61 years (SD = 7.12) at baseline and final wave of testing, respectively. Decedents completed from one to five assessment waves, with subsequent date of death confirmed through vital statistics records for the province of British Columbia, Canada. The mean interval between each decedent’s first wave of testing and subsequent death was approximately 8.1 years. Questionable dementia was listed as an antecedent condition (not primary cause) on death certificates for 33 decedents. Although VLS ledgers confirmed that these individuals were not demented at baseline, definite dementia diagnosis and date of incidence were unavailable in vital statistics records. Analyses were computed both with and without these cases; because identical patterns of statistical inference were observed, we included them in the present results (see Wilson et al., 2003). Additional demographic and health information on these participants is available in MacDonald and colleagues (2008).

Distinguishing between trajectories consistent with either terminal decline or terminal drop requires sufficient (a) numbers of decedents, (b) longitudinal waves of measurement, and (c) data observations within close proximity to the death event. Of the 265 decedents with available data, more than 50% completed two or more measurement occasions (see Table 1). A total of n = 9 decedents completed five measurement waves (3.4%), n = 18 completed four waves (6.8%), n = 49 completed three waves (18.5%), and n = 68 completed two waves (25.7%), with n = 121 (45.7%) completing a single wave. From baseline, the total number of observations (and associated percent) as a function of years before death were as follows: n = 22 within 1 year of death (4.2%), n = 38 within 2 years (7.3%), n = 42 within 3 years (8.1%), n = 38 within 4 years (7.3%), n = 50 within 5 years (9.6%), n = 50 within 6 years (9.6%), n = 45 within 7 years (8.6%), n = 36 within 8 years (6.7%), n = 49 within 9 years (9.4%), n = 31 within 10 years (6.0%), n = 17 within 11 years (3.3%), n = 34 within 12 years (6.5%), n = 27 within 13 years (5.2%), n = 16 within 14 years (3.1%), n = 21 within 15 years (4.0%), and n = 5 within 16 years (1.0%). Finally, Table 2 summarizes the number of individual cases with available data as a function of years to death and waves of testing completed. Considered together, these patterns confirm that sufficient data are available to achieve the study objectives.

Table 1.

Participant Attrition and Mortality Status for Each Measurement Wave

Attrition status	Wave of testing
	Wave 1	Wave 2	Wave 3	Wave 4	Wave 5	Wave 6
Sample 1 (year tested)	1986	1989	1992	1995	1998	2002
Returned	484 (100)	333 (68.8)	249 (74.8)	177 (71.1)	120 (67.8)
Dropped out
Personal health		10 (2.1)	15 (4.5)	9 (3.6)	12 (6.8)
Family health		6 (1.2)	1 (0.3)	3 (1.2)	7 (3.9)
Memory problems		2 (0.4)	0 (0.0)	0 (0.0)	1 (0.6)
Busy/not interested		48 (9.9)	15 (4.5)	15 (6.0)	7 (3.9)
Moved		9 (1.9)	8 (2.4)	2 (0.8)	3 (1.7)
Could not be located		4 (0.8)	7 (2.1)	0 (0.0)	0 (0.0)
Deceased		72 (14.9)	38 (11.4)	43 (17.3)	18 (10.2)	9 (5.1a)
Sample 2 (year tested)	1992	1996	1999	2002
Returned	530 (100)	410 (77.3)	327 (79.7)
Dropped out
Personal health		12 (2.3)	18 (4.4)
Family health		2 (0.4)	4 (1.0)
Memory problems		0 (0.0)	3 (0.7)
Busy/not interested		34 (6.4)	13 (3.2)
Moved		12 (2.3)	3 (0.7)
Could not be located		11 (2.1)	6 (1.5)
Deceased		49 (9.2)	30 (7.3)	6 (1.5a)

Notes: Values in parentheses reflect percentage of participants associated with a particular category. Column totals per sample may not sum to 100% due to rounding error.

^aAs of the most recent search of vital statistics records, these participants were confirmed deceased prior to follow-up testing.

Table 2.

Number of Individual Cases With Available Data as a Function of Years to Death and Waves of Testing Completed

Years to death	Waves of testing completed
	1 (n = 121)	2 (n = 68)	3 (n = 49)	4 (n = 18)	5 (n = 9)
1	5	7	6	1	3
2	8	13	10	3	4
3	13	16	7	4	2
4	14	4	4	4
5	13	3	1	1
6	9	7	3	4
7	8	7	6	1
8	8	3	2
9	11		7
10	2	3	3
11	2
12	11	4
13	6	1
14	8
15	2
16	1

Cognitive Measures

Indicators of five cognitive constructs (i.e., verbal speed, working memory, episodic memory, semantic memory, and vocabulary) sensitive to cognitive health, aging, and survival were selected from previous VLS confirmatory factor analyses (see Hertzog, Dixon, Hultsch, & MacDonald, 2003; Hultsch et al., 1998).

Verbal speed.—

Speed of verbal processing was indexed by a computer-based semantic verification task. Participants were asked to rapidly judge the plausibility of 50 test sentences (25 plausible and 25 implausible). The score used was the mean reaction time computed across trials.

Working memory.—

Working memory was assessed by a sentence construction task. Each of a series of sentences presented on cards contained a highlighted word to be maintained in memory for later recall in serial order to produce a new sentence. The outcome measure was the highest number of newly formed sentences (from sequences of three, four, five, and six sentences) correctly recalled for two out of three passage lengths.

Episodic memory.—

Two word lists were used, with each list consisting of six words from five taxonomic categories (e.g., birds) typed on a single page in unblocked order. Participants were given 2 min to study each list and 5 min to write their free recall. The average number of correctly recalled words was the outcome measure.

Semantic memory.—

Participants wrote their answers under self-paced conditions to two 40-item recall tests of world facts from multiple domains (e.g., science, history, sports). The outcome measure was the average number of correct items.

Crystallized ability.—

English vocabulary was indexed by a 54-item recognition vocabulary measure, with a 15-min response period. The score was the number of correct responses.

Data Imputation and Preparation

Full data across all relevant waves were available for 246 (93%) of the 265 decedents. Of the 19 decedents with at least one missing data point at any wave, most (n = 17) were missing data for only a single task on a single wave. Less than 1% of the participants had more than one missing data point across their waves of participation. Given the very small amount of missing data, a conservative imputation approach was adopted, favoring cognitive stability as opposed to change, whereby missing cognitive values were replaced with an individual’s own performance score from the immediately preceding measurement wave. For the few instances where individuals had not completed the first wave, the mean baseline score for the equivalent age group was substituted using series mean estimation (SPSS 17). To confirm the validity of the imputation procedures, we performed comparable multilevel models using full information maximum likelihood procedures assuming that missing data were missing at random; identical patterns of significance were observed.

Statistical Procedures

To specifically evaluate terminal decline versus drop accounts of cognitive change, we used HLM 6.06 (Raudenbush, Bryk, Cheong, & Congdon, 2004) to fit linear mixed models of within-person cognitive change, and acceleration in change, as a function of the number of years prior to death. For each of the five cognitive outcomes, linear and quadratic slopes were specified (see Equation 1) to further inform the shape of cognitive change in proximity to death. Cognitive performance for a given individual (i) at a given time (t) was modeled as a function of that individual’s performance centered 6 years prior to death (B_0i: the intercept), plus his/her average individual rate of change per year closer to death (B_1i: the linear slope), plus the acceleration or deceleration for each linear growth trajectory (B_2i: the quadratic slope), plus a random within-subject error term (r) representing prediction error holding intercept and slope constant. To control for an obvious confound, age at death (centered at 75 years of age) was entered as a continuous covariate in the corresponding between-subject portion of the models.

(1)

As depicted in Figure 1, we also computed linear mixed models with a change point to facilitate an alternative test of the terminal drop hypothesis (cf. Sliwinski et al., 2006; Wilson et al., 2003). This procedure permits more precise identification of the locus and rate of change prior to death (e.g., how many years prior to death does change increase or accelerate, and by what factor does change increase relative to normative age-related cognitive decline). Specifically, we fit a series of piecewise (i.e., two-slope) linear mixed models to the cognitive data (Raudenbush & Bryk, 2002). We estimated the knot of the spline (i.e., the change point), characterizing the number of years before death that the decedents deviated from the normal aging curve and exhibited accelerated cognitive decline, for each of the five cognitive outcomes. We allowed the change point to vary across models by 1-month increments, ranging from time of death to as many as 10 years preceding the death event. Whereas change during the preterminal phase (i.e., prior to the knot) was indexed using chronological age (i.e., years since birth from each individual measurement), the terminal slope following the change point was indexed as a function of time to mortality (i.e., years to death from each individual measurement). Whereas the average annual decline prior to the change point reflects the preterminal (i.e., normative age-graded) slope, average annual decline following the change point is derived by summing the preterminal and terminal slopes, reflecting both normative age-graded and pathological influences (cf. Sliwinski et al., 2006). After fitting a series of models with change points varying in 1-month increments prior to death, we subsequently employed the profile likelihood method and associated derivation of −2 log likelihood values to select the model with the best fitting change point for each cognitive outcome (for a more detailed description, see Hall et al., 2001).

RESULTS

Table 3 summarizes findings from the linear and quadratic models for each cognitive outcome. As expected, our test of the first research question showed that significant linear declines were observed per year closer to death for all cognitive measures. This general terminal decline pattern is consistent with much previous research and with the oft-observed linear decline pattern prior to death. Regarding the second and third research questions (i.e., testing for terminal drop across the cognitive measures), little evidence for more abrupt drop was observed, with the only significant quadratic effect found for semantic verification. As shown in Figure 2, the change trajectory for this measure of verbal processing speed revealed a significant quadratic slowing of response latencies per additional year closer to death, over and above the linear rate of slowing. Although the presence of a significant quadratic term is consistent with a terminal drop pattern of cognitive decline, the magnitude of acceleration for this particular quadratic effect is modest (see Figure 2).

Table 3.

Linear and Quadratic Change in Cognition as a Function of Years to Death

Variable	Intercept, γ00	Slope, γ10/γ20	SE	t
Semantic verification	3,370.37	117.28	15.63	7.50**
		7.21	2.30	3.14**
Sentence construction	4.74	−0.05	0.02	−2.37*
		0.00	0.00	1.57
Word recall	17.41	−0.33	0.05	6.31**
		−0.01	0.01	−1.56
Fact recall	20.14	−0.53	0.06	−8.51**
		−0.01	0.01	−1.02
Vocabulary	43.62	−0.16	0.07	−2.46*
		−0.00	0.01	−0.20

Notes: γ₀₀ = cognitive performance centered 6 years prior to death; γ₁₀ = average linear rate of cognitive change per additional year closer to death; γ₂₀ = average quadratic rate of cognitive change per year closer to death; t = t ratio. Intercept and slope coefficients reflect response latencies in milliseconds for semantic verification, values on a 0–6 scale for sentence construction, values out of 30, 40, and 54, respectively, for word recall, fact recall, and vocabulary. Age at death, centered at 75 years of age, was entered as a covariate for all models.

^*p < .05; **p < .01.

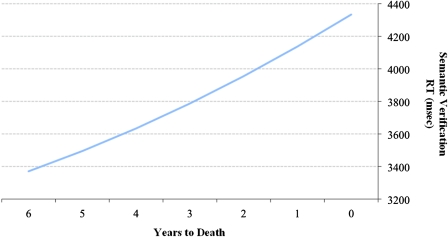
Figure 2.

Linear and quadratic change in response latency for the semantic verification task per year closer to death.

Our next set of analyses was designed to further determine whether the quadratic term yielded improved data fit. We computed a log-likelihood comparison of nested models, where the deviance statistic derived from the linear and quadratic model was subtracted from the deviance statistic for the linear-only model. Performing this calculation yielded a change in deviance (Δ deviance) between the two nested models (with a corresponding change of 1 degree of freedom) for all five cognitive measures: semantic verification (9.38), sentence construction (2.41), word recall (2.32), fact recall (1.00), and vocabulary (0.04). As the difference between deviance statistics of two nested models has an associated chi-square distribution, the calculated estimates could be compared with the critical value of chi-square with 1 df (3.84, p = .05). The change in deviance values exceeded the critical value for only semantic verification, indicating that the addition of the quadratic term fit the data significantly better than the linear model alone.

The random effects coefficient associated with the linear slope was significant for each cognitive measure, indicating between-person differences about the average linear rate of change. However, relative to the total amount of within- and between-person variance in cognitive functioning, very small proportions of variance were attributed to the random effects for slope (1.1% for semantic verification, 0.3% for sentence construction, 0.6% for word recall, 0.3% for fact recall, and 0.2% for vocabulary). This suggests that, although between-person differences in terminal decline trajectories are both present and significant, the magnitude of these individual differences is modest. Corresponding random effects for the quadratic slope were constrained in order to facilitate model convergence.

Finally, change-point models (cf. Hall et al., 2001) were fit to further examine evidence for abrupt cognitive impairment in close proximity to death. The two primary benefits of the change-point modeling approach, as compared with a linear or quadratic polynomial modeling approach, are the identification of (a) point estimates for the onset of acceleration in cognitive decline and (b) separate estimates of within-person change during the preterminal (time since birth) and terminal (time to death) periods. An index of terminal decline is provided by directly contrasting the change estimates from the preterminal and terminal phases. An indication of terminal drop is gained by taking into account both the proximity of the change point to death and the magnitude of decline following this inflection point.

Consistent with expectations, we were able to identify significant preterminal (i.e., age-based) cognitive decline for all but one cognitive outcome, as well as discernible change points for each measure ranging from 3.6 to 9.5 years prior to death (see Table 4). However, relative to the significant preterminal trajectories, further significant increases in cognitive decline following the change point (i.e., for the terminal phase) were observed only for semantic verification. Notably, this pattern was consistent with the earlier quadratic findings. Prior to the change point, each additional year increase in age was associated with an average 20.42 ms slowing. Following the change point, average annual linear decline within the terminal phase (i.e., preterminal slope + terminal slope) increased to 119.96 (20.42 + 99.54) ms, representing a fivefold increase in decline relative to age-related change. The change-point interval prior to death for semantic verification was broad (i.e., 9.5 years, effectively the entire follow-up interval), likely accounting for why significant age-related change was not observed. In examining the change-point findings for evidence of terminal drop (cf. Figure 1, trajectory labeled as “Change Point (NI)”), only a single change-point estimate was within 4 years of death (specifically, 3.5 years for sentence construction), and there was no evidence of abrupt drop following this inflection point (see Table 4).

Table 4.

Change-Point Models Estimating Preterminal and Terminal Cognitive Change

Variable	Intercept, γ00	Change point	Slope, γ10/γ20	SE	t
Semantic verification	2,985.33	9.5	20.42	30.91	0.66
			99.54	40.49	2.46*
Sentence construction	4.78	3.5	−0.05	0.01	−2.94**
			0.06	0.07	0.91
Word recall	17.09	6.8	−0.27	0.04	−7.24**
			−0.04	0.09	−0.51
Fact recall	20.15	8.2	−0.43	0.05	−8.37**
			−0.11	0.09	−1.11
Vocabulary	43.83	6.4	−0.13	0.06	−2.19*
			−0.07	0.12	−0.62

Notes: γ₀₀ = cognitive performance centered at 70 years of age and the specified change-point years prior to death; change point = number of years prior to death where the inflection between preterminal (age-based) and terminal (time-to-death) slopes yields the best model fit based on the highest likelihood value; γ₁₀ = average linear rate of cognitive change per additional year of age (centered at 70 years); γ₂₀ = average linear rate of cognitive change per year closer to death following the change point; t = t ratio. Intercept, slope, and change-point coefficients reflect response latencies in milliseconds for semantic verification, values on a 0–6 scale for sentence construction, values out of 30, 40, and 54, respectively, for word recall, fact recall, and vocabulary. Age at death, centered at 75 years of age, was entered as a covariate for all models.

^*p < .05; **p < .01.

DISCUSSION

Numerous studies have examined the impact of impending mortality on cognitive performance in older adults. However, only a few recent studies have considered longitudinal cognitive declines as a function of years to death and tested the potential differentiation of terminal decline from terminal drop. Conceptually, in contrast to the gradualness of terminal decline, terminal drop reflects a decline period interrupted by precipitous acceleration of cognitive impairment. Clinically, if terminal drop were to be observed and validated, the inflection point at which decline turns to drop could be useful as a marker of non-normative cognitive aging (e.g., due to neurodegenerative disease or dementia) or of impending mortality (e.g., due to engulfing biological compromise leading to imminent death). The present investigation employed linear mixed models to explore relative evidence for trajectories of terminal decline versus terminal drop. We used longitudinal cognitive change data in decedents from the VLS. Overall, the available longitudinal data and the multilevel analyses represent a significant improvement in precision for examining this question, especially as compared with some previous investigations employing cross-sectional analyses of longitudinal data or aggregate change techniques (e.g., repeated measures analysis of variance). Moreover, the present findings speak to the fundamental question of whether decline and drop are (a) equally observable and distinguishable phenomena and (b) terms that can be used interchangeably.

One feature of the present study was that we were able to test these models across five well-measured domains of cognition. Of these five cognitive outcomes, the linear effect was uniformly reliable, thus providing an unambiguous within-person confirmation of the terminal decline interpretation (cf. Palmore & Cleveland, 1976; Riegel & Riegel, 1972; Siegler, 1975). Notably, however, our index of verbal speed (semantic verification) also yielded a significant quadratic effect based on both the individual t test of the quadratic slope and the log-likelihood comparison of nested models (linear vs. linear + quadratic). Upon closer inspection of this quadratic effect, the magnitude of acceleration in proximity to death was slight. As shown in Figure 2, this was demonstrated by the modest parabolic slowing (i.e., increase) in response latencies for the 6 years preceding death (a period spanning almost the entire 8-year interval representing the average distance to death from the first wave of testing). This significant but modest slowing is comparable with the magnitude of quadratic effects for other studies examining measures of perceptual speed, including Ghisletta and colleagues (2006) and Thorvaldsson and colleagues (2006). On balance, the evidence regarding the shape of pre-death cognition as accumulated across five cognitive domains indicates that quadratic change could only be detected for our speed measure (and even then at a modest level). The consistency of this pattern suggests that mortality-related cognitive decline better approximates a terminal decline (accelerated but gradual) than a terminal drop (abrupt) pattern. Notably, the findings from the change-point analyses support this overall interpretation. Specifically, the change-point analyses showed that, although we identified inflection points that differentiated rates of change in proximity to death, a significant increase in cognitive decline during the terminal phase was only observed for semantic verification. Thus, both the polynomial and piecewise approaches support a general slow-but-steady terminal decline interpretation for all cognitive measures.

In the introduction, we expressed that three criteria were required for an interpretation of terminal drop. Our results indicate that only the weakest of these three criteria was satisfied. Specifically, (a) gradual terminal decline was indeed detectable a number of years preceding death for all measures, but (b) acceleration in proximity to death was largely absent, and (c) when acceleration was present, it was restricted to only one of the five cognitive outcomes (and not generalizable across the range of cognitive abilities represented in this battery). Although modest in magnitude, the fact that several studies have reported some evidence for terminal drop associated with speed measures suggests the potential value of exploring this domain further. In reflecting on more than 40 years of publications on mortality-related cognitive deficits, the best evidence for terminal drop (as compared with terminal decline) trajectories appear to come from several recent and methodologically sophisticated studies (e.g., Thorvaldsson et al., 2006; Wilson et al., 2003) and most consistently for speed measures. One methodological reason for the central importance of speed may be related to the superior psychometric properties of response latency measures in studies of mortality (Bäckman & MacDonald, 2006). Behavior is measured in terms of either speed or accuracy with all events taking place in time, and even when performance is error free, response latencies are either characterized by individual differences or there is no discernible change.

Because of the important theoretical and clinical implications, we consider several additional methodological attributes of our study that could inform previous inconsistencies in differentiating terminal decline from drop. First, Sliwinski and colleagues (2006) noted that some reports of terminal drop could reflect a conflation of rates of change for decedents and survivors. For this reason, we restricted our analyses to decedents who would die in as little as 1 month to as many as 16 years in the future, and subsequently observed only limited evidence for terminal drop. Second, the treatment of developmental time represents another critical methodological issue that could influence the pattern of results. To the extent that pre-death cognitive decline is due to pathological influences related to mortality, modeling change as a function of time to death (i.e., a process-based model) will more efficiently account for patterns of change than will models that use age or measurement occasion (i.e., time-based models) as a basis function (Sliwinski & Mogle, 2008). Finally, the use of measurement occasion to index time confounds terminal decline and normative aging effects. To circumvent this confound, we (a) parameterized cognitive decline as a function of time to death and controlled for age at death and (b) fit change-point models specifying preterminal and terminal decline slopes. We found little evidence for terminal drop. Although other methodological variations could account for discrepancies in the literature, the aforementioned issues of sample and time metric alone could largely account for incongruous results across studies.

Arguably, the novel strengths of the present investigation (e.g., broader cognitive battery, exclusive focus on decedents) provide a sensitive opportunity to detect evidence for terminal cognitive drop. We found very little such evidence. Extant reports of the linear nature of terminal decline coupled with the paucity of research directly contrasting terminal decline from drop could reflect a substantive effect but may also reflect shortcomings of research design (e.g., an artifact of measurement time scale or interval censoring). In future research, three important research design considerations might be considered. First, if available, researchers may wish to include narrower (i.e., <3 year) retest intervals, and thus increased occasion sampling, to improve design sensitivity for detecting terminal cognitive drop. Second, the sampling designs might oversample those at risk for mortality (e.g., individuals older than a certain age, or those who have select chronic diseases associated with mortality risk). Although promising, both design features also have challenging drawbacks, including the possibility of increased attrition due to testing burden (e.g., Deeg, van Tilburg, Smit, & de Leeuw, 2002), or generalized practice effects due to repeated exposure across narrow (e.g., annual) retest intervals (e.g., Rabbitt, Lunn, & Wong, 2006). Third, future research on this topic should strive to evaluate random effect change-point models that permit the inflection point to vary across individuals, effectively facilitating a within-person focus regarding the onset and rate of cognitive impairment in proximity to the death event. Such models require large samples, numerous measurement occasions, and narrow retest intervals.

Despite the methodological strengths of the present study, several limitations should be noted. First, key limitations that affect virtually all longitudinal studies of cognitive aging concern the issues of time scale and sampling. Statistically sensitive tests of the terminal drop hypothesis ultimately require retest intervals that are spaced closer than the expected duration of the terminal decline period, with sufficient sampling of cognitive performance in close proximity to death. The 3-year VLS retest intervals are indeed spaced closer than those of many corresponding longitudinal studies that have examined the terminal decline phenomenon, with some employing considerably longer retest intervals (e.g., 5–7 years). Nevertheless, future studies may wish to include even more closely spaced intervals. Clearly, the broader the interval between last time of cognitive assessment and subsequent death, the less precise such designs are for indexing terminal decline, and in particular for potentially differentiating terminal cognitive decline from drop. Wider retest intervals are also associated with greater interval censoring (loss of participant information during the critical drop period), resulting in difficulty fitting the post-node terminal decline portion of change-point models, and in turn directly limiting the given longitudinal design for contrasting terminal decline versus drop models. However, even designs that include annual retest intervals are not immune to attrition bias, as participants in the prodromal phase of select disease processes (e.g., dementia) often discontinue participation years prior to death.

A second limitation concerns the aggregation of terminal decline trajectories across many causes of death (e.g., cancer, cardiovascular disease)—a practice that may mask the identification of sudden terminal drop under some circumstances. As noted in the introduction, distinct causes of death may be associated with differentiable terminal decline signatures. Consequently, collapsing change trajectories across mortality classes characterized by individual differences in both severity and duration may result in the observed linearity of the terminal decline trend. Although plausible, a recent review (Anstey et al., 2006) suggests that similar trajectories of terminal cognitive decline are observed within homogeneous cause-of-death categories (stroke, cancer, and coronary heart disease), implying that declines in global (rather than disease-specific) biological vitality may account for a large share of the death–cognition relationship among older adults (see Berg, 1996; Rabbitt et al., 2002). Consistent with this interpretation, although all variance components for the linear terminal decline slopes were significant in the present study, the proportion of total variance associated with between-person differences in terminal decline was modest (ranging from 0.2% for vocabulary to 1.1% for semantic verification). Thus, if causes of death do moderate terminal trajectories, evidence from the present study suggests that the resulting individual differences in trajectories are modest.

Third, our current group of decedents is drawn from two VLS samples of initially healthy and typically aging adults who were living in a context of available health care. Given our previous work on speed (rate and inconsistency) as a marker of unhealthy cognitive aging (e.g., Dixon et al., 2007), it is possible that more quadratic shapes may occur for specific clinical samples developing and managing long-term conditions (e.g., mild cognitive impairment, specific health conditions). In contrast, focusing on decedents is methodologically advantageous, as previously described. Fourth, the sample of decedents (n = 265) is substantial but not as large as some other studies. Nevertheless, it was quite sufficient to support our analyses and actually fits comfortably in the range of several recent studies (e.g., n = 115, 404, and 445 decedents, respectively, for Wilson et al., 2007; Ghisletta et al., 2006; and Sliwinski et al., 2006). Finally, not all decedents completed five waves of testing, thus potentially limiting the estimation of quadratic effects. However, the range of one to five waves does readily facilitate change-point evaluations with fixed effects. Overall, our methodological strengths undergird clear results showing that, for the VLS data, the predominant shape of cognitive change before death is gradual decline rather than precipitous drop.

Theoretically, what might account for the general pattern of gradual decline before death? The slow-but-steady shape of the terminal decline function is inconsistent with generalized threshold models. In such models, pathology accumulates until a hypothetical threshold is reached, beyond which gradual change converts to manifest (or qualitative) decrements in cognitive decline—a transition that may be inevitable and rapid under some to-be-determined special circumstances (Richards & Sacker, 2003; Stern, 2002). Consider cognitive impairment associated with Alzheimer’s disease (AD). Stern’s model of cognitive reserve is a threshold model implying that AD pathology progresses at a similar rate in individuals characterized by low versus high reserve (e.g., based on years of education). However, the point of inflection where memory impairment becomes manifest occurs later for individuals with higher reserve and that the subsequent rate of cognitive impairment will be accelerated in those individuals due to greater pathology burden. Similarly, the “two-hit hypothesis” is also a threshold account of AD pathology and associated cognitive impairment, with both oxidative stress and abnormalities in mitotic signaling required to propagate disease pathogenesis (Zhu, Raina, Perry, & Smith, 2004). In the context of mortality-related cognitive decline, such models are consistent with terminal drop. In contrast, our overall results are more consistent with an alternative underlying process in which a more global decrease in cognitive reserve capacity reflects the gradual decline or failure of homeostatic systems (Berg, 1996). The underlying mechanisms of the terminal decline phenomenon remain to be tested in future research, and this question is beyond the scope of the present study. In addition, the door is still slightly open to the possibility that a combination of mechanisms may operate, with (a) the most predominant one being gradual but (b) a modest but abrupt acceleration occurring under some unknown set of conditions (e.g., perhaps represented by subsets of individual differences among the participants).

Regardless of underlying mechanism, one potentially beneficial application of the present results would be for researchers or clinicians to collect baseline or normative data on older healthy adults or patients and to subsequently use such data as a clinical screening tool for differentiating normal age-related from pathological cognitive decline. Although the present findings suggest that the terms terminal decline and terminal drop are broadly overlapping, design limitations (e.g., due to interval censoring) may ultimately render the question of whether terminal drop reflects an underlying disease pathology that would have been clinically manifest had individuals participated longer perhaps an intractable one (cf. Wilson, 2008). Indeed, terminal decline versus drop trajectories may not be mutually exclusive but could rather reflect distinct developmental trajectories within the same individual.

FUNDING

This research was supported by a grant from the National Institutes of Health/National Institute on Aging (R37 AG008235-20) to R. A. Dixon, who also acknowledges support from the Canada Research Chairs program. S. W. S. MacDonald was supported by a Career Investigator Scholar Award from the Michael Smith Foundation for Health Research. Portions of this investigation were conducted as part of S. W. S. MacDonald’s doctoral dissertation.