A heterogeneous population code for elapsed time in rat medial agranular cortex

Abstract

The neural mechanisms underlying the temporal control of behavior are largely unknown. Here we recorded from the medial agranular cortex in rats trained to respond on a temporal production procedure for probabilistically available food reward. Due to variability in estimating the time of food availability, robust responding typically bracketed the expected duration, starting some time before and ending some time after the signaled delay. This response period provided an analytic “steady-state” window during which the subject actively timed their behavior. Remarkably, during these response periods, a variety of firing patterns were seen which could be broadly described as ramps, peaks, and dips, with different slopes, directions, and times at which maxima or minima occur. Regularized linear discriminant analysis indicated that these patterns provided sufficiently reliable information to discriminate the elapsed duration of responding within these response periods. Modeling this across neuron variability showed that the utilization of ramps, dips, and peaks with different slopes and minimal/maximal rates at different times led to a substantial improvement in temporal prediction errors, suggesting that heterogeneity in the neural representation of elapsed time may facilitate temporally controlled behavior.

The perception of time in the seconds to minutes range, “interval timing”, plays a vital role in both human and non-human animal behavior (Gallistel, 1990). Besides providing the important ability to predict when specific events should occur, thereby allowing an organism’s behavior to match the temporal regularities in the environment, durations may also serve as important events in their own right, (e.g., a longer than normal pause in a colleague’s dialogue can be a cue requesting that one provide input to the discussion). Interval timing may also be essential for the computational processes underlying associative learning (Gallistel & Gibbon, 2000), adaptive foraging (Kacelnik & Bateson, 1996), and rate estimation (Brunner, Kacelnik, & Gibbon, 1992). However, despite its clear importance in the organization of behavior, and the sizeable literature on the psychological processes contributing to interval timing, relatively little is known about the neural mechanisms that support this perceptual capacity.

Interval timing behavior has been extensively investigated, and has two characteristic features, mean accuracy, which states that temporal estimates are closely related to the trained durations (Lejeune & Wearden, 2006), and scalar error, which is a form of Weber’s law that states that the error in temporal estimations grow in proportion to the intervals being timed (Gibbon, 1977). Both of these features are easily demonstrated by inspection of data from the peak-interval procedure (PI), a variant of a discrete-trial fixed interval procedure. In the PI, a proportion of trials (e.g., 50%) are reinforced following a fixed-interval schedule, such that reinforcement is provided following the first response after a criterion duration has elapsed since trial onset (typically indicated by onset of a continuously presented discriminative stimulus). Importantly, early responses have no programmed consequence, and as a result, plots of the average response rate on FI trials have the classic “scallop” form (Skinner, 1938), such that responding is low at the beginning of the trial and rises smoothly to maximal levels at the criterion duration. The remaining trials are non-reinforced probe trials, in which no reinforcement is provided and the discriminative stimulus remains on for an extended duration (typically three times the criterion duration). Plots of the average rate of responding as a function of elapsed time on these probe trials reveal a Gaussian, or peak shaped, form (see Figure 3). The mode of this average response distribution, the peak time, is taken as a measure of the animal’s temporal estimate. The characteristic of mean accuracy is seen in the PI as the peak time tends to fall close to the programmed criterion duration. The width of the distribution, the peak spread, is used as a measure of the animal’s error in estimating time. When timing different durations, peak spread grows in direct proportion to peak time, thereby showing the scalar property. This hallmark feature can be further demonstrated by normalizing the response functions by peak time and peak rate (the rate of responding at the peak time). Following normalization, the peak functions for different duration estimates superimpose.

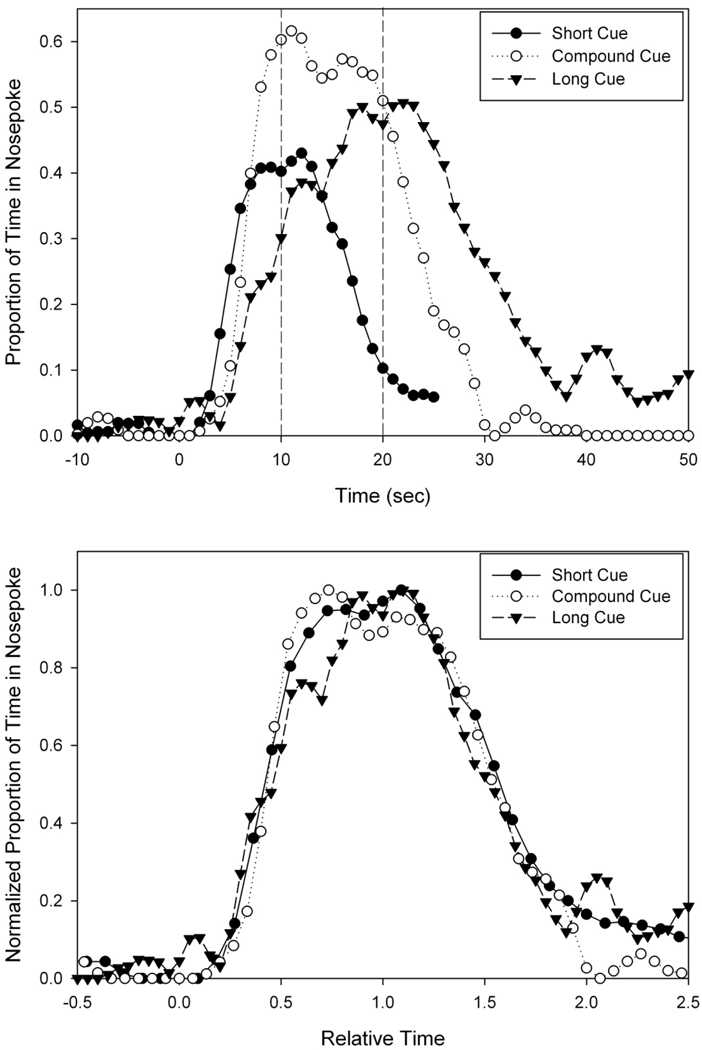
Figure 3.

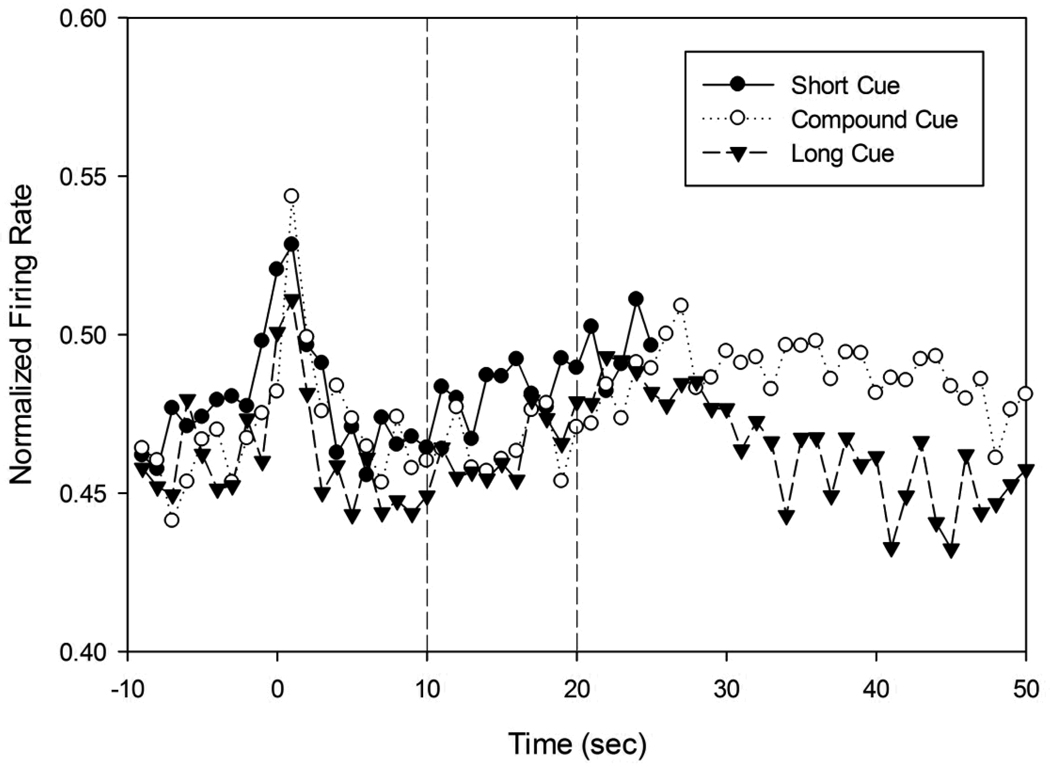
Peak functions from probe trials on a single session following Short, Compound, and Long cues. These peak functions plot the average proportion of time the rat’s snout was inserted into the nosepoke aperture as a function of time since signal onset. In the top panel, these peak functions are plotted in real time, while in the bottom panel, the axes have been scaled, thereby demonstrating superimposition of the peak functions. Stimulus onset at T=0, and stimuli remain on for 2.5× criterion duration (50s for non-reinforced compound trials). Dashed lines at 10s and 20s indicate the possible times of reinforcement.

The temporal control of behavior has been accounted for by information-processing models though three interacting components, a clock, memory, and decision stage (Church, 1997). The clock stage is thought to be composed of a pre-temporal signal, (i.e., some set of biological processes that vary or repeat in some manner as a function of time) which is then integrated to form a temporal signal; a one-to-one mapping of neural activity patterns to biologically relevant durations. It would intuitively seem that the temporal signal should develop in the form of linear or non-linear ramps or decay patterns (Gibbon, 1977; Staddon & Higa, 1999) thereby providing a monotonic representation of the amount of time that has passed. However, arguments have been made that there is not a continuously growing temporal percept(James, 1892), and temporally controlled behaviors could result when relevant times simply arise in a “time’s up” fashion, thereby implicating a peak-shaped or step function integration pattern (Matell & Meck, 2004). Upon the occurrence of a biologically relevant event, the signal value in the clock stage is stored in short or long term memory. On subsequent opportunities to time, an ongoing comparison is made between the continuously changing clock stage values and those retrieved from temporal memory. When the subject deems that the current clock value is sufficiently similar to the value in memory, it responds that “time’s up”.

Because a wide variety of models can account for temporally controlled behavior (Buonomano & Merzenich, 1995; Church & Broadbent, 1991; Gibbon, 1977; Grossberg & Schmajuk, 1989; Ivry & Richardson, 2002; Killeen & Fetterman, 1988; Matell & Meck, 2004; Staddon & Higa, 1999; Treisman, 1963), identifying the location(s) and pattern(s) of neural activity that contribute to the temporal signal has become a central quest in the field of interval timing. Electrophysiological (Macar, Vidal, & Casini, 1999) and functional imaging techniques in humans (Coull, 2004; Coull & Nobre, 1998; Coull, Vidal, Nazarian, & Macar, 2004; Ferrandez, et al., 2003; Harrington & Haaland, 1999; Lejeune, et al., 1997; Nenadic, et al., 2003; Rao, Mayer, & Harrington, 2001), electrophysiological investigations in primates (Genovesio, Tsujimoto, & Wise, 2006, 2009; Oshio, Chiba, & Inase, 2006; Roesch & Olson, 2005a, 2005b) and lesion (Dietrich, Frederick, & Allen, 1997; Meck, 2006a; Narayanan, Horst, & Laubach, 2006; Olton, 1989; Olton, Wenk, Church, & Meck, 1988) and electrophysiological (Matell, Meck, & Nicolelis, 2003c; Narayanan & Laubach, 2009; Shuler & Bear, 2006) investigations in rodents have suggested the involvement of a wide variety of cortical areas in timing.

Examinations of the patterns of activity that could serve to represent the passage of time have produced conflicting results. Brody et al. (2003) found that firing rates in the prefrontal cortex developed in a monotonic manner during the delay. When the delay length was increased on test trials, the vast majority of neurons scaled their activity patterns (e.g., a neuron that ramped to the choice time, now ramped more slowly, but to the same maximal rate). Similar results were seen in pre-motor (Lucchetti, Ulrici, & Bon, 2005) and pre-supplementary motor cortices (Mita, Mushiake, Shima, Matsuzaka, & Tanji, 2009), as well as supplementary eye fields (Ohmae, Lu, Takahashi, Uchida, & Kitazawa, 2008). In contrast, Kojima and Goldman-Rakic (1982) found that the majority of prefrontal neurons changed their firing pattern upon extension of the delay period, such that their rates increased up to the trained delay, but decayed during the extended delay, thereby showing a peak-like activation function. Peak-shaped patterns have also frequently been seen in studies in which extended delays were present throughout training (Leon & Shadlen, 2003; Matell, Meck, & Nicolelis, 2003a; Shuler & Bear, 2006; Tsujimoto & Sawaguchi, 2005). More recently, Oshio et al (2008) found that different neurons produced different activity patterns, with peaks seen in half the cells and ramps in a quarter of the cells with sustained or more complex patterns seen across the remaining neurons, indicating that a variety of neural activity patterns might be utilized for temporal control. Indeed, given that accurate temporal processing occurs concurrently with other behaviors that are required for survival (Boisvert & Sherry, 2006; Henderson, Hurly, Bateson, & Healy, 2006), the multi-faceted demands of the “real world” might require that temporal control be mediated by a rich ensemble of signals.

The medial agranular cortex of the rat “bears certain striking resemblances to the frontal eye field, supplementary motor, and arcuate premotor areas of monkey cortex” (Reep & Corwin, 1999); (see also Neafsey, et al., 1986). More recent work indicates that this cortical region sends bilateral projections to both dorsocentral (Reep, Cheatwood, & Corwin, 2003) and dorsolateral (Wu, Corwin, & Reep, 2009) striatum, a structure critical to the temporal control of behavior (Meck, 2006b) and central to the striatal beat frequency timing model (Matell & Meck, 2004). While the medial agranular cortex in the rat has been shown to contribute to movements of the head and neck area, including eyes, vibrissae, jaw and tongue movements, the possible homology to the pre- and supplementary-motor cortices of the primate, areas which have been linked to timing behavior, suggests that further investigation of its role in “higher” behavior functions may be fruitful. Indeed, in a recent meta-analysis of fMRI data, Wiener et al (2010) have concluded that the supplementary motor area is one of two sites active across all timing tasks (the other being the inferior frontal gyrus), whether sub- or supra-second, and whether motor or non-motor in nature. Coull & Nobre (2008) have also concluded that the pre-motor cortices (broadly defined) are intimately related to timing across both explicit and implicit domains. Consistent with this observation, Halsband et al (1993) demonstrated impairment on the continuation phase of paced finger tapping in patients with SMA lesions. Finally, recent work has shown that reversible inactivation of medial agranular cortex in the rat eliminates temporally predictive enhancement of reaction times (Smith, Horst, Liu, Caetano, & Laubach, 2010). With these possibilities in mind, we sought to assess the shape and reliability of firing patterns in rat medial agranular cortex that contain information related to elapsed time.

While most electrophysiological investigations of timing have been carried out in primates trained to remain motionless, imposing such extreme behavioral restrictions are considerably more difficult, if not impossible, to achieve in lower species such as rodents and pigeons, in which the majority of the behavioral investigations of timing have been done. Instead, the typical approach is to compare neural activity across time periods that are matched with respect to the subject’s behavior. To this end, we take advantage of the normal single trial steady-state response behavior displayed by rats when tested on the peak-interval (PI) procedure (Cheng & Westwood, 1993; Church, Meck, & Gibbon, 1994; Gibbon & Church, 1990; Gooch, Wiener, Portugal, & Matell, 2007; Matell, Bateson, & Meck, 2006). Unlike the smooth shape of the trial-averaged peak function, the response rate on single probe trials can be characterized as three discrete states: a low-rate “exploratory” state, a high-rate “goal-directed” state, and another low-rate “exploratory” state (see Figure 4). The transitions between these states are abrupt, and have been interpreted as reflecting the times at which the subject deems that currently elapsed time has become sufficiently similar to the remembered time of reinforcement to begin responding (start) and subsequently has become sufficiently dissimilar to terminate responding (stop). As the times at which the animal starts and stops responding at a high rate vary from trial to trial, the averaged data sets take on the Gaussian form described above. Importantly, because the response behavior during the high-rate state is roughly constant throughout the state, and any deviations measurable, we were able to evaluate the dynamics of cortical activity during this steady-state period in freely behaving animals, thereby removing the behavioral constraints imposed by the immobility-requirements used in most primate recording studies.

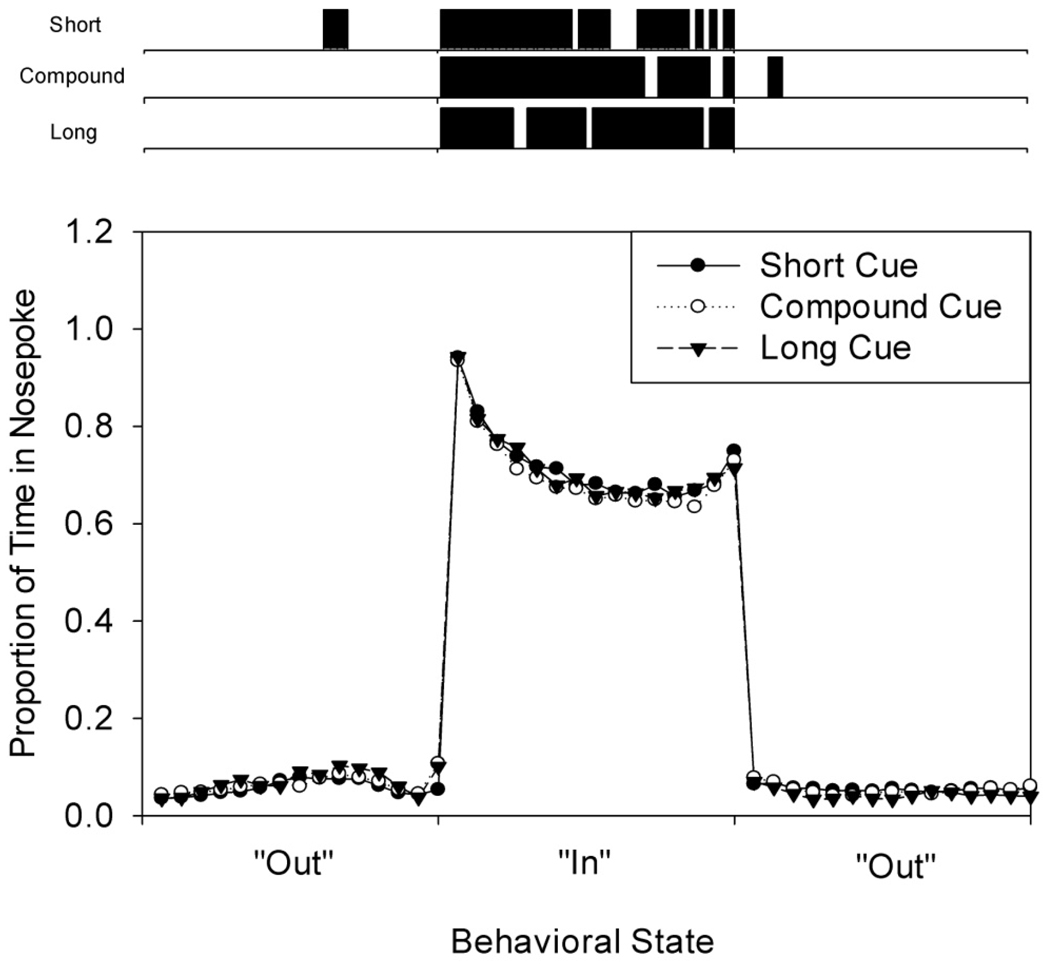
Figure 4.

Occupancy of the nosepoke aperture as a function of time on single trials. On each trial, the occupancy of the nosepoke as a function of time was characterized as a single step-function (out-in-out) by single trial analysis (see methods). As the placement and width of these step functions varied over trials, each state of occupancy was binned into 15 bins to demonstrate the abrupt state transitions, as well as the variation in occupancy as a function of time during the “In” state. The top panel shows occupancy of the nosepoke on a representative trial from each of the three trial types, lined up according to the onset and offset of each state. The lower panel shows the average proportion of time that the rats’ snouts were in the nosepoke aperture as a function of time and behavioral state.

Method

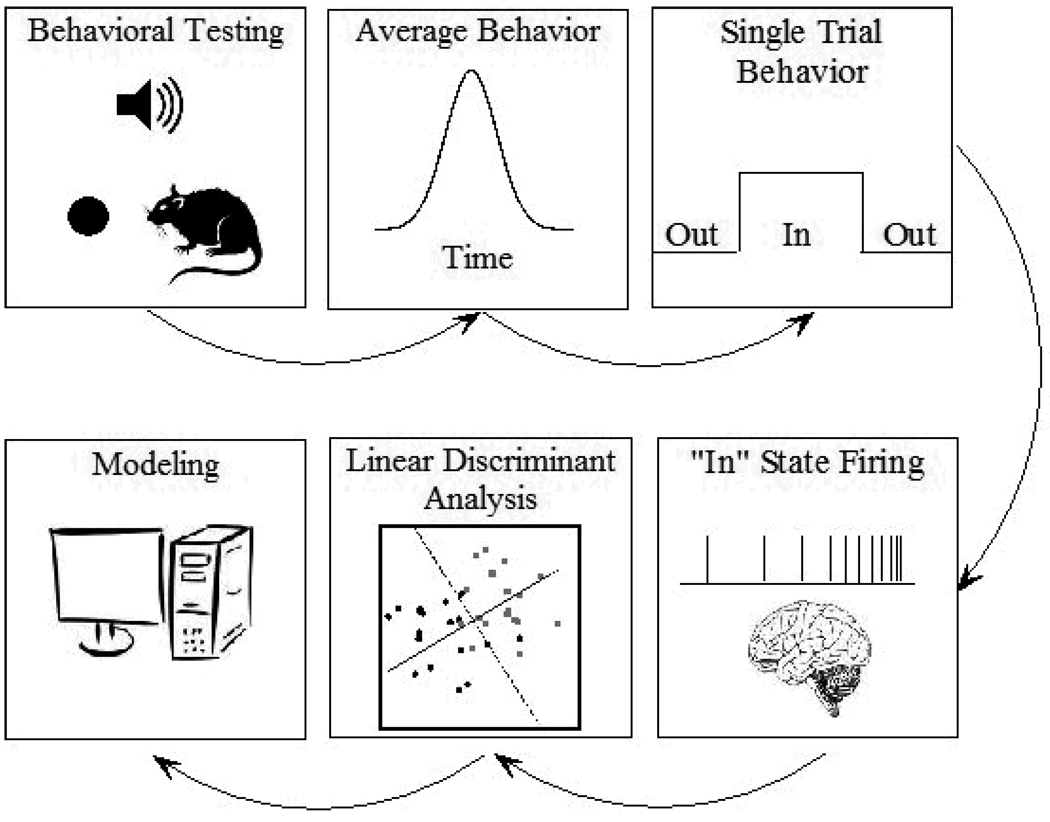
Figure 1 shows a schematic of the behavioral paradigm and sequence of analytic steps used in the present experiment. Briefly, rats were trained on a mixed-interval peak procedure in which one signal (e.g., a tone) indicated probabilistic availability of reward for a nosepoke response after a short duration (10 s), whereas a different signal (e.g., a light) indicated probabilistic reward availability for a nosepoke response after a long duration (20s). Single trial analysis techniques were used to identify the period of time on each trial in which responding was emitted at a high rate (the “In” state), and the firing rate and pattern during this state was analyzed for trial by trial reliability using regularized linear discriminant analysis. We followed this analysis with model development to examine the consequences of our results.

Figure 1.

Schematic of Experiment. A) Rats were trained to poke their snout into a nosepoke aperture to obtain probabilistic reinforcement after a stimulus had been on for a criterion duration. B) Plots of the session averaged probability of nosepoking as a function of time since stimulus onset show a smooth peak shape. C) On single trials, the response behavior is well described by a step function in which the rat abruptly switches from a behavioral state in which responding is unlikely, to a behavioral state where it is highly likely to have its snout in the nosepoke aperture. D) Single cell activity occuring during this “In” state are collected. E) Regularized linear discriminant analysis techniques are used to assess reliable patterns of activity across the “In” state in individual neurons. We found that these patterns were highly variable between neurons in shape (up-ramp, down-ramp, peak, dip), slope, and time of maximal (minimal) activity. F) Subsequent modeling demonstrated that such variability is beneficial in diminishing error in temporal estimates.

Subjects and Apparatus

Neurophysiological data are reported for four Spraque-Dawley male rats that were approximately 4 months old at the beginning of the study. Prior to electrode implantation, rats were housed in pairs with a 12 hour light-dark cycle, with lights on from 8 a.m. to 8 p.m. The animals were trained during the light phase of the cycle, and were given continuous access to water throughout the study. Subjects were kept on a restricted feeding schedule and their body weights were maintained at 85–90% of their free-feeding weights, adjusted for growth. On the first day of food restriction, approximately fifteen 45 mg sucrose pellets (Formula F; Noyes Precision, Lancaster, NH) were given to the rats in their home cage to familiarize them with the reinforcers used in the behavioral protocols. Following electrode implantation, rats were housed individually. All procedures were conducted in accordance with the Villanova University’s Institutional Animal Care and Use Committee (IACUC).

Training was carried out in 30.5 cm long × 25.4 cm wide × 30.5 cm high standard operant-conditioning chambers (Coulbourn Instruments, Allentown, PA). The sides of the chamber were ventilated and were made of Plexiglas, and the front wall, back wall and ceiling were made of aluminum. The floor was composed of stainless steel bars. A pellet dispenser attached to the back wall of the operant chamber delivered 45-mg sucrose pellets to a food magazine. Three nosepoke response detectors with LED cue lights were placed on the front wall of the chamber. Two aluminum “hallway” barriers (30.5 cm high × 8.2 cm deep) were attached to the front wall so that a rat could not nosepoke unless its body was parallel with the barriers (perpendicular to the front wall). The operant chambers were equipped with a houselight and a seven-tone audio generator. Behavioral data were transmitted to a computer program that recorded all events (Graphic State, Coulbourn Instruments, Allentown, PA). Following electrode implantation, all neural and behavioral data were recorded in a modified chamber in which the ceiling was raised to 43 cm with a slip-ring commutator at the top, and a food cup extended into the chamber. All stimuli and behavioral data were routed into an analog to digital data acquisition system (40 khz) used for recording neural activity (Recorder, Plexon, Dallas, TX) in order to synchronize the neural and behavioral event times.

Procedure

Nosepoke Training

Rats were given a single session of nosepoke training. In this phase of training, a sucrose pellet was delivered on a fixed ratio 1 schedule on the center and left nosepoke apertures, until 20 responses had been made in each nosepoke.

Fixed-Interval Training

Trials began with the onset of either the 10s “short” discriminative stimulus or the 20s “long” discriminative stimulus, with trial type selected at random. The discriminative stimuli for the two durations were a 1kHz tone or the houselight, with the duration-stimulus association counterbalanced (e.g., tone = 10s;light =20s or vice-versa). The discriminative stimuli remained on continuously throughout the trial. The first nosepoke into the center nosepoke aperture after the associated criterion duration elapsed was reinforced and the stimuli terminated. Responses prior to the criterion duration had no programmed consequence. Following a variable 30–70 sec inter-trial interval (ITI), a nosepoke into the left nosepoke aperture would initiate the next trial, although no cue was provided to indicate self-initiation availability. If the trial was not nosepoke-initiated within 3 min, the trial and corresponding stimuli were automatically initiated. Seven 2 hr sessions were run, at which point all rats showed fixed-interval scallops for both cues.

Peak-Interval Training

Peak-Interval training was identical to the Fixed-Interval training except that non-reinforced probe trials were presented in addition to the reinforced trials. Probe trials were identical to the fixed-interval trials, with random signal selection and continuous presentation of the discriminative stimulus, except that the trials terminated at a duration that was 2.5–3.5 times the criterion duration for that signal (e.g., “short” probe trials lasted 25–35 seconds) and no reinforcement was provided. The short cues were reinforced on 25% of the trials, whereas long cues were reinforced on 50% of the trials, in order to roughly equate reinforcement density for the two signals such that peak rates were similar between cues/durations, as was found previously (Swanton, Gooch, & Matell, 2009). Rats received a minimum of forty 2 hr sessions before electrode implantation.

Peak-Interval Testing

Peak-Interval testing began following recovery from electrode implantation. As we hypothesized that single neurons might show activity patterns (e.g., peaks) that were associated with a single trained duration, but which would also be associated with a specific cue modality, we sought to de-couple these factors by presenting non-reinforced compound cue probe trials, in which both the tone and house light commenced simultaneously. We had anticipated that neural activity on these trials would resemble that seen on one of the single modality trials, but that behavior would reflect influence from both trial types. Compound probe trials lasted 50–70 sec, and terminated independently of the subject’s behavior. Trial type was randomly sampled with compound probes making up 20% of the trials. Session length was increased to 4 hrs to allow greater data collection.

Surgery & Recording

Electrodes

Chronically implantable movable electrode ensembles were built using a design modified from that described in Bilkey & Muir (1999). Briefly, nine 25 µm teflon insulated tungsten microwires were assembled into a circular array (8 electrodes were used for recording, and 1 was used as a dedicated reference electrode). The microwires were held in place with epoxy and attached to the nib of a ballpoint pen, and the whole apparatus was encased in a microdrive. Through the use of a 0–80 drive screw, the “Scribe” microdrive allowed implanted electrode bundles to move ventrally through the brain by 80µm with a 1/4 screw turn. The diameter of the array was approximately 1 mm.

Implantation Procedure

Rats were anesthetized with 5% isoflurane via inhalation, followed by an intramuscular injection of ketamine (100mg/kg) and xylazine (10mg/kg), and placed in a stereotaxic frame. The skin and muscle on the skull were retracted, and a craniotomy made at the target coordinates for medial agranular cortex (center at AP +2.5, ML ±1.5). The dura was retracted and the array was lowered into cortex until cellular activity was detected (~0.2 mm). In addition to the electrode, four platinum skull screws were implanted to hold the electrode in place. A stainless steel wire was wound around the skull screws to serve as a ground for the electrode. The microdrive was attached to the skull and screws with dental cement. The wound was closed, and antibiotic ointment was applied. The animals were given one week to recover, during which they had free access to food and water.

Recording Procedure

Following recovery, electrophysiological recordings began once rats re-attained stable performance on the final version of the procedure. Before every session, the electrode assembly was lowered 80µm (1/4 screw turn) ventrally into cortex. A 20x gain headstage/cable assembly was plugged into the implant, and the rat was placed in the operant chamber with the sound attenuating cabinet door open in order to maximally differentiate contexts during spike thresholding. Spike signals were further amplified by 500×, highpass filtered above 150Hz, and passed to a data acquisition system running at 40kHz (Recorder, Plexon, Dallas, TX). The data acquisition system recorded all neural activity that surpassed a threshold voltage set independently on each microwire. All thresholded waveforms were simultaneously recorded during the session, along with all behavioral events that occurred, and stored for offline analysis. Single units recorded each day are treated as unique cells in the reported analysis, as the electrode was lowered 80µm per day, and no attempt was made to “match” cells from individual sessions.

Single Unit Discrimination

An off-line computer program (Offline Sorter, Plexon, Dallas, TX) was used to discriminate and isolate action potentials (“spikes”) from background noise and from one another. This program separates spikes from background noise by computing the principal components that maximally explain the variance in waveform shape. Single units were discriminated from noise by clustering in 3-d PCA space. Once single units were discriminated, the timestamps of spikes and behavioral events were examined through a neural analysis program (NeuroExplorer, Nex Technologies, Littleton, MA) and MATLAB (Mathworks, Natick, MA).

Behavioral Analysis

The proportion of time the rat’s snout was in each nosepoke as a function of time in the trial on probe trials was computed using 1 sec bins. For mean function analyses, the data for each rat were pooled across sessions. The resulting distribution, referred to as a peak function, relates the probability of responding to the subjective estimate of time passed. To obtain quantitative indices of these response functions, each distribution was fit with a 5 parameter Gaussian-type function [a*exp((−1/2)*(((abs(x−b))/c)^d))+e]. The first 3 parameters relate to the amplitude, the mean, and the width of the function. The 4^th parameter allowed the exponent of the function to vary in order to enable better fits in cases of low kurtosis, and the fifth parameter accounted for a baseline rate of responding. Peak rate was defined as [a+e], and peak time as [b]. Peak spread was defined to be the width of the function at half maximum as computed by [2*c*(2*log(2)^(1/d))]. The normalized spread is given by peak spread/peak time.

Single trial analyses were performed to identify the times at which the rat switched from being primarily outside the nosepoke aperture to being primarily inside the nosepoke aperture and then returned to being primarily outside the nosepoke aperture. These analyses have been described in detail previously (Gooch, et al., 2007; Matell & Portugal, 2007). Briefly, each 20 msec bin during a probe trial was assessed to determine whether the rat’s snout was in or out of the nosepoke aperture. This sequence of nosepoke occupancy states was then subjected to an exhaustive iterative process to find the best fitting step function (minimization of absolute deviations) in which the data were best described as 3 discrete states (outside the nosepoke, inside the nosepoke, outside the nosepoke). The bin at which the best-fitting step function went from “Out-to-In” was designated the start time, and the bin at which this step function went from “In-to-Out” was designated the stop time.

Neural Analysis

Peristimulus Time Histograms

To characterize the general firing rate changes over the course of a trial, we constructed a population PSTH (1s bins) using normalized (% max) firing rates to evaluate whether there was an average trend to the firing pattern within medial agranular cortex. To assess reliability of firing rate changes, individual PSTHs were binned into 10 segments (bin width proportional to probe length), and analyzed using a repeated measures ANOVA. The PSTHs of those neurons whose firing rate reliably changed over the trial were then separately fit with a Gaussian-like function (as described above for the behavioral peak fits) and a line. If the quality of the fit (R²) of these functions was greater than 0.5, the neuron was designated as having a peak or ramp shape. The peak fits were restricted to ensure that the times at which the peak function fell to half maximal levels occurred during the trial.

Analysis of neural activity during “In” states

In many cases, visual inspection of the neuronal PSTHs suggested a direct relationship with the nosepoking behavior. Further, in those neurons in which a relationship was not apparent, it would be premature to try to relate these neurons’ firing rate fluctuations to the passage of time, as the rats may be producing other behaviors during the “Out” states that may have contributed to the shape of the neural fluctations when examined as session-wide averages. Therefore, in order to evaluate the dynamics of neural activity as a function of time, we restricted the subsequent analyses to the period of time that the rat was engaged in nosepoking at a high rate, the “In” state. Because the “In” state is composed of the rat either holding its nose in, or repeatedly poking in and out of, the nosepoke aperture, it cannot be performing other overt behaviors that might covary with time (e.g., checking the food cup, rearing, general locomotion, etc). As such, this “In” state can be viewed as providing a similar framework for analysis as the period of motionlessness utilized in primate studies, but for a freely behaving animal.

Still, because the nosepoking behavior was not produced at an absolutely constant rate across the “In” state, and as this nosepoking might modulate the neural activity, we controlled for this change in nosepoking rate in two ways. First, we limited the analyses to a windowed subset of the “In” state in which the first and last 0.5 sec of the state were excluded. In this manner, neural activity associated with transitions between the states (i.e., initially entering and terminally exiting the nosepoke) would be minimized. Secondly, we assessed whether the neural activity was correlated with the nosepoke occupancy during this analysis window. In those neurons whose correlations were either moderately strong (R² > 0.25) or reliable (p < 0.2), instead of using the spike counts for the analyses, we used the residuals of the spike counts, after regressing to the nosepoking behavior. In this manner, we assessed whether the firing rates differed as a function of time after covariations in motor activity were taken into account.

Within-trial analysis -- encoding of elapsed time

To assess whether neuronal firing rates vary in a reliable manner as a function of time during the “In” state, we used regularized linear discriminant analysis (LDA) to compare the firing patterns produced early versus late through this state (Duda, Hart, & Stork, 2001 for a general overview on discriminant analysis). Specifically, the “In” state on each trial was split into 4 bins, and the number of spikes falling into each bin was determined. The first two sequential bins were labeled as “early” and the second two as “late” bins. The goal of LDA is to compare early vs. late bin counts, in order to determine whether neural activity varies predictably with elapsed time during the “In” state.

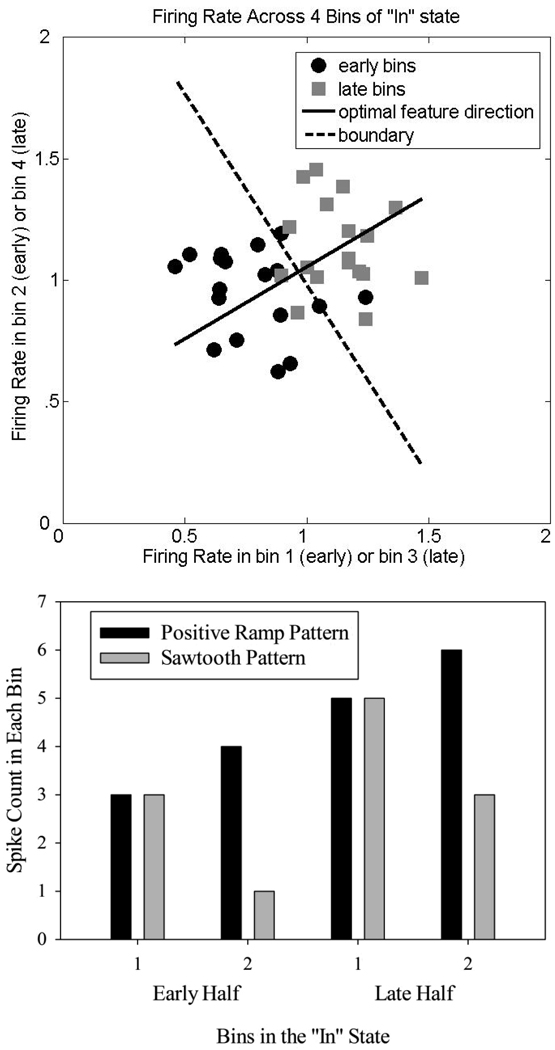
To illustrate LDA, a graphical representation is provided in Figure 2 showing the firing rate of a neuron on n short signal trials. Each half of the “In” state was split into two bins, and the single-trial firing rate during each of these bins, for n−1 trials, is plotted on a cartesian plane in which the firing rate during bin 1 is plotted along the abscissa, while firing rate during bin 2 is plotted along the ordinate. The firing rates during the first and second halves of the “In” state are plotted separately. As can be seen, the firing rate was consistently lower during the first half of the “In” state than during the second half. The dotted line serves as a boundary between the categories. The position and orientation of this boundary is determined based on the means and covariances of the data such that its position and direction are optimal for splitting the two categories of data (under standard assumptions about normally distributed data, and regularization to handle finite datasets (Duda, et al., 2001; Friedman, 1989). The “feature”, i.e., the dimension on which the data is optimally separated into two categories, is a line that runs in an orthogonal direction to the boundary.

Figure 2.

A graphical representation of linear discriminant analysis showing the firing rate of a neuron during the “In” state on short signal trials. Top Panel - The “In” state was split into early and late halves, and each half was split into 2 bins. Single-trial firing rates on each of n−1 individual trials are plotted as points, with rates for the 1^st bin along the abscissa and rates during the 2^nd bin along the ordinate (bins drawn from early vs. late periods during the trial are plotted separately; see text). The firing rate was consistently lower during early periods than during late periods. The orientation and position of the dotted boundary line separating the early and late data points is optimized based on the means and covariances of the data. The “feature”, i.e., the dimension on which the data is optimally separated into two categories, is a line that runs in an orthogonal direction to the boundary. The direction of the feature was always defined as pointing from the early half rates to the late half rates, so in this figure, the feature points towards Quadrant 1. Bottom Panel – Two hypothetical firing patterns which demonstrate that the feature direction does not uniquely specify the firing pattern. Both of these firing patterns produce features that point at the same angle (towards Quadrant 1) due to an equivalent change in the corresponding bins (e.g., Bin 1) from the first half to the second half.

To assess how reliably the two clusters are separated, we used a standard leave-one-out cross validation technique (see Duda, et al., 2001 for a general overview on discriminant analysis). Specifically, a data sample from the remaining trial is obtained (either early or late), and if this sample falls below this line, the sample is predicted to come from the early portion of the “In” state, whereas if it falls above the line, it is predicted to come from the late portion of the “In” state. The success of this prediction is recorded, and the process is repeated with every trial being left out, while the boundary line is constructed based upon the remaining trials. The cumulative success in predicting all of the data samples is used as the measure of categorization accuracy.

In the analysis described above, we used standard regularization methods (Friedman, 1989), implemented as part of our MATLAB codes. Specifically, we computed percentage of correctly classified trials with ten different levels of regularization, each corresponding to a different level of interpolation of the covariance matrix of the clusters between its measured value and a “diagonal” covariance matrix that would correspond to uncorrelated fluctuations in the data (the levels of interpolation used were equally spaced over the full possible range). The percent correct values reported are the best obtained over all levels of regularization. This procedure is designed to mitigate errors resulting from setting discrimination boundaries based on relatively small numbers of trials, and led to a slight increase in performance versus no regularization. While this regularization also slightly “improved” performance with data that were randomly categorized (i.e., “shuffled”), the improvement reflected a movement from spuriously incorrect predictions towards chance performance, (i.e., average accuracy without regularization = 48.4% correct, average accuracy with regularization = 49.6% correct). To assign signifance values to the percentages of correct trials we obtained, we computed the likelihood that each neuron would have n successful predictions out of x trials attempted, according to a binomial distribution, with an alpha level of 0.05. In order to assess whether the population as a whole performed at a level beyond that expected by chance, we compared the distribution of success rates of the neurons, with that obtained following random categorization, using a two sample t-test.

As the number of bins used to characterize the data increases, and/or as the number of trials decreases, there is an increased likelihood that the LDA will find a spurious dimension that best separates the data. As such, we ran the analysis only in the event that there were at least 6 trials for a particular trial type (i.e., short, compound, or long), and the step function on each trial was at least 5 seconds in length (the spread of typical temporally controlled steps is roughly equal to the duration being timed – (Church, et al., 1994). Additionally, we minimized the number of bins for each category (i.e., two), while still providing sufficient resolution to capture systematic patterns of activity (i.e., peaks or ramps). Because all evidence points to interval timing behavior being scalar (e.g., the width of the “In” state grows in rough proportion to the duration being timed), we varied the width of the bins as a function of the width of the “In” state, so that relative changes in activity, rather than absolute differences were responsible for classification. This normalization procedure also allowed us to make equivalent comparisons across durations without confound by the diminishing precision that is seen with increasing duration. We also minimized the influence of trial-by-trial variation in firing rate by expressing the firing rate as a fraction of the maximal rate on each trial. Analyses performed without these normalization techniques remained significant with equivalent qualitative patterns, although there was a decrease in the average performance of individual neurons, as well as a decrease in the absolute number of neurons showing significant performance. We ran the LDA separately for each trial type, and for all trials together without respect to trial type. In this latter analysis, the trials used were constrained to ensure that there were equivalent numbers of trials for each trial type.

Analysis of the “Shape” of the firing pattern

Returning to the example neuron shown in Figure 1, the pattern of firing in this neuron could be described as a positive ramp (i.e., showing a monotonic increase in spike rate across all 4 bins of the “In” state). As a result, the direction of the feature points toward quadrant 1. Conversely, firing patterns that smoothly ramp down across the “In” state would point towards quadrant 3, and firing patterns that peak or dip at the center of the “In” state would point towards quadrants 2 and 4, respectively. However, the feature direction can under-determine the qualititive “shape” of the firing pattern, as shown in Figure 2b for a hypothetical neuron.

Therefore, in order to clarify the “shape” of the firing pattern, and with the goal of providing a simpler description of the data for subsequent modeling, we characterized each neuron with significant discriminability on the LDA analysis as either peaking or ramping as follows. We rebinned the average firing pattern during the “In” state (or the residuals of the firing pattern in motor-correlated cells) into 3 bins (the minimum necessary to discriminate ramp from peak patterns), and characterized a cell as ramping if the rates changed in a monotonic manner (either positive or negative), and peaking (dipping) if the rates changed in a non-monotonic pattern. To represent these patterns graphically, we computed the change in rate from Bin 1 to Bin 2, and from Bin 2 to Bin 3. These two rate changes were normalized by the larger absolute rate change, and the relative rate change from Bin 1 to Bin 2 was plotted on the abscissa, and the relative rate change from Bin 2 to Bin 3 was plotted on the ordinate. In this manner, all firing patterns could be plotted on a square with corners at +/− 1, +/− 1 (see Figures 8 and 9). We found that there was substantial variability in the “shape” of the firing pattern across cells. Although we only characterized the shape of those neurons that were significant using LDA, we sought to confirm that the variability across cells was not due to finite sampling. To this end, we characterized the shape of firing of each neuron on each trial using the same methods, and compared the average within-neuron variability to the between-neuron variability.

Figure 8.

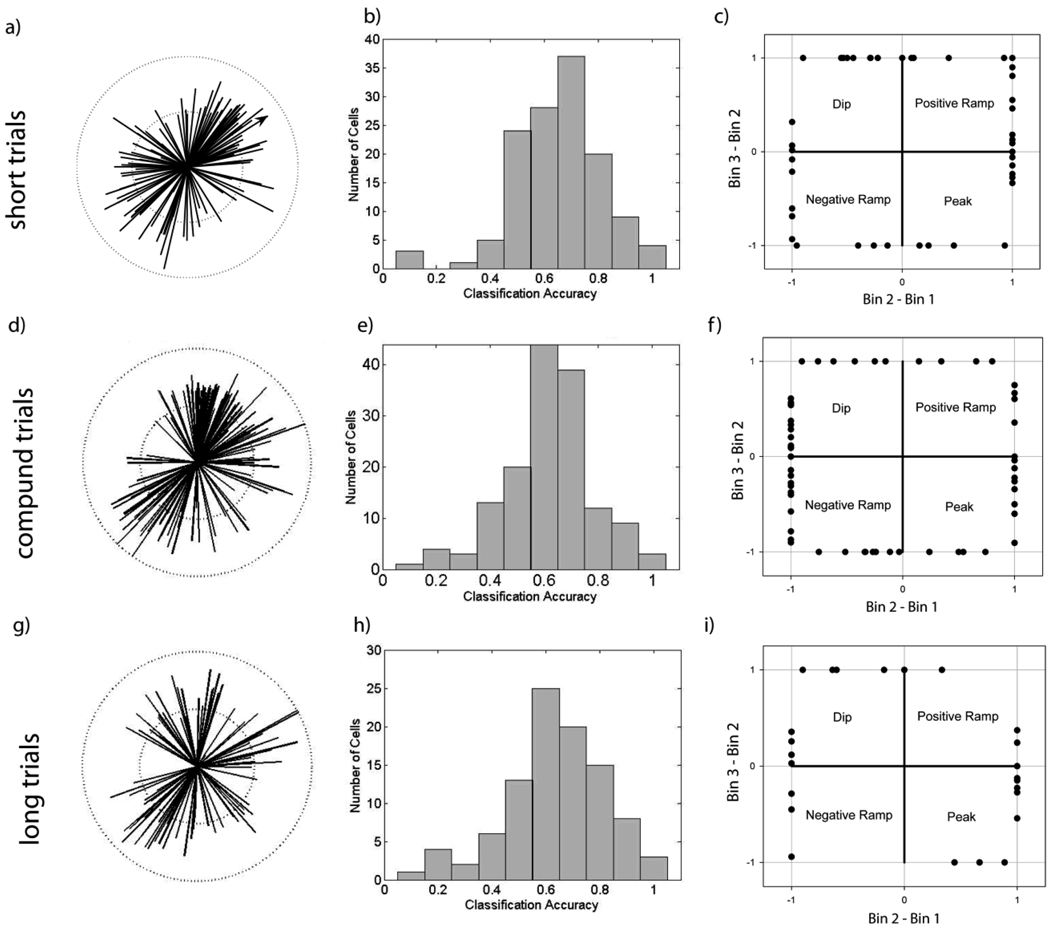
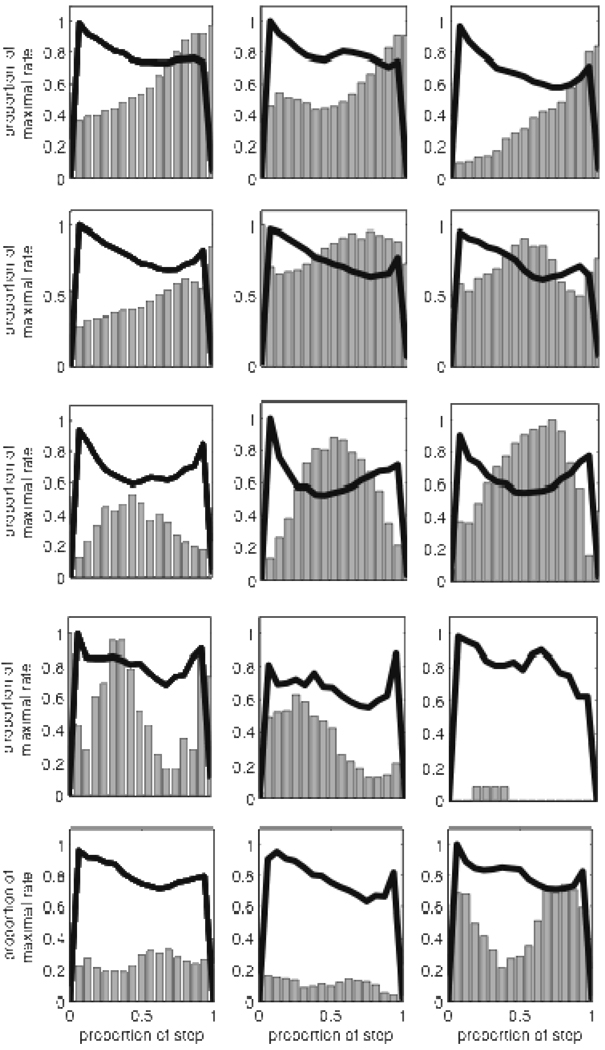
A variety of firing patterns provide reliable information about elapsed time during “In” state for individual trial types. Panels a), d), g) - Directions of features obtained from the regularized linear discriminant analyses comparing the firing rates during the early epoch (1^st half of “In” state) with the late epoch (2^nd half of “In” state). The length of the lines corresponds to each cell’s discriminative accuracy, and the dotted circles mark perfect (outer) and chance (inner) performance. Note the widely varying directions of the features. Panel a) shows accuracy from Short cue trials, panel d) shows accuracy from Compound cue trials, and Panel g) shows accuracy from Long cue trials. The line with the arrowhead in panel A corresponds to the feature obtained from the data shown in Figure 2. Panels b), d), f) – Distribution of classification success rates for neurons shown in panels a), d), g). Panels c), e), i) - Shape of the rate change across the “In” state using 3 bins to characterize pattern. The abscissa provides the change in rate from bin 1 to bin 2, while the ordinate provides the change in rate from bin 2 to bin 3. The rate changes were normalized by the larger of the two differences, such that all points fall along a square with corners at +/− 1, +/− 1. Points in quadrant 1 and 3 correspond to positive and negative ramps, respectively. Points in quadrants 2 and 4 correspond to dips and peaks, respectively.

Figure 9.

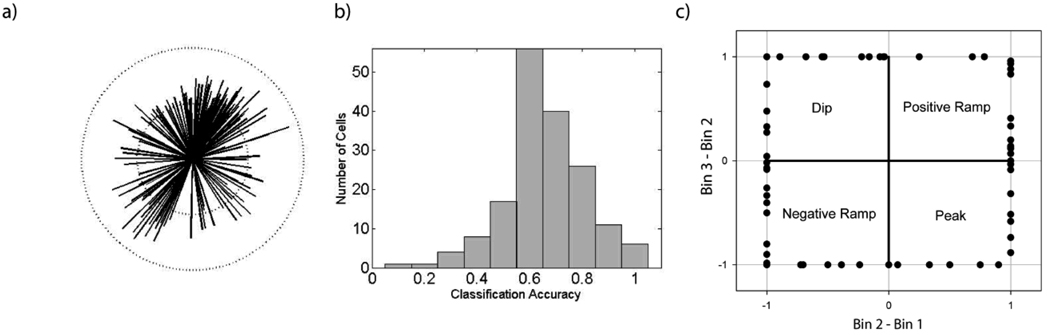
A variety of patterns provide reliable information irrespective of trial type. Panel a shows the direction and accuracy of the features obtained from the regularized linear discriminant analyses comparing the firing rates during the early epoch (1^st half of “In” state) with the late epoch (2^nd half of “In” state) when all trials were used, without regard to trial type. Panel b shows the distribution of classification success rates, and panel c reflects the shape of the rate change during the “In” state. Construction of the figures was identical to Figure 8.

Population Prediction

We were interested in determining how well the population of recorded neurons could collectively encode elapsed time. We produced a cross-validated estimate of that predictive capacity as follows. First, for each individual neuron, we “left out” a single trial, and used the remaining trials to identify a boundary discriminating early vs. late neural activity. Then, we replaced that trial, and allowed each neuron to “vote” according to the projection of the replaced trial onto the corresponding feature separating early vs. late trials. Specifically, the distance d to the discrimination boundary was computed, and a vote of v=+d assigned if the trial lay on the “correct” side of the boundary, and v=−d if it lay on the “incorrect” side. This procedure was repeated for every neuron in the population. The votes v for each neuron were then summed, and the population discrimination assessed as correct if this sum was positive and incorrect if it was negative. This was repeated over six different left-out trials (the minimum number of trials used for all LDA analyses) for as many randomly chosen neurons as necessary to form populations of various sizes as needed.

Results

Peak functions from a single rat on a single session are shown in Fig 3a. As can be seen, the average proportion of time the rat’s snout was in the nosepoke rose to a maximum roughly around the time that reinforcement would be provided. Across all rats and all sessions, the peak time (Mean (Std. Dev)) for the short stimulus was at 11.4 sec (0.9), while the peak spread was 10.4 sec (1.7), giving a normalized spread of 0.9 (0.1). For the long duration, the peak time was 17.2 sec (1.6), with a peak spread of 19.3 sec (6.9), providing a normalized spread of 1.1 (0.3). The rats also responded vigorously for the compound stimulus (simultaneous presentation of both short and long stimuli) at a time roughly midway in between the two anchor durations, despite the fact that reinforcement was never provided on compound trials. The average peak time, 14.5 sec (1.4) and peak spread, 16.1 sec (2.5) from these compound trials was longer than that from the short probe trials [t(3) = 3.06, one-tailed p<0.05; t(3) = 8.83, one-tailed p<0.005], and there was a strong trend [t(3) = 1.96, one-tailed p = 0.07] for the peak time to be shorter than that obtained on long probe trials, while there was no difference in peak spread between compound and long trials [t(3) = 1.37, n.s.]. As seen in previous reports regarding the behavior under compound stimulus trials (Swanton, et al., 2009), timing remained roughly scalar, as the normalized spread for the compound trials was 1.12 (0.27), with no significant differences in CV across the three trial types. Figure 3b shows the superimposition of peak functions after being normalized by peak rate and peak time.

Nosepoke responding on single probe trials of peak-interval procedures is typically described by a two-state step function (Cheng & Westwood, 1993; Church, et al., 1994; Matell, et al., 2006; Swanton, et al., 2009) in which the rat is primarily away from the operant manipulandum early in the trial (1st “Out” state), abruptly switches to being primarily active toward the manipulandum around the criterion time (“In” state), and then switches back to being primarily away from the manipulandum following the passage of the criterion time (2^nd “Out” state). Figure 4 shows these step functions for the three trial types from a single rat, on a single session, and Table 1 provides the mean times at which these events occurred across all rats and all sessions. As can be seen in Figure 4, the rat was in the nosepoke less than 10% of the time during the two “Out” states, whereas it was in the nosepoke roughly 60% of the time during the “In” state. While the nosepoking behavior is well described by these three states, the probability of being in the nosepoke was not constant throughout the “In” state, but rather showed a dip pattern. Although the high incidence of nosepoking on the edges of the step function is an artifact resulting from the requirement that the rat must be in the nosepoke for a behavioral state transition to be identified, the curvature in the center of the step remains even after excluding 0.5 sec intervals around the start and stop times, indicating that “In” state behavior was not stationary. Closer examination of the pattern of nosepoke occupation during the “In” state suggested that the rats typically made brief pauses (average maximal duration outside of the nosepoke during “In” state = 0.5 sec) in their response pattern. To account for this non-stationarity, we use occupancy of the nosepoke as a covariate when evaluating the neural responses during the “In” state, as discussed in the Methods.

Table 1.

Transition Times from Single Trial Analyses (sec)

	Start	Stop	Spread	Midpoint
Short	8.87	15.73	6.86	12.30
StDev	2.08	1.51	2.18	1.45
Long	18.29	28.32	10.03	23.31
StDev	3.66	3.33	4.76	2.56
Compound	13.29	24.67	11.37	18.98
StDev	3.79	1.27	4.65	1.61

Peristimulus Time Histograms

155 single units were recorded across the 4 rats (n=42, 32,48, 33/rat) from sessions with sufficient numbers of trials for statistical analysis (i.e., at least 6 probe trials from one trial type with temporally controlled behavioral responses). Figure 5 shows the population peristimulus time histogram over the entire trial period for the three signals. As can be seen, the population activity showed a phasic increase around trial onset followed by a slow positive ramp to trial end at 25 sec on short trials, or a positive ramp to 25 sec followed by either a gradual return to baseline rates (long trials) or sustained activity (compound trials). These differential patterns resulted in differences in mean firing rates between the three trial types [F(2,308) = 4.28, p < 0.05], as the mean firing rate on long trials (6.7 +/− 8.5 Hz) was significantly lower (p<0.05) than that on short trials (7.1 +/− 9.1 Hz) and nearly so (p = 0.056) on compound (6.9 +/− 8.8 Hz) trials, which did not differ. However, as can be seen by inspecting the scaling of the ordinate, the extent of common modulation across the population was small.

Figure 5.

Population peristimulus time histogram from probe trials showing phasic activation at cue onset, followed by slow ramping (short cue), ramping to plateau (compound cue), or peaking (long cue) in firing rate across the trial. The degree of common modulation is relatively low, largely due to different patterns of temporal dynamics across the population of 155 neurons. Stimulus onset at T=0. Dashed lines at 10s and 20s indicate the possible times of reinforcement.

Inspection of individual neuron data (Figure 6) revealed that this limited degree of modulation was due to a diversity of individual cell firing patterns that varied in both shape (e.g., peaks or ramps) and direction (i.e., increasing or decreasing) across many cells, rather than to temporal modulation being present in only a small number of cells, or to a limited degree. An examination of the reliability of firing rate fluctuations with repeated measures ANOVAs revealed that 46% (71/155) of the neurons had significant modulations of firing rate as a function of time in the trial. Of these 71 neurons, 25% had modulations on all trial types, 15% had modulations on just two trial types (e.g., just short and long trials), and 59% had significant modulations for just one trial type.

Figure 6.

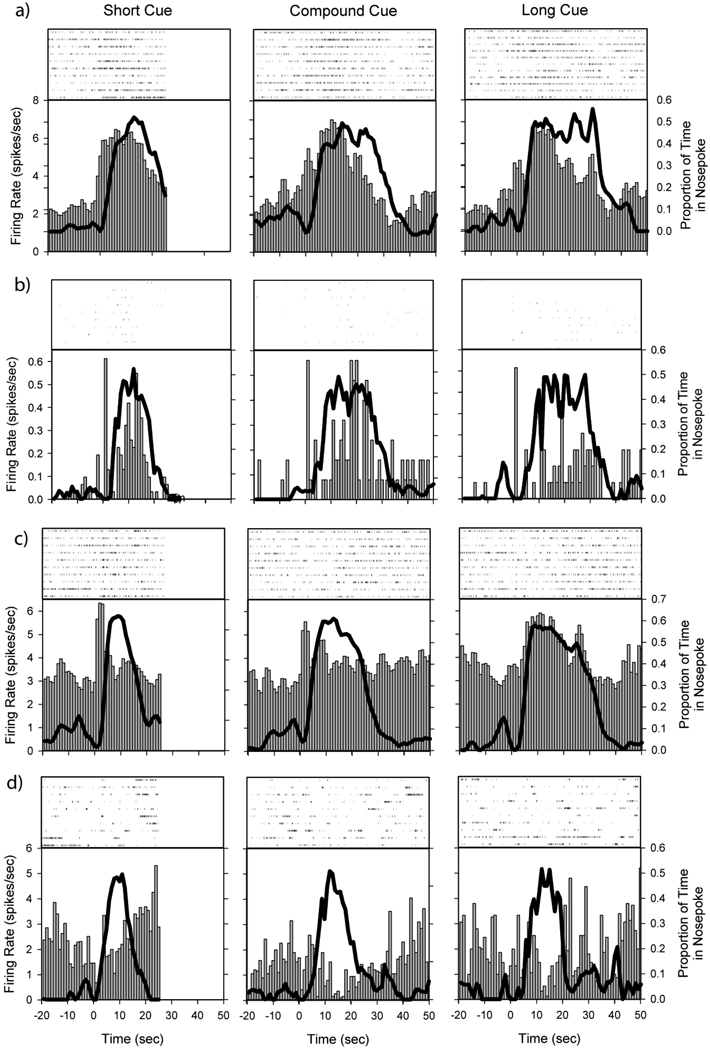
Peristimulus time histograms showing firing rate patterns from probe trials. Raster plots from a random subset of trials are shown above the PSTH. Responses to the Short cue are shown in the left panel, the Compound cues in the middle panel, and Long cue in the right panel. Each row shows a different neuron. The vertical bar graph represents the average firing rate of the neuron as a function of time in the trial, while the solid black line represents the average probability of having the snout within the nosepoke aperture as a function of time in the trial. Three of the neurons show peak shaped activity in response to one or more of the cues, while the bottom neuron shows ramping activity in response to the Short cue. Stimulus onset at T=0.

In order to provide a basic characterization of the pattern of neural firing across the trial, the PSTHs of those neurons showing reliable firing rate changes were separately fit with a linear function and a Gaussian-like function to broadly categorize them as ramping or peaking. Not surprisingly, given the motor-relation of the medial agranular cortex, coupled with the temporal control of behavior shown in Figure 3a, 59% (42/71) of the neurons were well characterized by a Gaussian-like function. Of these 42 cells, 76% (32/42) were peak shaped on only one trial type, 14% (6/42) had peaks across two, but not all three, trial types, and only two cells (5%) had peaks across all trial types. The cells differed in the degree to which their activity corresponded to the animal’s nosepoking behavior, with some cells showing a strong correspondence during at least one of the trial types, while others showed peaks that did not directly match the behavioral dynamics. In contrast, only 21% (15/71) of the neurons were well fit by a linear function on at least one trial type. 80% (12/15) of these latter cells were well fit by a linear function on only one trial type, one of these cells (7%) had a linear fit on two, but not all three trial types, and two of these cells (13%) showing a linear function across all trial types.

Within-trial analysis -- encoding of elapsed time

In many cells, visual inspection of the neuronal PSTHs suggested a direct relationship with the nosepoking behavior. Further, in those neurons in which a relationship was not apparent, it would be premature to try to relate these neurons’ firing rate fluctuations to the passage of time, as the rats may be producing other behaviors (see e.g., Killeen & Fetterman, 1988), particularly during the “Out” states, that may have contributed to the shape of the neural fluctations when examined as session-wide averages. Therefore, in order to evaluate the dynamics of neural activity as a function of time, we restricted the subsequent analyses to the period of time that the rat was engaged in nosepoking at a high rate, the “In” state. Because the “In” state is composed of the rat either holding its nose in, or repeatedly poking in and out of, the nosepoke aperture, it cannot be performing other overt behaviors that might covary with time (e.g., checking the food cup, rearing, general locomotion, etc). As such, the “In” state can be viewed as providing a similar “steady-state” framework for analysis as the period of motionlessness utilized in primate studies, but for a freely behaving animal.

Figure 7 shows the peristimulus time histograms of several representative cells during the “In” state across the three trial types. As can be seen, neural activity frequently varied quite strongly during the “In” state, and these firing patterns and/or rates frequently differed as a function of trial type. To quantitatively evaluate the extent and reliability of the firing rate changes over time, we compared neural firing rates and patterns between the first half (early) and second half (late) of “In” state responding using LDA with leave-one-out cross validation (see Figure 2 for a basic characterization of the analysis. To control for variations in nosepoke occupancy across the “In” state, we assessed whether the firing rates varied as a function of time after covariations in motor activity were taken into account.

Figure 7.

Peristimulus time histograms showing firing rate changes during the “In” state for the Short cue (left), Compound cue (middle) and Long cue (right). Due to trial by trial variability in the length of the “In” state, activity is shown as a function of the proportion of the “In” state by binning each trial’s activity into 15 bins, each 1/15 of the width of the “In” state for that trial. Each row is a different neuron. Notice the variation over time in the “In” state, as well as the difference in the patterns and/or rate of activity across trial types. Firing rates are shown as vertical bars, and occupancy in the nosepoke aperture is plotted as a thick black line. Firing rates within the “In” state have been smoothed with a 5s running mean for presentation, and were normalized by the maximum rate across trial types.

On short signal trials, 131 neurons came from sessions in which there were sufficient trials to perform the LDA analysis (19.0 +/− 8.2 trials per session). Of these neurons, 44 (34%) had spike trains that could be classified as to whether they came from the early or late epoch of the “In” state at better than chance levels. Across the 131 neurons, the average classification rate was 59% (p<0.001). The distribution of classification success is shown in Figure 8b.

What firing patterns lead to these discriminable differences in late vs. early activity in trials? As expected from the variety of PSTHs seen in Figure 7, the direction of the optimal feature varied widely across neurons as shown in Figure 8a. However, qualitatively different firing patterns can produce identical feature directions (e.g., the bottom of Figure 2 shows that hypothetical firing patterns that would be described as a ramp versus a rising sawtooth pattern have the same feature direction). Indeed, while the majority of significant neurons pointed towards quadrants 1 and 3, visual inspection of the firing patterns indicated that many of these neurons were best described as having an asymmetric peak shape. Thus, the varying feature directions by themselves are insufficient to characterize the variability of response patterns.

Therefore, to more adequately clarify the “shape” of the average firing pattern, with the goal of providing a simpler description for subsequent modeling, we re-binned the spike counts across the “In” state into 3 bins, and identified cells with monotonic changes across the bins as ramp-shaped, and cells with non-monotonic changes as peak-shaped. To provide a graphic representation of these shapes, the normalized change in rate from Bin 1 to Bin 2 was plotted on the abscissa and the normalized change in rate from Bin 2 to Bin 3 was plotted on the ordinate, such that all patterns would fall on a square with corners at +/−1, +/−1. As can be seen in Figure 8c the shape of the relative rate change across the “In” state was quite heterogenous, with cells corresponding to a broad mix of ramps of varying curvature (55% - Quadrants 1 and 3) and peaks (45% - Quandrant 2 and 4). Importantly, the variation in the shape of firing patterns between neurons (i.e., the spread of points around the square shown in Fig 8c) was significantly greater (p<0.001) than the average variation within a single neuron across trials.

On compound signal trials, 148 neurons were recorded on sessions with sufficient trials to run the discriminability and shape characterization analyses (15.5 +/− 6.6 trials/session). On these trials, 57 (39%) of the neurons’ spike trains were classifiable at better than chance levels. As shown in Figure 8e, the average classification rate was 63% (p<0.001). The diversity of optimal features for the compound trials (Fig 8d) was similar to that for the short trials, and the shape characterization plot revealed 49% ramp patterns and 51% peak patterns (Fig 8f), with greater heterogeneity of patterns between neurons than within (p<0.001).

On long signal trials, 97 neurons came from sessions with sufficient trials to run the analyses (9.5 +/− 2.7 trials/session). On these trials, 24 (25%) of the neurons’ spike trains were classifiable at better than chance levels. The diversity of optimal features for the long trials was similar to that for the short and compound trials (Fig 8g). Across neurons, the average classification rate was 62% (p<0.001). The distribution of success is shown in Figure 8h. The shape characterization plot (Fig 8i) again revealed a mix of ramp (33%) and peak patterns (67%). Again, there was greater heterogeneity in firing patterns between neurons as compared to average heterogeneity within a neuron (p<0.01).

Taken together, 55% (86/155) of the neurons produced classifiable changes in spike rate/pattern across the “In” state on one or more trial types. Of the 87 cells with sufficient trial numbers on both short and long trials, 14 (16%) changed in a reliable manner as a function of time for both trial types. Similarly, 17% (22/131) of cells provided classifiable information on both short and compound trials, and 13% (12/90) provided classifiable information on both long and compound trials. 10% (9/87) provided classifiable information on all three trial types.

We were also interested in assessing whether there were features of the firing pattern that transcended trial-type specific activity. To this end, we tested the ability of the neurons to discriminate the progression through the “In” state using all trials, irrespective of trial type. It should be noted that the statitistics reported in the preceding paragraph were obtained by pooling the results across multiple trial types, and did not assess whether the temporal dynamics allowing significant classification were similar across trial types (e.g., a neuron might ramp on short trials, but peak on long trials – see Figure 7b). In contast, the present across-trial analysis asks whether a feature of the firing patterns exists that is the same across all trials, irrespective of whether this feature is the optimal feature for any individual trial type. We found that 63 of the 148 (43%) neurons with sufficient trials to carry out the LDA had firing patterns that allowed us to predict whether the spike train came from the first or second half of the step function with significant accuracy. The increase in the number of significant neurons here compared to the single trial type analyses reported above results from an increase in the number of trials available for analysis by pooling across trials prior to performing the LDA. As in the single cue cases, the optimal feature directions varied across neurons (Figure 9a). Across the entire population of neurons, the average classification rate was 60% (p < 0.001), and the distribution of classification is shown in Figure 9b. The shape characterization plot (Figure 9c) was composed of a mix of ramp (56%) and peak patterns (44%). As in the single cue trials, the heterogeneity of firing patterns was significantly greater between neurons than within neurons (p<0.001).

Population encoding of elapsed time

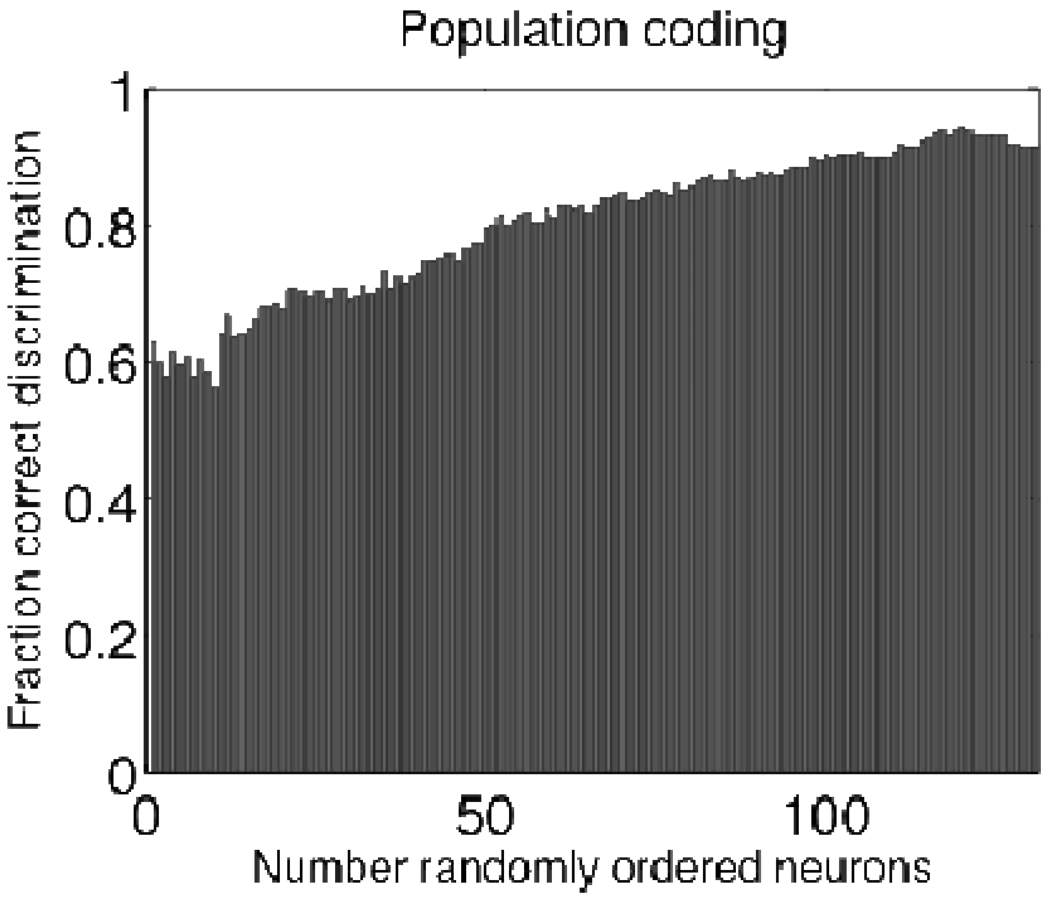
As the mean accuracy of single neurons in these categorizations was relatively low (~60%), we asked how well the population of recorded neurons could collectively encode elapsed time. This enabled us to quantify the increase in predictive capacity gained by sampling from multiple neurons. As shown in Figure 10, the addition of randomly chosen neurons led to an approximately linear increase in predictive success until nearly perfect predictability was obtained with approximately 150 neurons.

Figure 10.

Approximately linear improvement in classification accuracy following the addition of randomly chosen neurons to the ensemble.

Functional role of heterogeneous firing patterns in a simple model

Given our, and others’, results, it’s natural to ask what functional role is served by the heterogeneity among firing patterns of different cells. Here, we demonstrate one possible answer, by comparing the accuracy with which simple model populations of homogeneous vs. heterogeneous cells can be read out to produce an estimate of elapsed time. In particular, we show that heterogeneity can lead to more-accurate time estimates. Our analysis is similar to, and motivated by, that of Harper and McAlpine (2004) in a distinct setting.

The model cell populations we study consist of N=50 cells; each cell is assumed to fire spikes independently in a Poisson manner with a time-dependent firing rate (in other words, the j^th cell in the population is an inhomogeneous Poisson process with rate r_j(t)). For the different populations we study, individual cells might display, e.g., ramping or dipping firing rates over time.

To quantify how elapsed time can be estimated from a cell population, we apply basic results that describe the accuracy of an (unbiased) decoder that “observes” spike counts from the population at time, and makes the best-possible estimate of the current time t based on this observation. This accuracy is described by the r.m.s. error in this time estimate, i.e., the standard deviation std(t) of estimates made at time t. Our strategy is to compare values of std(t) obtained from homogeneous vs. heterogeneous cell populations; lower values of std(t) correspond to more accurate estimates of elapsed time.

The r.m.s. error std(t) for a given cell population is computed as follows. We assume that the decoder estimates elapsed time based on a running tally of the number of spikes that each cell has produced in a window of the previous T seconds; here, we take T=0.5 sec, though this precise value is of little consequence to our results. Thus, the decoder has access to a list of N spike counts, one for each cell; the temporal average of this spike count for cell j, which we will denote by s_j(t), is given by integrating r_j(t) from time t-T to t. By the Cramer-Rao bound (Dayan & Abbott, 2001), the standard deviation std(t) is given by the square root of the inverse of the Fisher information F(t) that the population of cells carries about elapsed time t:

$$\mathit{\text{std}}(t)=\frac{1}{\sqrt{F(t)}}.$$

Under the assumption of Poisson spiking given above, the Fisher Information has a simple form (Abbott and Dayan, 2001):

$$F(t)={\displaystyle \sum _{j=1}^N\frac{{\left(s_j\text{'}(t)\right)}^2}{s_j(t)}}$$

where, for each term in the sum, the numerator is the slope of the jth mean spike count vs. time (squared), and the denominator is the mean spike count itself. This shows how steep slopes, which correspond to greater temporal sensitivity of firing rates, give greater contributions to information about elapsed time; moreover, the contributions are also greater if a given slope occurs at a lower firing rate. Finally, average the r.m.s. error at all times in a range of interest [T_min, T_max], to extract a single number SD that characterizes a population’s encoding of elapsed time,

$$\mathit{\text{SD}}=\frac{1}{T_{\mathit{\text{max}}}-T_{\text{min}}}{\displaystyle \underset{T_{\text{min}}}{\overset{T_{\mathit{\text{max}}}}{\int }}\mathit{\text{std}}(t)\mathit{\text{dt}}},$$

which will be used to compare the coding of elapsed time by the different cell populations. Below, we take T_max = 30 sec. and T_min = 0 sec. (we allow firing rates to be defined for small negative times to compute s_j(t) for t near 0).

As a point of comparison for the heterogeneous population that we will consider below, we first compute SD for a homogeneous population made up entirely of identical cells that display one of the patterns observed in our recordings and are often reported in the literature (Brody, et al., 2003; Gontier, et al., 2009; Kojima & Goldman-Rakic, 1982; Niki & Watanabe, 1979; Pouthas, Maquet, Garnero, Ferrandez, & Renault, 1999): linear ramps, either increasing or decreasing over time. We restrict firing rates to lie between a minimum value of 1 Hz and a maximum of 40 Hz over the range from 0 to 30 sec., and perform an exhaustive search over all such ramps to find the one that gives the lowest value of SD. Specifically, each r_j(t) is defined by

$$r_j(t)=a+\frac{[b-a]}{30}t$$

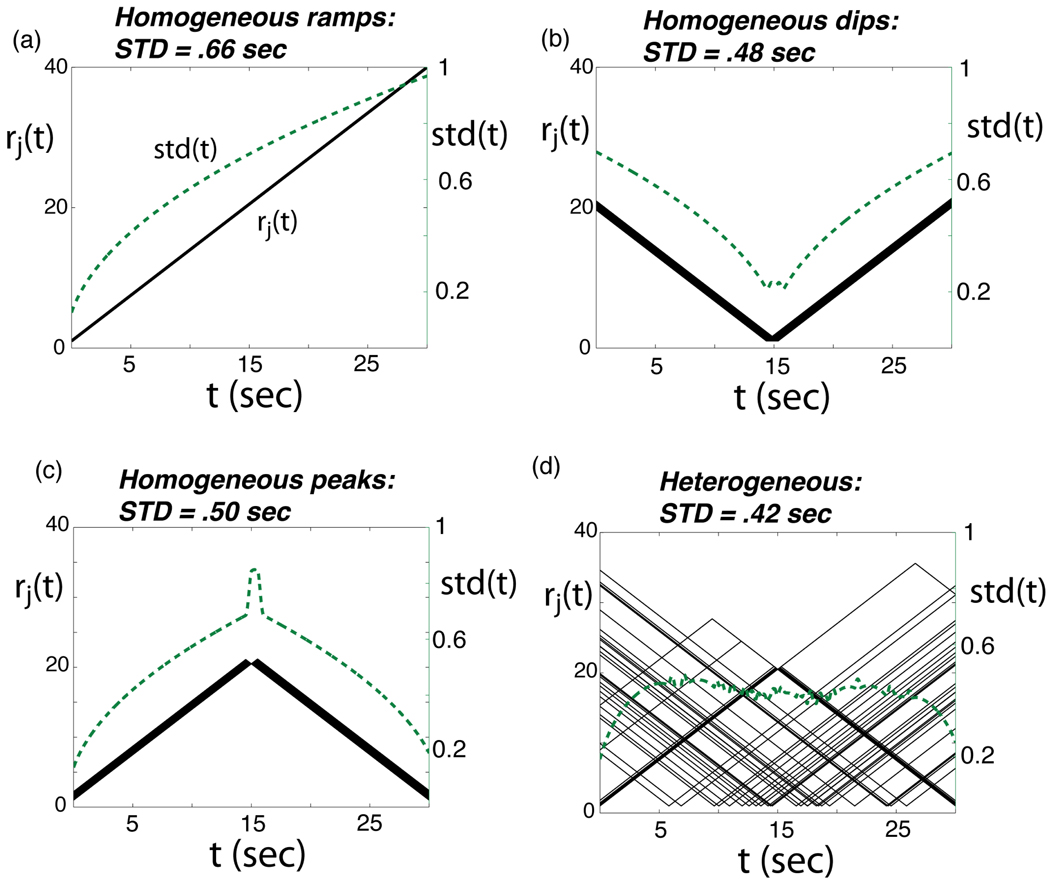
where a is the starting value of the ramping firing rate at t=0 sec. and b is its end point at t=30 sec., and we numerically evaluate SD for all possible a, b values and find the values that minimize it. The resulting optimal ramp increases from the minimum to the maximum rate (Fig. 11(a)), producing an average estimation error SD = 0.66 sec (an otherwise identical decreasing ramp gives the same value). Note from the plot of std(t) in Fig. 11(a) that the best-encoded times correspond to the lowest firing rates, as expected from the formulas above.

Figure 11.

Optimized firing rates r_j(t) (solid lines, scale on left of plot) for cells in different model populations with N=50 cells (see text). The accuracy with which elapsed times t could be estimated based on spikes produced by these populations is represented by the standard deviation in ideal time estimates std(t), plotted as a thick dashed line in each panel (scale on right of plot). a) Results for a homogeneous ramping population in which cell ramps identically between the same starting and the same ending firing rate; these starting and ending values are optimized to minimize average estimation error SD (see text). Likewise, for nearly homogeneous dipping (b) or homogeneous peaking (c) firing patterns (1 sec. of uniform jitter added, see text). Here, the location (again identical for all cells) of the minimum or maximum is optimized to minimize SD. d) For heterogeneous firing patterns with N/2=25 dipping and N/2=25 peaking cells, for each of which the dip or peak value is allowed to occur at a different time. The set of these times is optimized to minimize SD.

Next, we consider a different homogeneous population, this time displaying another common firing pattern from our data: piecewise-linear dips, obtaining a minimal firing rate at time t^min. The slope of these firing patterns is set to have the same (absolute) value as for the optimal ramps above, and the minima are likewise fixed to 1 Hz. We search over the range of possible values of t^min to find the one that optimizes SD: the optimal value, shown in Fig. 11(b), is nearly centered through the range being timed. (In our calculation, the minima in different cells is uniformly jittered over 1 sec., so as to avoid a pathological case in which std(t) becomes infinite.) This gives an optimal error SD=0.48 sec. This considerable improvement vs. the result SD=0.66 sec for ramping firing patterns can be understood via the formula for F(t) above: similar slopes s'(t) are obtained with, on average, smaller spike counts s(t). We obtain a similar result, shown in Fig. 11(c), for a homogeneous population of cells showing the other prominent pattern in our dataset, peaks, obtaining a maximal firing rate at times t^max. Here, the (absolute) slopes are as for the dipping patterns; values of maxima are set so that firing rates as low as possible while staying above the minimum rate of 1 Hz. The resulting optimal error is SD=0.50 sec., similar to the value for dips; once again, the optimal patterns are nearly centered in the time range.

Finally, we consider a heterogeneous population: we split the total of N=50 model cells into 25 dipping/peaking cells and 25 ramping cells. Moreover, we allow the times $t_j^{\mathit{\text{min}}}$ at which the minimum firing rate occurs for each dipping cell to vary freely, and likewise the times $t_j^{\text{max}}$ for each peaking cell -- as opposed to the cases considered above in which all cells in the population had identical ramping, dipping, or peaking patterns (firing patterns are otherwise constrained as for the previous cases). Note that this freedom allows for a mixture of ramping, dipping, and peaking cells: for example, $t_j^{\mathit{\text{min}}}=0$ for a dipping cell would correspond to an increasing ramp; $t_j^{\mathit{\text{min}}}=T^{\mathit{\text{max}}}$ to a decreasing ramp, and values in between to offset patterns that could resemble more closely either ramps or dips. Searching over different combinations of the $t_j^{\mathit{\text{min}}}\text{ and }{t}_j^{\text{max}}$ using a genetic algorithm, we find that the lowest values of SD are produced by populations with diverse firing patterns: see Fig. 11 (d) for an example. This heterogenous population gives SD = 0.42 sec, a 35.9% improvement over the homogeneous ramping population, 13.2% over the homogeneous dipping population, and 15.2% over the homogeneous peaking population.

Comparing panels (a)–(d) in Fig. 11 explains the role of the heterogeneity in decreasing the average estimation error SD: in our setup, each cell contributes most to decreasing std(t) when it has low firing rates, and heterogeneity allows for a cooperative code in which these contributions are spread out close to uniformly across the interval being timed. We note that peaking patterns are more clustered toward the center of the interval than the dipping patterns, which are broadly distributed; this may be understood based on the fact that centering a peaking pattern allows for it to have lower firing rates while obeying the lower bound of 1 Hz. Overall, we note that the optimization algorithm found many sets of firing patterns similar to that in Fig. 11(d) that gave similarly low values of the error SD; this indicates that a wide variety of heterogeneous population dynamics with the general characteristics discussed here all produce good timing performance.

We emphasize that our present study is intended only to give a qualitative illustration of the potential coding benefits of heterogeneity. A more involved study would account for an additional layer of heterogeneity in the range of possible firing rates displayed by each neuron in the population. Another interesting extension would be to more strongly weight the contribution to SD of estimation errors made at different times – perhaps those close to the task durations after which rewards are delivered. Overall, while details of optimal firing patterns will differ, we expect that the underlying mechanism of heterogeneous, cooperative coding improving overall estimates is likely to persist under these and other modeling assumptions (as in, e.g., Harper & McAlpine, 2004).

Discussion

The present experiment examined the firing patterns of medial agranular cortex neurons in rats while they freely behaved on a temporal production task, the peak-interval procedure. An analysis of trial-by-trial firing rates showed that roughly half of the recorded neurons were reliably modulated as a function of time in the trial, with average firing rates from individual neurons showing peak-like and/or ramp-like activity, as well as more complex activity patterns. However, given the co-occuring temporal dynamics of behavior in timing tasks (Fetterman, Killeen, & Hall, 1998; Gibbon, 1977; Killeen & Fetterman, 1988; Roberts, 1981; Swanton, et al., 2009), it is not clear whether these trial-wide neural activity patterns directly follow from the temporally varying behavior of the rats, or whether they serve as an information source guiding these behaviors.

Therefore, to facilitate an interpretation of the temporal dynamics of this neural activity, we restricted our analyses to windows of time in which the rats’ behaviors were essentially stable, the “In” state of responding (Cheng & Westwood, 1993; Church, et al., 1994; Gibbon & Church, 1990; Matell, et al., 2006; Matell & Portugal, 2007; Swanton, et al., 2009). Our experimental design provided a relatively small number of trials (i.e., < 20 trials) for any particular trial type (i.e., short, compound, or long), and as such, we were only able to characterize the firing pattern across the “In” state with 4 bin resolution, thereby allowing only a rough visualization of the neuronal dynamics (i.e., we could discern ramp and peak-like patterns of activity, but not more complex patterns). Nevertheless, similar to the variety of patterns seen in the peristimulus time histograms across the entire trial, we found a broad range of firing patterns during the “In” state. Importantly, in contrast to the heterogeneity between neurons, the variability within many of these neurons was small enough that an ideal observer could reliably identify whether the subject was responding in the first or second half of the response period. In other words, the subject could utilize the firing rate/pattern of these neurons to assess whether elapsed time in the trial was before or after the expected time of reinforcement, thereby allowing a decision to be made regarding the appropriate time to stop responding. Given that these analyses were restricted to the “In” state in order to provide interpretational control, it is important to note that our results are limited to this response window, and it remains unclear whether similar heterogeneous activity patterns provide accurate temporal information during the “Out” states. As tracking the passage of elapsed time prior to the “In” state is certainly necessary for deciding when to begin responding (Church, et al., 1994), and behavioral analyses have suggested that time following the “In” state is also tracked (Church, Miller, Meck, & Gibbon, 1991; Sanabria & Killeen, 2007), future work will be needed to evalaute whether the mechanisms underlying temporal control differ across behavioral states.

In addition to variation in firing rates over the course of the “In” state for a single stimulus, we also found that firing rates and/or patterns were reliably different in approximately one-third of the neurons when comparing one trial type with another trial type (see supplementary methods and results). However, there are a number of important psychological differences other than elapsed duration between the trial types, including, but not limited to, the different modalities of the stimuli used as cues, the different probabilities of reinforcement associated with these cues, and difference in incentive value due to delay and probability discounting. As such, it is premature to draw conclusions as to whether the differences in these activity patterns are related to the subjective perception of different durations. Nevertheless, the results showing a broad heterogeneity of activity patterns are consistent with the findings from the within-duration analyses, which do not suffer from these alternative interpretations.

In contrast to the reports reviewed in the introduction that highlighted either ramping activity or peaking activity during elapsing delays, the variety of firing patterns seen in the current data is similar to recent work conducted in non-human primates showing frontal cortex neurons displaying complex and heterogeneous activity patterns during memory delay tasks (Brody, et al., 2003; Genovesio, et al., 2009; Jun, et al., 2010; Miller, 1999; Romo, Brody, Hernandez, & Lemus, 1999; Romo, Hernandez, & Zainos, 2004). The basis for these different results is probably multi-faceted. One simple possibility is that it may reflect a decision by individual investigators to simplify presentation. Another possibility is that the construction of average population patterns may have diminished the influence of patterns which are counter-directional or vary in time across cells. For instance, recent work by Pastalkova et al. (2008) demonstrated that different hippocampal neurons peak at different times during a sustained delay period. Averaging such data would yield a flat population PSTH, similar to the relatively flat population-averages seen in our Fig 5. Similar findings have been reported by Oshio et al (2008). In contrast, the use of LDA to determine optimal features for classification as used here extracts the varied firing patterns that contribute to population activity in these cases.

Differing task demands may also be partially responsible for the diffences in firing patterns seen across studies. Many of the paradigms used to examine the temporal dynamics of cortical neurons were memory tasks, and subjects were not explicitly trained to discriminate the duration of the delay. As such, the neuronal activity patterns may be more directly related to working memory demands, rather than the perception of elapsed time. Additionally, non-human primates are typically required to remain motionless while the delay elapses before making a single response at the end of the interval. In contrast, subjects in the present experiment were free to move, and the steady-state “In” state behavior on which our primary analyses were based resulted from the “strategy” used by rats to obtain reinforcement at the earliest possible interval.

Related to the above issues are recent results from Machens et al (2010) in which they re-analyzed macaque prefrontal activity collected during a vibration frequency match to sample task. The authors introduced a novel analysis in which they identified covariations in neuronal responses that were related to both elapsing time and the stimulus frequency being remembered on each trial. Intriguingly, this analysis revealed that prefrontal firing patterns were composed of both ramping activity and peaking activity which were related to elapsed time in the delay and differences in rate (either static or rate of change) which were related to the vibration frequency held in memory. Importantly, different neurons were influenced by these task-related factors to different degrees, thereby generating the heterogeneity seen across the population. Similar evidence for multi-feature representation of duration, stimulus, and response components of the task is seen in the work of Genovesio et al (2009). Together, these data suggest that the different response patterns identified across studies are likely related to both task demands and the analytic/theoretic approach used.

The variety of neural patterns recently found within single neural structures poses difficulty for theories of interval timing that utilize unitary signal patterns, such as pulse accumulation (Church, 1984) or memory decay (Staddon & Higa, 1999). In these models, neural activity reflecting the clock should ramp (or decay), while neural activity reflecting a decision stage comparison process should peak (or dip). However, there apeears to be little neurobiological evidence supporting such simple serial models with one structure providing a clock signal and another structure comparing this clock signal to memory values. On the other hand, it is conceivable that the proportion of neurons contributing to these stages vary in a systematic manner as information flows from anterior planning and valuation areas to motor execution areas (see e.g., (Roesch & Olson, 2005a). However, to explain such findings, the serial information processing models of time may need to be modified to allow for dynamic feedback, such that output of the decision stage influences the functioning of the clock (Matell, Meck, & Nicolelis, 2003b). In this way, one might expect different neural areas to express both clock and decision processes. An alternative possibility that is not at odds with a serial model would place temporal processing within the domain of each cortical area. In this manner, temporal information related to the cognitive processes operated on by a cortical area would be computed locally, rather than globally, and one would expect to find a range of neural activity patterns in each recorded area. However, cross-modal transfer of temporal expectancy (Meck & Church, 1982) as well as the cross-modal temporal averaging seen in response to the compound stimulus in the current experiment and elsewhere (Swanton, et al., 2009; Swanton & Matell, in press) provides impediments to a purely local representation of time (see also (van Wassenhove, 2009)

A final possibility, as demonstrated by the simple model presented above, is that the utilization of a multitude of heterogeneous patterns provides an adaptive mechanism for diminishing error in temporal estimates. As shown above, the addition of each new pattern/slope/placement of maxima/minima resulted in increased accuracy. As such, the current results provide a benefit for proposing that the clock is not composed of a single signal, but rather that the internal clock is represented by a distributed code. One important aspect of any clock process is that it should be relatively sequestered from perturbation by outside influence. We speculate that distributed and/or heterogenous coding schemes may provide better insulation against such perturbation than local and/or homogeneous codes. Indeed, the inability to substantially modify temporal expectations via pharmacological and anatomical manipulations has been a hindrance to deciphering the mechanisms of interval timing (the largest shifts in temporal expectation following drug administration have been around 15% of the timed duration).

The Striatal Beat Frequency model of timing pointed out that striatal spiny neurons were in an ideal position to integrate neural activity from a broad array of cortical neurons with different firing statistics (Matell & Meck, 2000, 2004). The model specifically proposed a scenario in which cortical firing was oscillatory in nature, with different cortical neurons having different periodicities, an outcome that was not seen in the present data. However, the global framework of striatal integration of an array of cortical neurons could be easily applied to the present data. More generally, we suggest that a pattern detection, perceptron-style readout of multi-faceted, complex, evolving, cortical activity would be an effective mechanism for temporal control. Indeed, the state-dependent network models of Buonomano and colleagues (2000; 1995) utilized a similar scheme in which the dynamics of neuronal excitability (e.g., short-term synaptic plasticity) give rise to complex network states that can be used to discriminate intervals. While such states do not easily lend themselves to a monotonic representation of time, subsequent empirical work by this group demonstrated just such a non-monotonic representation of time in humans when discriminating short, sub-second, intervals (Karmarkar & Buonomano, 2007). In contrast, their results did not provide support for a non-monotonic representation of time for longer, supra-second intervals, such as those used here. Furthermore, given phenomenon such as matching behavior (Grace, 1999; Herrnstein, 1974), delay discounting (Green & Myerson, 2004; Mazur, 2001), and temporal memory averaging (Swanton, et al., 2009; Swanton & Matell, in press), at some point, time must be compatible with a monotonic representation. However, it remains unclear whether such a monotonic representation needs to reflect the temporal signal itself, or whether it might simply reflect the value associated with temporal memories, which could depend on the scalar variability associated with different durations, rather than the durations themselves. As such, the current heterogeneous activity patterns may serve as possible signals contributing to an internal clock.