Abstract
The correlations among seed yield components, and their direct and indirect effects on the seed yield (Z) of Russina wildrye (Psathyrostachys juncea Nevski) were investigated. The seed yield components: fertile tillers m-2 (Y1), spikelets per fertile tillers (Y2), florets per spikelet- (Y3), seed numbers per spikelet (Y4) and seed weight (Y5) were counted and the Z were determined in field experiments from 2003 to 2006 via big sample size. Y1 was the most important seed yield component describing the Z and Y2 was the least. The total direct effects of the Y1, Y3 and Y5 to the Z were positive while Y4 and Y2 were weakly negative. The total effects (directs plus indirects) of the components were positively contributed to the Z by path analyses. The seed yield components Y1, Y2, Y4 and Y5 were significantly (P<0.001) correlated with the Z for 4 years totally, while in the individual years, Y2 were not significant correlated with Y3, Y4 and Y5 by Peason correlation analyses in the five components in the plant seed production. Therefore, selection for high seed yield through direct selection for large Y1, Y2 and Y3 would be effective for breeding programs in grasses. Furthermore, it is the most important that, via ridge regression, a steady algorithm model between Z and the five yield components was founded, which can be closely estimated the seed yield via the components.
Introduction
Forages are the backbone of sustainable agriculture and environmental regeneration in arid land [1]. Perennial forage crops play a major role in providing high quality feed for the economical production of meat, milk and fiber products [2]. Perennial forage crops are also important in soil conservation and environmental protection [3], as they add organic matter to the soil and serve as a permanent ground cover preventing soil erosion [4]. In addition, perennial grasses are potentially useful for crop improvement as they possess important germplasm or genes for being tolerant to rigorous environment (field conditions) [5], [6].
Russian wildrye (Psathyrostachys juncea Nevski) is a perennial grass, which is growing rapidly, highly drought and CaCO3 tolerant and has a low fertility requirement [7], [8], [9], [10]. Russian wildrye is a cool-season forage species well adapted to semi-arid climates [3], [11]. It is a perennial bunchgrass and is characterized by dense basal leaves that retain their nutritive value better during the late summer and autumn than many other grasses [12].
Established stands of Russian wildrye provide excellent grazing for livestock and wildlife on semi-arid rangelands of the Intermountain West and the Northern Great Plains in North America [3], [13], [14]. Also, it is very competitive, high-yielding, an excellent source of forage for livestock and wildlife on semi-arid rangelands [12] in Eurasia and northwest China [4], [9], [10], [11], [15], [16], and it is also an important forage crop for revegetating rangeland in North America [17]and northwest China [1], [9]. In addition, Russian wildrye is cross-pollinated and relatively self-sterile [14]. It is the only agriculturally important species in the genus Psathyrostachys, which is a member of the Triticeae tribe [16], [18] and is also considered to be an important germplasm in crop improvement as it possesses resistance to barley yellow dwarf virus (BYDV) [1], [3], [10], [19].
There is a limited use of Russian wildrye due to its unsteadiness of seed production [1]. The reason is most probably that breeding programs has focused on developing Russian wildrys cultivars with a high biomass yield while improvement of seed yield has been neglected. Seed yield is a quantitative character, which is largely influenced by the environment and hence has a low heritability [20]. Therefore, the response to direct selection for seed yield may be unpredictable, unless there is good control of environmental variation. In order to select for higher seed yield there is the need to examine the mathematical relationships among various characters, especially between seed yield and key seed yield components and a certain amount of interdependence between them [21], e.g. seed yield components do not only directly affect the seed yield, but also indirectly by affecting other yield components in negative or positive ways [22]. In such situations, knowledge of the nature of genetic variability and interrelationships among seed yield and key yield components would facilitate with reference to breeding improvement for these traits [23]. Another possibility would be: To unravel the often complicated interdependence between seed yield components and seed yield knowledge of the nature on genetic variability and interrelationships among seed yield and seed yield components is important. This knowledge also merits future breeding programs in Russian wildrye. To our knowledge no information is available on the mathematical relationship between seed yield and seed yield components in Russian wildrye.
Path analysis provides a method of separating direct and indirect effects and measuring the relative importance of the causal factors involved. Several researchers have used this method to assess the importance of the components of yield [20], [23], [24], [25]. The advantage of path analysis is that it permits the partitioning of the correlation coefficient into its components, one component being the path coefficient that measures the direct effect of a predictor variable upon its response variable; the second component being the indirect effect(s) of a predictor variable on the response variable through another predictor variable [26]. In agriculture, path analysis has been used by plant breeders to assist in identifying traits that are useful as selection criteria to improve crop yield [26], [27].
For grass crops, the correlation of economic yield components with seed yield and the partitioning of the correlation coefficient into its components of direct and indirect effects have been extensively reported: e.g. highly significant associations of grain yield were observed with 1000-grain weight and tiller number per plant [28], [29], the number of filled grains per panicle and harvest index [30]. Grain yield has been influenced by high direct effects of total tillers and days to flowering [31], the number of panicles per plant, the number filled grains per panicle and 1000-grain weight, the number of filled grains per panicle and plant height, productive tillers, panicle length and flowering time [21], [32], plant height and tiller number, panicle number per plant, spikelet number per panicle, the number of effective tillers per plant, grains per panicle and 1000-grain weight, grains per panicle and productive tillers [33], the number of filled grains per panicle and 1000-grains weight [34] and biological yield, harvest index and 1000-grain weight, etc., but few of about grass seed yield components. Such detailed cause and effect mathematical relationships have not been examined in Psathyrostachys juncea Nevski.
However, morphological characters influencing yield are often highly inter-correlated, leading to multi-collinearity when the inter-correlated variables are regressed against seed yield in a multiple-regression equation. For such situations estimation of regression coefficients through ridge-regression was developed by Hoerl and Kennard [35] to ameliorate problems like inflation in absolute value of the regression coefficients and wrong sign of the regression coefficients resulting from these inter-correlated variables.
Based on multi-factor orthogonal design of various field experimental management, with big sample size, the main objective of this study was to examine the mathematical relationships between the seed yield (Z) and the key seed yield components: fertile tillers m-2 (Y1), spikelets per fertile tillers (Y2), florets per spikelet (Y3), seed numbers per spikelet (Y4) and seed weight (mg) (Y5) in Russian wildrye. Then there are formulas theoretically. Seed yield:
If one floret equals one seed embryo for grasses, then, Seed yield potential:
The mathematical relationship was examined using path coefficient and ridge regression analysis. Our hypothesis was that: 1) all the five seed yield components and the seed yield are inter-correlated, and all the five seed yield components are positively contributed to seed yield and 2) the relationship between seed yield and the five seed yield components should be a steady algorithm model which can be closely estimated the seed yield via the components.
Results
Pearson correlation coefficients for all the four years totally shows that seed yield components Y1, Y2 and Y4 are significantly (P<0.0001) positive correlated with the Z, while Y5 is significantly (P<0.01) negative correlated with the Z (Table 1). There was a negative significant correlation between Y1 and Y3 and between Y1 and Y5, while the correlation between Y2 and Y5 was non-significant it was still negative. The Pearson correlation of the Z and its components for individual years analyses of 2003, 2004, 2005 and 2006 showed that only Y1 in all the four years are positively significant correlated with Z and Y2 (P≤0.01), the correlation coefficients of the years order is: 2004>2003>2006>2005 and 2006>2004>2005>2003, respectively (Table 2). The Y3 with Y4 exhibited positively significant correlation in 2003, 2004 and 2005 along with the Y1 with Y3 in 2004, 2005 and 2006 and Y2 with Z in 2004, 2005 and 2003. The Y3 and Y4 with Y5 exhibited positively significant correlation in 2004 and 2005 (P<0.0001) (Table 2).
Table 1. Pearson correlation coefficients of Y1∼Y5, Z (Psathyrostachys juncea Nevski) for 4 years totally.
| Seed yield components | Y1 | Y2 | Y3 | Y4 | Y5 | Z(seed yield) |
| Y1 | 1.0000 | 0.4920*** | -0.3535*** | 0.2002*** | -0.3600*** | 0.8182*** |
| Y2 | 1.0000 | 0.2012*** | 0.2893*** | -0.0775 | 0.4554*** | |
| Y3 | 1.0000 | 0.5866*** | 0.4226*** | -0.0781 | ||
| Y4 | 1.0000 | 0.1865*** | 0.3570*** | |||
| Y5 | 1.0000 | -0.1745** | ||||
| Total sample size (n) | 3150 | 10080 | 9135 | 11970 | 3150 | 1260 |
F-values are presented along with statistical differences:
*P<0.05,
**P<0.01,
***P<0.0001. N = 315
Table 2. Pearson correlation coefficients of Y1∼Y5, Z (Psathyrostachys juncea Nevski) for each year.
| year | Y1 | Y2 | Y3 | Y4 | Y5 | Z | |
| Y1 | 2003 | 1.0000 | 0.3091** | 0.1067 | 0.1317 | -0.0081 | 0.7494*** |
| 2004 | 1.0000 | 0.5973*** | 0.2101* | 0.2428** | -0.0122 | 0.8045*** | |
| 2005 | 1.0000 | 0.5312*** | -0.4456** | -0.2632* | -0.5762*** | 0.3985** | |
| 2006 | 1.0000 | 0.6430** | -0.5561* | -0.0450 | 0.0269 | 0.6245** | |
| Y2 | 2003 | 1.0000 | -0.0712 | -0.1283 | -0.0217 | 0.1954* | |
| 2004 | 1.0000 | -0.1610 | -0.0160 | -0.1953* | 0.3783*** | ||
| 2005 | 1.0000 | -0.1024 | 0.1305 | -0.1588 | 0.3165* | ||
| 2006 | 1.0000 | -0.1111 | 0.1062 | -0.0717 | 0.4036 | ||
| Y3 | 2003 | 1.0000 | 0.9276*** | 0.1588 | 0.1276 | ||
| 2004 | 1.0000 | 0.7087*** | 0.3291*** | 0.3420*** | |||
| 2005 | 1.0000 | 0.6443*** | 0.6295*** | -0.0394 | |||
| 2006 | 1.0000 | 0.4531 | 0.1794 | 0.0271 | |||
| Y4 | 2003 | 1.0000 | 0.1223 | 0.1106 | |||
| 2004 | 1.0000 | 0.3210*** | 0.3121*** | ||||
| 2005 | 1.0000 | 0.5634*** | 0.0290 | ||||
| 2006 | 1.0000 | -0.0519 | 0.2654 | ||||
| Y5 | 2003 | 1.0000 | 0.2320* | ||||
| 2004 | 1.0000 | -0.0257 | |||||
| 2005 | 1.0000 | -0.979 | |||||
| 2006 | 1.0000 | 0.4398 |
F-values are presented along with statistical differences:
*P<0.05,
**P<0.01,
***P<0.0001. N = 105, 134, 60 and 16 for year 2003, 2004, 2005 and 2006, respectively.
Direct and indirect effects of Y1∼Y5 on the seed yield are presented in Table 3. In the individual years from 2003 to 2006 all five seed yield components had a significantly correlated relationship with Z in at least one year (Table 2), however, path analysis showed that only Y1 had strong direct effect (highlighted in bold in Table 3) on Z in the total 4 years (2003 and 2004 are at P≤0.0001, 2005 and 2006 are at P≤0.05), the coefficients are 0.7741, 0.8268, 0.4568 and 0.9417 respectively, thus Y1 had largest contribution to Z among them. And, Y5 in 2003 (0.2309 at P≤0.0001) and Y3 in 2004 (0.1672 at P≤0.05) significantly had direct effect on Z. Furthermore, via SAS, the results of ridge regression analysis and Duncan's Multiple Range Test for seed yield (z) and its components (Y1∼Y5) of the 4 years are showed in Table 4.
Table 3. Path analysis showing direct and indirect effect of Y1∼Y5 to Z (Psathyrostachys juncea Nevski).
| year | Indirect effect via | |||||
| →Y1→Z | →Y2→Z | →Y3→Z | →Y4→Z | →Y5→Z | ||
| Y1 | 2003 | 0.7741 *** | 0.0604 | 0.0136 | 0.0146 | -0.0019 |
| 2004 | 0.8268 *** | 0.2260 | 0.0719 | 0.0758 | 0.0003 | |
| 2005 | 0.4568 * | 0.1681 | 0.0175 | -0.0076 | 0.0564 | |
| 2006 | 0.9417 * | 0.2595 | -0.0150 | -0.0119 | 0.0118 | |
| Y2 | 2003 | 0.2317 | -0.0522 | -0.0091 | -0.0142 | -0.0050 |
| 2004 | 0.4805 | -0.1076 | -0.0551 | -0.0050 | 0.0051 | |
| 2005 | 0.2117 | 0.1009 | 0.0040 | 0.0038 | 0.0155 | |
| 2006 | 0.4015 | -0.1500 | -0.0030 | 0.0282 | -0.0315 | |
| Y3 | 2003 | 0.0799 | -0.0139 | 0.2082 | 0.1025 | 0.0368 |
| 2004 | 0.1691 | -0.0609 | 0.1672 * | 0.2212 | -0.0085 | |
| 2005 | -0.1776 | -0.0324 | 0.0956 | 0.0187 | -0.0616 | |
| 2006 | -0.3473 | -0.0448 | 0.4007 | 0.1202 | 0.0789 | |
| Y4 | 2003 | 0.0987 | -0.0251 | 0.1183 | -0.2195 | 0.0284 |
| 2004 | 0.1953 | -0.0061 | 0.2424 | 0.0229 | -0.0082 | |
| 2005 | -0.1049 | 0.0413 | -0.0254 | 0.0090 | -0.0552 | |
| 2006 | -0.0281 | 0.0429 | 0.0123 | 0.1597 | -0.0228 | |
| Y5 | 2003 | -0.0061 | -0.0042 | 0.0202 | 0.0135 | 0.2309 *** |
| 2004 | -0.0098 | -0.0739 | 0.1125 | 0.1002 | -0.0990 | |
| 2005 | -0.2300 | -0.0502 | -0.0248 | 0.0163 | 0.1161 | |
| 2006 | 0.0168 | -0.0289 | 0.0049 | -0.0138 | 0.3401 | |
| Total direct effect | 2.9994 | -0.2089 | 0.8717 | -0.0279 | 0.5881 | |
| Total effect | 3.9808 | 0.2489 | 1.3569 | 0.6346 | 0.6266 | |
F-values are presented along with statistical differences:
*P <0.05,
**P <0.01,
***P <0.0001.
The direct effects of Y1∼Y5 to z are highlighted in bold (on main diagonal cell); Arrows illustrate directions of effects. pye = 0.6117, 0.5556, 0.8949 and 0.5192 for year 2003, 2004, 2005 and 2006, respectively.
Table 4. Duncan's Multiple Range Test for seed yield (z) and its components (Y1∼Y5) of Psathyrostachys juncea Nevski of the 4 years, and of the ridge regression coefficients.
| year | N | Y1 | Y2 | Y3 | Y4 | Y5 | Z | |
| Duncan's Multiple Range Test | ||||||||
| 2003 | 105 | 205.67 c | 90.22 a | 4.590 a | 2.141 a | 3.461 a | 964.4 b | |
| 2004 | 134 | 542.31 a | 89.54 a | 2.358 b | 2.054 a | 3.093 b | 1483.8 a | |
| 2005 | 60 | 178.09 c | 82.34 b | 2.293 b | 1.587 c | 3.387 a | 541.3 c | |
| 2006 | 16 | 338.47 b | 81.14 b | 2.231 b | 1.749 b | 2.856 c | 714.4 c | |
| F Value | 89.35 | 31.93 | 548.55 | 70.62 | 39.34 | 55.35 | ||
| Pr > F | <.0001 | <.0001 | <.0001 | <.0001 | <.0001 | <.0001 | ||
| Ridge regression coefficients | ||||||||
| k | year | Intercept | Y1 | Y2 | Y3 | Y4 | Y5 | Z |
| 0.6 | 2003 | -892.634 | 2.188 | 4.607 | 15.461 | 3.201 | 263.961 | -1 |
| 0.6 | 2004 | -1611.481 | 1.164 | 7.456 | 510.828 | 274.322 | 7.807 | -1 |
| 0.7 | 2005 | -423.256 | 0.651 | 8.670 | 31.712 | 33.030 | 2.848 | -1 |
| 0.6 | 2006 | -827.011 | 0.667 | 5.076 | 73.065 | 159.624 | 161.698 | -1 |
Means with the same letter are not significantly different at Alpha = 0.05.
As for the contributions of Y1 to Y5 to Z, viewing totally the result of each 4 year as a group, the strongest indirect effect toward Z is Y2 via Y1 (the coefficients are 0.2317, 0.4805, 0.2117 and 0.4015), then orderly come Y1 via Y2 (0.0604, 0.2260, 0.1681 and 0.2595) and Y3 via Y4 (0.1025, 0.2212, 0.0187 and 0.1202). Y5 via Y2 had lightly a negative indirect effect to Z (-0.0042, -0.0739, -0.0502 and -0.0289). Combining the direct effects (highlighted in bold) of Y2 to Z had negative effects in 3 years (2003, 2004 and 2006) and positive effect in 1 year (2005), obviously, Y2 had least contribution to Z.
Y3 had positive effects to Z in four years, whereas Y4 and Y5 had a negative effect in one year respectively. In addition, Y5 had more contribution to Z than Y4 by comparing the coefficients between them from Table 3.
So, The contributions of the five seed yield components to the seed yield are orderly Y1>Y3>Y5>Y4>Y2. The order is the same as total direct effects (2.9994, -0.2089, 0.8717, -0.0279 and 0.5881 listed in Table 3) with Y4 and Y2 having negative effects, but the total effects order is Y1>Y3>Y4>Y5>Y2 (3.9808, 0.2489, 1.3569, 0.6346 and 0.6266 listed in Table 3).
Duncan's Multiple Range Test for seed yield (Z) and its components (Y1 to Y5) Showed that Z was significantly highest in 2004 followed by 2003 which was significant higher than 2005 and 2006 (Table 4). Y1 was the highest in 2004 and produced the highest Z. Except in 2003, Y3 was not significantly (P<0.05) different in the rest three years.
The ridge regression and multiple-regression was applied for avoiding the highly inter-correlated and multi-collinearity between Y1 to Y5 and Z [35], [36], [37],[38],[39].
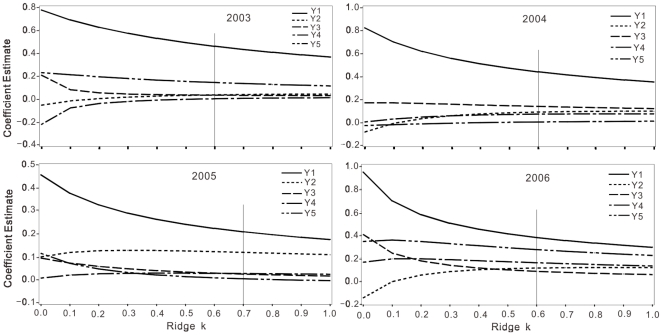
There are several procedures have been proposed for the selection of k in ridge regression analysis, although the optimal value of k cannot be determined with certainty [36], [37], [39], [40], and suggested that k should be determined from the ridge trace, with k selected such that a stable set of regression coefficients was obtained [38]. In this study, Figure 1 for year 2003, 2004, 2005 and 2006 respectively, showed the standard ridge traces, for various values of k, viewing the curves of Y1 to Y5 were asymptotically parallel to the horizontal axis when with the values of k estimated at the point 0.6, 0.6, 0.7 and 0.6 respectively, using the method of Horl and Kennard [35], [36], the ridge regression models were obtained at the selected values of the k for year 2003, 2004, 2005 and 2006, respectively. The resulting ridge regression coefficients are shown in Table 4. The ridge regression models were A, B, C and D, for year of 2003, 2004, 2005 and 2006, respectively:
Figure 1. Ridge traces of standard partial regression coefficients for increasing values of k for five yield components for year 2003, 2004, 2005 and 2006 respectively.
Y1 to Y5 are stand for fertile tillers m-2, spikelets per fertile tillers, florets per spikelet, seed numbers per spikelet and seed weight, respectively.
(Ridge k = 0.6; F = 33.11 Pr<0.0001)
(Ridge k = 0.6; F = 57.33 Pr<0.0001)
(Ridge k = 0.7; F = 2.68 Pr<0.0308)
(Ridge k = 0.6; F = 5.42 Pr<0.0114)
All of the ridge coefficients were positive whereas the values were various in the 4 years (Table 4). The highest ridge regression coefficients of Y1 and Y5, Y3 and Y4, and Y2 were in 2003, 2004, and in 2005 respectively (Table 4). Partly due to sample size, the ridge models in 2005 and 2006 was significant at Pr<0.05.
All of the Z and Y1 to Y5, 315 samples from the database of the 4 years totally, were taken the natural logarithm as S and C1 to C5, then S and C1 to C5 were taken in for ridge regression analyses, and got ridge regression model as:
| (1) |
(N = 315, F = 142.34, Pr<.0001)
Thus,
Above logarithmic model was transformed to exponential function as:
| (2) |
Formula (2) was used to estimate the seed yield of all the 315 samples and denoted as Zestimated. The actual seed yields were denoted as Zactual.
Then a general linear regression model was used to assess the Zactual as compared to the Zestimated. And analysis of variance for dependent variable Zactual and the parameter estimates of Zestimated was showed in Table 5 and 6. The linear line was presented in Figure 2 with the regression model as:
Table 5. Analysis of variance for dependent variable Zactual.
| Source | DF | Sum of squares | Mean square | F value | Pr > F |
| Model | 1 | 93271881 | 93271881 | 896.67 | <.0001 |
| Error | 313 | 32558436 | 104021 | ||
| Corrected total | 314 | 125830318 |
Table 6. Parameter estimates of Zestimated.
| Variable | DF | Parameter estimate | Standard error | t value | Pr > |t| |
| Intercept | 1 | 99.27080 | 37.71898 | 2.63 | 0.0089 |
| Zestimated | 1 | 0.95699 | 0.03196 | 29.94 | <.0001 |
Figure 2. Scatter plot to fit regression line of actual and estimated seed yield of the 4 years.
Zest were estimated by the model Z = e-0.26 Y 1 0.90 Y 2 0.14 Y 3 0.62 Y 4 0.17 Y 5 0.50.
| (3) |
(N = 315, F = 896.67, Pr<.0001)
So, via formula (3), the model was adjusted as:
| (4) |
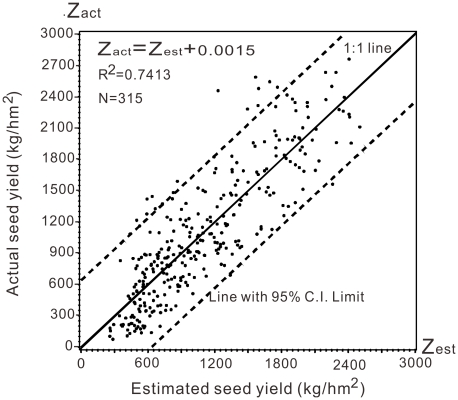
By variance test, the parameter estimates of intercept and Zestimated were 0.00153 and 0.99999 respectively (showed in Table 7). And the linear line, presented in Figure 3, was superposed on the 1:1 line.
Table 7. Parameter estimates of Zestimated after adjusted by the linear regression.
| Variable | DF | Parameter estimate | Standard error | t value | Pr > |t| |
| Intercept | 1 | 0.00153 | 40.65539 | 0.00 | 1.0000 |
| Zestimated | 1 | 0.99999 | 0.03339 | 29.94 | <.0001 |
Figure 3. Scatter plot to fit regression line of actual and estimated seed yield adjusted by Zact = 99.27+0.957·Z est of the 4 years.
It is superposed on the 1∶1 line.
Discussion
The results suggest that our first hypothesis that Y1 to Y5 and the Z are inter-correlated, and all the five key seed yield components are positively contributed to Z could not be validated. However, our second hypothesis that a steady algorithm model, which can estimate the seed yield via the components, was found.
Seed yield components and seed yield
Results show that total direct effects of Y1, Y3 and Y5 were positively contributed to Z but Y4 and Y2 were negatively; whereas the total effects (indirect + direct) of Y1∼Y5 to Z are positive. The negative effects of Y2 and Y4 were mainly canceled out by the effects of Y1 via Y2 (Y1→Y2) and Y3 via Y4 (Y3→Y4), respectively. There was no results available on negative effects of Y2 and Y4 in Russian wildrye. Firstly, Y2 is mostly genetic control [41], [42], there is not significantly different between 2003 and 2004 or between 2005 and 2006, and it decreases from 90.22 in 2003 to 81.14 in 2006 with increasing density because of aging (Table 4). Y4 has the same trend as Y2 with aging from 2.14 in 2003 to 1.75 in 2006. The large seed number (Y4) has a weak negative effect on seed yield maybe from the reason of limited soil nutrition with higher density [43]. Secondly, It maybe a true mathematical relationship resulting from a big sample size, e.g. both Y2 and Y4 are 4020 samples in 2004 in this research.
The seed yield component Y1 was the most important and effective component for seed yield, Z for significantly (P<0.0001 in 2003 and 2004; P<0.05 in 2005 and 2006) coefficients (0.7741, 0.8268, 0.4568 and 0.9417); this is in accordance with former experiments in Russian wildrye [44], [45], in fescues [46], [47], in zoysiagrass [48], in smooth brome [49], in perennial ryegrass [50] and in grasses [2], [51] and legumes [51], [52]. In addition, it was inferred that path-analysis could uncover the relationships between the components and the yield agreed with parallel results [53], [54], [55], [56]. As a seed yield component (Y1 to Y5) can affect other components positively or negatively, it is clear that measurement of simple linear relationships between two components with correlation analysis does not predict the success of selection. But, with standardized variables, path-analysis effectively determined the relative importance of direct and indirect effects on Z.
Steady algorithm model to estimate Z via Y1 to Y5
An exponential model was founded for estimating the Z via Y1 to Y5. Firstly, it deduced from the data of 315 samples in variously growing management in successive 4 years elaborate with more words. Secondly, it was of the same order of exponent values in the model as that of the contributions of the five components to Z; this mean that there was much correspondence between path-coefficients analysis and the ridge regressions. Thirdly, all of the four ridge regression models of the individual years were significant (2003 and 2004 at P<0.0001; 2005 and 2006 at P<0.05), and all with positive coefficients (Table 4). In addition, with multi-factor orthogonal experimental designs and big sample statistical analysis in field experiment, the significant (at P = 0.0001 and 0.01) coefficients of the correlation, path analyses and ridge regressions show that the models are reliable, and that ridge regression effectively overcome the problem of highly multi-correlated predictor variables (Y1 to Y5) [35], [36]. This research method may be one of the efficient and effective method in field crop experiment [39], [57], [58]. Unfortunately, the coefficients of the ridge regression models in individual years were various, ranged from 0.651 to 510.83 (Table 4), maybe mainly due to aging of the plant, designed field management and various climates.
Not all the five components and Z are inter-correlated
Though the experiment was set in various conditions with big sample size, the results of correlation analyses seems that theoretically accorded with biological theory in this experiment. Except Y1 with Y2 and Y1 with Z, the significant correlations were various. This was probably a consequence of the effects under climate of the individual year as the fields management are yearly repeats.
The relationships of Z and Ys are highly associated with the climate
Due to designed various field experimental management (experimental factor X1 to X10), there was a very wide range of seed yield and its yield components (Table S2), for example, in 2004 the maximum seed yield is 2763.89 kg/hm2, and the minimum 74.64 kg/hm2 (due to low/no irrigation, no fertilization and few plants) this plot have got a few irrigation, no any fertilizing and with the least fertilized tillers and plants, in terms of average, Psathyrostachys juncea Nevski. Z and its yield components (Y1, Y2, Y4 and Y5) are very different between the years of 2003∼2006 (Table S2); besides aging of the plant, this is the main effect of weather conditions of the 4 years (Figure S1). For example, that there were higher rainfall in June, which was the seed growing period, in 2003 and 2004 than in 2005 and 2006 partly result in higher seed yields as it in favor of pollination and grain filling. The most rainfall was in March 2005 which also had lower air temperature facilitated vegetative growing and decreased Y1 (Table 4) and consequently resulted in a lower Z. In comparison, the highest Z matched the higher temperature in March and April in 2004 than in other years. However, Y2 and Y3 were weakly decreased going with aging of the plant from 2003 to 2006; they might be controlled by its genotypes in some degree in this experimental site.
Conclusions
Via ridge regression analysis with big sample size in Psathyrostachys juncea Nevski, the model of seed yield with its five components was:
| (5) |
The total direct effects of the Y1, Y3 and Y5 to the seed yield were positive but Y4 and Y2 weakly negative; whereas the total effects (directs plus indirects) of the components were positively contributed to the seed yield by path analyses. Except Y3, Y1, Y2, Y4 and Y5 were significantly (P<0.001) correlated with the seed yield whereas Y2 were not significant correlated with Y3, Y4 and Y5 by Peason correlation analyses. Y1 was the major component presenting the most important and effective effect in the 5 components in the plant seed production. Therefore, selection for high seed yield through direct selection for large Y1, Y2 and Y3 would be effective for breeding programs in grasses.
The future study maybe consider the climate, e.g. rainfall and temperature in the seed growing stage, and different site locations for determining and testing the algorithm models of seed yield with the seed yield components in grasses.
Materials and Methods
Research Location and field conditions
Field experiments were conducted at the China Agricultural University Grassland Research Station located at the Hexi Corridor, in Jiuquan, Gansu province, northwestern China (latitude 39°37′N, longitude 98°30′E; elevation 1480 m) from 2003 to 2006. Soil at the site is Mot-Cal-Orthic Aridisols, classified as Xeric Haplocalcids (Soil Survey Staff, 1996). The 0.6 hm2 experimental site was tilled using a chisel plow in the fall and a disk-harrow in the spring for seedbed preparation. Russian wildrye (Psathyrostachys juncea Nevski) seeds (Cultivar: Bozoisky), were planted on 23 April 2002 at planting depth of 2.5 cm, a seeding rate of 5×106 seeds hm−2 and a row distances of 0.45 m. The former crop was alfalfa (Medicago sativa L.). Nitrogen (pure N) in rates of 104 kg hm−2 and phosphorus in rates of 63 kg hm−2 P2O5 was applied in bands 6 cm deep and 5 cm to the side of seed furrow. There was no seed yield in autumn 2002. This research trial was carried on in the next four years (2003 to 2006) with designed field managements (x1∼10), at yearly repeat (Table S1).
Experimental design
To simulate various growing conditions, the experiment used six groups (Group A to F) of multi-factor orthogonal field experimental designed plots [57], [59], [60], [61] (Table S1). Totally 143 experimental plots with different treatments combinations were arranged. Each one of individual plot areas 28 m2 (i.e. 4 m ×7 m), and with 1.5 m spacing between the adjacent plots. Weather for the experimental sites was provided by The Meteorological Working Station in Jiuquan, of Gansu province, P R China (Figure S1).
According to the orthogonal experimental designs, yearly repeated, under various field management, conditions from controlled growing environments, including regimes of fertilized (experimental factor: X1, X3, and X4), irrigation system (experimental factor: X2), planted density (experimental factor: X5), spray plant regulators (experimental factor: X6), irrigation time (experimental factor: X7), density manipulation (experimental factor: X8), time of cut post-harvest stubbles (experimental factor: X9), and burning post-harvest stubbles (experimental factor: X10), are listed in Table S1.
Data collection
Ten samples of 1 m length row were randomly selected for measuring the five seed yield components from anthesis to seed harvest during 2003 to 2006 respectively, for avoiding marginal utility, leave out 1 m from edge in the plots, which is means that samples were taken in the middle of the plot to avoid edge effect, the data of the seed yield components and seed yields of each one plot were collected by tactics as following: the samples of 1 m length row were randomly selected for measuring fertile tillers m-2 (Y1). Respectively, 30 to 36 fertile tillers and 27 to 54 spikelets were randomly selected for measuring the spikelets per fertile tillers (Y2), florets per spikelet (Y3) and seed numbers per spikelet (Y4). When the seed heads were ripen, four samples of 1 m length row were separately threshed by hand; yield of clean seed for each sample was weighted while the seed water content is at 7 to 10% for converting into seed yield (kg hm-2) (Z), and randomly taken 10 lots of 100-grains for determining seed weight (mg) (Y5) from the samples respectively. That total numbers of samples (n) of Y1 to Y5 and Z are 3150, 10080, 9135, 11970, 3150 and 1260 were determined respectively in the 4 years (Table 8). The sample size of been determined were listed in the individual years (Table 8), and then established experimental databases with Visio FoxPro (Version 6.0). Dates of flowering and seed harvesting in 2003 to 2006 (Table S3).
Table 8. The sample size of Y1∼Y5, z for each field experimental plot on Psathyrostachys juncea Nevski.
| year | Sample size of plots (N) (treatment) | Sample size of each field experimental plot | |||||
| Fertile tillers/m2Y1 (no.) | Spiklets/fertile tillersY2 (no.) | Florets/spikletY3 (no.) | Seed numbers/spikletY4 (no.) | Seed weightaY5 (mg) | Seed yieldZ (kg/hm2) | ||
| 2003 | 105 | 10 | 36 | 27 | 54 | 10 | 4 |
| Total sample size(n)b | 1050 | 3780 | 2835 | 5670 | 1050 | 420 | |
| 2004 | 134 | 10 | 30 | 30 | 30 | 10 | 4 |
| Total sample size(n) | 1340 | 4020 | 4020 | 4020 | 1340 | 536 | |
| 2005 | 60 | 10 | 30 | 30 | 30 | 10 | 4 |
| Total sample size(n) | 600 | 1800 | 1800 | 1800 | 600 | 240 | |
| 2006 | 16 | 10 | 30 | 30 | 30 | 10 | 4 |
| Total sample size(n) | 160 | 480 | 480 | 480 | 160 | 64 | |
| Total n of 4 years(n) | 3150 | 10080 | 9135 | 11970 | 3150 | 1260 | |
100-seed was taken as one sample, at a seed water content of 7∼10%, then 10 of the 100-seed sample in each plot were averaged to obtain one sample of seed weight (Y5) of the plot; the total sample size (n) of Y5 = 10×105 = 1050 in 2003.
Total sample size (n) = Sample size of plots (N) × Sample size of each plot (n), e.g., the number of spikelets fertile tiller-1 from 36 fertile tillers in each plot in 2003 was counted, then averaged as spikelets fertile tillers-1 (Y2) of the plot, so, the total sample size (n) of Y2 = 105×36 = 3780.
Statistics and Analytical Method
Analyses of variance and Pearson correlation analyses were performed using the SAS Version 8.2 program [62]. The general linear model (PROC GLM) was used to assess the ridge model. Then, a Qbasic program was written for the path coefficient analysis; furthermore, Duncan's multiple range test for Z and Y1 to Y5 were performed. Data were transformed when necessary using logarithmic and power transformations in order to avoid the effects of highly inter-correlated, leading to multi-collinearity among Y1 to Y5 with Z.
To establish a reliable model, combined data for all of the Z and Y1 to Y5 in Visio FoxPro, totaling 315 samples of Z (105+134+60+16 = 315) with their corresponding components (Y1 to Y5) over the four years studied, were taken as the natural logarithm because, mathematically, they did not influence the essential relations of the variables [37,39,63].
If S = In Z, Ci = In Yi, (i = 1 to 5), then S and C1 to C5 were used for the ridge regression analyses [39], ridge regression model is:
| (6) |
Where S is an n×1 vector of observations on a response variable, C is an n×p matrix of observations on p explanatory variables, ß is the p×1 vector of regression coefficients and u is an n×1 vector of residuals satisfying E (u ¯) = C ˙, E (uu′) = δ2 I. It is assumed that C and S have been scaled so that C′C and S′S are matrices of correlation coefficients [39]. Here n = 315, p = 5. Thus,
| (7) |
The above logarithmic model (7) was transformed to an exponential function as:
| (8) |
Where α, β are constants.
Formula (8) was used to estimate the Z of all 315 samples, and it was denoted as Zestimated; the actual seed yields were denoted as Zactual.
A general linear regression model was used to assess the Zactual, as compared to Zestimated, and an analysis of variance was used to assess the dependent variable Zactual and the parameter estimates of Zestimated.
The linear regression model is:
| (9) |
So, via formula (9), the model was adjusted to
| (10) |
The separate analyses for the four years provided useful information. Simple statistics (PROC MEAN) was made on the results and ridge plots were did.
Supporting Information
Monthly rainfall and mean temperature in Juquan, Guansu province, China in 2003, 2004, 2005 and 2006.
(TIF)
Field Experimental design and factors in (Psathyrostachys juncea Nevski).
(DOC)
Statistics of Y1∼Y5, Z (Psathyrostachys juncea Nevski) for year 2003 ∼ 2006.
(DOC)
Dates of flowering and seed harvesting in 2003, 2004, 2005 and 2006.
(DOC)
Acknowledgments
We are grateful to Dr. Luo Shuhang, Dr. Liu Fuyuan, Dr. Zhongyong, who are presidents of the Daye International Interest Co. Ltd., and my skilful technical assistants, Mr. Zhang Bing, Miss Yan Xuehua, Miss Han Juhoung, Mr. Zhang Xijun, Mr. Wang Shouguo and Mr. Zhang Guoqi, animal husbandry engineers, of Daye Institute of Forage & Grass Products in Jiuquan, Gansu Branch of Chengdu Daye International Interest Co. Ltd.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work was funded by the National Basic Research and Development Programme (grant number 973 project, 2007CB106805; http://www.973.gov.cn/), 948 Research Project (grant number 202099), Ministry of Agriculture of People's Republic of China. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Wang Y, Xu C-b. Advances in Studies on Psathyrostachys Nevski in China. Grassland of China. 2005;27:66–71. [Google Scholar]
- 2.Canode CL. London: P D Hebbletheaite ed; 1980. Grass-seed production in the intermountain pacific north-west, USA. Seed Production. pp. 189–202. [Google Scholar]
- 3.Wang ZY, Bell J, Lehmann D. Transgenic Russian wildrye (Psathyrostachys juncea) plants obtained by biolistic transformation of embryogenic suspension cells. Plant Cell Reports. 2004;22:903–909. doi: 10.1007/s00299-004-0772-4. doi: 10.1007/s00299-004-0772-4. [DOI] [PubMed] [Google Scholar]
- 4.Atul N, Hamel C, Forge T, Selles F, Jefferson PG, et al. Arbuscular mycorrhizal fungi and nematodes are involved in negative feedback on a dual culture of alfalfa and Russian wildrye. Applied Soil Ecology. 2008;40:30–36. doi: 10.1016/j.apsoil.2008.03.004. [Google Scholar]
- 5.Abreu ME, Munne-Bosch S. Salicylic acid deficiency in NahG transgenic lines and sid2 mutants increases seed yield in the annual plant Arabidopsis thaliana. Journal of Experimental Botany. 2009;60:1261–1271. doi: 10.1093/jxb/ern363. doi: 10.1093/jxb/ern363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tamura K, Kawakami A, Sanada Y, Tase K, Komatsu T, et al. Cloning and functional analysis of a fructosyltransferase cDNA for synthesis of highly polymerized levans in timothy (Phleum pratense L.). Journal of Experimental Botany. 2009;60:893–905. doi: 10.1093/jxb/ern337. doi: 10.1093/jxb/ern337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liu Y-c, Meng L, Mao P-c, Zhang G-f, Zhang D-g. Difference of Drought Resistance among 14 Psathyrostachys juncea Accessions at Seedling Stage. Chinese Journal of Grassland. 2009;31:64–69. [Google Scholar]
- 8.Definition CPCD, editor. United-States-Department-of-Agriculture. Psathyrostachys juncea(Fisch.) Nevski. Natural Resources Conservation Service---Conservation Plant Characeristics: United States Department of Agriculture. 2010.
- 9.Gu A, Holzworth L, Yun J. Establishment of Two Entries of Psathyrostachys juncea in the Arid and Semi-arid Areas in Inner Mongolia. Grassland of China. 1994;16:12–14. [Google Scholar]
- 10.Wang B. Biological and Economical Characteristic of Psathyrostachys Juncea Nevski. Grassland of China. 1990;12:17–20. [Google Scholar]
- 11.Berdahl JD, Ries RE. Development and vigor of diploid and tetraploid Russian wildrye seedlings. Journal of Range Management. 1997;50:80–84. [Google Scholar]
- 12.Asay KH. Breeding temperate rangeland grasses. Plant Breed Abstr. 1991;61:643–648. [Google Scholar]
- 13.Asay KH. Breeding potentials in perennial Triticeae grasses. Hereditas. 1992;116:167–173. [Google Scholar]
- 14.Asay KH. Wheatgrasses and wildryes: the perennial Triticeae; In: Barnes RF, Miller DA, Nelson CJ, editors. Ames: Iowa State University Press; 1995. pp. 373–394. [Google Scholar]
- 15.Jefferson PG, Muri R. Competition, light quality and seedling growth of Russian wildrye grass (Psathyrostachys juncea). Acta Agronomica Hungarica. 2007;55:49–60. doi: 10.1556/AAgr.55.2007.1.6. [Google Scholar]
- 16.Asay KH, Jensen KB. Cool-season forage grasses. In: Moser LE, Buxton DR, Casler MD, editors. Madison: American Society of Agronomy, Crop Science Society of America, Soil Science Society of America; 1996. pp. 725–748. [Google Scholar]
- 17.Dewey DR. New York: Plenim Press; 1984. The genomic system of classification as a guide to intergeric hybridization with the perennial Triticeae Gustafson JP, editor. pp. 209–279. [Google Scholar]
- 18.Liu Y, Meng L, Zhang G, Mao P, Zhang D. Genetic Diversity Analysis of 15 Psathyrostachys juncea Germplasm Resources by ISSR Molecular Marker. Acta Agriculturae Boreali-sinica. 2009;24:107–112. [Google Scholar]
- 19.Comeau A, Plourde A. Cell, tissue culture and intergeneric hybridization for barley yellow dwarf virus resistance in wheat. Can J Plant Pathol. 1987;9:188–192. [Google Scholar]
- 20.Ofori I. Correlation and path-coefficient analysis of components of seed yield in bambara groundnut (Vigna subterranea). Euphytica. 1996;91:103–107. [Google Scholar]
- 21.Firincioglu HK, Unal S, Erbektas E, Dogruyol L. Relationships between seed yield and yield components in common vetch (Vicia sativa ssp sativa) populations sown in spring and autumn in central Turkey. Field Crops Research. 2010;116:30–37. doi: 10.1016/j.fcr.2009.11.005. [Google Scholar]
- 22.Bidgoli AM, Akbari GA, Mirhadi MJ, Zand E, Soufizadeh S. Path analysis of the relationships between seed yield and some morphological and phenological traits in safflower (Carthamus tinctorius L.). Euphytica. 2006;148:261–268. [Google Scholar]
- 23.Das MK, Taliaferro CM. Genetic variability and interrelationships of seed yield and yield components in switchgrass. Euphytica. 2009;167:95–105. doi: 10.1007/s10681-008-9866-3. [Google Scholar]
- 24.El-Nakhlawy FS, Shaheen MA. Response of seed yield, yield components and oil content to the sesame cultivar and nitrogen fertilizer rate diversity. Electronic Journal of Environmental, Agricultural and Food Chemistry. 2009;8:287–293. [Google Scholar]
- 25.Rashidi M, Zand B, Abbassi S. Response of seed yield and seed yield components of alfalfa (Medicago sativa) to different seeding rates. American-Eurasian Journal of Agricultural and Environmental Science. 2009;5:786–790. [Google Scholar]
- 26.Milligan SB, Gravois KA, Bischoff KP, Martin FA. Crop effects on genetic relationships among sugarcane traits. Crop Science. 1990;30:927–931. [Google Scholar]
- 27.Dewey DR, Lu KH. A correlation and path coefficient analysis of components of crested wheat grass and seed production. Agronomy Journal. 1959;51:515–518. [Google Scholar]
- 28.Ram T. Character association and path coefficient analysis in rice hybrids and their parents. Journal Andaman Science Assoc. 1992;8:26–29. [Google Scholar]
- 29.Surek H, Korkut ZK, Bilgin O. Correlation and path analysis for yield and yield components in rice in a 8-parent half diallet set of crosses. Oryza. 1998;35:15–18. [Google Scholar]
- 30.Peiyan L. Inheritance of biological yield and harvest index and their relationship with grain yield in rice. Trop Agric Res Ser. 1988;21:230–233. [Google Scholar]
- 31.Amirthadevarathinam A. Genetic variability, correlation and path analysis of yield components in upland rice. Agricultural Journal. 1983;70:781–785. [Google Scholar]
- 32.Ibrahim SM, Ramalingan A, Subramanian M. Path analysis of rice grain yield nuder rainfed lowland condition. IRRN. 1990;15:11–15. [Google Scholar]
- 33.Sundarram T, Palanisarmy S. Path analysis in early rice. Madras Agricultural Journal. 1994;81:28–29. [Google Scholar]
- 34.Samonte SOPB, Wilson LT, McClung AM. Path analyses of yield and yield-related traits of fifteen diverse rice genotypes. Crop Science. 1998;38:1130–1135. [Google Scholar]
- 35.Hoerl AE, Kennard RW. Ridge regression: Applications to non-orthogonal problems. Technometrics. 1970;12:69–82. [Google Scholar]
- 36.Hoerl AE, Kennard RW. Ridge regression: biased estimation for non-orthogonal problem. Technometrics. 1970;12:55–67. [Google Scholar]
- 37.Marquardt DW, Snee RD. Ridge regression in practice. AmerStatist. 1975;29:3–14. [Google Scholar]
- 38.Newell GJ, Lee B. Ridge regression: an alternative to multiple linear regression for highly correlated data [in food technology]. Journal of Food Science (USA) 1981;46:968–969. [Google Scholar]
- 39.Chatterjee S, Price B. New York: John Wiley & Sons, Inc.; 1977. Regression analysis by example. [Google Scholar]
- 40.Lawless JF, Wang P. A simulation study of ridge and other regression estimators. Commun Stat Ser. 1976;A5:307–323. [Google Scholar]
- 41.Barrios C, Armando L, Berone G, Tomas A. Seed yield components and yield per plant in populations of Panicum coloratum L. var. makarikariensis Goossens; 2010 11-13 April 2010; Dallas, Texas.
- 42.Boelt B, Gislum R. 2010 11-13 April 2010; Dallas, Texas, USA; Seed yield components and their potential interaction in grasses- to what extend does seed weight influence yield? pp. 109–112. [Google Scholar]
- 43.Wang Q, Zhou H, Han J, Zhong Y, Liu F. Analysis on a model for water and fertilizer coupling effects on Psathyrostachys juncea seed yield. Acta Prataculturae Sinica. 2005;14:41–49. [Google Scholar]
- 44.Sun T. Beijing: China Agricultrural University; 2004. Effects of Fertilizer Application on Seed Yield Formation and Seed Physiological and Biochemical Characters during the Seed Development of Grasses.178 [Google Scholar]
- 45.Sun T, Han J, Zhao S, Yue W. Effects of fertilizer application on seed yield and yield components of Psathyrostachys juncea. Grassland of China. 2005;27:16–21. [Google Scholar]
- 46.Wang ZY, Ge YX. Agrobacterium-mediated high efficiency transformation of tall fescue (Festuca arundinacea). Journal of Plant Physiology. 2005;162:103–113. doi: 10.1016/j.jplph.2004.07.009. doi: 10.1016/j.jplph.2004.07.009. [DOI] [PubMed] [Google Scholar]
- 47.Meints PD, Chastain TG, Young WC, Banowetz GM, Garbacik CJ. Stubble management effects on three creeping red fescue cultivars grown for seed production. Agronomy Journal. 2001;93:1276–1281. [Google Scholar]
- 48.Ma C, Han J, Sun J, Zhang Q, Lu G. Effects of nitrogen fertilizer on seed yields and yield components of Zoysia japonica established by seeding and transplant. Agricultural Sciences in China. 2004;3:553–560. [Google Scholar]
- 49.Wang Q, Han J, Zhou H, Yong Zhong, Liu F. Correlation and Path Coefficient Analysis between Seed Yield Components and Seed Yield on Bromus inermis L. J Plant Genet Resour. 2004;5:324–327. [Google Scholar]
- 50.Deleuran LC, Boelt B. Establishment techniques in under-sown perennial ryegrass for seed production. Acta Agricultura Scandinavica Section B, Plant Soil Science. 2009;59:57–62. doi: 10.1080/09064710701855221. [Google Scholar]
- 51.Hampton JG, Fairey DT. Forage seed production, Volume 1: Temperate species; 1998. Components of seed yield in grasses and legumes. pp. 45–69. [Google Scholar]
- 52.Hampton JG, Fairey DT. Fairey DT, Hampton JG, editors. Components of seed yield in grasses and legumes. Forage Seed Production: CAB International. 1997.
- 53.Sodavadiya PR, Pithia MS, Savaliya JJ, Pansuriya AG, Korat VP. Studies on characters association and path analysis for seed yield and its components in pigeonpea (Cajanus cajan (L.) Millsp). Legume Research. 2009;32:203–205. [Google Scholar]
- 54.Ozturk O, Ada R. Correlation and Path Coefficient Analysis of Yield and Quality Components of Some Sunflower (Helianthus annuus L.) Cultivars. Asian Journal of Chemistry. 2009;21:1400–1412. [Google Scholar]
- 55.Lopes RR, Franke LB. Path analysis in white clover seed yield components. Revista Brasileira De Zootecnia-Brazilian Journal of Animal Science. 2009;38:1865–1869. [Google Scholar]
- 56.Golparvar AR, Ghasemi-Pirbalouti A. Correlation and path analysis of seed and oil yield in spring safflower cultivars. Research on Crops. 2009;10:147–151. [Google Scholar]
- 57.Schwabe R. New York: Springer; 1996. Optimum designs for multi-factor models. [Google Scholar]
- 58.Wang Q, Li Q, Cui J, Wang Y, Bai R, et al. Path analysis of seed yield and main agronomic traits in Caragana korshinskii K. Grassland of China. 2001;23:35–37. [Google Scholar]
- 59.Hedayat AS, Sloane NJA, Stufken J. Orthogonal Arrays: Theory and Applications. New York: Published by Springer-Verlag. 1999;363 [Google Scholar]
- 60.Wang XR. Beijing: Agricultural Press of China; 1996. Modern Fertilizer Experimental Deign. [Google Scholar]
- 61.Yandell BS. London: Chapman & Hall; 1997. Practical data analysis for designed experiments. [Google Scholar]
- 62.SAS-Institute-Inc. North Carolina: SAS Institute Inc; 1988. SAS/STAT User's Guide. [Google Scholar]
- 63.Gao S, Li Y, Jin H. Application of ridge regression models in economic increasing factors analysis. Statistics and Decision-making. 2005;5:142–144. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Monthly rainfall and mean temperature in Juquan, Guansu province, China in 2003, 2004, 2005 and 2006.
(TIF)
Field Experimental design and factors in (Psathyrostachys juncea Nevski).
(DOC)
Statistics of Y1∼Y5, Z (Psathyrostachys juncea Nevski) for year 2003 ∼ 2006.
(DOC)
Dates of flowering and seed harvesting in 2003, 2004, 2005 and 2006.
(DOC)