Abstract
Previous studies have shown that effective quantification of the cyclic variation of myocardial ultrasonic backscatter over the heart cycle might provide a non-invasive technique for identifying the early onset of cardiac abnormalities. These studies have demonstrated the potential for measurements of the magnitude and time delay of cyclic variation for identifying early onset of disease. The goal of this study was to extend this approach by extracting additional parameters characterizing the cyclic variation in an effort to better assess subtle changes in myocardial properties in asymptomatic subjects with type 2 diabetes. Echocardiographic images were obtained on a total of 43 age-matched normal control subjects and 100 type 2 diabetics. Cyclic variation data were generated by measuring the average level of ultrasonic backscatter over the heart cycle within a region of interest placed in the posterior wall of the left ventricle. Cyclic variation waveforms were modeled as piecewise linear functions, and quantified using a novel Bayesian parameter estimation method. Magnitude, rise time and slew rate parameters were extracted from models of the data. The ability of each of these parameters to distinguish between normal and type 2 diabetic subjects, and between subjects grouped by glycated hemoglobin (HbA1c) was compared. Results suggest a significant improvement in using measurements of the rise time and slew rate parameters of cyclic variation to differentiate (p < 0.001) the hearts of patients segregated based on widely employed indices of diabetic control compared to differentiation based on the magnitude of cyclic variation.
Keywords: diabetes mellitus, cardiomyopathy, ultrasonics, echocardiography, tissue characterization, Bayesian probability theory
Introduction
Type 2 diabetes mellitus is a known risk factor for coronary artery disease and subsequent heart failure. In addition, an increasing body of evidence indicates that diabetes can lead to heart disease independent of atherosclerosis, a condition known as “diabetic cardiomyopathy” (Fang et al., 2004; Hamby et al., 1974; Kannel et al., 1974; Witteles and Fowler, 2008; Rijzewijk et al., 2008). The mechanisms underlying the development of diabetic cardiomyopathy are not fully understood, but several studies suggest that lipid metabolic abnormalities may play a role in lipid accumulation in non-adipose tissue, including myocardium, and that the accumulation of lipids in myocardium contributes to cell dysfunction, cell death, and subsequently cardiomyopathy (Kusminski et al., 2009; Augustus et al., 2003; Carley and Severson, 2005; Peterson et al., 2004; Stremmel, 1988; Borradaile and Schaffer, 2005; Chiu et al., 2001; Finck et al., 2003; Nielsen et al., 2002; Rijzewijk et al., 2008; Zhou et al., 2000).
Ultrasonic backscatter from myocardium has long been known to vary systematically over the cardiac cycle (Madaras et al., 1983; Mottley et al., 1984; Barzilai et al., 1984; Wickline et al., 1985; Mobley et al., 1995; Naito et al., 1996; Bello et al., 1998; Hu et al., 2003; Holland et al., 2004, 2007, 2009; Gibson et al., 2009). Quantification of this cyclic variation of myocardial backscatter has provided a tool for non-invasive ultrasonic tissue characterization in a range of pathologies, including diabetes (Gibson et al., 2009; Holland et al., 2007; Wagner et al., 1995; Bello et al., 1995; Pérez et al., 1992). Traditionally, cyclic variation has been quantified by using the magnitude and time delay (phase) of the systematic variation of backscatter over the heart cycle. Both of these parameters have been shown to be useful for characterizing myocardial function (Holland et al., 2007; Gibson et al., 2009; Wagner et al., 1995; Bello et al., 1995; Hu et al., 2003; Finch-Johnston et al., 2000). However, other features of the cyclic variation waveform may be more sensitive to the early onset of diabetic cardiomyopathy. Because diabetic cardiomyopathies may first manifest themselves in the form of diastolic dysfunction, methods for characterizing cyclic variation that measure diastolic function could be useful for distinguishing between healthy hearts and those at higher risk for disease (Poirier et al., 2001; Schannwell et al., 2002). The current study introduces a novel method for modeling the cyclic variation of myocardial backscatter as a pulse waveform in order to extract parameters with the potential for identifying diastolic dysfunction. This model is then applied to a population of subjects that includes normal controls and asymptomatic type 2 diabetes patients to determine the ability of the model to discriminate between patient groups. Improved non-invasive methods for assessing the potential development of cardiomyopathies associated with type 2 diabetes could permit earlier and more effective intervention.
Methods
Normal control subjects (with a fasting glucose < 100 mg/dL) and subjects with a history of type 2 diabetes mellitus between the ages of 30 and 55 years were recruited for the study over a three-year span. All subjects underwent a screening medical history and physical exam and phlebotomy for routine laboratory blood tests. Participants were excluded from the study if they exhibited greater than Stage 1 hypertension as defined by the seventh report of the Joint National Committee (The Joint National Committee on the Prevention, Detection, Evaluation, and Treatment of High Blood Pressure, 2003); other systemic diseases (e.g. lupus); valvular disease; greater than trace or mild valvular regurgitation; an ejection fraction < 55%; ischemic heart disease as assessed by a screening stress echocardiography exam; or symptoms of heart failure. Study participants were also excluded if they were current smokers, postmenopausal, pregnant, or lactating. A total of 143 subjects was retained in the study, which included 43 normal controls and 100 type 2 diabetics. The average age of the subjects was 43 ± 7 years, and included 57 males and 86 females. Signed informed consent for participation was obtained from each of the subjects under a human studies protocol approved by the Washington University Human Research Protection Office (HRPO).
Laboratory tests
Subjects underwent fasting glucose, glycated hemoglobin, and lipid and protein level tests after an overnight fast. A standard echocardiographic exam was performed to assess cardiac function in addition to the echocar-diographic images acquired for ultrasonic tissue characterization.
Data acquisition
A General Electric Vivid 7 clinical imaging system (General Electric Medical Systems, Waukesha, WI, USA) was used to collect echocardiographic cineloops over approximately five heart cycles for each subject. The data were acquired from the parasternal long-axis view in harmonic imaging mode; the transmit frequency was 1.7 MHz, and the receive frequency was 3.4 MHz. The imaging system was configured such that there was a linear relationship between the displayed image grayscale value and changes in the level of ultrasonic backscatter expressed in decibels (dB). To verify this relationship, a series of measurements were performed on a tissue-mimicking phantom in which the imaging system gain was varied systematically in known dB steps. The average grayscale level was determined from within a region of interest placed on each phantom image at each gain setting to establish a conversion factor from image grayscale level to dB and to determine where the relationship was linear. The images were analyzed using NIH ImageJ software (National Institutes of Health, Bethesda, MD, USA).
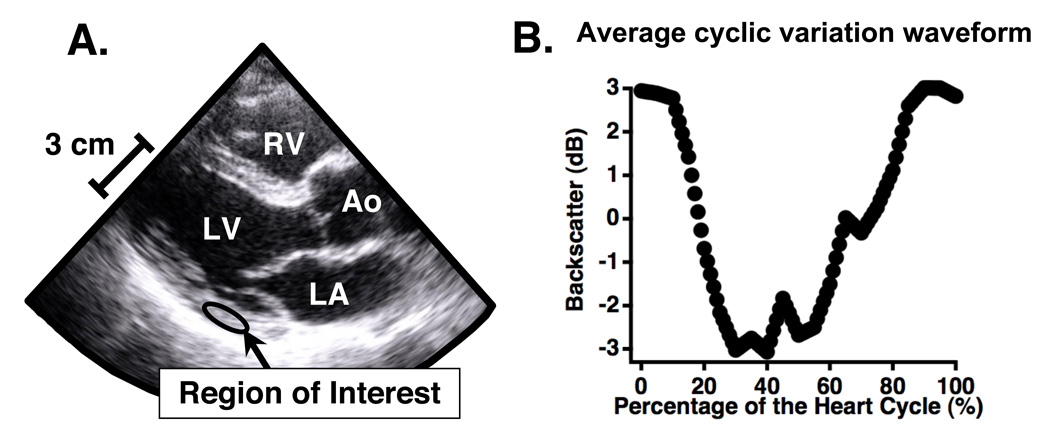
Subject images were acquired with the system gain set at a level that optimized the use of the available dynamic range of the imaging system configuration. Only data from consecutive heart cycles exhibiting normal sinus rhythm were analyzed. If a subject had an irregular heart rhythm while data were being acquired, a new set of data were collected. The acquired data were analyzed offline by using NIH ImageJ to draw a region of interest within the left ventricular free wall and manually tracking it over the several heart cycles in the cineloops. The average grayscale levels within the region of interest for each image frame was recorded and converted to decibels to obtain a measurement of backscattered signal level. The backscattered signal level in dB was plotted against time to obtain the systematic variation of ultrasonic backscatter from myocardium. This data was then averaged over the separate heart cycles and redimensioned so that it could be plotted as a percentage of the heart cycle, independent of heart rate. Only data from consecutive heart cycles exhibiting normal sinus rhythm were analyzed. If a subject exhibited an irregular heart rhythm while data were being acquired, a new set of data were collected. This processing results in average cyclic variation waveforms in which end-diastole is defined as the start (0%) and end (100%) of the heart cycle. A schematic of a region of interest within the posterior wall and the resulting average cyclic variation waveform is depicted in Fig. 1. More details of cyclic variation data acquisition and analysis are outlined by Gibson et al. (2009).
Figure 1.
Regions of interest were placed within the posterior left ventricular wall on each image frame (shown in Panel A) and tracked throughout the heart cycle. The average level of backscatter was determined for each frame and averaged across five heart cycles to obtain an average cyclic variation waveform, such as the one depicted in Panel B.
Model of cyclic variation data
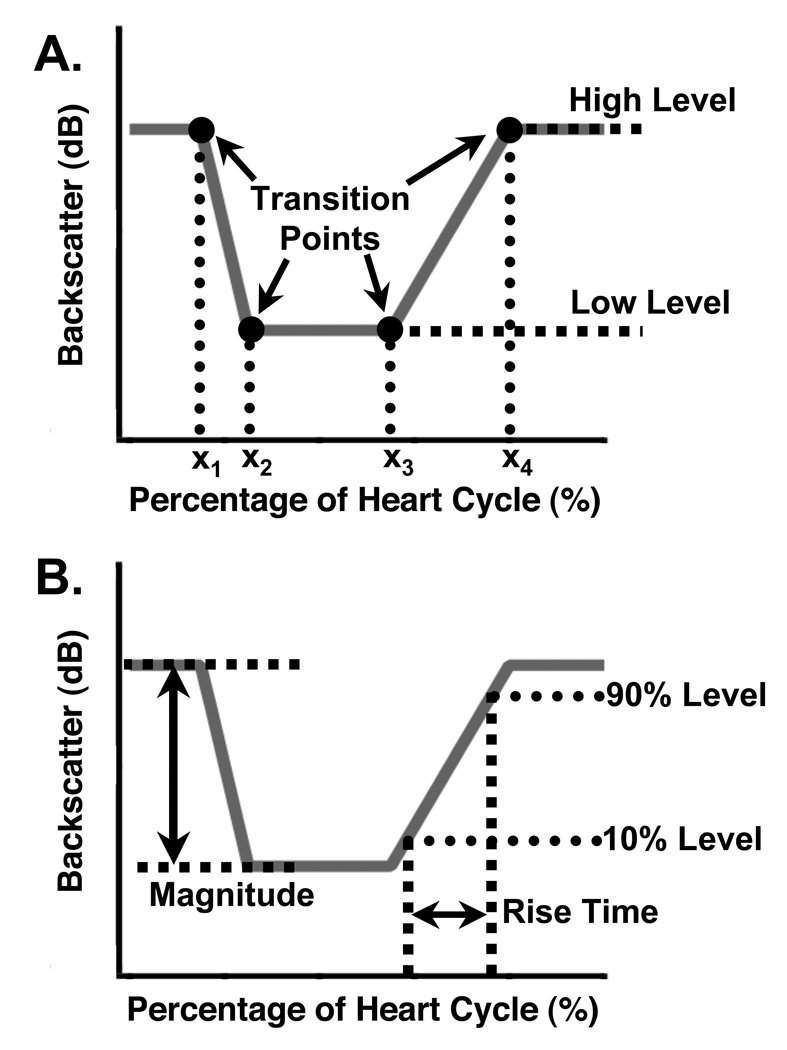
A piecewise linear model of cyclic variation was defined using six parameters to characterize a given cyclic variation waveform. Two parameters define the high and low levels for the waveform, and four parameters determine the placement (in time or percentage of the heart cycle) of the transition points between the line segments that comprise the model. The line segments are connected to form a continuous model waveform in the manner depicted in Panel A of Fig. 2. Mathematically, the model can be expressed as
| (1) |
where M(x) is the amplitude of the model waveform at a percentage of the heart cycle x, H is the high amplitude level for the waveform, L is the low amplitude level for the waveform, and the xi are the transition point parameters. The slopes of the line segments representing the transitions between the high and low levels, ma and mb, are given by
| (2a) |
| (2b) |
and the intercepts, ba and bb, are given by
| (3a) |
| (3b) |
Figure 2.
Panel A (top): Schematic of a model cyclic variation waveform and the parameters used to characterize it. The high and low amplitude levels determine the magnitude, and the four transition time parameters (x1, x2, x3, x4) mark the locations where the line segments join. Given a set of values for these six parameters, the model waveform (shown in gray) can be constructed. Panel B (bottom): Illustration of the pulse parameters derived from a model cyclic variation waveform. The magnitude is the difference between the high and low levels, and the rise time is the time taken to go from 10% of the magnitude to 90% of the magnitude on the rising edge. The slew rate is the difference between the 90% level and the 10% level, divided by the rise time.
This model can be used to characterize a generic positive-going or negative-going pulse with a variety of qualitatively different shapes, making it suitable for use on cyclic variation waveforms. Once a model for a specific waveform has been constructed, additional derived quantities can be extracted, such as the magnitude, rise time, fall time, slew rate, duration, and more.
Parameter estimation
Bayesian probability theory was used to estimate the six parameters {H, L, x1, x2, x3, x4} in the model of cyclic variation for each subject. In Bayesian probability theory, all of the information about a given parameter is represented by a probability density function. As an example, the probability for the parameter L is expressed as P(L|DI), where this notation is understood to denote the probability for L given the data D and available background information I. The posterior probability density functions for individual parameters can be computed from the joint posterior probability for all model parameters by marginalization, a process in which the joint posterior probability is integrated over all parameters except the one of interest. For instance, if all parameters are represented by Θ = {H, L, x1, x2, x3, x4}, then the marginal posterior probability for L is calculated by
| (4) |
where P(Θ|DI) is the joint posterior probability for all model parameters. Marginal posterior probabilities for the other parameters can be computed by using the same procedure, but integrating over the appropriate (different) sets of parameters. Thus, for the six-parameter model described in Eq. (1), a total of six integrals similar to Eq. (4) must be computed.
The joint posterior probability is obtained using Bayes’ theorem,
| (5) |
where P(Θ|I) is the prior probability for the parameters given only the background information I (i.e. before any data is analyzed), P(D|ΘI) is the likelihood, or direct probability for the data given the parameters and prior information, and P(D|I) is the evidence.
The calculation is performed under the assumption that the model parameters are logically independent; that is, each prior probability depends only on the parameter in question and not on any others. Note that the assumption of logical independence affects prior probability assignment, and does not preclude the final parameter estimates from being physically or physiologically dependent. For example, prior knowledge of L has no bearing on the prior knowledge of H, x1, or any other parameter. Under this assumption, the prior probability for the parameters can be factored using the product rule of probability theory, yielding
| (6) |
The terms on the right-hand side of Eq. (6) are prior probabilities for the individual parameters. These prior probabilities are assigned as bounded Gaussian functions defined by a low, high, mean, and standard deviation for each parameter. The prior information about the parameters is assumed to be vague, and hence the purpose of the prior probabilities is to provide order-of-magnitude estimates for the parameter values. The exact functional form of these prior probabilities has little effect on the final parameter estimates. Summaries of the Gaussian prior probability density functions are given in Table 1.
Table 1.
Summary of prior probability density functions used for each parameter in the Bayesian calculations. The means and standard deviations define Gaussian probability densities bounded by the low and the high values.
| Parameter |
||||||
|---|---|---|---|---|---|---|
| H | L | x1 | x2 | x3 | x4 | |
| (dB) | (dB) | (Percentage of Heart Cycle) | ||||
| Low | −10 | −10 | 0 | 0 | 0 | 0 |
| Mean | 0 | 0 | 50 | 50 | 50 | 50 |
| High | 10 | 10 | 100 | 100 | 100 | 100 |
| Standard Deviation | 10 | 10 | 50 | 50 | 50 | 50 |
The likelihood, P(D|ΘI), was assigned using a Gaussian prior probability to represent what was known about the noise. The standard deviation of this Gaussian was removed via marginalization using a Jeffreys prior (Jeffreys, 1961).
Evaluation of complicated multi-dimensional integrals such as those in Eq. (4) is difficult or impossible to achieve analytically. As such, the integrals were approximated using a Markov chain Monte Carlo simulation. The nested sampling algorithm was used to carry out the Markov chain Monte Carlo calculations and to draw samples from the joint posterior probability (Skilling, 2006). The nested sampling calculations used 25 live points and 1000 iterations, which provided a satisfactory sampling of the joint posterior probability. A detailed description of the nested sampling approach is given by Sivia (Sivia and Skilling, 2006) and Skilling (Skilling, 2006), and further details on Bayesian probability theory are given by Sivia and Skilling (Sivia and Skilling, 2006), Jaynes (Jaynes and Bretthorst, 2003), and Bretthorst (Bretthorst et al., 2005).
Data analysis
At the completion of the Markov chain Monte Carlo simulation for a given set of input data, the Monte Carlo samples of the joint posterior probability were used to extract means and standard deviations for each parameter. A model waveform for the input data was constructed using the most probable values for each parameter. Because the model waveform for each data set can be described as a negative-going pulse, additional parameters characteristic of pulsed waveforms can be derived. The parameters extracted from the model waveforms used in this study are illustrated in Panel B of Fig. 2. Each model waveform was analyzed to obtain magnitudes, rise times, and slew rates for each patient. The magnitude is defined as the difference between the high and low levels of the model waveform. The rise time is the time interval between the amplitudes representing 10% and 90% of the magnitude on the rising edge of the pulse. The slew rate is defined as the difference between 90% and 10% magnitude, divided by the rise time. The rising edge of the model waveform was chosen for this analysis because it corresponds to the timing of early diastolic relaxation, and therefore could serve as an indicator of diastolic dysfunction.
The subjects were separated into diabetic (n = 100) and normal control (n = 43) groups, and the magnitudes, rise times, and slew rates for each group were compared. Statistical significance was determined by a two-tailed, unpaired Student’s t-test. In addition, to examine further the impact glycemic control may have on the observed cyclic variation of backscatter, the subjects were divided into quartiles by glycated hemoglobin (HbA1c). Thus, although all subjects enrolled in this study had normal systolic function at rest and no evidence of significant obstructive coronary disease during stress echocardio-graphy, the highest quartile of HbA1c (n = 35) can in principle be considered to be “more at risk for cardiovascular complications” and the lowest quartile (n = 35) can be considered to be “less at risk” for the purposes of this study. Cyclic variation parameters for the highest and lowest quartiles were also compared using a two-tailed, unpaired Student’s t-test. A summary of the subject group characteristics is given in Tables 2 and 3, in which means and standard deviations for age, body mass index, and HbA1c are listed for each subject group.
Table 2.
Study group characteristics for the control and diabetic populations.
| Controls | Diabetics | ||
|---|---|---|---|
| Gender | M = 15 | M = 45 | |
| F = 28 | F = 55 | ||
| Age (y) | 41 ± 6 | 44 ± 7 | |
| p = n.s. | |||
| Body Mass Index (kg/m3) | 28 ± 6 | 34 ± 7 | |
| p < 0.001 | |||
| HbA1c (%) | 5.6 ± 0.4 | 7.6 ± 1.6 | |
| p < 0.001 |
Values are expressed as means ± standard deviations. n.s. = not significant.
Table 3.
Study group characteristics for the glycated hemoglobin (HbA1c) highest and lowest quartiles.
| Lowest Quartile | Highest Quartile | ||
|---|---|---|---|
| Gender | M = 13 | M = 16 | |
| F = 22 | F = 19 | ||
| Age (y) | 40 ± 6 | 42 ± 7 | |
| p = n.s. | |||
| Body Mass Index (kg/m3) | 27 ± 6 | 36 ± 6 | |
| p < 0.001 | |||
| HbA1c (%) | 5.4 ± 0.2 | 9.5 ± 1.2 | |
| p < 0.001 |
Values are expressed as means ± standard deviations. n.s. = not significant.
Results
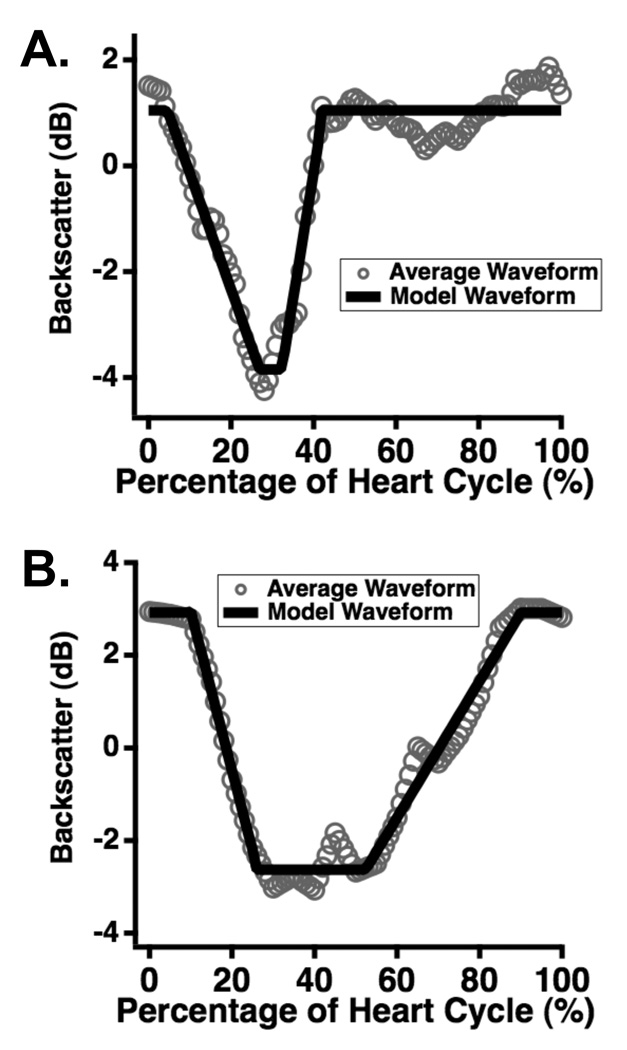
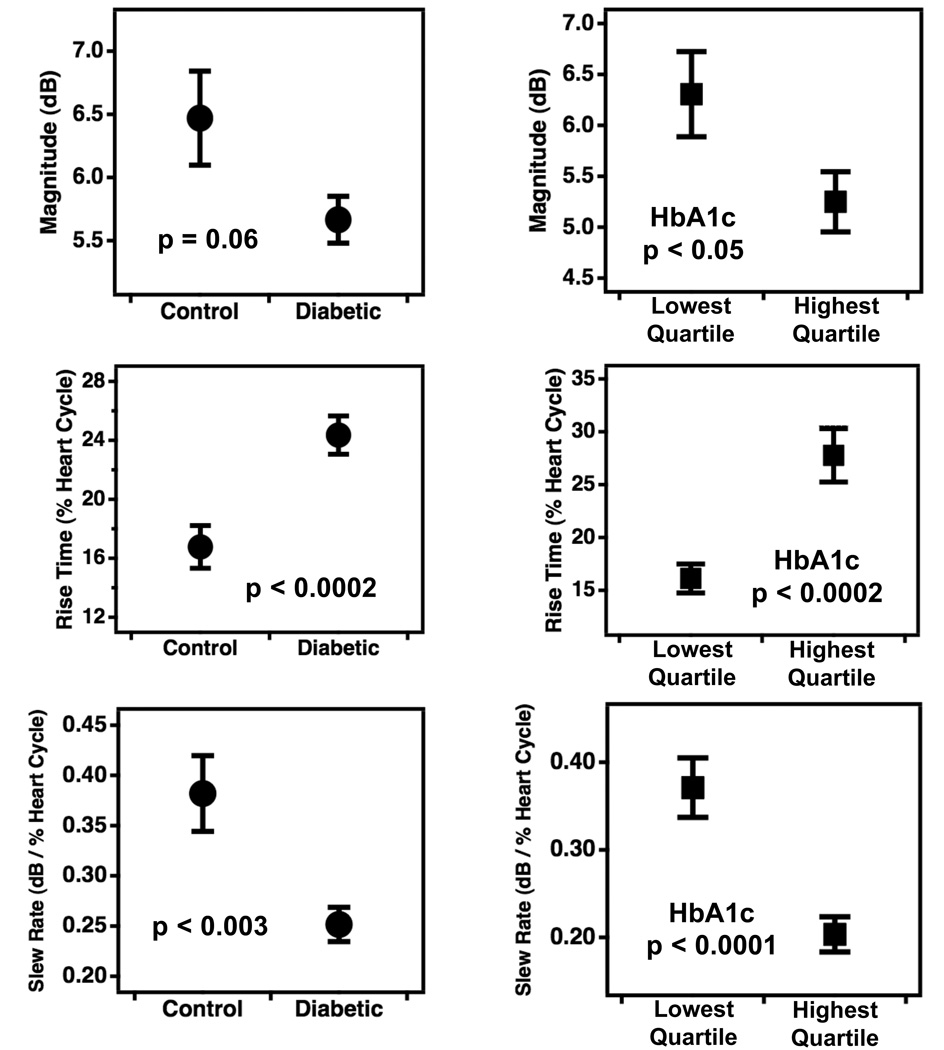
Representative data, along with corresponding model waveforms, are shown in Panels A and B of Fig. 3. The versatility of the piecewise linear model allows accurate representation of narrow cyclic variation waveforms that rise quickly back to baseline (Fig. 3, Panel A) as well as wider waveforms that take longer to return to baseline (Fig. 3, Panel B). Means and standard errors for the magnitude, rise time, and slew rate parameters for the different subject groups are shown in Fig. 4, with comparisons between the diabetic and control groups shown in the left-hand panels and those between the highest and lowest quartiles of HbA1c displayed in the right panels. As a group, the normal control subjects had shorter rise times and higher slew rates than their diabetic counterparts, indicating that on average, the cyclic variation of backscatter in the low-risk subject population returned to baseline more rapidly during diastole than in the high-risk population. Similar characteristics are evident between the highest and lowest HbA1c quartile groups. The rise time and slew rate parameters showed highly significant differences between the control and diabetic populations as well as the high and low HbA1c quartiles (p ranged between 0.003 and less than 0.0001). The differences in the magnitude of cyclic variation between the respective groups was either not significant (p = 0.06) or weakly significant (p < 0.05). A comparison of the error bars in the top panels of Fig. 4 indicates that the variance of the magnitude parameter is higher for the control subjects than for the diabetic subjects. This somewhat counter-intuitive observation likely arises because the control population exhibits a wide range of relatively low to relatively high magnitude values, whereas the diabetic subjects tend to have magnitudes clustered around lower values.
Figure 3.
Representative results for models of acquired cyclic variation data. The data, consisting of backscatter averaged over five heart cycles, are shown in gray circles; the models are shown in solid black lines. The flexible nature of the model allows good representation of both narrow (Panel A) and wide (Panel B) waveform data.
Figure 4.
Differences in the magnitude, rise time, and slew rate of the cyclic variation of backscatter from myocardium among the two subject groupings. Differences between normal control and type 2 diabetic subjects are shown in the left panels, and those between the highest and lowest quartiles of subjects grouped by glycated hemoglobin (HgA1c) are shown in the right panels. Data are presented as means ± standard errors. Corresponding p-values determined by two-tailed t-tests are included in each panel.
Discussion
Constructing models of cyclic variation data might provide further non-invasive tools for quantification of cardiac function that extend beyond the information obtained using conventional analysis of cyclic variation. Specifically, the shape of the waveform itself may provide indications of dysfunction that are independent or only weakly dependent on the traditionally reported magnitude of cyclic variation. The piecewise linear model examined in this study permits a relatively simple means of modeling such data, and the pulse parameters derived from it (rise time and slew rate) allow basic quantification of waveform characteristics that could have relevance to diastolic function. Although all subjects in the study exhibited clinically normal cardiac function, measurements of these novel cyclic variation parameters demonstrated highly significant differences between normal controls and individuals with type 2 diabetes, as well as between individuals with high and low HbA1c. Results for the magnitude parameter are consistent with previous studies involving type 1 and type 2 diabetics (Wagner et al., 1995; Gibson et al., 2009) in that higher magnitudes were observed in healthy individuals than in diabetics. However, the differences in rise time and slew rate between these two populations are stronger than the differences in the magnitude. Subjects without diabetes and subjects with low HbA1c tended to have lower rise times and higher slew rates than their counterparts. It is interesting to note that the results of this study appear consistent with recent reports of subclinical altered diastolic function in patients with altered metabolism.(Gong et al., 2009; Ng et al., 2009) Among other measures, these studies demonstrated a decreased early diastolic myocardial strain rate in subjects with metabolic syndrome (Gong et al., 2009) and uncomplicated type 2 diabetes mellitus (Ng et al., 2009) when compared with the values obtained from their respective control subjects. Hence, measurements of the rise time and slew rate of myocardial backscatter may indeed have a close correspondence with diastolic performance that appears consistent with the expectation that individuals subject to early onset of diabetic cardiomyopathy will first present with diastolic dysfunction.
The present study is limited by the absence of concrete evidence of cardiac metabolic or structural abnormalities. Indeed, it is impossible under the current study conditions to determine which, if any, subjects will develop a diabetic cardiomyopathy. A careful longitudinal study over many years could perhaps determine definitively whether differences in the parameters examined here are truly indicative of a high risk for cardiac dysfunction, but such an investigation is beyond the scope of the current study.
Additionally, the results presented are based on grouped data. The outcomes suggest that the parameters investigated may elicit differences in the means of the high-risk and low-risk study populations, which may in turn indicate promise for the role of rise time and slew rate in future analyses of the cyclic variation of backscatter from myocardium. However, caution should be exercised in extrapolating these methodological findings to individual clinical cases.
Finally, this study investigated cyclic variation in a localized portion of the posterior wall of the left ventricle. A more complete understanding of the relationship between cyclic variation and cardiac dysfunction could be complied by applying the current methods to measurements of cyclic variation in other portions of the myocardium. Nevertheless, cardiac dysfunction is expected to be present on a global cardiac scale, and the posterior wall is a convenient measurement area for demonstrating the viability of the new methodology described here.
In summary, analyses of model-derived parameters for cyclic variation data, especially rise time and slew rate, suggest that using a model-based approach could lead to enhancement or improvement in patient classification. Using these parameters in tandem with magnitude or time delay analyses could eventually lead to effective non-invasive monitoring of patients at higher risk for type 2 diabetic cardiomyopathy.
Acknowledgments
Funding Sources
This research was supported in part by NIH R01 HL40302, NIH R01 AR57433, National Science Foundation 57238 (FDA Scholar in Residence), NIH P20 RR020643, Burroughs Wellcome Fund (1005935), and a grant from the Barnes Jewish Hospital Foundation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Disclosures
The authors have no conflicts of interest to disclose.
References
- Augustus AS, Kako Y, Yagyu H, Goldberg IJ. Routes of FA delivery to cardiac muscle: modulation of lipoprotein lipolysis alters uptake of TG-derived FA. Am J Physiol Endocrinol Metab. 2003;284(2):E331–E339. doi: 10.1152/ajpendo.00298.2002. [DOI] [PubMed] [Google Scholar]
- Barzilai B, Madaras EI, Sobel BE, Miller JG, Pérez JE. Effects of myocardial contraction on ultrasonic backscatter before and after ischemia. Am J Physiol. 1984;247(3 Pt 2):H478–H483. doi: 10.1152/ajpheart.1984.247.3.H478. [DOI] [PubMed] [Google Scholar]
- Bello VD, Giampietro O, Matteucci E, Giorgi D, Bertini A, Piazza F, Talini E, Paterni M, Giusti C. Ultrasonic tissue characterization analysis in type 1 diabetes: a very early index of diabetic cardiomyopathy? G Ital Cardiol. 1998;28(10):1128–1137. [PubMed] [Google Scholar]
- Bello VD, Talarico L, Picano E, Muro CD, Landini L, Paterni M, Matteucci E, Giusti C, Giampietro O. Increased echodensity of myocardial wall in the diabetic heart: an ultrasound tissue characterization study. J Am Coll Cardiol. 1995;25(6):1408–1415. doi: 10.1016/0735-1097(95)00026-Z. [DOI] [PubMed] [Google Scholar]
- Borradaile NM, Schaffer JE. Lipotoxicity in the heart. Curr Hypertens Rep. 2005;7(6):412–417. doi: 10.1007/s11906-005-0035-y. [DOI] [PubMed] [Google Scholar]
- Bretthorst GL, Hutton WC, Garbow JR, Ackerman JJ. Exponential parameter estimation (in NMR) using Bayesian probability theory. Concepts Magn Reson. 2005;27A(2):55–63. [Google Scholar]
- Carley AN, Severson DL. Fatty acid metabolism is enhanced in type 2 diabetic hearts. Biochim Biophys Acta. 2005;1734(2):112–126. doi: 10.1016/j.bbalip.2005.03.005. [DOI] [PubMed] [Google Scholar]
- Chiu HC, Kovacs A, Ford DA, Hsu FF, Garcia R, Herrero P, Saffitz JE, Schaffer JE. A novel mouse model of lipotoxic cardiomyopathy. J Clin Invest. 2001;107(7):813–822. doi: 10.1172/JCI10947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang ZY, Prins JB, Marwick TH. Diabetic cardiomyopathy: evidence, mechanisms, and therapeutic implications. Endocr Rev. 2004;25(4):543–567. doi: 10.1210/er.2003-0012. [DOI] [PubMed] [Google Scholar]
- Finch-Johnston AE, Gussak HM, Mobley J, Holland MR, Petrovic O, Pérez JE, Miller JG. Cyclic variation of integrated backscatter: dependence of time delay on the echocardiographic view used and the myocardial segment analyzed. J Am Soc Echocardiogr. 2000;13(1):9–17. [PubMed] [Google Scholar]
- Finck BN, Han X, Courtois M, Aimond F, Nerbonne JM, Kovacs A, Gross RW, Kelly DP. A critical role for pparalpha-mediated lipotoxicity in the pathogenesis of diabetic cardiomyopathy: modulation by dietary fat content. Proc Natl Acad Sci U S A. 2003;100(3):1226–1231. doi: 10.1073/pnas.0336724100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson AA, Schaffer JE, Peterson LR, Bilhorn KR, Robert KM, Haider TA, Farmer MS, Holland MR, Miller JG. Quantitative analysis of the magnitude and time delay of cyclic variation of myocardial backscatter from asymptomatic type 2 diabetes mellitus subjects. Ultrasound Med Biol. 2009;35(9):1458–1467. doi: 10.1016/j.ultrasmedbio.2009.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong HP, Tan HW, Fang NN, Song T, Li SH, Zhong M, Zhang W, Zhang Y. Impaired left ventricular systolic and diastolic function in patients with metabolic syndrome as assessed by strain and strain rate imaging. Diabetes Res Clin Pract. 2009;83:300–307. doi: 10.1016/j.diabres.2008.10.018. [DOI] [PubMed] [Google Scholar]
- Hamby RI, Zoneraich S, Sherman L. Diabetic cardiomyopathy. JAMA. 1974;229(13):1749–1754. [PubMed] [Google Scholar]
- Holland MR, Gibson A, Kirschner C, Hicks D, Ludomirsky A, Singh G. Intrinsic myoarchitectural differences between the left and right ventricles of fetal human hearts: An ultrasonic backscatter feasibility study. J Am Soc Echocardiogr. 2009;22(2):170–176. doi: 10.1016/j.echo.2008.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holland MR, Gibson AA, Peterson LR, Areces M, Schaffer JE, Perez JE, Miller JG. Measurements of the cyclic variation of myocardial backscatter from two-dimensional echocardiographic images as an approach for characterizing diabetic cardiomyopathy. J Cardiometab Syndr. 2007 Aug;1(2):149–152. doi: 10.1111/j.1559-4564.2006.05493.x. [DOI] [PubMed] [Google Scholar]
- Holland MR, Wallace KD, Miller JG. Potential relationships among myocardial stiffness, the measured level of myocardial backscatter (“image brightness”), and the magnitude of the systematic variation of backscatter (cyclic variation) over the heart cycle. J Am Soc Echocardiogr. 2004;17(11):1131–1137. doi: 10.1016/j.echo.2004.06.004. [DOI] [PubMed] [Google Scholar]
- Hu X, Wang J, Sun Y, Jiang X, Sun B, Fu H, Guo R. Relation of ultrasonic tissue characterization with integrated backscatter to contractile reserve in patients with chronic coronary artery disease. Clin Cardiol. 2003;26(10):485–488. doi: 10.1002/clc.4960261010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaynes ET, Bretthorst GL. Probability theory: the logic of science. Cambridge Univ Press; 2003. [Google Scholar]
- Jeffreys H. Theory of probability. Oxford Univ Press; 1961. [Google Scholar]
- Kannel WB, Hjortland M, Castelli WP. Role of diabetes in congestive heart failure: the Framingham study. Am J Cardiol. 1974;34(1):29–34. doi: 10.1016/0002-9149(74)90089-7. [DOI] [PubMed] [Google Scholar]
- Kusminski C, Shetty S, Orci L, Unger R, Scherer P. Diabetes and apoptosis: lipotoxicity. Apoptosis. 2009;14:1484–1495. doi: 10.1007/s10495-009-0352-8. [DOI] [PubMed] [Google Scholar]
- Madaras EI, Barzilai B, Perez JE, Sobel BE, Miller JG. Changes in myocardial backscatter throughout the cardiac cycle. Ultrasonic imaging. 1983;5(3):229–239. doi: 10.1177/016173468300500303. [DOI] [PubMed] [Google Scholar]
- Mobley J, Banta C, Gussak H, Perez JE, Miller JG. Clinical tissue characterization: Online determination of magnitude and time delay of myocardial backscatter. Video Journal of Echocardiography. 1995;5(2):40–48. [Google Scholar]
- Mottley JG, Glueck RM, Perez JE, Sobel BE, Miller JG. Regional differences in the cyclic variation of myocardial backscatter that parallel regional differences in contractile performance. J Acoust Soc Am. 1984;76(6):1617–1623. doi: 10.1121/1.391608. [DOI] [PubMed] [Google Scholar]
- Naito J, Masuyama T, Mano T, Yamamoto K, Doi Y, Kondo H, Nagano R, Inoue M, Hori M. Influence of preload, afterload, and contractility on myocardial ultrasonic tissue characterization with integrated backscatter. Ultrasound Med Biol. 1996;22(3):305–312. doi: 10.1016/0301-5629(95)02061-6. [DOI] [PubMed] [Google Scholar]
- Ng AC, Delgado V, Bertini M, van der Meer RW, Rijzewijk LJ, Shanks M, Nucifora G, Smit JW, Diamant M, Romijn JA, de Roos A, Y LD, Lamb HJ, Bax JJ. Findings from left ventricular strain and strain rate imaging in asymptomatic patients with type 2 diabetes mellitus. Am J Cardiol. 2009;104:1398–1401. doi: 10.1016/j.amjcard.2009.06.063. [DOI] [PubMed] [Google Scholar]
- Nielsen LB, Bartels ED, Bollano E. Overexpression of apolipoprotein b in the heart impedes cardiac triglyceride accumulation and development of cardiac dysfunction in diabetic mice. J Biol Chem. 2002;277(30):27014–27020. doi: 10.1074/jbc.M203458200. [DOI] [PubMed] [Google Scholar]
- Péerez JE, McGill JB, Santiago JV, Schechtman KB, Waggoner AD, Miller JG, Sobel BE. Abnormal myocardial acoustic properties in diabetic patients and their correlation with the severity of disease. J Am Coll Cardiol. 1992;19(6):1154–1162. doi: 10.1016/0735-1097(92)90316-f. [DOI] [PubMed] [Google Scholar]
- Peterson LR, Herrero P, Schechtman KB, Racette SB, Waggoner AD, Kisrieva-Ware Z, Dence C, Klein S, Marsala J, Meyer T, Gropler RJ. Effect of obesity and insulin resistance on myocardial substrate metabolism and efficiency in young women. Circulation. 2004;109(18):2191–2196. doi: 10.1161/01.CIR.0000127959.28627.F8. [DOI] [PubMed] [Google Scholar]
- Poirier P, Bogaty P, Garneau C, Marois L, Dumesnil JG. Diastolic dysfunction in normotensive men with well-controlled type 2 diabetes: importance of maneuvers in echocardiographic screening for preclinical diabetic cardiomyopathy. Diabetes Care. 2001;24:5–10. doi: 10.2337/diacare.24.1.5. [DOI] [PubMed] [Google Scholar]
- Rijzewijk LJ, van der Meer RW, Smit JW, Diamant M, Bax JJ, Hammer S, Romijn JA, de Roos A, Lamb HJ. Myocardial steatosis is an independent predictor of diastolic dysfunction in type 2 diabetes mellitus. J Am Coll Cardiol. 2008;52(22):1793–1799. doi: 10.1016/j.jacc.2008.07.062. [DOI] [PubMed] [Google Scholar]
- Schannwell CM, Schneppenheim M, Perings S, Plehn G, Strauer BE. Left ventricular diastolic dysfunction as an early manifestation of diabetic cardiomyopathy. Cardiology. 2002 doi: 10.1159/000064682. [DOI] [PubMed] [Google Scholar]
- Sivia DS, Skilling J. Data analysis: a Bayesian tutorial. Oxford Univ Press; 2006. [Google Scholar]
- Skilling J. Nested sampling for general Bayesian computation. Bayesian Analysis. 2006;1(4):833–860. [Google Scholar]
- Stremmel W. Fatty acid uptake by isolated rat heart myocytes represents a carrier-mediated transport process. J Clin Invest. 1988;81(3):844–852. doi: 10.1172/JCI113393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner RF, Wear KA, Perez JE, McGill JB, Schechtman KB, Miller JG. Quantitative assessment of myocardial ultrasound tissue characterization through receiver operating characteristic analysis of Bayesian classifiers. J Am Coll Cardiol. 1995;25(7):1706–1711. doi: 10.1016/0735-1097(95)00038-6. [DOI] [PubMed] [Google Scholar]
- Wickline SA, Thomas LJ, Miller JG, Sobel BE, Pérez JE. The dependence of myocardial ultrasonic integrated backscatter on contractile performance. Circulation. 1985;72(1):183–192. doi: 10.1161/01.cir.72.1.183. [DOI] [PubMed] [Google Scholar]
- Witteles RM, Fowler MB. Insulin-resistant cardiomyopathy clinical evidence, mechanisms, and treatment options. J Am Coll Cardiol. 2008;51(2):93–102. doi: 10.1016/j.jacc.2007.10.021. [DOI] [PubMed] [Google Scholar]
- Zhou YT, Grayburn P, Karim A, Shimabukuro M, Higa M, Baetens D, Orci L, Unger RH. Lipotoxic heart disease in obese rats: implications for human obesity. Proc Natl Acad Sci U S A. 2000;97(4):1784–1789. doi: 10.1073/pnas.97.4.1784. [DOI] [PMC free article] [PubMed] [Google Scholar]