Slice Encoding for Metal Artifact Correction with Noise Reduction

Abstract

Magnetic resonance imaging (MRI) near metallic implants is often hampered by severe metal artifacts. To obtain distortion-free MR images near metallic implants, SEMAC (Slice Encoding for Metal Artifact Correction) corrects metal artifacts via robust encoding of excited slices against metal-induced field inhomogeneities, followed by combining the data resolved from multiple SEMAC-encoded slices. However, as many of the resolved data elements only contain noise, SEMAC-corrected images can suffer from relatively low signal-to-noise ratio (SNR). Improving the SNR of SEMAC-corrected images is essential to enable SEMAC in routine clinical studies. In this work, a new reconstruction procedure is proposed to reduce noise in SEMAC-corrected images. A singular value decomposition (SVD) denoising step is first applied to suppress quadrature noise in multi-coil SEMAC-encoded slices. Subsequently, the SVD-denoised data are selectively included in the correction of through-plane distortions. The experimental results demonstrate that the proposed reconstruction procedure significantly improves the SNR without compromising the correction of metal artifacts.

Introduction

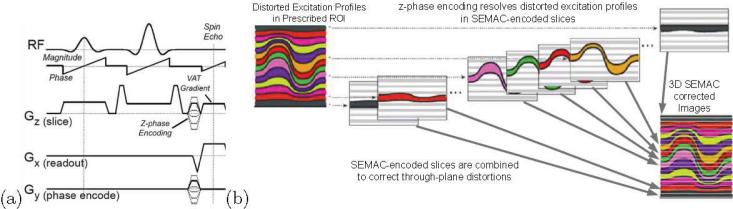
Distortion-free MRI near metal has great clinical potential in diagnosing millions of patients surgically treated with metallic implants. SEMAC (Slice Encoding for Metal Artifact Correction) [1] is a recently proposed imaging technique that corrects severe artifacts around metal in MR images. SEMAC extends a view-angle-tilting (VAT) [2] spin echo sequence with additional phase encoding along slice-select z axis (Figure 1a). The additional z-phase encoding resolves the spins subject to metal-induced susceptibility back to their actual slice locations. The complete correction of metal artifacts is then achieved by combining multiple resolved data elements in each voxel. Besides the signals of the spins that spatially locate in the same voxel but precess in different frequency bands, the resolved data elements also contain background noise. Therefore, the combination of the resolved data elements involves a trade-off between including signals and excluding noise.

Figure 1.

(a) Schematic diagram of SEMAC imaging sequence, which extends a VAT spin echo sequence with additional z-phase encoding. (b) Illustration of SEMAC working principle. The additional z-phase encoding resolves the distorted excitation profiles of SEMAC-encoded slices (highlighted in different colors). The reconstruction procedure of SEMAC assigns the resolved data back to their actual voxel locations, and corrects the through-plane distortions by combining multiple SEMAC-encoded slices.

Combination strategies play an important role in affecting the signal-to-noise ratio (SNR) and the performance of metal artifact correction. Simple combination strategies, such as maximum-intensity-projection which only include the data element with the maximum magnitude, result in superb SNR but also incomplete artifact correction. Another combination strategy, referred to as sum-of-squares combination, raises the magnitudes of all the data elements to the power of 2, followed by taking the square root of the combination result. The sum-of-squares combination is adopted by another recently proposed metal imaging technique, MAVRIC [3], which excites the spins in the region-of-interest (ROI) into multiple overlapping frequency bands with Gaussian radiofrequency (RF) pulses. MAVRIC overlaps the frequency bands in such a way that the sum-of-squares combination results in a flat spectral response.

SEMAC employs windowed-SINC RF pulses to excite multiple non-overlapping slabs. The non-overlapping excitation leads to better acquisition efficiency by exciting the spins in the ROI only once. However, as there is no overlapping between excited slabs, the sum-of-squares combination amplifies the differences between the resolved data elements, hence penalizing those elements with relatively small magnitudes. To obtain a flat spectral response in the correction of through-plane distortions, SEMAC adopts a linear complex sum to combine the resolved data elements in each voxel. In addition, the linear complex sum enables an arbitrary reconstruction order in accelerated SEMAC [4], which integrates SEMAC with acceleration techniques, such as parallel imaging and partial Fourier acquisition.

Lu et al. [1] shows that the linear complex sum of multiple resolved data elements leads to the penalty of signal-to-noise ratio (SNR) of the SEMAC-corrected images, as many of the data elements only contain background noise. Improving the SNR of SEMAC-corrected images is essential to enable SEMAC in imaging scenarios associated with SNR trade-off, such as incorporation with STIR (Short-TI Inversion Recovery) [5] for fat suppression and/or fast imaging techniques [6–8] for shorter scan times. In this paper, we propose a new reconstruction procedure for combining multi-coil SEMAC-encoded slices, which is developed to strike a balance between the SNR improvement and the correction of metal artifacts.

The proposed SEMAC reconstruction procedure consists of two consecutive steps. A singular value decomposition (SVD)-based denoising step is first applied to remove quadrature noise in all resolved data elements. Subsequently, a selective data inclusion step selects the SVD-denoised data elements that contain useful signals in the correction of through-plane distortions. The proposed technique is also extended to improve the SNR of the corrected images obtained using accelerated SEMAC. We demonstrate the efficacy of the proposed technique with both phantom and in vivo experiments. The experimental results show that the proposed technique leads to significantly higher SNR of the corrected images than the existing SEMAC reconstruction, without compromising the correction of metal artifacts.

Methods

Due to metal-induced field inhomogeneities, a SEMAC-encoded slice can contain spins residing at different locations in the slice-select direction, which are resolved by the additional z-phase encoding. Each SEMAC-encoded slice contains a three-dimensional resolved data set of size N_x×N_y×N_z, where N_x, N_y, and N_z are the numbers of frequency encoding, phase encoding, and z-phase encoding steps, respectively. To correct through-plane distortions, the data elements resolved from SEMAC-encoded slices are assigned back to their actual voxel locations.

SVD-based Denoising

The resolved data elements at each voxel form a vector v, whose length is equal to the number of SEMAC-encoded slices covering the voxel. When the vector v is received by a coil, the same coil sensitivity applies to all the elements of v, regardless of their frequencies. Denote the vector received by the i^th coil as v_i = w_iv+n_i, where w_i and n_i are the respective coil sensitivity and noise vector. The SVD-based denoising exploits the data redundancy in multi-coil SEMAC-encoded slices to suppress quadrature noise. Given the length of v equal to N_v and the number of coils equal to N_c, we can form a N_v × N_c matrix M, of which the i^th column is the signal vector v_i received by the i^th coil. In the absence of the noise vectors {n_i}_i=1,…,Nc, the rank of the matrix M is 1: all columns of M are the multiples of the vector v.

The data redundancy in the multi-coil SEMAC-encoded slices provides the basis to eliminate all noise orthogonal to the signal vector without explicit knowledge of the coil sensitivities. To remove the quadrature noise in the resolved data elements, a rank-1 approximation of the matrix M is performed to truncate all singular values of M except the largest one. Given the SVD of the matrix M = UΣV^⊺ of rank r, the rank-1 approximation of M is

$$\tilde{\mathrm{M}}={\sigma }_1{u}_1{v}_1^{⊺},$$ (1)

where U = [u₁ ⋯ u_r] and V = [v₁ ⋯ v_r] have orthonormal columns, and Σ is the diagonal matrix with the singular values in descending order σ₁ ≥ ⋯ ≥ σ_r > 0. The i^th column vector of $\tilde{\mathrm{M}}$ serves as the denoised vector v_s,i received by the i^th coil.

Selective Data Inclusion

After removing quadrature noise with the SVD-based denoising, the signals are less likely buried in noise. Subsequently, the correction of through-plane distortions is performed by excluding the resolved data elements that only contain noise. To this end, we exploit the fact that distorted excitation profiles are mostly sparse; i.e., the frequency dispersion in most voxels subject to metal-induced susceptibility is limited. Therefore, the signals that arise from a voxel subject to metal-induced field inhomogeneity can only spread into a limited number of resolved data elements. The selective data inclusion is equivalent to the recovery of the sparse distorted excitation profile.

In the following the coil dependence is dropped for notational simplicity. However, it should be understood that the selective data inclusion is performed for each coil separately, as the coils can have different noise levels. Let v_s denote the SVD-denoised signal vector at a voxel. The selection data inclusion is to approximate v_s with a sparse representation with few non-zero elements, which can be formulated into the following optimization problem:

$$\text{min}\frac{1}{2}{\parallel {\mathbf{v}}_s-{\mathbf{v}}_d\parallel }_2^2+\lambda {\parallel {\mathbf{v}}_d\parallel }_1,$$ (2)

where v_d is the optimization variable (i.e., the sparse representation of the SVD-denoised signal vector v_s), and λ determines the trade-off between the data consistency and the sparsity of v_d. The optimization problem in Eq. 2 can be solved by the following ”soft thresholding” [9]:

$${\mathbf{v}}_d\left(i\right)=\left\{\begin{array}{ccc}\hfill 0& \hfill \text{if}\mid \mathbf{v}\left(i\right)\mid <\lambda \hfill & \hfill \hfill \\ \hfill & \hfill \hfill & \hfill {\forall }_i=1,\dots ,N_v\hfill \\ \hfill \mathbf{v}\left(i\right)-\lambda & \hfill \text{if}\mid \mathbf{v}\left(i\right)\mid >\lambda \hfill & \hfill \hfill \end{array}\right\}$$ (3)

Eq. 3 simply states that a resolved data element should be selected only when its magnitude is greater than λ. In our implementation, the magnitude threshold λ is set to be $\sqrt{2}{\sigma }_n$, where σ_n is the standard deviation of noise. We estimate σ_n from the k-space edge, where noise dominates signals. After performing the selective data inclusion for all coils, the SEMAC-corrected images of multiple coils are combined using a sum-of-squares.

Extension to Accelerated SEMAC

To obtain clinically feasible scan times, the SEMAC acquisition needs to be accelerated through integration with fast imaging techniques. Hargreaves et al. [4] demonstrated that by exploiting the linearity of SEMAC reconstruction procedure, the correction of through-plane distortions can be performed in an arbitrary order with parallel imaging and partial Fourier reconstruction. However, as the proposed reconstruction procedure consists of non-linear operations—SVD-based denoising and selective data inclusion, the extension to accelerated SEMAC is performed such that the final SEMAC-corrected images have improved SNR and little reconstruction artifacts.

The extension of the proposed reconstruction procedure to accelerated SEMAC is as follows. First, a self-calibrated parallel imaging reconstruction technique, such as ARC (Auto-calibrated Reconstruction for Cartesian imaging) [10], is applied to interpolate missing k-space lines in each SEMAC-encoded slice. Subsequently, the SEMAC-encoded slices are subject to partial Fourier reconstruction with zero-filling such that the phase information is preserved for resolving distorted excitation profiles. After applying the SVD-based denoising to SEMAC data obtained from zero-filling partial Fourier reconstruction, the selective data inclusion is performed to correct through-plane distortions for each coil. To remove the zero-filling induced blurring, the corrected images are transformed back to (k_x, k_y, z) space. Due to the denoising process, there exists a small amount of signal leakage into the previously empty k-space region, which are simply set to 0. The resulting SEMAC-corrected partial Fourier data undergoes homodyne reconstruction [8] at each z slice location, followed by a sum-of-squares multi-coil combination.

Experimental Methods

All experiments were performed on a GE Signa 1.5 T scanner (General Electric Healthcare, Waukesha, WI) with gradients capable of 40 mT/m amplitude and 150 T/m/sec slew rate, and a readout bandwidth up to ±250 kHz. Windowed-SINC pulses with 3.2 ms pulse duration and 6.4 time-bandwidth product were used as both the 90° excitation pulse and the 180° refocusing pulse in the SEMAC imaging sequence. A readout bandwidth of 1 kHz/pixel was chosen such that the readout duration matched with the main lobe of the RF excitation pulse to minimize the VAT-associated blurring [11].

Phantom Study for SNR quantification

To demonstrate the SNR improvement brought by the proposed reconstruction procedure, we performed quantitative SNR measurements with an accelerated T1-weighted SEMAC acquisition of a titanium shoulder prothesis immersed in gel. The phantom was scanned with an eight-channel head phased-array coil and the following scan parameters: TE/TR = 9.5/469 msec, 320 × 144 matrix over 14 cm field-of-view (FOV), and 24 SEMAC-encoded slices with 2.5 mm thickness. The acceleration was achieved by incorporating parallel imaging (acceleration factor of 2) and partial Fourier ratio of 0.58 along y axis. Twenty four central k_y lines were used for calibration. The sub-sampled data set was reconstructed with ARC parallel imaging and partial Fourier reconstructions. For comparison, the reconstructed SEMAC-encoded slices were combined using the linear complex sum, the sum-of-squares combination, and the proposed procedure for noise reduction.

The SNR of reconstructed data sets was measured using the “pseudo multiple replica” method [12]. From the boundary regions of the fully sampled data set, we extracted few hundred lines of k-space data, which were used to empirically estimate the noise covariance matrix. The noise synthesized from the noise covariance matrix was added to each data set before reconstruction. The noise addition and reconstruction was repeated 30 times for each data set, and the mean and standard deviation were measured at each pixel over the 30 repetitions. SNR at each pixel was then quantified as the ratio of mean to standard deviation.

In-vivo Studies

The following in-vivo studies were imaged with the SEMAC sequence incorporated with 2× ARC parallel imaging and partial Fourier ratio of 0.58 along phase-encoding y-axis. The SEMAC-corrected images were obtained by the proposed reconstruction procedure and the following three means, namely combining all resolved data with (1) a complex sum, (2) a sum-of-squares, (3) a complex sum after applying the SVD-based denoising.

Accelerated SEMAC Acquisition

A subject with metallic implants in her neck was imaged with an eight-channel head/neck phased-array coil and the following scan parameters: TE/TR = 14/3751 msec with echo train length of 8, 256 × 192 matrix over 24 cm field-of-view, and 32 SEMAC-encoded slices with 3 mm thickness.

Accelerated SEMAC Acquisition with STIR

Fat-suppression near metal is challenging due to large metal-induced field inhomogeneities. While STIR is robust against field inhomogeneities, it causes further loss in SNR. A subject with metallic implants in her pelvis was imaged using the accelerated SEMAC sequence incorporated with STIR. An eight-channel cardiac phased-array coil and the following scan parameters were used: TE/TR = 9.6/3820 msec with echo train length of 8, 256 × 192 matrix over 36 cm FOV, and 24 SEMAC-encoded slices with 7 mm thickness.

Results

For all studies the proposed reconstruction procedure significantly improved the SNR compared to the existing SEMAC reconstruction, without affecting the artifact correction near metallic implants.

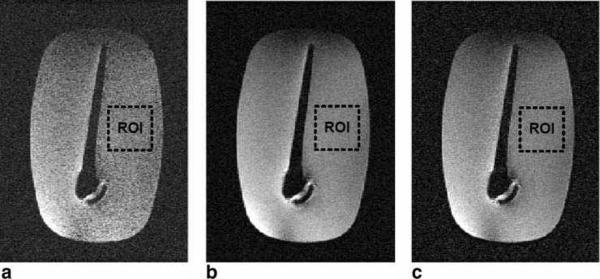
Figure 2 shows the comparison of phantom images acquired using the accelerated SEMAC; Fig. 2 (a,b,c) show the sample results obtained from the linear complex sum, the sum-of-squares combination, and the proposed reconstruction procedure, respectively. To quantify the SNR improvement, a uniform foreground region (ROI) was selected in the corrected images (highlighted with dashed boxes in Fig. 2). The SNR of each voxel inside the ROI was obtained from the “pseudo multiple replica” method. We performed an overall SNR comparison by averaging the SNR values over the ROI across slices. The empirically estimated SNR value is 4 for the images reconstructed using the existing SEMAC reconstruction. In their counterparts reconstructed using the sum-of-squares combination and the proposed technique, the SNR values are boosted to 10 and 8, respectively.

Figure 2.

Phantom image comparisons between (a) SEMAC with 2× ARC acceleration and 60% partial Fourier (ky) acquisition, and their counterparts (b, c) obtained from the sumof-squares combination and the proposed technique for noise reduction. It can be seen that both the sum-of-squares combination and the proposed reconstruction procedure significantly improved the SNR. To quantify the SNR improvement, a uniform foreground region was selected in the corrected images (highlighted with dashed box).

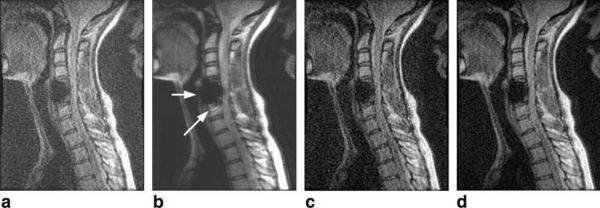
Figure 3 shows the comparison of the SEMAC-corrected images of the neck study at a sample slice location. Figure 3a shows the image obtained from the existing SEMAC reconstruction. Figure 3b shows the image obtained by combining all resolved data elements with a sum-of-squares, which have superior SNR; however, as compared to that in Figs. 3d, the result in b suffers from some signal drop (pointed by arrows), due to imperfect correction of signal voids near the metallic implant. In comparison, Figure 3c shows the image obtained by applying the SVD-based denoising to remove quadrature noise in the SEMAC-encoded slices. Figure 3d shows the image obtained from the proposed reconstruction procedure, which consists of both the SVD-based denoising and the selective data inclusion.

Figure 3.

Comparison of the SEMAC-corrected images of a neck study. This neck study was performed with accelerated SEMAC acquisition. The image in (a) was obtained from the existing post-processing procedure of SEMAC. The image in (b) was obtained by combining the resolved data with a sum-of-squares, which have superior SNR, but suffer from imperfect correction of signal voids near the metallic implant (arrows). In comparison, the image in (c) was obtained by applying the SVD-based denoising to remove quadrature noise. The image in (d) was obtained from the proposed post-processing procedure, which consist of both the SVD-based denoising and the selective data inclusion.

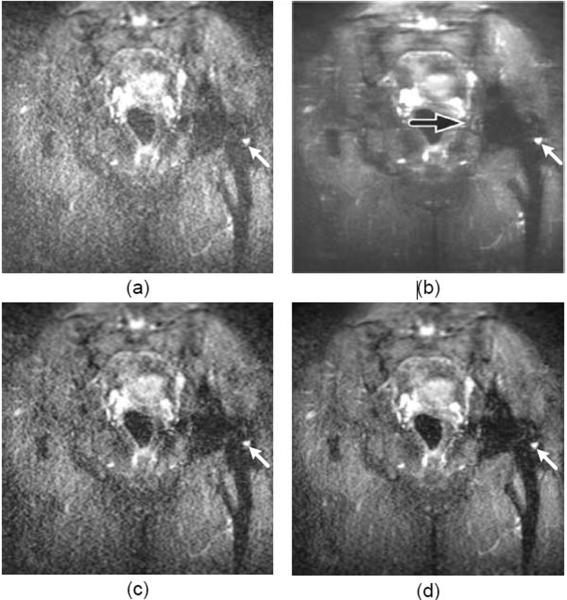
Figure 4 shows the comparison of the SEMAC-corrected images of the pelvis study. This pelvis study was performed with accelerated SEMAC acquisition with STIR. Figure 4a shows the image obtained from the existing reconstruction procedure of SEMAC. Figure 4b shows the image obtained by combining the resolved data with a sum-of-squares. In this case, the sum-of-squares combination causes two undesired side effects, namely altered image contrast due to the reduced dynamic range and the “ripple artifact” near the implant. In comparison, the image in Fig. 4c was obtained by applying the SVD-based denoising to remove quadrature noise. Figure 4d shows the image obtained from the proposed reconstruction procedure, which markedly improves the SNR of the STIR SEMAC image and preserves the unambiguous identification of fluid near the implant.

Figure 4.

Comparison of the SEMAC-corrected images of a pelvis study. This pelvis study was performed with accelerated SEMAC acquisition with STIR. The image in (a) was obtained from the existing SEMAC reconstruction procedure, which combines all resolved data with a complex sum. The image in (b) was obtained by combining all resolved data with a sum-of-squares. In this case, the sum-of-squares produces superior SNR, but causes two undesired side effects, namely altered image contrast due to the reduced dynamic range and the ”ripple artifact” near the implant (black arrow). In comparison, the image in (c) was obtained by applying the SVD-based denoising to remove the quadrature noise. The image in (d) was obtained from the proposed reconstruction procedure, which consist of both the SVD-based denoising and the selective data inclusion. The proposed reconstruction procedure markedly improves the SNR of the STIR SEMAC image and preserves the unambiguous identification of fluid near the implant (white arrow).

Discussion

SEMAC has shown great promise in obtaining distortion-free MR images near metallic implants. Nevertheless, the existing reconstruction procedure of SEMAC, which directly combines all resolved data elements with a complex sum, counteracts the SNR benefit brought by the long scan times associated with the additional z-phase encoding. To reclaim the SNR in the SEMAC-corrected images, we propose a new SEMAC reconstruction procedure that consists of SVD-based denoising and selective data inclusion.

Singular value decomposition (SVD) has been used for MR signal denoising in various applications, such as magnetic resonance spectroscopy [13] and combining multi-echo data sets [14]. The SVD-based denoising decomposes the resolved data into orthogonal components, followed by a low-rank approximation to keep those components that ideally correspond to signals. The SVD-based denoising of SEMAC multi-coil data removes the quadrature noise by retaining the signal component that corresponds to the largest singular value. By removing the quadrature noise, the resolved data elements containing useful signals can be more reliably differentiated from those only containing noise based on their magnitudes. This enables the selective data inclusion to exclude noise from the correction of through-plane distortions.

The key to the SVD-based denoising lies in determining the number of singular values preserved in the low-rank approximation. To uphold the rank-1 assumption of the SVD-based denoising, the extension of the proposed reconstruction procedure to accelerated SEMAC has to be carefully performed. Specifically, the parallel imaging reconstruction and the zero-filling partial Fourier reconstruction need to be performed prior to the denoising. By unfolding the aliasing in the phase encoding y direction with the parallel imaging reconstruction, we ensure that each resolved data element does not contain the signals from other voxels subject to different coil sensitivities. On the other hand, the zero-filling partial Fourier reconstruction introduces blurring [8], which causes the signal vector at one voxel to contain the data from its neighboring voxels. However, as coil sensitivities are smoothly varying (i.e., neighboring voxels' coil sensitivities are almost the same), the rank-1 assumption of the SVD-based denoising still holds; hence, the zero-filling induced blurring is acceptable for the denoising purpose.

There are different ways to combine the resolved data elements (e.g., the sum-of-squares combination and the complex-sum combination), which have different pros and cons in terms of implementation complexity, resultant SNR, and performance of artifact correction. The sum-of-squares is easy to implement, and results in a superior SNR than the linear complex sum. Even with the SVD denoising that completely removes quadrature noise, the linear complex sum still has higher noise level in the composite images, as shown with the experimental results. However, the sum-of-squares combination could be potentially problematic for the voxels that have large frequency dispersion, as the results in Figs. 3 and 4 show that the sum-of-squares combination can introduce undesirable intensity shading.

The linear complex-sum combination requires that the receiver and RF phase references in the SEMAC imaging sequence are carefully adjusted (Fig. 1) such that the data resolved from multiple slices can be coherently summed up without taking the magnitude operation. The proposed SEMAC reconstruction procedure aims to significantly improve the SNR of the SEMAC-corrected images obtained using the complex-sum combination without compromising the correction of metal artifacts. The efficacy of the proposed technique has been demonstrated in the clinically important imaging scenarios where SEMAC-corrected images are liable to relatively low SNR. These scenarios include the incorporation of SEMAC with high readout bandwidth for less VAT-associated blurring, STIR for fat suppression, and accelerated acquisition for shorter scan times.