Approximate Predictive Densities and Their Applications in Generalized Linear Models

Abstract

Exact calculations of model posterior probabilities or related quantities are often infeasible due to the analytical intractability of predictive densities. Here new approximations to obtain predictive densities are proposed and contrasted with those based on the Laplace method. Our theory and a numerical study indicate that the proposed methods are easy to implement, computationally efficient, and accurate over a wide range of hyperparameters. In the context of GLMs, we show that they can be employed to facilitate the posterior computation under three general classes of informative priors on regression coefficients. A real example is provided to demonstrate the feasibility and usefulness of the proposed methods in a fully Bayes variable selection procedure.

1 Introduction

Bayesian applications in a number of problems need to be able to evaluate marginal probability distributions of the data, often called predictive densities, or their ratios known as Bayes factors, for a set of competing models, which are often analytically intractable. Calculations of such quantities have been addressed by several authors, including sampling or Monte Carlo methods (e.g., Gelfand and Smith 1990, Verdinelli and Wasserman 1995, Han and Carlin 2001) and analytic approximations based on the Laplace method (e.g., Tierney and Kadane 1986, Tierney et al. 1989, Gelfand and Dey 1994, Raftery 1996, Boone et al. 2005). The first part of this paper presents new analytical methods to approximate the predictive densities, where we also discuss and compare their theoretical properties with those of Laplace approximations.

The proposed methods are then applied to Bayesian analysis of Generalized Linear Models (GLMs). Under a hierarchical Bayes setup for model uncertainty, we show that our proposed methods, when approximating predictive densities, are applicable to three general classes of informative priors, namely the normal prior (Dellaportas and Smith 1993, Meyer and Laud 2002), the conjugate prior (Diaconis and Ylvisaker 1979, Meyer and Laud 2002, Chen et al. 2008), and the power prior (Zellner 1988, Chen et al. 2000), for regression coefficients. The proposed approximations can also greatly facilitate the posterior computation. Raftery (1996) presented asymptotic analytics to approximate Bayes factors and accounted for model uncertainty in GLMs. He assumed independent normal priors on regression coefficients, which is a special case of our approach. Wang and George (2007) proposed several closed-form Bayesian selection criteria for GLMs, using normal priors with empirical covariance structures on regression coefficients. An integrated Laplace method was used to achieve the analytical tractability, which is a special case of our proposed methods; the classes of the conjugate and power priors were not discussed there. Chen et al. (1999) and Ibrahim et al. (2000) concentrated on variable selection for logistic and Poisson regression models, respectively. Their computation of model posteriors was purely sample based without using any analytic approximations. What distinguishes our work from these papers are the generality of our approach and the novelty of our analytical approximations.

The remainder of the paper is organized as follows. In Section 2 we introduce new analytic methods for approximating predictive densities. Section 3 describes their applications in GLMs. Section 4 presents two examples, one providing a simulation evaluation and comparison of various approximations, and the other using a real dataset with 19 predictors and a binary response variable to illustrate the approximations in a Fully Bayes variable selection procedure. Section 5 concludes the paper with discussions.

2 Methods for Approximating Predictive Densities

We consider the problem of approximating a predictive density of the form

$$I=\int L_n(\mathit{\beta })\pi (\mathit{\beta })\text{d}\mathit{\beta },$$ (1)

where β is a parameter vector whose domain Ω is R^m, L_n(β) is a likelihood function based on n observations, and π (β) is a prior density on β. In this paper we always assume that I exists and is finite.

2.1 The Case of Normal Priors

We begin with the case where π(β) is a normal prior density with a mean vector β₀ and a covariance matrix λΣ₀, λ > 0. The matrix Σ₀ reflects relative uncertainties of all parameters in β and the correlations among them. It can be specified a priori or empirically. After Σ₀ is chosen, the hyperparameter λ quantifies the strength of prior information relative to the data. When λ = 0, π reduces to a point mass at β₀. When λ gets large, π approaches a flat prior for β.

Theorem 2.1

Suppose π(β) ~ N(β₀, λΣ₀), and {l_n = logL_n(β) : n = 1, 2, …} is a Laplace-regular sequence of log-likelihood functions having strict local maxima {(β̂_n : n = 1, 2, …} and positive definite matrices { ${\mathbf{\Sigma }}_n={[-l_n^{″}({\widehat{\mathit{\beta }}}_n)]}^{-1}:n=1,2,\dots$}. Let

$$\stackrel{\sim }{I}=L_n({\widehat{\mathit{\beta }}}_n)·{\mid \lambda {\mathbf{\Sigma }}_0{\mathbf{\Sigma }}_n^{-1}+\mathbf{I}\mid }^{-\frac{1}{2}}exp\left\{-\frac{{({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}^T{(\lambda {\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_n)}^{-1}({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}{2}\right\},$$ (2)

where I is a n × n identity matrix. Then Ĩ = I(1 + O(n⁻¹)).

Laplace regularity has been discussed in depth in Kass et al. (1990). Briefly speaking, it requires that l_n(β) is six-time continuously differentiable, all partial derivatives (up to the sixth order) are bounded in the neighborhood of β̂_n, the determinants of the Hessians are bounded and positive, and l_n has a dominant peak at β̂_n. Note that the result in Theorem 2.1 is an analytical assessment for given sequences of well-behaved (i.e. Laplace-regular) data. In Kass et al. (1990), general conditions are discussed that guarantee the well-behaved data will occur with probability one. In particular, since those conditions hold for the exponential family, the results of Theorem 2.1 hold for GLMs almost surely.

A full proof of the theorem is given in Appendix A. Below is a brief description of the idea. When {l_n : n = 1, 2, …} is Laplace regular, we know from Lemma 2 in Kass et al. (1990) that, ∃ c > 0 and δ > 0, such that for all sufficient large n,

$${\int }_{\mathrm{\Omega }-B_{\delta }({\widehat{\mathit{\beta }}}_n)}exp\{l_n(\mathit{\beta })-l_n({\widehat{\mathit{\beta }}}_n)\}\pi (\mathit{\beta })\text{d}\mathit{\beta }<exp\{-nc\},$$ (3)

where B_δ (β̂_n) denotes an open ball centered at β̂_n with a radius δ. This reduces our consideration of I to the integral of L_n(β) π(β) over a neighborhood B_δ (β̂_n) because (3) ensures that I only depends on the behavior of L_n near its maximum when n is large. Thus Ĩ can be obtained by first approximating l_n(β) with a second-order Taylor series expansion at β̂_n, say l̂_n(β), over the region B_δ (β̂_n), and then inserting it in (1) and integrating out β from the approximate integrand exp{l̂(β)} π (β). As a result, Ĩ is derived by taking advantage of the normality assumption for π (β).

2.2 Comparison with the Laplace’s Method

Under the conditions of Theorem 2.1, the well-known Laplace’s method is legitimate for the integral I in (1). The resulting approximations are not unique, depending on how one defines the Laplace-regular sequence {l_n}.

Denning l_n = log L_n yields the standard-form Laplace approximation.

$${\stackrel{\sim }{I}}_L=L_n({\widehat{\mathit{\beta }}}_n)·{\lambda }^{-\frac{m}{2}}{\mid {\mathbf{\Sigma }}_0{\mathbf{\Sigma }}_n^{-1}\mid }^{-\frac{1}{2}}exp\left\{-\frac{{({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}^T{\mathbf{\Sigma }}_0^{-1}({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}{2\lambda }\right\}.$$ (4)

In practice, this approximation is easy to compute since it only requires the MLE of β and the observed Fisher information, which are reported by nearly all statistical software.

Next we consider the fully exponential form of Laplace’s method (Tierney and Kadane, 1986; Tierney et al., 1989) by defining l_n = log L_n + log π. Suppose {log L_n + logπ : n = 1, 2, …} have strict local maxima {β̃_n : n = 1, 2, …} and positive definite matrices { ${\mathrm{\Xi }}_n={[-l_n^{″}({\stackrel{\sim }{\mathit{\beta }}}_n)]}^{-1}:n=1,2,\dots$}. Then the approximation is given by

$${\stackrel{\sim }{I}}_{LF}=L_n({\stackrel{\sim }{\mathit{\beta }}}_n)·{\mid \lambda {\mathbf{\Sigma }}_0{\mathrm{\Xi }}_n^{-1}+\mathbf{I}\mid }^{-\frac{1}{2}}exp\left\{-\frac{{({\stackrel{\sim }{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}^T{\mathbf{\Sigma }}_0^{-1}({\stackrel{\sim }{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}{2\lambda }\right\}.$$ (5)

Usually Ĩ_LF is quite accurate, but it is computationally intensive because it requires the derivation of β̃_n (i.e., the posterior mode) and the inverse Hessian of log posterior evaluated at β̃_n, which are not directly available to users in most statistical software, and so have to be computed via numerical algorithms.

In addition, Raftery (1996) proposed a method for approximating Bayes factors based on the fully exponential form of Laplace’s method, followed by another approximation via Newton’s method to reduce the computational cost. For example, he approximated β̃_n from β̂_n using one step of Newton’s method. In our context, applying his idea yields the approximation

$${\stackrel{\sim }{I}}_R=L({\widehat{\mathit{\beta }}}_n)·{\mid \lambda {\mathbf{\Sigma }}_0{\mathbf{\Sigma }}_n^{-1}+\mathbf{I}\mid }^{-\frac{1}{2}}·exp\left\{-\frac{{({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}^T{(\lambda {\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_n)}^{-1}\left[{\mathbf{\Sigma }}_n{(\lambda {\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_n)}^{-1}+\mathbf{I}-{\mathbf{\Sigma }}_n{(\lambda {\mathbf{\Sigma }}_0)}^{-1}\right]({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}{2\phi }\right\},$$ (6)

which is less accurate but is easier to compute than Ĩ_LF.

Note that the errors of Ĩ, Ĩ_L, Ĩ_LF and Ĩ_R are all O(n⁻¹). Another similarity of the four is that for large λ with fixed Σ₀, Ĩ ≈ Ĩ_L ≈ Ĩ_LF ≈ Ĩ_R. This can be seen from the fact that as λ gets large, any pairwise ratio converges to 1, e.g., lim_λ→+∞ Ĩ/Ĩ_L = 1.

Since computing Ĩ is as easy as computing Ĩ_L and Ĩ_R, we first contrast Ĩ with Ĩ_L and Ĩ_R. First of all, when L_n(β) is proportional to ψ, the normal density function, (2) gives the exact value, i.e. Ĩ = I. However, it is easy to verify that Ĩ_L ≠ I and Ĩ_R ≠ I in the normal case. Secondly, for small λ with fixed Σ₀, approximations by Ĩ may differ substantially from those by Ĩ_L and Ĩ_R. The limit of I, as λ approaches zero, is lim_λ→0 I = L_n(β₀) since β is fixed at β₀ when λ = 0. For Ĩ,

$$\underset{\lambda \to 0}{lim}\stackrel{\sim }{I}=L_n({\widehat{\mathit{\beta }}}_n)·exp\left\{-\frac{{({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}^T{\mathbf{\Sigma }}_n^{-1}({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}{2}\right\}.$$ (7)

Thus,

$$\underset{n\to +\infty }{lim}\underset{\lambda \to 0}{lim}\stackrel{\sim }{I}=\underset{\lambda \to 0}{lim}I$$ (8)

whenever β̂_n → β₀ as n gets large, which occurs with probability one under mild regularity conditions for many commonly used models including GLMs. But this limiting equality does not hold for either Ĩ_L or Ĩ_R, since

$$\underset{\lambda \to 0}{lim}{\stackrel{\sim }{I}}_L=\{\begin{array}{cc}0& \text{if}{\mathit{\beta }}_0\ne {\widehat{\mathit{\beta }}}_n\\ +\infty & \text{if}{\mathit{\beta }}_0={\widehat{\mathit{\beta }}}_n\end{array},$$

and lim_λ→0 Ĩ_R = +∞. Neither of them converges to the true value. As a result, Ĩ is more accurate than Ĩ_L and Ĩ_R for small λ. This improvement in accuracy becomes important in situations where the predictive density needs to be evaluated for a range of values of λ including small ones, like a sensitivity analysis on λ or a Fully Bayes approach that entails choosing a prior on λ over (0, +∞).

Now we proceed to compare Ĩ with Ĩ_LF. Note that Ĩ_LF has excellent performance at small λ because lim_λ→0 Ĩ_LF = lim_λ→0 I holds for every n. As will be shown in our simulation, Ĩ can achieve nearly the same performance as Ĩ_LF, but requires much less computing time. In addition, in a fully Bayes (FB) method that treats λ as random, there does not exist a conjugate prior of λ based on Ĩ_LF. In contrast, when Σ₀ is chosen to be Σ_n, Ĩ can yield great analytical tractability when further integrating λ out. In this case, equation (2) becomes

$$\stackrel{\sim }{I}=L_n({\widehat{\mathit{\beta }}}_n)·{(\lambda +1)}^{-\frac{m+1}{2}}exp\left\{-\frac{{({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}^T{\mathbf{\Sigma }}_n^{-1}({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)}{2(\lambda +1)}\right\},$$

which suggests a conjugate prior of λ in the form of 1/(λ + 1) ~ Truncated Gamma(a, b). This would simplify the FB computation since a closed form of the posterior can be derived.

Finally, Table 1 summarizes the discussions about comparing the four analytical approximations to the integral I.

Table 1.

Comparison of different analytical approximations to the integral I. Note that the limiting properties when λ → 0 indicate their performance at small λ. And ψ denotes the normal pdf.

Approximations to I	Ĩ	ĨL	ĨLF	ĨR
Methods	Theory 2.1	standard Laplace	fully-exponential Laplace	fully-exponential Laplace + Newton
Normal case: Ln ∝ ψ	Ĩ = I	ĨL ≠ I	ĨLF = I	ĨR ≠ I
Convergence when λ → 0?	Yes for GLMs with large n	No	Yes	No
Existence of conjugate priors on λ?	Yes	Yes	No	No
Ease of computation?	Yes	Yes	No	Yes

2.3 The Case of General Priors

Here we discuss methods for approximating the predictive density in (1) with a general form of the prior π (β). A straightforward extension of Theorem 2.1 leads to the following result.

Corollary 2.1

Suppose {l_n = log L_n(β) : n= 1, 2, …} satisfy the same conditions as in Theorem 2.1; π (β) is a four-time continuously differentiate prior density on β with a mode β₀; and Σ₀ = {− λ [log π (β₀)]″}⁻¹ is positive definite, λ > 0. Let

$${\stackrel{\sim }{I}}^{\ast }=\stackrel{\sim }{I}+{\stackrel{\sim }{I}}_L^{\ast }-{\stackrel{\sim }{I}}_L,$$ (9)

where Ĩ is given in (2), Ĩ_L is given in (4) and ${\stackrel{\sim }{I}}_L^{\ast }={(2\pi )}^{m/2}{\mid {\mathbf{\Sigma }}_n\mid }^{1/2}{L}_n({\widehat{\mathit{\beta }}}_n)\pi ({\widehat{\mathit{\beta }}}_n)$. Then Ĩ^* = I(1 + O (n⁻¹)).

Proof

Let π^N(β) denote the pdf of N(β₀, λ Σ₀). Note that we can write

$$I=\int L_n(\mathit{\beta }){\pi }^N(\mathit{\beta })\text{d}\mathit{\beta }+\int L_n(\mathit{\beta })[\pi (\mathit{\beta })-{\pi }^N(\mathit{\beta })]\text{d}\mathit{\beta }.$$ (10)

Applying Theorem 2.1 to the first integral at the right-hand side of (10) and applying the standard-form Laplace approximation to the second integral yields (9) immediately.

One can treat Ĩ^* as an improved Laplace approximation to I under the condition that π (β) can be approximated by π^N(β), which is often satisfied when the prior is constructed from the likelihood or posterior of β based on historical or imaginary data with valid asymptotic normality. This is because in (9), ${\stackrel{\sim }{I}}_L^{\ast }$ is indeed the standard-form Laplace approximation to I; the remaining term Ĩ − Ĩ_L provides a correction factor, using the difference between the Laplace’s method and Theorem 2.1 based on the normality of π^N(β). This correction is useful when λ is small or when the prior sample size n₀ (i.e., the size of historical data) is not significantly smaller than n. Under this case, the standard-form Laplace approximation may not work well as L_n does not dominate π; Ĩ^* can achieve better performance because π − π^N is dominated by L_n when π is well approximated by π^N.

Like Ĩ for normal priors, an advantage of Ĩ* over a Laplace approximation to I is its nice limiting property. For example, when λ approaches 0, π (β) reduces to a point mass at its mode β₀ so that lim_λ→0 I = L_n(β₀); in this case, the Laplace approximation to the second integral in (10) is zero because π (β) = π^N(β). This leads to Ĩ^* = Ĩ and the equality lim_n→+∞ lim_λ→0 Ĩ^* = lim_λ→0 I follows directly from (8) whenever β̂_n → β₀. We also note that if β̂_n is within a small neighborhood of β₀, then ${\stackrel{\sim }{I}}_L^{\ast }\approx {\stackrel{\sim }{I}}_L$. This occurs sometimes in practice, for example, when the information contained in the current data agrees well with that in the historical data where the prior of β is from. In this case, I can be approximated by Ĩ only.

3 Application to Bayesian Inference in GLMs

3.1 Background

Suppose $\mathbf{Y}={(y_i)}_{i=1}^n$ are independent observations from an exponential family distribution

$$p(\mathbf{Y}\mid 𝛉,\phi )=exp\left\{\frac{{𝛉}^T\mathbf{WY}-{\mathbf{b}}^T(𝛉)\mathbf{WJ}}{\phi }+{\mathbf{c}}^T(\mathbf{Y},\phi )\mathbf{J}\right\},$$ (11)

indexed by unknown canonical parameters $𝛉={({\theta }_i)}_{i=1}^n$ and a dispersion parameter φ. The functions $\mathbf{b}(𝛉)={(b({\theta }_i))}_{i=1}^n$ and $\mathbf{c}(\mathbf{Y},\phi )={(c(y_i,\phi ))}_{i=1}^n$, assumed to be known, jointly determine the type of the distribution. The n × n matrix W is diagonal with its ith diagonal element being w_i, a known weight for the ith observation. And J is the n × 1 vector of all 1’s.

In the GLM setup θ may depend on p observed covariates X₁,…, X_p. Let γ = 1,…, 2^P index all subsets of the covariates, q_γ be the size of the γth subset, and X_γ be a n × (q_γ + 1) covariate matrix with 1’s in the first column and the γth subset of X_j’s in the remaining columns. Further, denote the entire data by = (Y, X, W), and the subset data for model γ by = (Y, X_γ, W). Under model γ, g(E(Y)) = X_γ/β_γ, where g is a known link function that by definition is monotonic and differentiable, and (β_γ is a(q_γ + 1)×1 vector of regression coefficients. Thus, the likelihood function of model γ is given by

$$L({\mathit{\beta }}_{\gamma },\phi ;{\mathcal{D}}_{\gamma })=exp\left\{\frac{{𝛉}^T({\mathbf{X}}_{\gamma }{\mathit{\beta }}_{\gamma })\mathbf{WY}-{\mathbf{b}}^T(𝛉({\mathbf{X}}_{\gamma }{\mathit{\beta }}_{\gamma }))\mathbf{WJ}}{\phi }+{\mathbf{c}}^T(\mathbf{Y},\phi )\mathbf{J}\right\}.$$ (12)

Here we denote θ(X_γβ_γ) explicitly for θ because θ = b′⁻¹ ◦ g⁻¹ (X_γβ_γ) under model γ, where ◦ denotes function composition.

Bayesian inferences of GLMs, when model uncertainty exists, often require the calculation of the model posterior, which reply heavily on the evaluation of the predictive density:

$$p(\mathbf{Y}\mid \gamma ,\lambda )=\int L({\mathit{\beta }}_{\gamma },\phi ;{\mathcal{D}}_{\gamma })\pi ({\mathit{\beta }}_{\gamma }\mid \gamma ,\lambda )\text{d}{\mathit{\beta }}_{\gamma }.$$ (13)

In (13), π(β_γ|γ, λ) is the prior on β_γ, where λ is a hyperparameter. Note that the dispersion parameter φ is assumed to be known throughout this paper. This indeed occurs in Poisson, Binomial and Negative Binomial GLMs, in which φ is 1. For other members of the exponential family, φ is usually unknown and might be replaced by an estimate (McCullagh and Nelder 1989). Alternatively one can assess a prior distribution on φ so that it can be integrated out from the model posterior (Raftery 1996 and references therein). In either case, it will not affect the evaluation of the predictive density.

We consider three classes of informative priors on β_γ in the literature, namely the normal, conjugate and power prior denoted by π^N, π^C and π^P, respectively. Let λ^N, λ^C and λ^P denote the hyperparameters introduced by these priors. The normal prior (Dellaportas and Smith 1993, Meyer and Laud 2002) is

$${\pi }^N({\mathit{\beta }}_{\gamma }\mid \gamma ,{\lambda }^N)\sim \mathbf{N}({\mathbf{m}}_{\gamma },{\lambda }^N\phi {\mathbf{U}}_{\gamma })\text{for}{\lambda }^N>0,$$ (14)

where m_γ is the prior mean and U_γ is a multiple of the prior covariance matrix of β_γ. The conjugate prior (Diaconis and Ylvisaker 1979, Meyer and Laud 2002, Chen et al. 2008) can be regarded as the likelihood of parameters (β_γ, λ^C φ) with data ${\mathcal{D}}_{\gamma }^C$:

$${\pi }^C({\mathit{\beta }}_{\gamma }\mid \gamma ,{\lambda }^C)\propto L({\mathit{\beta }}_{\gamma },{\lambda }^C\phi ;{\mathcal{D}}_{\gamma }^C)\text{for}{\lambda }^C>0,$$ (15)

where ${\mathcal{D}}_{\gamma }^C=({\mathit{\mu }}_0,{\mathbf{X}}_{\gamma },\mathbf{W})$ and μ₀ is the prior guess for Y. The power prior (Zellner (1988), Chen et al. 2000) is based on historical data 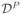= (Y₀, X₀, W₀) containing the same response and covariates as the current study:

$${\pi }^P({\mathit{\beta }}_{\gamma }\mid \gamma ,{\lambda }^P)\propto L^{1/{\lambda }^P}({\mathit{\beta }}_{\gamma },\phi ;{\mathcal{D}}_{\gamma }^P)\propto L({\mathit{\beta }}_{\gamma },{\lambda }^P\phi ;{\mathcal{D}}_{\gamma }^P,)\text{for}{\lambda }^P>0.$$ (16)

The three classes of priors are closely related via their large sample properties. The conjugate prior π^C is asymptotically normal as n → ∞:

$${\pi }^C({\mathit{\beta }}_{\gamma }\mid \gamma ,{\lambda }^C)\to \mathbf{N}({\widehat{\mathit{\beta }}}_{0\gamma }^C,{\lambda }^C\phi {\widehat{\mathbf{V}}}_{0\gamma }^C)$$ (17)

where ${\widehat{\mathit{\beta }}}_{0\gamma }^C$ is the MLE of β_γ using μ₀ rather than Y as the response vector; and ${\widehat{\mathbf{V}}}_{0\gamma }^C$ is minus the inverse of $\mathbf{H}({\mathit{\beta }}_{\gamma };{\mathcal{D}}_{\gamma }^C)$, the Hessian matrix of $L({\mathit{\beta }}_{\gamma },1;{\mathcal{D}}_{\gamma }^C)$ evaluated at ${\widehat{\mathit{\beta }}}_{0\gamma }^C$. This result can be obtained from Theorem 2.1 in Chen (1985) under some mild normality conditions. Similarly, the power prior π^P is asymptotically normal as the historical sample size n₀ → ∞:

$${\pi }^P({\mathit{\beta }}_{\gamma }\mid \gamma ,{\lambda }^P)\to \mathbf{N}({\widehat{\mathit{\beta }}}_{0\gamma }^P,{\lambda }^P\phi {\widehat{\mathbf{V}}}_{0\gamma }^P)$$ (18)

where ${\widehat{\mathit{\beta }}}_{0\gamma }^P$ is the MLE of β_γ based on the historical data ${\mathcal{D}}_{\gamma }^P$, and ${\widehat{\mathbf{V}}}_{0\gamma }^P$ is minus the inverse of $\mathbf{H}({\mathit{\beta }}_{\gamma };{\mathcal{D}}_{\gamma }^P)$, the Hessian matrix of $L({\mathit{\beta }}_{\gamma },1;{\mathcal{D}}_{\gamma }^P)$ evaluated at ${\widehat{\mathit{\beta }}}_{0\gamma }^P$.

As revealed by (14), (17) and (18), λ^N, λ^C and λ^P essentially play the same important role, each as a multiplier to the prior covariance matrix, weighing the impact of the prior information relative to the current data. Thus, our proposed methods can provide a unified way to compute the predictive densities (13) under the three classes of priors.

3.2 Approximate Predictive Densities

In what follows we will use λ to denote any of λ^N, λ^C and λ^P.

A direct application of Theorem 2.1 yields an approximation for p(Y|γ, λ) based on the normal prior (14), namely

$$\stackrel{\sim }{p}(\mathbf{Y}\mid \gamma ,\lambda )=L({\widehat{\mathit{\beta }}}_{\gamma },\phi ;{\mathcal{D}}_{\gamma }){\mid \lambda {\mathbf{U}}_{\gamma }{\widehat{\mathbf{V}}}_{\gamma }^{-1}+\mathbf{I}\mid }^{-\frac{1}{2}}exp\left\{-\frac{{({\widehat{\mathit{\beta }}}_{\gamma }-{\mathbf{m}}_{\gamma })}^T{(\lambda {\mathbf{U}}_{\gamma }+{\widehat{\mathbf{V}}}_{\gamma })}^{-1}({\widehat{\mathit{\beta }}}_{\gamma }-{\mathbf{m}}_{\gamma })}{2\phi }\right\}$$ (19)

where β̂_γ is the MLE of β_γ using the current data , and V̂_γ = −H⁻¹(β̂_γ; ). When Y is normally distributed so that the model is the familiar linear model, this approximation is exact, i.e. p̃(Y|γ, λ) = p(Y|γ, λ). This makes the results for linear models consistent with those for GLMs, as expected under the same Bayesian framework. However, it is not true if using the standard Laplace method or Raftery’s method. Another attractive feature of (19) is that, as discussed in Section 2.2, if U_γ is set to V̂_γ, it can provide great analytical tractability in a Fully Bayes approach that entails integrating λ out. As shown by Wang and George (2007), in the context of model selection, approximation (19) leads to selection criteria that have computational simplicity and adaptive performance.

Corollary 2.1 can be employed to approximate p(Y|γ, λ) in (13) with the conjugate and the power prior of β_γ. For notation simplicity, denote 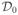the prior data, which is for the conjugate prior and is 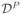for the power prior; denote β̂_0γ the MLE of β_γ based on , the prior data for model γ; denote V̂_0γ minus the inverse of H(β_γ; ) evaluated at β̂_0γ. First note that the normalizing constant ∫ L(β_γ, λφ; )dβ_γ in π(β_γ|γ, λ) varies from model to model, and thus cannot be ignored when model uncertainty is under consideration. We calculate the constant from the Laplace method, namely

$$\int L({\mathit{\beta }}_{\gamma },\lambda \phi ;{\mathcal{D}}_{0\gamma })\text{d}{\mathit{\beta }}_{\gamma }\approx {(2\pi )}^{\frac{q_{\gamma }+1}{2}}{\left|\lambda \phi {\widehat{\mathbf{V}}}_{0\gamma }\right|}^{\frac{1}{2}}·L({\widehat{\mathit{\beta }}}_{0\gamma },\lambda \phi ;{\mathcal{D}}_{0\gamma }).$$ (20)

Then Corollary 2.1 yields

$$\stackrel{\sim }{p}(\mathbf{Y}\mid \gamma ,\lambda )=L({\widehat{\mathit{\beta }}}_{\gamma },\phi ;{\mathcal{D}}_{\gamma })·\{{\left|\lambda {\widehat{\mathbf{V}}}_{0\gamma }{\widehat{\mathbf{V}}}_{\gamma }^{-1}+\mathbf{I}\right|}^{-\frac{1}{2}}exp\left\{-\frac{{({\widehat{\mathit{\beta }}}_{\gamma }-{\widehat{\mathit{\beta }}}_{0\gamma })}^T{(\lambda {\widehat{\mathbf{V}}}_{0\gamma }+{\widehat{\mathbf{V}}}_{\gamma })}^{-1}({\widehat{\mathit{\beta }}}_{\gamma }-{\widehat{\mathit{\beta }}}_{0\gamma })}{2\phi }\right\}+{\left|\lambda {\widehat{\mathbf{V}}}_{0\gamma }{\widehat{\mathbf{V}}}_{\gamma }^{-1}\right|}^{-\frac{1}{2}}\left[\frac{L({\widehat{\mathit{\beta }}}_{\gamma },\lambda \phi ;{\mathcal{D}}_{0\gamma })}{L({\widehat{\mathit{\beta }}}_{0\gamma },\lambda \phi ;{\mathcal{D}}_{0\gamma })}-exp\left\{-\frac{{({\widehat{\mathit{\beta }}}_{\gamma }-{\widehat{\mathit{\beta }}}_{0\gamma })}^T{\widehat{\mathbf{V}}}_{0\gamma }^{-1}({\widehat{\mathit{\beta }}}_{\gamma }-{\widehat{\mathit{\beta }}}_{0\gamma })}{2\lambda \phi }\right\}\right]\}$$ (21)

where β̂_γ and V̂_γ are defined in (19). Due to the asymptotic normality in (17) and (18), (21) is in general better than the standard-form Laplace approximation, as discussed in Section 2.3. When β̂_γ is close to β̂_0γ, the part following the “+” sign in the second line of (21) is about zero, so p(Y|γ, λ) can be approximated only by the first term, which simplifies the calculation in some degree.

One can easily calculate (19) and (21) using statistical packages for GLMs, in which MLEs and observed Fisher information matrices are often standard outputs. For example, V̂_γ can be calculated from the estimated covariance matrix divided by φ̂_γ that is fitted to estimate φ, based on the current data ; and V̂_0γ can be calculated in the same way but based on the prior data for the conjugate or power prior of β_γ.

4 Examples

4.1 Evaluation in a Simple Case

We first study the performance of the method proposed in Theorem 2.1 on a very simple Poisson linear model with a canonical link function. Two datasets, with n = 10 and 100 respectively, are simulated by generating (x_1i, x_2i) from N(0,I) and y_i from independent Poisson with mean μ_i, where log μ_i = 1 + x_1i, −0.5 x_2i for i = 1,…, n. Note β = (1,1, −0.5)^T, and φ = 1, b(θ_i) = μ_i = exp(θ_i) and c(y_i, φ) =− log(y_i!) in (12). For comparison, we adopt various methods to calculate the marginal likelihoods of the simulated data, p(Y|λ) = ∫ p (Y|β) π (β| λ)dβ, based on normal priors on β in the form of N(m_γ, λU_γ). For each dataset, we consider eight different λ values and two prior means, m_γ = (β¯₀, 0, 0)^T and m_γ = (1, 1, −0.5)^T, where β¯₀ is chosen to be the MLE of β₀ under the null model as in Chipman et al. (2003). Further, to see the impact of prior covariances, we consider two prior covariance matrices, U_γ = I and U_γ = V̂ _γ. The methods include Prop. (the method proposed in Theorem 2.1), SL (standard-form Laplace), FEL (fully-exponential Laplace), R (fully-exponential Laplace + Newton, Raftery 1996), and IS (Importance Sampling). The formulas for these methods are available in Appendix B. Since the true value of the integral is unknown, we keep generating blocks of 20, 000 sample units until the second decimal place of the log marginal likelihood value, estimated by IS cumulatively using all the generated blocks, stabilizes for 5 consecutive blocks. Since the absolute value of the log marginal likelihood varies from about 15 to 470, the variation in the third digit has a negligible impact on the relative error (i.e., the estimated value minus the true value, then divided by the true value). So the results from IS can be treated as surrogates of true values. Here we report the relative error in the log scale, |(log Ĩ − log I)/log I|, instead of the absolute error |Ĩ − I|. Thus, as n gets large, the relative error in log is not expected to decrease.

The absolute values of relative errors compared against estimates of IS are reported in Table 2. The proposed method is much better than SL and R for small λ. When λ is large, all methods work equally well. When λ is small, SL and R are sensitive to the prior variances U_γ as their relative errors for U_γ = I are much smaller than those for U_γ = V̂ _γ: by contrast, the proposed method appears to be robust to the choice of U_γ. Furthermore, all methods except for FEL are sensitive to m since their relative errors for m = β are smaller than m = (β¯₀, 0, 0)^T, but the proposed one appears to be less sensitive than the other two.

Table 2.

Absolute Values of Relative Errors in Approximate Log Marginal Likelihoods of Poisson Model

λ	n = 10, mγ = (β¯0, 0, 0), Uγ = I				n = 10, mγ = (β¯0, 0, 0), Uγ = V̂γ
	SL	R	Prop.	FEL	SL	R	Prop.	FEL
1.0E-10	3.E+08	3.E+08	0.031	0.000	4.E+09	4.E+09	0.031	0.000
0.0001	297.593	297.731	0.030	0.000	3524.682	3524.964	0.031	0.000
0.001	29.328	29.335	0.031	0.001	351.894	352.032	0.030	0.000
0.01	2.615	2.572	0.034	0.000	34.782	34.780	0.028	0.000
0.1	0.110	0.119	0.017	0.000	3.178	3.058	0.015	0.000
1	0.009	0.003	0.003	0.001	0.157	0.107	0.002	0.000
10	0.000	0.001	0.001	0.001	0.004	0.001	0.000	0.001
100	0.001	0.001	0.001	0.001	0.000	0.001	0.001	0.001
λ	n = 10, mγ = (1, 1, −0.5), Uγ = I				n = 10, mγ = (1, 1, −0.5), Uγ = V̂γ
	SL	R	Prop.	FEL	SL	R	Prop.	FEL
1.0E-10	1.E+07	1.E+07	0.001	0.000	1.E+08	1.E+08	0.001	0.000
0.0001	13.503	14.180	0.001	0.000	104.586	105.494	0.001	0.000
0.001	0.951	1.398	0.000	0.000	9.851	10.530	0.001	0.000
0.01	0.108	0.123	0.001	0.000	0.584	1.034	0.001	0.000
0.1	0.066	0.006	0.002	0.000	0.143	0.088	0.002	0.000
1	0.010	0.000	0.000	0.000	0.063	0.005	0.003	0.000
10	0.000	0.001	0.001	0.001	0.008	0.000	0.000	0.001
100	0.001	0.001	0.001	0.001	0.000	0.001	0.001	0.001
λ	n = 100, mγ = (β¯0, 0, 0), Uγ = I				n = 100, mγ = (β¯0, 0, 0), Uγ = V̂γ
	SL	R	Prop.	FEL	SL	R	Prop.	FEL
1.0E-10	2.E+07	2.E+07	0.077	0.000	6.E+09	6.E+09	0.077	0.000
0.0001	15.703	15.083	0.046	0.004	6309.329	6308.576	0.077	0.000
0.001	1.262	1.231	0.108	0.089	630.802	630.042	0.077	0.000
0.01	0.078	0.047	0.012	0.007	62.937	62.175	0.078	0.000
0.1	0.001	0.000	0.000	0.000	6.149	5.444	0.080	0.002
1	0.000	0.000	0.000	0.000	0.324	0.255	0.061	0.088
10	0.000	0.000	0.000	0.000	0.011	0.000	0.001	0.000
100	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
λ	n = 100, mγ = (1, 1, −0.5), Uγ = I				n = 100, mγ = (1, 1, −0.5), Uγ = V̂γ
	SL	R	Prop.	FEL	SL	R	Prop.	FEL
1.0E-10	6.E+05	6.E+05	0.001	0.000	1.E+08	1.E+08	0.001	0.000
0.0001	0.602	0.613	0.001	0.000	124.862	124.918	0.001	0.000
0.001	0.045	0.045	0.000	0.000	12.430	12.469	0.001	0.000
0.01	0.001	0.001	0.000	0.000	1.202	1.224	0.001	0.000
0.1	0.000	0.000	0.000	0.000	0.096	0.103	0.000	0.000
1	0.000	0.000	0.000	0.000	0.001	0.003	0.000	0.000
10	0.000	0.000	0.000	0.000	0.001	0.000	0.000	0.000
100	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000

It is helpful to discuss the methods from a computational perspective. SL, R and the proposed method only require the MLE of β, the estimated covariance matrix and likelihood, so they are easy to program using standard statistical software. FEL requires more programming efforts because one needs to calculate the posterior mode of β via an optimization algorithm and the corresponding posterior covariance matrix involving detailed formulas. IS, as a sampling-based method, is easy to code but requires fine tune for fast convergence. Turning to the CPU time, based on calculations for the dataset of size 100 and a fixed λ on a workstation with a 1.8 GHz Xeon processor and 1 GB of RAM, it takes 33 ms for SL, R and the proposed method, 68 ms for FEL, and for IS to get an estimate with an error within ±0.05, the time varies from 270 ms to 51 seconds for different λ. Overall, it appears that the proposed method is promising because of greater accuracy, less human efforts and faster computing speed.

4.2 Intensive Care Unit Data

We provide an example that incorporates our approximation methods in an application of Bayesian variable selection. We consider a dataset in Hosmer and Lemeshow (1989) with 200 subjects from a study on survival of patients following admission to an adult intensive care unit (ICU). The response STA is the vital status of a patient at the time of hospital discharge (0=Lived, 1=Died). There are 19 predictor variables in the dataset: (1) Age; (2) Sex; (3) Race (White/Black/Other); (4) Service at ICU admission (SER, Medical/Surgical); (5) Cancer Part of Present Problem (CAN, No/Yes); (6) History of Chronic Renal Failure (CRN, No/Yes); (7) Infection Probable at ICU Admission (INF, No/Yes); (8) CPR prior to ICU Admission (CPR, No/Yes); (9) Systolic Blood Pressure at ICU Admission (SYS); (10) Heart Rate at ICU Admission (HRA); (11) Previous Admission to an ICU within 6 Months (PRE, No/Yes); (12) Type of Admission (TYP, Elective/Emergency); (13) Long Bone, Multiple, Neck, Single Area, or Hip Fracture (FRA, No/Yes); (14) PO2 from Initial Blood Gases (PO2, > 60/≤ 60); (15) PH from Initial Blood Gases (PH, ≥ 7.25/< 7.25); (16) PCO2 from Initial Blood Gases (PCO, ≤ 45/> 45); (17) Bicarbonate from Initial Blood Gases (BIC, ≥ 18/< 18); (18) Creatinine from Initial Blood Gases (CRE, ≤ 60/> 60); (19) Level of Consciousness at ICU Admission (LOC, No Coma/Deep Stupor/Coma). The aim is to select models with highest posterior probabilities out of 2¹⁹ or 524288 possible logistic regression models to predict the probability of survival and study the risk factors associated with ICU mortality. Note for logistic regression, φ = 1, b(θ_i) = log(1 + e^θi) and c(y_i, φ) = 0 in (12).

Here, a fully Bayes method (FB) is used for illustration. Often, when a single value of λ is difficult to specify, like in this case, there is a general agreement that fully Bayes methods are well suited in summarizing posterior uncertainties, which entail integrating λ out:

$$p(\gamma \mid \mathbf{Y})\propto \pi (\gamma )\int p(\mathbf{Y}\mid \gamma ,\lambda )\pi (\lambda )\text{d}\lambda ,$$ (22)

where π(γ) and π(λ) denote the prior on γ and λ, respectively. Except for certain restricted examples, the resulting model posterior p(γ|Y) (up to a normalizing constant) is analytically intractable. Our approximation methods would allow MCMC algorithms to only sample over a two-dimension space of γ and λ. We consider conjugate priors (15) on regression coefficients and an inverse Gamma hyperprior IG(a, b) on the hyperparameter λ. For illustrative purposes, the prior mean μ₀ was obtained from a prior prediction using the logistic regression model reported in Lemeshow et al. (1988),

$$log\frac{{\mu }_{0i}}{1-{\mu }_{0i}}=-1.37+2.44LO{C}_i+1.81TY{P}_i+1.49CA{N}_i+0.974CP{R}_i+0.965I{NF}_i+0.0368AG{E}_i-0.0606SY{S}_i+0.000175SY{S}_i^2.$$ (23)

We explored four sets of (a, b) values with prior means of λ at 2, 5, 10, and 50, respectively. We found that the posterior of λ was sensitive to the choice of (a, b). Finally we chose (a, b) = (2.25, 62.5) because this hyperprior has a heavier right tail than the others, indicating the prior guess (23) is not to have much impact compared to the data. For prior model probabilities π(γ), to reflect no real prior information, we assigned equal probability to each possible model. To efficiently search high posterior models, the evolutionary Monte Carlo algorithm (Liang and Wong 2000) was applied in this example. Four chains were simulated in parallel with a temperature ladder {1,2,3,4} and each running 50,000 iterations. Within each iteration, for any proposed γ and λ, when calculating the transition and exchange probabilities, p(Y|λ, γ)π(λ|a, b) was approximated by p̃(Y|λ, γ)π(λ|a, b) using our methods, which greatly simplified the MCMC because there was no need to sample from the space of regression coefficients β_γ.

Table 3 reports the top 50 models from the MCMC search. The posterior probability of model γ was estimated from the frequency of γ in the chain divided by 40,000 (the first 10,000 iterations were discarded for the burn-in process). For comparison, we also give AIC and BIC values and ranks for each of the models: AIC_γ = log L(β̂_γ; ) − q_γ and BIC_γ = log L(β̂_γ; ) − q_γ log n/2. We can see from Table 3 that the “best” model selected by the FB procedure contains 6 covariates: RACE, SER, CAN, TYP, FRA, and LOC, denoted γ_FB; the “best” model given by AIC contains 10 covariates: AGE, RACE, SER, CAN, PRE, TYP, FRA, PH, PCO and LOC, denoted γ_A; and the “best” model given by BIC contains only three covariates: CAN, TYP, and LOC, denoted γ_B. It is well known that AIC tends to favor large models while BIC tends to favor small models, so it is interesting to see that γ_B ⊂ γ_FB ⊂ γ_A here. Also, γ_FB is a model that ranks high in both AIC and BIC (i.e., the model with a small rank sum). Another interesting feature for this dataset is, none of the top 50 models selected by AIC agrees with the top 50 models selected by BIC; for example, γ_A ranks 8098 in BIC, γ_B ranks 2588 in AIC, but both of them are in the top 50 list of the FB procedure.

Table 3.

Top 50 Models From MCMC for the ICU Data. Note that the estimated posterior probabilities π̂(γ|Y) were multiplied by 1,000.

Model	No. Variables	Est. Posterior	AIC (rank)	BIC (rank)
3,4,5,12,13,19	6	4.70	−51.20 (11)	−63.75 (61)
2,3,4,5,12,13,19	7	4.67	−51.72 (44)	−65.66 (593)
3,4,5,12,19	5	3.95	−52.28 (173)	−63.43 (41)
3,4,5,11,12,13,19	7	3.87	−51.12 (8)	−65.06 (312)
2,3,4,5,11,12,13,19	8	3.15	−51.74 (45)	−67.07 (2326)
3,4,5,6,12,13,19	7	2.70	−51.83 (58)	−65.76 (657)
1,3,4,5,8,11,12,13,16,19	10	2.55	−51.64 (33)	−69.76 (16867)
3,4,5,6,11,12,13,15,16,19	10	2.50	−51.79 (51)	−69.91 (18400)
1,3,4,5,11,12,13,19	8	2.45	−51.28 (12)	−66.61 (1501)
1,3,4,5,12,13,16,19	8	2.35	−51.14 (9)	−66.47 (1318)
2,3,4,5,11,12,13,18,19	9	2.20	−52.41 (228)	−69.13 (11251)
3,5,12,19	4	2.15	−53.44 (1435)	−63.19 (30)
3,4,5,12,13,15,19	7	2.07	−51.96 (87)	−65.89 (752)
3,4,5,6,10,12,13,19	8	2.00	−52.78 (470)	−68.11 (5364)
3,4,5,8,11,12,13,16,19	9	2.00	−52.00 (98)	−68.72 (8428)
3,4,5,12,13,16,19	7	1.97	−51.60 (31)	−65.54 (530)
2,3,4,5,6,12,19	7	1.87	−53.16 (916)	−67.10 (2382)
3,4,5,8,11,12,19	7	1.80	−52.87 (562)	−66.81 (1786)
3,4,5,11,12,13,14,19	8	1.80	−51.91 (78)	−67.25 (2696)
5,8,12,15,16,19	6	1.77	−53.42 (1399)	−64.57 (174)
3,4,5,11,12,19	6	1.77	−52.57 (301)	−65.11 (325)
2,3,4,5,6,8,11,12,13,19	10	1.75	−52.99 (701)	−71.10 (36334)
3,4,5,10,11,12,13,19	8	1.72	−52.10 (115)	−67.43 (3114)
5,12,19	3	1.67	−53.81 (2588)	−60.78 (1)
3,5,10,12,19	5	1.67	−54.17 (4250)	−65.32 (413)
1,2,3,4,5,12,13,15,16,19	10	1.65	−51.39 (19)	−69.51 (14521)
1,3,4,5,9,11,12,13,16,18,19	11	1.65	−52.79 (478)	−72.30 (64620)
3,4,5,12,15,19	6	1.57	−52.86 (556)	−65.41 (450)
1,2,3,4,5,12,13,16,19	9	1.57	−51.69 (37)	−68.41 (6714)
2,3,4,5,11,12,13,15,16,19	10	1.57	−51.38 (17)	−69.50 (14404)
3,4,5,7,8,10,12,13,19	9	1.55	−53.56 (1730)	−70.28 (23084)
1,3,4,5,12,13,15,16,19	9	1.50	−51.08 (7)	−67.81 (4238)
3,4,5,11,12,13,16,19	8	1.47	−51.30 (13)	−66.63 (1526)
3,4,5,8,12,19	6	1.45	−52.78 (468)	−65.32 (415)
3,4,5,8,12,13,19	7	1.42	−51.96 (89)	−65.90 (761)
3,4,5,11,12,15,19	7	1.32	−53.03 (742)	−66.96 (2065)
3,4,5,9,11,12,19	7	1.30	−52.97 (679)	−66.90 (1948)
1,3,4,5,11,12,13,15,16,19	10	1.30	−50.55 (1)	−68.67 (8098)
2,3,4,5,12,13,18,19	8	1.27	−52.51 (265)	−67.84 (4350)
2,3,4,5,12,19	6	1.25	−52.86 (549)	−65.40 (446)
5,12,15,19	4	1.22	−53.84 (2723)	−62.20 (7)
3,4,5,7,12,13,19	7	1.22	−51.70 (40)	−65.63 (579)
1,3,4,5,11,12,13,17,19	9	1.22	−52.27 (168)	−68.99 (10156)
3,4,5,9,11,12,13,15,16,19	10	1.22	−51.57 (28)	−69.69 (16167)
4,5,12,19	4	1.20	−53.02 (727)	−61.38 (2)
3,4,5,7,11,12,13,19	8	1.20	−51.66 (35)	−66.99 (2126)
3,4,5,8,11,12,13,16,17,19	10	1.20	−52.96 (669)	−71.08 (35795)
1,4,5,12,19	5	1.17	−53.11 (837)	−62.87 (14)
3,5,8,12,19	5	1.17	−53.47 (1519)	−64.62 (188)
3,4,5,6,9,12,19	7	1.17	−52.86 (554)	−66.80 (1776)

It is worth noting that the “best” model γ_FB represents only 0.47% of the total posterior probability, indicating a fair amount of model uncertainty in the ICU data. This reveals that in this example, model averaging may be more appropriate than simply selecting a “best” model. More importantly, our fully Bayes method gives the top 50 models covering more than 95% posterior probability, so that model averaging can be done over these 50 models (not all the 524,288 possible logistic regression models), with weights already provided.

In conclusion, our approximation methods, when applied to the fully Bayes variable selection, seem to work reasonably well.

5 Discussion

In this paper, we have proposed new methods to approximate predictive distributions that are easy to implement and computationally efficient, and discussed their performance both in theory and through simulation. In simulation studies we have shown that the relative error associated with the proposed methods is clearly superior to the Laplace-based methods when λ is small, say λ < 1. Whether the better performance of Ĩ at small λ has practical importance is worth discussing.

As we know, a large λ might be often used in practice to allow for a diffuse and vague prior distribution on (β). However, there exist situations when a wide range of λ, including small values, is of interest, like in a sensitivity analysis about λ or a Fully Bayes approach that entails choosing a prior on λ over the entire support (0,+∞). Using our proposed methods can help to avoid mathematical pitfalls that may be extremely hard to detect for practitioners, with little cost, as opposed to other existing analytical approximation methods.

Further, small λ can be chosen through empirical Bayes methods (George and Foster 2000) in data analysis. This can be seen from the formula given in George and Foster (2000) to estimate λ from data (in their denotation c is equivalent to λ):

$${\widehat{\lambda }}_{\gamma }={\left(\frac{{SS}_{\gamma }}{{\sigma }^2{q}_{\gamma }}-1\right)}_{+},$$ (24)

where (·)₊ is the positive part of the function, γ represents the γth regression model in the model space, q_γ is the number of variables in model γ; and SS_γ is the regression sum of squares of model γ, measuring the part of the variability of Y_is which can be explained by the regression line. Clearly, if the signal-to-noise ratio, measured by SS_γ/(σ²q_γ), is too low (say close to 1, or even small than 1), then λ would be chosen to be close to 0 or even 0 based on (24).

Finally, we would like to mention that in Bayesian applications of GLM, when model uncertainty can not be ignored, MCMC are commonly used to sample from a joint space of models and parameters. For large-sized problems, the computation of high-dimensional integrations via MCMC can be intensive or slow in convergence sometimes. As mentioned in Han and Carlin (2001), “…the ability of joint model and parameter search methods to sample effectively over such large spaces is very much in doubt” and they often require substantial time and effort (both human and computer). Thus, it would be useful for practitioners to try our proposed methods when MCMC-based algorithms do not work well.

A Proof of Theorem 2.1

This proof is similar in part to that of Theorem 1 in Kass et al. (1990). Without loss of generality, we consider the case m = 1 for simplicity. The higher-dimensional case involves straightforward modifications. Let h_n(β) ≡ −l_n(β)/n so that the integrand L_n(β)π(β) of (1) can be written as exp[−nh_n(β)]π(β), and let u ≡ n^1/2(β − β̂_n) so that for a fixed u, (β − β̂_n)^k is of O(n^−k/2). Now expanding nh_n(β) about β̂_n and e^−x about zero to the terms of order smaller than O(1) yields

$$exp[-{nh}_n(\mathit{\beta })]\pi (\mathit{\beta })=exp\left[-{nh}_n({\widehat{\mathit{\beta }}}_n)-\frac{1}{2}{h}_n^{″}({\widehat{\mathit{\beta }}}_n)u^2\right]·\left\{1-\frac{1}{6}{n}^{-1/2}{h}_n^{(3)}({\widehat{\mathit{\beta }}}_n)u^3+R_n(u)\right\}\pi (\mathit{\beta })$$

where R_n(u) is of order O(n⁻¹) uniformly on B_δ(β̂_n) defined in (3). Then

$${\int }_{B_{\delta }({\widehat{\mathit{\beta }}}_n)}exp[-{nh}_n(\mathit{\beta })]\pi (\mathit{\beta })\text{d}\mathit{\beta }=exp\left[-{nh}_n({\widehat{\mathit{\beta }}}_n)\right]·(E_1+E_2)$$

where

$$E_1={\int }_{B_{\delta }({\widehat{\mathit{\beta }}}_n)}exp\left[-\frac{1}{2}{h}_n^{″}({\widehat{\mathit{\beta }}}_n)u^2\right]\pi (\mathit{\beta })\text{d}\mathit{\beta }$$

and

$$E_2={\int }_{B_{\delta }({\widehat{\mathit{\beta }}}_n)}exp\left[-\frac{1}{2}{h}_n^{″}({\widehat{\mathit{\beta }}}_n)u^2\right]·\left\{-\frac{1}{6}{n}^{-1/2}{h}_n^{(3)}({\widehat{\mathit{\beta }}}_n)u^3+R_n(u)\right\}\pi (\mathit{\beta })\text{d}\mathit{\beta }.$$

Let’s look at E₁ first. Note by changing the variable from β to u, we have

$$E_1={\int }_{B_{\delta (n)}(0)}exp\left[-\frac{1}{2}{h}_n^{″}({\widehat{\mathit{\beta }}}_n)u^2\right]·\pi (n^{-1/2}u+{\widehat{\mathit{\beta }}}_n)·n^{-1/2}\text{d}u$$ (25)

where δ(n) = n^1/2 δ. Since the integration region B_δ(n)(0) is expanding at the rate O(n^1/2) as n → +∞, replacing this region by the whole real line incurs an error of exponentially decreasing order for the integral in (25), and yields (after some algebra)

$$E_1\approx exp\left[{nh}_n({\widehat{\mathit{\beta }}}_n)\right]·\stackrel{\sim }{I}$$ (26)

in which Ĩ is given in (2). For E₂, expanding π(β) about β̂_n and changing the variable from β to u, we have

$$E_2={\int }_{B_{\delta (n)}(0)}exp\left[-\frac{1}{2}{h}_n^{″}({\widehat{\mathit{\beta }}}_n)u^2\right]·\left\{-\frac{1}{6}{n}^{-1/2}{h}_n^{(3)}({\widehat{\mathit{\beta }}}_n)u^3+R_n(u)\right\}·\left\{\pi ({\widehat{\mathit{\beta }}}_n)+n^{-1/2}{\pi }^{\prime }({\widehat{\mathit{\beta }}}_n)u+S_n(u)\right\}{n}^{-1/2}\text{d}u$$ (27)

where S_n(u) is in the order O(n⁻¹) uniformly on B_δ(β̂_n). Using the same reasoning as for E₁, we replace B_δ(n)(0) by the real line in (27) and note that the third central moment of a normal distribution vanishes, so

$$E_2=O(n^{-1})$$ (28)

holds as long as the ith derivative of h_n(i ≤ 4) is uniformly bounded, which is satisfied automatically from the Laplace regularity of l_n. Combining (26), (28) and (3) yields Ĩ = I(1 + O(n⁻¹)), which completes the proof.

B Formulas For Calculations in Section 4.1

For a GLM described in (12), consider the marginal density of the data p(Y|γ, λ) based on a normal prior π(β_γ) in the form of N(m_γ, λφU_γ), λ > 0. Below are the formulas we derive for approximating p(Y|γ, λ) using the fully-exponential Laplace and the important sampling methods. The other methods involve trivial applications of formulas (2), (4) and (6).

1. Full-exponential Laplace

   $${\stackrel{\sim }{p}}_{LF}(\mathbf{Y}\mid \gamma ,\lambda )=L({\stackrel{\sim }{\mathit{\beta }}}_{\gamma },\phi ;{\mathcal{D}}_{\gamma })·{\left|\lambda {\mathbf{U}}_{\gamma }{\stackrel{\sim }{\mathbf{V}}}_{\gamma }^{-1}+\mathbf{I}\right|}^{-\frac{1}{2}}exp\left\{-\frac{{({\stackrel{\sim }{\mathit{\beta }}}_{\gamma }-{\mathbf{m}}_{\gamma })}^T{(\lambda {\mathbf{U}}_{\gamma })}^{-1}({\stackrel{\sim }{\mathit{\beta }}}_{\gamma }-{\mathbf{m}}_{\gamma })}{2\phi }\right\}$$
   where β̃_γ is the posterior mode of β_γ, ${\stackrel{\sim }{\mathbf{V}}}_{\gamma }={({\mathbf{X}}_{\gamma }^T{\mathbf{D}}_{\gamma }{\mathbf{X}}_{\gamma })}^{-1}$, D_γ is diagonal with its ith diagonal element equal to d_γi, and θ̃_γi = b′⁻¹ ◦ g⁻¹(X_γiβ̃_γ),

   $$d_{\gamma i}=\frac{1}{b^{″}({\stackrel{\sim }{\theta }}_{\gamma i}){[g^{\prime }(b^{\prime }({\stackrel{\sim }{\theta }}_{\gamma i}))]}^2}+[y_i-b^{\prime }({\stackrel{\sim }{\theta }}_{\gamma i})]\frac{{[b^{″}({\stackrel{\sim }{\theta }}_{\gamma i})]}^2{g}^{″}(b^{\prime }({\stackrel{\sim }{\theta }}_{\gamma i}))+b^{(3)}({\stackrel{\sim }{\theta }}_{\gamma i})g^{\prime }(b^{\prime }({\stackrel{\sim }{\theta }}_{\gamma i}))}{{[b^{″}({\stackrel{\sim }{\theta }}_{\gamma i})]}^3{[g^{\prime }(b^{\prime }({\stackrel{\sim }{\theta }}_{\gamma i}))]}^3}.$$
2. Importance Sampling:

   $${\stackrel{\sim }{p}}_{IS}(\mathbf{Y}\mid \gamma ,\lambda ,\phi )=\frac{1}{M}\underset{t=1}{\overset{M}{\Sigma }}\frac{p(\mathbf{Y}\mid \gamma ,{\mathit{\beta }}_{\gamma }^{(t)},\phi )\pi ({\mathit{\beta }}_{\gamma }^{(t)})}{h({\mathit{\beta }}_{\gamma }^{(t)})}$$

   where ${\mathit{\beta }}_{\gamma }^{(t)}$, t = 1, …, M, are independent samples, each with probability r generated from π(β_γ), i.e., N(m_γ, λφU_γ) and with probability 1 − r generated from N(β̂_γ, φV̂_γ); and h(β_γ) is the density of the mixture h(β_γ) = rπ (β_γ) + (1 − r) f(β_γ), where f(β_γ) is the pdf of N(β̂_γ, φV̂_γ). In our experiment, for λ = 1E − 20, we set r equal to 0.8; for λ = 0.001, we set r = 0.1 and for any larger λ, set r = 0.5. M is chosen to be large enough so that the estimate p̃_IS(Y|γ, λ, φ) stabilizes within a small region.