Electroosmotic pump performance is affected by concentration polarizations of both electrodes and pump

Abstract

Current methods of optimizing electroosmotic (EO) pump performance include reducing pore diameter and reducing ionic strength of the pumped electrolyte. However, these approaches each increase the fraction of total ionic current carried by diffuse electric double layer (EDL) counterions. When this fraction becomes significant, concentration polarization (CP) effects become important, and traditional EO pump models are no longer valid. We here report on the first simultaneous concentration field measurements, pH visualizations, flow rate, and voltage measurements on such systems. Together, these measurements elucidate key parameters affecting EO pump performance in the CP dominated regime. Concentration field visualizations show propagating CP enrichment and depletion fronts sourced by our pump substrate and traveling at order mm/min velocities through millimeter-scale channels connected serially to our pump. The observed propagation in millimeter-scale channels is not explained by current propagating CP models. Additionally, visualizations show that CP fronts are sourced by and propagate from the electrodes of our system, and then interact with the EO pump-generated CP zones. With pH visualizations, we directly detect that electrolyte properties vary sharply across the anode enrichment front interface. Our observations lead us to hypothesize possible mechanisms for the propagation of both pump- and electrode-sourced CP zones. Lastly, our experiments show the dynamics associated with the interaction of electrode and membrane CP fronts, and we describe the effect of these phenomena on EO pump flow rates and applied voltages under galvanostatic conditions.

1. Introduction

Electroosmotic (EO) micropumps require no moving parts, can be fabricated cheaply and compactly, and can deliver relatively high flow rates and pressures [1, 2]. EO pumps can also be used in applications requiring fairly low applied voltage (a few volts) and low applied power per volume flow rate [3]. A disadvantage of EO pumps, particularly in applications requiring high pump current density, is that electrolysis bubbles may eventually grow at a rate which interferes with pump performance [4, 5], and that long-term pumping can create electrochemically sourced pH gradients in the system [6]. EO pump systems often consist of a porous oxide structure, or frit, between two electrodes. The applied field exerts a Coulombic force on mobile counterions of electric double layers (EDL), and ion drag creates bulk fluid flow.

Recent work on EO pump optimizations have concluded that higher flow rate per power can often be achieved by: i) reducing frit pore size, and ii) reducing the ionic strength of the pumped electrolyte [7–9]. For example, Litster et al. [3], using a silica EO pump with 450 nm mean pore diameter and 1 mM ionic strength electrolyte, demonstrated the delivery of 10 μl/min and a few kPa pressure capacity with applied potential and power of 3 V and 75 μW, respectively. Each of the optimization strategies above increases the fraction of total ionic current carried by mobile EDL counterions (often referred to as surface conductivity), and thus increases the ratio of surface to bulk conductivity. This ratio is described by the Dukhin number [10], which for a binary electrolyte in a porous frit can be expressed as [11, 12],

$$Du=\frac{z_1{\upsilon }_1\frac{\mid s\mid }{l}}{{Fc}_o(z_1^2{\upsilon }_1+z_2^2{\upsilon }_2)}.$$ [1]

To express the Dukhin number in a simple manner, we assumed a spatially uniform surface charge density, s. The parameter l is a length scale representing the ratio of total electrolyte volume in the porous media to pore surface area [12], c_o is the pore centerline electrolyte concentration (for non-overlapped EDLs), υ is ionic mobility, z is ionic charge, and F is Faraday’s constant. Subscript 1 denotes the counter-ion and 2 the co-ion. Therefore, optimizing EO pumps by decreasing pore size (decreasing l), or decreasing electrolyte ionic strength (c_o), increases Dukhin number. If Dukhin number becomes of order unity or higher, concentration polarization (CP) effects become significant [11, 13]. In this regime, traditional models for EO pumps [8, 9], which ignore this phenomenon, no longer hold.

Applying an electric field to a frit with significant surface conductivity results in a higher flux of counterions than coions through the frit. For a negatively charged frit surface (typical of porous glass), this flux imbalance causes the formation of depletion and enrichment zones respectively at the anode and cathode sides of the frit [12, 14]. This effect is known as electrokinetic or ion concentration polarization (CP) [15, 16]. Mani et al. [11] and Zangle et al. [13] investigated CP in serial micro-nano-microchannel systems. They confirmed that, at nanochannel Dukhin numbers of roughly unity and above, CP can propagate in the form of shocks, featuring long-range growth of enrichment and depletion zones emanating from the nanochannel. However, few studies have focused on the effect of CP on EO pumps. Postler et al. [17] performed a numerical study of EO flow in a submicron channel, which showed non-linearity in EOF velocity with applied field. They attributed this non-linearity to surpassing the limiting current of the submicron channel. Strickland et al. [12] presented brief qualitative fluorescence visualizations which showed the formation of propagating CP fronts from a porous glass EO pump with roughly 500 nm diameter pores, while pumping 0.1 to 1 mM sodium borate buffer. Additionally, Litster et al. [3] observed distinct transients in EO pump flow rate when using a frit with submicron sized pores, which they hypothesized could be due to CP effects.

In this paper, we provide new quantitative experimental characterization of CP in EO pumps under galvanostatic conditions using simultaneous visualizations, flow rate and voltage measurements. We observe, at sufficiently high Du, a long-range propagation of enrichment and depletion fronts starting from the membrane through the connecting millimeter-scale channel (hereafter “millichannel”). Recently, Mani et al. [11] developed a theory explaining one mechanism for propagation of CP in systems involving micro and nano-scale channels. However, as we shall see, for our system their model is not applicable as our millichannel has negligible EDL current transport. Further, we show that fronts of perturbed concentration and pH are sourced by, and propagate from, the electrodes of our system. We show direct evidence of a sharp jump in electrolyte chemistry, in addition to a jump in electrolyte ionic strength, across the propagating anode enrichment front. We speculate as how this latter observation may explain the mechanism of millichannel CP propagation. Lastly, we report what is to our knowledge the first CP visualization combined with flow rate and voltage measurements. With these measurements, we elucidate key parameters affecting pump performance in the CP regime and show a scaling which collapses performance transients across all our experimental conditions.

2. Experimental setup

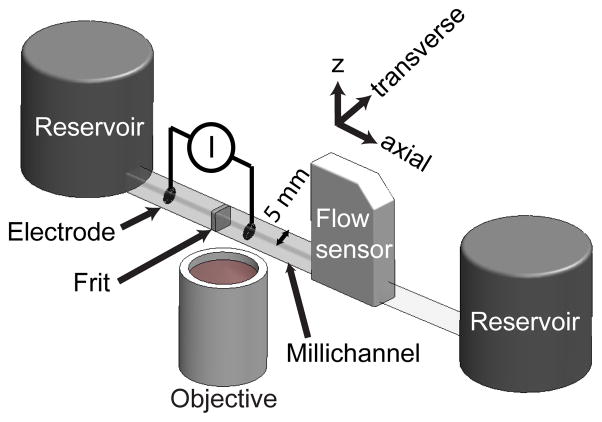
Figure 1 is a schematic of our experimental setup. We used a porous silica frit with mean pore radius of 225 nm (EoPlex, Redwood City, CA), similar to that used in studies by Litster et al. [3] and Strickland et al. [12]. The 1 mm thick frits were epoxied with clear UV cure epoxy (Norland, Cranbury NJ) into a clear, 5 × 5 mm square, borosilicate glass millichannel (Freidrich and Dimmock, Millville NJ). The frits were saturated with deionized (DI) water (Fischer Scientific, Waltham, MA) prior to the epoxy step to minimize the degree to which epoxy invaded the pores. Electrodes were made of coiled platinum, with coils approximately a millimeter apart, and inserted into the millichannel at various distances from the frit surface (cf. legend of Fig. 4). Two large diameter (3 cm) cylindrical end-channel reservoirs were filled to equal heights to insure no significant external pressure was applied to the pump system during operation. During experiments, we used 0.1 to 10 mM (Na⁺ concentration) sodium tetraborate decahydrate buffer (Mallinckrodt, Hazelwood, MO) to set ionic strength, where the borate salt was diluted in DI water. Our DI water had an initial, typical pH of 5.3 [18]. Our electrolyte solutions had pH values ranging from 5.5 to 9.2 for, respectively, 0.1 mM and 10 mM tetraborate decahydrate. We pumped with constant currents from 25 to 100 μA and measured applied potential with a Keithley 2410 sourcemeter (Cleveland, OH). Before each realization, we used a syringe pump (Harvard Apparatus, Holliston, MA) to flow at least 0.5 ml of new electrolyte through the frit. When switching to a borate solution of different ionic strength, we used first pressure-driven flow and then electroosmotic flow to each drive at least 0.5 mL of new solution through the frit. We found that the above pre-treatment allowed for repeatable flow rate versus time measurements, both in flow rate magnitude and transients observed (as will be shown in section 3.3). A micro flow sensor (ASL 1430–16, Sensirion, Switzerland) was used downstream of the pump to measure flow rate at a sampling frequency of 1 Hz.

Figure 1.

Schematic of the experimental setup used to perform simultaneous visualizations of concentration and qualitative pH fields, flow rate measurements, and voltage measurements under galvanostatic conditions. The frit was epoxied into a 5 mm square, clear borosilicate glass channel, and coiled platinum wire electrodes were positioned at variable locations along the channel. Visualizations were performed with an inverted epifluorescence microscope, and flow rate measurements were performed with a microflow sensor. Large diameter reservoirs were filled to equal heights to insure a negligible external pressure load.

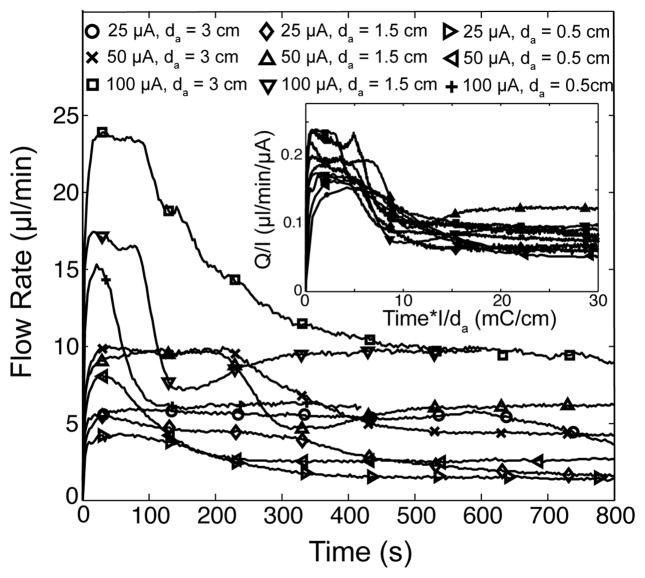
Figure 4.

Flow rate versus time plots for nine experimental conditions, where we vary applied current and anode-to-frit distances. The electrolyte was 0.1 mM borate, and all respective visualizations confirm the occurrence of propagating CP zones (e.g., Fig. 2c). In all realizations, flow rate initially increased sharply, approximately reached a temporary plateau, and then suffered a fairly rapid decay to a final steady value. The inset shows the same data but now flow rate is scaled with current and time is scaled with inverse applied current and anode-to-frit distance. This scaling approximately collapses the transition time between the plateau in flow rate and long-term value. Scaling involving 0.5 cm to 3 cm cathode-to-frit distances (not shown here) showed no such collapse of data. This evidence suggests the anode (in particular the time of arrival at the frit of the low pH anode enrichment zone) has a drastic effect on EO pump performance.

Simultaneous to our flow rate and voltage measurements, we obtained images of concentration and qualitative pH fields about our frit. We did not obtain concentration and pH field data within our frit, as the porous silica was effectively opaque. For all visualizations, we used an inverted epifluorescent microscope (Eclipse TE300, Nikon, Japan), a 1x, NA 0.04 objective (Nikon, Japan), and captured images with a CCD camera (MicroMAX, Princeton Instruments, Trenton, NJ) with a 6.7 μm pixel size. For simple concentration field visualizations (Fig. 2), we used an XF23 filter cube (Omega Optical, Brattleboro, VT) with peak excitation and emission wavelength ranges of 475–500 and 515–550 nm respectively. Also, for simple concentration field visualizations (Fig. 2), we observed the anionic, pH insensitive [19] tracing dye Alexa Fluor 488 (Invitrogen, Carlsbad, CA). The dye was at a concentration of 4 μM, over an order of magnitude lower than that of the sodium borate. For simultaneous pH and concentration field visualizations (Fig. 3), we used instead an XF53 dual pass filter cube (Omega Optical) with peak excitation wavelength ranges of 475–500 and 550–600 nm, and peak emission wavelength ranges of 500–550 and 600 to 675 nm, and a quad view (Micro-Imager, Photometrics, Tucson, AZ) to spatially separate concentration and pH field signals onto separate quadrants of the CCD chip. With the latter system, we simultaneously observed both the anionic Alexa Fluor 594 (Invitrogen) at 5 μM to measure concentration field, and a second anionic, pH-sensitive dye. The pH-sensitive dye used was Fluorescein (JT Baker Inc. Phillipsburg NJ) at 10 μM concentration [20, 21]. Fluorescein dye has four protolytic forms: dianionic, anionic, neutral, and cationic [21]. However, only the dianionic and anionic forms have emission bands which pass our filter cube and are recorded by our CCD chip, and thus in our system Fluorescein emissions likely drop to negligible values at a pH below 3 (see Sjoback et al. [21] for details on emission properties and equilibrium constants for Fluorescein protolytic forms).

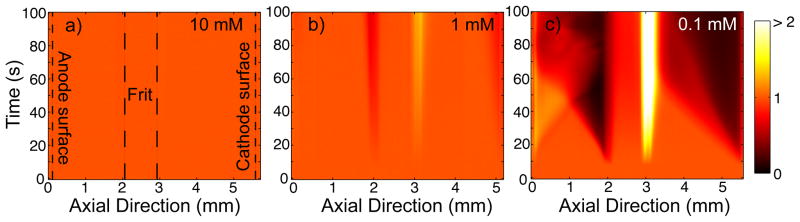
Figure 2.

Experimental visualizations of concentration fields in the millichannel about the silica frit (225 nm mean pore radius). We show visualizations at three borate ionic strengths (10, 1, 0.1 mM) and an applied current of 25 μA. The x-axis represents axial position along the borosilicate millichannel which houses the frit, and the ordinate is elapsed time (current is applied at 10 s). The colormap represents the concentration enrichment factor. In all realizations, the anode and cathode surfaces are at ~ 0 and 5.5 mm, respectively, and the frit between 2 and 3 mm. a) At 10 mM borate, no CP is observed. The frit and electrode boundaries are shown as dashed lines. b) At 1 mM, CP zones observably form but remain local to the frit surfaces. Additionally, a barely noticeable, apparently stationary depletion zone forms near the cathode surface. c) At 0.1 mM, CP fronts clearly propagate from the frit. Also, propagating enrichment and depletion zones are sourced by the anode and cathode, respectively.

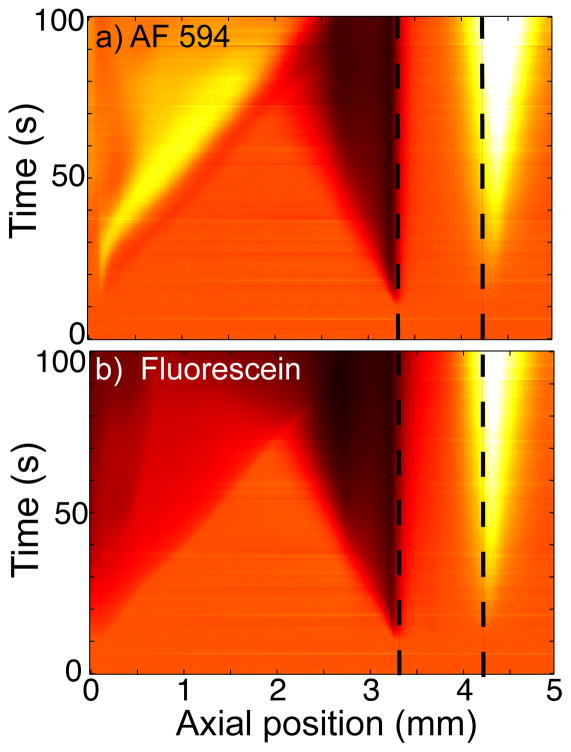
Figure 3.

Simultaneous visualizations of a) Alexa Fluor 594 and b) Fluorescein about our porous glass frit. As described in Section 2, we project the emissions of each dye onto separate quadrants of the CCD chip. The silica frit is located between the dashed lines, the anode surface is at 0 mm, and the cathode is 3 cm out of the field of view to the right. The background electrolyte is 0.1 mM borate buffer, and 25 μA current is applied at 10 s. The front sourced by and propagating from the anode is bright in the (pH-insensitive) Alexa Fluor images, but dark in the pH-sensitive Fluorescein images. This suggests the anode sources a propagating enrichment front of low pH. The anode front propagates at constant velocity and with a sharp front interface until it intersects and interacts with the CP depletion zone from the frit (past about 75 s).

3. Results

3.1 Frit-sourced propagating CP

Figure 2 illustrates typical results of concentration field visualizations in the millichannel around our silica frit. We show three visualizations for initial borate ionic strengths of 10, 1 or 0.1 mM (Fig. 2a-c), and 25 μA applied current. These results are plotted in spatiotemporal form where the abscissa is axial position along the millichannel, and the ordinate is elapsed time. The colormap represents concentration enrichment factor, which is the concentration averaged across the cross section of the millichannel and normalized by the initial value. The axial location of the frit is between about 2 and 3 mm in all cases, and the current is applied at t = 10 s. At 10 mM, no CP zones are detected, and ionic concentrations in the millichannels remain at the initial level. At 1 mM, enrichment and depletion zones are observable, but remain local to the frit surfaces. At 0.1 mM, the enrichment and depletion zone interfaces propagate at constant, order mm/min velocities away from the frit surface.

The transition from non-propagating to propagating CP with decreasing ionic strength (increasing Dukhin number) has been demonstrated for silica serial micro-nano-microchannel systems by Zangle et al. [13], and we demonstrate this transition here with porous glass in series with millichannels (Fig. 2). We note that the propagation mechanisms in these two cases are different. In the former case, propagation of the CP depletion zone in the microchannel was explained by nonlinear effects associated with a significant amount of axial transport of current through the microchannel EDL [11]. That is, one necessary condition for this mechanism is that the Dukhin number in the propagation channel should be finite. For a microchannel, Du of order unity is easily possible by depleting to concentrations of order 10 μM or below. However, for the millichannel in the current experiments, achieving Du order unity would require a concentration of order nM which is physically impossible with an aqueous electrolyte (due to the ionic strength associated with water autoprotolysis). Also note that in our millichannel experiment, the maximum change in resistance is by a factor of about 2 (see Fig. S1), and thus ionic strength in the depletion zone is several orders of magnitude higher than that required for non-negligible EDL current. Thus Du is negligibly small in the millichannel during the observed depletion zone propagation, and propagation must be due to another mechanism. We will describe a possible mechanism in section 3.2.

In addition to the frit-sourced CP, we see evidence of propagation of enrichment and depletion zones from electrodes at 0.1 mM (Fig. 2c). An enrichment zone is sourced at the anode, and a depletion front by the cathode (note the bright triangular regions adjacent to the x = 0 and x = 5.5 mm boundaries of the visualization). Less apparent, Figure 2b shows a weak, slowly or non-propagating depletion region near the surface of the cathode.

In the 0.1 mM case, at about t = 45 s, the propagating anode enrichment front interacts with the depletion front propagating from the EO pump frit. The two-dimensional visualizations show evidence of flow and/or transport instabilities (see Fig. S2 and video), and this shows up as disturbances in the spatiotemporal plot. In the same experiment, the cathode depletion zone interacts with the frit enrichment zone at about 60 s, but the scalar fields apparently acquire a steady state and do not show evidence of instability. These electrode CP fronts will be discussed further below in section 3.2. We also note that in our visualizations, we did not detect any significant perturbation of the electrolyte on the side of the electrode facing away from the frit surface.

3.2 Electrode-sourced propagating CP

When an electrode potential difference above roughly 1.2 V is applied to an aqueous electrolyte, the reactions at the anode and cathode are typically that of water electrolysis [22, 23], and under acidic conditions are given as [24]:

$$\mathit{Anode}:2{\text{H}}_2\text{O}\to 4{\text{H}}^{+}+4e^{-}+{\text{O}}_2,$$ [2]

$$\mathit{Cathode}:2{\text{H}}^{+}+2e^{-}\to {\text{H}}_2.$$ [3]

Thus, upon application of a DC current, positive hydronium ions are introduced into the electrolyte at the anode/electrolyte interface. Simultaneously, hydronium is removed at the cathode. This can result in the formation of enrichment and depletion zones about the anode and cathode, respectively. Ion concentration polarization at electrodes has been described previously by Probstein [25], and recently visualized by Garcia-Sanchez et al. [20]. In the latter study, the authors used ion tracers Bodipy and Rhodamine 6G, and the pH marker Fluorescein to visualize pH and concentration fields about a platinum electrode in a 100 μm high channel with 0.1 mM KCl electrolyte. They applied an AC potential to the electrode, and observed a zone of ion enrichment and low pH near the electrode for positive applied potentials (with respect to a counter electrode), which they attributed to the production of hydronium ions at the electrode.

To study whether the propagating electrode CP zones we visualized (Fig. 2) were sourced by water electrolysis, we performed simultaneous visualizations of both concentration field (Fig. 3a) and pH field (Fig. 3b) according to the procedure described in Section 2. In these visualizations, the frit is located roughly between 3 and 4 mm, the anode surface is located at 0 mm, and the cathode is about 3 cm out of the field of view to the right. We used 0.1 mM borate as the background electrolyte and an applied current of 25 μA (applied at 10 s). In Figures 3a and b, the concentration of both dyes increases and depletes at, respectively, the cathode and anode sides of the frit; consistent with frit-sourced CP. Also, in Figure 3a, the anionic Alexa Fluor dye indicates an ion enrichment front is propagating from the anode. However, simultaneously, the anionic Fluorescein dye shows a strong depletion propagating from the anode (Fig. 3b). The Fluorescein depletion and Alexa Fluor enrichment fronts emanating from the anode are nearly identical in spatial extent at all times. The depletion in pH-sensitive Fluorescein coupled with the enrichment in pH-insensitive Alexa Fluor is strong evidence that the anode enrichment front is also a region of low pH, likely lower than pH ~3 (see Section 2). It is therefore likely that the anode front is sourced by water electrolysis. Further, we note that the local pH about the anode is perturbed within the first few seconds of applying current. The anode front then intersects with the depletion front propagating from the frit and presumably mixes with this and eventually exposes the frit to relatively low pH (see Fig. 2c).

Therefore, similar to the visualizations of Garcia-Sanchez et al. [20], we visualize a low pH enrichment front near the anode of our system. However, unlike the latter work (which used AC applied potentials and a microchannel), we here report the anode front propagating through a millichannel at order mm/min velocity.

The results of Figure 3 directly show that both electrolyte concentration and chemical composition (i.e., pH) vary discontinuously across the anode CP zone interface as it propagates through the millichannel. We here hypothesize that the propagation of the anode front is driven by the observed jump in chemical composition, and thus current carrying species, across the interface. This jump can lead to propagation of concentration shocks (e.g., physics similar to isotachophoresis) [26]. We further hypothesize that this mechanism may also explain the propagation of a relatively sharp, frit-sourced depletion front through the millichannel. A jump in current carrying species across the frit depletion zone interface could feasibly occur if salt was depleted to the point that, for example, hydronium ions carried a significant portion of the current in the depletion zone. Our two-dye visualizations may not have picked up a jump in chemical composition across the frit depletion zone interface because, for example, this zone may be both an ionic depletion and low pH zone (and thus would deplete both Fluorescein and Alexa Fluor dyes).

3.3 EO pump performance in the CP regime

In Figure 4, we summarize the results of our flow rate measurements, which we used to explore the effects of CP on EO pump performance. We used 0.1 mM borate, and confirmed the onset of propagating electrode and frit CP fronts by simultaneous visualizations for all realizations. We varied applied current, the distance between the anode and the frit surface, d_a, and cathode-to-frit distances, d_c. In all realizations, we observed a rapid rise in flow rate, followed by an initial, locally-stable flow rate, and then a distinct transition to a significantly lower, steady flow rate (Fig. 4).

Scaling the time axis with inverse current and anode distance approximately collapses the time scale at which we see the step down to the final, steady flow rate (Fig. 4 inset). We found no such scaling trend involving the cathode distance. This result suggests that flow rate and pump performance are intimately coupled to the position of the anode, and likely the rate of propagation of the frit CP depletion and/or anode CP enrichment (and low pH) fronts. For example, when the anode is placed closer to the frit, and all other experimental conditions are kept constant, then the sudden decrease in flow rate occurs sooner. We therefore hypothesize the step-down in EO pump flow rate may be due to the sudden arrival of a front of anode-sourced low pH at the frit, which can then abruptly decrease pore surface charge. See for example (and most notably) Lambert et al. [27] for a discussion of abrupt changes in surface charge of electroosmotic flow systems exposed to very low pH electrolyte (pH ≤ 2). In all cases, the onset of the flow rate step-down occurs after the visualized interaction of the anode enrichment and frit depletion fronts (as seen in Fig. 2c and 3). As discussed by Yao et al. [8] and Litster et al. [3], EO pump flow rate per current is largely insensitive to local electric fields and very sensitive to in-pore ionic strength and zeta potential (and so surface charge).

While we presented clear evidence that pump flow rate at zero pressure load can deteriorate over time in the CP regime (cf. Fig. 4), we here do not attempt to conclusively answer the complex question as to whether (and when) CP may enhance or deteriorate pump performance. We hypothesize that CP effects will typically deteriorate pump performance due to the presence of low-conductivity (high electric field) depletion regions outside the pump. In galvanostatic operation, these create regions of significant voltage loss (cf. Figure S1), raising required power. In potentiostatic operation, these regions result in lower current across the pump and so lower flow rate and pressure. We further note that the CP (high Du number) regime is often associated with low ionic strength, and thus low buffering capacity. Therefore, pumping performance that is negatively affected by electrode reactions may be characteristic of this regime

4. Conclusion

We present an experimental study leveraging simultaneous visualizations of ion concentration and pH fields, and flow rate and voltage measurements under galvanostatic conditions. We used these measurements to characterize EO pump performance in the CP regime. The measurements captured a number of phenomena that require further study. First, at low electrolyte concentrations (high Dukhin number) we observe frit-sourced CP propagating through the connecting millichannel. The propagation of CP zones in millichannels is unexplained by current propagating CP theory, namely the theory developed for serial micro-nanochannel systems [11]. Second, we observe propagating enrichment and depletion fronts from the electrodes of our system. Simultaneous pH and concentration field visualizations near the anode revealed that the anode front is both a concentration enrichment and low pH zone relative to the initial electrolyte. We hypothesized that the propagation of both electrode and frit-sourced depletion zones is due to a jump in electrolyte chemistry across the CP zone-to-unperturbed electrolyte interface, and we directly visualize this jump for the anode CP front. Last, we performed flow rate measurements which showed a distinct step-wise decrease in flow rate characterizes performance in the CP regime. We reasoned that this sudden loss of performance may be due to the visualized arrival of the low pH anode front at the frit, and the consequent decrease in frit surface charge density. Scaling analyses of dynamic flow rate per current support this conclusion.

Biographies

Matthew E. Suss received his B.Eng. degree from McGill University, Montreal, in 2007, and M.Sc. at Stanford University, Stanford, CA in 2009. He is currently beginning a Ph.D. at Stanford where his research has been supported by an NSERC scholarship from the Canadian government. His work at the Stanford Microfluidics Laboratory focuses on the development of highly efficient electroosmotic micropumps and novel water desalination techniques.

Ali Mani is a research associate at Stanford’s Center for Turbulence Research and the Flow Physics and Computational Engineering group in the Mechanical Engineering Department. He earned his Ph.D. in mechanical engineering from Stanford University in 2009. His research interest is on multiphysics transport problems relating to electrokinetics, turbulence, and interfaces. He primarily uses mathematical models and numerical techniques to study detailed physical processes in these systems. His publications span across different disciplines in fluid mechanics including aero-optics, micro/nano-fluidics and aeroacoustics.

Thomas A. Zangle received his Ph.D. from Stanford University in mechanical engineering and is currently a post-doctoral fellow in the department of Laboratory & Pathology Medicine at the University of California, Los Angeles. He received his A.B. and B.E. degrees in Engineering Sciences from Dartmouth College. At Stanford he worked under the guidance of Prof. Juan G. Santiago in the Stanford University Microfluidics Laboratory working on experimental, theoretical and fabrication aspects of the integration of nanofluidic devices into microfluidic systems. His research at UCLA focuses on the development of new technologies to develop and study cellular models of cancer.

Juan G. Santiago is Associate Professor of Mechanical Engineering at Stanford University and Chair of the Thermosciences Group. He specializes in microscale transport phenomena and electrokinetics. He earned his PhD in Mechanical Engineering from the University of Illinois at Urbana-Champaign. Among other awards, he won the National Science Foundation Presidential Early Career Award for Scientists and Engineers (PECASE) (‘03–‘08). Santiago has presented 13 keynote and named lectures and over 100 additional invited lectures. His group has been awarded ten best paper and poster awards. He has authored/co-authored over 110 archival publications, authored/coauthored 200 conference papers, and holds 25 patents.