People’s Hypercorrection of High Confidence Errors: Did They Know it All Along?

Abstract

This study investigated the ‘knew it all along’ explanation of the hypercorrection effect. The hypercorrection effect refers to the finding that when given corrective feedback, errors that are committed with high confidence are easier to correct than low confidence errors. Experiment 1 showed that people were more likely to claim that they ‘knew it all along,’ when they were given the answers to high confidence errors as compared to low confidence errors. Experiments 2 and 3 investigated whether people really did know the correct answers before being told, or whether the claim in Experiment 1 was mere hindsight bias. Experiment 2 showed that (1) participants were more likely to choose the correct answer in a second guess multiple-choice test when they had expressed an error with high rather than low confidence, and (2) that they were more likely to generate the correct answers to high confidence as compared to low confidence errors, after being told they were wrong and to try again. Experiment 3 showed that (3) people were more likely to produce the correct answer when given a two-letter cue to high rather than low confidence errors, and that (4) when feedback was scaffolded by presenting the target letters one by one, people needed fewer such letter prompts to reach the correct answers when they had committed high, rather than low confidence errors. These results converge on the conclusion that when people said that they ‘knew it all along’, they were right. This knowledge, no doubt, contributes to why they are able to correct those high confidence errors so easily.

Do people know all along, the answers to high confidence errors?

It is generally agreed that providing corrective feedback to a person who has made an error is an effective means of rectifying those errors (Anderson, Kulhavy, Andre, 1971; Butler, Karpicke, & Roediger, 2008; Butler & Roediger, 2008; Kang, McDermott, & Roediger, 2007; Kulhavy, 1977; Lhyle & Kulhavy, 1987; Metcalfe & Kornell, 2007; Metcalfe, Kornell, & Son, 2007; Metcalfe, Kornell, & Finn, 2009; Pashler, Cepeda, Wixted & Roher, 2005). How beneficial the feedback will be, however, appears to be modulated by people’s confidence in their errors. In contrast to what might be expected, errors that are endorsed with higher confidence are more likely to be corrected on a final test than are errors endorsed with lower confidence (Butterfield & Mangels, 2003; Butterfield & Metcalfe, 2001; 2006; Fazio & Marsh, 2009; Kulhavy & Stock, 1989; Kulhavy, Yekovich & Dyer, 1976). This result is surprising because it indicates that people most easily overwrite the responses that they hold most strongly and correct the erroneous beliefs that are most deeply entrenched, while it seems intuitive that these beliefs and habits should be hardest to change.

In the standard paradigm used to investigate this ‘hypercorrection’ phenomenon (see, e.g., Butterfield & Metcalfe, 2001) participants were asked to generate the answersⁱ to general information questions and to rate their confidence in the correctness of each answer they produced. They were then given the correct answer. At later test, it was found that people were more likely to respond correctly to the questions that had produced high rather than low confidence errors. This result occurred despite the fact that most theoretical perspectives on memory and its relation to confidence (e.g., Gigerenzer, Hoffrage, & Kleinbolting, 1991; Hollingworth, 1913, who discusses Strong’s, 1912, confidence judgment-memory experiment; Koriat, l997; Koriat, Goldsmith, & Pansky, 2000; Murdock, 1974) indicate that responses that are made with high confidence are those in which the person believes most strongly, or which are the strongest in memory (e.g., Ebbesen & Rienick, 1998; Tulving & Thomson, 1971). As such, they should be most easily accessible and most resistant to interference. Certainly, in all data presented to date on the hypercorrection effect (including in this article), the overall correlation between confidence and correctness is very high. The responses, on average, in which people are highly confident are nearly always correct, and are thought to be the strongest, most entrenched responses associated with their respective cues. High confidence errors should, therefore, be difficult rather than easy to overwrite. Nevertheless, the empirical data indicate that these errors are the easiest, rather than the most difficult to change.

Two non-mutually exclusive explanations for this phenomenon have been proposed. The first is an attentional explanation. The idea is that when people are wrong with high confidence, they are surprised (and perhaps embarrassed), and they therefore rally their attentional resources to learn the correct item. Several lines of research (Butterfield and Mangels, 2003; Butterfield & Metcalfe, 2001, 2006; Fazio & Marsh, 2009) offer support for this explanation. For example, Butterfield and Metcalfe (2006) showed that people are more likely to miss detecting a soft tone in a concurrent task when it is presented during the interval during which visual feedback is given to a high confidence error, rather than a low confidence error. Presumably this result obtains because people’s attention is captured by the feedback, in the high confidence error condition, and they have less in reserve to detect the tone. Butterfield and Mangels (2003) investigated the hypercorrection effect by looking for a p300 or ‘late positivity’ event related potential, a deflection that is thought by most researchers to be an indication of enhanced attention to a novel stimulus. This late positivity is associated with enhanced memory (Paller & Wagner, 2002; Paller, Kutas, & Mayes, l987). Butterfield and Mangels (2003) observed a p300 event related potential associated with the presentation of corrective feedback to incorrect responses. Of critical importance was the fact that its magnitude was directly related to the person’s original confidence in the error. Feedback to high confidence errors produced a larger p300 than did feedback to low confidence errors. The authors interpreted this finding as indicating that people were paying more attention to the feedback to high than to low confidence errors. Finally, Fazio and Marsh (2009) found that memory for contextual aspects, such as the surface appearance, of the corrections to high confidence errors was enhanced, a finding that they attributed to increased attention to these corrections. While acknowledging the importance of attentional factors in this phenomenon, we here focus on the second explanation.

The second explanation for which there is some preliminary support is a familiarity account. The general idea is that there may be systematic differences in either the characteristics of general information questions and their answers that are related to high confidence errors, or that there may be individually based differences in the participant’s own familiarity with the domains of their own high as compared to low confidence errors. Because of a greater familiarity for high as compared to low confidence error domains, the correct answer may already have been partially learned in the more familiar domains of the high confidence errors, and less well learned, or not learned at all in the less familiar domains of the low confidence errors. Consider a typical high confidence error such as answering "Toronto” to the question: “What is the capital of Canada? “ When the person is told that actually the capital is Ottawa, they may find this response easy to learn because they already know that Ottawa is a city in Canada and they might even know that it is the capital of Canada, had they really thought about it. They might have known it all along, but made a slip in producing, instead, the more familiar, but incorrect, response, Toronto. Now consider a hypothetical low confidence error, such as saying that Bamako is the capital of Burundi. When the person is told that actually Bujambura is the capital of Burundi, they are probably not very familiar with Bujambura (and maybe not of Burundi, either) so more new learning is needed. They did not know it all along.

There is some evidence in support of this familiarity-based explanation. Butterfield and Metcalfe (2006) reanalyzed the data from their original 2001 article. The general information questions used in the 2001 paper were taken from Nelson and Narens’ (1980) article, which had presented the normative values of a correct response for each question in the set. Thus, Butterfield and Metcalfe (2006) were able to assess the normative probability of a correct response for errors committed at various levels of confidence. These were .19 for errors committed with low confidence, .18 for errors committed with medium confidence, and .28 for errors committed with high confidence. This difference in the characteristics of the questions as a function of people’s confidence in their errors was significant. They also found that the normative ease of questions answered incorrectly at first test was significantly correlated with later correct recall on the second, post feedback test. This familiarity or prior learning effect did not account for the whole hypercorrection effect. When they partialed out normative difficulty, there was still a significant residual contributing to the hypercorrection effect. But, even though it was not the whole story, familiarity was implicated.

Butterfield and Mangels (2003) asked their participants for subjective familiarity ratings following the presentation of the correct answer. They found that the correct answers presented following high confidence errors were retrospectively rated as more familiar than correct answers following low confidence errors. They also found, in their event related potential data, an inferior-temporal negativity occurring 300–600 ms after presentation of the correct answer that was sensitive to subsequent memory performance at both immediate and delayed retests, but only for answers containing familiar semantic information. They suggested that this negativity might reflect processes involved in the formation of an association between the question and pre-existing semantic information. These results on the familiarity of the answers to high confidence errors suggest that people might be more likely to have the answers in their semantic memory.

Here we test the possibility that when people make high confidence errors they actually know something about the correct answer, and more than they know about the correct answers to low confidence errors. The question we ask in the first experiment is: Do people exhibiting the hypercorrection effect assert, when the correct answers to high confident errors are presented, that they knew it all along?

Experiment 1

In this experiment, college students, queried with general information questions provided their answers, giving their confidence in each response, until they made 15 errors. After each error and confidence judgment, they were given corrective feedback followed immediately by the question of whether they had known the answer all along. Then a final cued recall test was given. We expected the participants to exhibit the hypercorrection effect, replicating previous research. We also hypothesized that people might, in response to the correct answer, say that they ‘knew it all along’ disproportionately to high confidence, rather than to low confidence errors.

Method

Participants

The participants were 25 undergraduates at Columbia University and Barnard College. They participated for course credit or cash. All participants were treated in accordance with APA ethical guidelines in this experiment and the experiments that follow.

Materials

Participants were asked general information questions from a pool of 191 general information questions, which had been taken from the set of Nelson and Narens (1980). A number of questions that were in the original pool were no longer relevant or correct and were eliminated from the pool. Examples of questions were, “What is the name of the unit of measure that refers to a six-foot depth of water?” (answer: Fathom) or “What is the name of the French author who wrote ‘The Stranger?’”

Procedure

At the beginning of the experiment participants were instructed that they would be answering general information questions, indicating how sure they were of their answers, that they would then be given the correct answers, and that, following feedback to errors, they would be asked if they knew the answers all along. They were presented, one at a time with general information questions, and instructed to enter their answers into the blank slot on the computer. They provided their confidence rating concerning the correctness of the answer, using a horizontal slider on the computer that ranged from “very unsure” on the left end to “very sure” on the right end. The slider bar was anchored to the middle of the scale at the onset of each question, and the individual had to move it away from that center rating to be either higher or lower, to have the confidence response register. Confidence ratings were coded along a scale from 0 to 1.00, with 0 indicating a selection of the lowest limit of the slider, at the very unsure end, and 1.00 indicating a selection of the highest limit, at the very sure end. In the analyses that follow we bifurcated the rating scale into high confidence and low confidence for above and below .50, we also analyzed as high or low confidence based on each participant’s median confidence rating, and we used the numerical values of the ratings.

When the participant’s answer was correct a chime sounded and the next general information question was presented. If their answer was incorrect, the correct answer was presented on the screen and participants were asked to indicate whether they knew that answer all along using a second slider anchored, initially, to the center position, which ranged from “That’s new to me” on the far left end to “I actually knew it all along” on the far right end. This process continued until participants had answered 15 items incorrectly. These 15 items became the items over which the person’s original confidence in their errors, as well as their ‘knew it all along’ judgments were computed. Once 15 incorrect items had been accumulated, the program randomized those 15 originally incorrect responses, and retested each, for a final cued recall test.

At the end of the experiment, all participants were thanked and debriefed.

Results

Each response of every participant to every question, in each of the three experiments presented here, was hand checked by the authors to be sure that no response was ever counted as incorrect because it was a spelling or typing mistake. Any such possibility was eliminated from the data analyzed.

Basic Data

On average, participants answered 20.48 (SE = .54) questions before they reached the 15 incorrect answer criterion. Participants’ initial confidence in their answers, including both correct and incorrect answers, was .36 (SE = .02). These confidence ratings were predictive of initial test performance. The mean gamma correlation (γ) between initial confidence ratings and initial recall performance, computed on each participant and then averaging over participants, was γ = .83 (SE = .03), which was significantly different from zero, t(24) = 26.92, p< .001. (In subsequent analyses we were sometimes unable to report a gamma correlation for some participants because some got everything right or everything wrong, or had too many ties and the statistic could not be computed. Thus, degrees of freedom listed for gamma correlations may differ from the total number of participants used in the experiment). For the items that were answered incorrectly on the initial test, mean pre-feedback confidence in the incorrect responses was .22 (SE = .02). Mean post feedback recall performance on the final test was .76 (SE = .03).

The Hypercorrection Effect

A hypercorrection effect would be in evidence if high confidence errors were more likely to be corrected on the final test than errors endorsed with lower confidence. Results showed a significant hypercorrection effect: The mean gamma correlation between confidence in the original error and retest accuracy was γ = .40, SE = .10, which was significantly greater than zero, t(22) = 4.04, p< .01.

Knew It All Along Judgments

Participants’ mean knew it all along judgment was .28 (SE = .03). The question of interest, concerning the possibility that high confidence errors were more likely to be thought to have been known all along, was whether the corrections to the errors that had been endorsed with high confidence were given higher knew it all along judgments than were the corrections to the errors endorsed with low confidence. The correlation between knew it all along judgments and confidence in the original error was γ = .30, (SE= .05), t(24)= 5.84, p <.001 (and τ_B= .25, SE = .04, when computed with Kendall’s Tau-b, t(24) = 5.73, p <.001). A further assessment showed that the mean ‘knew it all along’ judgment to the corrective feedback was higher for high confidence errors, than for low confidence errors, when high and low confidence were classified as judgments of .50 and greater for high confidence, and judgments of .49 or lower, for low confidence, the results were significant (Low Confidence: M = .25, SE = .03, High Confidence: M = .49, SE = .07, t(22) = 3.45, p < .01), and also when low and high confidence were assessed by using each participant’s median overall confidence rating as the split point (Low Confidence: M = .22, SE = .03, High Confidence: M = .46, SE = .05, t(24) = 4.86, p <.001).

Finally, we computed the correlation between knew it all along judgments and final test performance. The gamma correlation was .50 (SE = .09), which was significantly different from zero, t(22) = 5.57, p <.001. Thus, when they said they knew it all along, people were more likely to get the answer correct later.

Mediation Analyses

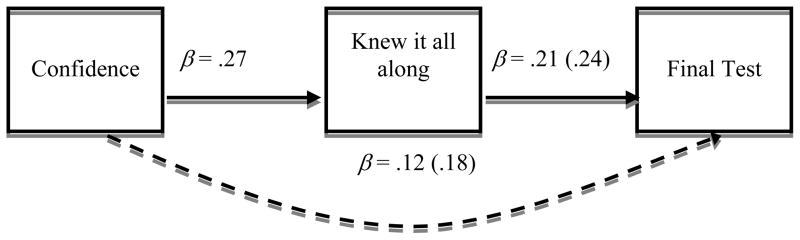
To examine the relationships among confidence, knew it all along judgments and final test performance further, we used a mediational model in which we assessed whether the effect of confidence on final test performance was mediated by the knew it all along judgments. Following the technique recommended by Baron and Kenny (1986), we found evidence of mediation of the impact of confidence on final test performance. There was a significant effect of confidence judgments on final test performance, β = .18, t(362) = 3.45, p < .01, and on knew it all along judgments, β = .27, t(362) = 5.43, p < .001. There was also a significant direct effect between knew it all along judgments and final test performance β = .24, t(362) = 4.77, p < .001. As illustrated in Figure 1, when both confidence judgments and knew it all along judgments were included as predictors in the regression equation, knew it all along judgments still predicted final test performance, β = .21, t(361) = 3.98, p < .001, as did confidence judgments, β = .12, t(361) = 2.30, p < .05. The decrease in the direct effect of confidence on final test performance was statistically significant, as measured by a Sobel test, z = 2.67, p < .01, indicating that the effect of confidence on final test performance was at least partially mediated by knew it all along judgments.

Figure 1.

Mediational model of direct and indirect effects of confidence and knew it all along judgments on final test performance, Experiment 1. Values in parentheses indicate the direct effect before the mediator was included in the analysis. All values were significant at p < .05.

Discussion

The results indicated that, at least some of the time, people believed they knew the correct answers all along. Furthermore, they were more likely to make this claim following the feedback to high as compared to low confidence errors. If they actually were more likely to know the answers to high as compared to low confidence errors, this would provide strong support for the familiarity explanation of the hypercorrection effect. This statement of belief, however, was assessed only after they had seen the correct answers. Whether their claim that they knew the answers all along was a pure hindsight bias, or whether it was an indication that they really did know something more than the incorrect answers at the time of making them, before getting corrective feedback, is the issue that is investigated in the second and third experiments.

Experiment 2

Experiment 2 examined the question of whether people showed any hint of knowing the answers to high confidence errors all along, before getting explicit feedback about those correct answers. If participants did have the correct information stored prior to receiving the feedback, then once alerted to the error, they might have been able to provide the correct answer. The ‘knew it all along’ claim, though, was selective to high confidence errors. Accordingly, we would expect that people would be able to produce the answers selectively following a high confidence error, but not following a low confidence error. The idea that people might be able to produce those answers, at least some of the time, is convergent on the notion that one reason people make high confidence errors, despite saying shortly after error commission that they knew it all along, was that the initial incorrect response had been impulsive.

Kornell and Metcalfe (2006b) observed that when people are in TOT states—states in which their metacognitive feelings of potentially knowing the answer are high--they have a good chance of retrieving the target later when given more time to do so (and see Schwartz, 2002). Furthermore, people are able to retrieve the correct answer when given more time or an additional retrieval opportunity, even when they were initially in what is called a ‘blocked’ TOT state in which an incorrect answer has come to mind. The difference between a blocked TOT state and the kind of high confidence error state observed in the preceding experiment, may primarily revolve around whether people know or do not know that the answer that came to mind was incorrect. But it is possible that in the high confidence error case as in the blocked TOT case, if given more time and effort, the correct answer might be recallable. Furthermore, it has been shown (O’Neill & Douglas, 1996) that boys who are impulsive spend less time trying to recall, and recall less as a result, than do typical non-impulsive boys. Finally, reminiscence effects (Payne, l987) suggest that additional retrieval effort may result in recall not apparent on the first attempt. These lines of research suggest that, given more time or further effort, high confidence errors might be correctible (though note that Dijksterhuis, 2007, showed that longer decision time resulted in worse rather than better decisions, contradicting the idea that more time necessarily leads to better results).

No experiments on the hypercorrection effect have included a condition in which no feedback is given, and in which people are simply given the final test. The first possibility that we explored was that even without feedback, people might be more likely to correct their high confidence errors than their low confidence errors on a subsequent test. Selective self-correction following no corrective feedback would constitute evidence that people might, indeed, have known the answers all along.

If they did not spontaneously produce the correct answers on the final test, they might have been able to do so--again, taking seriously the idea that they might know the answers all along at time of the first test--if we told them that they had been incorrect, and asked them to try again to generate the correct response before going on. Perhaps, at least some of the time, they could immediately generate the correct answer if we slowed them down and asked them to think again. Since the knew it all along responses were selective to high confidence errors, we expected that people would be more likely to generate the correct answer to questions that had evoked high rather than low confidence errors.

If they were unable to generate the correct response themselves, they might still have been able to correctly recognize the answer, from a list of alternatives, especially when they had made a high rather than low confidence error. This, too would suggest that their ‘knew it all along’ ratings had had some basis in fact, and were not purely a hindsight bias. These three conditions: the No Feedback condition, the Generate condition, and the Multiple Choice condition, were all contrasted to the Standard Feedback condition, in Experiment 2.

The fact that we asked people to make a second ‘guess’ in our generate condition and our multiple choice condition raises the possibility that these conditions might relate to the interesting work of Mozer, Pashler, and Homaei (2008) and Vul and Pashler (2008) in which they showed that having people make two guesses in a magnitude estimation task resulted in a better estimate of the true magnitude than did having them make only a single guess. This improvement in estimation with multiple sampling is a well-known finding, when the sampling is conducted by having different people make independent guesses about things like the weight of an ox. This finding is often dubbed the ‘wisdom of crowds.’ It also occurs, though, with estimates made by a single person who, at different times, takes different samples from memory, suggesting that there may be what the authors called ‘a crowd within’. Although, in our paradigm, we were not asking people to estimate a quantity, such as the weight of an ox, we were asking them to sample their memory more than once. As such, if multiple answers were available participants might also show the beneficial effects of ‘a crowd within’, and performance might improve, as Mozer et al. (2008) and Vul and Pashler (2008) found. Our question, however, was whether the space sampled was better with respect to the true answer when participants had made high rather than low confidence errors on the first sampling.

It was not necessarily the case that people would be able to show, in any of these three conditions, that they knew the answers all along preferentially for high confidence errors as they had so claimed, prior to feedback. Much research has shown that after people learn the outcome to a situation or the answer to a question they tend to exaggerate their ability to have seen it coming, claiming to have known the answer all along (see Hawkins & Hastie, 1990; Hoffrage & Pohl, 2003; Sanna & Schwartz, 2006). It was possible that the post-feedback knew it all along judgments we obtained in Experiment 1, were simply a demonstration of a classic hindsight bias (Fischhoff, 1975; Wood, 1978) and when a domain was familiar, the feedback was judged as already part of the person’s knowledge set even if it never could have been retrieved. Indeed, Werth and Strack (2003) showed that people were more likely to show a classic hindsight bias when an answer was judged as highly familiar.

Experiment 2 could potentially reveal either that people had some knowledge of the correct answers all along when they said they did, or that the claim that they had made, in the first experiment, was purely a hindsight bias. If it were a pure bias, then recalling the correct answer might not have been possible even with a second chance on a retest for which no corrective feedback was supplied. Asking the participants to make a second attempt to generate the answer, or giving them a multiple choice test that included the correct answer but did not include their original response, could fail to reveal any bias toward the high confidence errors in the correctness of the ‘second chance’ responses. If none of these three methods revealed evidence that people could demonstrate that they had greater knowledge for the correct responses to high confidence error questions than to low confidence error questions, then the results would provide support for the idea that the knew it all along judgments that they had made on the previous experiment were the result of pure hindsight bias, rather than actual prior knowledge. Such results would also suggest that differential attention to feedback to high and low confidence errors was entirely responsible for the hypercorrection effect.

Method

Participants

The participants were 45 undergraduates at Columbia University or Washington University in St. Louis. They received course credit or cash for participation.

Procedure

Participants answered general information questions, until they had reached 36 errors. The questions were randomly drawn from a larger pool of 493 questions taken from Nelson and Narens (1980) as well as a variety of difficult trivia questions that elicit high confidence errors added since the earlier pool was constructed, but which followed the form of Nelson and Narens’ general information questions.

The questions were presented one at a time, in a random order, and after each response, which, in this experiment, unlike Experiment 1, was forced (i.e., the participant had to provide a response to get the program to continue), the participants made a confidence judgment about the correctness of their response. The answers were computer scored online by an algorithm, developed by Brady Butterfield, that computed proportion letter overlap and order, assigning each item a value between 0 and 1, where a score of .75 corresponds fairly well to what human scorers would call a minor spelling mistake. The item was counted as correct if the score was .75 or higher; otherwise it was treated as an error. When the response was incorrect a low pitched honk sounded, and one of four within participants feedback conditions, randomly determined, occurred: (1) Standard Feedback, (2) No Feedback, (3) Generation, or (4) Multiple Choice. Immediately following each feedback treatment, participants were asked: ‘Did you know that all along?’ and had to click either a ‘yes’ or ‘no’ button. There were 9 replications in each of the 4 treatment conditions, giving 36 errors in all. After the 36^th error, participants were given a cued recall test, in which the 36 items that had been answered incorrectly were randomized and each question was presented for the participant to type the correct answer in to the computer. Participants had no restrictions on the amount of time they could take to answer each question.

In the Standard Feedback condition, after indicating their confidence in their incorrect answer, participants were simply told, “Actually the correct answer is x”, and the correct answer was presented in the response window on the computer screen. This condition allowed us to ascertain that the basic paradigm from Experiment 1 replicated. In the No Feedback condition, aside from the fact that participants had heard the chime when they were correct and the low sound when incorrect, and so would have known that they had been incorrect, no corrective feedback was given, nor was there a chance to come up with a second guess. This condition allowed us to investigate whether, without any corrective feedback at all, people might, on the final test, change their answers to be correct. In the Generation condition, the computer told the participants: “Please choose another answer. If you do not know the answer, please guess.” After they typed in a new response, they made a knew-it-all-along judgment and were not told whether their response was correct or not. This condition was directed at the possibility that high confidence errors were the result of impulsiveness, and that if people were told that they were incorrect and asked to give another response they might be able to produce the correct answers. Finally, in the Multiple Choice condition, a message stated, “Actually, the answer is one of these 6 options. Please choose one.” A randomized array of six options, including the correct answer was presented and participants could choose a new response. The program randomly selected the six options from a set of nine potential options. If the participant’s original error was included in the list of 6 options first selected by the computer, that option was replaced, randomly, with one of the remaining 3 options. After selecting their forced choice response, participants made a knew it all along judgment and then moved onto the next question.

Results

Basic Data

On average participants answered 51.82 (SE = 1.44) questions before they reached the 36 incorrect answer criterion. Participant’s initial confidence in their answers was .38 (SE = .02). Their confidence ratings were predictive of their initial test performance. The mean of gamma correlations taken over participants, between initial confidence ratings and initial recall performance, was γ = .81 (SE = .02), and was significantly different from zero, t(44) = 45.59, p< .001. These basic analyses showed no effect of feedback condition with any measure. This was as expected since the feedback manipulation followed the initial test and confidence ratings.

Using only the items that were answered incorrectly on the initial test, of course, there was a significant effect of feedback condition on final test performance, F(3, 132) = 226.70, MSE = .02, p <.001, η_p² = .84 (effect size was computed using partial eta squared, here and throughout). The Standard Feedback condition showed the highest final test performance (M = .70, SE = .03), followed by the Multiple Choice condition (M = .30, SE = .03), the Generate condition, (M = .07, SE = .01), and finally the No Feedback condition, (M = .04, SE = .01). All feedback conditions were significantly different from zero (all t >1, all p<.05). All comparisons between the feedback conditions showed significant differences, all t >1, all p <.05, except for the comparison between the No Feedback and Generate conditions, which showed a marginally significant difference, t(44) = 2.48, p =.10 (all pairwise comparisons in this analysis, and in the analyses that follow were Bonferroni-corrected to the .05 level).

Since only the standard feedback condition appropriately measured the hypercorrection effect, insofar as none of the other conditions provided corrective feedback, the question of whether or not there was a hypercorrection effect will be addressed below, with regard to that condition alone.

Standard Feedback condition

All of the basic effects that were seen in Experiment 1, replicated in this experiment. First, there was a hypercorrection effect. Errors that were committed with higher confidence were more likely to be corrected than errors committed with lower confidence (γ = .28, SE = .08, t(40) = 3.57, p <.01). There was a significant ‘knew it all along’ effect, such that participants were more likely to say they knew it all along when given the feedback to high confidence errors than to low confidence errors, when confidence was split based on the center of the scale (Probability of saying they knew it all along| Low confidence error: M = .10, SE = .02, Probability of saying they knew it all along| High confidence error: M = .21, SE = .05, t(34) = 2.11, p <.05). This effect was only marginally significant when confidence was split based on each participants median confidence rating over all responses, however (Probability of saying they knew it all along| Low confidence error: M = .09, SE = .02, Probability of saying they knew it all along| High confidence error: M = .17, SE = .04, t(40) = 1.49, p =.07, one-tailed). When assessed with gamma correlations computed between confidence and whether or not the person said that they knew it all along, the effect was significant (γ = .31, SE = .11, t(25) = 2.84, p <.01). Finally, participants were more likely to be correct on the final test if they had claimed that they knew the answer all along, as measured by a phi correlation, r_ϕ = .30, t(23) = 9.48, p <.001).

No Feedback condition

There were very few correct answers in the no feedback condition (M =.04, SE = .01). For the participants upon which it could be computed--but there were few of them, so this null result should be viewed with caution-- we found that the correlation between initial confidence and final accuracy was not significantly different from zero, t(12) = 1.16, p>.05.

Generation condition

First, and germane to the question of whether there was any evidence that people knew the answers all along, there was a significantly greater probability of generating a second guess correct response following a high confidence error than when an error had been produced with low confidence. This result was found whether we divided confidence at the center of the scale, (Probability of generating a correct second guess| Low confidence error: M = .04, SE = .01, Probability of generating a correct second guess| High confidence error: M = .18, SE = .05, t(37) = 2.80, p <.01), by using a median split (Probability of generating a correct second guess| Low confidence error: M = .04, SE = .01, Probability of generating a correct second guess| High confidence error: M = .15, SE = .04, t(41) = 2.94, p <.01), or we computed gamma correlations between original confidence and whether a correct second guess was or was not generated, γ = .48, SE = .14, t(23) = 3.49, p<.01. This effect is shown in Figure 2. Furthermore, items that produced errors, in this condition, that were committed with higher confidence were more likely to produce correct answers on the final test than were items that produced errors committed with lower confidence, γ = .53, SE = .12, t(22) = 4.43, p <.001.

Figure 2.

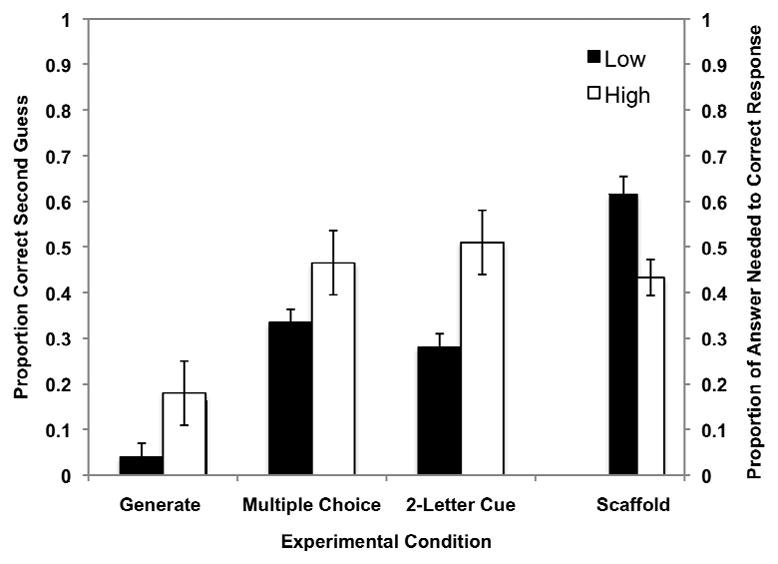
Probability of a correct second guess for low and high confidence errors, when participants were asked to generate a second response (Experiment 2, far left); when they were asked to choose the correct response in a 6 alternative multiple choice test (Experiment 2, center left); when they were given a 2-letter cue (Experiment 3, center right), and, the proportion of the word that needed to be revealed to allow participants to produce the correct answer for low and high confidence errors (Experiment 3, far right).

The probability of producing the correct answer on the final test was higher when the answer had been produced on the second guess test, (Final recall| incorrect second guess: M = .00, SE = .00; Final recall | correct second guess: M = .81, SE = .08; t(23) = 10.34, p<.001). Final test performance was higher when the original error had been made with high confidence when the split was based on the center of the scale, (Final recall | Low confidence error: M = .04, SE = .01, Final recall | High confidence error: M = .17, SE = .05, t(30) = 2.39, p<.05), and when the split was based on participants median confidence ratings, (Final recall | Low confidence error: M = .04, SE = .01, Final recall | High confidence error: M = .13, SE = .03, t(41) = 2.56, p=.01). There was no difference between the second guess performance and the final recall, with the former being .08, SE = .01 and the latter being .07, SE = .01, t(44)<1, p>.05. Note that this analysis used data from all participants, since each had a score, while in the conditionalized analysis presented just prior to this result, a number of participants were excluded from the paired comparison because they did not have any high confidence observations (which is why there were only 30 degrees of freedom in that t-test). These results indicate that adults did, at least to some extent, know the answer all along, when they said they did--namely for the high confidence errors.

Multiple Choice condition

When people had committed a high confidence error there was a greater probability of choosing the correct response on the multiple choice test, than when an error had been produced with low confidence (Probability of correct multiple choice response | Low Confidence error: M = .32, SE = .03; Probability of correct multiple choice response | High Confidence: M = .46, SE = .08; t(31) = 1.91, p(one-tailed) = .03. when the split was based on the middle of the scale. This difference did not reach significance, however, when the split was based on participants’ median response confidence (Probability of correct multiple choice response | Low Confidence error: M = .34, SE = .04; Probability of correct multiple choice response | High Confidence: M = .41, SE = .06; t(35) = 1.00, p>.05) and was not significant when gamma correlations between original confidence and whether the multiple choice was correct or incorrect, were computed, γ = .04, SE = .16, t<1, p>.05. Twelve participants (seven in the median confidence split), who had no high confidence responses at all were included in the gamma analyses, and their inclusion, as well as the increased weighting of the many low confidence responses in the gamma analysis may have diluted the effect.

Errors that were committed with higher confidence were more likely to be correctly recalled on the final recall test than were errors committed with lower confidence, γ = .21, SE = .09, t(38) = 2.40, p <.05. The probability of producing the correct final answer was higher when the correct choice was made on the multiple choice test than when it had not (Probability of correct final recall | Incorrect multiple choice response: M = .07, SE = .02; Probability of correct final recall | Correct multiple choice response: M = .69, SE = .05, t(42) = 11.13, p <.001). If the person not only picked the correct answer on the multiple choice but also said, following that choice, that they knew it all along, their final test performance was .95, SE =.04, as compared to when they picked the correct answer but said that they did not know it all along, M = .58, SE = .08, (t(25)=4.51, p<.01). Final recall test performance was higher when the original error had been made with high confidence (Final recall | Low confidence error: M = .27, SE = .03; Final recall | High confidence error: M = .52, SE = .08, t(33) = 3.05, p<.01). There was a significant difference between multiple choice test performance and final recall (Multiple Choice: M = .35, SE = .03, Final Recall: M = .30, SE = .03, t(44) = 2.60, p <.05), but this difference is difficult to interpret because there was a .17 guessing probability in the multiple choice test. When the person did choose the correct answer on multiple choice, the probability of a correct final answer was higher than their final test mean, t(42) = 9.24, p<.01. These multiple-choice data provide some support (though, perhaps, more equivocal than those provided in the generate condition) for the idea that the participants did know all along at least some of the correct answers to their high confidence errors.

Discussion

In Experiment 2, once again, the hypercorrection effect result itself was replicated. People also claimed that they knew it all along more frequently to high than to low confidence errors, thus, confirming the basic findings of Experiment 1. Simply retesting people on the questions to which they had given the wrong answers, or even asking them to generate a second response, produced very small (but not zero) final recall benefits. Final proportion recalled when the participant had made an error and received no feedback, except yes/no feedback, was given was extremely low: .04. When people were explicitly asked to immediately try to generate the correct answer to their errors--knowing only that they were errors--their final recall performance was also very low, though numerically slightly higher: .07. Clearly, giving more complete feedback has a much greater beneficial effect than giving minimal feedback, consistent with the review of the feedback literature on this issue by Pashler et al. (2005).

The question of primary interest in Experiment 2, though, concerned whether people actually knew the answers to high confidence errors all along. Two lines of evidence, from this experiment, suggest that they did have some knowledge of the correct answers to high confidence errors, that is, that their claim that they knew it all along--that was selective to these kinds of errors--had some basis in fact. First, participants were able to generate the answers to errors that they had made with high confidence to a greater extent than to errors they had made with low confidence. Second, they were able to pick the correct answers on a second guess multiple choice test more frequently to their high confidence errors, than to their low confidence errors. When they did pick the correct answer and said they knew it all along, they almost invariably got the answer right on the final test, even without having been given feedback about whether they had been correct on the multiple choice test or not.

Thus, the knew it all along claim appeared to be based, partially at least, on the fact that they did know the correct answers preferentially when they had made high rather than low confidence errors. The claim did not appear to be a pure hindsight bias. In Experiment 3, we sought additional evidence bearing on this possibility.

Experiment 3

In the third experiment we sought to test the ‘knew it all along’ hypothesis using a different method of evoking a response without necessarily providing full corrective feedback. The overarching rationale for Experiment 3 was the same as for Experiment 2. If people did actually know the answers all along more often when they made high confidence than low confidence errors, then they should be more likely to produce the correct answer to those high confidence questions more easily. In the third experiment, we gave them clues to help them.

There were two conditions in this experiment: the 2-letter cue condition and the scaffold feedback condition. In the former condition, after committing an error, people were given the first two letters of the target word, and asked to generate the correct answer. In the second condition, participants were given scaffolded feedback (Carpenter & DeLosh, 2006; Finn & Metcalfe, 2010) after having committed an error. First they were asked to make a second guess. If that was not successful, they were given the first letter, and again asked to make a guess. Then they were given the second letter, third letter, and so on, with presentation of each successive letter intervened by an opportunity to guess the target, until they had correctly guessed the target. After receiving feedback about the target in this way, they were asked whether they knew it all along. The hypothesis, with respect to this second condition was that people would need fewer letters for the high confidence errors, and once they had seen the entire word, would be more likely to affirm that they knew it all along, than for the low confidence errors.

Method

The general method was the same as in Experiment 2, with the changes noted below.

Participants

The participants in this experiment were 24 students at Columbia University or Barnard College, who received course credit for participating.

Procedure

The procedure was the same as that of Experiment 2 except that participants were told that if they were incorrect, half of the time the computer would give them the first two letters of the correct answer, and that they should try to type in the correct answers from this clue. After being given the first two letters, if they typed in a word that was the correct answer a ding would sound. Then they would then be asked whether they knew the answer all along or not. The other half of the time, when they made an incorrect response, they were told that the computer would start by giving them one letter, and they should guess if they could. The computer would continue to give them one letter at a time until they had either produced the correct answer, or the entire answer had been revealed. Then they would be asked whether they knew the answer all along.

A total of 72 errors were accumulated, 36 of which were randomly assigned to the 2-letter clue condition, and 36 of which were assigned to the scaffold feedback condition. Once all 72 errors had received this feedback, a final test was administered in which participants were asked to provide the correct answer to all 72 questions that had just been answered erroneously.

Results

Basic Data

On average participants answered 99.42 (SE = 2.49) questions before they reached the 72 incorrect answer criterion. Participant’s initial confidence in their answers was .34 (SE = .02). Their confidence ratings about their initial answers were predictive of the accuracy of their initial test performance; γ = .83, t(23) = 61.56, p< .001.

Using only the items that were answered incorrectly on the initial test, there was an effect of feedback condition on final test performance, t(23) = 11.24, p <.001: the scaffold condition produced better results than did the 2-letter cue condition (with proportion recall of .61, SE = .03 and .31, SE = .02 respectively).

2-letter cue condition

People were more likely to generate a second guess correctly when given two letters when they had given their erroneous answer high confidence than when they had ascribed low confidence to their answer, assessed by dividing confidence at the center of the scale, (Probability of correct response to 2-letter cue | Low confidence error: M = .29, SE = .02; Probability of correct response to 2-letter cue | High confidence error: M = .48, SE = .06, t(23) = 3.32, p <.01) and assessed by splitting the data at participants’ median confidence (Probability of correct response to 2-letter cue | Low confidence error: M = .27, SE = .02; Probability of correct response to 2-letter cue | High confidence error: M = .42, SE = .05, t(22) = 3.11, p <.01). The gamma correlation between original confidence and whether a correct second guess was or was not generated was significant, γ = .19, SE = .08, t(23) = 2.30, p<.05. When participants produced a correct second guess to the two-letter cue, the probability of saying that they knew it all along was .40, SE =.05, which was significantly greater than zero, t (23)=1.90, p<.05.

On the final test, they were more likely to be correct on those questions to which they had originally ascribed high rather than low confidence. The proportions correct on the final test were almost identical to those observed during the process of attempting to generate the correct answer from 2-letter cues (with 50:50 split: Probability of correct final recall |Low confidence error: M = .28, SE = .02; Probability of correct final recall | High confidence error: M = .51, SE = .07, t(23) = 3.58, p >.01, with median split: Probability of correct final recall |Low confidence error: M = .26, SE = .02; Probability of correct final recall | High confidence error: M = .43, SE = .05, t(22) = 3.55, p >.01) (See Figure 2). The mean gamma correlation between original confidence in the errors and final performance was: .22 (SE = .09), t(23) = 2.58, p <.05. These results offer support for the idea that people did, at least to some extent, know the answers all along when they made high confidence errors.

Scaffold feedback condition

When people had committed a high confidence error the number of letters that they needed to produce the correct answer was significantly fewer than when they had produced an error with low confidence (Number of letters required to correct answer |High confidence error: M = 2.65, SE = .27; Number of letters required to correct answer |Low confidence error: M = 4.15, SE = .13, t(23) = 5.00, p <.001, with 50/50 split; Number of letters required to correct answer |High confidence error: M = 3.27, SE = .21; Number of letters required to correct answer |Low confidence error: M = 4.31, SE = .15, t(22) = 4.32, p <.001, with median split). The average length of the correct answer was longer for low confidence errors (M = 6.59 letters, SE = .06) than for high confidence errors (M = 6.13 letters, SE = .16, t(23) = 2.51, with 50/50 split). This difference (Low confidence: M = 6.56, SE = .16, High confidence: M = 6.46, SE = .10) was not, however, significant with a median split, t<1, p> .05. Because the direction of the difference in the word length between the high and low confidence errors favored the relation of shorter, higher frequency words with high confidence rather than low confidence errors--as might be expected by the familiarity view of the hypercorrection effect--we also analyzed for the reduced cuing effect by computing, for each response, the proportion of the target word that was necessary to generate a correct response. This analysis was directed at the possibility that the cuing effects might be due to the shorter nature of the words rather than to people knowing the words, in the high confidence condition. Again, though, even when controlling for number of letters, the results favored the high confidence error condition. The analysis showed that a smaller proportion of the word needed to be revealed to allow correct target completion, both when we examined the data with a 50/50 split on confidence (Proportion of the word that needed to be revealed for correct response| High confidence error: M = .43, SE = .04; Proportion of the word that needed to be revealed for correct response| Low confidence error: M = .61, SE = .02, t(23) = 3.93, p <.001). The same pattern emerged when we examined the data using a median split (Proportion of the word that needed to be revealed for correct response| High confidence error: M = .50, SE = .03; Proportion of the word that need to be revealed for correct response| Low confidence error: M = .64, SE = .02, t(22) = 4.70, p <.001). These results favor the idea that people did know the answers all along preferentially to the high confidence errors.

The probability of correct responding on the final test was plotted as a function of the proportion of letters that had to be revealed, as is shown in Figure 3. Proportions were grouped into bins of 25%. Correct final performance was greater for answers that required fewer rather than more letters to be revealed, F(3, 69) = 33.55, MSE = .03, p <.001, η_p² = .59, suggesting that the knew it all along factor was important for later correct responding. Because complete feedback was given in this condition--though in a piecemeal way-- we were able to look at whether participants claimed that they knew the answers all along for the high as compared to the low confidence errors. They did: the proportion of knew it all along responses, using a 50/50 split, was .45 (SE = .06) for the high confidence errors, as compared to .19 (SE = .02) for the low confidence errors, t(23) = 4.14, p <.001. The proportions were .36 (SE = .04) and .17 (SE = .03) respectively, t(22) = 5.60, p <.001, when we used a median split. Finally, there was a hypercorrection effect, such that performance on the final test was better for high than low confidence errors. The mean gamma correlation between original confidence and final performance was γ = .17 (SE = .07), t(23) = 2.50, p <.05. Additionally, in this condition, we had sufficient responses per participant to allow us to plot the relation of original confidence in the error and final performance, dividing the data into confidence quartiles, as is shown in Figure 4.

Figure 3.

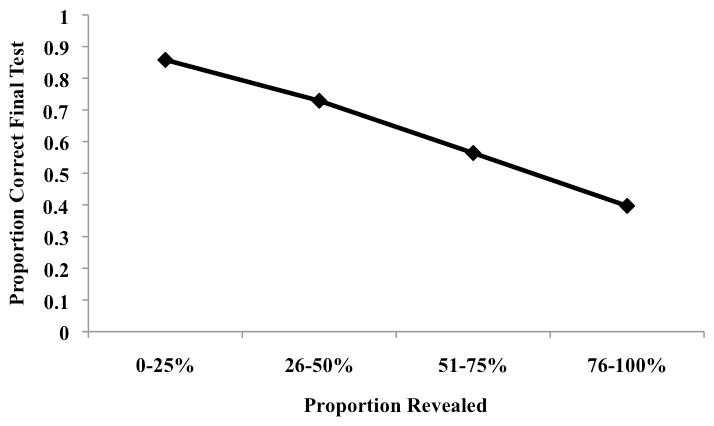
Probability of correct final recall as a function of the proportion of letters revealed in the scaffold condition, Experiment 3.

Figure 4.

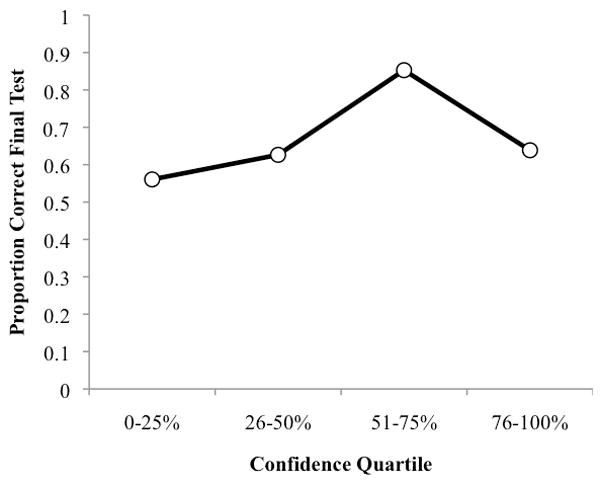
Probability of correct final recall, in the scaffold condition, as a function of confidence in original error, Experiment 3.

Additional analysis of item characteristics of high and low confidence errors

Finally, to examine the possible effects of the characteristics of the items themselves, and whether there were item differences that distinguished high from low confidence errors, we conducted a latent semantic analysis (LSA, Landauer & Dumais, 1997, and see http://cwl-projects.cogsci.rpi.edu/msr/) to examine the association strength between the error that was generated and the target item, when it was a high confidence error and when it was a low confidence error. To do so the LSA value of every error-target pair was determined, and then these pairs were grouped into low confidence pairs and high confidence pairs, on a participant by participant basis, for analysis. If an error was not a word, or could not be found in the data base, it was eliminated from this analysis. Although we below report each contrast separately, in every case, the associative relation of the low confidence error to the target was lower than was the associative relation of the high confidence errors to the target. This was found when the confidence split was based on the midpoint of the scale, and collapsed over all three experiments, (Low Confidence: M _{LSA error-target}= .20, SE = .01, High Confidence: M _{LSA error-target} = .31, SE = .01, t(89) = 7.35, p <.001). The same pattern resulted when a participant based median split was used (Low Confidence: M _{LSA error-target} = .19, SE = .01, High Confidence: M _{LSA error-target} = .30, SE = .01, t(90) = 8.98, p <.001). The Experiment 1 means were: Low Confidence: M_{LSA error-target} = .25, SE = .02, High Confidence: M _{LSA error-target} = .37, SE = .04, t(21) = 3.37, p <.01, for mid-split; Low Confidence: M _{LSA error-target} = .24, SE = .03, High Confidence: M _{LSA error-target} = .36, SE = .03, t(23) = 3.14, p <.01, for median split. The Experiment 2 means were: Low Confidence: M _{LSA error-target} = .18, SE = .01, High Confidence: M _{LSA error-target} = .29, SE = .02, t(43) = 5.77, p <.001 for mid-split; Low Confidence: M _{LSA error-target} = .16, SE = .01, High Confidence: M _{LSA error-target} = .28, SE = .01, t(43) = 8.18, p <.001, for median split. The Experiment 3 means were: Low Confidence: M _{LSA error-target} = .21, SE = .01, High Confidence: M _{LSA error-target} = .29, SE = .02, t(23) = 3.42, p <.01 for mid-split; Low Confidence: M _{LSA error-target} = .18, SE = .01, High Confidence: M _{LSA error-target} = .28, SE = .01, t(22) = 7.17, p <.001, for median split. These differences, like the differences in the normative probability correct for high versus low confidence errors reported by Butterfield and Metcalfe (2006) indicate that there were important differences in the characteristics of the items that evoke high versus low confidence errors, and provide additional support for the familiarity explanation of the hypercorrection effect.

General Discussion

These experiments replicated the finding (Butterfield & Metcalfe, 2001) that subjective confidence in one’s errors plays a role in which errors are most likely to be amended: errors that are endorsed with high confidence are hypercorrected following corrective feedback. We do not dispute our own finding and those of others (Butterfield & Mangels, 2003; Butterfield & Metcalfe, 2006; Fazio & Marsh, 2009) that when a person makes a high confidence error they give the corrective feedback to that error extra attention. This attentional boost undoubtedly contributes to the hypercorrection of those errors.

However, as the present results demonstrate, increased attention to feedback following a high confidence error does not appear to be the whole story behind the hypercorrection effect. People claimed, after receiving the corrective feedback following high confidence errors that they ‘knew it all along.’ When we investigated whether the ‘knew it all along’ claim had any basis in fact, we found that it did. People were able to selectively generate the correct answers to high confidence, as compared to low confidence errors, when they were asked to take a second try. They did this rarely, but they did it more frequently for high confidence errors than low confidence errors (to which they almost never generated a correct second response). They were also sometimes able to select the correct answer in a multiple choice test, following high confidence erroneous responses, without first having had corrective feedback. They were more likely to produce the correct answer after seeing the minimal cue of the first two letters of the correct answer, if the error had been made with high rather than low confidence. And, finally, when we gave participants scaffolded cues, such that they got one letter at a time in the answer until they were able to produce the answer, they needed fewer such cues to produce the correct responses to high confidence errors than to low confidence errors. Thus, the selective claim that people had made after having been given the correct responses to high confidence errors--that they knew the answers all along--appears not to be merely a hindsight bias. It appears to have some basis in fact.

The finding that adults did sometimes have knowledge of the correct answer even when they committed a high confidence error, and that they are easily able to correct high confidence errors given standard corrective feedback (while they almost never corrected them given no feedback) suggests that those items that evoke high confidence errors may be inside what we have previously called the person’s region of proximal learning (RPL, Kornell & Metcalfe, 2006; Metcalfe, 2002, 2009; Metcalfe & Kornell, 2003, 2005). The individual’s RPL is thought to be comprised of materials that are almost, but not quite learned, and that will benefit the most from additional study opportunities. The materials in the person’s RPL are thought to not be difficult to learn, but without further study (or in this case, feedback, which provides an excellent study opportunity) the individual may fail to learn these items. A small investment of effort has large payoffs. Our no-feedback condition attests to the fact that without such an additional study opportunity, final performance on errors remained at roughly a 4% level of performance. Errors are not spontaneously self-correcting. Given a moment of standard corrective feedback, memory performance climbed to 70% or more. High confidence errors given corrective feedback reached 82%. Thus, all items benefited from feedback. But high confidence errors, those items that a priori might have been thought to be impervious to correction, were the easiest to correct both because of the extra attention allocated to the corrective feedback and because people appear--according to the present results-- to know quite a bit about those answers all along.

In practical terms, it would appear that encouraging students to generate their own responses, and thereby reaping the benefit of the generation or testing effect (Butler & Roediger, 2007; McDaniel, Anderson, Derbish, & Morrisette, 2007; McDaniel & Fisher, 1991; McDaniel, Roediger, & McDermott, 2007; Roediger & Karpicke, 2006a, 2006b; Slamecka & Graf, l978) is likely to be highly beneficial to their learning. The only potential problem with doing so had been the possibility that the errors that people make, in such a generation or test procedure, might prove to be problematic. If making an error entrenched that error in memory, and made it harder to learn the correct answer, one might rationally opt not to encourage generation and testing, because of the inevitable errors that it entails. This logic would seem to apply most pointedly to the errors that the person believed in most strongly, namely their high confidence errors. The present results argue strongly against this rationale for avoiding having students generate the answers. The very high levels of recall on what had earlier been errors, once those errors have been given corrective feedback, indicates that the commission of errors does not harm eventual memory performance, at least in normal college students. Some caution should be exercised in this claim that errors may have few long term detrimental effects since our participants were restricted to being typical college students. The commission of errors may have a more detrimental effect in people with memory disorders (Baddeley & Wilson, 1994; Glisky, Schacter & Tulving, 1986) and perhaps in people with learning disorders. More research on these special populations is needed to determine the limitations and boundary conditions of the conclusions we reach here concerning the effects of errors.

However, with normal college students, the avoidance of generation or testing procedures, which are otherwise beneficial for memory, would not seem to be justified on the grounds that such procedures inevitably result in errors and the commission of errors poses problems for later memory. Indeed, with just a few moments of corrective feedback, the errors themselves are not recommitted, but rather are corrected, at a very high rate. High confidence errors are particularly easy, not difficult, to correct. Furthermore, as Butterfield and Metcalfe (2006) showed, the correct answers to high confidence errors are maintained over time. The one obvious caveat to the idea that committing errors does not harm future memory with typical college students, is that those errors do need to be corrected. Feedback is essential. Metcalfe et al. (2009) have shown that the errors do not necessarily have to be corrected immediately. However, as we have shown here, without correction, little or no remediation can be expected.