Symmetry Numbers for Rigid, Flexible and Fluxional Molecules: Theory and Applications

Abstract

The use of molecular simulations and ab initio calculations to predict thermodynamic properties of molecules has become routine. Such methods rely upon an accurate representation of the molecular partition function or configurational integral, which in turn often includes a rotational symmetry number. However, the reason for including the symmetry number is unclear to many practitioners, and there is also a need for a general prescription for evaluating the symmetry numbers of flexible molecules; i.e., for molecules with thermally active internal degrees of freedom, such as internal rotors. Surprisingly, we have been unable to find any complete and convincing explanations of these important issues in textbooks or the journal literature. The present paper aims to explain why symmetry numbers are needed and how their values should be determined. Both classical and quantum approaches are provided.

Introduction

The symmetry number of a molecule appears in the denominator of its molecular partition function. In classical statistical thermodynamics, it reduces the volume of phase space occupied by the molecule, and in quantum statistical thermodynamics, it reduces the number of eigenstates the molecule can occupy. Although the symmetry number is introduced in many textbooks and used in many papers, this is almost always done in relation to rigid or near-rigid molecules with simple chemical structures. Such treatments were adequate in the earliest applications of thermochemistry, which focused on simple molecules like ammonia and ethane, but they are difficult to extend to the complex systems studied today by computational methods, such as carbon nanostructures and biomolecules. As a consequence, practical and conceptual problems regarding the symmetry number can arise in many current applications of computational chemistry.

In particular, it can be difficult to conceptualize, compute and apply the symmetry number of a complex, flexible molecule. Several specific questions arise. If a potentially symmetric molecule is so flexible that it virtually never adopts a symmetric conformation at room temperature, can its symmetry number be greater than 1? Should the symmetry number account for both external symmetries and internal ones, such as the 3-fold symmetry of a methyl rotation? Does the symmetry number influence binding affinities in the context of noncovalent molecular recognition? Does the symmetry number depend upon temperature? Finally, is there a practical approach to computing the symmetry number of a molecule with complicated symmetries?

The present paper addresses these issues by reviewing the theoretical basis of the symmetry number from a classical perspective and then from the quantum mechanical standpoint. We provide a practical method of computing symmetry numbers in challenging cases and resolve conceptual issues that arise in applications of computational chemistry and molecular modeling.

Theory of Symmetry Numbers

Symmetry Numbers in Classical Statistical Thermodynamics

Historically, the symmetry number was first introduced for rigid molecules treated by classical statistical mechanics.¹ Only later was the concept elaborated for flexible molecules and reinterpreted in the light of quantum mechanics, with its notion of indistinguishable particles. Here, we begin with the classical starting point, for the sake of its historical interest and also for the clarity and insight it offers. The classical treatment also bears to some degree on how one conceptualizes the treatment of symmetry in classical molecular simulations. We first introduce the symmetry number for rigid molecules and then address systems of increasing flexibility, due to molecular vibrations, internal rotors, and fluxionality (that is, degenerate chemical rearrangement), using simple molecules as examples. We then describe a practical method of computing symmetry numbers that is readily applied even to flexible molecules with multiple symmetries. This presentation draws in particular upon a number of valuable publications that introduce, develop and explicate the concept of the symmetry number.^1–8

Rigid molecules and the origin of the symmetry number

We start with the elementary case of a system of M identical, interacting atoms. If one ignores quantum indistinguishability, which was not known when Ehrenfest and Trkal first introduced the molecular symmetry number,¹ then the configuration integral is

$$Z_{\mathit{disting}}=\int exp\left[-\beta U({\mathit{r}}_1,\dots ,{\mathit{r}}_N)\right]{d\mathit{r}}_1\dots {d\mathit{r}}_N$$ (1)

where U is the potential energy as a function of the Cartesian coordinates r_i of the atoms i, and β = (k_BT)⁻¹, where k_B is Boltzmann’s factor and T is absolute temperature. If we define a configuration as a set of atomic coordinates irrespective of the indices of the atoms at each location, then every configuration in the domain of this integral occurs M! times, where each occurrence differs from the others only in respect of which atom is at which position. Similarly, if the system has M₁ atoms of elemental type 1 (e.g., carbon), M₂ of element 2 (e.g., nitrogen), and so forth, then the integral in Eq 1 has ${\displaystyle \prod _j}{M}_j!$ configurations that are identical except for interchanges of indices of atoms of like type (element). Because we are, for now, treating all atoms as distinguishable, each of these configurations is considered to contribute to the configuration integral. Therefore, this configuration integral does not overcount configurations due to its interchange of identical atoms with different indices, and Eq (1) is correct as it stands.

Now, following Ehrenfest and Trkal’s derivation,¹ we consider the same atoms to be formed into N rigid molecules, where each molecule contains n₁ atoms of element type 1, etc., so that M_j=Nn_j. (Ehrenfest and Trkal characterized the internal coordinates of a rigid molecule as “non-excited”, while Einstein, in a related derivation,² said the internal coordinates were “asleep”.) A first draft of the configuration integral for this system may be written as an integral over the positions R_i and overall orientations Ω_i of the molecules,

$$Z_{\mathit{draft}}\equiv \int exp\left[-\beta U({\mathit{R}}_1,\dots {\mathit{R}}_N,{\mathbf{\Omega }}_1,\dots {\mathbf{\Omega }}_N)\right]{d\mathit{R}}_1\dots {d\mathit{R}}_N{d\mathbf{\Omega }}_i\dots {d\mathbf{\Omega }}_N$$ (2)

where a Jacobian term stemming from the transformation from Cartesian atomic coordinates is omitted for simplicity, and the external (translational and orientational) coordinates of molecule i, R_i and Ω_i respectively, are defined so that they do not affect the conformation of the molecule. Within the classical approximation, such a separation into internal and external coordinates is readily effected within the Flexible Molecule approach.⁹ The formulation in Eq (2) has the merit of restricting the integral to configurations in which the atoms form the molecules of interest, rather than including dissociated configurations. However, it has the further consequence that, for each configuration, it includes only a subset of all possible interchanges of indices of like atoms: those resulting from the N! interchanges of whole-molecule coordinates, due to the integrals over the translational coordinates R_i, and those resulting from any rotational symmetry of the molecules, due to the integrals over molecular orientations Ω_i. For example, the integrals over orientation include the interchange of identical atoms in an H₂ molecule, and there are 12 orientations of rigid benzene that replicate any single molecular configuration with different atom numberings. Accordingly, H₂ and benzene are said to have symmetry numbers, σ, of 2 and 12, respectively. If a molecule has σ orientations that superimpose identical atoms, then the orientational integrals in Eq (2) account for σ^N interchanges of like atoms. Based on these considerations, it is apparent that Z_draft includes σ^NN! instances of each configuration of the system, where the various instances differ only in the indices at each atomic position. However, because we are deliberately ignoring quantum indistinguishability for now (see above), our configuration integral ought to include the full set of ${\displaystyle \prod _j}(N{n}_j)!={\displaystyle \prod _j}{M}_j!$ instances of each identical configuration, just as in the general system of interacting atoms presented at the start of this subsection. Since we know that Z_draft includes σ^NN! instances of each configuration, we can correct to the full configuration integral as follows:

$$Z_{\mathit{disting}}=\frac{{\displaystyle \prod _j}(N{n}_j)!}{N!{\sigma }^N}{Z}_{\mathit{draft}}$$ (3)

The correction factor before Z_draft in Eq (3) accounts for additional interchanges of subsets of identical atoms between molecules. Eq (3) demonstrates that, as shown by Ehrenfest and Trkal,¹ the symmetry number is needed even if we assume that all atoms are distinguishable. This result is perhaps unexpected to the modern reader, who is trained to view the symmetry number as a consequence of quantum indistinguishability. In this purely classical approach reviewed here, the symmetry number originates from the fact that the typical form of a configuration integral written in molecular coordinates undercounts the number of distinct atomic labelings associated with each configuration of the system. The factor in Eq (3) corrects for this undercounting.

We now introduce the idea that certain atoms in a system are indistinguishable from each other, so that interchanging them does not affect the energy or any measurable property of the system. Indistinguishability is most frequently considered to result from quantum indistinguishability; i.e., from the constraint that the wave function be either symmetric or antisymmetric with respect to the interchange of two identical nuclei, as discussed in detail below. However, indistinguishability also appears in a classical system if all measurable properties are invariant to the interchange of certain atoms, as previously noted (e.g. footnote 20 in ref. 10). This holds when two atoms are identical, and also can hold to a good approximation when two atoms are very similar. For example, when other (e.g., vibrational) isotope effects are negligible, one may legitimately treat different isotopes of an element as indistinguishable. When atoms are considered indistinguishable, on whatever basis, interchanging them does not generate a distinct new state to be counted in the configuration integral. Thus, if the identical interacting atoms in the gas described by Eq (1) are considered indistinguishable, then Eq (1) must be multiplied by a factor of (M!)⁻¹ to correct for the fact that it generates M! indistinguishable instances of each configuration. Similarly, Z_draft in Eq (2) should be adjusted so that it no longer counts the σ^NN! instances of each configuration separately, but instead counts each configuration once. The corrected configuration integral takes the following familiar form:

$$Z_{in\mathit{disting}}=\frac{1}{N!{\sigma }^N}{Z}_{\mathit{draft}}$$ (4)

Eq 4 shows how the symmetry number arises when identical atoms are considered indistinguishable, as in the case of quantum indistinguishability. In this case, it is used to correct for the fact that the typical form of a molecular configuration integral overcounts states, rather than undercounting as when all atoms are considered distinguishable, above.

In summary, the symmetry number is needed whether or not identical atoms are treated as distinguishable. One may therefore consider that the symmetry number does not originate in quantum indistinguishability, as often explained, but from the mathematical manner in which the configuration integral of a molecular system is conveniently and typically formulated, namely as an integral over the rotations and translations of distinguishable molecules without any explicit interchange of atoms. In this sense, the symmetry number is a mathematical artifact rather than a physical property of a molecule.

Applicability of symmetry numbers to flexible molecules and supramolecular complexes

Molecules are not really rigid, and the configuration of a molecule at T > 0 is constantly randomized by heat energy. As a consequence, a molecule that could potentially adopt a rotationally symmetric three-dimensional configuration will essentially never do so. One may therefore ask about the relevance of symmetry numbers to real molecules subject to thermal motion. Another aspect of flexibility is that a molecule may possess a rotatable bond whose rotation interchanges two or more potentially identical groups. Examples include the 3-fold interchange of hydrogen atoms by a methyl rotation or the 2-fold interchange of atoms in a pendant phenyl group. Such rotations suggest that the concept of the symmetry number may need to be enlarged to account for internal molecular rotations. The present section addresses these issues in the context of the classical formulation of statistical thermodynamics, while treating identical atoms as indistinguishable in the customary manner.

Molecular vibrations

We first relax the assumption of molecular rigidity by considering small-amplitude vibrational motions; i.e., configurational fluctuations around a single energy minimum such that no vibrational motion away from equilibrium leads to a new configuration of equal energy where atoms have been interchanged. The draft configuration integral for a system of N such molecules now ranges not only over molecular translation and orientation, as in Eq (2), but also over the internal coordinates s_i of each molecule i:

$$Z_{\mathit{draft}}=\int exp\left[-\beta U({\mathbf{r}}_1,\dots {\mathbf{r}}_N,{\mathbf{\Omega }}_1,\dots {\mathbf{\Omega }}_N,{\mathit{s}}_1\dots {\mathit{s}}_N)\right]{d\mathbf{r}}_1\dots {d\mathbf{r}}_N{d\mathbf{\Omega }}_i\dots {d\mathbf{\Omega }}_N{d\mathit{s}}_1\dots {d\mathit{s}}_N$$ (5)

Whether this expression must be adjusted by a molecular symmetry number depends upon whether the integral overcounts configurations, as discussed above. This question arises because even a nominally symmetrical molecule, such as benzene, has perfect three-dimensional rotational symmetry in only a subspace of the overall configurational space, due to the constant randomization of its shape by internal vibrations. As a consequence, the integration over molecular orientations, Ω_i, does not, on its own, overcount configurations through the interchange of identical atoms, as occurred for a rigid, symmetrical molecule. Nonetheless, the integral in Eq (5) does overcount the molecular configurations of a symmetric molecule, due to the interchange of identical atoms by combined changes in orientational and internal coordinates.

Figure 1 illustrates how this comes about for the example of benzene. Suppose that one benzene molecule is twisted and stretched into some entirely asymmetric configuration, as shown; there are still 12 different combinations of internal distortion and overall rotation that can regenerate this configuration via permutations of identical atoms. Because the integral in eq. (5) ranges over all of these identical configurations, it still leads to configurations that are identical save for interchanges of identical atoms. Hence, it overcounts by a factor of σ^N, and must be corrected by the same prefactor of 1/(σ^N N!) that was required for the rigid treatment of benzene, where the factor of 1/N! again corrects for the translational interchange of molecules in identical configurations.

Figure 1.

Twelve indistinguishable configurations of benzene encompassed by the vibrational and rotational integrals. The corresponding coordinate permutations are as follows:

$$\begin{array}{l}1:\left(0,0,0,x_1^0,y_1^0,z_1^0,x_2^0,y_2^0,z_2^0,x_3^0,y_3^0,z_3^0,x_4^0,y_4^0,z_4^0,x_5^0,y_5^0,z_5^0,x_6^0,y_6^0,z_6^0\right);2:\left(\pi ,0,0,x_1^0,y_1^0,-z_1^0,x_2^0,y_2^0,z_2^0,x_3^0,y_3^0,z_3^0,x_4^0,y_4^0,z_4^0,x_5^0,y_5^0,z_5^0,x_6^0,y_6^0,z_6^0\right);\\ 3:\left(0,0,\frac{\pi }{3},x_2^0,y_2^0,z_2^0,x_3^0,y_3^0,z_3^0,x_4^0,y_4^0,z_4^0,x_5^0,y_5^0,z_5^0,x_6^0,y_6^0,z_6^0,x_1^0,y_1^0,z_1^0\right);4:\left(\pi ,0,\frac{\pi }{3},x_2^0,y_2^0,z_2^0,x_3^0,y_3^0,z_3^0,x_4^0,y_4^0,z_4^0,x_5^0,y_5^0,z_5^0,x_6^0,y_6^0,z_6^0,x_1^0,y_1^0,-z_1^0\right);\\ 5:\left(0,0,\frac{2\pi }{3},x_3^0,y_3^0,z_3^0,x_4^0,y_4^0,z_4^0,x_5^0,y_5^0,z_5^0,x_6^0,y_6^0,z_6^0,x_1^0,y_1^0,z_1^0,x_2^0,y_2^0,z_2^0\right);6:\left(\pi ,0,\frac{2\pi }{3},x_3^0,y_3^0,z_3^0,x_4^0,y_4^0,z_4^0,x_5^0,y_5^0,z_5^0,x_6^0,y_6^0,z_6^0,x_1^0,y_1^0,-z_1^0,x_2^0,y_2^0,z_2^0\right);\\ 7:\left(0,0,\pi ,x_4^0,y_4^0,z_4^0,x_5^0,y_5^0,z_5^0,x_6^0,y_6^0,z_6^0,x_1^0,y_1^0,z_1^0,x_2^0,y_2^0,z_2^0,x_3^0,y_3^0,z_3^0\right);8:\left(\pi ,0,\pi ,x_4^0,y_4^0,z_4^0,x_5^0,y_5^0,z_5^0,x_6^0,y_6^0,z_6^0,x_1^0,y_1^0,-z_1^0,x_2^0,y_2^0,z_2^0,x_3^0,y_3^0,z_3^0\right);\\ 9:\left(0,0,\frac{4\pi }{3},x_5^0,y_5^0,z_5^0,x_6^0,y_6^0,z_6^0,x_1^0,y_1^0,z_1^0,x_2^0,y_2^0,z_2^0,x_3^0,y_3^0,z_3^0,x_4^0,y_4^0,z_4^0\right);10:\left(\pi ,0,\frac{4\pi }{3},x_5^0,y_5^0,z_5^0,x_6^0,y_6^0,z_6^0,x_1^0,y_1^0,-z_1^0,x_2^0,y_2^0,z_2^0,x_3^0,y_3^0,z_3^0,x_4^0,y_4^0,z_4^0\right);\\ 11:\left(0,0,\frac{5\pi }{3},x_6^0,y_6^0,z_6^0,x_1^0,y_1^0,z_1^0,x_2^0,y_2^0,z_2^0,x_3^0,y_3^0,z_3^0,x_4^0,y_4^0,z_4^0,x_5^0,y_5^0,z_5^0\right);12:\left(\pi ,0,\frac{5\pi }{3},x_6^0,y_6^0,z_6^0,x_1^0,y_1^0,-z_1^0,x_2^0,y_2^0,z_2^0,x_3^0,y_3^0,z_3^0,x_4^0,y_4^0,z_4^0,x_5^0,y_5^0,z_5^0\right)\end{array}$$

Here the first three coordinates (bold font) are rotational, the first being the polar angle off the z-axis, the second being the azimuthal angle around the z-axis, and the third being a body rotation around the z-axis. The remaining coordinates are Cartesians, the notation being chosen to highlight the generic nature of their interchanges.

This analysis highlights the difference between a three-dimensional molecular symmetry, which is never perfectly reached due to thermal randomization, and a “topological” symmetry of the molecule’s chemical graph,^11–13 which allows every configuration, in general asymmetric, to be replicated with multiple permutations of internal and orientational coordinates. (Several algorithms have been developed to identify such topological symmetries.^11–14) The present analysis also shows that symmetry numbers remain applicable and requisite, even when the approximation of molecular rigidity is relaxed to allow for vibrational motions.

Molecules with rotatable bonds and low-barrier inversions

The vibrational model just considered is an artificial simplification in the sense that it treats identical atoms as distinguishable. If one could forcibly interchange two identical atoms within a molecule, one would break and reform covalent bonds to generate a new instance of the same stable conformation, rather than the artificial high-energy state predicted by the vibrational model. That is, the Hamiltonian is invariant with respect to the interchange of identical atoms. Nonetheless, the vibrational model works well when such atom-atom interchanges are blocked by high energy barriers. Moreover, if such interchanges were included in the configuration integral, they would lead to further overcounting of configurations, so it is reasonable to use a vibrational potential function that excludes, albeit artificially, such interchanges. On the other hand, the energy barrier to the interchange of identical atoms can be low, such as when the interchange is effected by a bond-rotation with a low energy barrier. We now consider whether and when the symmetry associated with such an interchange should contribute to the molecule’s symmetry number, using the time-honored example of ethane.^4,15–17

If the methyl groups of ethane are treated as rigid and symmetrical, then rotating one relative to the other by 120° or 240° cyclically permutes its (indistinguishable) hydrogen atoms. As a consequence, a configuration integral in which the hydrogen torsions are considered to range from 0 to 360° will overcount configurations by a factor of three. This overcounting can be corrected by including a factor of 3 in the molecule’s symmetry number. Alternatively, one may recognize the symmetry before writing the configurational integral and therefore restrict the torsional range to 0–120°; in classical statistical thermodynamics, these two corrections will yield identical results. In addition, when one considers that thermal fluctuations of the methyl groups actually perturb their symmetry, one still obtains a symmetry number contribution of 3, according to reasoning analogous to that described above for the vibrations of benzene and diagrammed in Figure 1. In the case of ethane, thermal fluctuations essentially guarantee that the methyl group will never be symmetric at any particular moment: the three CH bond-lengths, CCH bond-angles, and HCCH torsional angles will differ, so that merely rotating the group about the C-C bond will not perfectly permute the coordinates of the hydrogens. Nonetheless, a configuration integral ranging over all nine of these hydrogen coordinates will still generate three instances of every (in general asymmetric) configuration of the methyl group, each instance having a different permutation of the hydrogens. Thus, the methyl rotation will still generate a factor of 3 in the symmetry number.

It may be helpful to interpret a classic discussion of the symmetry number of ethane in the terms of this analysis. Mayer and Mayer¹⁸ wrote that the symmetry number of ethane depends upon temperature, with the methyl rotation contributing a factor of 3 to the symmetry number when k_BT is larger than the rotational energy barrier, and 1 when k_BT is smaller. The potentially puzzling concept of a temperature-dependent symmetry number follows from their different choices of the range allowed for the methyl rotation when computing its partition function at low versus high temperature. At high temperature, where the methyl readily crosses the rotational barrier, they chose to integrate the rotational coordinate from 0 to 360°, requiring a symmetry number of 3. At low temperature, they chose to consider only a single well of the torsional potential, integrating the rotational coordinate from 0 to 120°, avoiding interchange of hydrogen atoms and leading to a symmetry number of 1. Pitzer made a similar point in relation to the inversion of the ammonia molecule: one can either integrate over both energy wells and include a factor of 2 in the symmetry number, or else integrate over only one well so that the inversion does not contribute to the symmetry number.⁸ The analyses of Pitzer and of Mayer and Mayer confirm that the correct choice of symmetry number is not a physical property of a molecule, but depends upon how the configurational integral is formulated. It determines the number of times that identical configurations are overcounted. Thus, Mayer remarked that the symmetry number “....is less a characteristic of the molecule itself, than of the coordinate system and Hamiltonian which is used.”¹⁹

Fluxional molecules

Molecules in which atoms can interchange by mechanisms other than bond rotations may be termed fluxional. In phosphorus pentafluoride, a classic example, equatorial and axial ligands can exchange positions by Berry pseudorotation.²⁰ A configuration integral over the full range of spherical coordinates for each F atom will lead to 5! different permutations of the fluorines, so that one must set the symmetry number to 5!.

Noncovalent complexes and binding free energies

We now consider a supramolecular complex comprising multiple molecules held together by noncovalent forces, such as hydrogen bonds and dispersion forces, where one or more of the component molecules possess topological symmetry. Once again, the symmetry number by which the configuration integral of this complex should be divided depends upon how the configuration integral is written. If the integral ranges over configurations that are identical except for the interchange of symmetry-related atoms, then the symmetry number must be greater than 1 to compensate for the resulting overcount. Consider, for example, a complex of β-cyclodextrin with benzene (Figure 2). If the configuration integral ranges over all possible orientations of the complex and also of the benzene molecule relative to its cyclodextrin host, then the integral will overcount by a factor of 7 due to the topological symmetry of the host and by a factor of 12 due to the topological symmetry of the benzene guest, leading to a symmetry number of 7 × 12 = 84. Alternatively, and equivalently, one may restrict the ranges of these rotations in the configuration integral so that overcounting does not occur, in which case the configuration integral will not need to be corrected by a symmetry number. Whether or not a particular configuration integral ranges over such internal rotations can depend upon the computational approach. For example, a computer simulation may or may not surmount the energetic barrier separating symmetry-related conformations, and it is incumbent upon the practitioner to determine whether a symmetry number is required.

Figure 2.

Two views of a molecule of β-cyclodextrin (a cyclic polymer of 7 glucoses) with a bound benzene molecule. Cyan: carbon atoms. Red: oxygen atoms. Hydrogen atoms are suppressed for simplicity.

Group theory and symmetry numbers

One may be tempted to compute the symmetry number of a molecule with multiple internal and external symmetries by identifying its symmetry elements and multiplying their orders. For example, benzene has one 6-fold rotational symmetry, three 2-fold rotations around axes defined by diametrical carbons, and three more 2-fold rotations around the centers of diametrical bonds, so one might imagine its symmetry number to be (6)(2³)(2³)=384, for the case where one integrates over the full range of its rotational coordinates. However, these symmetry elements are not independent; for example, it is not possible to have the six-fold axis and only one perpendicular two-fold axis. As a consequence, the total number of identical permutations – i.e., the symmetry number – is less than or equal to the product of the orders of the symmetry elements. Thus, for the benzene example, there are only 12 permutations, not 384. The question, then, is how to determine the true number of permutations generated by a set of identified symmetry elements.

Group theory provides an elegant solution to this problem. The set of atomic permutations associated with a molecule’s symmetry elements has the properties of closure, and associativity, as well as existence of an identity element and of inverses. As a consequence, these permutations constitute a mathematical group, and the count of its elements is the order of the group. Importantly, the closure property of groups means that applying redundant symmetry operations causes no change in the number of resulting permutations, since those operations were already included implicitly. For example, if the configuration integral for benzene includes the full range of rotations, then the six-fold rotation plus any two-fold rotation can be used to generate the full group. Adding and applying more of benzene’s two-fold rotational symmetries does not enlarge the group, since those “new” rotations are merely products of the initial two operations. Since each molecular orientation corresponds to a symmetry operation, the symmetry number is equal to the number of distinct elements in the group of symmetry operations that are implicit in the configuration integral. This number is the order of the group.^5,7,21 A practical approach to computing molecular symmetry numbers, based on group theory, is provided in a later section of this paper.

Note that the relevant symmetry group is not necessarily the same as the molecular point group, which may contain reflections, inversion, and other operations whose corresponding permutations are not included in the configuration integral. Likewise, it is different from the permutation-inversion group (or molecular symmetry group) used in molecular spectroscopy.^6,22 In the case of benzene, the relevant symmetry group contains 12 independent operations: the identity operation, five rotations about the six-fold axis [rotation through n(60°), where n=1, 2, 3, 4, and 5], and the six additional two-fold rotations described earlier.

Summary of symmetry numbers in the classical case

The configuration integral overcounts states because it includes states that are identical but for a permutation of indistinguishable atoms. To correct this overcounting, the configuration integral must be divided by a symmetry number, σ. Thus, the symmetry number is equal to the number of different permutations of indistinguishable atoms generated by the configurational integral. The value of σ depends upon how the configuration integral is formulated, in particular upon the ranges over which its conformational variables are integrated. Although a flexible molecule at nonzero temperature essentially never adopts a perfectly symmetrical conformation, due to random thermal motion, it still can have a symmetry number greater than 1, because any topological symmetries that it possesses allow multiple permutations of its atomic coordinates to correspond to the same configuration of indistinguishable atoms. As a consequence, the symmetry number remains meaningful for a flexible molecule randomized by thermal agitation. In addition, because the topological symmetry of a molecule is preserved even as the molecule thermally samples geometrically asymmetric conformations, there appears to be no need, in this context at least, for using continuous symmetry numbers²³ or assigning different symmetry numbers to different conformers²⁴. Analogous reasoning holds as well for fluxional molecules and supramolecular complexes comprising one or more molecular components with topological symmetry. The symmetry number of a molecule is equal to the order of the mathematical group whose elements are the indistinguishable permutations of identical atoms associated with the molecule’s topological symmetries. Thus, the problem of computing the symmetry number is equivalent to finding the order of this group.

Symmetry Numbers in Quantum Statistical Thermodynamics

Quantum-mechanical partition functions are typically computed in the ideal-gas approximation, so that one may focus on the molecular partition function of a single molecule. The molecular partition function for a given temperature, T, can be written as

$$Q(T)=\sum _{i}exp(-\beta {\epsilon }_i),$$ (6)

where ε_i is the i^th quantized energy level for a single molecule, and the sum is over all energy levels. No level degeneracies or symmetry numbers are included in eq. (6), and indeed they are unnecessary. However, eq. (6) is rarely used in practice because such a table of individual energy levels is usually inconveniently large, and because an adequate table is seldom available from experimental measurements. Instead, a simplified model is used to describe the molecular energy levels.

For a reasonably rigid molecule, the simplest and most popular partition function is based upon the rigid-rotor/harmonic-oscillator (RRHO) model, in which translation, rotation, and vibration are assumed uncoupled and separable. Thus, the molecular partition function is a product of translational, rotational and vibrational parts, each with its own quantum numbers:

$$Q(T)=Q_{\text{trans}}(T)Q_{\text{rot}}(T)Q_{\text{vib}}(T)$$ (7)

Electronic degeneracies and excited states are included when appropriate, as for free radicals, but electronic degrees of freedom are not discussed here. Internal and spin nuclear degrees of freedom are not included in practical thermodynamic tables because they do not change during ordinary chemical reactions.^25,26

The point here is that the simple rigid-rotor partition function, Q_rot(T), includes all rotational levels, including any forbidden levels. Certain levels may be forbidden because of the Pauli exclusion principle, which constrains the symmetry of the wavefunction (in our case, the nuclear wavefunction). This constraint, described in many textbooks, is that the wavefunction, ψ, must be either antisymmetric (for fermions) or symmetric (for bosons) with respect to the interchange of any two identical nuclei. (Fermions and bosons have, respectively, half-integer or integer values of the spin quantum number.) The RRHO model neglects this constraint, so it may over-count the rotational energy levels. The rotational partition function it yields must therefore be divided by a rotational symmetry number, σ, to correct this overcounting. This correction modifies the entropy by −Rln(σ) but does not influence the heat capacity or the enthalpy because only derivatives of ln(Q) appear in the latter quantities. Note that, since the quantum treatment is based upon the energy levels (i.e., stationary states), it is not necessary to consider instantaneous distortions due to molecular vibration, as in the classical treatment. A vibrational energy level corresponds to a time-independent vibrational wavefunction, which is spatially delocalized.

In a classical calculation, the symmetry number provides an exact correction, because the indistinguishable configurations have identical energies. However, as noted by Davidson,²⁷ in quantum mechanics the use of a symmetry number is an approximation. The correction is not for overcounting of configurations, but for overcounting of energy levels, typically rigid-rotor energy levels. The energy levels occur in sets of σ levels of which only one is allowed, as shown below. Dividing the partition function, Eq (6), by σ is not exact because those σ levels have somewhat different energies and therefore make unequal contributions to Eq (6). This is a good approximation when the spacing between rotational levels is much smaller than kT. But at low temperatures it is necessary to use eq. (6), including only allowed levels in the sum.

These ideas are elaborated in the following subsections. We first review the symmetry number of the hydrogen molecule at the textbook level, and then discuss it again through the lens of group theory. We then generalize the approach to discuss the symmetry numbers of molecules with multiple, arbitrary symmetry elements, including internal rotors and degenerate rearrangements.

Textbook presentation of the hydrogen molecule

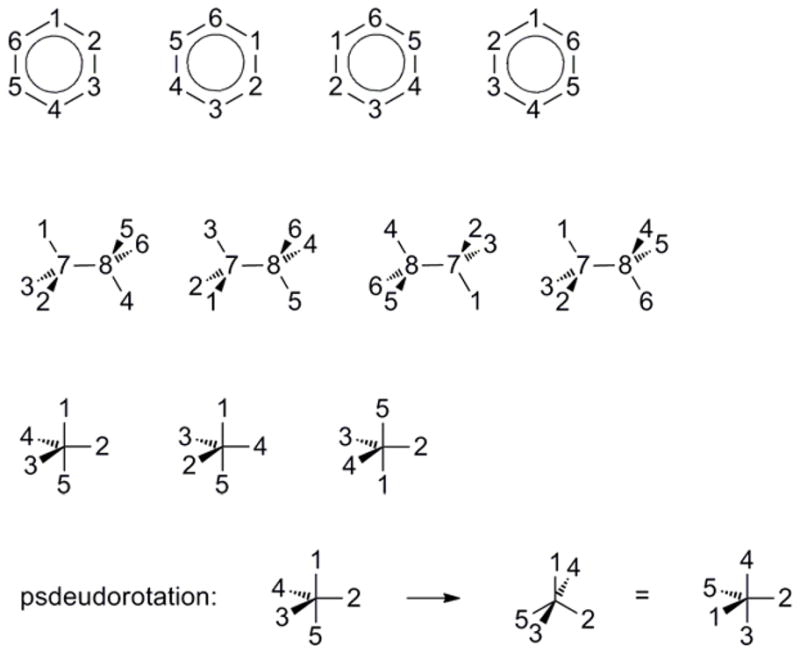
The H₂ molecule is the only example typically treated in textbooks. The hydrogen nucleus has spin quantum number I = ½, making it a fermion. Denoting the axial projection of spin m_I = ½ as α and m_I = −½ as β, in the usual convention, the four possible nuclear spin functions ψ_spin are αα, (αβ + βα), ββ (the three triplet components, known as ortho-hydrogen), and (αβ − βα) (the singlet, para-hydrogen). The triplet state is symmetric (that is, unchanged) with respect to interchange of the two nuclei, while the singlet state is antisymmetric (changes sign). The Pauli principle requires the total wavefunction, ψ = ψ_spinψ_rot, to be antisymmetric. Thus, when ψ_spin is the triplet (symmetric), ψ_rot must be antisymmetric, and when ψ_spin is the singlet (antisymmetric), ψ_rot must be symmetric. Molecular rotation serves to interchange the nuclei, so ψ_rot is antisymmetric for odd values of the rotational quantum number, J, and symmetric for even values. The conclusion is that for the triplet spin function (ortho H₂), only odd rotational levels are allowed, and for the singlet spin function (para H₂) only even rotational levels are allowed. In other words, regardless of the nuclear spin function, only half of the rigid-rotor rotational levels are allowed. Thus, the simple rigid-rotor model overcounts states by a factor of 2 and the required symmetry number is σ = 2. In the case of D₂, the deuterium nucleus has spin quantum number I = 1 and is a boson, requiring that ψ be symmetric. Reasoning as above leads to the conclusion that only even values of J are allowed for symmetric spin functions and only odd values are allowed for antisymmetric spin functions. The symmetry number is still σ = 2 because, for any spin state, only half of the rotational levels are allowed. For the HD molecule there are no identical nuclei, so there are no constraints from the Pauli principle. The symmetry number is therefore σ = 1; all rigid-rotor rotational levels are allowed and there is no overcounting.

Although H₂ is a commonly used example, it is arguably the worst possible choice because of its large rotational constant. Pairs of energy levels are far from degenerate. For example, the difference between the two lowest levels is Δε/k_B ≈ 175 K, and the spacing increases for higher levels. The symmetry number correction is crude for this molecule and the rigid-rotor model should be avoided.

Explicit group theory for hydrogen

The usual reasoning for H₂, reproduced above, is difficult to generalize to molecules with larger numbers of identical, symmetrically arranged nuclei. An alternative presentation, based upon rotational symmetry groups,²⁸ is given below. Note that spectroscopists have long used group theory and the Pauli principle to explain line intensities, although symmetry numbers are not used in spectroscopy.²² For their purposes, spectroscopists determine the fraction of possible nuclear spin functions that are compatible with a given rotational eigenfunction. Conversely, the symmetry number is the reciprocal of the fraction of possible rotational eigenfunctions that are compatible with a given nuclear spin function. As shown below, this fraction is the same for all possible choices of nuclear spin function and is the same for both fermions and bosons.

In the RRHO model, only rotations interchange identical nuclei, so consider the rotational group C₂ for the H₂ molecule. (We use bold italic for the name of a group and normal italic for the name of a symmetry operation.) Its character table is shown in Table 1 as in textbooks, except that we have added (+) or (−) above each symmetry operator to indicate whether is corresponds to an even (+) or odd (−) number of pairwise interchanges of identical nuclei. The (+) parity means that the sign of the wavefunction under that operation never changes, regardless of the sign of the corresponding character. For the operation C₂ (rotation by 180°), the (−) parity means that a character of −1 changes sign and a character of +1 does not change sign.

Table 1.

Character table for rotation group C₂.

C2	(+)E	(−)C2
A	1	1
B	1	−1

We require that the total wavefunction ψ= ψ_spinψ_rot be antisymmetric with respect to nuclear pair interchange. In terms of Table 1, we require that the character of the irreducible representation Γ = Γ_spin × Γ_rot (the direct, or outer, product) be −1 under C₂ because C₂ has negative parity. The character under E must be +1 because E has positive parity. Thus, we require Γ = B for the total wavefunction. First, consider ψ_spin. To determine the relevant irreducible representations, it does not matter which linear combination of basis functions we choose. Instead of the symmetrized spin functions used above, we choose the simpler basis {αα, αβ, βα, ββ} because it is easier to generalize. The characters of its representation are [4, 2], since all four functions are preserved under the identity operation E and two functions (αα and ββ) are preserved under C₂. This representation can be reduced to 3A + B. The A representations constitute the triplet and the B representation is the singlet. Since both A and B are possibilities, we will consider Γ_spin = A and Γ_spin = B in turn.

Next, consider ψ_rot. In his treatment of five polyatomic molecules, Wilson used explicit rotational wavefunctions.²⁹ Instead, for simplicity and generality, we use the rotational operations to represent rotational wavefunctions. This is equivalent to considering rotations semi-classically, and is the central approximation in the present treatment. To justify it, we note that the rotational states fall into sets that span all irreducible representations of the rotational symmetry group.⁴ Thus, for H₂ we use the basis ¹⁵, which are exactly the symmetry operations of the group, instead of a basis of rotational wavefunctions. The characters of its representation are Γ_rot = [2, 0], since both operations are unchanged by E and neither is preserved by C₂. Γ_rot is the reducible representation for any one of the sets of rotational states, as represented semi-classically by the corresponding rotational operations. In reduced form, Γ_rot = A + B. Consequently, the weights for A and B are equal.

To obtain the symmetry representation for ψ = ψ_spinψ_rot, we take the direct product of the representations for ψ_spin and ψ_rot. The four possible situations are shown in Table 2. For ψ to have symmetry B when ψ_spin has symmetry A, ψ_rot must have symmetry B. Since B has a weight of ½ within Γ_rot (the dimensionality of the B representation divided by the dimensionality of the Γ_rot representation), only half the rotational levels are allowed. Likewise, when ψ_spin has symmetry B, ψ_rot must have symmetry A. Once again only half the rotational levels are allowed. Since only half the rotational levels are allowed, regardless of the spin function, the over-counting of rotational states can be corrected (approximately) by using the symmetry number σ = 2.

Table 2.

Representations of wavefunctions for H₂ under the group C₂. The fractions (½) are the weights of the irreducible representations within Γ_rot= A + B.

Γspin	×	Γ rot	=	Γ
A	×	A (½)	=	A
A	×	B (½)	=	B
B	×	A (½)	=	B
B	×	B (½)	=	A

For D₂ (bosons instead of fermions), the reasoning is similar except that ψ must have symmetry A to be symmetric with respect to interchange. Deuterons have I = 1, so m_I = 1, 0, or −1. There are now 3² = 9 basis spin functions, {11, 10, 1 1̄, 01, 00, 01̄, 1̄1, 1̄0, 1̄1̄} with representation [9, 3] = 6A + 3B. Again we consider all possibilities, Γ_spin = A and Γ_spin = B, in turn. The rotational functions are the same as for H₂, Γ_rot = A + B, so the weights are still ½ for A and ½ for B. From Table 2, to achieve Γ = A we see that the symmetry number is again σ = (½)⁻¹ = 2. For HD, we could treat the problem formally using the C₁ rotation group. This group has only one irreducible representation, A. All possibilities are allowed and σ = 1.

Three-fold symmetry: chloromethane

Chloromethane, CH₃Cl, has three identical nuclei that can be interchanged by molecular rotation. The point group for the molecule is C_3v but we use the rotational sub-group C₃ because the vertical reflection operations are not part of the RRHO model; i.e., the corresponding motions are not included in the partition function. The character table is given in Table 3, where we have combined the conjugate complex-valued irreducible representations, for convenience. All operations have positive parity because they all correspond to an even number of pair interchanges. Thus, both fermions and bosons require that the character of the irreducible representation of Γ be +1 under E, under C₃, and under $C_3^2$. That is, ψ must have symmetry A.

Table 3.

Condensed character table for rotation group C₃.

C3	(+)E	(+)	(+) $C_3^2$
A	1	1	1
E	2	−1	−1

There are 2³ = 8 basis spin functions, {ααα, ααβ, αβα, αββ, βαα, βαβ, ββα, βββ} with representation [8, 2, 2] = 4A + 2E. Note that the only information we need is the list of possible values for Γ_spin (that is, A and E); the numerical weights (4 and 2) of the spin functions are irrelevant. We again take the rotational basis functions semi-classically as the operations of the group, {E, C₃, $C_3^2$} with representation Γ_rot = [3, 0, 0] = A + E. Since E is a two-dimensional representation (see Table 3), the weights are 1/3 for A and 2/3 for E. The possible products Γ = Γ _spin × Γ_rot are shown in Table 4. When ψ_spin has symmetry A, ψ_rot must also have symmetry A, which occurs for only 1/3 of the possible rotational states. When ψ_spin has symmetry E, ψ_rot must also have symmetry E, which is 2/3 of the possible rotational states. However, the resulting ψ = ψ_spinψ_rot has symmetry A for only 2/4 of the E × E product states, for a total weight of (2/3)(2/4)= 1/3. Thus, the symmetry number σ = (1/3)⁻¹ = 3 regardless of ψ_spin.

Table 4.

Representations of proton wavefunctions for CH₃Cl under the group C₃. The fractions are the weights of the irreducible representations within Γ_rot = A + E and d_spin is the degeneracy of Γ_spin.

dspin	Γspin	×	Γrot	=	Γ
1	A	×	A (1/3)	=	A
1	A	×	E (2/3)	=	E
2	E	×	A (1/3)	=	E
2	E	×	E (2/3)	=	2A + E

For CD₃Cl there are (2I+1)³ = 27 basis spin functions with representation [27, 3, 3] = 11A + 8E, so ψ_spin can again have symmetry A or E. Since the deuteron is a boson, ψ must have character +1 for operations of either parity. Thus, we require ψ to have symmetry A. By the same reasoning as for CH₃Cl, the symmetry number σ = 3. If the three hydrogen atoms are not identical, as in the isotopologue CH₂DCl, there are no molecular rotations that interchange a pair of identical nuclei and the Pauli principle is not constraining. Thus, the appropriate rotational group is C₁ and the symmetry number σ = 1.

In the general C₃ case, we consider all possible symmetries for ψ_spin, that is, Γ_spin = A and E in turn. As in the case of chloromethane, Γ_rot = A + E. All operations have positive parity so ψ must have symmetry A for either fermions or bosons. From Table 4, we find σ = 3 generally.

General quantum mechanical case

The group theory approach to the hydrogen and chloromethane molecules, above, can be repeated for any point group, although it becomes tedious for higher-order groups and for multiple rotational axes. The essential point is that ψ must obey the Pauli principle. If the identical nuclei are bosons, then the irreducible representation of ψ must have a character of +1 for every operation in the group. If the identical nuclei are fermions, then the irreducible representation of ψ must have a character of +1 for every even-parity operation and a character of −1 for every odd-parity operation.

The only operations affected by the Pauli principle are those that interchange identical nuclei. Thus, in the RRHO model, only molecular rotations are of interest. For each possible irreducible representation of ψ_spin, the symmetry of ψ is obtained as the direct product with the reducible representation of ψ_rot, representing a set of rotational states. Only some of the possible rotational states are allowed (by the Pauli principle) for each possible symmetry of ψ_spin. Although the symmetry of ψ_spin affects which rotational states are allowed, the fraction of states that are allowed is found to be independent of the particular spin state. This fraction is the reciprocal of the symmetry number.

More quantitatively, suppose for generality that ψ_spin can be of any symmetry, so that every irreducible representation in the group is considered, one at a time, for Γ_spin. Next obtain Γ_rot in the basis of rotational operations, as in the preceding examples, as a semi-classical surrogate for a basis of rotational wavefunctions. Since those are the same rotational operations that compose the group of interest, the representation is Γ_rot = [h, 0, 0, …, 0], where h is the order of the group. It follows that

$${\mathrm{\Gamma }}_{\text{rot}}=\sum _i{\mathrm{\Gamma }}_i,$$ (8)

where the Γ_i are the irreducible representations of the group. (This may be recognized as the regular representation of the group.^30,31) Depending upon the nuclear spin and the orders of the rotational axes, the allowed, one-dimensional, irreducible representation for ψ will be either the totally symmetric representation (often called A) or that with characters of −1 under all odd-parity operations and +1 under all even-parity operations (often called B). Call this allowed one-dimensional representation Γ_Pauli. By analogy with the previous examples, the fraction of allowed rotational states is then given by eq. (9). In the denominator, one factor of h is for the dimensionality of Γ_rot, as noted above, and the other factor of h is the usual normalization factor for projecting out Γ_Pauli. The divisor d_spin is the dimensionality of Γ_spin.

$${\sigma }^{-1}=\frac{({\mathrm{\Gamma }}_{\text{spin}}\times {\mathrm{\Gamma }}_{\text{rot}})·{\mathrm{\Gamma }}_{\text{Pauli}}}{d_{\text{spin}}{h}^2}$$ (9)

Applying eq. (8), the direct product between the parentheses is [d_spinh, 0, 0, …, 0] for any choice of Γ_spin. Since Γ_Pauli is one-dimensional, the numerator then simplifies to d_spinh. Thus, the symmetry number is equal to the order of the group,

$$\sigma =h.$$ (10)

Since the group includes one operation for every possible orientation of the molecule, this is the same as the classical value, discussed above.

Internal symmetry numbers

When a molecule is flexible, so that it contains rotatable groups, the internal rotations are often incorporated into the partition function by using a hindered rotor approach.^32–36 The hindered rotor model is more sophisticated than the RRHO model and should give more reliable results. However, since it introduces additional possibilities for interchange of identical nuclei, an “internal” symmetry number may be required to correct the model to satisfy the Pauli principle. Fortunately, no new concepts are introduced and Eqs. (9) and (10) still apply for the total symmetry number. Now the relevant symmetry group includes intramolecular motions in addition to rotations of the whole molecule. The group should include all symmetry operations that are included in the model partition function being used, and no others.

There is sometimes confusion about when an internal symmetry number should be used and what its value should be. In particular, some practitioners worry that it introduces arbitrariness and discontinuities into the computed thermodynamic functions. On the contrary, the symmetry number ensures continuity.^8,18,19 This may be appreciated by considering a hypothetical molecule with one symmetrical, internal rotor.^18,27 If the barrier to rotation is very high, the molecule can be considered rigid and we may use the RRHO model; no internal symmetry number is needed. However, even with a high barrier, we can choose to use a hindered-rotor model instead. This will lead to state degeneracies because the rotor can be in any of its equivalent orientations with negligible splitting. Since there are more states in the hindered-rotor model, the partition function is larger. But since the molecule has not changed, all our models should produce essentially the same partition function. Thus, the hindered-rotor model requires an internal symmetry number to offset its additional states.

Evaluation of Symmetry Numbers

As discussed above, in both the classical and quantum settings, the symmetry number equals the order of the symmetry group implied by the choice of partition function or configuration integral. As a consequence, group theory is useful for determining the symmetry number. In particular, the closure property of groups means that applying redundant symmetry operations causes no change in the group, so one is protected from overestimating the symmetry number. For example, if the configuration integral for benzene includes the full range of rotations, then the six-fold rotation plus any two-fold rotation generate the molecule’s full symmetry group, but adding more of benzene’s two-fold rotational symmetries does not enlarge the group, since those added rotations are already present as products of the initial two operations.

Given a set of symmetry operations, the freely available Groups, Algorithms, Programming (GAP)³⁷ software for group theory can be used to evaluate the symmetry number of a molecule with complicated symmetries. One simply inputs a list of topological symmetries, expressed as permutations of identical atoms, and then asks for the order of the group they define. The procedure may be described as follows.

1. Draw the molecule with the atoms numbered. It is only necessary to number enough atoms to specify all symmetry operations, but numbering additional atoms will give the same result.

2. For each molecular symmetry element, draw at least one representative atomic permutation. It is only necessary to specify enough symmetry elements to generate the desired group, but specifying additional, redundant elements does not lead to error and is recommended when in doubt.

3. Enter the atom permutations from step (2) into the GAP program and compute the order of the resulting group.

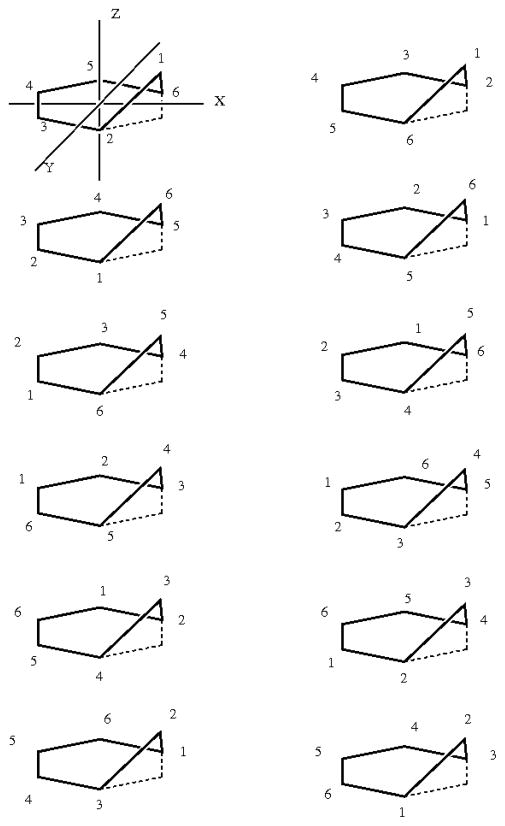
Consider benzene as an initial example. (1) It is drawn, with atoms numbered, in Scheme 1. Hydrogen atoms are omitted for simplicity; including them does not affect the result. (2) The six-fold rotation (through 60°) may be described as the atom ordering [6,1,2,3,4,5] and one of the two-fold rotations, around an axis bisecting C-C bonds, as [6,5,4,3,2,1] (see Scheme 1). The other two-fold rotations are omitted because they are redundant with the six-fold and the first two-fold. However, including the other two-folds is not wrong and will yield the same result. It is also unnecessary to include the initial permutation, [1,2,3,4,5,6], because it corresponds to the identity operation and is included automatically. (3) The two permutations are entered into GAP by defining variables (here called “c6” and “c2”) as the corresponding permutations:

Scheme 1.

gap> c6:= PermList( [6,1,2,3,4,5]);
(1,6,5,4,3,2)
gap> c2:= PermList( [6,5,4,3,2,1]);
(1,6)(2,5)(3,4)

(After each variable is defined, GAP echoes the permutation in cycle notation. This is a standard notation, but is not important in the present application.) Next, use the “Group” command to generate a group, which we name “Benzene”, from these two permutations; and finally, the “Order” command computes the order of this group, which is the desired symmetry number.

gap> Benzene:= Group(c6, c2);
Group([(1,6,5,4,3,2), (1,6)(2,5)(3,4)])
gap> Order(Benzene);
12

(Note that the GAP language is case-sensitive.) As discussed above, an additional permutation (here called “c2a”) associated with another two-fold rotational symmetry is redundant and therefore does not change the order of the group:

gap> c2a:= PermList( [1,6,5,4,3,2]);
(2,6)(3,5)
gap> Benzene:= Group(c6, c2, c2a);
Group([(1,6,5,4,3,2), (1,6)(2,5)(3,4), (2,6)(3,5)])
gap> Order(Benzene);
12

One may furthermore write out all the different permutations within the group in order to check that the symmetry operations of the group make sense. Naming the carbons C1, C2, C3, C4, C5, C6, we have:

gap> AtomNames:= [“C1”, “C2”, “C3”, “C4”, “C5”, “C6”];
[“C1”, “C2”, “C3”, “C4”, “C5”, “C6”]
gap> Orbit(Benzene, AtomNames, Permuted);
[[“C1”, “C2”, “C3”, “C4”, “C5”, “C6”],
[“C3”, “C4”, “C5”, “C6”, “C1”, “C2”],
[“C5”, “C6”, “C1”, “C2”, “C3”, “C4”],
[“C2”, “C3”, “C4”, “C5”, “C6”, “C1”],
[“C4”, “C5”, “C6”, “C1”, “C2”, “C3”],
[“C6”, “C1”, “C2”, “C3”, “C4”, “C5”],
[“C1”, “C6”, “C5”, “C4”, “C3”, “C2”],
[“C3”, “C2”, “C1”, “C6”, “C5”, “C4”],
[“C5”, “C4”, “C3”, “C2”, “C1”, “C6”],
[“C2”, “C1”, “C6”, “C5”, “C4”, “C3”],
[“C4”, “C3”, “C2”, “C1”, “C6”, “C5”],
[“C6”, “C5”, “C4”, “C3”, “C2”, “C1”]]

As a second example, consider ethane. (1) Start by numbering the atoms as shown in the left-hand side of Scheme 1. Although we have included numerical labels for the carbon atoms in this example, this is not necessary. (2) If the configuration integral encompasses the full range of all external and internal rotational variables, then there is an overall symmetry corresponding to rotation by 120° around the three-fold axis defined by the 7–8 bond, which may be expressed by the representative permutation [3,1,2,5,6,4,7,8] (see Scheme 1). The two-fold rotation in the plane of the paper is represented by [4,5,6,1,2,3,8,7], and the internal rotation can be expressed as the rotation of a single methyl group, [1,2,3,6,4,5,7,8]. Application of GAP tells us that the combined and repeated action of these permutations upon each other, until closure, generates a group of order 18.⁴ The character table for this group has been derived by Wilson.¹⁷

gap> c3:= PermList( [3,1,2,5,6,4,7,8]);
(1,3,2)(4,5,6)
gap> c2:= PermList( [4,5,6,1,2,3,8,7]);
(1,4)(2,5)(3,6)(7,8)
gap> torsion:= PermList( [1,2,3,6,4,5,7,8]);
(4,6,5)
gap> Ethane:= Group(c3, c2, torsion);
Group([(1,3,2)(4,5,6), (1,4)(2,5)(3,6)(7,8), (4,6,5)])
gap> Order(Ethane);
18

Finally, we consider phosphorus pentafluoride, which has a three-fold symmetry axis and three two-fold axes (Scheme 1). In addition, equatorial and axial fluorine atoms can interchange by the Berry pseudorotation mechanism.²⁰ Recognizing that the full set of two-fold rotations would be redundant, we include only one of them, and write the set of representative permutations shown in Scheme 1 and processed as follows with GAP:

gap> c3:= PermList( [1,4,2,3,5] );
(2,4,3)
gap> c2:= PermList( [5,2,4,3,1] );
(1,5)(3,4)
gap> berry:= PermList( [4,2,1,5,3] );
(1,4,5,3)
gap> PF5:= Group(c3, c2, berry);
Group([(2,4,3), (1,5)(3,4), (1,4,5,3)])
gap> Order(PF5);
120

Thus, the order of this group equals 120, which is the symmetry number of PF₅ when the configuration integral includes psdeudorotation. (The reader can confirm that including all the redundant two-folds does not change this result.) Since the symmetry operations lead to all possible interchanges of the fluorines, this is also the number of permutations of five objects, 5!.

The Appendix presents additional worked examples.

Applications and Implications

We now consider some of the implications of this analysis for chemical thermodynamics and computations. Note that the treatment of symmetry numbers in chemical rate calculations has recently been discussed,³⁸ so it is not specifically addressed here.

Molecular symmetry and binding affinity

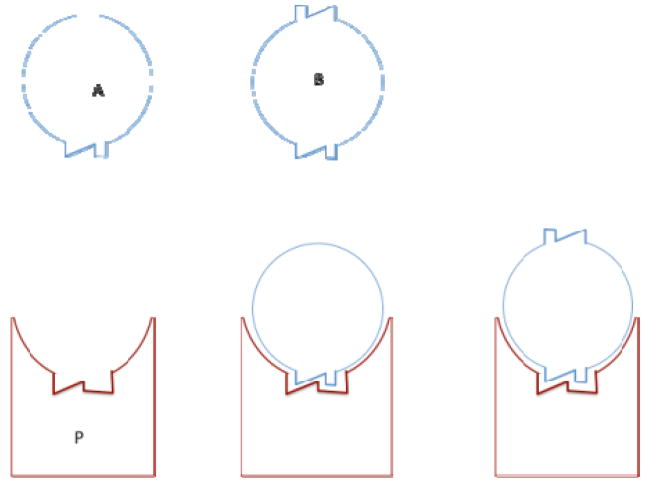
In medicinal chemistry and drug design, the question sometimes arises whether a more symmetric drug-like ligand will tend to bind a targeted protein P with higher affinity than a less symmetric one. A potential rationale for this expectation is that a highly symmetric ligand will have less entropy in its unbound state, reducing the entropic penalty for binding. One may analyze this question by comparing two rigid ligands that bind analogously but possess different symmetry. Figure 3 diagrams such a comparison: compound A has a symmetry number of 1 and has only one way to bind the target; compound B has 2 symmetrically disposed groups that can interact with the target just as compound A does, and has a symmetry number of 2 if the configuration integral is written as ranging over all orientations. To isolate any consequences of symmetry, we assume that, when compound B is bound, the other binding moiety that does not fit the target’s binding site makes no contribution to the affinity. For simplicity, we consider binding to take place in vacuo rather than in solvent. (Including solvent formally would only make the equations more complicated without changing the final result.) Given these simplifications, and accounting for quantum indistinguishability, the configuration integrals of the free forms of A and B are related as follows:

$$Z_A=2Z_B$$ (11)

Figure 3.

Competitive binding of asymmetric and symmetric ligands to a protein.

Thus, the free form of A has a statistical weight twice that of B, suggesting that A might bind less strongly than B. However, in the bound complex, the rotational symmetry of B becomes a two-fold internal symmetry of the complex, analogous to the three-fold rotational symmetry of a methyl group. As a consequence,

$$Z_{AP}=2Z_{BP}$$ (12)

Note that the 2-fold ratios in these two expressions hold whether we integrate the rotation of B around its symmetry axis from 0 to 2π and divide by the internal symmetry number of 2, or instead integrate from 0 to π and use a symmetry number of 1. The binding constant is directly related to the ratio of the bound to free configuration integrals,^39,9 and it is evident that

$$\frac{Z_{AP}}{Z_A}=\frac{Z_{BP}}{Z_B}$$ (13)

We conclude that the greater symmetry of ligand B leads neither to increased nor decreased affinity relative to the less symmetric, but otherwise matched, ligand A, because the symmetry has an equal effect on the statistical weights of the bound and free states. Note that, if one neglects indistinguishability, then Z_A=Z_B and Z_AP=Z_BP, so again, there is no difference in affinity. Similar considerations apply to the entropies of fusion and sublimation, as discussed below.

Exploitation of symmetry to speed free energy calculations

Calculating the free energy of a molecule, or a free energy change, typically requires time-consuming sampling of all of its low-energy conformations. If a molecule has symmetries, then these can sometimes be used to reduce the work of sampling. For example, the full configuration integral of the bound state of ligand B in the prior example can be obtained by sampling only one of its two potential bound conformations. One need only be careful to treat symmetries consistently between the free and bound states. Thus, if one samples only one bound state of B, then one must divide the rotational part of the configurational integral of B in the free state by 2. In thermodynamic integration and free-energy perturbation calculations, these ideas can be implemented by applying artificial restraints to prevent a molecule from sampling symmetry-related conformations.^40–43 In the mining minima approach,^44,45 the energy minima generated by conformational sampling are filtered to remove symmetry-related repeats, based upon a program that computes root-mean-square conformational differences while accounting for internal and external symmetries.

Isotopologues

Isotopic substitution is another common point of confusion. For benzene, the symmetry number of 12 corresponds to a contribution to the entropy of −Rln(12). But for asymmetrically labeled benzene, such as with one atom of ¹³C and one atom of ²H bonded elsewhere, the symmetry number is 1. This means that its absolute entropy in the gas phase is 20.6 J mol⁻¹ K⁻¹ greater than that of homoisotopic benzene. This is a big difference, which one might expect to be easily measureable, for example during the sublimation or melting of the solid. However, the difference is essentially unmeasurable because of the difficulty of obtaining a perfect, isotopically aligned crystal of the labeled material. Since the isotopically disordered crystal contains all twelve possible orientations of the labeled molecules, its entropy exceeds that of the perfect crystal by an amount that exactly cancels the theoretical increase in entropy of sublimation or fusion. Thus, treating ¹²C and ¹³C as indistinguishable here would not lead to a measurable error, as touched on in the text preceding Eq 5.

On the other hand, in isotopic substitution reactions, changes in symmetry numbers may be the dominant influence. For example, an undergraduate laboratory exercise uses the reaction⁴⁶

$${{}^{131}\text{I}}^{-}+{{}^{127}\text{I}}_2={{}^{127}\text{I}}^{-}+{{}^{131}\text{I}}^{127}\text{I}.$$ (14)

As usual, the equilibrium constant K = exp(−ΔG/RT) = exp(−ΔH/RT)exp(ΔS/R). To a good approximation, ΔH = 0 so that K ≈ exp(ΔS/R). Since ΔS is dominated by the change in symmetry number from 2 (product of symmetry numbers of the reactants) to 1 (product of symmetry numbers of the reaction products), ΔS ≈ Rln(2) and K ≈ 2 as observed.⁴⁶ This prediction is not surprising and the same result may be reached by using a simple statistical argument. Indeed, Ehrenfest and Trkal demonstrated that symmetry contributes a factor of 2 to the equilibrium constant for the reaction

$$\text{ABA}=\text{AAB}$$ (15)

where A and B are different elements, even though their work preceded the discovery of quantum indistinguishability. It is also worth noting that, if one were unable experimentally to distinguish between ¹²⁷I₂ and ¹³¹I¹²⁷I, then the reaction in Eq 14 would not be detectable and one might as well treat the two isotopes as indistinguishable.

Conclusions

In both classical and quantum statistical thermodynamics, mathematically convenient formulations of the partition function have the physically inconvenient property of overcounting states, and the symmetry number corrects this overcounting. From the perspective of classical statistical thermodynamics, the symmetry number corrects for miscounting of phase-space states in the partition function. From the perspective of quantum mechanics, the symmetry number is a consequence of the requirement that identical particles obey the Pauli principle. In either analysis, the symmetry number equals the order of the group of atomic permutations that are included in the selected partition function. The symmetry number thus arises as a mathematical consequence of the ways we typically compute molecular partition functions. Changing the formulation of the partition function can change the symmetry number, and using the correct symmetry number ensures that the value of the partition function, which is directly related to observable quantities, is independent of how it is formulated.

We are now in a position to answer the questions posed in the Introduction. First, even if a molecule is highly flexible, it can have a symmetry number greater than 1, because it is the topological symmetry, rather the average or instantaneous shape, that leads to the overcounting in a partition function. Second, the symmetry number should account for all external and internal symmetries that are subsumed by the partition function, but no more. Third, a more symmetrical molecule will bind a receptor with the same affinity as a less symmetrical one, all other things being equal. Fourth, the symmetry number is independent of temperature, except in the sense that the appropriate symmetry number can change if one chooses to formulate a different partition function at a different temperature. Finally, the group theory program GAP can be used to assist in the calculation of symmetry numbers for molecules with complex symmetries.

Appendix: Additional examples

These examples follow the quantum analysis, but the resulting symmetry numbers are equally appropriate for the corresponding classical partition functions.

GAP programming language

Numerical results can be obtained easily using the freely available GAP software package for computational group theory.³⁷ No detailed understanding of group theory is needed, but it is necessary to specify a minimal set of symmetry transformations. For example, a transformation that moves atoms 1, 2, and 3 into positions 2, 3, and 1 is denoted as [2, 3, 1], which is simply the list of new positions. Once the necessary transformations are entered, one command generates a group and another command computes the order of the group, which is the required symmetry number.

Methane

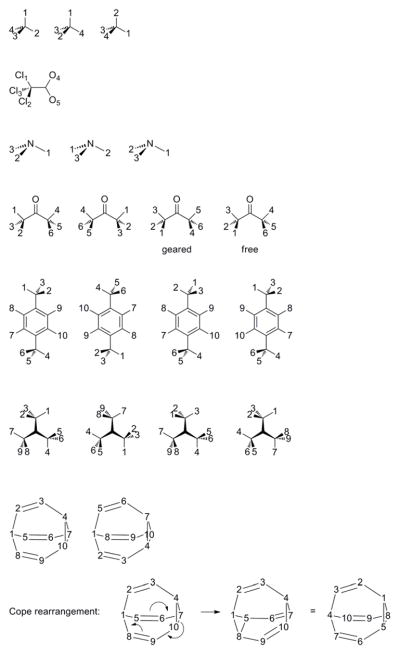
The (homoisotopic) methane molecule has full point-group symmetry T_d, which has order 24. However, this includes 12 operations (reflections and improper rotations) that are not part of the RRHO model. The sub-group that includes only rotational operations is T, which has order h = 12. Thus, the symmetry number is σ = 12. If not all hydrogen nuclei are identical, the number of symmetry operations is reduced, lowering the symmetry number. For example, σ = 2 for CH₂D₂ (C₂ sub-group of point group C_2v). Four commands are needed to obtain this number using GAP. First, number the hydrogen atoms (and the carbon atom, if you wish) in a drawing of methane, as in Scheme 2. Rotation around the vertical three-fold axis maps atoms 1-2-3-4 into positions [1,4,2,3] (see Scheme 2). Rotation around the two-fold axis in the plane of the paper is [2, 1, 4, 3]. The following commands in GAP specify the symmetry operations.

Scheme 2.

gap> c3:= PermList( [1, 4, 2, 3] );
gap> c2:= PermList( [2, 1, 4, 3] );

Finally, generate the group and determine its order (12) using the following commands.

gap> grp:= Group( c3, c2 );
gap> Order( grp );

CCl₃NO₂

The rigid molecule has point-group symmetry C_s, which has order 2. Deleting the irrelevant reflection operation leaves only the C₁ sub-group with σ = 1 in the RRHO approximation. Allowing internal rotation in the homoisotopic molecule, equivalent configurations can be obtained by three-fold internal rotation of the CCl₃ moiety and by two-fold internal rotation of the NO₂ moiety. Combining those operations leads to a group of order h = 6 (isomorphic with C₆), so the symmetry number σ = 6. The torsional potential energy function is six-fold symmetric,⁴⁷ but recall that the symmetry number derives from the Pauli principle and the choice of partition function, not merely the symmetry of the potential energy function. The symmetry and potential energy function for CH₃NO₂ and related molecules were first analyzed by Wilson et al.⁴⁸ To get the symmetry number using GAP, number the atoms, such as 1-2-3 for the chlorines and 4–5 for the oxygens (Scheme 2). The trichloromethyl rotation is then [3,1,2,4,

gap> ccl3:= PermList( [3,1,2,4,5] );
gap> no2:= PermList( [1,2,3,5,4] );
gap> grp:= Group( ccl3, no2 );
gap> Order( grp );

The natural abundances of chlorine isotopes are 75.8% ³⁵Cl and 24.2% ³⁷Cl. Thus, only (0.758³ + 0.242³) = 45.0% of the molecules are homoisotopic with σ = 6. The other 55.0% lack the three-fold operation so have only σ = 2. To be fastidious, the entropy of natural CCl₃NO₂ could be computed as a mixture of the various isotopologues, including the so-called “entropy of mixing” (really an entropy of mutual dilution). Practical thermochemical tables, however, are computed for a single, fictitious isotope with an average mass,²⁵,⁴⁹ which is essentially equivalent to the fastidious treatment.²⁷

CH₃NH₂

As for CCl₃NO₂, the rigid molecule has σ = 1. Allowing methyl rotation leads to a group of order 3. Umbrella inversion of the NH₂ moiety is not a symmetry operation, but its combination with internal rotation of the NH₂ group (through 180°) is a symmetry operation. The resulting group has order 6 as for CCl₃NO₂, so σ = 6 for methylamine when internal rotation and amine inversion are included in the model partition function. To obtain this result mechanically, label the hydrogen atoms in some way, such as 1-2-3 for the methyl group and 4–5 for the amine group. Methyl rotation corresponds to [3,1,2,4,5]. Amine inversion combined with rotation by 180° is [1,2,3,5,4]. These functions, which are the same as in the CCl₃NO₂ example, yield the same group of order 6.

NH₃

Rigid, pyramidal ammonia has point group symmetry C_3v, but only the subgroup C₃ is appropriate for the RRHO approximation, so σ = 3. Using GAP, the corresponding three-fold rotation is [2, 3, 1] and generates a group of order 3. The molecule can undergo an umbrella-like inversion with a modest barrier. Combined with overall two-fold rotation, this is a symmetry operation denoted [1, 3, 2] (Scheme 2). The generated group has order 6, so this is the appropriate symmetry number for a partition function that permits inversion.

Acetone

Rigid acetone has point-group symmetry C_2v, which has order 4. Deleting the non-RRHO operations leaves the C₂ sub-group, so σ = 2 for acetone in the RRHO approximation. In a model that permits internal (three-fold) rotation of both methyl moieties, the resulting group has order h = 18, so the symmetry number is σ = 18. In a model for acetone that allows only geared (cog-like) internal rotation, the methyl torsions are interdependent. The resulting group has order 6, so the symmetry number for such a model is σ = 6. This result can be obtained using GAP and numbering such as in Scheme 2. The two-fold rotation is [4,5,6,1,2,3]. Geared torsion corresponds to [3,1,2,5,6,4]. The generated group is of order 6.

para-Xylene

This molecule may be drawn with point-group symmetry C_2h, but only the two-fold rotation is included in the RRHO model, for which the symmetry number is therefore 2. A model that includes methyl rotation will also include a two-fold rotation of the aromatic ring, or equivalently, rotation of both methyl groups followed by a co-axial two-fold rotation of the entire molecule. Using the numbering in Scheme 2, overall two-fold rotation in the plane is [4,6,5,1,3,2,9,10,7,8], methyl rotation is [2,3,1,4,5,6,7,8,9,10], and C₆H₄ rotation is [1,2,3,4,5,6,10,9,8,7]. The resulting group has order 36.¹⁵

tert-Butylradical

In a rigid conformation with the carbon atoms slightly pyramidal and the methyl groups in the same orientation, t-butyl radical (C₄H₉) has point-group symmetry C_3v. Deleting the irrelevant reflection element leaves the C₃ sub-group, so σ = 3. In a model that allows the methyl groups to rotate, the symmetry number is σ = 3×3³ = 81. However, the barrier for pyramidal inversion is very low. If this is included in the partition function, combining it with molecular re-orientation results in a new symmetry operation and a final symmetry number σ = 81×2 = 162. For mechanical calculation, hydrogen atoms could be numbered sequentially (see Scheme 2) so that [7,8,9,1,2,3,4,5,6] represents the three-fold molecular rotation, [3,1,2,4,5,6,7,8,9] is the methyl torsion, and [1,2,3,7,8,9,4,5,6] is the inversion/rotation/torsion. The resulting group has order 162.

Fe(Cp*)₂

Rigid decamethylferrocene, FeC₂₀H₃₀, can be drawn with point-group symmetry D_5d (staggered cyclopentadienyl rings). Deleting the inversion and reflection operations, which are absent from the RRHO model, leaves D₅, which has order 10. Allowing internal, five-fold rotation of the Cp* rings leads to a group of order 50. Allowing the methyl groups to rotate leads to a large group. When groups are combined (direct product) to create a larger group, the order of the new group is the product of the orders of the original groups.³⁰ For example, our group of order 50 is the product of C₅ (order 5) and C₂ (order 2) and the five-fold torsion group (order 5). Each of the ten methyl rotors constitutes a separate subgroup of order 3. Thus, the fully rotating model has a symmetry number of 50(3)¹⁰ = 2,952,450. When applying this shortcut one must be careful not to count any symmetry operation more than once. The same result is obtained mechanically, and more safely, using GAP, but the procedure is too tedious (30 hydrogen atoms) to display here.

Benzene

As discussed above, the symmetry number for benzene is 12 in the RRHO model. At high temperature, however, the automerization reaction interchanges adjacent methine units.⁵⁰ For a partition function that includes this transformation, the corresponding permutation [2,1,3,4,5,6] must be included, leading to a group of order 720 = 6!. If the hydrogen atoms are furthermore allowed to rearrange independently of the carbon atoms,⁵¹ the appropriate symmetry number is 518,400 = (6!)².

Bullvalene

This C₁₀H₁₀ isomer (Scheme 2) has an equilibrium structure with point-group symmetry C_3v. Deleting the reflection operations, which are absent in the RRHO model, leaves the sub-group C₃, which has order 3. However, this molecule is famous for its rapid, degenerate Cope rearrangement, which scrambles all methine units.⁵² A partition function that includes this rearrangement requires a large symmetry number. It can be determined mechanically by labeling as in Scheme 2, where only the carbon atoms are represented. The three-fold rotation is [1,8,9,10,2,3,4,5,6,7]. A Cope rearrangement forming the new bond between atoms 5 and 8, combined with overall molecular re-orientation (see Scheme 2), corresponds to [4,3,2,1,10,9,8,7,6,5]. These two operations generate a group of order 3,628,800 = 10!, which is the appropriate symmetry number for such a partition function.

Excited vibronic states

The discussion of ψ in the present paper presumes that the molecule is in a totally symmetric vibronic state. If it is not, then one must consider the total wavefunction, ψ = ψ_elecψ_vibψ_spinψ_rot, as either antisymmetric (fermions) or symmetric (bosons) with respect to nuclear interchange. The analysis is the same as before, except that Γ_spin is replaced by Γ_elec × Γ_vib × Γ_spin. Every possible irreducible representation is considered for this product, as was done above for Γ_spin alone. The allowed rotational levels may differ but their fraction within Γ_rot, and hence the symmetry number, is not affected.