Validated Finite Element Models of the Proximal Femur Using Two-Dimensional Projected Geometry and Bone Density

Abstract

Two dimensional finite element models of cadaveric femoral stiffness were developed to study their suitability as surrogates of bone stiffness and strength, using two dimensional representations of femoral geometry and bone mineral density distributions. If successfully validated, such methods could be clinically applied to estimate patient bone stiffness and strength using simpler and less costly radiographs. Two dimensional femur images were derived by projection of quantitative computed tomography scans of 22 human cadaveric femurs. The same femurs were fractured in a fall on the hip configuration. Femoral stiffness and fracture load were measured, and high speed video was recorded. Digital image correlation analysis was used to calculate the strain distribution from the high speed video recordings. Two-dimensional projection images were segmented and meshed with second-order triangular elements for finite element analysis. Elastic moduli of the finite elements were calculated based on the projected mineral density values inside the elements. The mapping of projection density values to elastic modulus was obtained using optimal parameter identification in a set of nine of the 22 specimens, and validated on the remaining 13 specimens. Finite element calculated proximal stiffness and strength correlated much better with experimental data than areal bone mineral density alone. In addition, finite element calculated strain distributions compared very well with strains obtained from digital image processing of the high speed video recordings, further validating the two-dimensional projected subject-specific finite element models.

Introduction

The risk for hip fracture increases exponentially with age due to the combination of increased fall rates [1] and decreased bone strength [2]. Osteoporosis, an age-related musculoskeletal disease affecting bone mineral content, is regarded as a major cause of decreased hip strength [3]. Hip fractures require hospital admission and may result in severe disability and an increase in the mortality rate, especially in older patients [4]. Osteoporotic fractures are associated with a cost of ∼$20 billion per year in the United States and ∼$30 billion per year in the European Union [5]. Despite the extent of this problem, there is currently no accurate, fast and low-cost method for non-invasive measurement of bone strength.

Clinically, areal bone mineral density (aBMD) is assessed by imaging techniques such as dual X-ray absorptiometry (DXA) or quantitative computer tomography (QCT) and is used to measure bone density in a particular area of interest such as the proximal femur [6]. By itself, aBMD has had limited success in predicting bone strength, because it does not consider other factors such as the anatomical bone geometry or the spatial bone density distribution [7, 8]. Therefore, much attention has been directed towards the development of three-dimensional (3D), subject-specific finite element analysis (FEA) to predict femoral strength [9]. This procedure consists of 1) obtaining a 3D finite element mesh based on a QCT-scan of the femur, 2) determining the material properties for each element based on the CT grayscale numbers of the voxels in the elements, and 3) simulating the model response under specific loading conditions. Three dimensional QCT/FEA methods hold promise for achieving accurate predictions of femoral strength [10,11].

However, clinical implementation of 3D QCT/FEA methods is currently not widespread, in part due to the requirement of expensive computer hardware to achieve solutions of 3D finite element models within a clinically acceptable time, as well as the availability of robust 3D segmentation and meshing techniques. Segmentation, meshing and finite element analysis of a 2D geometry, on the other hand, can be accomplished fast and is potentially more robust than 3D QCT/FEA [12]. A method for 2D FEA of the femur was previously developed, based on the assumption that the stresses and strains during a fall on the hip lie predominantly in the coronal plane of the hip [13]. The 2D FEA method incorporated the 2D projection of the femoral geometry and density values similar to a DXA scan [13] or QCT image projection [12]. The elastic (Young's) moduli of the elements of the 2D mesh were calculated based on the bone density pixel values inside the element. Two dimensional FEA-predicted strains showed good agreement with strains measured on a fiberglass replica of the femur [13], but no validation on human specimens was reported. In addition, the relation between the projection density values and the Young's modulus of human femurs is currently unknown. Therefore, it remains unclear if a 2D FEA method could increase the prediction of femoral strength as compared to aBMD alone.

The first aim of this study was to improve the 2D FEA technique by developing an optimal parameter identification method for the calibration of the density-elastic modulus relationship. The second aim was to validate the 2D FEA method using experimental data. To achieve both aims, we conducted in vitro fracture experiments on human cadaveric specimens in a fall on the hip configuration. The 2D FEA method was first validated using experimental measurements of overall femoral stiffness and trochanteric fracture force. For further validation, FEA-predicted strain fields were compared with strain fields obtained by digital image correlation analysis of high speed video recordings of the fracture.

Materials and Methods

Femurs

Twenty-two human cadaveric femurs were provided by the Musculoskeletal Transplant Foundation (Edison, NJ) from donors over 55 years of age. The femurs were divided into an estimation group (n = 9) and a validation group (n=13). To cover a wide range for the stiffness and strength values, the estimation group was chosen such that it consisted of three ‘normal’, three ‘osteopenic’ and three ‘osteoporotic’ femurs as classified by femoral neck aBMD according to the standards of the World Health Organization [14]. The validation group consisted of the remaining femurs that were available for this study (three ‘normal’, seven ‘osteopenic’, and three ‘osteoporotic’ femurs). Table 1 summarizes the properties of the experimentally tested specimens. Despite a small, but statistically significant difference in age, values for femoral neck aBMD, stiffness and strength were similar in both groups. Coefficients of determination (R²) were calculated independently for the two groups to estimate the robustness of the current models to using a different data set. In addition, R² values were calculated for the combined set (n = 22).

Table 1.

Age, areal bone mineral density (aBMD), stiffness and strength of the estimation and validation group (*p<0.05 validation group vs. estimation group)

	Estimation group (n=9)		Validation group (n=13)
	Mean ± SD	Range	Mean ± SD	Range
Age (years)	70 ± 10	62-93	63 ± 4*	57-69
Neck aBMD (g cm-2)	0.53 ± 0.14	0.31-0.75	0.57 ± 0.16	0.26-0.75
Stiffness (N mm-1)	1573 ± 479	922-2350	1694 ± 482	1016-2417
Strength (N)	4021 ± 1399	1636-5825	4441 ± 1558	2485-7852

Radiographs of the femurs were taken in two planes to rule out the presence of fractures and tumors. Soft tissue was removed from the proximal 300 mm of the femurs, taking care not to cause any damage to the bone. The femurs distal end was removed leaving the proximal 250 mm for testing. Material was removed from 25-35 mm of the distal medullary canal. Using an in-house designed holder, 100 mm of the remaining distal end was embedded in dental cement (Coltène/Whaledent, Cuyahoga Falls, OH). While the cement cured, the holder maintained the orientation of the bone such that the neck was internally rotated 15° for later testing, as per a previous study testing femurs in a fall on the hip configuration [15].

Generation of projection images from QCT data

The femurs were removed from the freezer ∼20 hours prior to scanning and allowed to warm to room temperature. The wraps were removed and the exposed bones placed in plastic bags, which were tightly wrapped around the bones and sealed to prevent dehydration. Femurs were scanned in a clinical Siemens Somatom Definition 64-slice CT scanner (Siemens, Malvern, PA). In-plane resolution was 0.29 to 0.41 mm pixel-on-a-side, depending on the field of view (512 × 512 matrix). Slice thickness was 0.40 mm. The X-ray tube was operated at 120 kVp and 216 mA. Before each scan, the fixture holding the femur was carefully aligned with the scanner axis using laser alignment. The scanning position of the femur was with the shaft at a 10° angle with the horizontal and the neck at a 15° internal rotation, identical to the fracture testing position used later during the experiments.

A CT calibration phantom (Mindways Inc., San Francisco, CA), containing five rods of different solid reference materials calibrated against liquid K₂HPO₄/water solutions, was placed under the femur for conversion of CT Hounsfield number to equivalent K₂HPO₄ density (ρ_K2HPO4), yielding the following linear relation between Hounsfield units (HU) and ρ_K2HPO4:

$${\rho }_{\text{K}2\text{HPO}4}=7.0\cdot {10}^{-4}\cdot \text{HU}$$ (1)

It was assumed that ρ_K2HPO4 was identical to the bone ash density ρ_ash, in agreement with a previous study on QCT using different calibration phantoms [16]. The bone mineral content of each voxel was then calculated as the product of ρ_ash and voxel volume. The total bone mineral content in the voxels along the anterior-posterior axis was obtained by summing the values for ρ_ash in these voxels, such that a projection in the coronal plane was obtained. This projection plane was chosen under the assumption that the stresses and strains during a fall on the hip lie predominantly in this plane [13]. The resulting sum was divided by the 2D pixel area in the coronal plane to obtain 2D distributions of the bone mineral density (ρ_2D, [g cm^-2[). The average of ρ_2D was then calculated from the pixels belonging to the femoral neck in a 10 mm wide rectangle, perpendicular to the femoral neck axis (Fig. 1A), using custom MATLAB (The Mathworks, Natick, MA) code. This value was used as a measure for femoral neck aBMD (g cm^-2). A nomenclature of the different density metrics used in this study is given in Table 2.

Figure 1.

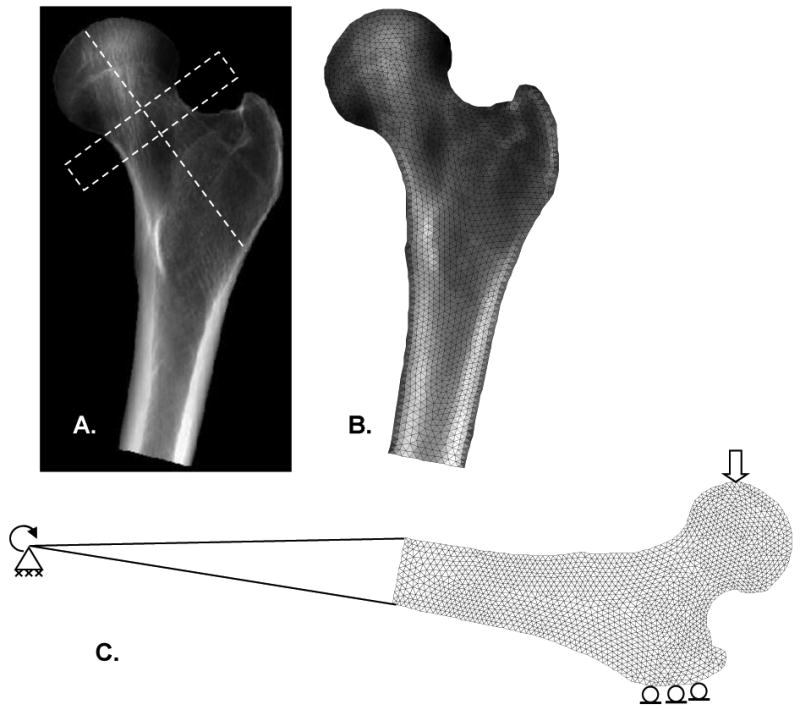
(A) Projection image of QCT scan. Average values for aBMD were calculated from pixels belonging to the femoral neck inside a 10 mm high rectangle perpendicular to the femoral neck axis. (B) Triangular mesh with material property distribution. (C) Boundary conditions consisted of a fixed joint support at the distal end, zero vertical displacement at the greater trochanter, and a 1.0 mm vertical displacement at the femoral head.

Table 2.

Descriptions of different density metrics used.

Abbreviation	Unit	Description
ρK2HPO4	g cm-3	Equivalent K2HPO4 density in the voxels of the QCT scans, obtained after conversion of Hounsfield numbers using a calibration phantom.
ρash	g cm-3	Bone ash density in the voxels of the QCT scans. Assumed to be equal to ρK2HPO4.
ρ2D	g cm-2	Bone density distribution in the 2D projection image generated from the QCT scan.
ρele	g cm-2	Average bone density in each element of the finite element mesh, obtained by integration of ρ2D in the element.
aBMD	g cm-2	Areal bone mineral density, obtained by averaging ρ2D in the femoral neck area.

Mechanical testing

An in-house designed fixture was used in conjunction with a standard mechanical testing system (MTS, Minneapolis, MN) to test the femurs to fracture. The hydraulic ram was displacement controlled and moved at a velocity of 100 mm s^-1. The maximum displacement was set to 25 mm, which was sufficient to ensure fracture in all the tested bones. A single-axis 13 kN load cell (Transducer Techniques, Temecula, CA) measured the vertical force applied to the greater trochanter. Just before testing the greater trochanter was placed in an aluminum cup, which was then filled with dental cement. The femoral head was fitted into an aluminum cup connected to the upper fixture of the MTS. The upper fixture was attached to the MTS test machine through linear bearings, permitting frictionless displacement in the horizontal plane. The femurs were placed in the fixture at a 10° shaft angle and a 15° internal neck rotation. Furthermore, the femur was allowed to rotate about the x-axis, mimicking knee rotation. This loading configuration has been used in previous studies to experimentally simulate femoral fracture during a fall on the hip [11, 15, 17]. Femoral fracture tests were recorded with a high speed video camera (Photron Inc., San Diego, CA) with a resolution of 1024 × 512 at a capture rate of 6000 fps. High-intensity lights were used to achieve sufficient illumination of the specimens.

Digital Image Correlation

Digital image correlation (DIC) was used to calculate deformation and strain fields from the high speed video recordings during the mechanical testing of femurs. The 24-bit color (Red (R), Green (G) and Blue (B)) frames of the high speed video recordings were converted to grayscale by summing up the R, G and B values for each pixel. The grayscale image was then divided by 765 (i.e., 3 × 255) to ensure all the values were between zero and one. The video frame right before the onset of the ram movement was used to manually define a region of interest, by tracing the bone contour. A uniform grid with a distance of five pixels in between nodes was generated within this region of interest. The movement of the grid points from frame to frame was calculated based on a normalized two-dimensional cross-correlation method with sub-pixel resolution available in MATLAB. Time steps corresponding to 50 frames duration were taken to track the displacement field in the linear elastic region. The horizontal and vertical displacement fields U(x,y) and V(x,y) were filtered with a 5 × 5 points moving average filter. The strains were then calculated by spatial differentiation of the displacement field using a central difference. Plane stress conditions were assumed and the components of the strain tensor were calculated according to the infinitesimal strain theory:

$$\begin{array}{lll}{\varepsilon }_x=\frac{\partial U}{\partial x},\hfill & {\varepsilon }_y=\frac{\partial V}{\partial y},\hfill & {\varepsilon }_z=\frac{\nu }{1-\nu }\left(\frac{\partial U}{\partial x}+\frac{\partial V}{\partial y}\right)\hfill \\ {\varepsilon }_{xy}=\frac{1}{2}\left(\frac{\partial U}{\partial y}+\frac{\partial V}{\partial x}\right),\hfill & {\varepsilon }_{xz}={\varepsilon }_{yz}=0\hfill \end{array}$$ (2)

Here ε_x, ε_y, and ε_z are the normal strains and ε_xy, ε_xz, and ε_yz are the shear strains in the Cartesian coordinate system. The Poisson's ratio v was assumed to be 0.3. The equivalent (von Mises) strain was determined as:

$${\varepsilon }_{\mathit{\text{eqv}}}=\frac{1}{(1+\nu )\sqrt{2}}\sqrt{{({\varepsilon }_x-{\varepsilon }_y)}^2+{({\varepsilon }_y-{\varepsilon }_z)}^2+{({\varepsilon }_z-{\varepsilon }_x)}^2+6{\varepsilon }_{xy}^2}$$ (3)

Contour plots of the equivalent elastic strains were plotted using the deformed grid, and superimposed on the high speed video frame.

2D Finite Element Analysis

The model assumed plane stress conditions with a constant thickness. The femurs were segmented from the projection QCT image (Fig. 1A) by manually tracing bone contours. An unstructured mesh with 6-node quadratic triangular elements was generated in ANSYS Mechanical APDL (ANSYS Inc, Canonsburg, PA), as shown in Fig. 1B. For each element, the average element bone mineral density value ρ_ele, [g cm^-2]) was calculated using 3-point Gaussian integration using the pixel values closest to the midpoint of each side of the triangular elements. The following power law was assumed between the Young's modulus E and ρ_ele:

$$E=a\cdot {{\rho }_{\text{ele}}}^b$$ (4)

where a and b are constants, the values of which were determined as described below. To mimic the experimental conditions, boundary conditions were applied (Fig. 1C). The nodes at the distal end of the shaft were connected with rigid beam elements to a rotation point, which corresponded with the rotation axis during the experiments. The displacements of the rotation point were set to zero in all directions, but in-plane rotation was allowed to mimic knee rotation. At the greater trochanter, the displacement in the vertical direction was set to zero, but horizontal displacement was allowed. At the femoral head, a 1 mm vertical displacement was applied. The finite element model was solved in ANSYS, using custom code programmed in Tcl. Computation times varied from 15 to 45 seconds on a workstation with an AMD Opteron 2.59 GHz processor and 16 GB internal memory.

The reaction force F_T,1mm at the greater trochanter as a result of the 1.0 mm displacement was calculated and the 2D FEA-predicted femoral stiffness K_f,FEA was computed as:

$$K_{f,\mathit{\text{FEA}}}=\frac{F_{T,1\text{mm}}}{1.0\text{mm}}$$ (5)

A mesh convergence study was performed to evaluate the influence of mesh density on the predicted stiffness. A linear regression model was used to fit experimental femoral strength to 2D FEA stiffness. Finally, Eqs. 2 and 3 were also used to calculate the elastic equivalent strain field predicted by 2D FEA.

Calculation of bone density-elastic modulus relationship

The experimentally measured stiffness K_f,measured was obtained as the slope of the initial linear part of the trochanter load - femoral head displacement curve. For the estimation data set (n=9), the difference between K_f,FEA and K_f,measured was minimized using the Nelder-Mead simplex search algorithm available in MATLAB, such that:

$$[a,b]=\arg \text{min}\sum _{i=1}^9{(K_{f,\text{FEA}}(a,b)-K_{f,\text{measured}})}^2$$ (6)

The 2D FEA analyses were automatically executed and post-processed using custom MATLAB code. The computed values for a and b were incorporated into (Eq. 4 and subsequently used in the 2D FEA method to predict the stiffness and strength for the 14 femurs in the validation set.

Results

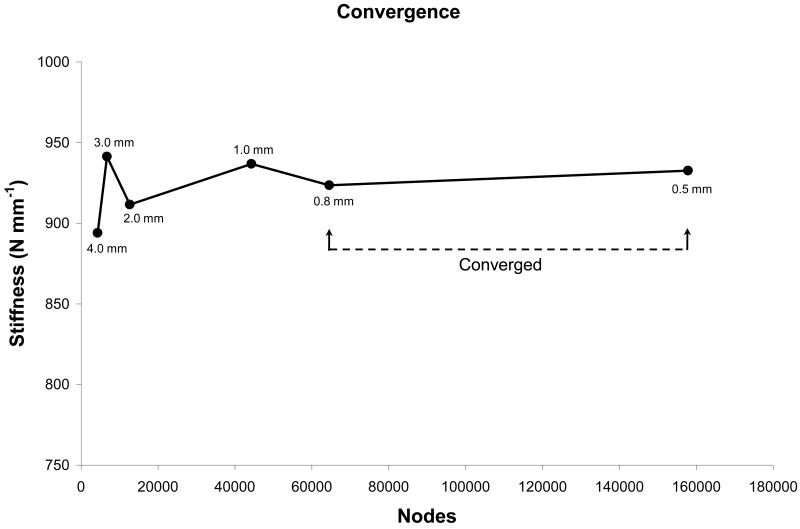
A mesh convergence analysis of a representative femur (Fig. 2) showed the convergence of the 2D FEA-predicted stiffness upon decreasing the element edge length and thereby increasing the number of nodes in the model. The models were fully converged at element size of 0.5 mm, and at element size 0.8 mm the obtained stiffness was within 1% of the fully converged value. For an optimal balance between computational cost and precision, we used an element size of 0.8 mm to mesh all the femur projected images. This resulted in meshes with an average of 54292 ± 5980 nodes and 26843 ± 2979 elements.

Figure 2.

Mesh convergence study for a typical femur. The maximum element edge length is indicated for each data point.

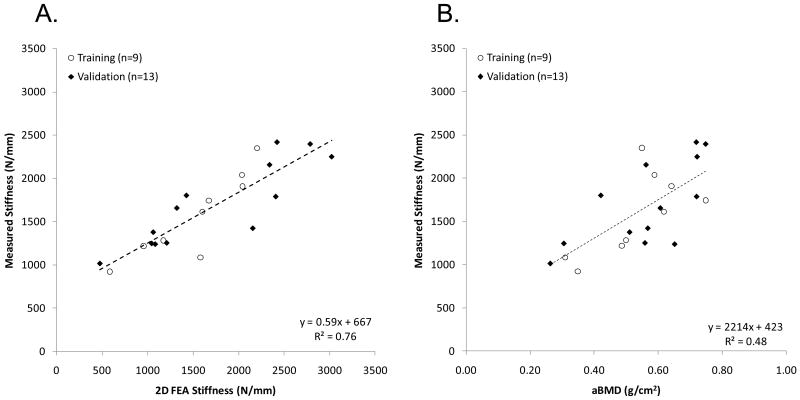
The minimum search algorithm successfully determined the parameters of the density-elastic modulus relationship (Eq. 4) as a = 29.8 GPa and b = 1.56 in the estimation set. The coefficient of determination calculated between 2D FEA-predicted and measured stiffness was R² = 0.80 for the estimation set, R² = 0.77 for the validation set (R² = 0.76 in the entire data set), as shown in Fig. 3A. In contrast, a poor correlation between measured stiffness and femoral neck aBMD was found with R² = 0.48 for the estimation set and R² = 0.47 for the validation set (R² = 0.48 for the entire set), as shown in Fig. 3B.

Figure 3.

Correlation between (A) measured stiffness, and stiffness predicted by two-dimensional finite element analysis (2D FEA) and (B) measured stiffness, and areal bone mineral density (aBMD). Coefficient of determination (R²) shown corresponds to all data.

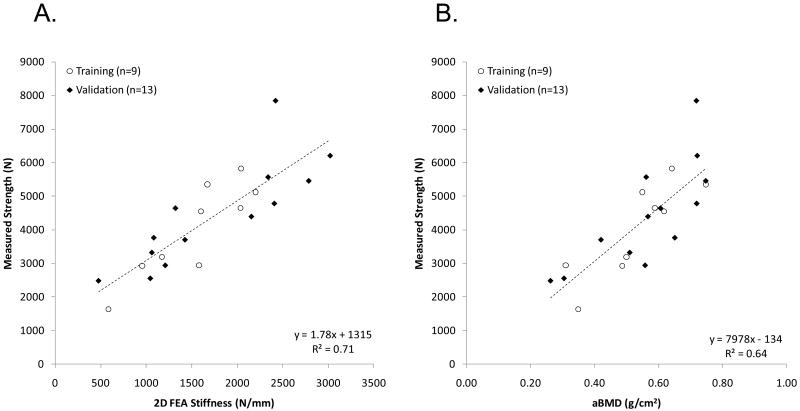
The correlation between 2D FEA-predicted stiffness and measured strength was R² = 0.77 for the estimation set, and R² = 0.69 for the validation set (R² = 0.71 for the entire data set), as shown in Fig. 4A. Correlation between femoral neck aBMD and strength was lower at R² = 0.74 for the estimation set and R² = 0.58 for the validation set (R² = 0.64 for the entire data set), as shown in Fig. 4B.

Figure 4.

Correlation between (A) measured strength, and stiffness predicted by two-dimensional finite element analysis (2D FEA) and (B) measured strength, and areal bone mineral density (aBMD). Coefficient of determination (R²) shown corresponds to all data.

The equivalent strain fields in the initially linear elastic region of the experimental load-displacement curves were obtained from high speed video recordings using digital image correlation and compared with the elastic equivalent strain field obtained with the 2D FEA method (Fig. 5). Regions of high strain were observed at the femoral head and at the superolateral cortex, in both the experimental data and the finite element analysis.

Figure 5.

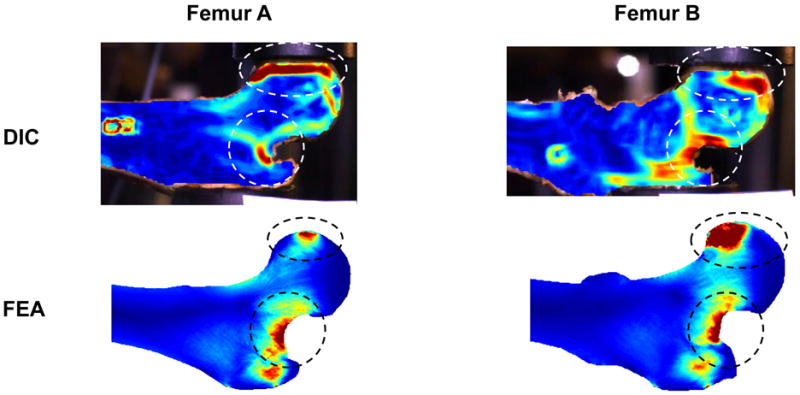
Elastic equivalent strain distributions in two representative femurs as measured by digital image correlation (DIC) and as predicted by two-dimensional finite element analysis (2D FEA).

Discussion and conclusion

In this study, we demonstrated the capability of a subject-specific 2D FEA method, with geometry and material properties obtained from projected QCT-images, to predict femoral fracture loads in a sideways fall on the hip configuration. Our results show that the 2D FEA method yields substantially more accurate predictions of the femoral stiffness and ultimate proximal femur strength than femoral neck aBMD. To that end, we used our ex vivo fracture data to obtain an empirical relationship between projection values of bone density and Young's modulus for use in plane stress finite element models of the proximal femur.

The 2D FEA method was previously reported to be a promising tool for proximal femur strength estimation by Testi et al. [13], who performed validation studies using a synthetic fiberglass femur. In the current work, we provided a more extensive validation on a set of 22 human cadaveric femurs. We used nine of the femurs as estimation set to obtain the parameters of the power law relation between bone density values and Young's modulus. The prediction power of the obtained model was then further investigated using the remaining 13 femurs. The results showed that our optimization procedure resulted in a good correlation between 2D FEA stiffness predictions and measured femoral stiffness. Linear regression was subsequently used to predict strength from stiffness, resulting in a better correlation than femoral neck aBMD (R² = 0.71 vs. 0.64 for the entire sample).

A novelty of the present study was the calculation of 2D strain fields from high speed video recordings using DIC. This method has been previously shown to yield accurate strain calculations at sub-pixel resolutions in deforming bovine humeral heads [18] and in the periodontium during tooth crown placement [19]. The use of DIC to determine the equivalent strain field in the linear elastic region of the mechanical testing revealed great similarities between the DIC strain field and the 2D FEA-predicted strain field. In particular, high strains were observed on the superolateral cortex of the femoral neck, which has been suggested to be the initiation site of compressive failure during a fall on the hip [17]. The good similarity between strain fields obtained by DIC and 2D FEA increased our confidence in the modeling technique.

We obtained the 2D distributions of bone mineral density using a method employing the projection of QCT images similar to the method reported by Langton et al. [12]. Potentially, this 2D FEA method could also be applied to 2D images obtained by X-ray projection methods, such as dual-energy X-ray absorptiometry (DXA), the current clinical standard for determining femoral neck aBMD, or radiographs. This would require substantially less radiation than CT-scans, rendering the method even more attractive for clinical implementation. However, in the in vivo scenario, the acetabulum will be in the field of view for DXA or X-ray scans, most likely resulting in overestimation of the Young's modulus for a portion of the femoral head. This would likely result in an increase in the 2D FEA-predicted stiffness and strength. Therefore, as a preliminary feasibility study, we chose to generate our projection images from QCT scans. Future validation studies should evaluate the performance of the 2D FEA method under clinical conditions.

Our parameter estimation technique led to a new power law equation between the Young's modulus and projected bone mineral density, $E=29.8\cdot {\rho }_{\text{ele}}^{1.56}\text{GPa}$. Although no other relationships between projected bone mineral density and Young's modulus have been previously reported, there exist some data on equations relating bone ash density (ρ_ash) to Young's modulus for 3D FEA scenarios. For example, from Morgan et al. [20] we derived E = 14.6 · ρ_ash^1.49 GPa for proximal femurs, assuming the ratio of apparent density to ash density to be 0.6 [21,22]. Furthermore, Keller [23] reported E = 10.2 · ρ_ash^2.01 GPa for femoral specimens. As an interesting observation, our value for the exponent in the power law (1.56) was in the range of the exponents obtained from bone coupon testing as reported in the literature.

The in-house designed mechanical testing apparatus may have had an influence on the experimental results of this study. First, the speed of testing was set constant at 100 mm s^-1. Although this value is assumed to result in a realistic rate of bone deformation [15], this rate depends on external factors such as patient's weight, height, and impact surface properties. Future work is needed to investigate the rate of bone deformation by applying different loading speeds. In addition, the boundary conditions, i.e. contact of the apparatus with the greater trochanter and femoral head, may have influenced the fracture strength and fracture pattern. Although it is difficult to measure the effects of these boundary conditions, the observed fracture patterns (trochanteric and cervical) were deemed comparable with clinical fracture patterns by an orthopaedic surgeon. Additionally, there were no fractures that occurred at the femoral head or greater trochanter as a result of unrealistically high contact stresses. Finally, the orientation of the femur is likely to influence fracture strength. Future studies with different orientations of the femora are needed to investigate the influence of femur orientation.

In conclusion, despite inherent assumptions made by 2D finite element analysis methods, the stiffness derived from computationally inexpensive plane stress FEA of projection images of bone geometry and mineral density is a more accurate predictor of femoral stiffness and strength during a sideways fall on the hip than femoral neck aBMD. In the modeling process, a power law was established and optimized for the empirical mapping of projection bone density values to Young's modulus. Still, given the predictive power of about 70%, there is room for improvement. Incorporation of a yield and/or damage model into the analysis may result in better strength predictions. Despite the need for further studies, we have shown that a 2D finite element analysis from projected bone geometries and densities holds potential for future clinical implementation and surpass the accuracy of aBMD in predicting proximal femur strength and stiffness.