Incorporating priors on expert performance parameters for segmentation validation and label fusion: a maximum a posteriori STAPLE

Abstract

In order to evaluate the quality of segmentations of an image and assess intra- and inter-expert variability in segmentation performance, an Expectation Maximization (EM) algorithm for Simultaneous Truth And Performance Level Estimation (STAPLE) was recently developed. This algorithm, originally presented for segmentation validation, has since been used for many applications, such as atlas construction and decision fusion. However, the manual delineation of structures of interest is a very time consuming and burdensome task. Further, as the time required and burden of manual delineation increase, the accuracy of the delineation is decreased. Therefore, it may be desirable to ask the experts to delineate only a reduced number of structures or the segmentation of all structures by all experts may simply not be achieved. Fusion from data with some structures not segmented by each expert should be carried out in a manner that accounts for the missing information. In other applications, locally inconsistent segmentations may drive the STAPLE algorithm into an undesirable local optimum, leading to misclassifications or misleading experts performance parameters.

We present a new algorithm that allows fusion with partial delineation and which can avoid convergence to undesirable local optima in the presence of strongly inconsistent segmentations. The algorithm extends STAPLE by incorporating prior probabilities for the expert performance parameters. This is achieved through a Maximum A Posteriori formulation, where the prior probabilities for the performance parameters are modeled by a beta distribution. We demonstrate that this new algorithm enables dramatically improved fusion from data with partial delineation by each expert in comparison to fusion with STAPLE.

1. Introduction

Among numerous tools for the evaluation of automatic segmentation algorithms with respect to manual delineations [1–4], an algorithm named STAPLE (for Simultaneous Truth And Performance Level Estimation) [5] was proposed by Warfield et al. as a novel way to compute simultaneously a reference segmentation and performance parameters from a set of segmentations. This algorithm is very versatile as it allows the evaluation of intra- and inter-rater variability as well as the comparison of segmentation algorithms with respect to multiple manual segmentations. It has therefore been used for many applications. Among them, it has been either embedded in new atlas construction methods [6], utilized to fuse segmentation decisions in multiple atlas-based segmentation [7], or to compute atlas segmentations from registered manual delineations [8].

Manual delineation is a very time consuming and burdensome task, even more when several structures have to be segmented in each image. Applications of manual segmentation, such as delineation of brain structures for neuroscience research, may be accelerated, and the quality of each segmentation improved, by having more experts who each delineate fewer structures. Some structures may then be missing in each rater segmentation. Performance estimation however requires observations of segmentation decisions of each structure by each rater. This can cause STAPLE to fail to provide accurate estimates of the reference standard and expert performance parameters. It would therefore be extremely valuable to take into account the missing structures to get accurate estimates of the reference and performance parameters. This would also help for existing datasets delineated in clinical conditions where structures are missing.

With this objective, Landman et al. [9] proposed an ad-hoc solution by fixing the parameters for missing structures and ignoring background voxels. This approach cannot be extended easily to take into account any prior on the expert parameters. This would however be valuable as the estimation of the parameters and reference segmentation may be incorrect when strong inconsistencies exist between the input segmentations. Inconsistent delineations may indeed lead the algorithm to an undesired local maximum where the performance parameter estimates converge to values incompatible with our prior information about rater performance. We can introduce an explicit prior model for rater performance parameters to drive the estimation algorithm to a better local optimum.

We propose a new algorithm that incorporates a prior probability for the performance parameters estimated through STAPLE. This is performed by extending the expression of the expected value of the complete data log-likelihood to a Maximum A Posteriori formulation incorporating prior probabilities as a beta distribution on each performance parameter. We applied our algorithm to label fusion with missing structures, and demonstrate its efficiency for improving label fusion and reducing manual rater delineation burden.

2. Method

2.1. Summary of STAPLE

We first summarize the principle of STAPLE [5]. It takes as an input a set of segmentations from J experts (either manual or automatic segmentations). These segmentations may be binary or multi-category segmentations, i.e. several structures are delineated with each structure represented by one specific label. The labeling of each voxel, in an image of I voxels, provided by the segmentation generators is referred to as segmentation decisions d_ij, indicating the label given by each expert j for voxel i, i ∈ [1 … I]. The goal of STAPLE is then to estimate both a reference standard segmentation T, and parameters θ = {θ₁, …, θ_j, …, θ_J} describing the agreement between each expert and the reference standard. Each θ_j is represented by an L × L matrix, where L is the number of labels, and θ_js’s is the probability that the expert j gave the label s′ to a voxel i when the reference standard label is s, i.e. θ_js’s = P(d_ij = s′|T_i = s).

If the reference standard was known, then estimating the performance parameters for each expert would be straightforward. However, as this reference standard is unknown, an Expectation-Maximization approach [10, 11] is used to estimate T and the expert performance parameters through the maximization of the expected value of the complete data log-likelihood Q(θ|θ^(k)):

$$Q(\theta \mid {\theta }^{(k)})=\sum _i\sum _j\sum _s{W}_{si}log({\theta }_{{jd}_{ij}s})$$ (1)

where W_si denotes the posterior probability of T for label s: P(T_i = s|D, θ^(k)). The EM algorithm, which is guaranteed to converge to a local maximum, proceeds to identify the optimal estimate θ̂ by iterating two steps:

• E-Step: Compute Q(θ| θ^(k)), the expected value of the complete data log-likelihood given the current estimates of the expert parameters at iteration k: θ^(k). This requires computing P(T|D, θ^(k)), i.e. the W_si values [5].

• M-Step: Estimate new performance parameters θ^(k+1), maximizing Q(θ|θ^(k)).

2.2. Introducing Priors: a Maximum A Posteriori Formulation

We consider the possibility of utilizing a prior probability for the performance parameters to modify the local maximum to which the estimator converges. This can be done by utilizing Maximum A Posteriori (MAP) estimation rather than Maximum Likelihood. MAP estimation is equivalent to augmenting the expected value of the complete data log-likelihood Q(θ|θ^(k)) with a term log(P(θ)) corresponding to the prior probability of the parameters:

$$Q_{\mathit{MAP}}(\theta \mid {\theta }^{(k)})=Q(\theta \mid {\theta }^{(k)})+log(P(\theta ))$$ (2)

As the performance parameters for each label are independent, P(θ) can be expressed as a product of the independent probabilities P(θ_js’s). The appropriate form for the prior probability density function for each parameter θ_js’s must be chosen. Several properties are desirable for this prior distribution:

• θ_js’s is a probability and therefore must take its values in [0, 1],

• it must be able to model any prior on the parameters (close to 1 e.g. diagonal parameters, close to 0 e.g. non-diagonal parameters, or uniform prior),

• a function for which the logarithm is easily obtained as well as its derivatives.

The beta distribution, B_α,β, is particularly well suited to these requirements. Its support ranges between 0.0 and 1.0 and it allows, based on two parameters α and β, to consider a broad range of prior distributions for the parameters for each expert (particularly the specific combination α = β = 1 corresponds to the uniform prior used in the regular STAPLE). Further, the relative weight of each prior in Q can be modified by modeling the prior distribution as:

$${(B_{\alpha ,\beta }(x))}^{\gamma }={\left(\frac{1}{Z}{x}^{\alpha -1}{(1-x)}^{\beta -1}\right)}^{\gamma }$$ (3)

with γ ≥ 0.0 a scaling parameter. Z is the normalizing constant of the beta distribution. Moreover, the logarithm and the derivatives of B_α,β are easily computed.

2.3. Solving the MAP formulation in the Multi-Category Case

We associate each parameter θ_js’s with a prior defined as a γ-weighted beta distribution (B_α,β(x))^γ. The new expected value of the complete data log-likelihood function for the expert j is then expressed as:

$$Q_{\mathit{MAP}}^{\prime }({\theta }_j\mid {\theta }^{(k)})=\gamma \sum _{s^{\prime }}\sum _s\left(({\alpha }_{j{s}^{\prime }s}-1)log({\theta }_{{js}^{\prime }s})+({\beta }_{j{s}^{\prime }s}-1)log(1-{\theta }_{j{s}^{\prime }s})\right)+\sum _i\sum _s{W}_{si}log({\theta }_{j{d}_{ij}s})$$ (4)

The computation of the posterior probability of the reference standard segmentation P(T|D, θ^(k)) remains the same as in [5]. It indeed only depends on the current estimates θ^(k) and not on the prior on these parameters. However, the M-Step is modified by the prior distribution on the parameters.

M-Step: A Fixed Point Iterative Solution

The new estimates of the expert performance parameters are computed by differentiating $Q_{\mathit{MAP}}^{\prime }$ with respect to each θ_js’s and equating the derivatives to 0 under the constraint that Σ_s′ θ_js’s = 1. This leads to the following system for the parameters of each expert j:

$${\theta }_{j{s}^{\prime }s}=\frac{\left({\sum }_{i:d_{ij}=s^{\prime }}{W}_{si}\right)+\gamma ({\alpha }_{j{s}^{\prime }s}+{\beta }_{j{s}^{\prime }s}-2)+\gamma \frac{{\beta }_{j{s}^{\prime }s}-1}{{\theta }_{j{s}^{\prime }s}-1}}{{\sum }_{n^{\prime }}\left[\left({\sum }_{i:d_{ij}=n^{\prime }}{W}_{si}\right)+\gamma ({\alpha }_{j{n}^{\prime }s}+{\beta }_{j{n}^{\prime }s}-2)+\gamma \frac{{\beta }_{j{n}^{\prime }s}-1}{{\theta }_{j{n}^{\prime }s}-1}\right]}$$ (5)

In this form, we can readily see that, for a particular label s and the set of decisions s′, the expression in the numerator is calculated once for each s′ and the denominator is simply the sum of the numerators. When using a uniform prior on parameters (α_js’s = β_js’s = 1) this system further simplifies to the regular STAPLE M-Step [5]. It also admits a closed form in two specific cases: first in the binary case, where the non-diagonal parameters are entirely determined by the values of the diagonal parameters, and also when all prior parameters β_js’s = 1.

In the general multi-category case, with β_js’s ≠ 1, this system of equations does not admit any closed form solution. We therefore propose a simple iterative method to solve this system of equations. Equation (5) is a continuous mapping of the form θ_j = f(θ_j), with f: ]0, 1[^N→]0, 1[^N (where N is the number of parameters to compute for expert j). The iterative approach consists of applying the f mapping recursively to the current estimate, i.e. computing the sequence {x_n}_n≥1 where x_n+1 = f(x_n) until convergence to the fixed point. Because of the configuration of the mapping f, Schaefer’s fixed point theorem applies, which guarantees that a fixed point solution to this system (θ_j = f(θ _j)) exists.

The {x_n} sequence can be initialized from the previous parameters estimates ${\theta }_j^{(k)}$ or from the regular STAPLE parameters estimates. These initializations ensure that the sequence rapidly converges to the fixed point ${\theta }_j^{(k+1)}=f({\theta }_j^{(k+1)})$.

3. Results

We have applied our algorithm to multi-label segmentations fusion with missing data. The manual segmentation of all structures in the entire brain is very long and costly. Repeated segmentations of the same images are necessary to estimate intra- and inter-rater variability, but this further increases the burden on each rater. It would be much more practical if each rater could focus on only a subset of structures, therefore lowering the segmentation burden of each rater. However this leads to segmentations in which some structures are missing and in which different error rates, associated with different raters, are present.

To simulate this situation, we have used a database of 15 adult images (T1 images, size 256 × 256 × 175, 1 mm³) where all structures (CSF, subcortical, cortical and cerebellar grey matter, white matter, cerebellar white matter) were delineated over the whole brain (see images (a,c,e,g) on Fig. 1). For each image, we then removed randomly 4 structures out of 6 (by replacing their labels with background label 0, see images (b,d,f,h) on Fig. 1) in such a way that all structures are segmented an equal number of times overall subjects.

Fig. 1. Database of Segmentations.

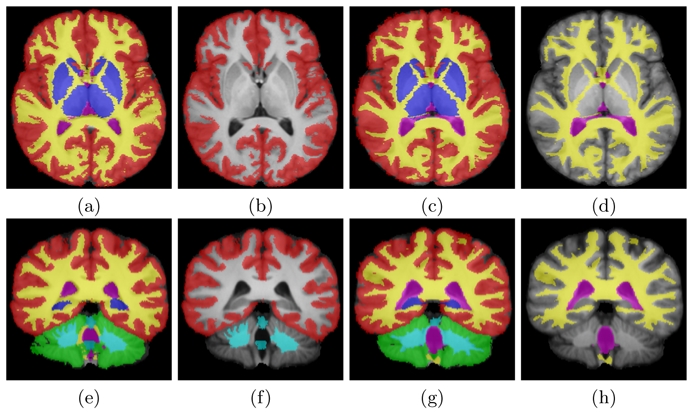
Individual manual segmentations registered on an average image. (a,c,e,g): original segmentations, (b,d,f,h): segmentations with 4 missing structures. Legend: red, blue, green: cortical, sub-cortical and cerebellar grey matter, yellow: white matter, pink: CSF, cyan: cerebellar white matter and brainstem.

We have aligned these images in a common template using Guimond et al.’s method [12], and run STAPLE first without taking into account missing structures (regular STAPLE algorithm as proposed in [5]). Then, we have run MAP STAPLE with a weight γ = 10, assuming a prior distribution close to 1 (α = 5, β = 1.5) on diagonal elements for the delineated structures, on the background for missing structures, and a prior close to 0 (α = 1.5, β = 5) on other parameters. These results as well as a regular STAPLE on the dataset without missing structures are presented in Fig. 2. Another option to account for missing structures would be to consider the case where raters were asked to delineate structures on an image where voxels are initially given an illegal label (e.g. −1) and ignore in STAPLE those voxels with the illegal label. We implemented this option with and without priors on parameters and the conclusions were similar.

Fig. 2. Results on Label Fusion with Missing Data.

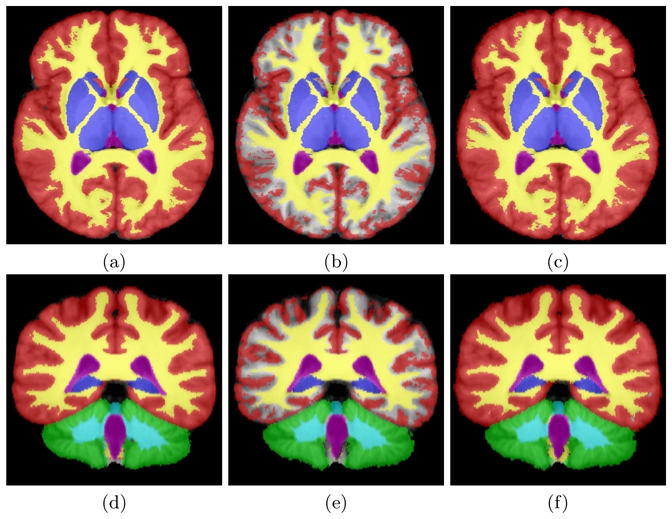
(a,d): reference label fusion (all structures used), (b,e): label fusion with a third of the segmentations, (c,f): label fusion with a third of the segmentations with prior information.

Not taking into account the missing structures in the STAPLE algorithm leads to erroneous label fusion. We can indeed see on images (b) and (e) in Fig. 2 that the interface between cortical grey matter and white matter gets segmented as the background. Because missing structures are not taken into account, experts who segmented the structures obtain poor performance scores and the background becomes the most typical structure in this region. On the contrary, when taking into account the missing structures (images (c) and (f)) by introducing an appropriate prior for the performance parameters values, the label fusion is much closer to what would be expected and also very close to regular STAPLE with all structures.

This qualitative evaluation is confirmed by the Dice scores (shown in Table 1) between the results from the two methods and the reference segmentation obtained from all structures. The MAP STAPLE formulation therefore facilitates the accurate estimation of the reference segmentation and performance parameters by enabling accurate label fusion when expert raters are each asked to delineate only some of the brain structures.

Table 1. Quantitative Evaluation of MAP STAPLE.

Dice scores between the STAPLE reference estimated from all segmentations (images (a,d) on Fig. 2) and from the dataset with missing delineations using the regular STAPLE or MAP STAPLE.

Structure	CGM	CeGM	SCGM	WM	CeWM	CSF
Regular STAPLE	0.678	0.959	0.957	0.866	0.940	0.939
MAP STAPLE	0.939	0.960	0.958	0.947	0.939	0.939

CGM, CeGM, SCGM: cortical, cerebellar and sub-cortical grey matter, WM, CeWM: brain and cerebellar white matter, CSF: cerebrospinal fluid.

4. Conclusion

We have presented a new algorithm to incorporate in STAPLE prior information for each of the expert performance parameters. This is obtained by utilizing a Maximum A Posteriori formulation for the expected value of the complete data log-likelihood and modeling the prior probability for each expert performance parameter with a beta distribution, whose parameters α and β allow for any prior distribution. We have derived a simple fixed point iterative solution for the performance parameters estimates for the most general multi-category case. Further, we identified specific cases where closed forms can be derived.

The MAP formulation we have presented may have many applications in validation studies and label fusion. We have illustrated our algorithm on a database with missing delineations (e.g. some structures are not segmented and assigned the background level), showing how MAP STAPLE allows to deal with these images and produce meaningful results. This experiment is particularly interesting as it will allow in the future for the design of validation experiments with multiple experts and multiple structures while minimizing the delineation burden for the experts. Apart from this application, this algorithm may be used to drive the STAPLE algorithm out of undesirable local maxima and obtain realistic tissue classifications even in the presence of strongly inconsistent input segmentations. This could be of great interest in the future to take into account registration errors or inconsistencies among manual segmentations.

In the future, we will use this algorithm to define new validation protocols with a lower delineation burden on the experts. This could be achieved for multiple structures as proposed here, or, for large structures, by asking the experts to delineate different slices and fuse them using our multi-category MAP algorithm, assigning each slice with a different label. Finally, the parameters α, β for each θ_js’s and the weight γ may have an important effect on fusion results. We will perform a cross-validation study on these parameters and determine if γ can be optimized automatically to get the best trade-off between prior and data.