A hierarchical state space approach to affective dynamics

Abstract

Linear dynamical system theory is a broad theoretical framework that has been applied in various research areas such as engineering, econometrics and recently in psychology. It quantifies the relations between observed inputs and outputs that are connected through a set of latent state variables. State space models are used to investigate the dynamical properties of these latent quantities. These models are especially of interest in the study of emotion dynamics, with the system representing the evolving emotion components of an individual. However, for simultaneous modeling of individual and population differences, a hierarchical extension of the basic state space model is necessary. Therefore, we introduce a Bayesian hierarchical model with random effects for the system parameters. Further, we apply our model to data that were collected using the Oregon adolescent interaction task: 66 normal and 67 depressed adolescents engaged in a conflict interaction with their parents and second-to-second physiological and behavioral measures were obtained. System parameters in normal and depressed adolescents were compared, which led to interesting discussions in the light of findings in recent literature on the links between cardiovascular processes, emotion dynamics and depression. We illustrate that our approach is flexible and general: The model can be applied to any time series for multiple systems (where a system can represent any entity) and moreover, one is free to focus on whatever component of the versatile model.

Introduction

The role affect and emotions play in our daily life can hardly be overestimated. Affect and emotions produce the highs and lows of our lives. We are happy when a paper gets accepted, we are angry if a colleague intentionally spreads gossip about us and we feel guilty when we cross a deadline for a review. For some people, their affect is a continuous source of troubles because they suffer from affective disorders, such as a specific phobia or depression.

As for any aspect of human behavior, emotions are extremely complex phenomena, for several reasons. First, they are multicomponential, consisting of experiential, physiological and behavioral components (Gross, 2002). If you are afraid when walking alone on a deserted street late at night, this may lead to bodily effects such as heart palpitations but also to misperceptions of stimuli in the environment and a tendency to walk faster. Second, an emotion fluctuates over time. Without going into the muddy waters of what the exact definition of an emotion is (see Bradley & Lang, 2007), it is clear that emotions function to signal relevant events for our goals (Oatley & Jenkins, 1992). Because of their communication function, they have a clear temporal component (see e.g., Frijda, Mesquita, Sonnemans, & Van Goozen, 1991) and therefore a genuine understanding of emotions implies an understanding of the underlying dynamics. Third, emotional reactions are subject to contextual and individual differences (see e.g., Barrett, Mesquita, Ochsner, & Gross, 2007; Kuppens, Stouten, & Mesquita, 2009).

The aforementioned complicating factors make the study of affective dynamics a challenging research domain, which requires an understanding of the complex interplay between the different emotion components across time, context and individual differences (Scherer, 2000, 2009). Despite its importance and complexity, research on emotion dynamics is still in its infancy (Scherer, 2000). Next to the lack of a definite theoretical understanding of affective phenomena, a large part of the reason for this lies in the complexity of the data involved in such an enterprise. For instance, because of the prominent physiological component of affect, biological signal processing techniques are required and these are typically not part of the psychology curriculum. On the other hand, the existing methods, traditionally developed and studied in the engineering science, are not directly applicable. As we explain below, we think one of the major bottlenecks according to us is the existence of individual differences. Indeed, as noted by Davidson (1998), one of the most striking features of emotions is the presence of large individual differences in almost all aspects involved in their elicitation and control. Incorporating such differences is therefore crucial, not only to account fully for the entire range of emotion dynamics across individuals in itself, but also for studying the differences between individuals characterized by adaptive or maladaptive emotional functioning.

As an example, let us introduce the data that will be discussed and investigated below. Two groups of adolescents (one with a unipolar depressive disorder and the other without any emotional or behavioral problems) engaged in an interaction task with their parents during a few minutes in which they discussed and tried to resolve a topic of conflict. During the task, several physiological measures were recorded from the adolescent. Moreover, the behavior of the adolescent and parents was observed and coded. All measures were obtained on a second-to-second basis. Several possible research questions are: In what way do the physiological dynamics differ between depressed adolescents and normals? What is the effect of the display of angry behavior by a parent on the affective physiology observed in the adolescent, and is this effect different for depressed and normal adolescents?

A powerful modeling framework that is capable for addressing the above questions is provided by state space modeling. State space models will be explained in detail in the next section, but for now it suffices to say that they have been developed to model the dynamics of a system from measured inputs and outputs using latent states. Usually, it is a single system that is being studied with such models. However, in the particular example in this paper there are as many systems as participants. Because a single state space is already a complex model for statistical inference, studying several of these state space models simultaneously is a daunting task. However, in the present paper we offer a solution to this problem by incorporating state space models in a Bayesian hierarchical framework, which allows to study multiple systems (e.g., individuals) simultaneously, and thus allows to make inferences about differences between individuals in terms of their affective dynamics. Markov chain Monte Carlo methods make the task of statistical inference for such hierarchical models more digestible and the Bayesian approach lets us summarize the most important findings in a straightforward way.

In sum, the goal of this paper is to introduce a hierarchical state space framework allowing us to study individual differences in the dynamics of the affective system. The outline of the paper is as follows. In the next section, we introduce a particular state space model, the linear Gaussian state space model, and extend it to a hierarchical model. In subsequent section, we illustrate the framework by applying it to data consisting of cardiovascular and behavioral measures that were taken during the interaction study introduced above. By focusing on various aspects of the model, we will show how our approach allows to explore several research questions and address specific hypotheses that are discussed in the literature on the physiology and dynamics of emotions. Finally, the discussion reviews the weak and strong aspects of the model, and we make some suggestions for future developments.

Hierarchical state space modeling

We will present a model for the affective dynamics of a single person and then extend this model hierarchically: The basic model structure for each person’s dynamics will be of the same type, and the hierarchical nature of the model allows for the key parameters of the model to differ across individuals.

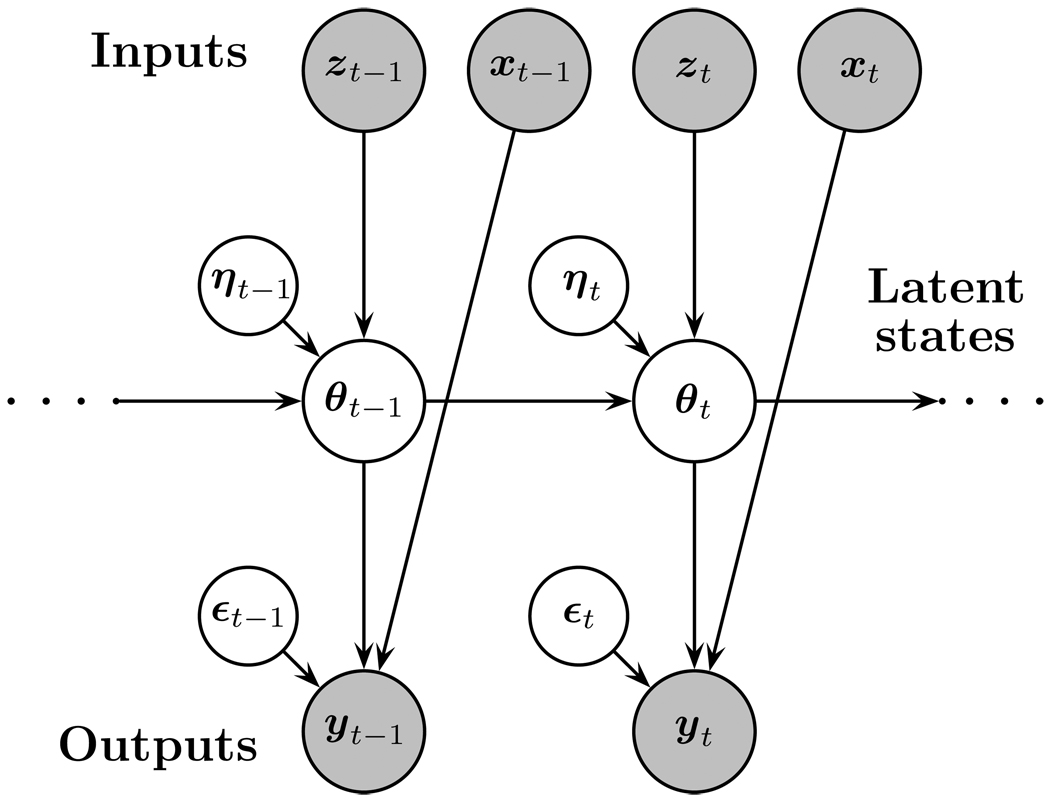
The single individual’s model will be a linear dynamical systems model, cast in the state space framework. In the next paragraphs, the key concepts will be explained verbally and in the next subsections, the mathematical aspects of the model will be described. Our coverage of dynamical systems theory will be sufficient to understand the remainder of the paper, but readers who wish a deeper study of the topic can consult Grewal and Andrews (2001), Ljung (1999) or Simon (2006). Suppose we have a set of observable output variables measured at time t (t = 1, 2, …, T) collected in a vector y_t (e.g., heart rate and blood pressure measured every second from an adolescent) and a set of observable input variables (e.g., an indicator coding whether a parent is angry or not), collected in the vectors x_t and z_t, that are believed to have, respectively, a direct and indirect influence on the outputs. It is believed that the input and output are part of a system, which is a mathematical description of how inputs affect the outputs through state variables (denoted by θ_t). The state variables are a set of latent variables of the system that exhibit the dynamics. A graphical illustration of a state space system is given in Figure 1. In this paper, we will work in discrete time (as opposed to continuous time, for which t ∈ ℝ). The dynamics of the states are then described by a stochastic difference equation where the stochastic term is called the process noise or the innovation, denoted by η_t. As a result, θ_t cannot be perfectly predicted from θ_t−1. On the observed level, it is assumed that the measurements of the output variables are noisy and the measurement error at time t is denoted by ε _t.

Figure 1.

Graphical representation of a dynamical linear system.

The state space modeling framework has been applied in a wide variety of scientific disciplines: From the Apollo space program to forecasting in economical time series to robotics and ecology. The important breakthrough for the practical application of state space models was the seminal paper by Kalman (1960) on the estimation of the states in a linear model.¹ The paper introduces what became known as the Kalman filter, which is a recursive least squares estimator of the state vector θ_t at time t given all observations up to time t (i.e., y₁, … , y_t). Note that the Kalman filter can be derived from a Bayesian argumentation (see Meinhold & Singpurwalla, 1983; see also below).

The Kalman filter is used in state space modeling to obtain an estimate of the latent states, but depending on the context, the researcher may or may not be interested in the values of these states. As an example of the former attitude let us consider an aerospace application. Here the latent states can be the position coordinates of a spacecraft and the parameters of the dynamical system are entirely known (because they may be governed by well-known Newtonian mechanics). In such case, the question of interest is to determine where the spacecraft is, and if necessary, to correct its trajectory (i.e., exerting control by changing the input). However, in other application settings, the dynamics of the process are not exactly known and the interest lies in inference on the parameters of the model. Estimating the states, for instance through the Kalman filter, is only a necessary step in the process of inferring the dynamics of the system. This is the topic of system identification (Ljung, 1999): constructing a mathematical dynamical model based on the noisy measurements.

The specific type of state space model that will be used to model the dynamics of a single individual is a linear state space model: The state dynamics are described using a linear difference equation (with the random process noise term added). Although the kind of processes we will model may be considered to be inherently nonlinear, linear dynamical systems often serve as a good approximation that may reveal many aspects of the data, even when it is known that the underlying system is nonlinear (Van Overschee & De Moor, 1996).

In the following subsections, we will explain in more detail the linear Gaussian state space model and then discuss the hierarchical extension.

The linear Gaussian state space model

The state space model consists of two equations: A transition (or state) equation and an observation equation. Let us start with the transition equation that represents the dynamics of the system. As defined above, θ_t is the vector (of length P) of latent state values at time t. In addition, suppose there are K state covariate measurements collected in a vector z_t. The type of transition equation we use in this paper can be written as follows:

$${\mathit{\theta }}_t|{\mathit{\theta }}_{t-1},\dots ,{\mathit{\theta }}_{t-L}~N\left({\displaystyle \sum _{l=1}^L{\mathbf{\Phi }}_l{\mathit{\theta }}_{t-l}+\mathbf{\Delta }{\mathit{z}}_t,{\mathbf{\Sigma }}_{\eta }}\right).$$ (1)

From Equation 1, it can be seen that the P-dimensional vector of latent processes θ_t is modeled as the combination of a vector autoregression model of order L (denoted as VAR(L)) and a multivariate regression model.² The order of the vector autoregressive part is the maximum lag L. The transition matrix Φ_l of dimension P × P (for l = 1, …, L) consists of autoregression coefficients on the diagonal and crossregression coefficients in the off-diagonal slots. The autoregression coefficient ϕ_[a,a]l represents the dependence of latent state θ_[a]t on itself l time points before, that is, the effect of state θ_[a]t–l. The crossregression coefficient ϕ_[a,b]l represents the influence of state θ_[b]t–l on θ_[a]t. The regression coefficient matrix Δ of dimension P × K contains the effects of the K covariates in z_t on the latent processes θ_t. The innovation covariance matrix Σ_η of dimension P × P describes the Gaussian fluctuations and covariations of the P-dimensional innovation vectors η_t.

The model presented in Figure 1 corresponds to a model for which L = 1 (i.e., VAR(l)) in Equation 1. However, if we ignore the contribution of the state covariates in Equation 1, the general VAR(L) process can also be defined as a VAR(l) process as follows:

$${\mathit{\theta }}_t^{*}|{\mathit{\theta }}_{t-1}^{*}~N\left(\mathit{F}{\mathit{\theta }}_{t-1}^{*},e_1{e}_1^{\prime }\otimes {\mathbf{\Sigma }}_{\eta }\right),$$ (2)

where the definition of the new state vector is: ${\mathit{\theta }}_t^{*}=({\mathit{\theta }}_t^{\prime },\dots ,{\mathit{\theta }}_{t-L}^{\prime })\prime$ or in words, the non-lagged and lagged state vectors combined in a new state vector ${\mathit{\theta }}_t^{*}$. The symbol ⊗ represents the Kronecker product³. The new transition matrix F of dimension PL × PL is equal to

$$\mathit{F}=\left[\begin{array}{ccccc}\hfill {\mathbf{\Phi }}_1\hfill & \hfill {\mathbf{\Phi }}_2\hfill & \hfill \cdots \hfill & \hfill {\mathbf{\Phi }}_{L-1}\hfill & \hfill {\mathbf{\Phi }}_L\hfill \\ \hfill \mathit{I}\hfill & \hfill \mathbf{0}\hfill & \hfill \cdots \hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathit{I}\hfill & \hfill \dots \hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \dots \hfill & \hfill \mathit{I}\hfill & \hfill \mathbf{0}\hfill \end{array}\right],$$ (3)

where I represents a P × P identity matrix and 0 refers to a P × P matrix of zeros. This technique of reformulating a dynamical system of order L into one of order 1 is common in state space modeling, but is also used in differential equation modeling (see Borrelli & Coleman, 1998). Because in our new formulation, some parts of ${\mathit{\theta }}_t^{*}$ and ${\mathit{\theta }}_{t-1}^{*}$ are exactly equal to each other (there is no randomness involved), the covariance matrix in Equation 2 is degenerate:

$$e_1{e}_1^{\prime }\otimes {\mathbf{\Sigma }}_{\eta }=\left[\begin{array}{cccc}\hfill {\mathbf{\Sigma }}_{\eta }\hfill & \mathbf{0}& \cdots & \cdots \\ \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\\ ⋮& ⋮& \ddots & ⋮\\ \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\end{array}\right],$$ (4)

where e₁ is the L-dimensional first standard unit vector (with 1 in the first position and zero otherwise). Equation 2 shows that it is most important to study the VAR(1) process since higher order processes can always be reduced to a lag 1-model. For instance, a useful result is that if the process in Equation 2 is stationary, all eigenvalues of F should lie inside the unit circle (see e.g., Hamilton, 1994). The state covariate regression part can be easily added to Equation 2 by inserting in the mean structure: e₁ ⊗ Δ z_t.

The second equation in a state space model is the observation equation, which reads for the model as presented in Equation 1 as follows:

$${\mathit{y}}_t|{\mathit{\theta }}_t~N(\mathit{\mu }+\mathbf{\Psi }{\mathit{\theta }}_t+\mathbf{\Gamma }{\mathit{x}}_t,{\mathbf{\Sigma }}_{\mathbf{\epsilon }}),$$ (5)

where the observed output at time t is collected in a Q-dimensional vector y_t. The observation equation maps the vector of latent states θ_t at time t to the observed output vector y_t also at time t (hence there are no dynamics in this equation). The observation equation also contains a P-dimensional mean vector μ and a Q × P design matrix Ψ that specifies to which extent each of the latent states influence the observed output processes. In addition, there is the influence of the J observation covariates collected in a vector x_t, with the corresponding regression coefficients being organized in the Q × J matrix Γ. The Q × Q measurement error covariance matrix Σ_ε describes the Gaussian fluctuations and covariations of the measurement errors (denoted as ε_t).

It should be noted that we consider in this paper a restricted version of the state space model in which each observed output is tied directly to a latent state. This means that P = Q and Ψ = I_P. Stated otherwise, each observed process has a corresponding latent process that is not corrupted by measurement error.

If the model from Equation 2 is used as the transition equation, then the observation equation needs to be modified as well because the definition of the latent states has changed:

$${\mathit{y}}_t|{\mathit{\theta }}_t^{*}~N\left(\mathit{\mu }+\left(e_1^{\prime }\otimes \mathbf{\Psi }\right){\mathit{\theta }}_t^{*}+\mathbf{\Gamma }{x}_t,{\mathbf{\Sigma }}_{\epsilon }\right),$$ (6)

where e₁ is again the first standard unit vector.

As mentioned before, the graphical representation in Figure 1 is in fact much more general than it appears. It seems to be only valid for a restricted dynamical model of only lag 1, but as we have shown the lag 1 dynamical model also has the lag L model as a special case after an appropriate definition of the state vector. Figure 1 is not only an appealing illustration of some of the general components of the model; it also gives a concise and detailed description of the basic properties of the model. Graphical modeling is a popular method for visualizing conditional dependency relations between the various components of the model. For instance, one can read off quite easily that the Markov property holds for the transition equation on the latent state level: Given knowledge of state θ_t, there is independence between θ_t−1 and θ_t+1. In the language of graphical models (see e.g., Pearl, 2000), this means that θ_t−1 and θ_t+1 are d-separated by θ_t (i.e., θ_t blocks the path from θ_t−1 to θ_t+1) and therefore θ_t−1 and θ_t+1 are conditionally independent given θ_t. Using the same reasoning, it can be seen that there is no conditional independence between y_t−1 and y_t+1 given y_t because the latter one does not block the path from y_t−1 to y_t+1. Hence, while the dynamical properties are limited to the latent dynamical system and they are Markovian, the dependency relations between the observed outputs y_t are not Markovian but more complex.

Hierarchical extension

In the previous subsection we have described a dynamical linear model for a single system. In many scientific domains one can stop there and discuss how the statistical inference for such a single-system dynamical linear model can be performed. However, in psychology, if the system refers to processes within one individual, the study of individual differences in such processes requires studying many systems and the differences between them simultaneously. There are several options for doing this.

A first option is to analyze the data from all subjects simultaneously. However, such an approach is hard to reconcile with the existence of individual differences unless a model structure is chosen that allows for states to be unique for different individuals. A disadvantage of such an approach is that the state vector quickly becomes very large and the computations unwieldy. A second option is to apply a separate dynamical linear model to the data of each participant. Although this approach allows for maximal flexibility in terms of how people may differ from each other, it is not without risk. In many cases, data from single participants are not very informative. In the example to be discussed in detail later on, the anger responses of the parents will be considered input for the cardiovascular system. Unfortunately, many parents show angry behavior only at rare occasions, which yields uninformative data and therefore may hamper the inferential process.

An interesting modeling approach that allows for individual differences but at the same time does not collapse under the weight of its flexibility is hierarchical dynamical linear modeling. In hierarchical models, person specific key parameters are assumed to be a sample from a distribution, typical for the population that is investigated, allowing to model both individual differences and group effects (Shiffrin, Lee, Kim, & Wagenmakers, 2008; Lee & Webb, 2005).

To explain the hierarchical extension, let us first reconsider the state space model and make it specific for person i (with i = 1, …, I):

$$\begin{array}{ccc}\hfill {\mathit{y}}_{t,i}|{\mathit{\theta }}_{t,i}& ~& N({\mathit{\mu }}_i+{\mathit{\theta }}_{t,i}+{\mathbf{\Gamma }}_i{x}_{t,i},{\mathbf{\Sigma }}_{\mathit{\epsilon }})\hfill \\ \hfill {\mathit{\theta }}_{t,i}|{\mathit{\theta }}_{t-1,i},\dots ,{\mathit{\theta }}_{t-L,i}& ~& N\left({\displaystyle \sum _{l=1}^L{\mathbf{\Phi }}_{l,i}{\mathit{\theta }}_{t-l,i}+{\mathbf{\Delta }}_i{\mathit{z}}_{t,i},{\mathbf{\Sigma }}_{\eta }}\right),\hfill \end{array}$$ (7)

such that all parameters are specific for individual i, except the error covariance matrices Σ_η and Σ_ε. Although it would be realistic, we have chosen not to allow these covariance matrices to vary between individuals because hierarchical models for covariance matrices are not yet very well understood (for an exception, see Pourahmadi & Daniels, 2002).

The size of the vectors and matrices in Equation 7 is the same as in the corresponding Equation 1 and Equation 5. In order to have a parsimonious notation scheme, we will denote elements of the person specific vectors and matrices with an index i and the appropriate row and column indicators between square brackets. For instance, the p^th element of μ_i is then equal to μ_[p]i and the element (j,k) of Φ_l,i is ϕ_[j,k]l,i.

A next step in constructing a hierarchical model is to specify the population distributions from which it is assumed that the person specific parameters are sampled. For each element of these system parameters, an independent hierarchical multivariate normal distribution is assumed. For notational convenience, the population mean is always denoted by α (mean) or α (mean vector) and the population variance by β (variance) or B (covariance matrix). An appropriate subscript will be used to specify for which particular parameter hierarchical parameters are defined. For example, the personspecific mean μ_i is assumed to be sampled from a multivariate normal distribution with mean vector α_μ and covariance matrix B_μ:

$${\mathit{\mu }}_i~N({\mathit{\alpha }}_{\mu },{\mathit{B}}_{\mu }).$$ (8)

The other person specific parameters are all organized into matrices and to specify their corresponding population distributions, we need the vectorization operator vec(·) (or vec operator; see Magnus & Neudecker, 1999), which transforms a matrix into a column vector by reading the elements row-wise and stacking them below one another. Let us illustrate this for the transition matrix Φ_1,i. Assuming that P = 2 (i.e., there are two latent states), Φ_1,i is a 2 × 2 matrix that is vectorized as follows:

$$\text{vec}({\mathbf{\Phi }}_{1,i})=\text{vec}\left(\left[\begin{array}{cc}{\varphi }_{[1,1]1,i}& {\varphi }_{[1,2]1,i}\\ {\varphi }_{[2,1]1,i}& {\varphi }_{[2,2]1,i}\end{array}\right]\right)=\left[\begin{array}{c}{\varphi }_{[1,1]1,i}\\ {\varphi }_{[1,2]1,i}\\ {\varphi }_{[2,1]1,i}\\ {\varphi }_{[2,2]1,i}\end{array}\right].$$ (9)

As for the hierarchical distributions for these matrix parameters Φ_l,i (for l = 1, …, L), Γ_i and Δ_i, we assume multivariate normal distributions for all vectorized parameters. For the regression coefficients of the observation covariates x_t,i, the population distribution reads as:

$$\text{vec}({\mathbf{\Gamma }}_i^{\prime })~N({\mathit{\alpha }}_{\mathbf{\Gamma }},{\mathit{B}}_{\mathbf{\Gamma }})$$ (10)

and for the regression coefficients of the state covariates z_t,i, it is

$$\text{vec}({\mathbf{\Delta }}_i^{\prime })~N({\mathit{\alpha }}_{\mathbf{\Delta }},{\mathit{B}}_{\mathbf{\Delta }}).$$ (11)

For the transition matrices Φ_l,i (with l = 1, …,L), it is in principle the same but with the additional constraint that the dynamic latent process is stationary (i.e., that the eigenvalues of the F_i matrix fall inside the unit circle). This constraint is denoted as I(|λ(F_i)| < 1) in subscript of the multivariate normal distribution:

$$\left(\begin{array}{c}\text{vec}({\mathbf{\Phi }}_{1,i}^{\prime })\\ ⋮\\ \text{vec}({\mathbf{\Phi }}_{L,i}^{\prime })\end{array}\right)~N{({\mathit{\alpha }}_{\mathbf{\Phi }},{\mathit{B}}_{\mathbf{\Phi }})}_{I(|\mathrm{\lambda }({\mathit{F}}_i)|<1)}.$$ (12)

The covariance matrices can be unstructured (i.e., all variances and covariances can be estimated freely) but in the application section we will impose some structure (because it is the first time the model has been formulated and we do not want to run the risk of having weakly identified parameters that cause trouble for the convergence and mixing of the MCMC algorithm). In this paper, it is assumed that all person specific parameters have a separate variance, but that all covariances are zero.

Statistical inference

In this section we will outline how to perform the statistical inference for the hierarchical dynamical linear model, i.e. how to estimate the model parameters with Bayesian statistics. Concerning the estimation of the parameters of a (non-hierarchical) dynamical linear model, there is a huge literature mainly in engineering (e.g., Ljung, 1999) and econometrics (e.g., Hamilton, 1994; Kim & Nelson, 1999), but also in statistics (e.g., Shumway & Stoffer, 2006; Petris, Petrone, & Campagnoli, 2009). However, to the best of our knowledge, the hierarchical extension as presented in this paper is new and estimating the model’s parameters requires some specific choices, of which opting for the Bayesian approach is the most consequential one.⁴

Besides the theoretical appeal of Bayesian statistics, it also offers the possibility to use sampling based computation methods such as Markov chain Monte Carlo (MCMC, see e.g., Gilks, Richardson, & Spiegelhalter, 1996; Robert & Casella, 2004). Especially for hierarchical models this is very helpful because the multidimensional integration against the random effects densities may not have closed form solutions and if the latter do not exist, numerical procedures are practically not feasible. For instance, in the model defined in the preceding section, an integral of very high dimension has to be calculated: P + LP² + PK + QJ, where the contributions in the product come from respectively the mean vector, the transition matrices, the state covariate regression weights, and the observation covariate regression weights. Even for a model with no covariates, two states and five time lags, the dimension is already 22. For this reason, we resort to Bayesian statistical inference and MCMC.

To sample the parameters from the posterior distribution, we have implemented a Gibbs sampler (Casella & George, 1992; Gelfand & Smith, 1990). In this method, the vector of all parameters is subdivided into blocks (in the most extreme version, each block consists of a single parameter) and then we sample alternatively from each full conditional distribution: The conditional distribution of a block, given all other blocks and the data. For our model, all full conditionals are known and easy-to-sample distributions (i.e., normals, scaled inverse chi-squares). Sampling iteratively from the full conditionals creates a Markov chain with as an equilibrium or stationary distribution the posterior distribution of interest. Although strictly speaking convergence is only attained in the limit, in practice one lets the Gibbs sampler run for a sufficiently long “burn-in period” (long enough to be confident about the convergence) and after the burn-in the samples are considered to be simulated from the true posterior distribution. Convergence can be checked with specifically developed statistics (for instance R̂, see Gelman, Carlin, Stern, & Rubin, 2004). The inferences are then based on the simulated parameter values (for instance, the sample average of a set of draws for a certain parameter is taken to be a Monte Carlo estimate of the posterior mean for that parameter). More information on the theory and practice of the Gibbs sampler and other MCMC methods can be found in Gelman et al., 2004 and Robert & Casella, 2004.

For describing the specific aspects of the Gibbs sampler used in this paper, we start by reconsidering the observation and transition equations, see Equation 7. It can be seen that if the latent states θ_t,i were known for all time points t = 1, …, T for a specific subject i, the problem of estimating the other parameters reduces to estimating the coefficients and residual variances in a regression model (see Gelman et al., 2004). Unfortunately, the latent states θ_t,i are not known, but they can be considered as “latent data” or “missing data” and their full conditional (given the model parameters and the data) can be derived as well. Note that considering the latent states as missing data and sampling them will enormously simplify the sampling algorithm. After running the sampler, the sampled latent states may be used as well for inference or they can be ignored (and this option actually means that one integrates the latent states out of the posterior).

The Gibbs sampler consists of three distinct large components: (1) sampling the latent states, (2) sampling the system parameters, and (3) sampling the hierarchical parameters. These components will be discussed separately in the next paragraphs.

Component 1: Sampling the latent states

In the first component, we estimate the latent states with the forward filtering backward sampling algorithm (FFBS; Carter & Kohn, 1994). Let us define Θ_1:t,i as the collection of latent state vectors of individual i up to time t. Likewise, y_1:t,i contains all observations for individual i up to time t. In addition, collect all parameters of the model in a vector ξ. The FFBS algorithm draws a sample from the conditional distribution of all states for an individual i, given all data for person i and the parameters: p(Θ_1:T,i|y_1:T,i,ξ) The FFBS algorithm is also called a simulation smoother (Durbin & Koopman, 2001). To simplify notation, we will suppress the dependence upon the parameters ξ in the following paragraphs. We also note that in our derivation we will assume a lag 1 dynamical model for the states. However, if one considers a more general lag L dynamical model, then Θ_1:t,i has to be replaced by ${\mathbf{\Theta }}_{1:t,i}^{*}$ (containing all latent states ${\mathit{\theta }}_{t,i}^{*}$ defined as in Equation 2 up to time t).

In explaining the FFBS algorithm, it is important to note that our graphical model for a single person is a Directed Acyclic Graph (DAG; directed because all links have an arrow and the graph is acyclic because there is no path connecting a node with itself) with all specified distributions being normal (both marginal and conditional distributions). As shown in Bishop (2006), in a DAG with only normal distributions, the joint distribution p(Θ_1:T,i, y_1:T,i) is also (multivariate) normal. Therefore, the conditional distribution p(Θ_1:T,i|y_1:T,i) will also be multivariate normal.

Instead of sampling directly from p(Θ_1:T,i|y_1:T,i) one could use in principle samples from the full conditional of a single θ_t,i. In that case, the full conditional of θ_t,i given the latent states, parameters and data is used: p(θ_t,i|θ_1:t−1,i, θ_t+1:T,i,y_1:T,i) = p(θ_t,i|θ_t−1,i, θ_t+1:,i, y_t,i) This identity holds, because given θ_t−1,i, θ_t+1,i and y_t,i, θ_t,i is independent from all other states and data (again this can be checked in the graphical model because these three nodes block all paths to the state at time t). Carter and Kohn (1994) call this the single move sampler and note that it may lead to high autocorrelations in the sampled latent states. Therefore, we opt for the multimove sampler such that Θ_1:T,i is sampled as a whole from p(Θ_1:T,i|y_1:T,i)

However, sampling efficiently from p(Θ_1:T,i|y_1:T,i) is not a straigthforward task because it may be a very highdimensional multivariate normal distribution (e.g., if there are 60 time points and four latent states, it is 240-dimensional). Carter and Kohn (1994) described an efficient algorithm (see also Kim & Nelson, 1999). The basic idea is based on the following factorization (repeated from Kim & Nelson, 1999):

$$\begin{array}{c}p({\mathbf{\Theta }}_{1:T,i}|{\mathit{y}}_{1:T,i})\hfill \\ =p({\mathit{\theta }}_{T,i}|{\mathit{y}}_{1:T,i})p({\mathbf{\Theta }}_{1:T-1,i}|{\mathit{\theta }}_{T,i},{\mathit{y}}_{1:T,i})\hfill \\ =p({\mathit{\theta }}_{T,i}|{\mathit{y}}_{1:T,i})p({\mathit{\theta }}_{T-1,i}|{\mathit{\theta }}_{T,i,}{\mathit{y}}_{1:T,i})p({\mathbf{\Theta }}_{1:T-2,i}|{\mathit{\theta }}_{T,i},{\mathit{\theta }}_{T-1,i},{\mathit{y}}_{1:T,i})\hfill \\ =p({\mathit{\theta }}_{T,i}|{\mathit{y}}_{1:T,i})p({\mathit{\theta }}_{T-1,i}|{\mathit{\theta }}_{T,i,}{\mathit{y}}_{1:T,i})p({\mathit{\theta }}_{T-2,i}|{\mathit{\theta }}_{T,i},{\mathit{\theta }}_{T-1,i,}{\mathit{y}}_{1:T,i})p({\mathbf{\Theta }}_{1:T-3,i}|{\mathit{\theta }}_{T,i,}{\mathit{\theta }}_{T-1,i}{\mathit{\theta }}_{T-2,i},{\mathit{y}}_{1:T,i})\hfill \\ =\dots \hfill \\ =p({\mathit{\theta }}_{T,i}|{\mathit{y}}_{1:T,i})p({\mathit{\theta }}_{T-1,i}|{\mathit{\theta }}_{T,i,}{\mathit{y}}_{1:T,i})p({\mathit{\theta }}_{T-2,i}|{\mathit{\theta }}_{T-1,i},{\mathit{y}}_{1:T,i})p({\mathit{\theta }}_{T-3,i}|{\mathit{\theta }}_{T-2,i},{\mathit{y}}_{1:T,i})\dots p({\mathit{\theta }}_{1,i}|{\mathit{\theta }}_{2,i},{\mathit{y}}_{1:T,i})\hfill \\ =p({\mathit{\theta }}_{T,i}|{\mathit{y}}_{1:T,i})p({\mathit{\theta }}_{T-1,i}|{\mathit{\theta }}_{T,i},{\mathit{y}}_{1:T-1,i})p({\mathit{\theta }}_{T-2,i}|{\mathit{\theta }}_{T-1,i},{\mathit{y}}_{1:T-2,i})\hfill \\ p({\mathit{\theta }}_{T-3,i}|{\mathit{\theta }}_{T-2,i},{\mathit{y}}_{1:T-3,i})\cdots p({\mathit{\theta }}_{1,i}|{\mathit{\theta }}_{2,i},{\mathit{y}}_{1:1,i})\hfill \\ =p({\mathit{\theta }}_{T,i}|{\mathit{y}}_{1:T,i}){\displaystyle \prod _{t=1}^{T-1}p({\mathit{\theta }}_{t,i}|{\mathit{\theta }}_{t+1,i},{\mathit{y}}_{1:t,i}).}\hfill \end{array}$$ (13)

The factorization shows that we can start sampling θ_T,i given all data and then going backwards, each time conditioning on the previously sampled value and the data up to that point. It is here that the Kalman filter comes into play because p(θ_T,i|y_1:T,i) is the so-called filtered state density at time T: It contains all information in the data about θ_T,_i. Although we will not present the mean and covariance matrix for the normal density p(θ_T,i|y_1:T,i) (see e.g., Meinhold & Singpurwalla, 1983; Bishop, 2006; Kim & Nelson, 1999), it is useful to stress that the Kalman filter equations can be seen as a form of Bayesian updating with p(θ_T,i|y_1:T−1,i) as the prior, p(y_T,i|θ_T,i) as the likelihood and p(θ_T,i|y_1:T,i)as the posterior (all distributions are normal).

The other densities p(θ_t,i|θ_t+1,i, y_1:t,i) involved in the factorization in Equation 13 can also be found through applying the Kalman filter. For instance, p(θ_t,i|θ_t+1,i, y_1:t,i) is simply the Kalman filtered density for the state at time t after having seen all data up to time t and an additional “artificial” observation θ_t+1,i, that is, the sampled value for the next state. Hence, this involves another one-step ahead prediction using the Kalman filter.

In practice, the FFBS algorithm works by running the Kalman filter forward and thus calculating the filtered densities for the consecutive states given y_1:t,i (with t = 1,…, T). After this forward step, the backward sampling is applied and this involves each time (except for the first sampled value θ_T,i) another one-step ahead Kalman filter prediction, starting from observed sequence y_1:t,i and adding a new “observation” θ_t+1,i, (with an appropriate likelihood p(θ_t+1,i|θ_t,i) which is in this case the transition equation and the prior is the filtered density p(θ_t,i|y_1:t,i))

Component 2: Sampling the system parameters

In the second component, we sample the individual effect parameters μ_i, Φ_l,i (for l = 1, …, L), Γ_i, Δ_i and also the covariance matrices Σ_η and Σ_ε from their full conditionals. Because the sampling distributions condition on the values for the latent states, obtained in the FFBS, the observation and transition equations for individual i as in Equation 7 reduce to multivariate linear regression equations in which the regression coefficients and the covariance matrices are to be estimated. The hierarchical distributions serve as prior distributions for the random effects. Because this is a well-known problem in Bayesian statistics, we refer the reader to the literature for more information (see e.g., Gelman et al., 2004). More information about the derivation of the full conditionals can be found in Appendix A.

Component 3: Sampling the hierarchical parameters

In this component, the hierarchical mean vectors α_μ, α_Φ, α_Γ and α_Δ and the hierarchical covariance matrices B_μ, B_Φ, B_Γ and B_Δ are sampled. These parameters only depend on the individual effects that were sampled in the previous component. Hence, given the sampled individual system parameters, the problem reduces to estimating the mean vector and covariance matrices for the normal population distribution. Technical details are explained in Appendix A.

Easy-to-use software WinBUGS is available for free and used in various research standard in Bayesian modeling (Lunn, Thomas, Best, & Spiegelhalter, 2000). However, for optimal tuning and the implementation of complex subroutines in the MCMC sampling scheme, custom written scripts are a better alternative, certainly for complex models as the one presented here. For the hierarchical state space model, the implementation of a Gibbs sampler was especially written in R (R Development Core Team, 2009).⁵

Before turning to the application, we want to make two comments about the estimation procedure. A first observation is that when estimating the model using artificial data (simulated with known true values), we obtained estimates that were reasonably close to the population values. An illustration of this can be found in Appendix B. A second point is that the R code can be speeded up by coding some parts or the whole code in a compiled programming language (e.g., C++ or Fortran). At this stage, we have not yet done this because the R code is more transparant and allows for easy debugging and monitoring but future work will include translating the program into C++ or Fortran.

Application to emotional psychophysiology

We will now apply the presented hierarchical state space model to the data that reflect the affective physiological changes in depressed and non-depressed adolescents during conflictual interactions with their parents (Sheeber, Davis, Leve, Hops, & Tildesley, 2007). The study was carried out with adolescents because one is especially at risk for mood disorders at that age. Depression, cardiovascular physiology and affective dynamics form a three-node graph for which all three edges have been extensively documented in the literature. For instance, overviews of studies supporting the link between depression and cardiovascular physiology can be found in Carney, Freedland, and Veith (2005) and Gupta (2009). Evidence on the link between affective dynamics and depression is documented by Sheeber et al. (2009). The relation between cardiovascular aspects of emotion are described by Bradley and Lang (2007).

In this application section, we will combine the three aforementioned aspects (depression, cardiovascular physiology and affective dynamics) in a state space model to study three specific questions to be outlined below. This section starts with a description of the study and the data, some discussion of the fitted model and basic results and then we consider in detail the three specific research questions.

Oregon adolescent interaction task

The participants were selected in a double selection procedure in schools, consisting of a screening on depressive symptoms using the Center for Epidemiologic Studies Depression scale (CES-D; Radloff, 1977) followed by diagnostic interviews using the Schedule of Affective Disorders and Schizophrenia-Children’s Version (K-SADS; Orvaschel & Puig-Antich, 1994) when the CES-D showed elevated scores. The selected participants were 133 adolescents⁶ (88 females and 45 males) with mean age of 16.2 years. From the total group, 67 adolescents met the DSM-IV criteria for major depressive disorder and were classified as “depressed” whereas 66 adolescents did not meet these criteria and were classified as “normal”.⁷

As part of the study, the adolescent and his/her parents were invited for several nine-minute interaction tasks in the laboratory: two positive tasks (e.g., discuss nice time together), two reminiscence tasks (e.g., discuss salient aspects of adolescenthood and parenthood) and two conflict tasks (e.g., discuss familial conflicts). During these interactions, second-to-second physiological measures were taken from the adolescent and second-to-second behavioral measures were derived from videotaped behavior of adolescent and parents, resulting in 540 measurements for each task per participant.

The physiological measurements consisted of various measures of heart rate (heart rate, finger pulse heart rate, interbeat interval), blood pressure (blood pressure, diastolic and systolic blood pressure, moving window blood pressure), respiration (respiratory sinus arrhythmia, tidal volume, respiratory period) and skin conductance (skin conductance level, skin conductance response). The behavioral measurements were coded from the videotaped interactions using the Living In Family Environment coding system (LIFE, Hops, Davis, & Longoria, 1995). The behavior of adolescent and parents was classified on a second-to second basis as either neutral, happy (happy non-verbal or verbal behavior), angry (aggressive/provoking non-verbal or verbal behavior) or dysphoric (sad non-verbal or verbal behavior).

Model specification

The Oregon adolescent interaction data set has a large number of variables and a large number of time points. It is impossible to model everything in a single step. Therefore, we have restricted our attention in this paper to a subset of the available data. First, we focus on capturing the dynamics of adolescent’s physiology in terms of their heart rate (HR) and blood pressure (BP). Both HR and BP are seen as indicators of sympathetic autonomic arousal and are considered to be part of the emotional stress-reponse (e.g., Levenson, 1992). Second, in deciding in which context such reponses could best be studied, we decided to focus on the conflictual interaction task, as this task was specifically designed to study conflict and the ensuing stress responses. Third, we focused on the dynamics of these physiological indicators and studied the effect of parental anger (denoted as AP). Fourth, we focus only on the third minute (seconds 121 to 180) of the first conflict task. The reason for the restriction of the number of observation points is that we want to illustrate the usefulness of the hierarchical framework in weakly informative data. Thus, to summarize, the three time-varying measures of interest are HR, BP (both outputs) and AP (input), and this in the third minute of the first conflictual task.

HR was derived from the measured electrocardiograph (ECG) signal and its unit is BPM (beats per minute). BP was obtained with the Portapres portable device, with its unit being mmHg (millimeter of mercury). The behavioral measure AP was obtained by aggregation of two measures that were obtained after analysis of the videotaped interactions with the LIFE coding system. The constituent variables AngerFather (AF) and AngerMother (AM) were binary: They were equal to 0 when the behavior of respectively father or mother was classified an “not angry” and 1 if it was classified as “angry”. Then AP was derived as the sum of AF and AM, taking values of 0 (none of the parents show angry behavior), 1 (at least one parent shows angry behavior) and 2 (both parents show angry behavior). In Figure 2, an example of the data is shown for two random participants.

Figure 2.

Example data for two randomly chosen participants, showing their fluctuations in heart rate (HR; full line), blood pressure (BP; dotted line) and anger parents (AP; background shading: white = 0, light grey = 1 and dark grey = 2).

The hierarchical state space model is based on the observable outputs HR and BP and the observable input (or state covariate) AP. The model for individual i is

$$\begin{array}{c}{\mathit{y}}_{t,i}|{\mathit{\theta }}_{t,i}~N({\mathit{\mu }}_i+{\mathit{\theta }}_{t,i},{\mathbf{\Sigma }}_{\epsilon })\\ {\mathit{\theta }}_{t,i}|{\mathit{\theta }}_{t-1,i},\dots ,{\mathit{\theta }}_{t-5,i}~N\left({\displaystyle \sum _{l=1}^5{\mathbf{\Phi }}_{l,i}{\mathit{\theta }}_{t-1,i}+{\mathbf{\Delta }}_i{z}_{t-1,i},{\mathbf{\Sigma }}_{\eta }}\right)\end{array}$$ (14)

where the vector of observed processes y_t,i consists of y_[1],t,i (observed HR of individual i at time t) and y_[2],t,i (observed BP of individual i at time t), the vector of latent processes θ_t,i consists of θ_[1],t,i (latent HR of individual i at time t) and θ_[2],t,i (latent BP of individual i at time t) and the scalar covariate z_t−1,i equals the observation of AP at time t for individual i. The number of lags for the transition matrices was set at 5 seconds (lag 5), which is consistent with earlier findings that this is the appropriate time window to look at (see e.g., Matsukawa & Wada, 1997).

The random effects distributions for the means, covariate effects and transition matrices are defined as in Equations 8, 11 and 12 respectively. The mean vector α_μ consists of the elements α_μ1 (hierarchical mean of HR) and α_μ2 (hierarchical mean of BP), and the diagonal of B_μ consists of the elements β_μ1 and β_μ2 (the corresponding hierarchical variances). The population mean α_Φl has elements α_ϕ[1,1]l (hierarchical mean of the autoregressive effect HR for lag l), α_ϕ[1,2]l (hierarchical mean of the crosslagged effect BP on HR for lag l), α_ϕ[2,1]l (hierarchical mean of the crosslagged effect HR on BP for lag l) and α_ϕ[2,2]l (hierarchical mean of autoregressive effect BP for lag l). In addition, the diagonal of B_Φl contains elements β_ϕ[1,1]l, β_ϕ[1,2]l, β_ϕ[2,1]l and β_ϕ[2,2]l, (the corresponding hierarchical variances). Finally, α_Δ consists of the elements α_δ1 (hierarchical mean of the regression effect of AP on HR) and α_δ2 (hierarchical mean of the regression effect of AP on BP) and the diagonal of B_Δ consisting of the elements β_δ1 and β_δ2(the corresponding hierarchical variances).

The introduced hierarchical state space model is estimated separately for data of the normal and the depressed adolescents, using a Gibbs sampler that was implemented in R. The prior distributions were chosen to be conjugate to the model likelihood.⁸ For each analysis, we obtained three independent chains of 6000 samples of which the first 1000 were discarded as burn-in. To monitor convergence of the MCMC chains, R̂ (Gelman et al., 2004) was calculated for each single parameter and convergence was obtained for most parameters according to R̂.⁹ In Table 1, the posterior medians and the 95% credibility intervals are reported for selected parameters from the analysis of the normal and depressed adolescents. This is to give the reader a general idea of the values of the parameters in the estimated model. Specific parameters will be discussed below in the context of specific questions. We will elaborate on this in the following paragraphs.

Table 1.

Posterior medians (q.500) and 95% credibility interval ([q.025,q.975]) for a selection of parameters in the analysis of the hierarchical model for the normal and depressed adolescents. Abbreviations used are HM (hierarchical mean), HV (hierarchical variance), AR (autoregression), CR (crossregression), HR (heart rate), BP (blood pressure) and AP (anger parents).

		Normals			Depressed
	Description	q.025	q.500	q.975	q.025	q.500	q.975
	Hierarchical parameters μ
αμ1	HM for general mean HR	73.01	75.46	77.92	76.19	78.96	81.69
αμ2	HM for general mean BP	83.86	87.44	91.10	88.67	91.82	94.88
βμ1	HV for general mean HR	70.98	99.94	144.43	91.33	127.71	184.43
βμ2	HV for general mean BP	157.05	221.30	320.31	113.90	158.09	229.16
	Hierarchical parameters Φ1
αϕ[1,1]1	HM for AR effect HR	0.85	0.93	1.01	0.85	0.93	1.00
αϕ[1,2]1	HM for CR effect BP → HR	−0.23	−0.16	−0.10	−0.22	−0.17	−0.11
αϕ[2,1]1	HM for CR effect HR → BP	0.11	0.17	0.22	0.11	0.17	0.23
αϕ[2,2]1	HM for AR effect BP	0.40	0.46	0.53	0.33	0.40	0.47
βϕ[1,1]1	HV for AR effect HR	0.04	0.06	0.09	0.03	0.04	0.07
βϕ[1,2]1	HV for CR effect BP → HR	0.03	0.04	0.07	0.02	0.04	0.05
βϕ[2,1]1	HV for CR effect HR → BP	0.02	0.03	0.05	0.02	0.04	0.06
βϕ[2,2]1	HV for AR effect BP	0.04	0.06	0.08	0.04	0.06	0.09
	Hierarchical parameters Δ
αδ1	HM for effect AP → HR	−0.79	−0.27	0.23	−0.88	−0.38	0.13
αδ2	HM for effect AP → BP	0.14	0.78	1.47	−0.12	0.38	0.86
βδ1	HV for effect AP → HR	0.13	0.41	1.60	0.30	1.08	3.49
βδ2	HV for effect AP → BP	0.27	1.26	4.17	0.13	0.41	1.26
	Error variances
${\sigma }_{\epsilon ,1}^2$	Measurement error variance HR	0.25	0.58	1.03	0.49	0.82	1.30
${\sigma }_{\epsilon ,2}^2$	Measurement error variance BP	0.22	0.79	1.51	0.12	0.40	0.99
${\sigma }_{\eta ,1}^2$	Innovation variance HR	16.66	17.59	18.60	14.63	15.47	16.39
${\sigma }_{\eta ,2}^2$	Innovation variance BP	15.50	16.34	17.2	21.57	22.65	23.78

Question 1: Tachycardia & hypertension?

Literature on psychophysiology and psychiatry recognizes that major depressive disorder is associated with various physiological processes (Gupta, 2009). For instance, tachycardia (elevated heart rate) was found to be linked to depression (Carney et al., 2005; Dawson, Schell, & Catania, 1977; Lahmeyer & Bellur, 1987). More extensively studied is the link between depression and hypertension (high blood pressure): Depressed individuals seem to generally have a higher blood pressure than normals (Davidson, Jonas, Dixon, & Markovitz, 2000; Jonas, Franks, & Ingram, 1997; Rutledge & Hogan, 2002; Scherrer et al., 2003), although in some studies the effect was not replicated (Wiehe et al., 2006; Lake et al., 1982) or even a reverse effect was observed (Licht et al., 2009). Various explanations for the link between hypertension and depression were investigated such as psychosocial stressors (Sparrenberger et al., 2006; Bosworth, Bartash, Olsen, & Steffens, 2003), antidepressant use (Licht et al., 2009) and sleep (Gangwisch et al., 2010).

To investigate this particular difference in physiology for depressed and non-depressed individuals, we focus in the hierarchical state space model on the estimated posterior distributions for the elements of the hierarchical parameter vector α_μ for the group of normals and depressed. In Figure 3, the estimated posterior densities for the elements α_μ1 and α_μ2 are compared and visual inspection suggests that average heart rate and blood pressure are higher for depressed than for normals.

Figure 3.

Estimated posterior densities for normals (full lines) and depressed (dotted lines) of the parameters α_μ1 and α_μ2, the hierarchical means of respectively HR and BP.

As a formal test, Bayes factors are estimated to quantify the support of the comparisons. Bayes factor estimation is performed with the encompassing prior method (see e.g., Klugkist & Hoijtink, 2007; Hoijtink, Klugkist, & Boelen, 2008). This method easily allows to estimate the Bayes factor to test whether a parameter θ is larger or smaller than a fixed value. Given that the prior distribution of θ gives equal prior mass to both scenarios M₁ : θ < 0 and M₂ : θ > 0, an estimate for the Bayes factor BF₂₁ (in favor of M₂) is equal to the ratio of the posterior proportions of parameter θ being consistent with each of the models: B̂F₂₁ = P̂r(θ > 0 | Y)/P̂r(θ < 0 | Y) To test a difference between the populations of normal and depressed individuals, a difference parameter was derived (e.g., θ^diff = θ^depr – θ^norm) and the encompassing prior method was applied to the estimated posterior distribution of this difference parameter.

We find strong support for heart rate (BF = 30.12) and blood pressure (BF = 25.60) being higher for depressed than for normals.¹⁰ These findings are consistent with many studies in the literature that suggest a link between depression, tachycardia and hypertension. Although the particular setting of our study strongly differs from most studies about tachycardia and hypertension, our results demonstrate that the associations with depression remain even during stressful interactions.

Question 2: Emotional inertia?

As mentioned in the introduction, emotions are dynamic in nature. Not “despite” but “because of” the fact that our emotional state constantly changes, we are able to experience emotions. The concept of emotional inertia poses that an individual lingers in a certain emotional state for a while (Kuppens, Allen, & Sheeber, in press). A high level of emotional inertia implies a lack of flexibility in adapting emotions to the surrounding context and in response to regulation efforts. In line with this reasoning, Kuppens et al. (in press) demonstrated that the emotional behavior or experience of depressed individuals is characterized by higher levels of inertia than that of their non-depressed counterparts. An important research question in this respect is whether this increased emotional inertia observed in the behavioral expression of emotions also extends to the dynamics of physiological emotion components. Along these lines, previous research has suggested that depressed individuals are characterized by slower HR recovery after physical exercise (Hughes et al., 2006). The question is, however, whether such slower recovery will also be observed in a psychologically demanding setting, a finding that would moreover be in line with the idea of higher inertia.

To explore the dynamics of state space models, we can work with impulse response functions (see Hamilton, 1994) which have been applied extensively in the domain of cardiovascular modeling as well (see e.g., Matsukawa & Wada, 1997; Nishiyama, Yana, Mizuta, & Ono, 2007; Panerai, James, & Potter, 1997; Triedman, Perrott, Cohen, & Saul, 1995). The impulse response function represents how a one unit innovation impulse of a process affects the process itself (autoregressive impulse response) or another process (crossregressive impulse response) over time. This temporal effect is compared to a baseline of 0, to be interpreted as “there was no impulse”. The values in the impulse response functions are calculated from parameter estimates in time series models (for more details about the calculation, see Hamilton, 1994; Matsukawa & Wada, 1997).

In Figure 4, the autoregressive and crossregressive impulse response functions for HR and BP are shown for the groups of normal and depressed adolescents. These response functions were derived from the posterior means of α_Φ and reflect the impulse response functions at the hierarchical level. To guide interpretation, let us first focus on the autoregressive effect for HR in Figure 4.a. When HR is incremented with a “pulse” of one BPM at time t = 0, it stays elevated for t = 1,…,4. However, around 5 seconds, a downward correction occurs (until about 8 seconds) and thereafter, the effect fades out. The autoregressive impulse response function for BP in Figure 4.d shows a recovery to “no effect” in about 5 seconds and has a less obvious oscillatory component. These impulse effects are similar for the normal and depressed population, which suggest that emotional inertia for physiological emotion components is not stronger for depressed individuals, contrary to what was found for the behavioral expression of emotion (Kuppens et al., in press), which displayed increased inertia in depression.¹¹ These results thus point to a possible dissociation between the dynamical properties of emotional expression and physiology, indicating that both may be governed by different types of regulatory control. Expressive emotional behavior can indeed be thought to be strongly governed by social and self-representational concerns (like display rules, see Darwin, Ekman, & Prodger, 2002), whereas physiology is obviously primarily dictated by much more autonomous processes.The fact that higher levels of inertia in depression are observed for the former rather than the latter processes, may thus indicate that the emotional dysfunctioning associated with this mood disorder may be particularly manifested in emotion components that have implications for the social world (for the importance of social concerns in depression, see e.g., Allen & Badcock, 2003).

Figure 4.

Hierarchical impulse response functions for the groups of normal and depressed individuals with (a) the HR autoregression effect, (b) the BP to HR crossregression effect, (c) the HR to BP crossregression effect and (d) the BP autoregression effect. The impulse response functions were derived from the posterior median of the hierarchical mean vector α_Φ, as explained in Hamilton (1994).

When considering the crossregressive impulse response functions in Figure 4.b and Figure 4.c, we find them to be strongly asymmetric. This observation is consistent with previous studies and reflects a basic dynamical relation of these cardiovascular processes (Matsukawa & Wada, 1997; Triedman et al., 1995; Nishiyama et al., 2007).

The impulse response functions in Figure 4 handled the dynamical patterns of the physiological processes on population level. However, impulse response functions can also be derived for each individual i, based on estimated posterior medians of [Φ_i,1,…,Φ_i,5]. In Figure 5, the individual autoregressive impulse response functions are shown for 10 random participants of both groups, with the estimated population impulse response functions as a reference. This illustrates the individual differences within the populations. The strong variations reflect the problem of data: Only very little data are available for each individual, resulting in quite unique forms for the individual impulse response functions. The hierarchical parameter distribution stabilizes these individual estimates and allows for inference at the population level. Moreover, the complex forms of the impulse response functions rationalize our approach to choose a lag equal to 5. If only one lag was relevant, all impulse response functions would fade out monotonously without any quadratic or sinusoidal tendency.

Figure 5.

Individual differences in the autoregressive IRF for HR in normals and depressed, respectively (a) and (b), and individual differences in the autoregressive IRF for BP in normals and depressed, respectively (c) and (d). The bold lines represent the hierarchical IRF, the thin lines the individual ones. Each plot is based on a random subset of 15 participants. The impulse response functions were derived as explained in Hamilton (1994), with the individual functions based on the posterior medians of the set of transition matrices [Φ_1,i Φ_2,i Φ_3,i Φ_4,i,Φ_5,i] and the hierarchical functions based on the posterior median of the hierarchical vector α_Φ.

Question 3: Emotional responsitivity?

The research literature on emotional reactivity in depression argues that depressed differ from non-depressed individuals in how they emotionally respond to specific eliciting events or stimuli. The findings regarding the nature or direction of this difference are inconsistent, however. In terms of reactivity to negative stimuli or events, on the one hand, there is research suggesting that depressed individuals are characterized by increased responsivity to negative or aversive stimuli, while on the other hand there is also research that points to the opposite, namely that depressed are characterized by decreased emotional reactivity, something that has been labeled emotion context insensitivity (ECI; Rottenberg, 2005). A recent meta-analysis of laboratory studies found most support for the ECI view across self-report, behavioral and physiological systems (Bylsma, Morris, & Rottenberg, 2008), but there remained a large variability between findings from different studies. However, most of this research examined emotional responding to standardized, non-idiographic stimuli (such as standardized emotional pictures or film clips). In contrast, the current data allows to study emotional reactivity in a context that is highly personally relevant to the individual (i.e., the own family environment). The question that arises is thus whether depressed will indeed differ from non-depressed in how they emotionally respond to a personally meaningful and stressful event (anger displayed by the parent), and if so, in what way they differ, as indicated by changes in their HR and BP.

The parameter of interest here is α_Δ, the hierarchical mean vector of the regression coefficient vectors δ_i, containing the effects of AP. In Figure 6, the estimated posterior densities of the elements α_δ1 and α_δ2 are shown for the depressed and normal group. Concerning HR (see left panel of Figure 6), we found positive support in favor of an inhibitory effect of parental anger for both depressed (B̂F = .08) and normals (B̂F = .17), and these effects are found to be equally strong (B̂F = .62). A heart rate deceleration has been theoretically linked to an orienting response, related to information intake and orientation towards a salient stimulus (Cook & Turpin, 1997). The observed HR response thus suggests that participants are alerted by anger expression by the parent and orient their attention to such behavior.

Figure 6.

Estimated posterior densities for normals (full lines) and depressed (dotted lines) of the parameters α_δ1 and α_δ2, the hierarchical regression effects of AP on respectively HR and BP.

On the other hand, concerning BP (see right panel of Figure 6), positive (B̂F = 11.69) and strong (B̂F = 89.36) support was found in favor of an excitatory effect of parental anger for respectively depressed and normal individuals. The effect is stronger for normal individuals as compared to depressed (B̂F = .19). These results show that angry parental behavior elicits a blood pressure increase, indicative of a stress response. The fact that the effect is much stronger for normals than for depressed supports the ECI hypothesis, in that depressed do not show the typical emotional reactivity observed in normal individuals, even in response to a stressful, idiographically highly relevant event (parental anger). Instead, they are characterized by a insensitivity to such stimuli, in line with predictions and findings from emotion context sensitivity research (Rottenberg, 2005).

Discussion

In this paper, we introduced a hierarchical extension for the linear Gaussian state space model. The extended model proved to be very useful when studying individual differences in the dynamics of emotional systems. Applying it to the Oregon adolescent interaction data led to interesting discussions about hypotheses on the relations between cardiovascular processes, emotion dynamics and depression. On the whole, it was clear that applying the hierarchical state space approach to these data provides a detailed picture of several central characteristics of the dynamics underlying physiological emotion components and its determinants (both contextual and individual differences). As such, it allowed to address several research questions that are central to the study of emotion dynamics in relation to psychopathology.

Although the model is very flexible, we must remark that it has several strong assumptions that we might want to relax in the future. For instance, the assumptions of linearity and Gaussian error distributions might not always be realistic, especially when considering psychological data (e.g., outliers, sudden changes in level, discrete processes). Also, random effects distributions for the error covariance matrices might be added, allowing to study differences in for instance the link between heart rate variability and depression (Frasure-Smith, Lesperance, Irwin, Talajic, & Pollock, 2009; Licht et al., 2008; Pizzi, Manzoli, Mancini, & Costa, 2008). However, for some generelizations, the appealing traditional Gibbs sampling approach with closed form full conditionals, as discussed in Appendix A, might not be possible anymore.

Regarding more invasive extensions for the future, an explanatory model can be added on the hierarchical level, such that individual differences can be interpreted in function of other individual characteristics (e.g., emotional inertia is associated to only particular depression symptoms). Further, the design matrix Ψ (which was fixed to an identitiy matrix in our approach) can be considered as a free parameter for each individual, which turns the model into a hierarchical dynamic factor model. Finally, complex hypotheses might be tested when discrete output variables might be allowed, whereas the truly observed discrete outputs are connected to the underlying unobserved continuous outputs through linking functions.

Maybe one of the most important advantages of the model is its generality: In practice, it can be applied beyond the context of physiological emotion responses, to any type of time series and in various research domains, whether one wants to make inferences about the values of the latent states or investigate differences in the system parameters for several dynamical systems.

Appendix A

Derivation of full conditionals distributions

A Gibbs sampler consists of full conditionals for single parameters or blocks of parameters. When iteratively sampling from these full conditional distributions, convergence is obtained in infinity.¹² After convergence, samples are considered to be simulations of the true posterior distribution of these parameters and thus these posterior distributions can be approximated with a large set of samples. The main principle of deriving these full conditionals is to combine the likelihood function of the parameter with its prior distribution. To obtain a closed form distribution, the likelihood and prior should match, i.e., some kernel elements in their formulas should be combined such that a new distribution is obtained. As the likelihood function is determined by the model, which is fixed, the prior distribution can be chosen in such a way that it can be combined with the likelihood, which is called a conjugate prior.

In the section on statistical inference, we distinguished three categories of parameters in the Gibbs sampler: (1) the latent states, (2) the system parameters and (3) the hierarchical parameters. The latent states were sampled with the forward filtering backward sampling algorithm (Carter & Kohn, 1994; Kim & Nelson, 1999), as explained in that section, and the remaining parameters are sampled using full conditional distributions that are derived by combining the likelihood function with conjugate prior distributions. In this appendix, we provide more details on the derivation of the full conditionals. For every type of parameter, we illustrate the technique for one parameter and generalize it to the other parameters of the same type. The parameter types that are discussed in the respective order are variances, hierarchical mean vectors and individual effects.

Full conditionals for variances

The covariance matrices in the hierarchical state space model, as described in Equations 7, 8, 10, 11 and 12, are Σ_ε, Σ_η, B_μ, B_Φ, B_Γ and B_Δ All matrices are assumed to be diagonal matrices, with the variances on the diagional and the covariances on the off-diagional elements fixed to 0.¹³ We illustrate how to derive the full conditional for β_μ1, i.e., the first diagonal element of B_μ.

In the hierarchical state space model, the only equation that is relevant for the likelihood function of B_μ is Equation 8. As all covariances in B_μ are fixed to 0 and thus all elements in vector μ_i are independent, we can isolate the first element μ_[1]i and express it as a univariate Normal,

$${\mu }_{[1]i}~N({\alpha }_{{\mu }_1},{\beta }_{{\mu }_1}).$$

The likelihood function for β_μ1 can be expressed and simplified as follows:

$$\begin{array}{ccc}\ell ({\beta }_{{\mu }_1})\hfill & =\hfill & {\displaystyle \prod _{i=1}^{I}N({\mu }_{[1]i}|{\alpha }_{{\mu }_1},{\beta }_{{\mu }_1})}\hfill \\ \hfill & \propto \hfill & {\displaystyle \prod _{i=1}^I{({\beta }_{{\mu }_1})}^{-\frac{1}{2}}\text{exp }\left(-\frac{{({\mu }_{[1]i}-{\alpha }_{{\mu }_1})}^2}{2{\beta }_{{\mu }_1}}\right)}\hfill \\ \hfill & \propto \hfill & {({\beta }_{{\mu }_1})}^{-\frac{I}{2}}\text{exp }\left(-\frac{{\displaystyle \sum _{i=1}^I{({\mu }_{[1]i}-{\alpha }_{{\mu }_1})}^2}}{2{\beta }_{{\mu }_1}}\right)\hfill \\ \hfill & \propto \hfill & {({\beta }_{{\mu }_1})}^{-\frac{I}{2}}\text{exp }\left(-\frac{SS}{2{\beta }_{{\mu }_1}}\right),\hfill \end{array}$$ (15)

with SS being the sum of squared residuals ${\displaystyle \sum _{i=1}^I{({\mu }_{[1]i}-{\alpha }_{{\mu }_1})}^2}$. In this structure, the kernel of a scaled inverse χ² distribution is recognized. Therefore, a conjugate scaled inverse χ² prior distribution for β_μ1 is chosen, with ν₀ degrees of freedom and scale $s_0^2$, resulting in a scaled inverse χ² full conditional distribution with ν₁ degrees of freedom and scale $s_1^2$:

$$\begin{array}{ccc}P({\beta }_{{\mu }_1}|\mathit{D},\mathit{P})\hfill & \propto \hfill & P({\beta }_{{\mu }_1})\ell ({\beta }_{{\mu }_1})\hfill \\ \hfill & \propto \hfill & {({\beta }_{{\mu }_1})}^{-\frac{{\nu }_0}{2}+1}\text{exp }\left(-\frac{{\nu }_0{s}_0^2}{2{\beta }_{{\mu }_1}}\right){({\beta }_{{\mu }_1})}^{-\frac{I}{2}}\text{exp }\left(-\frac{SS}{2{\beta }_{{\mu }_1}}\right)\hfill \\ \hfill & \propto \hfill & {({\beta }_{{\mu }_1})}^{-\frac{{\nu }_0+I}{2}+1}\text{exp }\left(-\frac{{\nu }_0{s}_0^2+SS}{2{\beta }_{{\mu }_1}}\right)\hfill \\ \hfill & ~\hfill & SI{\chi }^2({\nu }_1,s_1^2),\hfill \end{array}$$ (16)

with D representing the set of all data and P representing the set of all model parameters but β_μ1. The specific values of the full conditional parameters are

$$\begin{array}{ccc}{\nu }_1\hfill & =\hfill & {\nu }_0+I\hfill \\ s_1^2\hfill & =\hfill & \frac{{\nu }_0{s}_0^2+SS}{{\nu }_1}.\hfill \end{array}$$

.

The derivation is parallel for all other variances. To obtain ν₁, the prior degrees of freedom ν₀ are incremented with the “amount of residuals”, which is I for the random effects variances on the diagonals of B_μ, B_Φ, B_Γ and B_Δ and IT for the error variances on the diagonals of Σ_ε and Σ_η (these parameters are constant over I individuals and T measurement occasions). To obtain $s_1^2$, we need to calculate SS, the sum of squared residuals. For the random effects variances, the residuals are the differences between the individual parameters and hierarchical means for i = 1,…,I. For the error variances in Σ_ε and Σ_η, the residuals are the deviations of the data or latent states to the mean term in respectively the observation and transition equation. For instance, the residuals in the observation equation are equal to ε_t,i = y_t,i – μ_i – θ_t,i – Γ_ix_t,i for t = 1,…,T and i = 1,…,I. When focusing on a particular variance on the diagonal of Σ_ε, the corresponding vector element in ε_t,i should be considered.

Full conditionals for hierarchical mean vectors

The hierarchical mean vectors in the hierarchical state space model are α_μ, α_Φ, α_Γ and α_Δ. Contrary to the covariance matrices, these vector elements are not independent in the sampling process. We illustrate the derivation for α_μ.

The only Equation in the hierarchical state space model that contains α_μ is Equation 8(repeated) :

$${\mathit{\mu }}_i~N({\mathit{\alpha }}_{\mu },{\mathit{B}}_{\mu }),$$

, thus, the likelihood for α_μ is expressed as

$$\begin{array}{ccc}\ell ({\mathit{\alpha }}_{\mu })\hfill & =\hfill & {\displaystyle \prod _{i=1}^I\mathit{N}({\mathit{\mu }}_i|{\mathit{\alpha }}_{\mu },{\mathit{B}}_{\mu })}\hfill \\ \hfill & \propto \hfill & {\displaystyle \prod _{i=1}^I\text{exp }\left(-\frac{1}{2}\left[({\mathit{\mu }}_i-{\mathit{\alpha }}_{\mu })\prime {\mathit{B}}_{\mu }^{-1}({\mathit{\mu }}_i-{\mathit{\alpha }}_{\mu })\right]\right)}\hfill \\ \hfill & \propto \hfill & \text{exp }\left(-\frac{1}{2}\left[{\displaystyle \sum _{i=1}^I{\mathit{\alpha }}_{\mu }^{\prime }{\mathit{B}}_{\mu }^{-1}{\mathit{\alpha }}_{\mu })-{\displaystyle \sum _{i=1}^I({\mathit{\mu }}_i^{\prime }{\mathit{B}}_{\mu }^{-1}{\mathit{\alpha }}_{\mu })-{\displaystyle \sum _{i=1}^I({\mathit{\alpha }}_{\mu }^{\prime }{\mathit{B}}_{\mu }^{-1}{\mathit{\mu }}_i}}}\right]\right)\hfill \\ \hfill & \propto \hfill & \text{exp }\left(-\frac{1}{2}\left[({\mathit{\alpha }}_{\mu }^{\prime }[I{\mathit{B}}_{\mu }^{-1}]{\mathit{\alpha }}_{\mu })-({\mathit{S}}_{\mu }^{\prime }{\mathit{B}}_{\mu }^{-1}{\mathit{\alpha }}_{\mu })-({\mathit{\alpha }}_{\mu }^{\prime }{\mathit{B}}_{\mu }^{-1}{\mathbf{S}}_{\mu })\right]\right),\hfill \end{array}$$ (17)

where ${\mathit{S}}_{\mu }={\displaystyle \sum _{i=1}^I{\mathit{\mu }}_i}$. Now, a conjugate multivariate normal prior for μ_α is formulated as

$${\mathit{\alpha }}_{\mu }~N({\mathit{\mu }}_0,{\mathbf{\Sigma }}_0).$$

The result is a multivariate normal full conditional distribution for α_μ:

$$\begin{array}{ccc}P({\mathit{\alpha }}_{\mu }|\mathit{D},\mathit{P})\hfill & \propto \hfill & P({\mathit{\alpha }}_{\mu })\ell ({\mathit{\alpha }}_{\mu })\hfill \\ \hfill & \propto \hfill & \text{exp }\left(-\frac{1}{2}\left[({\mathit{\alpha }}_{\mu }-{\mathit{\mu }}_0)\prime {\mathbf{\Sigma }}_0^{-1}({\mathit{\alpha }}_{\mu }-{\mathit{\mu }}_0)\right]\right)\hfill \\ \hfill & \hfill & \text{exp }\left(-\frac{1}{2}\left[{\mathit{\alpha }}_{\mu }^{\prime }[I{\mathit{B}}_{\mu }^{-1}]{\mathit{\alpha }}_{\mu })-({\mathit{S}}_{\mu }^{\prime }{\mathit{B}}_{\mu }^{-1}{\mathit{\alpha }}_{\mu })-({\mathit{\alpha }}_{\mu }^{\prime }{\mathit{B}}_{\mu }^{-1}{\mathit{S}}_{\mu })\right]\right)\hfill \\ \hfill & \propto \hfill & \text{exp }\left(-\frac{1}{2}\left[({\mathit{\alpha }}_{\mu }^{\prime }{\mathbf{\Sigma }}_0^{-1}{\mathit{\alpha }}_{\mu })-({\mathit{\mu }}_0^{\prime }{\mathbf{\Sigma }}_0^{-1}{\mathit{\alpha }}_{\mu })-({\mathit{\alpha }}_{\mu }^{\prime }{\mathbf{\Sigma }}_0^{-1}{\mathbf{\mu }}_0)\right]\right)\hfill \\ \hfill & \hfill & \text{exp }\left(-\frac{1}{2}\left[{\mathit{\alpha }}_{\mu }^{\prime }[I{\mathit{B}}_{\mu }^{-1}]{\mathit{\alpha }}_{\mu })-({\mathit{S}}_{\mu }^{\prime }{\mathit{B}}_{\mu }^{-1}{\mathit{\alpha }}_{\mu })-({\mathit{\alpha }}_{\mu }^{\prime }{\mathit{B}}_{\mu }^{-1}{\mathit{S}}_{\mu })\right]\right)\hfill \\ \hfill & \propto \hfill & \text{exp }\left(-\frac{1}{2}[{\mathit{\alpha }}_{\mu }^{\prime }({\mathbf{\Sigma }}_0^{-1}+I{\mathit{B}}_{\mu }^{-1}){\mathit{\alpha }}_{\mu }-({\mathit{\mu }}_0^{\prime }{\mathbf{\Sigma }}_0^{-1}+{\mathit{S}}_{\mu }^{\prime }{\mathit{B}}_{\mu }^{-1}){\mathit{\alpha }}_{\mu }-{\mathit{\alpha }}_{\mu }^{\prime }({\mathbf{\Sigma }}_0^{-1}{\mathit{\mu }}_0+{\mathit{B}}_{\mu }^{-1}{\mathit{S}}_{\mu })]\right)\hfill \\ \hfill & ~\hfill & N({\mathit{\mu }}_1,{\mathbf{\Sigma }}_1)\hfill \end{array}$$ (18)

where

$$\begin{array}{c}{\mathbf{\Sigma }}_1={({\mathbf{\Sigma }}_0^{-1}+I{\mathit{B}}_{\mu }^{-1})}^{-1}\hfill \\ {\mathit{\mu }}_1={\mathbf{\Sigma }}_1({\mathbf{\Sigma }}_0^{-1}{\mathit{\alpha }}_0+{\mathit{B}}_{\mu }^{-1}{\mathit{S}}_{\mu }).\hfill \end{array}$$

The structure of μ₁ and Σ₁ is logical. The precision of the full conditional is the sum of the precisions originating from the prior distribution and the likelihood function, while the mean of the full conditional is a weighted average of the prior mean and μ̄, the sample mean of the individual effects μ_i (S_μ = I × μ̄). A parallel strategy is followed for obtaining full conditionals for the other hierarchical mean vectors α_Φ, α_Γ and α_Δ For each sample of α_Φ, the stationarity condition I(|λ(F_i)| < 1) is checked (see text). If the condition is not satisfied, we reject and resample.

Full conditionals for individual effect parameters

Finally, full conditional distributions are derived for the individual effects μ_i, Φ_1,i, …, Φ_L,i, Γ_i and Δ_i. Although this technique strongly resembles the one used for the hierarchical mean vectors as explained in the previous paragraphs, there are some complicating factors that need some extra calculations and transformations. Before we combine the likelihood and the prior distribution, we correct the data or states for non-relevant constants in the model and subsequently we define a vectorized model that takes into account all measurements at once. We will illustrate this approach for Γ_i, the matrix of regression effects for the observation covariates x_i,t.

As the focal variable is Γ_i, only the observation equation is relevant for the likelihood function and thus the transition equation can be ignored for now. To keep the notation simple, we group non-relevant constants (we also drop the conditioning notation at the left hand side of the equation):

$$\begin{array}{ccc}\hfill {\mathit{y}}_{t,i}& ~& N({\mathit{\mu }}_i+{\mathit{\theta }}_{t,i}+{\mathbf{\Gamma }}_i{\mathit{x}}_{t,i},{\mathbf{\Sigma }}_{\epsilon })\hfill \\ \hfill {\mathbf{y}}_{t,i}-{\mathit{\mu }}_i-{\mathit{\theta }}_{t,i}& ~& N({\mathbf{\Gamma }}_i{\mathit{x}}_{t,i},{\mathbf{\Sigma }}_{\epsilon })\hfill \\ \hfill {\mathbf{y}}_{t,i,cor}& ~& N({\mathbf{\Gamma }}_i{\mathit{x}}_{t,i},{\mathbf{\Sigma }}_{\epsilon }),\hfill \end{array}$$ (19)

where the subscript cor indicates that the observation vector y_t,i was corrected for μ_i and θ_t,i, which are both assumed to be known in this stage of the Gibbs sampler. The likelihood function is based on Equation 19. However, continuing to consider Γ_i as a matrix will bring us into trouble later. Therefore, we have to reparametrize Equation 19 in such a way that Γ_i is expressed as a vector. The solution lies in considering the P × T (corrected) observation matrix Y_i,cor instead of the P-dimensional (corrected) observation vectors y_t,i,cor for t = 1,…,T, which are in fact columns in Y_i,cor. By vectorizing this matrix with the vec(·) operator, we obtain the following model:

$$\text{vec}({\mathit{Y}}_{i,cor})~N\left(\text{vec}\left({\mathit{X}}_i^{\prime }{\mathbf{\Gamma }}_i^{\prime }\right),{\mathbf{\Sigma }}_{\epsilon }\otimes {\mathit{I}}_T\right),$$ (20)

with X_i being the J × T matrix with the J-dimensional observation covariate vectors x_t,i for t = 1,…,T as its columns. A Kronecker product (⊗) was used to expand the covariance matrix Σ_ε over all PT elements of vec (Y_i,cor). Using a basic property of vectorization and the Kronecker product, the vectorized mean term can be further decomposed as follows:

$$\text{vec}({\mathit{Y}}_{i,cor})~N\left(\left(I_P\otimes {\mathit{X}}_i^{\prime }\right)\text{vec}\left({\mathbf{\Gamma }}_i^{\prime }\right),{\mathbf{\Sigma }}_{\epsilon }\otimes I_T\right)$$ (21)

For notational convenience, we use the *-notation, indicating that we work in the vectorized model.

$${\mathit{Y}}_{i,cor}^{*}~N({\mathit{X}}_i^{*}{\mathbf{\Gamma }}_i^{*},{\mathbf{\Sigma }}_{\epsilon }^{*}),$$ (22)

with ${\mathit{Y}}_{i,cor}^{*}=\text{vec}({\mathit{Y}}_{i,cor}),{\mathit{X}}_i^{*}=\left(I_P\otimes {\mathit{X}}_i^{\prime }\right),{\mathbf{\Gamma }}_i^{*}=\text{vec}\left({\mathbf{\Gamma }}_i^{\prime }\right)$, and ${\mathbf{\Sigma }}_{\epsilon }^{*}={\mathbf{\Sigma }}_{\epsilon }\otimes I_T$. The likelihood of ${\mathbf{\Gamma }}_i^{*}$ can now be expressed as a multivariate normal. Moreover, the hierarchical distribution defined in Equation 10 serves as an informative multivariate normal prior distribution for $\text{vec}\left({\mathbf{\Gamma }}_i^{\prime }\right)={\mathbf{\Gamma }}_i^{*}$. They are combined into a multivariate normal full conditional distribution:

$$\begin{array}{ccc}\mathbf{P}({\mathbf{\Gamma }}_i^{*}|\mathit{D},\mathit{P})\hfill & \propto \hfill & P({\mathbf{\Gamma }}_i^{*})\ell ({\mathbf{\Gamma }}_i^{*})\hfill \\ \hfill & \propto \hfill & N({\mathbf{\Gamma }}_i^{*}|{\mathit{\mu }}_0,{\mathbf{\Sigma }}_0)\times N({\mathit{Y}}_{i,cor}^{*}|{\mathit{X}}_i^{*}{\mathbf{\Gamma }}_i^{*},{\mathbf{\Sigma }}_{\epsilon }^{*})\hfill \\ \hfill & \dots \hfill & \hfill \\ \hfill & ~\hfill & N({\mathit{\mu }}_1,{\mathbf{\Sigma }}_1)\hfill \end{array}$$ (23)

with

$$\begin{array}{c}{\mathbf{\Sigma }}_1={\left({\mathbf{\Sigma }}_{\mathbf{\Gamma }}^{-1}+{\mathit{X}}_i^{*\prime }{\mathbf{\Sigma }}_{\epsilon }^{*-1}{\mathit{X}}_i^{*}\right)}^{-1}\hfill \\ {\mathit{\mu }}_1={\mathbf{\Sigma }}_{\mathbf{1}}\left({\mathbf{\Sigma }}_{\mathbf{\Gamma }}^{-1}{\mathit{\mu }}_{\mathbf{\Gamma }}+{\mathit{X}}_i^{*\prime }{\mathbf{\Sigma }}_{\epsilon }^{*-1}{\mathit{Y}}_{i,cor}^{*}\right)\hfill \end{array}$$

We don’t report all steps in the derivation because the procedure is parallel to the technique discussed for the hierarchical mean vectors in Equation 18. Returning from the *-notation to the original notation, we use properties of Kronecker product and vectorization:

$$\begin{array}{c}{\mathbf{\Sigma }}_1={({\mathbf{\Sigma }}_{\mathbf{\Gamma }}^{-1}+{\mathbf{\Sigma }}_{\epsilon }^{-1}\otimes ({\mathit{X}}_i{\mathit{X}}_i^{\prime }))}^{-1}\hfill \\ {\mathit{\mu }}_1={\mathbf{\Sigma }}_{\mathbf{1}}\left({\mathbf{\Sigma }}_{\mathbf{\Gamma }}^{-1}{\mathit{\mu }}_{\mathbf{\Gamma }}+\text{vec}({\mathit{X}}_i{\mathit{Y}}_{i,cor}^{\prime }{\mathbf{\Sigma }}_{\epsilon }^{-1})\right).\hfill \end{array}$$

.

To sample Γ_i, we sample ${\mathbf{\Gamma }}_i^{*}$ from its multivariate normal full conditional and transform it back to its matrix form Γ_i. The procedure is parallel for deriving full conditionals for μ_i, Φ_l,i (for l = 1,…,L) and Δ_i, with the only difference that μ_i is already a vector and the vectorization step can be skipped. Moreover, the stationarity condition is checked for the Φ_l,i (for l = 1,…,L), as explained in Equation 12.

Appendix B

Parameter recovery

To evaluate the quality of the Gibbs sampler routine that we implemented in R, we report a small simulation study that shows the parameter recovery of one simulated set of observations. We explain the process of data simulation and parameter estimation and report our findings. It is not our goal to set up an intensive simulation study to investigate specific properties of the algorithm. We only want to illustrate that the algorithm obtains estimated values that are close to the population values.

Data simulation

The data simulation was based on the results of the hierarchical analysis for the depressed population of 67 individuals (see the application section). In a first step, we sampled the individual level parameters from hierarchical normal distributions. The estimated¹⁴ hierarchical mean vectors α̂_μ, α̂_Φ and α̂_Δ and hierarchical covariance matrices B̂_μ, B̂_Φ and B̂_Δ were used to define hierarchical Gaussian sampling distributions (see Table B1).

Table B1.

The left side of the table contains the estimated posterior quantiles q.025, q.500, q.975 (obtained with the Oregon data), which were used as population values for the data simulation. At the right side of the table, the estimated posterior quantiles are listed for the model identical model that was applied on the simulated data.

		Depressed			Simulated
	Description	q.025	q.7.500	q.975	q.025	q.500	q.975
	Hierarchical parameters μ
αμ1	HM for general mean HR	76.19	78.96	81.69	76.22	79.11	82.02
αμ2	HM for general mean BP	88.67	91.82	94.88	91.52	95.52	99.36
βμ1	HV for general mean HR	91.33	127.71	184.43	96.32	140.57	211.22
βμ2	HV for general mean BP	113.90	158.09	229.16	191.16	266.25	384.84
	Hierarchical parameters Φ1
αϕ[1,1]1	HM for AR effect HR	0.85	0.93	1.00	0.59	0.66	0.73
αϕ[1,2]1	HM for CR effect BP → HR	−0.22	−0.17	−0.11	−0.17	−0.11	−0.04
αϕ[2,1]1	HM for CR effect HR→ BP	0.11	0.17	0.23	0.05	0.12	0.19
αϕ[2,2]1	HM for AR effect BP	0.33	0.40	0.47	0.27	0.34	0.41
βϕ[l,l]l	HV for AR effect HR	0.03	0.04	0.07	0.03	0.05	0.07
βϕ[1,2]1	HV for CR effect BP → HR	0.02	0.04	0.05	0.03	0.05	0.08
βϕ[2,1]1	HV for CR effect HR → BP	0.02	0.04	0.06	0.04	0.06	0.09
βϕ[2,2]1	HV for AR effect BP	0.04	0.06	0.09	0.04	0.05	0.08
	Hierarchical parameters Δ
αδ1	HM for effect AP → HR	−0.88	−0.38	0.13	−0.46	−0.23	−0.01
αδ2	HM for effect AP → BP	−0.12	0.38	0.86	0.19	0.39	0.59
βδ1	HV for effect AP → HR	0.30	1.08	3.49	0.24	0.46	0.82
βδ2	HV for effect AP → BP	0.13	0.41	1.26	0.10	0.22	0.45
	Error variances
${\sigma }_{\epsilon ,1}^2$	Measurement error variance HR	0.49	0.82	1.30	2.26	3.19	4.36
${\sigma }_{\epsilon ,2}^2$	Measurement error variance BP	0.12	0.40	0.99	5.33	7.08	9.25
${\sigma }_{\eta ,1}^2$	Innovation variance HR	14.63	15.47	16.39	18.57	19.91	21.35
${\sigma }_{\eta ,2}^2$	Innovation variance BP	21.57	22.65	23.78	21.19	22.70	24.27

After sampling from the hierarchical parameter distributions, a bivariate series ${\mathit{y}}_i^{\text{sim}}$ of T = 60 observations was simulated for each of 67 individuals, using parameter sets {μ̃_i, Φ̃_1,i, Φ̃_2,i, Φ̃_3,i, Φ̃_4,i, Φ̃_5,i, Δ̃_i, Σ_ε, Σ_η} and a covariate ${\mathit{z}}_i^{\text{sim}}$ to account for the regression effect Δ̃_i in the transition equation. The tilde (˜) indicates that parameters have been sampled from the hierarchical distributions. The values of Σ_ε and Σ_η were set to the estimated values in the application (see Table B1). The values for covariate ${\mathit{z}}_i^{\text{sim}}$ were simulated for each individual i from a standard normal distribution. The data, consisting of ${\mathit{y}}_i^{\text{sim}}$ and ${\mathit{z}}_i^{\text{sim}}$ for 67 individuals, are available as an R workspace at http://sites.google.com/site/tomlodewyckx/downloads

Model estimation

With the simulated observations ${\mathit{y}}_i^{\text{sim}}$ and covariate ${\mathit{z}}_i^{\text{sim}}$, we estimated the hierarchical state space model as described in the application in equation 14: a bivariate state-space model of order five, with a regression effect in the transition equation. We estimated three Markov chains of 5000 values, after removing a burn in of 1000 values.

Results simulated data

Convergence is controlled with R̂ and very similar values are found as for the analysis of the depressed individuals. The estimated posterior quantiles for the parameters, using the simulated data, are reported in Table B1. In general, we see that the parameter values approximate the population values. There are some remarkable differences between the population values and the ones based on the simulation. For instance, the dynamic parameters in α_Φ1 and the regression effects in α_Δ are lower than in the population, which is compensated for with an overestimation of the error variances in Σ_ε and Σ_η.

Despite these differences, the general trend is more or less the same. Increasing the amount of observation moments T and individuals N should bring the estimates closer to the population values. An extensive simulation study, varying the population values, should reveal more information on how the algorithm performs.