Integrated Analysis of Pharmacologic, Clinical, and SNP Microarray Data using Projection onto the Most Interesting Statistical Evidence with Adaptive Permutation Testing

Abstract

Powerful methods for integrated analysis of multiple biological data sets are needed to maximize interpretation capacity and acquire meaningful knowledge. We recently developed Projection Onto the Most Interesting Statistical Evidence (PROMISE). PROMISE is a statistical procedure that incorporates prior knowledge about the biological relationships among endpoint variables into an integrated analysis of microarray gene expression data with multiple biological and clinical endpoints. Here, PROMISE is adapted to the integrated analysis of pharmacologic, clinical, and genome-wide genotype data that incorporating knowledge about the biological relationships among pharmacologic and clinical response data. An efficient permutation-testing algorithm is introduced so that statistical calculations are computationally feasible in this higher-dimension setting. The new method is applied to a pediatric leukemia data set. The results clearly indicate that PROMISE is a powerful statistical tool for identifying genomic features that exhibit a biologically meaningful pattern of association with multiple endpoint variables.

1. Introduction

Integrated data analysis is an important emrging challenge in computational biology. It is increasingly common for researchers to collect multiple forms of biological data (e.g. clinical, pharmacologic, gene expression microarray, genotype microarray) on the same set of subjects. The objective of collecting such data is to gain insights regarding the biological processes underlying the development and treatment of disease. The exciting potential and intellectual challenge of integrated data analysis has drawn the attention of researchers from diverse fields such as engineering, biology, computer science, and statistics.

Recently, Projection Onto the Most Interesting Statistical Evidence (PROMISE) has been developed as a procedure to perform an integrated analysis of microarray gene expression data with multiple endpoint variables [1]. PROMISE identifies genes with expression values that exhibit a specific pattern of correlations with the endpoint variables defined by prior biological knowledge. Thus, PROMISE incorporates prior biological knowledge into an integrated analysis of gene expression data and multiple endpoint variables.

In principle, PROMISE can be adapted to other settings, such as the analysis of SNP microarray data. However, this can be quite challenging in practice because PROMISE is a computationally demanding algorithm that uses permutation to determine statistical significance. PROMISE computes a test statistic for each genomic variable across a large number of permutations of the assignment of genomic data to endpoint data. For instance, the published implementation of PROMISE is not computationally feasible for SNP microarray data sets, which typically have 100 to 1000 fold more variables than do microarray gene expression data sets.

Here, we introduce an adaptive permutation testing (APT) algorithm to make it computationally feasible to use PROMISE to perform an integrated analysis of SNP microarray data, pharmacologic data, and clinical response data. APT greatly reduces the computational effort expended in the analysis for non-significant genomic features without compromising the statistical precision of p-values for highly significant features. Furthermore, the advantages of the PROMISE procedure previously observed in the analysis of gene expression microarray data are also observed in the analysis of SNP microarray data.

In section 2, we briefly describe the PROMISE procedure and its statistical properties. Section 3 introduces the APT algorithm. Section 4 describes the application of PROMISE and APT to the analysis of a leukemia data set. Discussion is provided in section 5.

2. The PROMISE Procedure

Suppose that data is collected for j = 1, …, k endpoint variables on i = 1, …, n subjects. Assume that data is collected for each of g = 1, …, m genomic variables (expression of genes, genotypes of SNPs, etc) on the same set of subjects. For all j and g, let T_jg be a statistic that measures the evidence that genomic variable g is associated with endpoint variable j. Without loss of generality, assume that −1 ≤ T_jg ≤ 1 for all g and j, where T_jg = −1 is the strongest evidence for a negative association between variables j and g and T_jg = 1 is the strongest evidence for a positive association between variables j and g. (Note that correlation statistics satisfy this requirement and that other statistics can be transformed to satisfy this requirement.) For each g, let T_g = (T_1g, …, T_kg) be a k × 1 vector of statistics measuring the associations of genomic variable g with all k endpoint variables.

Assume that the biological relationships of the endpoint variables with one another have been well-established by prior research. For each g, this knowledge about the biological relationships among the endpoint variables can be used to define a k × 1 vector d of the biologically most interesting values for T_g. In many applications, the entries of d equal ± 1 with the signs determined by prior biological knowledge. The entries of d indicate the most interesting result that genomic feature g is fully correlated with each of the k endpoint variables in a pattern concordant with the known biological relationships.

Given the definition of d implied by the biological relationships, PROMISE defines a test statistic as

$$R_g={\mathit{T}}_g\cdot \mathit{d}$$

for each g. The dot-product R_g is proportional to the magnitude of the projection of T_g onto d (the projection onto the most interesting statistical evidence). A large positive value for R_g indicates that the observed correlations in T_g are similar to the biologically most interesting result d. Conversely, a large negative value for R_g indicates that the observed correlations in T_g are strong in magnitude and opposite in direction to the most interesting result d. In many applications, negative value of R_g with large magnitude may also be a very interesting result from a biological perspective.

Consider an example from leukemia research. From previous studies, it is well-known that increasing concentrations of chemotherapy in leukemic cells leads to a reduction of tumor burden [2]. The Total 13B and Total 15 clinical trials [3,4] collected genotype data for g = 1,…,m genomic features with Affymetrix SNP microarrays and measured the following endpoints on study participants: concentrations of chemotherapy in leukemic cells following 42–44 hours of treatment (endpoint j = 1), tumor burden after 3 days of treatment (endpoint j = 2), and tumor burden following 6 weeks of treatment (endpoint j = k = 3). For a specific genomic variable g, T_g = (T_1g, T_2g, T_3g) is the observed correlations of genomic feature g with the 3 endpoints. The most interesting result for T_g is d = (+1,−1,−1) In light of prior biological knowledge, d = (+1,−1,−1) indicates that the genomic variable g has a therapeutically beneficial correlation of greatest possible magnitude with each of the k = 3 endpoints (i.e. higher values of variable g associate with values of the endpoints that relate with therapeutic efficacy). Additionally, −d indicates that higher values of the genomic variable g are associated with therapeutically detrimental values of the 3 endpoint variables. Given the definition of d and observed values for T_g, calculation of the PROMISE statistic R_g is straightforward. For instance, T_g = (+0.3, −0.1, −0.2) and d = (+1,−1,−1) gives R_g = 0.6.

The statistical significance (i.e. p-value) of R_g can be empirically determined via permutation testing [5]. The value of R_g is computed using the observed data and also using a large number B of data sets obtained by random reassignments (permutations) of the genomic data to endpoint data. Assuming that R_g = 0 is expected under the null hypothesis; the p-value for R_g is simply the proportion of permutations giving a value of R_g with greater magnitude than does the observed data. For example, suppose that R_g = 0.6 is computed from the observed data as described above. Also, suppose that new values of R_g are computed for each of 100,000 permutations and that 1,000 of those data permutations give |R_g| ≥ 0.6. In this case, R_g = 0.6 has p = 0.01.

In principle, PROMISE may be adapted to a wide variety of applications. As technological advances enable the collection of ever-larger data sets, the computational burden of permutation testing must be reduced in order to make PROMISE feasible for these exciting applications.

3. The APT Algorithm

The classical approach to permutation testing wastes much computational effort when it is utilized in the exploratory statistical analysis of genomic data. Typically, the vast majority of associations explored are not statistically significant. Performing a very large number of permutations for statistically insignificant associations simply improves the precision of uninterestingly large p-values.

Permutation tests can be viewed as procedures for sampling from the set of all possible permutations of the data [5]. Each permutation is labeled a “success” or “failure” depending on how its permutation statistic compares with the observed statistic. Thus, each permutation is a Bernoulli trial with success probability π equal to the proportion of all permutations that yield a “success” (e.g., the exact p-value) [5]. In practice, an approximate p-value is computed by sampling from the set of possible permutations because it is infeasible to compute the statistic for all possible permutations.

The classical approach to permutation testing selects a fixed number B of permutations and the p-value is the proportion of selections yielding a success. Thus, the classical permutation p-value has a binomial distribution [6] with form

$$\mathrm{Pr}\left(\mathrm{p}\text{-value}=\frac{x}{B}\right)=\left(\begin{array}{c}\hfill B\\ \hfill x\end{array}\right){\pi }^{xq}1-{\pi }^{B-x},$$

where

$$\left(\begin{array}{c}\hfill B\hfill \\ \hfill x\hfill \end{array}\right)=\frac{B!}{x!B-x!},$$

x is the number of successes, and π is the exact p-value.

Here, we propose an adaptive permutation testing (APT) algorithm that greatly reduces the computational burden of permutation-based exploratory analysis of high-dimensional data without sacrificing the required precision for the most significant p-values. APT utilizes a different strategy for sampling from the set of possible permutations. APT selects permutations until obtaining a fixed number b of successes or until a fixed maximum number B have been selected. Therefore, the number v of permutations performed by APT follows a truncated negative binomial distribution [5] with form

$$\mathrm{Pr}(v=x)=\{\begin{array}{cc}\hfill \left(\begin{array}{c}\hfill x-1\hfill \\ \hfill x-b\hfill \end{array}\right){\pi }^b{(1-\pi )}^{x-b}\hfill & \hfill \text{for}x=b,\dots ,B-1\hfill \\ \hfill 1-\sum _{x=b}^{B-1}\mathrm{Pr}(v=x)\hfill & \hfill \text{for}x=B.\hfill \end{array}\phantom{\}}$$

As with classical permutation testing, the APT p-value is the proportion of permutations yielding a success.

APT computes a large number of permutation statistics only for those tests with small exact p-value. For a statistical test with exact p-value π, the expected number of permutations performed by APT is approximately min(B, b/π). For example, APT will perform approximately 100b permutations for a statistical test with exact p-value π = 0.01. This will be much smaller than B, but still large enough that the p-value will have sufficient precision. In the case that π = 0.01, b = 200 and B = 10⁶, there is a 99% probability that APT will perform between 16,562 and 23,811 permutations (~ 20,000) and the permutation p-value will fall in the interval (0.0084, 0.0121). In this case, APT computes 98.6% fewer permutations than classical permutation does. Additionally, this number of permutations provides adequate precision for exploratory analyses of genomic data from the perspective that a p-value of 0.0084 will not be among the most significant results in most genome-wide analyses. In general, the truncated negative binomial distribution shown above can be used to choose B and b to satisfy specific requirements for precision of the p-values in terms of the number v of permutations to be performed. Table 1 summarizes the distribution of v for various values of π, b, and B.

Table 1.

The expected value E(v), 0.5 percentile, and 99.5 percentile of the number of permutations v performed by APT given the exact p-value π, maximum number of permutations B, and targeted number of successes b.

π	B	b	E(v)	0.5%	99.5%
10−1	104	200	2,000	1,672	2,363
≤10−2	104	200	104	104	104
10−1	104	103	9,880	9,245	104
≤10−2	104	103	104	104	104
10−1	105	200	2,000	1,672	2,363
10−2	105	200	20,000	16,562	23,811
≤10−3	105	200	105	105	105
10−1	105	103	104	9245	10791
lO−2	105	103	98,745	92,082	105
≤10−3	105	103	105	105	105
10−1	106	200	2,000	1,672	2,363
10−2	106	200	20,000	16,562	23,811
10−3	106	200	200,000	165,469	238,284
≤10−4	106	200	106	106	106

In an actual analysis of high-dimensional data, the computational effort of APT depends on the exact p-values of the statistical tests to be performed. A different number of permutation statistics may be computed for each statistical test. A relatively small number of permutation statistics will be computed for the vast majority of statistical tests that have insignificant exact p-values. A very large number of permutation statistics will be computed only for the typically very small number of statistical tests with exceedingly small exact p-values.

In most genomics applications, the computational savings of APT will be tremendous. For an application with m statistical tests having exact p-values uniformly distributed over (0, 1], APT computes approximately bm×(1+ln(B/b)) permutation statistics instead of the Bm permutation statistics computed by classical permutation. This approximation indicates that APT with B = 10⁶ and b = 200 computes 99.8% fewer permutation statistics than does classical permutation with the same B.

In our application, we use permutation to perform several statistical tests (the PROMISE analysis and analyses for the individual endpoints) for each genomic variable. Thus, we modified the APT procedure to perform permutations for one genomic variable until b successes are observed for each statistical test involving that genomic variable. Nevertheless, the computational savings realized by incorporating APT into the PROMISE procedure made the analysis computationally feasible.

4. Application to Leukemia Data Set

Our example application includes pharmacologic, clinical, and SNP microarray data for 656 patients enrolled on the Total 13B and Total 15 clinical trials for children with newly diagnosed acute lymphoblastic leukemia conducted at St. Jude Children's Research Hospital [3,4].

4.1 Description of the Data Set

In the Total 13B clinical trial, patients were randomly assigned to receive one of three regimens for initial therapy: intravenous mercaptopurine alone (1 g/m² over 6 hours); low-dose oral methotrexate (30 mg/m² every 6 hours for a total of 6 doses) followed by intravenous mercaptopurine (1 g/m² over 6 hours); or high-dose intravenous methotrexate (1 g/m² over 24 hours) immediately followed by intravenous mercaptopurine (1 g/m² over 6 hours). In the Total 15 clinical trial, patients were randomly assigned to receive initial therapy consisting of intravenous methotrexate given over a period of 4 or 24 hours. Some patients in Total 15 did not consent to the randomization. For both clinical trials, subsequent therapy was risk-adapted according to initial treatment response and a set of clinical and molecular factors observed at diagnosis.

Genetic, pharmacologic, and clinical data were collected from the participants of these studies. The Affymetrix 500K SNP microarray was used to determine the germ-line genotype for blood samples collected during remission from each patient. Genotypes were determined using the BRLMM algorithm [7]. Concentrations of methotrexate polyglutamates (MTX PG, the active metabolites of methotrexate) in leukemic cells were measured at 42–44 hours after starting therapy in both the Total 13B and Total 15 studies [8]. In the first few days of therapy, the white blood count (WBC) is a measure of tumor burden. Our statistical analysis uses the WBC on the third day of therapy adjusted by linear regression for its baseline value. The level of minimal residual disease (MRD) determined by flow cytometry [9,10] after 46 days of therapy is another measurement of tumor response. In our statistical analysis, the MRD is characterized as negative (no detectable disease), low positive (some disease is present), and high positive (a large amount of disease persists). There were 380 patients with MTX PG data, 414 with WBC data, and 598 with MRD data. All 656 patients had SNP microarray data. All patients with data for a given phenotype were included in the calculation of the individual phenotype analysis and the PROMISE analysis.

4.2 Definition of Association Statistic

Rank-based association statistics were used to measure the association of the genotype of each SNP (characterized as the number of “B” alleles) with each of the three endpoint variables (MTX PG, WBC, and MRD). Let l = 1,…,6 index the six therapy assignments (mercaptopurine alone on Total 13B, low-dose MTX on Total 13B, high-dose MTX on Total 13B, 4-hour infusion of MTX on Total 15, 24-hour infusion of MTX on Total 15, and non-randomized on Total 15). Also, let j = 1,..,3 index the three endpoint variables and let g = 1,…,m index the SNP markers genotyped in the study. For each g and l, let i_gjl = 1,…,n_jgl index the subjects given therapy l with data available for endpoint j and SNP marker g. Note that g, j, and l may be shown at the same level of subscripting as i for simplicity of notation. For a given g, j, and l, let x_igjl be the value of endpoint j for subject i and let y_igjl be the number of B alleles observed for SNP marker g. For each i, g, j, and l, define

$$r_{igjl}=\text{rank}(x_{igjl}∕g,j)-\frac{n_{gjl}+1}{2},$$

where rank(x_igjl | g,j) is the rank of x_igjl among the values of endpoint j for subjects with available data for SNP marker g and endpoint variable j who were assigned to therapy l. Define

$$S_{igjl}=\text{rank}(y_{igjl}∕g,j)-\frac{n_{gjl}+1}{2},$$

where rank(y_igjl | g,l) is the rank of y_igjl among the values of endpoint j for subjects with available data for SNP marker g and endpoint j who were assigned to therapy l. Note that the rank-transformed variables are centered at zero. Let r_gjl = {r_gj1, …, r_gjn} and s_gjl = {s_gj1, …, s_gjn}. Now, define

$$T_{jgl}=\frac{{\mathit{r}}_{gjl}\cdot {\mathit{s}}_{gjl}}{\sqrt{\Vert {\mathit{r}}_{gjl}\Vert \Vert {\mathit{s}}_{gjl}\Vert }},$$

as the rank-based correlation of endpoint variable j and SNP marker g among subjects assigned therapy l. Finally,

$$T_{jg}=\frac{\sum _{l=1}^4{n}_{jgl}{T}_{jgl}}{\sum _{l=1}^4{n}_{jgl}}$$

was used as the statistic to measure the association of marker g with endpoint j stratified by therapy

4.3 Definition of PROMISE Analysis

Prior research has established a paradigm that characterizes the biological relationships among the endpoint variables. Leukemic cells die as MTX PG accumulates in them. Thus, an increase in MTX PG leads to a reduction in tumor burden as measured by day 3 WBC and day 46 MRD. Based on this knowledge, higher values of MTX PG and lower values of WBC and MRD are considered to be therapeutically beneficial. Therefore, for any SNP g, the most interesting values for the association statistics that suggest the B allele is therapeutically beneficial are T_1g = 1, T_2g = −1, and T_3g = −1 where the indices j = 1, 2, and 3 correspond to MTX PG, WBC, and MRD respectively. Thus, d = {+1,−1,−1} defines the most interesting statistical evidence and we used

$$R_g=(T_{1g}-T_{2g}-T_{3g})∕3$$

as the PROMISE statistic in our analysis. The statistic was scaled by 1/3 so that −1 ≤ R_g ≤ 1. A negative value of R_g suggests that the B allele of SNP g has a therapeutically detrimental pattern of association with the endpoints; a positive value of R_g suggests that the B allele has a therapeutically beneficial pattern of association with the endpoints.

The statistical significance of T_1g, T_2g, and T_3g, and the PROMISE statistic R_g for each SNP was determined using the APT algorithm described in section 3. For each SNP, permutations were performed until obtaining b = 200 permutation statistics with greater absolute value than the observed statistic for each of the four statistical tests (MTX PG alone, WBC alone, MRD alone, and PROMISE) or until B = 10⁶ permutations were performed. For each SNP, the same set of permutations was used for all four statistical tests. The permutations were stratified by therapy (i.e., reassignments were performed within each therapy-defined group of subjects).

4.4 Results

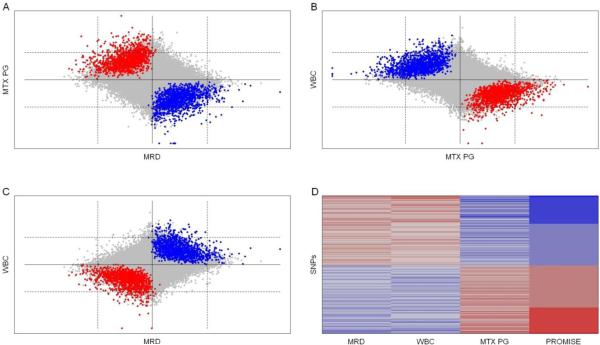
The individual endpoint analyses identified 1686, 598, and 600 SNPs as significantly associated with MTX PG, WBC, and MRD, respectively (p ≤ 0.001 was defined as significant in each analysis). The pattern of associations was concordant with the biological relationship among the three endpoints for 1138 of the 1686 (67.5%) SNPs associated with MTX PG, 396 of the 598 (66.2%) SNPs associated with WBC, and 387 of the 600 (64.5%) SNPs associated with MRD. There was very limited overlap among the three lists of significant SNPs. Only 9 SNPs were significantly associated with both MRD (Figure 1A) and MTX PG and only 6 SNPs were significantly associated with both MTX PG and WBC (Figure 1B). No SNPs were significantly associated with both MRD and WBC (Figure 1C). Consequently, no SNPs were significantly associated with all three endpoints.

Figure 1.

Visualization of Results. In the scatter plots (panels A, B, and C), each point represents the results for one SNP in our analysis. The axes correspond to the signed log₁₀ p-value for the indicated single-endpoint analysis. The sign is assigned to match that of the corresponding rank-based correlation statistic. The solid vertical and horizontal lines correspond to log₁₀(p) = 0, or equivalently p = 1. The dashed lines correspond to −log₁₀(p) = 3, or equivalently p = 0.001. Thus, SNPs significant at the p = 0.001 in an individual endpoint analysis will appear as points beyond the dashed lines perpendicular to the corresponding axis. The color of the point indicates that the B allele of the SNP has a significant (PROMISE p-value ≤ 0.001) detrimental pattern of association with the endpoints (blue), a significant (PROMISE p-value ≤ 0.001) beneficial pattern of association with the endpoints (red), or a non-significant (PROMISE p-value > 0.001) pattern of association with the endpoints. In panel D, the heat map indicates the sign of the correlation statistic for the individual endpoints and the PROMISE statistic for the 2473 significant SNPs from the PROMISe analysis. The color increases in intensity with statistical significance.

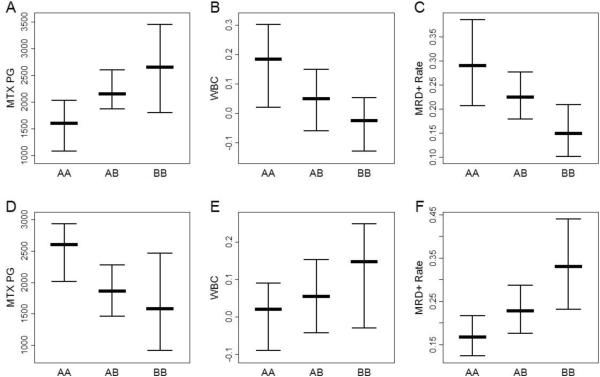
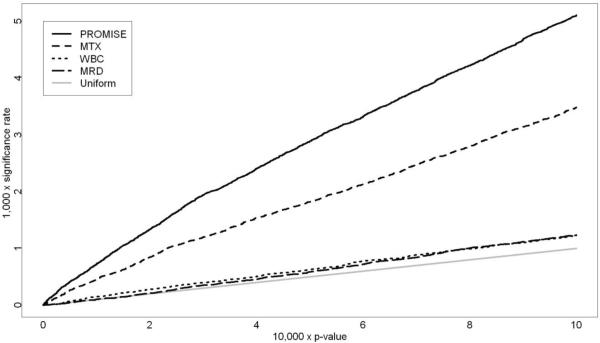
The PROMISE analysis dominates each of the individual endpoint analyses in terms of the number of discovered SNPs and the concordance of the significant SNPs with the biological relationships among the endpoints. The PROMISE analysis identified 2473 SNPs as significant at the p = 0.001 level, an improvement of 46.7% or more over any of the individual endpoint analyses. Additionally, 2460 of the 2473 (99.5%) SNPs showed a pattern of association with the endpoints that was consistent with the known biological relationships among the endpoint variables (Figures 1A–1D). Examples of the therapeutically beneficial and therapeutically detrimental patterns identified by this analysis are shown in Figure 2. Moreover, PROMISE identified many more SNPs than individual endpoint analyses for any p-value threshold between 0 and 0.001 used to define statistical significance (Figure 3).

Figure 2.

Therapeutically beneficial and detrimental patterns of association. For a SNP with a therapeutically beneficial B allele, an increase number of B alleles is associated with an increase in MTX PG (panel A), a decrease in WBC (panel B), and a decrease in the MRD+ rate (panel C). For a SNP with a therapeutically detrimental B allele, an increase in the number of B alleles is associated with a decrease in MTX PG (panel D), an increase in WBC (panel E), and an increase in the MRD+ rate (panel F). Panels A, B, D, and E show the median MTX PG or median WBC with error bars defined by the sign-test based confidence interval for the median. Panels C and F show the proportion of subjects with detectable minimal residual disease (MRD) after 46 days of therapy with error bars defined by the confidence interval based on the binomial distribution. The confidence intervals in this figure are intended solely for visualization because they are not adjusted for therapy group. The confidence intervals are computed using the sign-test method and binomial distribution have been previously described [11].

Figure 3.

Proportion of SNPs identified as significant (significance rate) as a function of the p-value threshold.

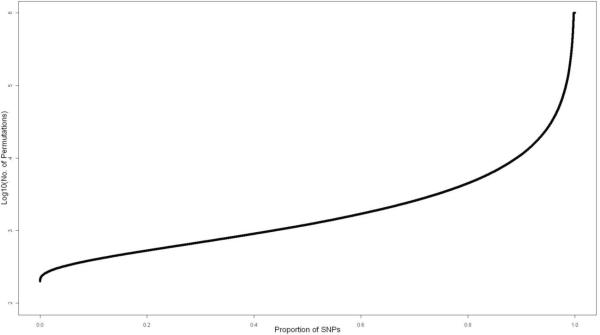
The APT algorithm greatly reduced the computational burden of completing this analysis. The APT procedure performed 10⁵ or more permutations for only 1.7% of all SNPs (Figure 4). Overall, in this analysis, APT computed 98.9% fewer permutation statistics than would classical permutation using B = 10⁶. This immense savings in computational effort was achieved by computing a very large number of permutation statistics only for those SNPs with the most statistically significant p-values. The actual reduction of 98.9% in the number of permutation statistics computed is similar to the approximate reduction of 99.8% derived in section 3.

Figure 4.

Number of Permutations Performed. The figure above plots the number of permutations (on the log₁₀ scale) versus the proportion of SNPs. In this figure, SNPs are ordered by the number of permutations performed in the analysis.

5. Discussion

PROMISE is a powerful and flexible procedure that incorporates prior biological knowledge into an integrated analysis of genomic data with multiple endpoint variables. The prior biological knowledge is incorporated into the form of the test statistic used in the analysis. Prior knowledge about the relationships among the endpoint variables implies a specific pattern of association of the endpoint variables with the genomic variable. This pattern of association dictates the form of the test statistic. Notably, the prior biological knowledge involves only the endpoint variables and not the genomic variables. This strategy does not bias the analysis towards selecting a specific list of genomic variables that is preferred by the investigator.

In this application, PROMISE showed much greater statistical power than did any of the individual endpoint analyses. PROMISE identified 787 more SNPs at the p = 10⁻³ level than did any of the individual endpoint analyses (Figure 2). Additionally, 99.5% of the identified SNPs at this level showed a pattern of association with the endpoint variables that is concordant with the therapeutically beneficial or therapeutically detrimental patterns derived from our well-established biological paradigm, a result that increases our confidence in the biological validity of the results. We are further encouraged by the finding that many of the most statistically significant SNPs identified by PROMISE are located within genes known to be involved in oncogenesis and drug response. These interesting biological findings will be published elsewhere.

To our knowledge, PROMISE is the first statistical procedure designed to determine whether a variable exhibits a specific pattern of correlations with a set of other variables [1]. As such, PROMISE differs fundamentally from widely used approaches that identify genomic variables which are associated with a single endpoint variable, and offers an alternative approach for evaluating genomically based pleiotropic phenotypes – applicable when related phenotypes may share at least some common genotypic basis. The unique objective of PROMISE also differs from that of other multivariate statistical methods. Among other multivariate statistical methods [12], canonical correlation analysis (CCA) has the most similar analysis objective. However, CCA is designed to determine whether two sets of variables have any pattern of non-zero correlations. Thus, CCA has less power than PROMISE to detect the specific pattern of correlations that is of greatest biological interest [1]. Additionally, PROMISE can handle a much wider variety of data types than CCA. CCA is applicable only to data that can be accurately modeled with the multivariate Gaussian distribution [12], whereas PROMISE can be applied to quantitative, ordinal, qualitative, and censored time-to-event variables [1].

In this application, statistical significance of the PROMISE statistic was determined by the APT algorithm. The APT algorithm reduced the number of permutation statistics to be computed by 98.9%, thus making our application computationally feasible. Additionally, APT is a general-purpose permutation procedure that may be used in place of classical permutation in many other analysis methods.

We plan to incorporate gene-set enrichment analysis (GSEA) [13] into PROMISE for the analysis of SNP array data as we have done previously for gene-expression microarray data [1]. We anticipate that incorporating GSEA into PROMISE using APT may prove to be a computationally efficient and statistically powerful tool for biological discovery. However, implementation of APT for GSEA is not as straightforward as for analysis of individual genomic variables. Implementing APT for GSEA requires computing permutation statistics for all genomic variables included in a gene-set until the requirements for the permutation statistics for the gene-set is satisfied. Future research should focus on incorporating GSEA into PROMISE using the APT algorithm to determine statistical significance.

Efforts should also be made to adapt PROMISE to other applications and explore whether alternative definitions of the PROMISE statistic may enhance statistical power. One interesting extension would be to implement PROMISE to perform an integrated analysis of microarray gene expression, microarray SNP genotype, and clinical endpoint data. Anticipated challenges in developing such a procedure include defining the PROMISE statistic in a biologically meaningful way and determining which sets of data should be permuted for computing the p-value. Accurate analytical expressions for the distribution of PROMISE statistics may mitigate the need for permutation and thus alleviate the computational effort required to implement PROMISE in these interesting and challenging applications.

It is important to recognize that the p-values from PROMISE may not be meaningful if the results of individual endpoint analyses are used to define the PROMISE statistic [1]. We recommend to use the current PROMISE procedure only in applications for which prior biological knowledge can be used to unambiguously define the most interesting statistical evidence vector d. PROMISE may be modified to identify genomic variables showing an unspecified pattern of association with endpoint variables by using the sum of squared correlation statistics as the PROMISE statistic. Another area of potentially rewarding research would be to develop extensions of PROMISE that find interesting patterns of association which are not pre-specified.

For previously discussed technical reasons, there are some restrictions on how the permutations should be performed [1]. In particular, the endpoint data should be permuted jointly to preserve the correlation of endpoints among themselves. For some applications, stratified permutations should be performed.

An R package that implements the PROMISE procedure with classical permutation testing is available from Bioconductor (www.bioconductor.org) and our website (www.stjuderesearch.org/depts/biostats). We plan to provide an option to perform adaptive permutation testing with future releases of the package.