Introduction
Image registration is the process of transforming images acquired at different time points, or with different imaging modalities, into the same coordinate system. It is an essential part of any neurosurgical planning and navigation system because it facilitates combining images with important complementary structural and functional information to improve the information basis on which a surgeon makes critical decisions.
Magnetic Resonance Imaging (MRI) can be used to generate both structural and functional neurological images and thus plays an important role in planning neurosurgical procedures (Figure 1). High-resolution anatomical MR images can be used to discriminate between healthy and pathological tissue, functional MRI (fMRI) can be used to identify the location, and extent, of important cognitive areas of the brain while Diffusion Tensor Imaging (DTI) can be used to identify the white matter connectivity of the brain. If important cognitive areas are injured or removed during surgery, it can have an adverse effect on the patient's quality of life post surgery.
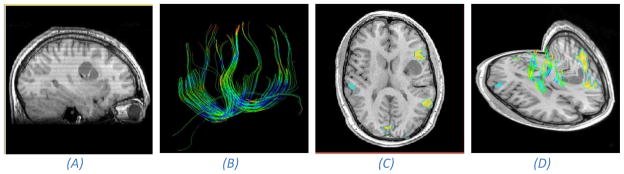
Figure 1.
Anatomical and functional MR information acquired pre-operatively48. (A) An anatomical T1 scan of a patient with a lesion in the left frontal region. (B) Extracted white matter tracts using tractography from DTI. (C) Speech areas found with fMRI overlaid on an axial anatomical slice. Notice that one of the speech centers is adjacent to the tumor and should be conserved during surgery. (D) Composite view of the anatomical MR image and functional DTI and fMRI.
It is especially important to put these complementary images into the same coordinate system when functional areas are located adjacent to a tumor. A map of important anatomical structures and surrounding functional areas can then be built and used by the surgeon to plan the surgical procedure1. Because the brain is enclosed by the skull, a rigid transformation which consists of a translation and rotation is adequate to align these images. The importance of fMRI in planning of tumor resections is underlined by the findings of Petrella et al.2 where the effect of therapeutic decision making in patients with brain tumors was studied. Treatment plans before and after seeing the fMRI differed in 19 out of 49 patients, with a more aggressive approach recommended after imaging in 18 patients. The availability of fMRI resulted in reduced surgical time in 22 patients who underwent surgery, a more aggressive resection in 6 patients and a smaller resection in 2 patients.
Other modalities than MRI have been and are also currently being used in neurosurgical navigation systems. Positron Emission Tomography (PET) allows analyzing function and metabolism of the brain. It is mainly used to localize the most malignant parts of brain tumors, but has also been used to locate eloquent areas of the cortex. However, it does not provide useful structural information and is therefore combined with high resolution structural images, e.g. MRI and Computed Tomography (CT), to accurately locate the functional areas in relation to anatomical structures3. For planning of neurosurgical procedures, PET images are usually combined with MRI because they provide the best tissue contrast. fMRI has now superseded PET as a functional imaging modality for locating eloquent cortex because it eliminates any radiation exposure.
Registration also plays an important role in other neurosurgical guidance applications besides tumor removal, for instance in resection of suspected epileptogenic centers. The epileptogenic centers are located using information from subdural electrodes and the location of these electrodes extracted from CT. By registering the CT with structural MRI, the centers can be precisely located within the brain anatomy and used to plan the resection4.
Because of brain-shift, tissue resection and retraction, the pre-operative image information does not necessarily reflect the intra-operative anatomy the surgeon sees during surgery, even after rigid registration. Brain-shift, a deformation of the brain tissue that occurs after the craniotomy and opening of the dura mater, is caused by various combined factors: cerebrospinal fluid (CSF) leakage, gravity, edema, tumor mass effect and administration of osmotic diuretics5,6. A clinical example of brain-shift is shown in Figure 2. Reported deformations of the brain tissue caused by brain-shift are up to 24mm7–9, and further deformations may be induced because of tissue manipulation during the resection5,10.
Figure 2.
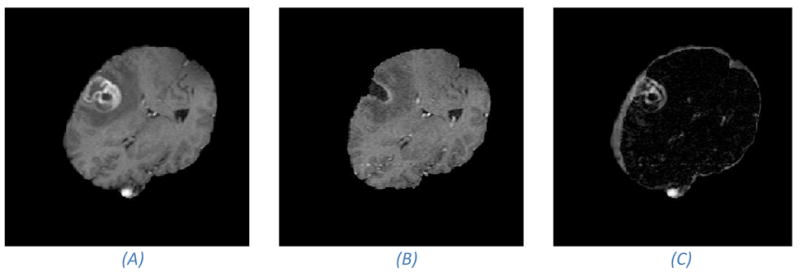
Pre- and intra-operative MR images that shows brain-shift and resection. (A) Pre- operative image. (B) Intra-operative image. Notice the cavity which is a result of the tumor resection. (C) Absolute difference image of the images in (A) and (B). Notice the large intensity differences around the tumor site. Large image gradients and image intensity differences are often the driving force in image registration methods. However, in the case of resections, these image forces should be contained to prevent them from driving the registration into false minima.
As a way of acquiring up to date anatomical information during surgery, intra-operative MRI has been introduced into the surgical workflow11,12. Intra-operative imaging during neuro-surgical procedures helps identify any residual tumor tissue and leads to a significant increase in the extent of tumor removal and survival times13. However, intra-operative images are often of a degraded quality compared to the pre-operative images. Many factors lead to reduced quality in intra-operative MRI: fast acquisition protocols which are used to reduce the surgical time, intra-operative MRI scanners often operate on lower magnetic field strengths than diagnostic MRI scanners, surface coils are used instead of head coils, and disturbances to the main magnetic field caused by the surgery.
Ultrasound (US) is another imaging modality used to acquire up-to-date images during neurosurgery 14. Compared to MRI, acquisition is faster and does not require the patient to move, but image quality and soft tissue discrimination is reduced. US can identify functional information such as blood flow, but not cognitive functions such as motor, visual and language cortices. Reliable and accurate acquisition of intra-operative fMRI is in general not feasible, either because of factors such as time constraint, the requirement that the patient be conscious during acquisition of fMRI, and disturbances of the magnetic field from the surgical procedure1.
How then can we accurately and robustly provide the surgeon with the location of these important eloquent areas in relation to the intra-operative anatomy? Non-rigid transformations have a high degree of freedom and are capable of accommodating the local brain deformations that occur during surgery. Non-rigid intra-operative registration has therefore been introduced as a way of mapping the pre-operative functional information into the intra-operative space. In practice, a transformation cascade is constructed to facilitate intra-operative navigation of the pre-operative image data (see Figure 3). First, the functional images, typically fMRI and DTI, are rigidly registered to a high-resolution pre-operative anatomical image. Next, the pre-operative anatomical image is non-rigidly registered with the intra-operative image. Finally, to facilitate navigation of these images, the intra-operative image is registered with the physical patient space by estimating a rigid transformation from corresponding (fiducial) landmarks identified in the image and on the patient. Most commercial neuro-surgical navigation systems register the pre-operative images to the intra-operative space using fiducial markers and rigid registration and do not take into account the non-rigid deformations caused by brain-shift15.
Figure 3.
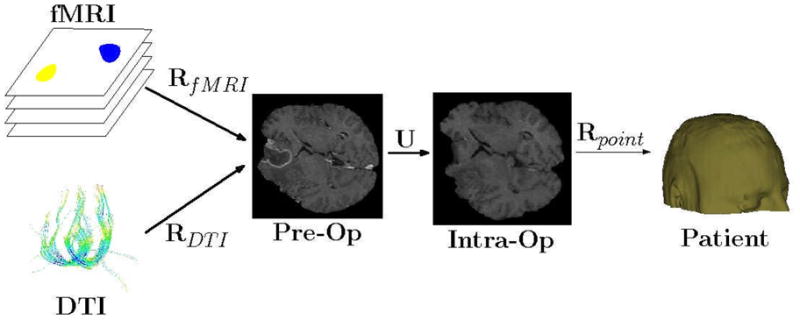
Transformation cascade. Three steps are needed to map the functional images, fMRI and DTI, into the intra-operative physical space. First, rigid, or affine, transforms, RfMRI and RDTI are estimated to align the functional images with the pre-operative anatomical image. A rigid transform is generally adequate because the brain is still enclosed in the skull and assumed to move rigidly up until the start of the surgery. Secondly, a non-rigid transform U is estimated to align the anatomical pre-operative image with the anatomical intra-operative image. A non-rigid transform is required to capture the non-linear movements due to for instance brain-shift. A rigid transform Rpoint is estimated from homologous points extracted from the patient space and the intra-operative image. In some intra-operative MR scanners, for instance the GE Signa SP 0.5T which was in use at BWH until 2007, the physical tracking space and the image space were aligned and the estimation of Rpoint was unnecessary. Consequently, points X in the pre-operative functional space can be mapped to the patient (physical) space with the following transformation cascade: Rpoint (U(RfMRI(X))). This enables navigation of the functional images in a neuro-surgical navigation system.
Brigham and Women’s Hospital (BWH), an affiliate of Harvard Medical School, has been one of the pioneers in developing intra-operative registration methods for aligning pre-and intra-operative images of the brain12. In this paper we present a general overview of intra-operative registration and highlight some of the recent developments at BWH. The rest of the paper is organized as follows. First we introduce patient-to-image registration followed by a discussion of the error involved in such estimations. Next, we provide an introduction of image-to-image registration and the specific challenges of intra-operative registration and, finally, present an overview of the research that has been carried out to handle these challenges.
Patient-to-Image Registration
The primary requirement of a neuro-surgical navigation system is to relate both pre- and intra-operative images to the physical patient space, i.e. to insure that when the surgeon points a tracked device to an easily identifiable structure on the patient, the navigation system shows the pointer at the correct location in the images. The common approach is to identify a set of homologous points in the two spaces, the image space and the physical patient space. One example would be to record the positions, f = {f1, ...fn}, of a set of n fiducial markers attached to the skull as located using a tracking device and the corresponding set of points, m = {m1, ...mn}, in the image. The transformation is established by finding a rigid body transformation Rpoint which minimizes the root mean square (RMS) distances between the homologous points
Because the skull is a rigid object, this transformation is generally considered to be rigid consisting of a translation and rotation.
It is important to understand that there are errors and uncertainties involved in such calculations. For point-based registration, the error is usually separated into three parts16:
Fiducial Localization Error (FLE) is the error in localizing the fiducials in both physical and image space.
Fiducial Registration Error (FRE) is the RMS error between corresponding points after registration.
Target Registration Error (TRE) is the distance between homologous points, other than the fiducials used to compute FRE, after registration.
FRE is the only error that is easily computed as it is the minimum of the cost function we are minimizing. The expected value of FRE is dependent on the number of fiducials and the squared value of FLE, but independent of the fiducial configuration. A more critical and important measure, the TRE, can tell us something about the error around the site that will be operated on. However, in contrast to FRE, the expected value of TRE does in some way depend on the fiducial configuration. Recent results by Shamir and Joskowicz17 showed that for realistic configurations of the FLE, the TRE and FRE are uncorrelated, regardless of the target location and the number of fiducials and their configuration. Assume FRE is less than its expected value: according to Fitzpatrick18, we may not assume that the TRE will also be less than its expected value. Thus, Fitzpatrick argues, the FRE for a given patient does not provide useful information about the true registration accuracy (TRE) for a specific patient and should be warily used as a measure for registration accuracy.
Intra-Operative Image-to-Image Registration
Although current commercial image-guided navigation systems use rigid registration to establish the mapping between the pre- and intra-operative spaces, we are starting to see a shift towards non-rigid registration which is necessary to accommodate the non-rigid movement of brain-tissue caused by e.g. brain-shift19. A reason for the late adoption of non-rigid registration in image guided neurosurgical systems are the strict constraints and tough challenges that intra-operative registration face:
Brain-shift: The craniotomy and opening of the dura mater may induce a considerable high-dimensional warp of the brain tissue.
Time constraints: A registration algorithm should in general not affect the surgical workflow and not extend the total surgical time. Hence, only a limited time period is available to register the pre- to the intra-operative images. It should in general not exceed the time it takes to get the patient ready for surgery after acquiring the intra-operative images, which is approximately 5–10 minutes.
Resection and Retraction: Manipulation of the brain tissue by the surgeon leads to discontinuities in the movement of tissue due to retraction of tissue, and a non-bijective mapping because of missing tissue due to resection.
Uncertainty: Registration uncertainty is a nearly neglected topic in the non-rigid registration community. The surgeon is provided with registered images, but never with an estimate of how much the registered image data can be trusted, i.e. the uncertainty of the estimated transformation. We believe that in the future, it should be mandatory for intra-operative registration methods to report the registration uncertainty alongside the registered data because critical surgical decisions are taken based on the registered data.
In the following sections we will first define what we mean by image registration and introduce the different components that make up a registration method with a focus on brain-shift. Next we will discuss methods for accommodating resection and retraction followed by methods for quantifying the registration uncertainty.
Basic Image-to-Image Registration
Given two images, f and m, the goal of a registration algorithm is to find a transformation u which spatially aligns homologous structures in the two images. A distance (similarity) function D is used to estimate how well points in the images overlap given a transformation, while a regularization function R generally reduces the space of permissible transformations to physically realistic ones. Basically we are looking for the transformation u that minimizes D (f, u(m)) + α R(u). The constant α controls the relative importance of the regularization term versus the distance function. A high-level diagram of a general registration algorithm is shown in Figure 4 and general image registration surveys can be found in Maintz and Viergever20 and Zitova and Flusser21.
Figure 4.
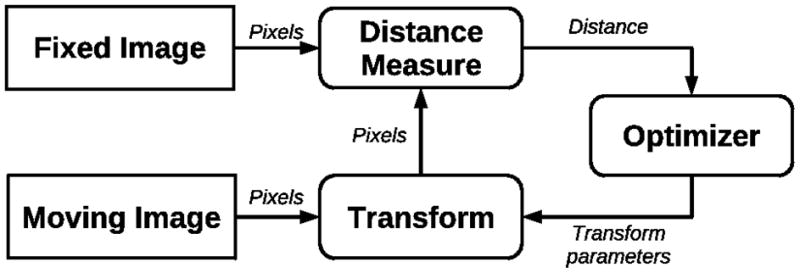
This diagram shows the general flow of a registration algorithm. It is generally an iterative process where the transformation parameters are estimated to minimize the “distance” between two images. The distance measure can measure anything from image intensities to the distance between homologous points in the two images.
Distance Measuresin Image Registration
Much of the early work in image-to-image registration was in registering brain images of the same patient (intra-subject) acquired with different imaging modalities (intra-modality). Researchers were especially focused on finding robust distance (similarity) measures for aligning images acquired from different modalities where there is not necessarily a simple relationship between intensities in the images. Woods et al.22 presented some early work registering PET-MRI by minimizing the standard deviation of the PET pixel values that correspond to each MRI pixel value. Today, however, most inter-modality registration is based on different variants of Mutual Information23 which was introduced in 1996. MI is a generally applicable similarity measure because it only assumes a probabilistic relationship between intensities and has been used for registering a variety of different modalities24. Sometimes, the intensity differences are not of a global character which is often seen in intra-operative MR images because of disturbances in the magnetic field. Clatz et al.25 introduced a block matching algorithm that was robust to local intensity changes by estimating local displacements and from them estimating a global transformation where local displacements that diverged from permissible global transformations were discarded. Some authors have totally circumvented the direct use of intensities by registering sparsely measured displacements instead, e.g. cortex and ventricle surfaces extracted from images26.
Transformation
Depending on the situation, the transformation can range from a simple rigid transformation (translation and rotation) to a non-rigid transformation. Before the introduction of intra-operative imaging, a rigid body approximation was adequate to estimate the movement of the brain in intra-subject registration because there is minimal change to the brain shape and position within the skull between scans22. However, registering pre- with intra-operative images require high-dimensional transformation models where local movements of the brain is allowed. Popular high-dimensional transformation models used in registration of the brain include splines27, Finite Element Models (FEM)25 and optical flow based methods28. Spline-based models determine a globally smooth deformation field by interpolating displacements defined at control points in the image, e.g. corresponding landmarks. The main disadvantage of spline methods is that special measures are sometimes required to prevent folding of the deformation field. FEM models divide the image into cells and provide a high degree of freedom in defining the granularity of the deformation. In areas where highly local deformations are expected, many degrees of freedom can be used, while areas which are assumed to move rigidly, e.g. bones, can be modeled with few degrees of freedom. Optical flow methods are usually used when speed is important and can provide highly localized deformations, but their main disadvantage is that they are not robust with regards to intensity differences.
Regularization
Images only partially constrain the transformation. For transformations with many degrees of freedom, regularization is used to constrain the transformation to mimic underlying physical properties of the tissue we are registering. Depending on the tissue, such properties can include smoothness, volume preservation or elasticity. State-of-the-art non-rigid registration methods for registering brain-images use physically-based regularization; they use biomechanical models for including patient specific modeling, e.g. mechanical properties of different biological tissues. In the context of intra-operative registration, deformation of brain tissue is often well approximated with linear elastic models25,29. Elastic models allow us to use different material properties, i.e. stiffness and compressibility, for the different tissue types we are modeling. Methods that use the linear elastic model can in general be divided into two groups, those that exclusively use image information as the driving force in the registration25–26, and those that use externally measured displacements using for instance laser scanners30, stereo-vision31, or alternatively using some combination of intensities and landmarks32. More sophisticated physical models such as hyper-elastic, hyper-viscoelastic33 models or coupling of fluid and elastic34 models have also been investigated. However, Wittek et al.35 have shown that using more advanced models than linear elastic may not affect the estimated results significantly enough to justify the added complexity and computational time.
A substantial uncertainty is involved in determining exact values for the material properties of brain tissue, and consequently the reported estimates of material parameters are quite divergent36. In addition, medication, radiation, and other factors related to the surgical procedure may significantly change the material parameters. Because the literature reports divergent values for the material parameters, most authors make more or less qualified guesses as for the values of these parameters. We have recently introduced a probabilistic registration framework37 where, instead of using point-estimates for the material parameters, we modeled them with broad prior distributions and jointly estimated the posterior distribution over deformations and the material parameters. We showed that we could accurately recover the deformation and also recover plausible material parameters for CSF, and grey and white matter.
Modeling Resection and Retraction
When a tumor is located deep in the brain, it is necessary to retract brain tissue to create an access channel to the tumor. This is commonly performed by making an incision in the brain tissue down to the tumor, inserting a device called a retractor, and pulling the brain tissue apart to leave an open space through which the surgeon can resect the tumor. Most intra-operative images are acquired some time after the start of the resection, either to check that all tumor tissue has been resected, or to confirm that important functional or structural areas are not compromised. Because of the resected, or “missing”, tissue, there is no longer a one-to-one (bijective) correspondence between the pre- and intra-operative anatomy. Consequently, a discontinuous and non-bijective deformation model is required to capture the motion of the brain tissue10.
One result of the resection, especially in intensity-based registration approaches, is that unwanted image forces are likely to occur in the non-bijective areas because of large image gradients and image intensity differences. The majority of non-rigid registration methods assume a bijective deformation field and regularize the deformation field accordingly. With a few notable exceptions, researchers have usually not included models for accommodating the non-bijectivity that is caused by retraction and resection. Periaswamy et al.38 proposed a registration framework which handles missing data by applying the expectation maximization method to alternately estimate the missing data and the registration parameters. Miga et al.39 introduced a bio-mechanical FEM model that explicitly handles resection and retraction. The FEM mesh was split along the retraction, while nodes in the area of resection were decoupled from the FEM computations. They included no automatic means of determining the resected and retracted areas—they needed to be manually delineated. The main drawback of using a conventional FEM method for modeling retraction and resection is that it requires re-meshing which is a complex and time consuming process.
Non-physically based registration methods are in general computationally efficient, robust, provide straightforward implementations and require minimal manual interaction. However, the main drawback with non-physically based methods is that they do not include any domain specific modeling to encourage realistic deformations of biological tissues. The Demons method is a widely used non-physically based non-rigid registration method based on optical flow 28. It is an iterative method where each iteration consists of a two-step procedure. First, an unconstrained update to the transformation is estimated to improve the distance measure. Secondly, the updated transformation is regularized by applying a Gaussian smoothing filter. It has proved to be fast enough for intra-operative use, but is in general constrained to intra-modal registration. A version of the method that could handle affine intensity correspondences was introduced by Guimond et al40, but at the cost of a considerable increase in computation time. In recent work41,42 we have extended the Demons method to handle both retraction and resection by adapting the regularization step of the method to accommodate discontinuities and missing data. We showed that we could reach speeds adequate for intra-operative registration and we achieved increased registration accuracy near the resection compared to a traditional Demons based methods.
Another approach is taken by Toews and Wells43 who focus on automatically identifying and registering informative local image features between pre-operative MR and intra-operative US images. The goal is to robustly determine a sparse set of image-to-image correspondences in the case where underlying tissues may not be present or visible in both of the images to be registered, either due to resection or modality- specific characteristics. The correspondences identified can potentially be useful in constraining further registration or analysis of more difficult, less informative image regions.
Registration Uncertainty
Registration uncertainty is another important, but mostly neglected, topic in non-rigid image registration. Most authors are focused on finding the most likely estimate of their registration problem, and disregard any treatment of uncertainty in their estimate. In the case of intra-operative registration, it is likely that the registration uncertainty increases around the tumor because of intensity differences due to contrast enhancement, degraded image quality and missing data due to the resection. Registration uncertainty is closely tied to surgical risk. Registration uncertainty means the lack of complete certainty, i.e. the existence of more than one possible transformation that will align two images. A surgical risk exists whenever we have a set of possible transformations that might lead to an undesirable outcome. In the case of intra-operative registration, one of the possible transformations might lead the surgeon to believe that resecting a certain part of the brain will not affect any cognitive areas, while another possible outcome might indicate the opposite. Hence, it is critical that intra-operative registration reports the registration uncertainty to increase the surgeon's confidence level and their ability to make better intra-operative decisions that are less risky.
In point-based rigid body registration, registration uncertainty has been studied extensively to quantify the distribution of the Target Registration Error (TRE)44 which can be important information to provide to the surgeon, e.g. during image-guided biopsies.
However, few authors have reported methods for quantifying non-rigid registration uncertainty. Hub et al.45 developed a heuristic method for quantifying uncertainty in B-spline image registration by perturbing the B-spline control points and analyzing the effect on the similarity criterion. Kybic et al.46 consider images to be random processes and proposed a general bootstrapping method to compute statistics on registration parameters. This is a computationally intensive approach, but is applicable to a large set of minimization based registration algorithms.
We have taken another approach and introduced a Bayesian registration framework where we aim to characterize the posterior distribution over deformation parameters instead of estimating the conventional point estimates47. The posterior distribution contains information about the modes, and the corresponding uncertainty, of the transformation parameters. We introduced methods for summarizing the marginal posterior distributions on deformation parameters and showed how these summaries can be visualized in a clinical meaningful way. An example is included in Figure 5.
Figure 5.
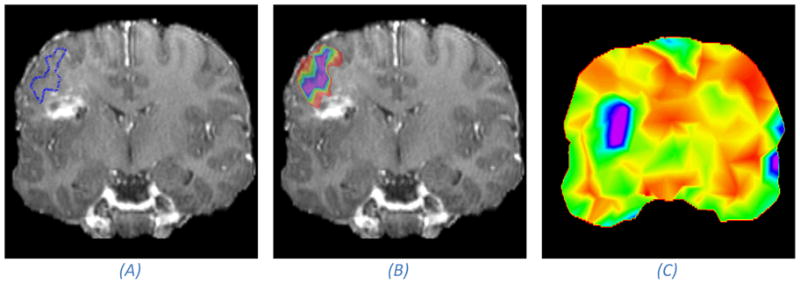
Illustration of the effect of registration uncertainty on mapping of functional areas from the pre-operative to the intra-operative space. The anatomical image is a post-operative image, acting as a proxy for an intra-operative image, acquired from the same patient we show pre-operative images of in Figure 1. (A) A coronal MRI slice with the estimated boundary of a speech activated functional area after registration. (B) Takes into account the registration uncertainty, and rather than visualizing the point-estimate as in (A), it visualizes the marginal probability that a certain voxel is inside the functional area (purple denotes a probability of one which falls off normal to the iso-contours down to red which is close to a zero probability). If we assume that the hyper intense area is the site of the resection, then we can conclude with a small probability that the functional area was touched during surgery because the outer rim of the color map touches on the “resected” area. Image (C) shows an uncertainty map. The uncertainty is measured as the dispersion of the marginal posterior distribution over deformation parameters. We have colored high uncertainty with purple and low uncertainty with red. It can be seen that the registration uncertainty is higher close to the resection than away from the resection. It is important to keep in mind that a high uncertainty in the registration does not necessarily mean that the registration is inaccurate, but the chance that it is less accurate is higher.
Discussion
Neurosurgical navigation systems depend on image registration methods to relate images acquired from different sources or time points. Most registration methods that are available in commercial systems are point-based and constrained to rigid transformations. It is important to understand the limitations of these methods and the error associated with the registration. The point-based methods commonly report the Fiducial Registration Error (FRE) which is the distance between the fiducials after registration. In this paper we have pointed out that the FRE is not necessarily a good estimate of the real registration error (TRE) and should be used warily as a measure of registration error.
Rigid registration methods cannot account for the highly non-rigid warps caused by, e.g., brain-shift. Non-rigid registration methods have not reached a level of maturity, especially with regards to handling the tough challenges of intra-operative registration, to be routinely used in commercial registration systems. Some of the remaining challenges are to handle discontinuities and missing data in the registration algorithms due to for example retraction and resection, and to meet the time requirements of intra-operative registration. However, perhaps most importantly is to develop methods that not only provide registration results, but also report the uncertainty associated with registration results because it will increase the surgeon’s confidence level in the registered image data and help reduce the risk involved in making important clinical decisions.
Acknowledgments
This work was supported by Grants: R01CA138419, P41RR13218, P41RR19703 from National Institutes of Health
Footnotes
The authors have nothing to disclose.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Petter Risholm, Department of Radiology, Brigham & Women’s Hospital, Harvard Medical School.
Alexandra J. Golby, Department of Neurosurgery, Brigham and Women’s Hospital, Harvard Medical School.
William M. Wells, III, Department of Radiology, Brigham & Women’s Hospital, Harvard Medical School.
Bibliography
- 1.Tharin S, Golby A. Functional brain mapping and its applications to neurosurgery. Neurosurgery. 2007;4:185–201. doi: 10.1227/01.NEU.0000255386.95464.52. [DOI] [PubMed] [Google Scholar]
- 2.Petrella JR, Shah LM, Harris KM, et al. Preoperative Functional MR imaging Localization of Language and Motor Areas: Effect on Therapeutic Decision Making in Patients with Potentially Resectable Brain Tumors. Radiology. 2006;240(3):793–802. doi: 10.1148/radiol.2403051153. [DOI] [PubMed] [Google Scholar]
- 3.Nabavi A, Kacher DF, Gering DT, Pergolizzi RS. Neurosurgical procedures in a 0.5 Tesla, Open-Configuration Intraoperative MRI: Planning, Visualization and Navigation. Automedica. 2001;00:1–35. [Google Scholar]
- 4.Ken S, Di Gennaro G, Giulietti G. Quantitative evaluation for brain CT/MRI coregistration based on maximization of mutual information in patients with focal epilepsy investigated with subdural electrodes. Magnetic Resonance Imaging. 2007;25(6):883–888. doi: 10.1016/j.mri.2007.02.003. [DOI] [PubMed] [Google Scholar]
- 5.Hartkens T, Hill DLG, Catellano-Smith AD, et al. Measurement and analysis of brain deformation during neurosurgery. IEEE Transactions on Medical Imaging. 2003;22(1):82–92. doi: 10.1109/TMI.2002.806596. [DOI] [PubMed] [Google Scholar]
- 6.Nimsky C, Ganslandt O, Cerny S, Hastreiter P, Greiner G, Fahlbusch R. Quantification of, visualization of, and compensation for brain shift using intraoperative magnetic resonance imaging. Neurosurgery. 2000 November;47(5):1070–1079. doi: 10.1097/00006123-200011000-00008. [DOI] [PubMed] [Google Scholar]
- 7.Hastreiter P, Rezk-Salama C, Soza G, et al. Strategies for Brain Shift Evaluation. Medical Image Analysis. 2004;8(4):447–464. doi: 10.1016/j.media.2004.02.001. [DOI] [PubMed] [Google Scholar]
- 8.Nabavi A, Black PML, Gering DT, et al. Serial intraoperative mr imaging of brain shift. Neurosurgery. 2001;48(4):787–798. doi: 10.1097/00006123-200104000-00019. [DOI] [PubMed] [Google Scholar]
- 9.Roberts DW, Hartov A, Kennedy FE, Miga MI, Paulsen KD. Intraoperative brain shift and deformation: a quantitative analysis of cortical displacement in 28 cases. Neurosurgery. 1998 October;43(4):749–758. doi: 10.1097/00006123-199810000-00010. [DOI] [PubMed] [Google Scholar]
- 10.Platenik L, Miga M, Roberts D, et al. In vivo quantification of retraction deformation modeling for updated image-guidance during neurosurgery. IEEE Transactions on Biomedical Engineering. 2002 August;49(8):823–835. doi: 10.1109/TBME.2002.800760. [DOI] [PubMed] [Google Scholar]
- 11.Claus E, Horlacher A, Hsu L, et al. Survival rates in patients with low-grade glioma after intra-operative magnetic resonance image guidance. Cancer. 2005 March;103(6):1227–1233. doi: 10.1002/cncr.20867. [DOI] [PubMed] [Google Scholar]
- 12.Warfield S, Haker S, Talos I, et al. Capturing intraoperative deformations: research experience at brigham and women's hospital. Medical Image Analysis. 2005 April;9(2):145–162. doi: 10.1016/j.media.2004.11.005. [DOI] [PubMed] [Google Scholar]
- 13.Wirtz CR, Knauth MA, Subert MMB, Sartor K, Kunze S, Tronnier VM. Clinical evaluation and follow-up results for intraoperative magnetic resonanceimaging in neurosurgery. Neurosurgery. 2000 January;46(5):1112–1120. doi: 10.1097/00006123-200005000-00017. [DOI] [PubMed] [Google Scholar]
- 14.Rasmussen IA, Lindseth F, Rygh OM, et al. Functional neuronavigation combined with intra-operative 3D ultrasound: initial experiences during surgical resections close to eloquent brain areas and future directions in automatic brain shift compensation of preoperative data. Acta neurochirurgica. 2006;149(4):365–378. doi: 10.1007/s00701-006-1110-0. [DOI] [PubMed] [Google Scholar]
- 15.Shamir RR, Joskowicz L, Spektor S, Shoshan Y. Localization and registration accuracy in image guided neurosurgery: a clinical study. International Journal of Computer Assisted Radiology and Surgery. 2009 January;4(1):45–52. doi: 10.1007/s11548-008-0268-8. [DOI] [PubMed] [Google Scholar]
- 16.Fitzpatrick JM, West JB. The distribution of target registration error in rigid body point-based registration. IEEE Transactions on Medical Imaging. 2001 September;20(9):917–927. doi: 10.1109/42.952729. [DOI] [PubMed] [Google Scholar]
- 17.Shamir RR, Joskowicz L. Geometrical analysis of registraiton errors in point-based rigid-body registration using invariants. Medical Image Analysis. 2010 doi: 10.1016/j.media.2010.1007.1010. In Press, Corrected Proof. [DOI] [PubMed] [Google Scholar]
- 18.Fitzpatric JM. Fiducial registration error and target registration error are uncorrelated. Paper presented at: Medical Imaging 2009: Visualization, Image-Guided Procedures, and Modeling; 2009. [Google Scholar]
- 19.Archip N, Clatz O, Whalen S, et al. Non-rigid alignment of pre-operative MRI, fMRI and DT-MRI with intra-operative MRI for enhanced visualization and navigation in image-guided neurosurgery. NeuroImage. 2007;35(2):609–624. doi: 10.1016/j.neuroimage.2006.11.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Maintz J, Viergever M. A survey of medical image registration. Medical Image Analysis. 1998;2(1):1–36. doi: 10.1016/s1361-8415(01)80026-8. [DOI] [PubMed] [Google Scholar]
- 21.Zitova B, Flusser J. Image registration methods: a survey. Image Vision Computing. 2003;21(11):977–1000. [Google Scholar]
- 22.Woods RP, Mazziotta JC, Cherry SR. MRI-PET registration with automated algorithm. Journal of Computer Assisted Tomography. 1993;17:536–546. doi: 10.1097/00004728-199307000-00004. [DOI] [PubMed] [Google Scholar]
- 23.Wells WM, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi-modal volume registration by maximization of mutual information. Medical Image Analysis. 1996;1(1):35–51. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]
- 24.Pluim JPW, Maintz JBA, Viergever MA. Mutual Information based registration of medical images: a survey. IEEE Transactions of Medical Imaging. 2003;22(8):986–1004. doi: 10.1109/TMI.2003.815867. [DOI] [PubMed] [Google Scholar]
- 25.Clatz O, Delingette H, Talos IF, et al. Robust nonrigid registration to capture brain shift from intraoperative mri. IEEE Transactions on Medical Imaging. 2005 November;24(11):1417–1427. doi: 10.1109/TMI.2005.856734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Vigneron LM, Boman RC, Ponthot JP, Robe PA, Warfield SK, Verly JG. Enhanced fem-based modeling of brain shift deformation in image guided neurosurgery. Journal of Computational and Applied Mathematics. 2010 August;234(7):2046–2053. [Google Scholar]
- 27.Holden M, Schnabel JA, Hill DLG. Quantification of small cerebral ventricular volume changes in treated growth hormone patients using non-rigid registration. IEEE Transactions of Medical Imaging. 2002;21:1292–1301. doi: 10.1109/TMI.2002.806281. [DOI] [PubMed] [Google Scholar]
- 28.Thirion JP. Image matching as a diffusion process: an analogy with Maxwell's demons. Medical Image Analysis. 1998;2(3):243–260. doi: 10.1016/s1361-8415(98)80022-4. [DOI] [PubMed] [Google Scholar]
- 29.Ferrant M, Nabavi A, Macq B, et al. Serial Registration of intraoperative mr images of the brain. Medical Image Analysis. 2002 December;6(4):337–359. doi: 10.1016/s1361-8415(02)00060-9. [DOI] [PubMed] [Google Scholar]
- 30.Miga MI, Sinha TK, Cash DM, Galloway RL, Weil RJ. Cortical surface registration for image-guided neurosurgery using laser-range scanning. IEEE Transactions on Medical Imaging. 2003;22(8):973–985. doi: 10.1109/TMI.2003.815868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Skrinjar O, Nabavi A, Duncan J. Model-driven brain shift compensation. Medical Image Analysis. 2002;6(4):361–373. doi: 10.1016/s1361-8415(02)00062-2. [DOI] [PubMed] [Google Scholar]
- 32.Paul P, Morandi X, Jannin P. A surface registration method for quantification of intra-operative brain deformations in image-guided neurosurgery. IEEE Transactions on Information Technology in Biomedicine. 2009;13(6):976–983. doi: 10.1109/TITB.2009.2025373. [DOI] [PubMed] [Google Scholar]
- 33.Wittek A, Miller K, Kikinis R, Warfield S. Patient-specific model of brain deformation: application to medical image registration. Journal of Biomechanics. 2007 February;40(4):919–929. doi: 10.1016/j.jbiomech.2006.02.021. [DOI] [PubMed] [Google Scholar]
- 34.Hagemann A, Rohr K, Stiehl HS. Coupling of fluid and elastic models for biomechanical simulations of brain deformations using FEM. Medical Image Analysis. 2002;6(4):375–388. doi: 10.1016/s1361-8415(02)00059-2. [DOI] [PubMed] [Google Scholar]
- 35.Wittek A, Hawkins T, Miller K. On the unimportance of constitutive models in computing brain deformation for image guided surgery. Biomechanics and Modeling in Mechanobiology. 2009;8(1):77–84. doi: 10.1007/s10237-008-0118-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hagemann A, Rohr K, Stiehl H, Spetzger U, Gilsbach J. Biomechanical modeling of the human head for physically based nonrigid image registration. IEEE Transactions onImage Processing. 1999 October;18(10):875–884. doi: 10.1109/42.811267. [DOI] [PubMed] [Google Scholar]
- 37.Risholm P, Samset E, Wells WM. Biomedical Image Registration (WBIR) Vol. 6204. LNCS, Springer; Berlin/Heidelberg: 2010. Bayesian Estimation of Deformation and Elastic Parameters in Non-Rigid Registration; pp. 104–115. [Google Scholar]
- 38.Periaswamy S, Farid H. Medical image registration with partial data. Medical Image Analysis. 2006;10(3):452–464. doi: 10.1016/j.media.2005.03.006. [DOI] [PubMed] [Google Scholar]
- 39.Miga M, Roberts DW, Kennedy FE, et al. Modeling of retraction and resection for intraoperative updating of images. Neurosurgery. 2001;49(1):75–85. doi: 10.1097/00006123-200107000-00012. [DOI] [PubMed] [Google Scholar]
- 40.Guimond A, Roche A, Ayache N, Meunier J. Three-dimensional brain warping using the demons algorithm and adaptive intensity corrections. IEEE Transactions of Medical Imaging. 2001;20(1):58–69. doi: 10.1109/42.906425. [DOI] [PubMed] [Google Scholar]
- 41.Risholm P, Samset E, Talos I, Wells WM. Information Processing In Medical Imaging (IPMI) Vol. 5636. LNCS, Springer; Berlin/Heidelberg: 2009. A Non-Rigid Registration Framework that Accommodates Resection and Retraction; pp. 447–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Risholm P, Samset E, Wells WM. Validation of a Non-Rigid Registration Framework that Accommodates Tissue Resection. SPIE Medical Imaging. 2010;7623:762319. [Google Scholar]
- 43.Toews M, Wells WM. Information Processing in Medical Imaging (IPMI) Vol. 5636. LNCS, Springer; Berlin/Heidelberg: 2009. Bayesian Registration via Local Image Regions: Information, Selection and Marginalization; pp. 435–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Moghari M, Abolmaesumi P. Distribution of target registration error for anisotropic and inhomogenous fiducial localization error. IEEE Transactions on Medical Imaging. 2009 June;28(6):799–813. doi: 10.1109/TMI.2009.2020751. [DOI] [PubMed] [Google Scholar]
- 45.Hub M, Kessler M, Karger C. A stochastic approach to estimate the uncertainty involved in b-spline image registration. IEEE Transactions on Medical Imaging. 2009 November;28(11):1708–1716. doi: 10.1109/TMI.2009.2021063. [DOI] [PubMed] [Google Scholar]
- 46.Kybic J. Bootstrap resampling for image registrationuncertainty estimation without ground truth. IEEE Transactions on Image Processing. 2010 January;19(1):64–73. doi: 10.1109/TIP.2009.2030955. [DOI] [PubMed] [Google Scholar]
- 47.Risholm P, Pieper S, Samset E, Wells WM. Medical Image Computing and Computer Assisted Interventions. (MICCAI) Vol. 6362. LNCS, Springer; Berlin/Heidelberg: 2010. Summarizing and Visualizing Uncertainty in Non-Rigid Registration; pp. 554–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Pace D, Hata N. Image Guided Therapy in Slicer3: Planning for Image Guided Neurosurgery. Surgical Planning Laboratory, Brigham and Women's Hospital; 2008. http://www.spl.harvard.edu/publications/item/view/1608. [Google Scholar]